Lettre d’Ampère à Berthollet

Auteur :

André-Marie Ampère (1775-1836)

Auteur de l'analyse: Pierre Laszlo, chimiste, professeur honoraire à l’École polytechnique

Publication :

« Lettre de M. Ampère à M. le Comte Berthollet, sur la détermination des proportions dans lesquelles les corps se combinent, d’après le nombre et la disposition respective des molécules dont leurs parties intégrantes sont composées », Journal des mines, vol. 37, n° 217, janvier 1815, pp. 5-40 et figures pl. I et II [réédition de l’article original In Annales de chimie, tome 94, 30 avril 1814, pp.43-86 et planches]

Année de publication :

1814

Nombre de pages :

Résumé :

Ampère imagine les figures géométriques de polyèdres selon lesquelles pourraient s’organiser les molécules – la position et l’ordonnancement des atomes dans les molécules et cristaux (ce qu’on appelle la stéréochimie) conditionnent leurs propriétés.

Source de numérisation :

Bibliothèque de Mines-ParisTech

Ampère et la « forme représentative » des molécules

Pierre Laszlo, chimiste, professeur honoraire à l’École polytechnique

Introduction

L’histoire des sciences va au delà d’une redite, plus ou moins à l’identique, et contextualisée dans une époque donnée. Elle est relecture. Les évolutions, continuités et filiations sont tout aussi importantes que la reconstitution de ce qui s’est exprimé dans un passé plus ou moins lointain.

Ainsi, le présent article replace l’histoire de la stéréochimie dans la longue durée. Il comporte trois parties. En premier lieu, j’attire l’attention sur les contributions de Wollaston et d’Ampère, ainsi que sur les raisons probables de leur manque d’impact public. Je me focaliserai ensuite sur la seule publication d’Ampère, qui définit pour la première fois, avant de la décrire comme polyédrique, la structure des molécules. Elle donna chair aux notions du cristallographe René-Just Haüy (1743-1822), qui prônait déjà une approche géométrique de la structure des molécules (pour user de termes actuels). Cette vision géométrique participe d’une mentalité pythagoricienne. Elle fait le lien entre des savants, séparés parfois par des siècles mais réunis par une même intuition de l’importance des solides platoniciens, de Kepler et Robert Hooke à Alfred Werner (1). La plupart partagèrent aussi leur volonté de baser la structure en chimie sur l’incisive physique mathématique de Descartes. Je conclurai en dénonçant le cliché suivant lequel la stéréochimie naquit en 1874 de la proclamation de l’atome tétraédrique de carbone, par Achille Le Bel et Jacobus Henricus van’t Hoff (2). Cette sous-discipline est d’une ancienneté bien plus grande.

Mon analyse porte essentiellement sur la publication d’Ampère aux Annales de Physique et de Chimie en 1814.

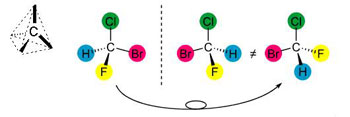
Figure 1 : Importance de la configuration spatiale (stéréochimie) : cas de la chiralité

Figure 1 : Importance de la configuration spatiale (stéréochimie) : cas de la chiralité (3). À gauche, en noir, l’atome de carbone « tétraédrique » : il peut se lier à quatre atomes aux sommets d’un tétraèdre dont il est le centre. Une telle répartition dans l’espace d'atomes différents – par exemple autour d'un point (C au milieu) – conduit à des configurations non superposables dans un miroir, donc à des objets chimiques différents. En couleurs, les deux molécules (séparées par un tireté symbolisant la trace d’un miroir) sont l'image l'une de l'autre dans un miroir : si on tourne la première (ce qui conduit à la troisième, à droite), on voit qu'elle n'est pas superposable à la seconde, au milieu. Elle constitue un composé chimique différent : la molécule initiale est dite chirale : elle n’est pas superposable à son image dans un miroir.

La conférence bakerienne de Wollaston

William Hyde Wollaston (1766-1828), natif de Dereham, dans le Norfolk, est davantage connu pour sa production du platine au moyen d’un procédé qu’il garda confidentiel et qui s’avéra hautement lucratif, en collaboration d’abord avec Smithson Tennant (1761-1815), puis, à partir de 1805, avec William Cary (1759-1825). Mais il eut de nombreux autres centres d’intérêt, la cristallographie entre autres. Il perfectionna le goniomètre que René-Just Haüy avait conçu pour mesurer les angles des faces d’un cristal. Il publiait dans les Philosophical Transactions en 1809 sa conception d’un goniomètre par réflexion. Il était donc familier des travaux et des idées de Haüy. De plus, il s’était intéressé de près à la théorie atomique, à la fois critiquant et modifiant les idées de John Dalton.

Figure 2 : L’abbé René-Just Haüy, inventeur de la cristallographie

Figure 2 : L’abbé René-Just Haüy, inventeur de la cristallographie. C’était le frère de Valentin Haüy (1745-1822), fondateur de la première École pour aveugles.

Ces préoccupations se retrouvent dans la Bakerian Lecture qu’il donna en 1812 à la Royal Society, publiée en 1813. Wollaston prit comme point de départ une remarque de Robert Hooke dans sa Micrographia sur la construction de solides géométriques comme le tétraèdre à partir de corpuscules sphériques. Wollaston hésite : faut-il choisir le tétraèdre ou l’octaèdre comme module de base en cristallographie ? La forme rhomboédrique du spath d’Islande le fascine aussi. Il montre à son auditoire comment on aboutit, en assemblant des objets sphériques, au choix, à un tétraèdre, un octaèdre, un rhomboèdre, un prisme hexagonal, etc.

Au passage, il décrit ce que nous savons à présent être la structure cristalline du chlorure de sodium, réseau cubique alternant deux types de particules. Je citerai ici ce seul autre passage de cette conférence, pour sa lucidité :

Bien que l’existence d’ultimes atomes physiques insécables doive encore être démontrée, elle est loin d’être indispensable aux hypothèses avancées ici, qui impliquent seulement des points mathématiques sujets à des forces d’attraction et de répulsion égales de tous côtés, d’ampleur donc virtuellement sphérique [nous dirions, des forces radiales]. Ainsi, de l’union de telles particules résulteraient les mêmes solides que de la combinaison de sphères dures impénétrables.

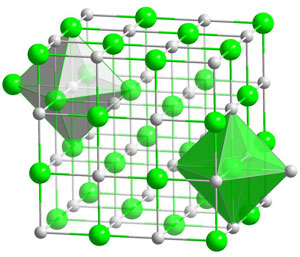
Figure 3 : Schéma de la structure cristalline du NACl (chlorure de sodium)

Figure 3 : Schéma de la structure cristalline du NACl (chlorure de sodium). C’est un réseau dit « cubique à faces centrées » où les ions chlore (en vert) occupent les sommets d’un cube, et où les ions sodium (en gris) occupent les centres des arêtes de ce cube, ou vice-versa. On remarque aussi que les ions sodium sont répartis en octaèdres autour de chaque ion chlore (octaèdre vert à droite) (dessin Wikimedia Commons, Solid state)

L’article d’Ampère

En 1814, l’année qui suivit celle de la publication de Wollaston, parut une Lettre de M. Ampère à M. le Comte Berthollet sur la détermination des proportions dans lesquelles les corps se combinent, d’après le nombre et la disposition respective des molécules dont leurs particules intégrantes sont composées. Ses contemporains chimistes n’y prêtèrent guère attention, ce qui explique l’oubli dans lequel ce magnifique article sombra. Ampère n’était peut-être pas chimiste, mais fut sans aucun conteste une figure majeure de la chimie. Pour en offrir un autre exemple, il s’essaya à une classification systématique des éléments en des familles, anticipant donc de plusieurs décennies celle de Mendeleïev.

Dans cet article de 1814, Ampère pose l’existence des molécules dans l’espace à trois dimensions. Si chacun des atomes occupe le sommet d’un polyèdre, ce dernier constituera la forme représentative de la molécule :

… un polyèdre dont chaque molécule occupera un sommet, et il suffira de nommer ce polyèdre pour exprimer la situation respective des molécules dont se compose une particule. Je donnerai à ce polyèdre le nom de forme représentative de la particule (4).

D’autre part, en conséquence des lois des gaz qu’établit Louis-Joseph Gay-Lussac (1778-1850), les nombres relatifs des atomes dans une molécule se déduisent des volumes des gaz. Ampère rattache comme suit sa démarche à celles de Gay-Lussac et d’Avogadro, qu’il cite tous deux (5) :

Je suis parti, pour cela, de la supposition que, dans le cas où les corps passent à l’état de gaz, leurs particules [molécules] seules soient séparées et écartées les unes des autres par la force expansive du calorique, à des distances beaucoup plus grandes que celles où les forces d’affinité et de cohésion [les forces d’attraction entre atomes d’une molécule] ont une action appréciable, en sorte que ces distances ne dépendent que de la température et de la pression que supporte le gaz, et qu’à des pressions et à des températures égales, les particules de tous les gaz, soit simples, soit composés, sont placés à la même distance les unes des autres. Le nombre des particules est, dans cette supposition, proportionnel au volume des gaz.
(…)
l’eau en vapeur contenant, d’après les belles expériences de M. Gay-Lussac, un volume égal d’hydrogène, et la moitié de son volume en oxygène, une de ses particules [la molécule d’eau] sera composée d’une particule entière d’hydrogène [une molécule d’hydrogène, soit deux atomes d’hydrogène], et de la moitié d’une particule d’oxygène [soit un atome d’oxygène]

Ampère va distinguer cinq modules de base pour la géométrie moléculaire, le tétraèdre, l’octaèdre, le parallélépipède, le prisme hexagonal et le dodécaèdre rhomboédrique. Ampère voit la combinaison chimique comme assemblage congruent de deux polyèdres, chacun étant forme représentative des molécules en cours d’union. Une conséquence logique de cette théorie est la possibilité de déduire la composition élémentaire de telles considérations géométriques; et Ampère en fournit des exemples.

Exemples donnés par Ampère sur la structure des molécules

La première construction donnée par Ampère est (p.12) celle d’un parallélépipède avec deux tétraèdres. Elle se fait en deux étapes : dans la première étape, Ampère prend (bas de p.11) deux lignes égales et perpendiculaires formant une croix, dans un plan, puis les écarte d’une certaine distance « en les tenant toujours dans une situation parallèle à celle qu’elles avaient dans ce plan », il obtient un tétraèdre régulier.

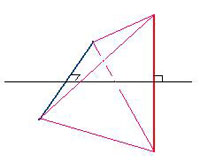
Figure 4 : Construction d’un tétraèdre à partir de deux lignes droites, telle qu’indiquée par Ampère.

Figure 4 : Construction d’un tétraèdre à partir de deux lignes droites, telle qu’indiquée par Ampère. La vue est ici en perspective, dans deux plans perpendiculaires (celui du segment rouge et du trait noir ; celui du segment bleu et du trait noir). On a écarté le segment rouge et le segment bleu, à l’origine perpendiculaires dans le même plan (situation d’origine non représentée). Une fois ces deux segments écartés depuis leur milieu commun, on joint (en mauve) une extrémité du segment rouge à celles du segment bleu, puis l’autre. On obtient un tétraèdre, à quatre sommets (chacune des extrémités des deux segments) et quatre faces.

La seconde étape est basée sur la première :

Si l’on suppose, dans le cas du tétraèdre, qu’on mène par les deux lignes dont nous avons parlé, deux plans parallèles entre eux, et qu‘on place dans chacun d’eux une ligne qui représente la position où se serait trouvée la ligne de l’autre plan avant qu’on les eût écartés, les extrémités de ces deux nouvelles lignes seront les quatre sommets d’un tétraèdre symétrique (…), et les huit sommets de ces deux tétraèdres, réunis de cette manière, seront ceux d’un parallélépipède. C’est ainsi que la forme parallélépipède résulte de la réunion de deux tétraèdres.

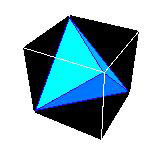
Figure 5 : Construction d’un cube à partir de deux tétraèdres, telle qu’indiquée par Ampère.

Figure 5 : Construction d’un cube à partir de deux tétraèdres, telle qu’indiquée par Ampère. Ici on n’a représenté qu’un tétraèdre – au passage on voit bien la situation de la figure 2, avec un segment en haut (la diagonale de la face supérieure du cube), équivalent d’un des deux segments de la figure 2, et un segment en bas (la diagonale de la face inférieure du cube), équivalent à l’autre segment. Dans la phrase ci-dessus, Ampère propose de bâtir un second tétraèdre (non représenté) à partir de l’autre diagonale de la face supérieure, et de l’autre diagonale de la face inférieure. Les deux tétraèdres définissent à eux deux huit sommets, qui sont ceux du cube (image Académie de Nouméa).

Ampère fait certaines déductions sur les formes des molécules. Il prend l’exemple d’un corps A, « dont les particules [molécules] ont pour forme représentative un tétraèdre », et un corps B, représenté par un octaèdre. Il essaie de combiner géométriquement tétraèdres et octaèdres en diverses proportions et tenter d’aboutir à des polyèdres :
Si l’on essaie, par exemple, de combiner des tétraèdres et des octaèdres, de manière que le nombre des premiers soit la moitié de celui des seconds, on ne trouve que des formes bizarres qui ne présentent aucune régularité (…) On doit donc en conclure [que le corps A et le corps B] ne s’uniront pas de manière qu’il y ait dans la combinaison une proportion de A et deux proportions de B ; cette combinaison sera facile au contraire, entre deux proportions de A et une de B, puisque deux tétraèdres et un octaèdre forment, par leur réunion, un dodécaèdre.

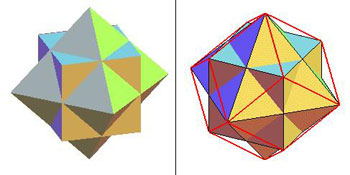
Figure 6 : Construction d’un dodécaèdre rhombique à partir de deux tétraèdres et d’un octaèdre, telle qu’indiquée par Ampère.

Figure 6 : Construction d’un dodécaèdre rhombique à partir de deux tétraèdres et d’un octaèdre, telle qu’indiquée par Ampère. On a vu que deux tétraèdres imbriqués forment un cube (figure 5). On imbrique maintenant un octaèdre dans le cube ainsi formé (à g.). On relie par des traits rouges l’enveloppe des sommets (à dr.) : on obtient ainsi un polyèdre à 12 faces en forme de losange et à 14 sommets (les six sommets du cube et les 8 du tétraèdre). Le polyèdre semi-régulier obtenu est le dodécaèdre (12 faces) dit rhombique, à faces losangiques – à ne pas confondre avec le dodécaèdre régulier, solide de Platon, à faces pentagonales (6) (images site Mathcurve)

Dans le cas d’impossibilité de combinaison géométrique en polyèdre, Ampère enfonce le clou :
Ces formes doivent être rejetées ; et on observe, en effet, que les proportions qu’elles supposeraient dans les combinaisons chimiques, ne se rencontrent point dans la nature.
Mais la combinaison de A et de B « en deux proportions de A et une de B » n’est pas la seule possible, Ampère indique une combinaison possible en proportions égales, avec deux constructions possibles (p.16) :
- Réunion d’un tétraèdre et d’un octaèdre en un « hexadécaèdre », tel que le désigne Ampère.
- Réunion de deux octaèdres et de deux tétraèdres en un « triacontaèdre », tel que le désigne Ampère.

Figure 7 : Extrait de la planche de figures en fin d’article, le « triacontaèdre ».

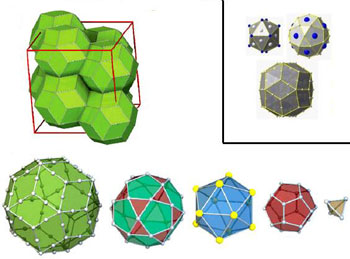
Figure 7bis : Une structure de triacontaèdre dans un quasicristal de Cadmium-Ytterbium, dit Cd5,7Yb (mis en évidence en 2000).

Figure 7 : (en haut) Extrait de la planche de figures en fin d’article, le « triacontaèdre ». Ce n’est évidement pas un solide de Platon, mais un polyèdre à faces trapézoïdales et triangulaires, inscrit dans une sphère.
Figure 7bis : (en bas) Une structure de triacontaèdre dans un quasicristal de Cadmium-Ytterbium, dit Cd5,7Yb (mis en évidence en 2000). Même le triacontaèdre postulé par Ampère a son répondant avec la structure de certains composés chimiques. On reconnaît le triacontaèdre en bas à gauche, avec ses faces en losanges et en parallélogrammes, comme ci-dessus. Ces polyèdres s’encastrent à plusieurs dans des structures cubiques (en haut à gauche). Ils sont formés de plusieurs couches (en gris le cadmium, en jaune l’ytterbium) : une première couche tétraédrique de cadmium (4 atomes) – une seconde couche dodécaédrique de cadmium (20 atomes) – une troisième couche icosaédrique d’ytterbium (12 atomes), chacune des 20 faces de l’icosaèdre ayant en son centre l’atome de cadmium de la couche antérieure (voir détail dans la figure encadrée) – une quatrième couche icosidodécaédrique de cadmium (30 atomes), chacune des 12 faces pentagonales de l’icosidodécaèdre ayant en son centre l’atome d’ytterbium de la couche antérieure (voir détail dans la figure encadrée) – enfin une cinquième couche triacontaédrique.
(image ESRF, sauf encadré CNRS)

Ampère était bien conscient de l’importance de ses déductions. Son introduction et sa conclusion sont éloquentes à cet égard (conclusion p.39-40) :

Les résultats que je viens d’indiquer ne sont qu’une très petite partie de ceux qu’on peut déduire de la considération des formes représentatives des particules des corps, appliquée à la détermination des proportions des composés inorganiques. La chimie des corps organisés [organiques] offre aussi de nombreuses applications de cette théorie (…) J’en ai tiré (…) plusieurs déterminations relatives à la composition de différentes substances tirées du règne végétal, qui s’accordent trop bien avec les résultats de l’expérience pour laisser des doutes sur l’utilité dont elle peut être dans cette partie de la chimie.

De fait Ampère estima plus tard ses contributions en chimie comme le meilleur de son œuvre scientifique (7). Le commentateur moderne n’a pas lieu d’en douter.

Ampère bâtissait sur des fondations solides, de deux types. Gay-Lussac avait établi que des gaz se combinent entre eux suivant des rapports numériques simples. René-Just Haüy, qui en eut l’idée à fracasser un cristal de calcite, découvrit que la maille élémentaire d’un cristal, dans notre langage d’aujourd’hui, se reproduit indéfiniment par translation dans chacune des trois dimensions. De la sorte, la forme géométrique épousée par un cristal réel, à l’échelle du laboratoire, nous informe de la structure à l’échelle microscopique. Cette intuition de Haüy, remarquons-le, peut s’identifier à la mise en abyme, une figure de style familière aux littérateurs des dix-septième et dix-huitième siècles.

L’article d’Ampère se situe explicitement dans la mouvance des idées de Haüy. Pour ce dernier, la molécule intégrante, notion qu’Haüy introduisit dès 1784 dans son Essai d'une théorie sur la structure des cristaux, devait être un polyèdre minuscule, puisque la forme macroscopique d’un cristal ne faisait qu’amplifier les modules microscopiques en son sein. Le clivage d’un cristal, que ce soit concrètement ou par une opération de la pensée, révélerait la forme primitive qu’il partage avec toute une famille de minéraux apparentés : on ne peut s’empêcher de penser aux archétypes platoniciens. Ampère ne se contente pas de reprendre ce concept de molécule intégrante, qu’il renomme “particule”. Il se ressert aussi de cinq des six formes primitives de Haüy, à l’exception du dodécaèdre aux faces triangulaires isocèles. Ampère se démarque, un peu, de Haüy lorsqu’il identifie molécules intégrantes et formes primitives.

Qu’Haüy en a-t-il pensé ? En 1814, il avait conservé toute son agilité d’esprit : à preuve, l’année suivante, il formulait sa loi de symétrie, par laquelle il clôturait son œuvre de cristallographe. On ne peut douter que les articles de Wollaston et d’Ampère lui furent signalés.

Leurs contemporains virent bien l’étroitesse des rapports. L’évaluation la plus incisive fut, de manière un peu inattendue, le fait du critique littéraire Sainte-Beuve (1804-1869) qui écrivit en 1843 :

la découverte de M. Gay-Lussac sur les proportions simples que l'on observe entre les volumes d'un gaz composé et ceux des gaz composants, lui [Ampère] devenait un moyen de concevoir, sur la structure atomique et moléculaire des corps inorganiques, une théorie qui remplace celle de Wollaston (8).

De plus, il pourrait bien s’agir là de la première attestation de l’expression “structure atomique et moléculaire” !

Ampère, quant à lui, introduisit l’expression forme représentative. Elle est d’un grand intérêt, car apparemment redondante. Son utilisation suggère qu’Ampère dès 1814 conduisait une réflexion épistémologique, du type de celles qui le mobiliseraient entièrement à partir de 1828. S’il s’était attaché à la forme d’une particule, c’est-à-dire à une propriété moléculaire (pour user de notre terminologie actuelle), on aurait pu le taxer de glisser d’une hypothèse scientifique à de la spéculation pure et simple. Mais, en ayant l’habileté de recourir à l’expression forme représentative d’une particule, Ampère mettait l’accent sur ce que les formes polyédriques qu’il conjecturait étaient des propriétés projetées par l’esprit sur la matière, plutôt que des qualités intrinsèques. Cette forme représentative était inhérente à la description, pas nécessairement à l’objet décrit. Voilà ce qu’implique cette apparente tautologie de la forme représentative. En d’autres termes, cet article de 1814 est écrit d’un point de vue cryptoristique et non cryptologique, pour user du vocabulaire d’Ampère dans sa Classification des sciences : découvrir quelque chose de caché, plutôt qu’élucider les causes des faits observés.

L’article d’Ampère est important pour sa généralisation des idées de Haüy de la minéralogie aux composés chimiques dans leur ensemble. Il comporte aussi une intuition fondamentale, à vertu programmatique hélas non perçue durant le dix-neuvième siècle, suivant laquelle la composition élémentaire se déduit de la structure moléculaire ; l’analyse chimique pourrait de la sorte, non pas précéder, mais suivre la détermination structurale. Ampère publie même un tableau de correspondance. Il affirme :

la considération des formes représentatives fait prévoir (…) combien, dans un corps composé, il doit entrer de molécules [lire: atomes] de chacun de ses éléments.

Le peu d’impact de l’article d’Ampère

Cet article magistral tomba dans un vide. Comme on sait, l’hypothèse d’Avogadro-Ampère fut ignorée jusqu’à ce que Stanislao Cannizzaro la ressuscite au congrès de Karlsruhe en 1860. Fut-elle une découverte prématurée ? John H. Brooke y répondit par la négative, après avoir émis une douzaine d’hypothèses quant à la raison du délai d’un demi-siècle entre la publication d’Avogadro et le congrès de Karlsruhe. Son argumentation est généralisable aux théories de Wollaston et d’Ampère.

Le rejet des idées d’Ampère eut deux causes, l’une et l’autre explicites. Elles étaient spéculatives, pire encore elles étaient le fait d’un physicien. Comme l’exprima Jean-Baptiste Dumas (Leçons de philosophie chimique, 1836) :

L’hypothèse d’Ampère, quelque ingénieuse qu’elle soit, est absolument inadmissible. Tel est le sort, et cette circonstance est à remarquer, tel est le sort des systèmes d’affinités et des systèmes de groupements moléculaires présentés par les physiciens. Lors même qu'ils possèdent, comme M. Ampère, des notions exactes sur les phénomènes et les lois de la chimie, le défaut d'habitude de la pratique de cette science se fait toujours sentir chez eux.

Que se passa-t-il entre 1814, date de la lettre d’Ampère à Berthollet, et 1836, lorsque Dumas balaie d’un revers de main la théorisation d’Ampère ? Toute une génération de chimistes eut l’occasion d’étudier les notions géométriques d’Ampère appliquées à la forme des molécules. Dans leur ensemble, ils les rejetèrent. Pourquoi ?

Outre les raisons alléguées par Brooke dans le cas d’Avogadro, j’en vois quatre. En les ordonnant par importance croissante, 1° - du fait de l’état des publications scientifiques en Europe au début du dix-neuvième siècle, les contributions d’Avogadro, de Wollaston et d’Ampère arrivèrent en ordre dispersé ; qui plus est, dans une large mesure, ils s’ignorèrent mutuellement; s’ils avaient pu faire bloc, cela aurait pu changer le tableau; 2° - ces contributions ne furent pas jugées utiles ou applicables, elles souffraient aussi d’incohérences tant internes qu’externes (avec la théorie atomique de John Dalton); 3° - elles s’inscrivaient dans le programme newtonien d’une physique mathématique, que la disparition scientifique et politique (avec la Restauration de Louis XVIII) de la Société d’Arcueil avait condamné en France ; 4° - effectivement, ces trois contributions avaient des relents de physique mathématique qui effrayaient : elles tendaient à gommer le clivage entre chimie et physique, au moment même où ces deux disciplines amorçaient leurs professionnalisations.

Néanmoins, il y eut des jeunes chimistes pour prendre au sérieux les idées d’Ampère. Ce fut le cas de Marc-Antoine Gaudin (1804-1880). Ayant assisté aux cours d’Ampère, il se convertit à ses idées. Il résolut en conséquence de se vouer à la description de la forme des molécules, et à déduire l’architecture moléculaire de la structure cristalline. Ses contributions ne furent même pas rejetées, elles restèrent ignorées tout du long. Personne ne le prit au sérieux. Il ne faisait pas partie du système établi, c’était un poids plume, une quantité négligeable. Alexandre-Édouard Baudrimont (1806-1880) était un réaliste du même tonneau qu’Ampère, ainsi qu’un antipositiviste. Ce scientifique, dans la mouvance intellectuelle d’Ampère, se battit en vain pour une chimie structurale en amont des études de réactivité. Il fut lui aussi tenu à l’écart du courant dominant de la chimie française des années 1830-1880. Médecin et pharmacien de formation, il fut nommé à une chaire de chimie à Bordeaux en 1849 et contraint, de ce fait, à une influence limitée.

Le retour du refoulé

à une date aussi tardive que 1856, le jeune William Henry Perkin (1838-1907) restait suffisamment convaincu de ce que la composition élémentaire était en correspondance biunivoque avec la structure moléculaire pour tenter une synthèse de la quinine (C₂₀H₂₄N₂O₂) par simple doublement de l’allyltoluidine (C₁₀H₁₃N); ce qui le gratifia de la découverte inattendue d’un nouveau colorant, la mauvéine.

La mauvéine, premier colorant « industriel »

En 1856, par un artefact, Perkin, nettoyant le récipient contenant des résidus de son essai raté de synthèse de la quinine, s’aperçoit que certains d’entre eux sont solubles dans l’alcool, formant une solution violette. Le premier colorant industriel pour le teinture de la soie et de l’étoffe est né – une usine pour la fabrication de mauvéine est construite à Greenford, à l’ouest de Londres. Les colorants industriels de synthèse remplaceront progressivement les pigments naturels colorés.

Figure 8 : Un échantillon de tissu coloré à la mauvéine

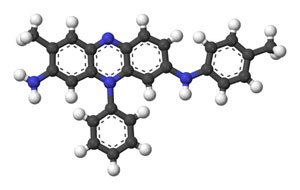
La formule complète de la mauvéine

Figure 8 : (en haut) Un échantillon de tissu coloré à la mauvéine, joint à une lettre du fils de William Perkin (image WikiCommons Henry Rzepa). (en bas) La formule complète de la mauvéine – elle n’a été connue que tardivement (en bleu les atomes N, en noir les atomes C, en blanc les atomes H)

Cet épisode comporte deux leçons. En 1856, l’analyse des molécules organiques pour en déterminer la composition était pratiquée vigoureusement depuis une bonne génération déjà. Justus von Liebig (1803-1873), dans son laboratoire de Giessen, à l’influence profonde et durable, tenu comme un modèle dans toute l’Europe, y forma les jeunes chimistes de 1824 à 1852. Une telle analyse élémentaire constituait la base de cette formation.

Les chimistes de cette époque caractérisaient les substances qu’ils isolaient par leur composition, que venaient compléter le point de fusion, le point d’ébullition et quelques autres constantes physiques. La tentative de synthèse de la quinine par Perkin, qui de notre perspective apparaît d’une grande naïveté, indique bien combien, à la veille même de l’épanouissement de la chimie structurale dans la foulée du congrès de Karlsruhe (1860), la détermination de la composition élémentaire prenait le pas sur toute autre considération.

En revanche, les chimistes n’avaient guère pris conscience de l’immense prolifération des molécules de la chimie organique. La géniale gaffe de Perkin ouvre sur une mentalité collective ne prenant pas la mesure de toutes les conséquences de l’isomérie, de combien elle est prodigue de molécules ayant en partage une même composition. Ce phénomène avait pourtant été découvert 30 ans plus tôt par Liebig et Friedrich Wöhler (1800-1882), et reçu son nom de Berzelius en 1830-31. Les chimistes l’acceptaient du bout des lèvres ; mais ceci ne les empêchait pas de rester convaincus de ce que la composition élémentaire servait de signature suffisante et complète pour toute molécule.

D’où leur venaient leurs œillères ? Durant toute la première moitié du dix-neuvième siècle, la chimie fut sous-tendue par un programme de recherche visant à élaborer des classifications des composés chimiques sur le modèle des différentes systématiques des organismes biologiques. Les chimistes de cette période visaient un schéma de classification à deux termes, analogue à la classification linnéenne, dans laquelle un mot définit le genre et un autre l’espèce. Cette mentalité s’ancrait dans l’analyse chimique, une routine stricte usant de l’outil inventé par Liebig, son kaliapparat. Les débuts de la professionnalisation de la chimie qui intervinrent à la même époque, puis l’industrialisation de la chimie des colorants qui suivit la découverte de Perkin, ne firent que sceller cette notion simpliste d’une correspondance biunivoque d’une formule élémentaire et d’une molécule.

Comme on ne le sait que trop, changer une mentalité est extrêmement difficile. Seuls des francs-tireurs s’y essaient. Ce fut le cas de deux jeunes chimistes, l’un français, Auguste Laurent (1807-1853), l’autre britannique, Archibald Couper (1831-1892), qui de ce fait eurent maille à partir avec l’establishment. Ce n’est que vers le milieu des années 1850 que cette mentalité, rebelle aux idées d’Ampère, commença d’évoluer. La collecte empirique de données brutes, dans un esprit de positivisme, le céda peu à peu à une analyse, lexicale et syntactique, des formules chimiques à l’instar de mots.

Cette mutation vit l’introduction de nouvelles formules, dites développées, porteuses d’information sur la connectivité des atomes dans une molécule. Ce fut là une découverte multiple (l’historien des sciences Sarton nota que la plupart des découvertes sont simultanément le fait de plusieurs personnes) attachée aux noms de Couper (1858), Kekulé (à partir de 1857), Loschmidt (1861), Crum Brown (1861), Wurtz (1864), Hofmann (1865) …

Le tableau noir venait s’ajouter à la paillasse. La science chimique se retourna vers la méthode hypothético-déductive, dans laquelle Ampère avait tenté de l’orienter. L’exemple de Friedrich August Kekulé (1829-1896) et de son évolution intellectuelle est des plus parlants à cet égard. En 1858, il tenait toujours pour équivalentes une “formule rationnelle” et Umsetzungformeln, c’est-à-dire une sorte de sténographie de l’ensemble des faits d’observation, relatifs aux transformations qu’un composé donné avait subies. En 1866, avec sa formulation cyclique du benzène, Kekulé avait accompli un basculement de Gestalt. La formule, qu’elle fût hexagonale ou triangulaire (selon qu’on se fie à la formule de Kekulé ou aux alternatives proposées par ses contemporains) — retour aux formes géométriques d’Ampère — était devenue construction intellectuelle a priori. Elle était une hypothèse à confronter aux données expérimentales.

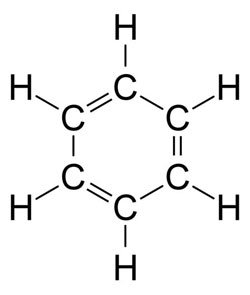
Figure 9 : Formule développée du benzène C6H6

Figure 9 : Formule développée du benzène C₆H₆. Cette forme représentative hexagonale, avec les doubles liaisons Carbone, a été mise en évidence vers 1864 par August Kekulé von Stradonitz (1829-1896) (image WikiCommons Leyo).

Histoire de la stéréochimie et longue durée

Commençons par noter que les deux termes, “stéréoisomère” et “stéréochimie” datent de 1888. De telles dénominations sont des indicateurs, plutôt que de l’ouverture d’un nouveau champ disciplinaire, de son âge adulte. De manière générale, les disciplines et les sous-disciplines se dotent d’une organisation, d’une appellation, d’une terminologie, d’un périodique spécialisé, d’un programme de formation des jeunes chercheurs, après que la pousse initiale (mise au point d’instruments et de procédures, établissement de concepts) s’est déjà lignifiée en une telle institutionnalisation.

Si donc nous posons que la stéréochimie, en tant que mentalité, était parvenue à maturité dans les années 1880, quand donc a-t-elle commencé ? Les divers récits historiques divergent sur ce point. On trouve deux écoles principalement. L’une choisit la date de 1874 qui vit les annonces du carbone tétraédrique, quasi-simultanément par Le Bel et van’t Hoff. D’autres auteurs choisissent l’année 1847, et le début des travaux de Pasteur sur les acides tartriques. Ce qui ne fait guère que 30 ans de différence, la durée d’une génération.

Quoi qu’il en soit, que l’on choisisse l’une ou l’autre date, la décision est minée par l’existence de toute une préhistoire à la stéréochimie. Dans la première option, n’est-il pas avéré que van’t Hoff trouva l’idée d’une représentation tridimensionnelle (pour le carbone tétraédrique) dans le laboratoire de Kekulé à Bonn, où il séjourna en 1872-73 ? Kekulé lui-même ne fut-il pas influencé par la conjecture de Butlerov en 1862, suivant laquelle les affinités du carbone irradiaient des sommets d’un tétraèdre carboné ? L’hypothèse tétraédrique de van’t Hoff, comme il l’admit lui-même, eut encore comme autre source l’étude des acides lactiques en 1869 par Johannes Wislicenus, ce dernier concluant à une isomérie provenant de la différence de disposition des atomes dans l’espace. Wislicenus écrivit à ce sujet, en 1873 :

si des molécules peuvent être identiques dans leurs structures et posséder néanmoins des propriétés différentes, cela ne peut s’expliquer que si la différence provient de l’arrangement différent des atomes dans l’espace.

Qu’Achille Le Bel bénéficia des idées pasteuriennes est tout aussi patent. Pasteur lui-même n’innova pas dans le vide. Sa séparation des isomères droit et gauche des acides tartriques ne fut pas une innovation ex-nihilo. Il en était redevable à Auguste Laurent, qui lui avait suggéré d’étudier les cristaux des tartrates pour son travail doctoral.

Ces indications suffiront à nous convaincre de la légèreté qu’il y aurait à faire partir la stéréochimie de 1874, voire de 1847. A mon sens, la seule perspective dans laquelle replacer l’histoire de la stéréochimie ne peut être que la longue durée braudélienne, celle d’«une histoire quasi immobile, celle de l'homme dans ses rapports avec le milieu qui l'entoure ; une histoire lente à couler, à se transformer, faite souvent de retours insistants, de cycles sans cesse recommencés », une histoire « presque hors du temps ».

Esquissons ici ce que serait une histoire de la stéréochimie inscrite de la sorte dans la longue durée. Elle est intimement liée, à toutes les étapes, au développement de la cristallographie. Elle remonte donc au moins à la Renaissance.

Les croyances pythagoriciennes dans la numérologie s’écrivirent dans le ciel lorsque sa mystique néo-platonicienne incita Kepler à inscrire les orbites planétaires dans les polyèdres platoniciens. Il eut cette idée en 1595. Elle lui permit, en 1618, d’énoncer sa troisième loi, qualifiée d’harmonique, pour décrire le système solaire. Sommes-nous très éloignés de la forme des molécules ? Assurément non, puisque le même Kepler (Strena sive de nive sexangula) rendit compte en 1609 de la symétrie d’ordre six des cristaux de glace par l’empilement de minuscules gouttelettes, élémentaires, de l’eau constituante. Il y eut là un tout premier stade dans l’histoire de la géométrie moléculaire, et donc aussi de la stéréochimie.

Durant le dix-septième siècle, cette intuition de Kepler fut reprise et développée par Descartes, Bartolin, Boyle, Hooke et Huygens. Robert Hooke, par exemple, montra l’invariance des angles des faces dans un cristal indépendamment de sa dimension. Alors que Kepler avait vu les solides platoniciens dans divers minerais, Sténon délaissa les solides platoniciens pour des mesures exactes de cristaux d’hématite venant de l’île d’Elbe. Un siècle d’observations s’accumulèrent, jusqu’à ce que Haüy formule son hypothèse réticulaire en 1802. De plus, et pour retourner aux flocons de neige que Kepler avait scruté si attentivement, nous sommes redevables à Haüy d’avoir reconnu que la symétrie sénaire n’était compatible qu’avec des particules constituantes (nos molécules) coudées. C’était de sa part une inférence visionnaire.

Le second stade dans la graduelle mise en abyme du monde matériel fut ainsi atteint à la fin du dix-huitième siècle lorsque le même Haüy représenta les formes des cristaux, les basant sur des polyèdres réguliers pris comme blocs de base. L’idée platonicienne, héritée de la Renaissance, en vint alors à englober l’ensemble de la minéralogie.

Le troisième fut la lettre ouverte d’Ampère à Berthollet en 1814, que nous commentons ici. Dorénavant, on pourra décrire — bien que peu de chimistes s’y aventurèrent — la structure moléculaire par des atomes situés aux sommets de polyèdres réguliers, dans des arrangements redevables de relations mathématiques simples. Ampère fut un pionnier, en cela qu’il spécifia les notions de structure et d’architecture moléculaires comme des buts à atteindre : pour que la science chimique les établisse et les explique ; pour que les chimistes s’en servent pour dénouer l’écheveau des lois régissant les combinaisons chimiques.

Le quatrième stade, si vous m’en croyez, un écho vraisemblable à la lettre d’Ampère de 1814, est la thèse de doctorat d’Auguste Laurent en 1837. Ce chimiste, très averti en cristallographie, familier des textes de René-Just Haüy, rédigea sa thèse sur la réactivité des molécules organiques à l’égard des additions et substitutions. Il conçut un noyau hydrocarboné, à forme de parallélépipède, comportant huit atomes de carbone et douze d’hydrogène. Ce faisant, Laurent conjecturait un solide régulier, un polyèdre qui résumerait et rassemblerait l’ensemble des métamorphoses qu’une molécule organique était susceptible de subir. Ce fut l’une des graines d’où éclorait en 1858 la tétravalence du carbone telle que Kekulé la conçut (cinquième stade).

Le sixième, dans cette mise en abyme qui se poursuivit, lente mais majestueuse, au cours des âges, fut la découverte par Le Bel et van’t Hoff en 1874 : le tétraèdre, l’un des cinq solides platoniciens, s’avéra un parfait descripteur de la tétravalence comme de la possible asymétrie de l’atome de carbone. Durant la décennie 1890, Alfred Werner tira parti de l’octaèdre, un autre des solides platoniciens, comme un gabarit pour la classe tout entière des complexes de coordination, ou “composés d’ordre supérieur”, comme il les désignait, et pour rendre compte de leurs isomérie.

@@@@@@@

C’est ainsi que la lettre d’Ampère de 1814 jette un pont entre Haüy et Werner. La contribution de Werner mettait de l’ordre dans la prolifération des composés de coordination. Elle les organisait en trois classes ou familles, de coordinences quatre, six et huit. Lui aussi fit appel à des polyèdres réguliers, tout particulièrement l’octaèdre pour la coordinence six. Les contributions d’Ampère et de Werner sont l’une et l’autre d’inspiration géométrique. Le prix Nobel fut décerné à Alfred Werner en 1913. Dans son discours de réception, Werner mentionna “les groupements, potentiellement symétriques, de quatre, six ou huit points autour d’un centre, lorsque les points adjacents sont équidistants”, donnant ainsi une description de la sphère de coordination autour d’un atome central.

Figure 10 : Alfred Werner (1866-1919), prix Nobel de chimie 1913.

Figure 10 : Alfred Werner (1866-1919), prix Nobel de chimie 1913.

Ce n’est pas tout, la mise en abyme esquissée ici ne s’interrompit pas avec la théorisation que Werner donna de la coordination. Ensuite, au tout début du vingtième siècle, Gilbert N. Lewis fut intrigué par la coexistence de deux types d’interaction de liaison interatomique, la covalence normale dans les molécules organiques, la liaison dative dans les complexes de coordination de Werner. Cela l’incita, dès le 28 mars 1902, à représenter la configuration électronique, au dos d’une enveloppe, par encore un autre solide platonicien, le cube. Dans son schéma, les électrons formaient une couche, occupant graduellement et de manière symétrique les sommets d’un cube. Il se convainquit de ce que, suivant ses propres mots,

la paire d’électrons constitue leur groupement stable, et, de façon plus générale, c’est la paire d’électrons et non leur groupe de huit qu’on doit considérer comme étant l’entité fondamentale.

Cela lui donna la notion de la liaison chimique à deux électrons, et il rendit compte aussi de cette manière de l’atome de carbone tétraédrique. Lewis fut amené de la sorte à conclure que les électrons allaient par paires comme s’ils étaient retenus par des petits aimants ; ce qui anticipa sur la découverte du spin de l’électron et sur le principe de Pauli. J’y vois le huitième stade dans ce qu’on pourrait dénommer la platonisation du monde matériel. Ce fut une étape majeure aussi dans la réouverture d’un dialogue entre les chimistes et les physiciens, durant les trois premières décennies du vingtième siècle. Elle s’acheva par l’importation, dont nous sommes redevables à Linus Pauling, des principales idées de la mécanique quantique ; tandis que des physiciens, comme Hans Bethe, Fritz London, Julius R. Oppenheimer, Edward Teller, et quelques autres, qui s’étaient aventurés en chimie, battaient en retraite, écœurés par la complexité de cette autre discipline. La découverte du neutron par Chadwick y fut aussi pour beaucoup, ils retrouvèrent la physique avec un charme pour eux de ce fait accru. Les deux sciences divergèrent ensuite, la chimie se donnant des modèles prédictifs, en un développement de Fourier, par l’acquisition d’information de qualité inférieure sur un domaine de plus en plus étendu. Un physicien, par contre, vise typiquement à se donner une capacité prédictive ou interprétative, dans un développement en série de Taylor, sur un cas-prototype comme celui de l’atome d’hydrogène, par l’acquisition d’une information la meilleure possible, tant sur le prototype que sur des cas voisins.

Qui plus est, la numérologie sous-jacente aux structures atomique et nucléaire, que des physiciens comme Elsasser et Goeppert-Meyer établirent durant les décennies ultérieures, améliora encore notre connaissance de la nature, allant du macrocosme au microcosme, toujours sur la base d’harmonies pythagoriciennes.

@@@@@@@

Pour revenir à nos moutons, c’est-à-dire aux formules moléculaires et à la postérité de la lettre d’Ampère, mentionnons très brièvement, à titre d’étapes ultérieures de la mise en abyme graduelle se déroulant inlassablement depuis l’époque d’Albrecht Dürer et Johannes Kepler, l’heuristique annoncée en 1957 par plusieurs chimistes sous le nom de valence shell electron pair repulsion (théorie VSEPR ou de Gillespie-Nyholm); la réunification par Earl R. Muetterties dans les années 1960, toujours dans l‘esprit d’Ampère, des structures minérales et organiques, qu’il s’agisse d’agrégats d’atomes, de molécules ou de complexes de coordination ; la découverte par Aaron Klug des virus icosaèdres ; la synthèse à la fin du vingtième siècle d’hydrocarbures isomorphes de solides platoniciens (Philip E. Eaton pour le cubane ; Leo Paquette pour le dodécaédrane); et la découverte fortuite (Richard Smalley, Harold Kroto et Robert Curl) du fullerène C60, à géométrie d’icosaèdre tronqué.

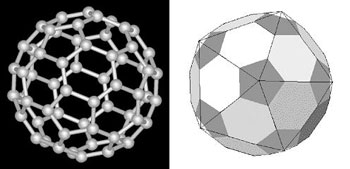
Figure 11 : (à g.) La molécule de fullerène C60, découverte en 1985. Sa découverte vaudra le prix Nobel de chimie en 1996 à Smalley, Kroto et Curl. Elle a une géométrie de 20 faces hexagonales et de 12 faces pentagonales, dite d’icosaèdre tronqué. (à dr.) Le ballon de football a lui aussi la même géométrie : les 12 sommets de l’icosaèdre sont coupés, se transformant en 12 faces pentagonales ; les 20 faces triangulaires de l’icosaèdre deviennent 20 faces hexagonales.

Octobre 2010

Logo BibNum

(1) Alfred Werner (1866-1919), chimiste suisse, prix Nobel de chimie 1913 pour son explication de la structure de certains métaux.
(2) Achille Le Bel (1847-1930) et Jacobus Henricus van’t Hoff (1852-1911, premier prix Nobel de chimie 1901) ont travaillé ensemble à Paris dans le laboratoire de chimie d’Adolphe Wurtz pendant leurs études.
(3) Sur la propriété de chiralité et le pouvoir rotatoire des molécules, tel qu’analysé par Fresnel en 1822, voir l’analyse BibNum faite par Jeanne Crassous.
(4) Il convient d’être vigilant dans la lecture d’Ampère : il désigne par molécule ce que nous appelons actuellement atome, et par particule ce que nous désignons comme molécule.
(5) Voir les dossiers BibNum correspondants : l’article de Gay-Lussac (1809) analysé par Pierre Radvanyi, et celui d’Avogadro (1811) par Bernard Fernandez.
(6) Ampère ne donne pas cette précision, mais la figure 5 de la planche I à la fin de son article montre clairement qu’il parle du dodécaèdre rhombique.
(7) Dans une lettre du 11 mars 1814 à son ami Roux, Ampère évoque en ces termes la loi de combinaison des corps chimiques proposée dans son article : « une loi de la nature dont la découverte sera peut-être, après ce que j'ai fait l'été passé en métaphysique, ce que j'aurai conçu de plus important dans toute ma vie » (cité par Michelle Sadoun-Goupil , “Esquisse de l'œuvre d'Ampère en chimie”, Revue d'histoire des sciences, année 1977, 30, numéro 30-2, pp. 125-141 (en ligne sur Persée).
(8) Charles-Augustin Sainte-Beuve. "Notice sur M. Ampère", In : André-Marie Ampère, Essai sur la philosophie des sciences, t. II, Paris, 1843, p. I-LIX (en ligne sur Gallica).

À LIRE (BibNum)

Bernard Fernandez, « Les deux hypothèses d’Avogadro en 1811 », BibNum, janvier 2009, (lien)

Jeanne Crassous, « La double réfraction de Fresnel et les molécules pharmaceutiques chirales », BibNum, février 2009 (lien)

À LIRE (LIVRES)

Henri Kagan, La stéréochimie organique, PUF, Paris, 1975.

Robert Halleux et Pierre Laszlo, Représentations anciennes du savoir chimique et alchimique, Bibliothèque centrale de l’université de Liège, décembre 1980, 195 pp. n° 32.

Kurt Mislow, Introduction to Stereochemistry, New York, Dover Publications, 2003 (réédition d’un ouvrage publié en 1965).

Robert Locqueneux et Myriam Scheidecker-Chevallier, Ampère, encyclopédiste et métaphysicien, EDP Sciences, 2008.

À LIRE (ARTICLES D'HISTOIRE DES SCIENCES)

Myriam Scheidecker-Chevallier, “Ampère et la chimie”, Bulletin de la Sabix, 2004, no 37 , pp. 39-52 (lien)

Myriam Scheidecker-Chevallier, « La chimie géométrique de André-Marie Ampère (1775-1836) et de Marc-Antoine Gaudin (1804-1880) », L’Actualité Chimique, 1999 - Paris: Société chimique de France.

Myriam Scheidecker-Chevalier, “L'hypothèse d'Avogadro (1811) et d'Ampère (1814) : la distinction atome/molécule et la théorie de la combinaison chimique”, Revue d’histoire des sciences, 1997, vol. 50, no1-2, pp. 159-194

À LIRE (ARTICLES DE CHIMIE)

Muetterties, E. L.. “Polytopal form and isomerism”. Tetrahedron (1974), 30(12), 1595-604.

Muetterties, E. L.; Guggenberger, L. J. “Idealized polytopal forms. Description of real molecules referenced to idealized polygons or polyhedra in geometric reaction path form”. Journal of the American Chemical Society (1974), 96(6), 1748-56.

Muetterties, Earl L.. “General structural-stereochemical principles an topological analysis”. Record of Chemical Progress (1971), 31(2), 51-88.

Muetterties, Earl L.; Storr, A. T. “Topological analysis of polytopal rearrangements. Sufficient conditions for closure”. Journal of the American Chemical Society (1969), 91(11), 3098-9.

Embarquer le document

Voir le code

Envoyer la référence de la page