Figure 1 : Arthur Stanley Eddington, 1882-1944 (WikiCommons, photo du fonds George Grantham Bain Collection, Library of Congress).
Introduction
Ce chapitre au titre étonnant (On the Nature of Things) conclut le best-seller d'Eddington Space, Time & Gravitation (1920), un des premiers livres à présenter au public anglophone la théorie de la relativité d'Einstein sous une forme relativement vulgarisée, qui plus est dans un style magnifique et, nous allons le voir, dans un cadre épistémologique et philosophique singulier.
Arthur Stanley Eddington (1882-1944), astrophysicien, physicien et philosophe britannique de la première moitié du XXe siècle, peu connu en France, faisait partie des rares personnes (selon la légende au nombre de trois !) à maîtriser la théorie de la relativité générale d'Einstein au moment de sa publication (fin 1915). C'est lui qui, en 1916, fait connaître à la communauté scientifique anglo-saxonne les travaux de ce dernier dans un contexte (Première Guerre mondiale) peu propice à la circulation des travaux scientifiques entre l'Allemagne et la Grande-Bretagne. Eddington sera un fervent défenseur de la théorie de la relativité générale, et le premier à la vérifier expérimentalement lors d'une expédition sur l'île de Principe (1919) où il observe, conformément à la théorie, la déviation de rayons lumineux d'étoiles observables à proximité du Soleil lors d'une éclipse (cf. figures 2, 2bis et 2ter).
Pendant les années 1920, Eddington sera à la pointe de la physique théorique, prenant part à de nombreuses tentatives d'unification pour remédier à la fragmentation insatisfaisante de la discipline, comme celle de la gravitation et de l'électromagnétisme, à l'instar du mathématicien Hermann Weyl, et, plus tard, de la relativité générale et de la mécanique quantique.
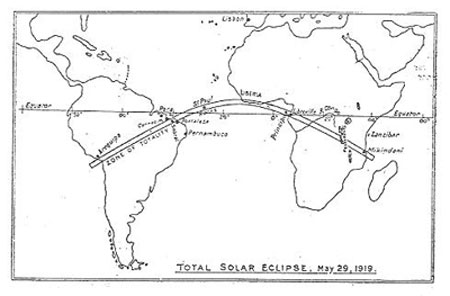
Figure 2 : Parcours de l’éclipse solaire de 1919 (image revue Nature, 1919, n°102). L’expédition d’observation menée par Eddington sur l’île de Principe (golfe de Guinée), en parallèle d’une seconde expédition à Sobral (Brésil), permet d’apporter, malgré une précision médiocre, la première vérification expérimentale de la théorie de la relativité générale. La déflexion gravitationnelle, très faible, de rayons lumineux ne pouvant être mise en évidence qu’auprès de corps suffisamment grands et massifs tels que le Soleil, il faut alors une éclipse totale pour pouvoir l’observer. L’expédition frappe aussi les esprits parce que c’est une équipe de savants anglais (de la Royal Astronomical Society) qui vérifie la théorie d’un savant allemand, Einstein, et ce juste après la fin de la Première Guerre mondiale.
Figure 2bis : Principe d’observation de la déflexion de rayons lumineux frôlant la surface du soleil (schéma issu de l’ouvrage d’Eddington, 1920) : la trajectoire de la lumière issue de l’étoile P (considérée à l’infini) est courbée au voisinage du Soleil et, atteignant la Terre en E, semble provenir de P’. La mesure de l’angle de déflexion (par rapport à la situation sans Soleil, avec comme référence des étoiles plus éloignées), double de celui prédit par la théorie newtonienne, est conforme à la prévision de la relativité générale (soit 4GMs/Rsc², avec des notations évidentes).
Figure 2ter : Matériel d’observation de l’éclipse de 1919 à Sobral, Brésil (photographie issue de l’ouvrage d’Eddington, 1920) : deux télescopes, deux miroirs cœlostats et l’horloge dirigeant le plus grand miroir (à gauche, sur le piédestal).
Mais, à partir des années 1930, sa physique sera de plus en plus gouvernée par sa philosophie, au point de lui faire perdre pied avec l'orthodoxie scientifique. Il sera progressivement mis au banc de la communauté scientifique ; ses dernières tentatives de réconciliation de la relativité générale et de la mécanique quantique en une « théorie fondamentale
(1) », par ailleurs toujours mal comprise, seront taxées de pythagorisme
(2).
Notre propos ici n'est évidemment pas d'analyser dans son ensemble la philosophie, très complexe et parfois incohérente, d'Eddington, mais de comprendre comment, dans un de ses premiers textes, s'exprime déjà sa conception très particulière des lois physiques, différente de ce que l'on attendrait de la part d'un scientifique professionnel, et annonçant ce que d'aucuns appelleront par la suite son « idéalisme
(3) ». Dans ce chapitre, qui conclut l'ouvrage et la présentation de la théorie de la relativité (avec des considérations plus générales sur la géométrie ou l'électromagnétisme), Eddington aborde, à partir de cette dernière, des thèmes canoniques de la philosophie des sciences, qui dépassent son cadre et intéressent tous les champs scientifiques : le réalisme scientifique (dans quelle mesure les entités des théories scientifiques existent-elles vraiment ou, au contraire, sont-elles des fictions qui ont un rôle purement épistémologique ?), la définition de l'objectivité, le rapport entre les mathématiques et la réalité physique...
Dès les premières pages du chapitre, partant d'une posture réaliste classique, il bascule vers une conception antiréaliste des théories scientifiques qui privilégie leur structure mathématique. Définissant la réalité physique comme « synthèse de tous les points de vue possibles », il pousse à bout la philosophie de la relativité pour, à partir de la géométrie la plus générale et objective qu'il a précédemment élaborée, véritablement construire la réalité physique. Le milieu du chapitre, un peu plus technique, se focalise sur les équations d'Einstein, à partir desquelles Eddington, « inversant » leur interprétation, tire une conception
a priori, totalement géométrisée, de la matière – plus encore, c'est la géométrie qui est véritablement « matérialisée ». Les dernières pages témoignent de sa conception des lois physiques en tant que projection de notre entendement, faisant montre d'un certain idéalisme qui n'est pas sans rappeler celui de Kant
(4).
Figure 3 : Une édition de 1675 du De Rerum Natura de Lucrèce (99–55 av. J-C.). Le titre du chapitre d’Eddington, "On the nature of things", en est peut-être inspiré. Une émission de radio "On the nature of things" a existé à la BBC dans les années 1950 : c’est dans une de ces émissions que le physicien Fred Hoyle a inventé, par dérision, le terme de "Big Bang", qui est resté.
La théorie de la relativité
Un bref rappel de la théorie de la relativité d'Einstein (restreinte et générale), à laquelle Eddington fait référence en début de chapitre et dont la structure influence grandement son épistémologie, peut être utile pour les lecteurs qui n'en sont pas familiers.
La meilleure façon d'aborder cette théorie est peut-être de souligner, comme l'a lui-même reconnu Einstein par la suite, à quel point elle porte mal son nom. En effet si la relativité établit qu'il n'existe de mouvement que relatif, et non absolu (comme le croyait Newton), son essence consiste à affirmer l'invariance des lois physiques, qui gardent la même forme dans tous les référentiels. Historiquement c'est Galilée qui, le premier (en 1632 dans son Dialogue sur les deux grands systèmes du monde), introduit le concept de relativité en physique avec sa célèbre expérience de pensée du bateau : dans un bateau en mouvement uniforme, les sauts d'un passager dans un sens ou dans l'autre auront la même longueur ; aucune expérience de physique (sans référence à un élément extérieur) ne permet de dire si le bateau est en marche ou immobile. En somme rien ne permet de distinguer le mouvement uniforme de l'état de repos.
La théorie de la relativité restreinte
La théorie de la relativité restreinte naît ainsi d'une insatisfaction : les équations de Maxwell (1865), qui régissent les lois de l'électromagnétisme classique, ne sont pas invariantes dans les transformations de Galilée mais dans les transformations de Lorentz inventées à la fin du siècle. Une autre incompatibilité se fait jour, celle de l'additivité galiléenne des vitesses avec la vitesse maximale de propagation c des ondes électromagnétiques.
Einstein parvient, en 1905, à concilier mécanique newtonienne et électromagnétisme avec sa théorie de la relativité restreinte, dont l'élaboration, purement déductive, repose sur deux postulats
(5) :
1. le principe de relativité « étendu », selon lequel toutes les lois de la nature (incluant l'électromagnétisme) sont les mêmes dans tous les référentiels galiléens ; 2. l'universalité de la vitesse de la lumière, qui stipule que la vitesse de la lumière dans le vide (c) est la même dans tous les référentiels galiléens, et indépendante du mouvement de la source lumineuse.
S'ensuivent, au niveau formel, la fusion des coordonnées spatiales et temporelles en des « évènements » de l'« espace-temps » à quatre dimensions de Minkoswki
(6) ; au niveau conceptuel, la disparition du concept de temps absolu de Newton identique pour tous les référentiels, la simultanéité étant relative au référentiel considéré.
La théorie de la relativité générale
La relativité générale prend en compte la gravitation, contrairement à la relativité restreinte où elle est négligée. Elle achève de répondre aux deux problèmes conceptuels qui demeurent inexpliqués dans la théorie newtonienne de la gravitation : 1. la vitesse de propagation infinie de l'interaction gravitationnelle, qui est en contradiction avec le postulat de relativité d'Einstein ; 2. le principe d'équivalence locale entre masse inerte et masse pesante.
Une conséquence du principe d'équivalence newtonien est que les lois de la mécanique sont les mêmes dans un référentiel en chute libre soumis à la gravitation (un ascenseur, pour reprendre l'exemple d'Einstein) et un référentiel galiléen en l'absence de gravitation. Cela signifie que localement, les effets de la gravitation sont éliminés par le passage à un référentiel accéléré (la gravité étant assimilable à un champ d'accélération).
Avec la relativité générale, Einstein généralise ce principe à la totalité des lois physiques : dans un référentiel en chute libre occupant une région suffisamment petite de l'espace-temps, toutes les lois de la physique sont celles de la relativité restreinte. La relativité générale constitue ainsi l'extension de la relativité restreinte (où les référentiels considérés sont galiléens) aux mouvements non uniformes.
Les équations d'Einstein :
relient le tenseur (7) d'Einstein Gμν, construit à partir du tenseur de courbure (qui représente la géométrie de l'espace-temps), au tenseur énergie-impulsion Tμν qui représente la distribution de matière (G étant la constante de Newton).
Un des tenseurs de la relativité générale
Le tenseur de courbure de Riemann-Christoffel, qui exprime une propriété géométrique intrinsèque de la variété, est défini par
où → X, Y, Z sont des champs de vecteurs tangents (appartenant à l’espace tangent à la variété au point considéré, dont une base est constituée par les dérivées partielles ∂/∂xi un champ de vecteur pouvant être vu comme un opérateur de différentiation d’ordre un), et W un champ de vecteur dual (une forme linéaire sur les vecteurs tangents, dont une base est constituée par les différentielles dxi) ; → ∇X désigne la dérivée covariante par rapport au vecteur tangent X (généralisation de la notion de dérivée sur une variété de dimension supérieure à 1, qui nécessite de définir la direction dans laquelle se déplace le point, et qui permet de dériver des tenseurs de manière indépendante des coordonnées) ; → [X,Y] = XY – YX désigne le crochet de Lie (ou commutateur) des deux champs de vecteurs X,Y.
La gravitation, figurant dans le terme de gauche de l’équation (1), est totalement géométrisée et représentée par la courbure (une quantité géométrique). Lorsque l'espace est vide, ces équations s'écrivent donc Gμν= 0.
Il nous faut quelques instants réfléchir à cela, afin de comprendre l’interprétation singulière qu’Eddington en fait. En première analyse, le terme de gauche de
(1) est assimilable au «contenant» (l'espace-temps), et le terme de droite au «contenu» (la matière, l'énergie) ; mais, en fait d'analogie, c'est plutôt de métonymie qu'il s'agit. En effet, la lecture initiale classique de l'équation, « machienne
(8) », va de droite à gauche : la matière déforme l'espace-temps,
i.e. la métrique (le « contenant ») est déterminée par la distribution de matière (le « contenu », représenté par le tenseur énergie impulsion).
Cependant, la seule donnée du tenseur énergie-impulsion ne suffit pas à déterminer la métrique, car justement l’expression de ce dernier nécessite en général d'avoir explicitement recours à la métrique. Réciproquement, la seule donnée de la métrique ne suffit pas à déterminer le tenseur énergie-impulsion, car il ne correspondra pas en général à un champ de matière physiquement admissible. En somme, l'égalité des équations d'Einstein énonce une interaction dynamique, une sorte d’ « harmonie » entre la métrique et la distribution de matière, dont la résolution doit être recherchée conjointement
(9).
La géométrisation de la physique
Concluons ce court aperçu de la théorie de la relativité par une de ses caractéristiques les plus remarquables, à savoir sa nature fondamentalement géométrique, à laquelle Eddington sera particulièrement sensible. En effet, l'utilisation d'une géométrie de plus en plus complexe, qui devient une sorte de langage naturel, confère à la théorie une physique de plus en plus simple. Ainsi en est-il du principe d'inertie, qui fait décrire à un corps en l'absence de force : - en mécanique newtonienne, une droite de l'espace à vitesse constante – la « dispersion » disciplinaire se répartissant entre cinématique, dynamique et géométrie (euclidienne) ; - en relativité restreinte, une droite de l'espace-temps – la dispersion se réduisant à la dynamique et la géométrie (minkowskienne ou pseudo-euclidienne) ; - en relativité générale (en incluant la gravitation), une géodésique – en ayant recours uniquement à la géométrie (non-euclidienne).
Notion de géodésique en relativité générale
La géodésique est la généralisation du concept de droite (plus court chemin entre deux points) aux espaces courbes (ou variétés). Une variété constitue la généralisation du concept d'espace euclidien dans les géométries non euclidiennes. Ainsi, l'espace-temps de la relativité générale peut être considéré comme une succession de petits espaces de Minkowski de la relativité restreinte, de même que la surface de la Terre peut être approximée comme une succession de petits plans à deux dimensions. Le principe d'équivalence stipule alors que la trajectoire d'une particule libre (soumise uniquement à la gravitation) est approchée par un ensemble de segments de droite infinitésimaux qui la décrivent localement dans une suite de référentiels en chute libre. Plus précisément, l'équation de la géodésique signifie que l'accélération est nulle dans la direction de la surface, et perpendiculaire au plan tangent à la surface en chaque point de la courbe : c’est précisément ainsi que le mouvement des particules est complètement déterminé par la courbure de l'espace-temps. La géodésique apparaît alors comme une sorte de chemin naturel, l'équation du mouvement des particules dans un champ gravitationnel ne faisant pas intervenir la notion de force, par opposition aux trajectoires de la mécanique newtonienne issues de forces.
Le réalisme structural
Venons-en maintenant au texte lui-même. L'épigraphe en apparence énigmatique du chapitre
(10), une citation du
Songe d'une nuit d'été de Shakespeare,
est en fait, comme il se doit, révélateur de la teneur des propos qui suivent. En effet, si l'on substitue par exemple à cette « chose » (stuff) les théories scientifiques, on comprend que pour Eddington elles ne seront que des « ombres » (shadows), qui tirent leur valeur de l'esprit qui les pense. D'emblée, cette citation poétique annonce sa posture antiréaliste.
En effet, même s'il démarre le chapitre par un plaidoyer pour la théorie de la relativité, très vite il émet des réserves quant à une adhésion réaliste naïve aux théories scientifiques. Citons son analogie amusante du jeu d'échecs – il suppose que le jeu disparaît et que dans trois mille ans des « antiquaires » retrouvent un livre de partie transcrites :
Les parties d’échecs décrites ce sont nos expériences physiques. Les règles du jeu que l’étude de ces expériences permet de fixer, ce sont les lois de la physique. L’échiquier hypothétique à soixante-quatre cases, c’est l’espace-temps de quelque observateur ou joueur particulier […] Les pièces du jeu d’échecs deviennent des entités de la physique – électrons, particules ou points-événements […] L’étude expérimentale ne peut rien nous apprendre sur la nature et même sur l’apparence de ces entités. Mais cette connaissance est étrangère à la question car nous pouvons nous en passer pour apprendre le « jeu » avec toutes ses combinaisons.
Figure 4 : Pièces de jeu d’échecs (figurine de Lewis, XIIe s., Europe du Nord ; photo WikiCommons, © Andrew Dunn). Eddington compare les pièces d’échecs aux entités physiques : l’antiquaire, dans trois mille ans, peut comprendre le jeu d’échecs sans connaître la forme des figurines, ou même savoir que ce sont des « pièces en bois sculpté ». Il en est ainsi des entités, électrons, etc. L’analogie est poussée plus loin, puisque, pour paraphraser Eddington, les règles du mouvement de chacune des pièces (roi, reine, pion, fou,…) pourraient être comparées aux champs de rayonnement émanant des particules – champs électrique ou gravitationnel.
Ainsi les pièces – dont la nature, inaccessible, est de toute façon inutile aux futurs « antiquaires » pour comprendre le jeu – sont les entités auxquelles les théories font appel, et les règles – nécessaires en revanche et seules accessibles – sont les lois physiques. Eddington prend en fait une posture proche de ce que l'on qualifierait aujourd'hui de
réalisme structural, selon lequel le progrès continu des théories scientifiques vers une description vraie du monde s'effectue à travers une accumulation de
structure, de
forme des relations mathématiques qu'elles postulent, et non de contenu, d'entités. Il est à cet égard fortement influencé par la théorie de la relativité, à l'instar d'Ernst Cassirer qui, peu après dans un ouvrage au titre éloquent (
Substance and Function)
(11), montrera comment elle opère le passage d'une physique « substantialiste », basée sur la constance des choses, à une physique « de principes » basée sur des relations universelles :
La théorie de la relativité ramène tout, en physique, à des relations; autrement dit, c’est la structure, non la substance, qui compte.
On peut y voir une référence à la covariance
(12) des équations postulée par le principe de relativité, mais aussi à la géométrisation de la physique (avec le recours massif aux tenseurs, cf. plus bas) en relativité générale, démarche qu'il va pousser en quelque sorte jusqu’au bout. À propos du tenseur d'Einstein, il écrit encore :
L’expression Gμν est donc d’une forme définie, mais son contenu est indéterminé. C’est par sa forme seule qu’elle doit rendre compte de toutes les propriétés physiques de la matière ; jamais l’investigation physique ne pourra pénétrer au-dessous de la forme.
La conception qu'a Eddington des mathématiques, en tant que science purement formelle, sans contenu, « vide » en somme, va dans ce sens [cf. l’étonnant prologue de l'ouvrage : What is Geometry?] :
The fact that he has to deal with entities of unknown nature presents no difficulty to the mathematician. As the mathematician in the Prologue explained, he is never so happy as when he does not know what he is talking about […] The pure mathematician never “deviates into sense”.
C'est pourquoi cette connaissance structurale, qui ne dit rien sur le monde, sera pour lui insatisfaisante, et appellera autre chose :
And yet, in regard to the nature of things, this knowledge is only an empty shell – a form of symbols. It is knowledge of structural form, and not knowledge of content.
L'objectivité comme géométrie dépersonnalisée
Toujours dans la continuité du principe de relativité affirmant l'invariance des lois physiques (indépendamment des mouvements des différents référentiels), Eddington livre une définition classique de l'objectivité, traditionnellement considérée comme étant ce qui ne dépend pas d'un point de vue particulier, mais commun à tous les observateurs. Au niveau formel, il est fortement influencé par l'outillage tensoriel auquel la théorie de la relativité a massivement recours, qui d'une part assure la covariance des équations (toute loi physique devant s'écrire comme l'égalité de grandeurs de même nature : scalaires, vecteurs ou tenseurs), d'autre part constitue un facteur d'unification de la physique (des grandeurs n'ayant pas de relation en physique classique étant réunies en relativité, comme l'espace et le temps dans les quadrivecteurs par exemple).
Ainsi, il définit la réalité comme « la synthèse de tous les aspects physiques possibles de la nature », prenant l'exemple de la dualité ondes/corpuscules de la lumière, ou, plus prosaïquement, d'un penny que l'on regarde sur la tranche ou sur l'une ou l'autre face. Mais il faut aller plus loin :
La réalité n’est obtenue que lorsqu’on fait entrer dans la combinaison tous les points de vue imaginables.
Pour cela, il faut opérer la synthèse de tous les points de vue « impersonnels » possibles : non seulement ceux des observateurs en mouvement uniforme (relativité restreinte), puis quelconque (générale), mais aussi ceux de « taille variable
(13) ». Après quoi, le recours à
une diversité de points de vue plus personnels serait peut-être nécessaire pour parvenir à l’objectivité suprême,
même si la question sort du cadre de « l’Univers réel de la physique ». S'arrêter en chemin, exclure des observateurs potentiels, consisterait alors à sombrer dans le solipsisme
(14):
Qu’elle soit soutenable ou non cette hypothèse que ce que nul n’observe n’existe pas, la science la repousse fermement.
Le mouvement de géométrisation croissante opéré par la théorie de la relativité puis par la géométrie encore plus générale de Weyl permet ainsi de tendre vers cette réalité impersonnelle, mathématisée au maximum, indépendante non seulement des types d'observateurs (domaine de la physique) mais aussi de leur existence même (domaine de la conscience) – à partir de laquelle la conscience humaine va constituer, presque « choisir » une réalité physique comme nous allons le voir
(15). L'interprétation qu'Eddington fait des équations d'Einstein en constitue l'exemple le plus flagrant.
Figure 5 : Le mathématicien allemand Hermann Weyl (1885-1955), et sa signature (photographie Wikicommons, source ETH-Bibliothek Zürich, Bildarchiv)
L'« inversion » des équations d'Einstein : la géométrie matérialisée
Attardons-nous ici sur un passage particulièrement intéressant du chapitre, à savoir l'interprétation extrême, « unilatérale », que fait Eddington des équations d'Einstein – il est semble-t-il le premier à la faire. C’est le point d'orgue de l'ouvrage, fondateur de son épistémologie.
Il faut rappeler ici l'influence de facteurs « formels » déjà évoqués : la géométrisation croissante de la théorie (en particulier l'équivalence entre champ gravitationnel et champ d'accélération – ce dernier, contrairement à la vitesse, ne nécessite pas de matière environnante pour être défini), ainsi que l'importance « intrinsèque » des tenseurs (la nullité d'un tenseur ou l'égalité avec un autre est une propriété intrinsèque, indépendante du système de référence).
Eddington commence par présenter, selon ses propres termes, la vision « classique », machienne, des équations, même si pour lui la nullité du tenseur d'Einstein en l'absence de matière constitue déjà une sorte de prescription sur la manière dont doivent s'arranger les « évènements » du monde. L'irruption de la matière « perturbe » ces relations naturelles, conformément à l'interprétation initiale d'Einstein.
Ainsi nous avons trouvé deux formules absolues qui semblent pleinement confirmées par l’observation, à savoir : dans un espace vide, Gμν = 0 dans un espace contenant de la matière, Gμν = Kμν où Kμν renferme certaines grandeurs physiques qui nous sont des plus familières : la densité et l’état du mouvement de la matière dans la région considérée.
Mais très vite, de manière assez brutale, il renverse l'interprétation des équations :
Nous avons décidé que dans un espace vide G
μν s’annulerait
(16) […] À défaut d’une autre interprétation nous dirons que cette égalité [G
μν =0] signifie que là où elle est vérifiée, il y a le vide ; ainsi, dire que G
μν n’est pas nul c’est caractériser un espace qui n’est pas vide.
Il est intéressant de voir (sans entrer dans le détail car cela nous emmènerait trop loin) comment Eddington combine à sa conception géométrique « prioritaire » une certaine physique des sensations :
Les deux équations [concernant Gμν ci-dessus] ne sont par suite que de simples définitions – définitions des impressions que nous avons de certains états de l’Univers [...] Quand nous percevons que telle région de l’Univers est vide, c’est simplement que nos sens reconnaissent que cette région n’a pas une courbure d’un degré supérieur au premier. Si au contraire nous avons la sensation que la région contient de la matière, c’est que nous y reconnaissons une courbure intrinsèque de l’Univers [...]
À partir de sa conception géométrique impersonnelle (la géométrie la plus générale de Weyl évoquée plus haut), il montre ainsi comment c'est nous, en tant qu'humains à la recherche de « permanence », qui voyons de la matière là où il n'y a que courbure
(17), ce qui l'amène à asséner ce verdict incroyable :
We need not regard matter as a foreign entity causing a disturbance in the gravitational field; the disturbance is matter […] This view, that matter is a symptom and not a cause, seems so natural that it is surprising that it should be obscured in the usual presentation of the theory.
Alors Eddington, prenant le contre-pied de l'opérationnalisme
(18) d'Einstein qui bâtit sa théorie (de la relativité restreinte) avec des mesures de distance et de temps, voit dans l'introduction trop hâtive de règles et d'horloges une « inversion logique » dans laquelle les quantités physiques de l'équation sont déjà bien définies, ce qui masque leur nécessaire égalité :
The result of this logical inversion is that by the time the equation Gμν= Kμν is encountered, both sides of the equation are well-defined quantities. Their necessary identity is overlooked, and the equation is regarded as a new law of nature. This is the fault of introducing the scale and clock prematurely. Four our part we prefer first to define what matter is in terms of the elementary concepts of the theory ; then we can introduce any kind of scientific apparatus ; and finally determine what property of the world that apparatus will measure.
Eddington prend ainsi clairement parti du côté de l'a priori : les équations d'Einstein sont indépendantes de l'expérience, nécessaires et universelles. Le champ gravitationnel est ainsi l'expression d'un état du monde, qui se manifeste également dans la géométrie naturelle déterminée par des instruments de mesure. Ce n'est pas la physique qui est géométrisée, mais elle est au contraire littéralement dérivée de la géométrie
(19) : la géométrie est rendue physique, « matérialisée ».
Historiquement, Eddington prendra ainsi le parti de De Sitter contre Einstein dans l'interprétation cosmologique des équations : tandis que le second affirmera la nécessité de masses pour leur trouver une solution, le premier ne voudra pas faire dépendre la structure cosmique de l'Univers de facteurs physiques contingents, et affirmera la possibilité de trouver une solution sans introduire de masses, ce qui l'amènera à un univers fermé et non borné (sphérique ou cylindrique).
@@@@@@@
Il est par ailleurs intéressant d'évoquer les analogies entre Eddington et un autre mathématicien «hétérodoxe» de son temps, Alfred North Whitehead (1861-1947), qui livrera
(20) également une interprétation « alternative » de la théorie de la relativité, selon laquelle la gravité n'est pas assimilable à la courbure de l'espace temps, mais à une interaction physique (un champ) sur fond d'espace-temps de Minkowski. Il sera en cela guidé par ce qu'il appellera le «sens commun» (non pas le «bon sens» des opinions partagées, mais l'intuition basique de la réalité partagée également par tous, une sorte de sixième sens qui intègre tous les autres), que les théories scientifiques n'ont selon lui pas le droit d’enfreindre, car alors les physiciens sont en contradiction en théorie avec ce qu'ils présupposent en pratique. C'est ainsi que Whitehead conserve la structure a priori de la relativité restreinte, que l'on présuppose inévitablement lorsqu'on effectue des mesures (qui nécessitent le concept de congruence, donc l'uniformité de l'espace-temps)
(21), et qui lui permettra de rompre la circularité d'une lecture « machienne » des équations d'Einstein.
Figure 6 : Le philosophe et mathématicien britannique Alfred North Whitehead (1861-1947) (en page de garde d’un ouvrage de 1941 d’édition de ses œuvres par Paul Arthur Schilpp, catalogue en ligne de la bibliothèque de McMaster University, Hamilton, Ontario, CA).
Ainsi, les deux interprétations alternatives d'Eddington et de Whitehead de la relativité générale apparaissent en quelque sorte comme symétriques : partant de leur rejet commun du point de vue machien (de la matière qui détermine la métrique), elles s'opposent quant à leur interprétation des équations d'Einstein (tandis que Whitehead rejette la courbure de l'espace-temps, pour Eddington c'est elle qui définit tout), comme le font plus généralement leurs conceptions du rapport entre science objective et perceptions subjectives (tandis que Whitehead voudra ancrer la première dans la pratique, Eddington soulignera le fossé qui les sépare, que seule la conscience permet de franchir).
L'idéalisme eddingtonien
Nous voici donc, après cet aperçu de l'épistémologie d'Eddington, en mesure de comprendre « (...) why the world must of necessity be as we have described it ». En effet :
We see now that the choice of a permanent substance for the world of perception necessarily carries with it the law of gravitation, all the laws of mechanics, and the introduction of the ordinary space and time of experience. Our whole theory has really been a discussion of the most general way in which permanent substance can be built up out of relations; and it is the mind which, by insisting on regarding only the things that are permanent, has actually imposed these laws on an indifferent world.
Eddington considère donc les lois physiques comme une sorte de spécialisation, de restriction effectuée par notre esprit en quête de permanence parmi toutes les géométries formellement possibles (dont celle de Weyl constitue l'exemple le plus général), impersonnelles et « objectivées » au maximum. Ainsi s'énonce l'idéalisme transcendantal
(22) d'Eddington, qui rappelle directement celui de Kant, pour qui « notre connaissance ne doit pas se conformer aux objets », mais « ce sont les objets qui doivent se conformer à notre connaissance ». La conception eddingtonienne des lois physiques,
[...] the conclusion is that the whole of those laws of nature which have been woven into a unified scheme - mechanics, gravitation, electrodynamics and optics - have their origin, not in any special mechanism of nature, but in the workings of the mind.
[...] And, moreover, we have found that where science has progressed the farthest, the mind has but regained from nature that which the mind has put into nature.
fait ainsi directement écho à la conception transcendantale kantienne (23) :
L'ordre et la régularité dans les phénomènes, ce que nous appelons nature, est donc notre œuvre à nous, et nous ne l'y trouverions pas, si elle n'y avait pas été mise d'abord par nous, ou par la nature de notre esprit
(24).
Ainsi, si la connaissance scientifique ne fournit qu'une connaissance formelle et structurelle, faites de symboles, simple « coquille vide » comme nous l'avons vu, c'est la conscience qui constituera, par la suite, le matériau de base de l'épistémologie eddingtonienne, annonçant son idéalisme croissant :
All through the physical world runs that unknown content, which must surely be the stuff of our consciousness.
C'est la conscience qui, en « choisissant » le monde de la physique tel que nous le connaissons parmi toutes les géométries a priori possibles, va en quelque sorte l’« actualiser » (au sens anglo-saxon), lui donner sa réalité
(25).
@@@@@@@
On voit donc, pour conclure, quelle réponse l'épistémologie eddingtonienne apporte à la question canonique du rapport entre les mathématiques et la réalité physique : commencer par construire le formalisme mathématique, logiquement prioritaire et objectivement supérieur (car élaboré « du point de vue de personne en particulier »), puis l'identifier aux caractéristiques physiques du monde réel (défini comme « la synthèse de tous les points de vue possibles »), construites par la suite (comme la matière) par l'intermédiaire de la conscience.
Si, historiquement, la théorie de Weyl sera expérimentalement mise en défaut par Einstein
(26), Eddington la généralisera davantage encore
(27), en séparant encore plus la partie géométrique de son interprétation physique, au point presque de s’affranchir de toute question de réalisme scientifique ou de « vérité ». Si sa démarche de prolonger la philosophie de la relativité générale est compréhensible, il la portera à un tel point (jusqu'à éliminer tout observateur) que seul un idéalisme radical lui fournira une porte de sortie, au prix de retomber par la suite – ironie du sort, en recherchant l'objectivité la plus impersonnelle – dans un point de vue subjectif.
Si elle peut sembler un exemple extrême d'élaboration théorique, que l'on pourrait croire à l'opposé des principes de la recherche en science physique, nécessairement reliée à l'expérimentation, l'épistémologie d'Eddington trouve un écho inattendu dans les recherches contemporaines de « grande unification » en gravité quantique, dont la géométrisation sophistiquée (de plus en plus générale) et le caractère spéculatif (en raison de l'inaccessibilité expérimentale des gammes d'énergie requises) emprunte également une telle démarche aprioriste, dont nombre de physiciens théoriciens se réclament d'ailleurs.
Février 2012
(1) Arthur Eddington, Fundamental Theory, Cambridge : at the University Press, 1946.
(2) Qui consiste, conformément à la doctrine attribuée au mathématicien Pythagore, à faire du nombre la loi suprême de toute chose, à considérer que l'Univers est d'essence mathématique.
(3) L'idéalisme est un terme équivoque qui revêt des sens différents selon les systèmes philosophiques considérés. De manière très générale, il indique une conception philosophique qui privilégie la pensée à la réalité, mais, de Platon (idéalisme platonicien) à Hegel (idéalisme dialectique), en passant par Descartes (idéalisme méthodique), Berkeley (idéalisme absolu) ou Kant (idéalisme transcendantal), sa signification varie grandement. Nous aurons l'occasion d'y revenir en analysant celui d'Eddington (nous nous excusons par avance pour le recours, réduit autant que possible, à certains « -ismes », dont la philosophie est friande mais qui sont parfois nécessaires pour manipuler ses concepts).
(4) La revue proposée de ce chapitre n'est aucunement exhaustive : en particulier nous ne traitons pas des références à la “géométrie purement infinitésimale” de Weyl (abordée au chapitre précédent Electricity and Gravitation), ni à la théorie quantique naissante (dont la conception épistémologique qu'en a Eddington est totalement opposée à celle qu’il a de la relativité), qui nous emmèneraient trop loin, préférant nous focaliser sur la relativité, qui constitue le cœur de l'ouvrage et, d’une certaine manière, la spécialité d’Eddington.
(5) Auxquels Einstein rajoute les hypothèses d'homogénéité et d'isotropie de l'espace (absence de point ou de direction privilégiés de l'espace) et d'homogénéité du temps.
(6) Résumée dans sa célèbre tirade de 1908 [Minkowski, Raum und Zeit, Gesammelte Abhandlungen, Chelsea N.Y., 1967, p. 431] : « Désormais, l'espace en soi et le temps en soi seront réduits à de simples ombres et seule une union des deux conservera une existence autonome ».
(7) Un tenseur est un objet mathématique qui généralise la notion de scalaire (assimilable à un tenseur de rang 0) et de vecteur (tenseur de rang 1). Dans un espace à 3 dimensions, suite à un changement d'axes (une rotation) : un scalaire (un nombre : temps, masse, ...) est invariant ; un vecteur (un ensemble de trois nombres : impulsion, force, ...) a ses trois composantes qui se transforment comme les trois composantes du vecteur position ; un tenseur de rang 2 (un ensemble de neuf nombres : tenseur des contraintes, des déformations...) a ses neuf composantes qui se transforment comme les produits deux à deux des composantes de deux vecteurs. Pour plus de détails, cf. le texte de Feynman et l'analyse de B. Diu sur BibNum.
(8) Du nom d'Ernst Mach (1838-1916), physicien et philosophe autrichien à l'origine du principe dont s'est inspiré Einstein dans l'élaboration de la relativité générale, et dont la formulation vague – que l'on peut résumer au fait que la matière “engendre” l'espace qui est autour d'elle – admet une multitude d'interprétations.
(9) C'est pourquoi l'on dit qu'en relativité générale la « structure de fond » que représente l'espace-temps en relativité restreinte (distinct des objets qu'il contient et non influencé par eux) disparaît, l'espace-temps devenant lui-même un objet physique, une structure dynamique influencée par la matière (et c'est la structure différentiable sous-jacente qui joue alors le rôle de « structure de fond »).
(10) Cette citation de Shakespeare est remplacée dans la traduction française par une citation d’Henri Poincaré (La Valeur de la Science, 1905) : « Cette harmonie que l’intelligence humaine croit découvrir dans la nature, existe-t-elle en dehors de cette intelligence ? Non, sans doute, une réalité complètement indépendante de l’esprit qui la conçoit, la voit ou la sent, c’est une impossibilité. Un monde si extérieur que cela, si même il existait, nous serait à jamais inaccessible. Mais ce que nous appelons la réalité objective, c’est, en dernière analyse, ce qui est commun à plusieurs êtres pensants, et pourrait être commun à tous ; cette partie commune, nous le verrons, ce ne peut être que l’harmonie exprimée par des lois mathématiques ».
(11) Ernst Cassirer, Substanzbegriff und Funktionsbegriff: Untersuchungen über die Grundfragen der Erkenntniskritik, Berlin: Bruno Cassirer, 1910. Trad. Substance and Function, Chicago: Open Court, 1923 (p. 197).
(12) Une équation est covariante (on dit aussi invariante) si elle garde la même forme dans tous les référentiels.
(13) Cf. le ch. 11, il s’agit d’une référence à la « géométrie purement infinitésimale » d'H. Weyl, généralisation de la géométrie de la relativité générale, qui sort du cadre de cet article, et qui remet en cause la comparaison à distance des longueurs autorisée dans la géométrie riemannienne de la relativité générale, au moyen des connexions (outils permettant un transport parallèle des vecteurs), et qui constituera le cadre formel de sa tentative d'unification entre gravitation et électromagnétisme.
(14) Doctrine extrême selon laquelle le monde n'existe que pour celui qui le pense.
(15) Weyl, une fois construite sa « géométrie du monde » mathématique et impersonnelle, retrouve, par une identification purement formelle, les équations de Maxwell, puis l’identifie au monde physique par un choix de « jauge » (définissant le tenseur métrique à un facteur de conformité près) particulier [Weyl, Raum, Zeit, Materie, Berlin: Julius Springer, 1918].
(16) Il s'agit ici, avec les notations usuelles d'aujourd'hui, du tenseur de Ricci noté Rμν (et non du tenseur d'Einstein), qui s'annule également en l'absence de matière.
(17) Du fait de la divergence identiquement nulle du tenseur d’Einstein, Eddington, par analogie avec les relations de conservation en mécanique des fluides, y voit la condition caractéristique de la permanence, et le candidat idéal pour l’identifier au tenseur énergie-impulsion, dont la divergence est également nulle suite à la conservation de l’énergie [Eddington, The Mathematical Theory of Relativity, Cambridge: at the University Press, 1923]. La distinction entre matière et courbure relève alors de l’esprit.
(18) L’opérationnalisme consiste à définir les quantités physiques par la manière dont elles sont mesurées.
(19) Ce qu'il résume dans la première phrase du chapitre précédent “Electricity and Gravitation” : “The relativity theory deduces from geometrical principles the existence of gravitation and the laws of mechanics of matter. Mechanics is derived from geometry” [p. 167].
(20) The Principle of Relativity with Applications to Physical Science. Cambridge Uni. Press, 1922.
(21) Par exemple Whitehead soulignera la contradiction consistant à utiliser les photographies prises par Eddington de l’éclipse pour valider la relativité générale, donc ce faisant à présupposer en pratique l’uniformité de l’espace-temps (pour permettre une comparaison des mesures avec et sans Soleil) tout en la niant en théorie.
(22) En deux mots, “[Kant] appelle idéalisme transcendantal de tous les phénomènes la doctrine d'après laquelle nous les considérons sans exception comme de simples représentations, non des choses en soi. ”, c'est-à-dire que la connaissance scientifique est considérée uniquement en relation avec les conditions subjectives de la représentation humaine.
(23) Ainsi qu’à celle de Whitehead dans The Concept of Nature : “Cartesian reason is entirely based on the implicit assumption that the mind can only know that which it has itself produced and retains in some sense within itself”.
(24) Kant (Immanuel), Kritik der reinen Vernunft, 1787. Trad. J. Tissot, Critique de la raison pure, Paris : librairie philosophique de Ladrange, 1845 (citation p. 148).
(25) Ce qui sera plus tard dénommé, de façon explicite, le subjectivisme sélectif d’Eddington.
(26) Qui lui fera remarquer qu’elle contredit la constance des spectres atomiques.
(27) Qualitativement, tandis que la géométrie de Weyl autorise la comparaison des magnitudes de vecteurs de directions différentes au même point, celle d’Eddington requiert en plus qu’elles soient identiques [Eddington, The Mathematical Theory of Relativity, 1923, op. cit.]. La géométrie de Weyl, tout comme celle la géométrie riemannienne, en constituent alors un cas particulier.
se fait généralement de droite à gauche (lecture « machienne ») : la matière déforme l'espace-temps, i.e. la métrique (le « contenant », représenté par le tenseur de courbure G) est déterminée par la distribution de matière (le « contenu », représenté par le tenseur énergie-impulsion T). Eddington en fait une lecture inverse : la physique est littéralement dérivée de la géométrie. Ce n’est pas la matière qui créée une perturbation, mais la matière qui est intriquée à la géométrie : la géométrie est rendue physique, « matérialisée ».Eddington indique : « La matière est un symptôme et non une cause ». C’est une vue idéaliste poussée à l’extrême qu’aura Eddington dans sa carrière de philosophe, et de physicien : elle le marginalisera progressivement dans la communauté scientifique.
Une sélection de livre sur la relativité, faite sur le site science.gouv (voir plus spécifiquement les livres de T. Damour, Cherche-Midi et de J. Eisenstaedt, CNRS Éditions).
Butterfield J. & Earman J. ed., Philosophy of Physics, Elsevier, 2007 (articles Classical Relativity Theory par D. Malament et Symmetries and Invariances in Classical Physics par K. Brading et E. Castellani).
