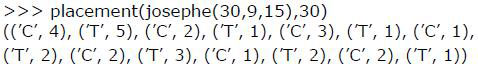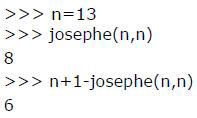Textes fondateurs de la science
analysés par les scientifiques d´aujourd´hui
analysés par les scientifiques d´aujourd´hui
Autour du problème de Josèphe
- INFORMATION
- ACTUALITÉ
- ANALYSE
- EN SAVOIR PLUS
- À TÉLÉCHARGER
Autour du problème de Josèphe
Auteur : Flavius Josèphe (ca. 37-100) - Historien judéen
Auteur de l'analyse :
Laurent Signac - Laboratoire d'Informatique et d'Automatique pour les Systèmes (LIAS - Université de Poitiers) & École Nationale Supérieure d'Ingénieurs de Poitiers (ENSIP).
Publication :
Histoire des Juifs, écrite par Flavius Josèphe (75-79 ap. J.-C.), traduite par M. Arnauld d’Andilly, Tome Cinquième, à Paris, chez Gissey, avec approbations et privilège du Roy, 1744 ; extrait Livre III, chapitre XXVI, p. 427-430.
Année de publication :
79
Nombre de Pages :
n.s.
Résumé :
Une enquête sur le problème dit de décimation, attribué à Flavius Josèphe, et la façon dont il est repris par divers mathématiciens à travers les âges.
Source de la numérisation :
Par l’auteur (Laurent Signac)
Mise en ligne :
septembre 2012
Décimer… C’est sélectionner une personne sur dix – mais comme l’écrit avec humour l’auteur, « le terme sera à présent employé même si on sélectionne une personne sur n avec n différent de 10 ». Décimer… C’est aussi prendre un soldat sur dix et le tuer – ancienne punition militaire romaine. Comment être placé dans une file ou un cercle (qui change à chaque disparition) pour être le dernier, épargné ? Une récréation mathématique qui ne l’a pas toujours été : ni récréative (il fallait sauver sa peau) ni théorique (id.) ! L’auteur nous propose ici une passionnante enquête sur la façon dont ce problème a été traduit de Josèphe, ou présenté et traité à travers les âges par divers auteurs, mathématiciens ou non : un certain Hégésippe ou « pseudo-Hégésippe » (IVe siècle), Bachet de Méziriac (1581-1638), pionnier des « récréations mathématiques », Nicolas Chuquet (ca. 1445/1455-1487), Niccolò Tartaglia (1499-1557), avec ses turcs et ses chrétiens sur un bateau, Cardan (1501-1576), et plus près de nous Édouard Lucas (1842-1891) et Ernest Dudeney (1857-1890) avec son jeu du chat et des souris. On trouvera ci-dessous une photo de l’auteur plongé dans ces diverses références.
To decimate… is to select one person in ten – but as the author playfully points out, “the term will be used here even if a person is selected from a group of n people, where n is other than 10”. To decimate… is also to execute one soldier in ten – a military punishment in ancient Rome. Where should one position oneself in a line or circle (which changes with each execution) to be the last person standing – and therefore spared? This example of recreational maths was not always so: it was neither recreational (one had to save one’s skin) nor theoretical (id.)! The author offers a fascinating inquiry into how the Josephus problem has been translated, presented or treated throughout the ages by various authors, some mathematicians and some not: a certain Hegesippus or “pseudo-Hegesippus” (4th c.); Bachet de Méziriac (1581–1638), a pioneer of “mathematical recreations”; Nicolas Chuquet (ca. 1445/1455–1487); Niccolò Tartaglia (1499–1557) with his Turks and Christians aboard a boat; Cardano (1501–1576); and, closer to our time, Édouard Lucas (1842-1891), and Ernest Dudeney (1857–1890) with his cat-and-mice game. Below, a photo of the author – surrounded by his many books on the Josephus problem.
Laurent Signac est chercheur au Laboratoire d'Informatique et d'Automatique pour les Systèmes (LIAS, EA 1219, université de Poitiers), et Maître de conférence en Informatique à l'École Nationale Supérieure d'Ingénieurs de Poitiers (ENSIP).
Autour du problème de Josèphe
Laurent Signac - Laboratoire d'Informatique et d'Automatique pour les Systèmes (LIAS - Université de Poitiers) & École Nationale Supérieure d'Ingénieurs de Poitiers (ENSIP).
S’il est un petit problème amusant duquel on décroche difficilement, c’est bien le problème de Josèphe. Il s’agit d’un divertissement arithmétique relativement connu, qui revient régulièrement dans la littérature de vulgarisation mathématique ou même informatique. Il appartient à la famille des problèmes de décimation. L’origine un peu sanglante (1) de ce mot prend d’ailleurs tout son sens dans le cas du problème de Josèphe.
L’énoncé en est fort simple : 41 personnes sont disposées en cercle et une origine est choisie (figure 1a).
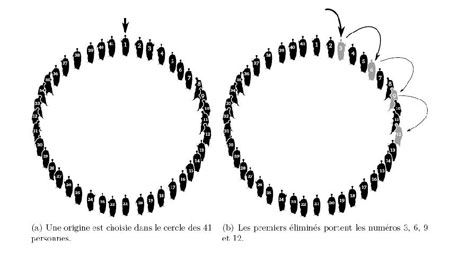
Figure 1 : Procédé de décimation.
En commençant sur cette personne, on compte : 1, 2, et la troisième personne est supprimée (2). Puis on continue : 1, 2 et on supprime la troisième personne. Les premières personnes qui sortent du cercle portent donc les numéros : 3, 6, 9, 12... comme indiqué figure 1b. Le même procédé est répété tout autour du cercle (figure 2a). Attention, après un tour complet, il y a des places vacantes, et ça se complique. Voici les numéros des malheureux perdants dans l’ordre de leur élimination (figure 2b) :
3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 1, 5, 10, 14, 19, 23, 28...
La question est : Où se placer dans le cercle d’origine pour être le dernier survivant ? Autrement dit, quel sera le dernier numéro restant dans le cercle ?
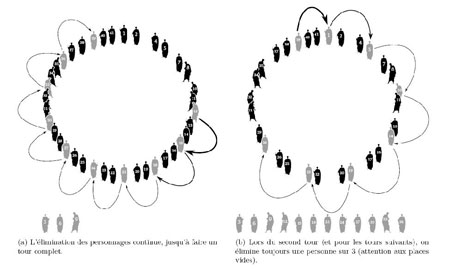
Figure 2 : Poursuite du procédé de décimation.
I - Guerre des Juifs
Le problème précédent est généralement rattaché à l’histoire de Flavius Josèphe, « historien » du Ier siècle, qui a raconté cet épisode de sa vie (il faisait partie des 41 personnes) dans son ouvrage : Guerre des Juifs. Chaque personne désignée par le procédé qui vient d’être détaillé était alors tuée par la personne désignée après elle. Flavius Josèphe a donc manifestement su résoudre le problème.
Mathématiquement, dans le cas général (pour un nombre de personnes quelconque, et un comptage qui n’est pas forcément de 3 en 3), la solution ne peut pas être obtenue par un calcul direct (3). C’est d’ailleurs probablement l’absence de solution directe générale qui a fait résister le problème au temps et le rend intéressant aujourd’hui encore. En outre, il est assez facile, quelles que soient les données de départ cette fois-ci, de simuler la phase de décimation avec un ordinateur, pour finalement obtenir comme réponse le numéro du dernier survivant dans le cercle et plus généralement l’ordre d’élimination : un tel programme est même assez amusant à faire et les programmeurs potentiels sont encouragés à ne pas consulter la solution proposée à la fin de cet article avant d’avoir trouvé par eux-mêmes.
Enfin, la dimension historique ne peut qu’aiguiser la curiosité et il est difficile de ne pas être tenté de rechercher des détails supplémentaires sur la façon dont le héros d’origine s’est tiré d’affaire en ces temps reculés. On lit en effet dans les présentations contemporaines que l’histoire se serait déroulée lors du siège de Jotapata par Vespasien (4), en 67, alors que les 41 personnes (Flavius Josèphe, alors gouverneur de la cité, et 40 soldats) étaient acculées dans une caverne, refusant de se rendre. Le contexte historique nous permet de mesurer plus facilement la prouesse de Flavius Josèphe : sa situation, terré dans une caverne assiégée, sachant que la moindre erreur de calcul lui coûtera la vie, n’est pas particulièrement propice au repos de l’esprit nécessaire à la résolution du problème de tête pour un cercle de 41 personnes.
La tentation est donc grande de rechercher des précisions non plus dans un texte de divertissements mathématiques, mais plutôt dans une des nombreuses traductions issues de manière plus ou moins directe du texte de Flavius Josèphe. La première version qui s’est présentée est disponible sur Gallica. Il s’agit des Œuvres complètes de Flavius Josèphe, publiées à partir de 1911 sous la direction de Théodore Reinach, et traduites du grec par René Harmand. Le passage est situé dans le Livre III de la Guerre des Juifs, chapitre VIII (5) :
Voici le passage en question :
Puisque, dit-il, nous sommes résolus à mourir, remettons-nous en au sort pour décider l’ordre où nous devons nous entretuer : le premier que le hasard désignera tombera sous le coup du suivant et ainsi le sort marquera successivement les victimes et les meurtriers, nous dispensant d’attenter à notre vie de nos propres mains [...] À la fin, soit que le hasard, soit que la Providence divine l’ait ainsi voulu, Josèphe resta seul avec un autre : alors, également peu soucieux de soumettre sa vie au verdict du sort ou, s’il restait le dernier, de souiller sa main du sang d’un compatriote, il sut persuader à cet homme d’accepter lui aussi la vie sauve sous la foi du serment.
Algorithmiquement parlant, on reste un peu sur sa faim. Il est plus question de hasard et de Providence divine que de calculateur prodige. Excepté le nombre de personnes, qui est effectivement 41 dans ce texte (on le trouve dans les pages qui précèdent), il n’est pas fait mention d’un cercle, ni d’un quelconque moyen algorithmique de désigner les personnes à exclure du cercle en comptant de 3 en 3.
Le traducteur René Harmand émet d’ailleurs dans une note de bas de page quelques réserves sur l’authenticité de l’histoire contée par Flavius Josèphe, tout en admettant qu’elle a, depuis la Renaissance, donné naissance à un « piquant sujet de problème ».
Enfin, le texte sous-entend qu’au moment où il ne reste plus que Josèphe et son compagnon comme survivants, le premier propose d’arrêter le processus de décimation craignant de mourir ou de devoir donner la mort. Or, à ce moment, Josèphe sait nécessairement dans quelle situation parmi les deux possibles il se trouve. Si le dernier meurtre a été commis par lui (ce qui est peu probable, puisqu’il se soucie alors de ne pas devenir un meurtrier), c’est à son tour de mourir. Si en revanche il a été commis par son compagnon, c’est à Josèphe de prendre le rôle d’assassin et il a l’assurance d’être le seul survivant. Comme il se trouve très probablement dans la seconde situation, il s’en suit que Josèphe a réellement épargné un compagnon, probablement pour ne pas devenir lui-même un meurtrier. Cette imprécision enlève encore un peu à la crédibilité de l’histoire.
Cependant, la traduction que nous avons utilisée a bien sûr été réalisée à partir de textes qui ne sont pas les textes originaux (6) (a priori perdus). Il est tout à fait concevable qu’il existe plusieurs versions de ce passage, contenant plus ou moins de détails sur le procédé et l’astuce de Flavius. Voici par exemple le même passage, situé dans le volume 5 de l’Histoire des Juifs, livre III, chapitre XLIV. Cette traduction du grec, due à Arnauld d’Andilly, a été publiée de nombreuses fois depuis le XVIIe siècle (ci-dessous, l’édition de 1744) :
Nous pouvons y lire :
Puisque vous êtes résolus de mourir, jetons le sort pour voir qui sera celui qui devra être tué le premier par celui qui le suivra : & continuons toujours d’en user de la même sorte [...] Ainsi le sort fut jeté : & celui sur qui il tombait, tendit la gorge à celui qui le devait tuer : ce qui continua jusqu’à ce qu’il ne resta plus que Joseph & un autre, soit que cela arrivât par hasard, ou par une conduite particulière de Dieu. Alors Joseph voyant que s’il eût encore jeté le sort, ou il lui aurait fallu tremper ses mains dans le sang d’un de ses amis, il lui persuada de vivre, après lui avoir donné parole de le sauver.
Même s’il apparaît un peu plus clairement ici que Josèphe a épargné l’avant-dernier survivant, on reste là-encore sur sa faim en ce qui concerne le procédé précis employé pour la décimation : pas de cercle, c’est le sort qui désigne les victimes, et Josèphe s’en tire sans calcul.
@@@@@@@
Signalons enfin une troisième version, appelée Prise de Jérusalemn, écrite en slavon (russe ancien) et tirée de différents manuscrits des XVe et XVIe siècles contenant le texte entier ou des bribes mêlées à d’autres chroniques. Ces différents manuscrits pourraient provenir de traductions slavonnes plus anciennes (XIIe ou XIIIe siècle) de textes encore plus anciens et maintenant perdus. En effet, la version paléo-slave diffère sur plusieurs points des versions européennes que l’on connaît. Elle contient en particulier des détails sur la vie de Jésus ou de Jean le Baptiste. Savoir si ces détails ont été ajoutés par le traducteur slave ou s’il a utilisé pour sa traduction une version maintenant perdue qui contenait déjà ces détails reste de la spéculation. Il est possible qu’il y ait un peu des deux.
Une traduction en français du texte en vieux russe, réalisée par Pierre Pascal, a été publiée en deux tomes par l’Institut d’Études Slaves en 1934 et 1938, sous le nom La prise de Jérusalem de Josèphe le Juif. Le texte russe a été imprimé en regard du texte français. Plus tard, en 1965, la même traduction, mais sans le texte russe, a été publiée aux Éditions du Rocher.
Dans la version paléo-slave figure l’épisode de la caverne. Voici la traduction qui est donnée par P. Pascal :
Alors Josèphe, confiant son salut à la tutelle de Dieu, dit : «Puisque Dieu a voulu que nous mourions, tuons nous en comptant les chiffres : celui sur qui tombera la fin du compte recevra la mort du suivant». Ayant ainsi parlé, il compta les chiffres avec habileté et par là les trompa tous. Ils se tuèrent tous les uns les autres, sauf un. Josèphe, soucieux de ne pas souiller sa main du sang d’un compatriote, le supplia, et tous deux sortirent vivant.
Cette version est bien différente de celles que nous avons vues pour l’instant. S’il est toujours question de confier son salut à la tutelle de Dieu, la phase « il compta les chiffres avec habileté et par là les trompa tous» laisse peu de place à l’ambiguïté.
Voici une copie manuelle du texte slavon :
Le terme traduit par habileté en français (
) peut aussi être interprété comme sagesse, donnant un sens différent (proche de la résignation) à la phrase.
) peut aussi être interprété comme sagesse, donnant un sens différent (proche de la résignation) à la phrase.
La trace du Josèphe calculateur n’est pas inexistante, mais il manque les détails techniques sur le procédé de décimation. De plus, les possibilités d’investigations sur ce texte sont réduites. Aussi, plutôt que de rechercher de nouvelles traductions issues du récit de Josèphe, reprenons le problème dans l’autre sens et cherchons à savoir où les auteurs de divertissements mathématiques ont déniché leur idée de problème arithmétique. Peut-être trouverons-nous les références d’une version particulière de la Guerre des Juifs.
II - Récréations arithmétiques
Le problème étant presque « passé dans les mœurs », les ouvrages récents présentent le fameux passage de la caverne sans donner de source exacte. Il faut se tourner vers des auteurs spécialisés des XIXe et XXe siècles pour obtenir de nouvelles informations. Plus particulièrement, des problèmes identiques ou similaires se retrouvent (par exemple) chez Édouard Lucas, bien connu pour son jeu des tours de Hanoï, source inépuisable de tracasseries pour les étudiants en informatique, et Ernest Dudeney.
L’ouvrage en langue anglaise Amusements in mathematics d’Ernest Dudeney, publié en 1917, présente un problème similaire à celui de Josèphe, à base de chats et de souris. Il ne permet pas vraiment d’avancer dans la quête de la vérité sur la prouesse calculatoire de Flavius, mais propose une variante amusante.
L’ouvrage de Dudeney est mis à disposition par le projet Gutenberg (7). Voici une traduction en français du problème 232 accompagnée de la figure illustrant l’énoncé dans l’ouvrage original.
« Ne triche pas ! » dit la souris. « Tu connais les règles du jeu. » « Je connais les règles », dit le chat. « Je dois tourner tout autour du cercle, en restant dans le même sens que vous, et manger chaque fois la treizième souris, mais je dois garder la blanche comme gâterie finale. Treize est un nombre qui porte la poisse, mais je vais faire de mon mieux pour vous satisfaire. » « Dépêche-toi alors », hurla la souris. « Laissez-moi un peu de temps pour réfléchir », dit le chat, « je ne sais pas par laquelle d’entre vous commencer. Je dois faire le calcul. » Alors que le chat résolvait le casse-tête, il s’endormit et, le sort étant ainsi rompu, les souris rentrèrent chez elles saines et sauves. Par quelle souris le chat aurait-il dû commencer pour que la souris blanche fût la dernière mangée ?
C’est bien le même problème. Il donne l’impression d’être posé à l’envers mais passer d’une solution « à la Josèphe » (qui est le dernier ?) à une solution « à la chat » (par qui commencer pour terminer sur une position prédéterminée ?) est immédiat (8). Le problème du chat est amusant, mais ne fait malheureusement pas avancer sur l’origine du problème de Josèphe. De son côté, Édouard Lucas nous livre sa version dans l’Arithmétique amusante, publiée de manière posthume en 1895 (9). Après avoir exposé une autre variante que nous évoquerons plus loin, il donne des indices sur l’origine du problème de Josèphe :
Nous lisons que :
Bachet, dans la préface au lecteur de la seconde édition de ses Problèmes plaisants et délectables qui se font par les nombres, nous donne l’origine de ce curieux problème : « Hégésippus, au troisième Livre de la Guerre de Jerusalem, rapporte la mémorable histoire de Josèphe, [...] Josèphe les disposa de sorte, et choisit pour lui une si bonne place, que la tuerie étant continuée jusqu’à la fin, il se trouva seul en vie [...] »
Non seulement Lucas semble confirmer que la survie de Josèphe n’a pas été un fait du hasard, mais nous avons maintenant deux références supplémentaires :
- Claude Gaspard Bachet, sieur de Mériziac, un auteur du XVIIe siècle que l’on considère souvent comme étant le premier auteur français de divertissements mathématiques, - et surtout, une autre version de la Guerre de Juifs, intitulée Guerre de Jerusalem, écrite par un certain Hégésippus et dans laquelle on doit trouver que: Josèphe les disposa de sorte, et choisit pour lui une si bonne place...
@@@@@@@
Penchons-nous en premier lieu sur le texte de Bachet. La seconde édition des Problèmes plaisants et délectables datant de 1624 (la première a été publiée 12 ans plus tôt), est disponible sur Gallica (10) :
Nous lisons dans la préface :
Finalement, pour prouver encore que ce livre n’est point du tout inutile, & que la connaissance de ces Problèmes peut servir grandement en quelque occasion, je ne veux employer que le témoignage d’Hégésippus, au troisième livre de la prise de Jérusalem. Là il rapporte la mémorable histoire de Josèphe, ce fameux auteur qui nous a laissé par écrit la même guerre des Juifs [...] il fut contraint de se retirer dans une citerne (11)[...] alors sans doute c’était fait de sa vie, s’il n’eût eu l’esprit de se défaire de ces hommes furieux, par l’artifice de mon 23 Problème. Car feignant d’adhérer à leur volonté [...] [il les] persuada facilement [...] [qu’] il valait mieux se ranger par ordre en quelque façon, et commençant à compter par un bout, massacrer toujours le tantième (l’auteur n’exprime pas le quantième) jusqu’à ce qu’il n’en demeurât qu’un seul, lequel serait obligé de se tuer soi-même. [...] Josèphe les disposa de sorte, et choisit pour lui une si bonne place [...] il se trouva seul en vie.
Le problème 23 dont il est question, une variante avec des turcs et des chrétiens sur un bateau, est celui dont s’est inspiré Édouard Lucas. En voici le texte, issu de la même édition de 1624 :
L’objectif, pour le capitaine du bateau mentionné dans cette histoire, est de disposer 30 personnes (15 chrétiens et 15 turcs) de façon qu’en supprimant 15 d’entre elles en comptant de 9 en 9, les 15 restantes soient les chrétiens. Bachet propose un moyen mnémotechnique pour retenir les positions à donner aux turcs et aux chrétiens :
Mort tu ne falliras pas En me livrant le trépas
Chaque voyelle est affectée à un numéro (1 pour a, 2 pour e, 3 pour i, 4 pour o et 5 pour u) et la phrase donne donc la série de chiffres : 4, 5, 2, 1, 3, 1, 1, 2, 2, 3, 1, 2, 2, 1 qui indique que la disposition est : 4 chrétiens, 5 turcs, 2 chrétiens...
La disposition finale obtenue est donnée figure 3. De nombreuses autres phrases mnémotechniques, dans diverses langues (Lucas en donne une en latin, que nous retrouverons bientôt), existent pour ce problème que nous appellerons dans la suite la variante 15-15, où les chrétiens et les turcs sont parfois remplacés par des personnes habillées en blanc ou en noir, des pions de différentes couleurs, des enfants sages et des garnements...
Figure 3 : Variante 15-15 : en décimant 1 sur 9, les 15 premiers éliminés seront les personnages grisés. Les 5 premiers sont désignés par les flèches.
Bachet conclut son 23e problème en revenant sur celui de Josèphe :
Nous pouvons y lire :
Or comme j’ai touché en la préface de cette œuvre, c’est par cette invention que Josèphe sauva très subtilement dans Jotapata ainsi qu’on recueille évidemment des paroles d’Hégésippus touchant ce fait au 3 livre de la Guerre de Jerusalem. Et bien qu’il ne particularise pas assez cette action, toutefois par ce qu’il dit nous pouvons imaginer comme le tout se passa. Car ainsi qu’il raconte, il y eut 40 soldats qui se sauvèrent avec Josèphe dans le lac si bien qu’à conter ledit Josèphe ils étaient en tout 41. Partant, supposons qu’il ordonna que comptant de trois en trois, on tuerait toujours le troisième : il est certain que procédant de la sorte, tu trouveras en fin par la règle donnée en la démonstration qu’il faut que Josèphe se mit le trente-unième après celui par lequel on commençait à conter, au cas qu’il visait à demeurer en vie lui tout seul. Mais s’il voulut sauver un de ses compagnons, il le mit en sa seizième place, & s’il en voulut sauver encore un autre, il le mit en la trente-cinquième place.
Il semble, à la lecture de ce passage, que ce soit le choix de Bachet de compter de 3 en 3 (il précise dans la préface citée précédemment que la valeur du tantième n’est pas donnée par Hégésippus). Même si cette valeur n’est pas précisée dans la Guerre de Jerusalem, cet ouvrage devrait contenir, toujours d’après Bachet, le protocole d’élimination utilisé par Josèphe, certes peu détaillé, mais suffisant pour nous confirmer que Josèphe ne s’en est pas simplement remis à la Providence divine.
Notons au passage que, contrairement à une information qu’on rencontre parfois, pour autant que nous puissions en juger, Bachet ne s’est pas trompé sur le nombre de personnes (il y en a bien 41), ni sur la solution au problème (16 et 31). Ces valeurs sont tout aussi correctes dans la première édition de 1612.
L’ouvrage de Bachet a été réédité beaucoup plus tard, en 1874 (troisième édition), commenté et détaillé par A. Labosne. Une version ultérieure (la cinquième), publiée en 1884, est disponible sur le site du Conservatoire numérique des Arts et Métiers (12).
Dans cette cinquième édition, une note de Labosne, ajoutée dans la préface au lecteur, nous met en garde contre une mauvaise interprétation du texte de Josèphe dont le sort aurait été livré au hasard ou à la Providence. Néanmoins, Bachet insistant, comme Lucas, sur la version d’Hégésippus (13) : il semble naturel de se mettre en quête de cette version particulière qui n’a a priori pas de raison d’être moins véridique qu’une autre.
III - L’Hégésippe
Gallica propose plusieurs versions de L’Hégésippe, dont une belle édition manuscrite (14) du XIIIe siècle. Le passage se trouve au verso du feuillet 77 :
Une traduction, réalisée par I. Millet de Saint-Amour et publiée en 1556, est accessible par Google Books (15) :
Nous y lisons :
Compagnons, je serais d’opinion, si vous en êtes d’accord, que le sort soit juge de l’ordre que nous devons tenir à trouver la fin de nos vies [...] celui à qui premièrement le sort viendra sera tué par son suivant, et ainsi des autres consécutivement [...] Cette offre leur fut tant agréable qu’ils ne se doutèrent aucunement de ruse, quelle qu’elle fut, ainsi y donnèrent prompt consentement d’une voix : tellement que sans contradiction ils s’entretuaient les uns les autres, comme le sort leur tombait dessus, le suivant mettant à mort celui qui le précédait. De sorte que tous occis Josèphe demeura seul avec son compagnon, étant nécessaire qu’il mourut, comme les autres, ou que du moins, il fût contaminé du sang de son prochain qu’il épancherait.
Une nouvelle fois, la piste s’arrête. Même si les propos sont ambigus (les mots sort et ruse se côtoient), il n’est pas mentionné dans ce texte que les soldats aient été disposés d’une façon particulière, ni que Josèphe ait choisi sa si bonne place. Le mot ruse apparaît en revanche, alors qu’il était absent des versions non-Hégésippe de la Guerre des Juifs. Les deux passages importants, mentionnant le système de tirage au sort et le fait que les soldats ne se doutent pas d’une ruse, sont présents aussi dans la version latine manuscrite mentionnée un peu plus haut (bien qu’une hypothétique ruse n’y soit pas aussi clairement indiquée) :
Se peut-il que Bachet soit l’auteur du problème, inspiré par la simple évocation, dans la traduction de l’Hégésippe, d’une ruse possible ? La première édition des Problème plaisants et délectables a été publiée en 1612. Le passage dans la préface est un peu différent dans la forme, mais identique sur le fond. Et le problème (le XX dans l’édition de 1612) est identique. La trace la plus ancienne du Flavius Josèphe certainement calculateur est donc pour le moment celle laissée par Bachet en 1612.
IV - Traité des jeux mathématiques
C’est le traité sur l’histoire des jeux mathématiques, publié par Wilhelm Ahrens au début du siècle dernier, à notre connaissance uniquement en Allemand, qui va nous fournir des compléments de réponse. Le chapitre xv est consacré au Jeu de Josèphe. La première édition de Mathematische Unterhaltungen und Spiele (Jeux mathématiques et divertissements), publiée en 1901 est disponible en ligne (16) :
Ahrens indique (second paragraphe de la page) :
Le même problème avait déjà été traité par Cardan, qui l’avait baptisé « le jeu de Josèphe (ludus Joseph) », en référence à l’histoire racontée plus haut.
La note de bas de page précise :
D’après Cantor, notre jeu se trouve mentionné dans les travaux de Nicolas Chuquet, travaux imprimés pour la première fois au début des années 1880 et jusqu’alors diffusés dans des versions manuscrites.
V - Chuquet, Cardan et Tartaglia
Parmi les sources citées par Ahrens, la plus ancienne est celle concernant Nicolas Chuquet. Ce dernier a, en effet, rédigé son manuscrit en 1484. La bibliothèque nationale en conserve un exemplaire. L’histoire ce cet ouvrage est intéressante : possédé par Estienne de La Roche au XVIe siècle, ce dernier l’a utilisé pour écrire son propre traité, Larismetique, publié en 1520 (17) (certains estiment qu’Estienne de La Roche a honteusement copié des passages du manuscrit de Chuquet sans citer sa source). Puis, l’ouvrage de Chuquet a été «oublié» pendant plus de 300 ans, avant d’être redécouvert par Aristide Marre qui l’a fait imprimer en 1880 et 1881 dans les Bullettino di bibliografia e di storia delle scienze matematiche e fisiche> (18).
Le passage qui nous intéresse est situé dans les Problèmes numériques faisant suite et servant d’application au Triparty en la Science des nombres de Nicolas Chuquet et constitue le problème 146 (page 453). C’est très exactement le problème raconté par Bachet, bien que les religions des protagonistes ne soient pas les mêmes. Il s’agit aussi de compter de 9 en 9, et de sélectionner 15 personnes prédéterminées parmi 30. La figure 4 est une reproduction de l’illustration du problème 146 dans le manuscrit de Chuquet (cette illustration n’a pas été reprise dans l’imprimé de 1881).
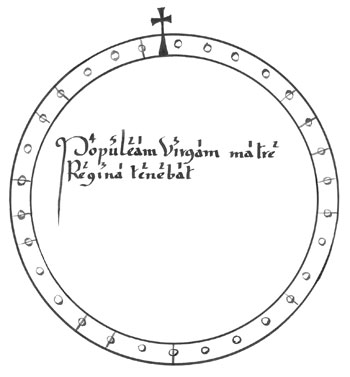
Figure 4 : Reproduction du dessin illustrant le problème 146 de Chuquet. Les cercles représentent la position de ceux qui seront sauvés, et les cercles barrés, la position de ceux qui périront. Notons, sur cette illustration, la phrase mnémotechnique (en latin) utilisée par Chuquet pour se souvenir de la manière d’agencer les 30 individus (Lucas donnait une phrase presque identique à la fin du XIXe siècle) : Populeam virgam matre regina tenebat (19).
Dans son ouvrage, Chuquet ne mentionne en revanche pas Josèphe ni de problème similaire. Il ne s’intéresse qu’au problème du partage 15-15.
Une autre source donnée par Ahrens concerne l’ouvrage de Cardan, Practica Arithmeticae, publié en 1536. Entre la première édition des Mathematische Unterhaltungen und Spiele en 1901, et la dernière, en 1918, Ahrens affine sa position en indiquant que :
La première mention du jeu de Josèphe – «Ludus Joseph», comme il l’appelle – est apparue dans les Practica Arithmeticae de Cardan.
Le texte de Cardan peut être consulté dans son édition de 1536 (20) ou dans une édition ultérieure (les Opera Omnia (21)). Le texte est le même dans les deux cas, et le passage qui nous intéresse est situé au milieu du paragraphe 18, à la fin du chapitre LXI, De extraordinariis & Ludis.
Voici une traduction en français du bref passage concernant les jeux de décimation :
[…] de la même manière, on pose en cercle autant de tablettes qu’on le souhaite et on sélectionne les blanches tout en écartant les noires ; disons qu’il y en ait 15 planches blanches et tout autant de noires, mais cela peut se faire avec n’importe quel nombre ; on connaît le jeu de Josèphe, qui avec celui-ci infligea la mort à ses compagnons de telle sorte que, dit-on, ceux-ci pensaient qu’elle leur arrivait par le sort, tandis que lui-même, vu que ceux-ci étaient pris au dépourvu, a été sauvé avec un compagnon seulement ; on dispose en cercle autant de petits cailloux qu’on le souhaite et pour deux comptés on en fait sortir un que l’on a choisi ; ce jeu, comme d’autres, semble admirable à ceux qui n’ont pas de jugement, bien que la chose soit simple...
Cardan donne ici de manière très succincte les énoncés des deux problèmes. La version 15-15, avec des planchettes noires et blanches, et le jeu de Josèphe. Les règles qu’il donne sont étonnamment incomplètes : s’il mentionne bien le fait que l’on compte de 3 en 3 (22), il ne précise pas le nombre de personnes (qui est pourtant le seul élément précisé dans Guerre des Juifs), et ne donne donc pas non plus la solution au problème.
Nous avons vu que le problème de décimation en version 15-15 était plus ancien que l’ouvrage de Cardan, puisque Chuquet le mentionne déjà. Bien qu’il soit impossible de le vérifier, on peut penser que la version du problème reliée à Josèphe était probablement elle aussi en circulation avant que Cardan ne la mette par écrit. Dans le cas contraire, il aurait probablement mieux cité l’ouvrage de Josèphe, et aurait sans doute donné plus de détails (nombre de personnes, solution...).
@@@@@@@
Avant de terminer ce tour d’horizon du problème de Josèphe à travers les âges, mentionnons l’ouvrage de Niccolò Tartaglia, General trattato di numeri, et misure publié entre 1556 et 1560, qui contient le problème sous la forme 15-15. Il est à peu près sûr que Tartaglia, au moment où il a écrit son ouvrage, avait pris connaissance de celui de Cardan, car il avait recherché dans ce dernier, avec angoisse, la méthode de résolution des équations polynomiales de degré 3, qu’il avait communiquée à Cardan, mais ne souhaitait pas voir publiée (23).
Le texte de Tartaglia est mis à disposition en version numérique par l’Université de Strasbourg (24) : le paragraphe qui concerne le problème de décimation est le 203. Voici une traduction en français du début du paragraphe :
Si quelqu’un veut me faire le plaisir suivant, à savoir mettre 30 pions sur un jeu de dames, dont 15 blancs et 15 noirs, de telle manière qu’en les numérotant du premier au dernier, tu soulèveras les noirs un à un tout en ne déplaçant aucun des blancs. Comme si dans une barque il y avait 15 chrétiens et 15 turcs, cette barque étant trop chargée, il était besoin d’en jeter dehors la moitié, savoir les asseoir de telle manière et dans tel ordre qu’en les numérotant tu pourras jeter tous les turcs hors de la barque, et ainsi sauveras les chrétiens, on demande comment ce faire. Je dis si tu veux le savoir que tu dois garder à l’esprit toutes les syllabes des vers ci-dessous et mettre autant de pions de telle couleur (ou faire asseoir autant de chrétiens) de la manière figurée par ces dites syllabes.
Tartaglia donne ensuite la correspondance voyelle/chiffre que nous avons déjà mentionnée, et termine par une liste très fournie de phrases mnémotechniques permettant de retrouver la disposition des 30 personnes selon que la décimation est faite de 3 en 3 , de 4 en 4 etc...
Même s’il n’a pas traité du jeu de Josèphe, Tartaglia semble avoir abordé le problème de manière plus sérieuse que Cardan, ou tout au moins plus systématique, et a apporté sa pierre à l’édifice en proposant de nouvelles phrases mnémotechniques pour des variantes du jeu.
VI - Conclusion
Il n’est pas très satisfaisant de conclure tant les versions du texte historique de Josèphe comme les ouvrages de divertissements arithmétiques contenant le problème ou une variante sont nombreux. Chaque trouvaille se ramifie presque systématiquement en plusieurs nouvelles pistes à explorer.
Néanmoins, à défaut d’être originaux, nous pouvons tout au moins confirmer, textes à l’appui, que ni les versions «classiques», traduites du grec, ni la version de pseudo-Hégésippe de la Guerre des Juifs ne contiennent d’éléments établissant que Josèphe ait été un féru de problèmes arithmétiques.
Le cas de la version slavonne est moins évident. Nous pensons cependant que les traducteurs, slaves puis français, ont pu être influencés par la connaissance préalable du problème de décimation et l’ont ainsi intégré à l’histoire.
En ce qui concerne la paternité du problème de Josèphe, et même si Cardan l’a mentionné dans ses Practica Arithmeticae, le plus gros travail revient, pour ce que nous avons vu, à Bachet et à ses Problèmes plaisants et délectables publiés en 1612.
Le témoignage de Cardan nous laisse toutefois penser que, contrairement à d’autres divertissements dont l’auteur peut revendiquer la paternité, le problème de Josèphe a émergé de la nébuleuse des problèmes de décimation (comme la version 15-15 des turcs et des chrétiens) bien avant d’être publié. Cardan n’a probablement fait que rapporter un problème qui était alors bien connu. Dans le cas contraire, il aurait certainement donné plus de détails. La paternité du problème de Josèphe, de ce point de vue là, ne revient donc sans doute ni à Bachet, ni à Cardan...
En ce qui concerne les problèmes de décimation en général, et plus précisément le problème 15-15 (partage en deux groupes) que nous avons vu apparaître plusieurs fois, les origines sont bien plus anciennes que celle que nous donnons ici (Chuquet, 1484) – ce type de problème apparaîtrait en effet déjà dans des ouvrages du XIIe siècle.
Septembre 2012
(1) Le terme de décimation trouve son origine dans une punition militaire romaine qui consistait à «éliminer» une personne sur dix dans un groupe. On procédait probablement par tirage au sort.
(2) Le terme de décimation sera maintenant employé même si on sélectionne une personne sur n avec n différent de 10.
(3) Il existe des solutions basées sur des récurrences, d’autres basées sur le calcul de suites annexes (suites géométriques « arrondies »), mais pas de calcul direct dans le cas général.
(4) Qui deviendra empereur deux ans plus tard.
(6) Flavius Josèphe aurait écrit en araméen, puis aurait lui même rédigé une traduction en grec. Les traductions latines ne seraient apparues que plus tard.
(8) On passe d’un problème à l’autre en modifiant simplement l’origine de la numérotation, autrement dit en décalant les numéros.
(9) Disponible sur le site archive.org (lien).
(11) La caverne est ici devenue une citerne. Ce n’est pas très surprenant, et le dictionnaire historique de la Bible du révérend Calmet nous indique que les termes lac (que nous verrons plus loin), citerne, caverne ou même tombeau peuvent désigner tous les quatre des réserves d’eau ou des sépultures.
(13) Ce point n’est pas développé ici, mais ajoute à la confusion de l’affaire : la Guerre de Jérusalem (De excidio urbis Hierosolymitana), écrite vers 370, n’a pas été écrite par Hégésippe, qui vécut au IIe siècle, mais probablement par Saint-Ambroise de Milan (cette thèse n’est pas unanimement partagée et certains identifient pseudo-Hégésippe à un certain Isaac).
(16) Page du site OpenLibrary.
(17) Larismetique est consultable sur Google Books.
(18) Les publications de 1880 et 1881 sont accessibles en ligne (ici et là).
(19) La reine mère tenait une branche de peuplier.
(21) Page Universota degli Studi di Milano.
(22) L’ouvrage de Cardan contient donc la plus ancienne mention du comptage de 3 en 3 que nous ayons trouvé.
(23) Elle le sera néanmoins dans l’Ars Magna (1545) de Cardan après que celui-ci aura découvert que Tartaglia n’était pas le premier inventeur de la méthode de résolution de ces équations, mais que, toujours d’après Cardan, Scipione Dal Ferro l’avait précédé.
(24) Page site Université de Strasbourg.
Annexe : résolution informatique
Il serait impossible de terminer sans proposer une solution moderne au problème de Josèphe. La fonction Python suivante indique pour n personnes, et un comptage de p en p, quelle est la place à occuper pour être sauvé. Le troisième paramètre, facultatif, permet d’indiquer le nombre de personnes à sauver. Le réponse donnée est la liste des positions qu’elles doivent occuper dans le cercle.
On peut vérifier ainsi que la 31 place est bien celle que Josèphe devait occuper :
Il est ainsi immédiat de savoir que si vous vous trouviez dans une légion romaine comptant 6000 hommes et devant subir le sort des compagnons de Josèphe :
votre meilleur(e) ami(e) et vous devriez choisir les places 3949 et 5864.
@@@@@@@
La solution au problème des turcs et des chrétiens est obtenue en demandant la liste des 15 derniers survivants pour une liste de 30 personnes et une décimation de 9 en 9 :
L’ajout de la fonction suivante permet d’obtenir le placement tel qu’il est donné par Bachet :
Nous obtenons ainsi :
On reconnaît la série : 4 chrétiens, 5 turcs, 2 chrétiens...
@@@@@@@
Enfin, il est possible de résoudre le problème du chat tel que l’a posé Dudeney ainsi :
La dernière souris mangée sera la 8ème. Par conséquent, pour terminer sur la souris blanche, le chat doit commencer à compter «1» sur la souris située 6 positions après la souris blanche.
Septembre 2012
Je remercie les éditions H&K qui m’ont permis de réutiliser des figures de l’ouvrage Divertissements mathématiques et informatiques (2011). Merci à Céline Michaud, pour ses précisions sur la traduction de l’anglais (Dudeney), à Alexandre Moatti pour sa traduction de l’italien (Tartaglia), à Nima Yeganefar pour sa traduction de l’allemand (Ahrens), à Sergueï Martemianov pour ses indications sur le slavon, et à Anne-Sophie Traineau-Durozoy, pour sa traduction du latin (pseudo-Hégésippe, Cardan,...) et son aide précieuse en général.
LIVRES
Laurent Signac, Divertissements mathématiques et informatiques, H&K, 2011 (site associé) [Contient la résolution informatique pas à pas de plusieurs récréations mathématiques, dont le problème de Josèphe]
Alex Bellos, Alex au pays des chiffres, Robert Laffont, 2011 [De nombreux problèmes abordés à la fois sous l’angle de l’histoire, du reportage, du voyage initiatique et bien sûr des mathématiques]
Ian Stewart, Mon cabinet de curiosités mathématiques, Flammarion, 2009 [Recense des problèmes amusants, parfois faciles et parfois difficiles, dont bon nombre se prêtent à une interprétation ou adaptation informatique.]
Malcolm E. Lines, Dites un Chiffres, Champs Flammarion, 1999 [De celèbres problèmes mathématiques abordés de manière assez détaillée et très pédagogique]
Flavius-texte.pdf
>> Téléchargez le texte de Flavius Josèphe
Histoire des Juifs (extrait) - Version PDF (8.92 Mo)
flavius-analyse-1.pdf
>> Téléchargez l'analyse de Laurent Signac
Autour du problème de Josèphe - Version PDF (13.7 Mo)
flavius-joseph-analysis-en.pdf
>> Download Laurent Signac's analysis
On the Josephus problem - PDF Version (3.21 Mo)
société des amis de la bibliothèque de l'X