Fermat et la factorisation des entiers

 

 

Pierre de Fermat était un mathématicien très habile avec les nombres et il savait facilement effectuer des calculs opératoires avec des entiers à dix ou douze chiffres. Cette maîtrise technique s’accompagnait de beaucoup d’astuce et d’ingéniosité de sa part. Nous savons cela aujourd’hui grâce aux nombreuses correspondances qu’il a eues avec ses contemporains.

Pour bien se rendre compte des talents arithmétiques de Fermat, voici l’étude de deux de ses lettres, chacune datant de 1643, dans lesquelles il factorise des entiers à 10 et 12 chiffres.

 

 

Figure 1 : Pierre de Fermat (ca 1601-1665) (gravure de François Poilly, 1623-1693).

 

1. La méthode de factorisation de Fermat - Fragment d’une lettre de 1643

La question de savoir factoriser un nombre entier est cruciale de nos jours : de nombreux systèmes cryptographiques (dont le fameux RSA) reposent sur cela. Mais, au XVII^e siècle, du temps de Fermat, savoir factoriser un entier n’avait absolument aucune application pratique ; le seul intérêt de trouver une factorisation était éventuellement ludique.

Fermat avait trouvé une méthode de factorisation qu’il exposa dans une lettre datée de 1643, dont voici un extrait :

 

 

 

Comme on le constate, Fermat expose sa méthode sans réelle explication, ni justification. Nous allons donc détailler cette méthode, et cela, à l’aide d’un formalisme plus contemporain.

 

1.1 Une idée simple mais brillante

Soit N un entier naturel qu’on veut factoriser. La méthode de Fermat découle de l’idée toute simple suivante : si on peut écrire N comme une différence de deux carrés N = a² – b², alors N = (a – b)(a + b). Le problème de la factorisation se ramène donc à un problème de soustraction. Par exemple, 15 = 4² – 1² = (4 – 1)(4 + 1) = 3 X 5.

Remarquons que si N est un nombre impair, une telle factorisation existe toujours. En effet, si N = 2n+1   alors vous pouvez vérifier que N=(n+1)²-n² . Il faut faire tout de même attention car dans ce cas nous avons a=n+1  et b=n , ce qui donne a-b=1  et a+b=2n+1=N: la factorisation obtenue est donc triviale (savoir que N=NX1  n’a aucun intérêt, vous en conviendrez).

 

1.2 Deux conditions nécessaires

Dans toute la suite, on supposera que  n’est pas un carré (car sinon, la factorisation de  est facile à trouver: c’est 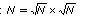). Si on est capable de trouver une décomposition en une différence de deux carrés, autrement dit si N=a²-b² alors,

    1.  a²-N est un carré

    2. 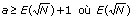   est la partie entière de .

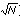Explication : Le 1. est évident. Pour le 2., il faut remarquer que a²-N+b²>N  (strict car N n’est pas un carré) et donc 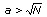 , ce qui implique  .

 

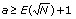1.3 Principe général de la méthode de Fermat

On note toujours N  le nombre à factoriser et on pose 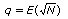. Puisque l’idée est de trouver a et b  tels que  N=a²-b² et puisqu’on a vu (cf. le paragraphe précédent sur les conditions nécessaires) que si  existe alorsa>q+1 , alors on va choisir successivement a=q+1, a=q+2 , a=q+3 , ... jusqu’à ce qu’il y ait un a tel que  a²-N soit un carré. Facile, non ? Voici un exemple simple pour illustrer cette méthode : supposons qu’on souhaite factoriser N=799 . On a  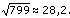donc q=28.

 

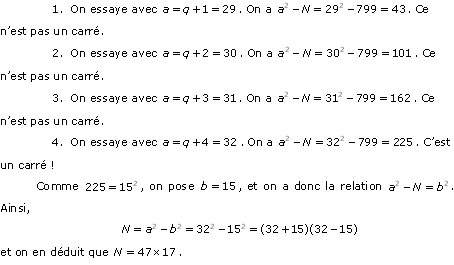
1.4 Raffinement

Dans le cas où le nombre N est très grand, le nombre d’étapes et de calculs est potentiellement très élevé. Pour que cette méthode soit utilisable d’un point de vue pratique, il va falloir minimiser le nombre de calculs, et pour cela, nous allons essayer de voir comment réutiliser les calculs déjà effectués au fur et à mesure. En particulier, il va être possible de calculer les a² -N facilement.

Puisqu’on pose successivement a=q+1, a=q+2 , etc. nous allons donc utiliser la notation 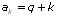 . Essayons de trouver une relation de récurrence:

                                

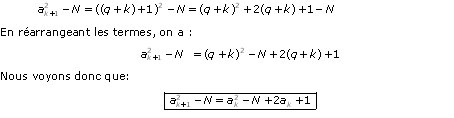
Il reste maintenant à voir sur un exemple pratique comment utiliser cette relation de récurrence pour exécuter la méthode de Fermat.

 

1.5 Analyse de l’exemple donné par Fermat dans sa lettre

Dans sa lettre, Fermat décrit en pratique sa méthode pour factoriser le nombre N=2027651281. En posant 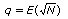=45029 , voici ce que cette méthode donne sous forme de tableau:

 

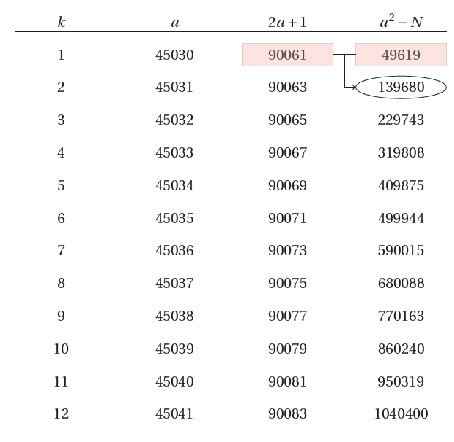
Vous voyez que ce tableau est très facile à remplir car:

    1.  a augmente de 1 à chaque fois

    2.  2a+1 augmente de 2 à chaque fois

    3.   a² -N s’obtient en faisant la somme des deux cases situées au-dessus (à la manière du triangle de Pascal) et cela vient de la relation de récurrence que nous avons démontrée au paragraphe précédent. Il n’y a donc aucune multiplication à faire, ni aucun carré à calculer ! (à part pour la première ligne bien sûr – c’est-à-dire le calcul de a² -N).

Dans l’exemple ci-dessus, on s’est arrêté dès qu’on est tombé sur un carré dans la dernière colonne: en effet, on a  1040400=1020² et donc, comme énoncé par Fermat dans son texte, on a

 

N = 45 041²-1020²=(45 041+1020)(45041-1020)=46 061X44 021

 

Comme vous l’avez sans doute constaté dans la lettre, Fermat savait directement reconnaître un nombre qui n’est pas un carré, s’épargnant ainsi un calcul de racine carrée. Il utilisait la condition nécessaire suivante: si un nombre est un carré alors ses deux derniers chiffres sont 00, 01, 04, 09, 16, 21, 24, 25, 29, 36, 41, 44, 49, 56, 61, 64, 69, 76, 81, 84, 89, ou 96 (mais attention, ce n’est pas une condition suffisante). Dans l’exemple ci-dessus, vous voyez immédiatement que les seuls nombres qui peuvent potentiellement être des carrés dans la dernière colonne sont 499 944 et 1 040 400.

 

2. La factorisation de 100 895 598 169 - Lettre du 7 Avril 1643

Dans une lettre envoyée à Fermat en 1643, le père Mersenne[1] (prêtre qui a donné son nom aux fameux nombres de Mersenne) demanda à Fermat de factoriser le nombre 100 895 598 169. Il reçut aussitôt une lettre de Fermat (datée du 7 avril 1643) dans laquelle on pouvait lire ceci[2] :

 

Vous me demandez si le nombre 100 895 598 169 est premier ou non, et une méthode pour découvrir, dans l’espace d’un jour, s’il est premier ou composé. À cette question, je réponds que ce nombre est composé et se fait du produit de ces deux : 898 423 et 112 303, qui sont premiers.
 

Sans calculatrice et en moins d’un jour, Fermat a réussi à factoriser un nombre à 12 chiffres ! Impressionnant ! Mais comment Fermat a-t-il fait pour factoriser ce nombre ? Car malheureusement il n’a pas décrit sa méthode dans cette lettre... (c’était une habitude il faut croire !)

 

 

Figure 2 : Le père Marin Mersenne (1588-1648) (WikiCommons, portrait s.d.)

 

 

2.1 Échec de la précédente méthode de Fermat

Tout d’abord, il est peu probable que Fermat ait utilisé la méthode de factorisation que nous avons décrite précédemment. En effet, lorsqu’on programme cette méthode sur un ordinateur pour factoriser N=100895598169, on trouve qu’il faudrait k=187723 étapes avant que l’algorithme ne se termine !
Et on a alors

     

c’est-à-dire N=898423X112303 . On retrouve bien la réponse donnée par Fermat à Mersenne mais il est difficile d’imaginer que Fermat a effectué à la main le calcul de ces 187 723 étapes… La méthode qu’il a utilisée ici est plus astucieuse et s’appuie sur la nature même du nombre 100895598169 , qui n’a pas été proposé par hasard par Mersenne. Pour comprendre le raisonnement de Fermat, commençons par donner un plus grand extrait de sa correspondance.

 

2.2 Quelques éclaircissements sur cette lettre

Voici donc l’extrait plus large de cette lettre datant du 7 avril 1643 :

 

Dans cet lettre, Fermat affirme que le nombre:

         

               

est égal à 5 fois la somme de ses diviseurs propres, c’est-à-dire de tous les diviseurs de N sauf N. Si on note σ (N) la somme de tous les diviseurs de N (y compris N lui-même), cela signifie que

                                       σ (N)-N=5N

ce qui est bien entendu équivalent à σ (N)=6N. Nous allons calculer  et voir comment, grâce à cela, Fermat a pu faire apparaître la factorisation de 100 895 598 169.

 

2.3 Calcul de σ (N)

Commençons par remarquer^[3] que 169=13², que 961=31², que 6561=3⁸ , que  823543=7⁷ et que 214748364800000=2³⁶X5⁵.

Nous pouvons en déduire que  se décompose de la façon suivante:

Hormis 100 895 598 169 dont on cherche la factorisation, tous les facteurs de cette décomposition de N sont des puissances de nombres premiers^[4]. Tous ces facteurs sont donc premiers entre eux deux à deux et l’on peut supposer que les facteurs premiers de 100 895 598 169 sont distincts des autres facteurs premiers de N. Pour le voir rigoureusement, on peut faire successivement la division de 100 895 598 169 par 2, 3, 5, 7, ..., 7019 et 616 318 177 pour voir que le reste n’est jamais nul.

Savoir que ces facteurs sont premiers entre eux est important car on sait que la fonction σ est multiplicative, c’est-à-dire que  σ(mn)=σ(m)σ(n) dès lors que m et n  sont premiers entre eux. Pour calculer σ(N), il suffit donc de calculer les σ(p^k) où p^k parcourt tous les facteurs de N donnés au-dessus. Mais cela est aisé car on sait que si p est premier, on a la formule  .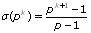

Voici donc le calcul de tous lesσ(p^k) :

Dans la dernière ligne apparaît le facteur 898 423, qui est premier. Fermat avait sans doute dû vérifier sa primalité.

Le nombre noté σ(100895598169) ne peut pas être calculé pour le moment, donc on le notera s. On obtient la décomposition de σ(N) en faisant le produit de tous les nombres de la colonne de droite et, après regroupement des termes, on obtient :

 

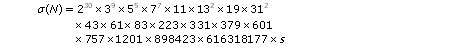
2.4 Un facteur commun à N et σ(N)

En regardant les décompositions de N et σ(N) , on se rend compte que le nombre

                               

Rappelons que la question posée à Fermat était d’étudier si σ(N) est égal à un multiple de N . Si c’était le cas, on aurait  pour un certain entier  ce qui donnerait la relation:

           MX3X898423Xs=kXMX2⁶X7019X100 895 598 169                    

Après simplification par M, cela implique que, soit le facteur premier 898 423 divise k , soit il divise 100 895 598 169. Cela a sans doute conduit Fermat à tenter de diviser 100 895 598 169 par 898 423, et il se trouve justement que cette division est exacte puisque 100 895 598 169 divisés par 898 423 égalent 112 303^[5] – ce qui donne à Fermat la deuxième partie de sa réponse à Mersenne.

 

2.5  Fin de la réponse...

A partir de là, Fermat pouvait répondre à la question globale de Mersenne qui était de savoir si la somme des diviseurs propres de  N est un multiple de N. Si  k est un entier tel que  alors σ(N)=kN alors

                 MX3X898423Xs=kXMX2⁶X7019X100 895 598 169 

ce qui donne, en simplifiant par  et par 898 423:

                                              

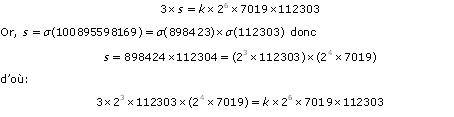
ce qui entraïne que k=6 . Ainsi, σ(N)=6N et donc, comme l’avait affirmé Fermat dans sa lettre en parlant de sous-quintuple des parties, on a bien σ(N)-N=5N .

 

 

 

(juillet 2015)