
Figure 1 : Cercles de Villarceau en perspective sur un tore.
C’est pour moi un plaisir extrême de rédiger un texte sur les cercles de Villarceau
(1). Car ils sont doublement et fortement liés à ma vie personnelle. Voici pourquoi. Ma première rencontre avec ces cercles exotiques arriva ainsi. En classe terminale au lycée en 1943-1944, outre les livres de mathématiques normalement conseillés, j’avais sous la main l’ouvrage que mon père avait eu dans la même classe, le titre précis de ces deux gros volumes était « Traité de Géométrie » et les auteurs s’appelaient Rouché et de Comberousse. Ils traitaient certes intégralement le programme de géométrie de terminale (scientifique), mais fourmillaient d’appendices hors programme, à l’époque importants car liés à la géométrie postérieure à ce programme. Amoureux un peu fou de la géométrie, feuilletant le deuxième tome, dans un appendice je découvre ce fait surprenant (c’est une litote), pour moi mais probablement aussi pour vous cher lecteur, qu’un tore (s’entend comme toujours à l’époque, un tore de révolution), contenait toujours beaucoup d’autres cercles autres que les méridiens et les parallèles. Je fus tellement surpris que, au lieu de regarder la démonstration, en grand paresseux, ma première réaction fut d’essayer une démonstration physique, à savoir de scier un anneau de tringle de rideau en bois. Avec des scies primitives, manuelles, et surtout avec un anneau finalement trop mince, l’opération se révéla non concluante. Pour ce qui est d’une démonstration élémentaire, et d’autres de tous les niveaux, dont une donnée en classe préparatoire de ce résultat qui reste toujours spectaculaire, voir plus bas. En tout cas j’avais ensuite complètement oublié ces cercles, plongé dans un thèse, et autres travaux de géométrie différentielle (de toutes dimensions).
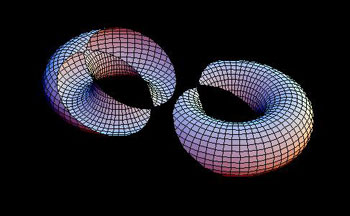
Figure 2 : Coupe d’un tore par un plan bitangent (tangent en-dessus et en-dessous). Voici la coupe que l’auteur n’avait pas réussi à faire, muni de sa scie, sur un anneau de tringle à rideaux. On sépare donc le tore en deux morceaux, et sur le morceau de gauche on voit apparaître les deux cercles de Villarceau, avec leurs deux points de rencontre, points de bitangence (en haut et en bas) (image Académie de Nancy-Metz).
Figure 2bis : Représentation du plan bitangent, coupe verticale de l’opération réalisée sur le tore (dessin Marcel Berger)
Le second événement arriva ainsi. Muni de cette thèse et d’un poste de maîtres de conférences à Strasbourg, et y visitant le musée de l’Œuvre Notre-Dame, essentiellement dévoué aux de sculptures moyenâgeuses, et accédant au premier étage par un magnifique escalier en vis, je découvre un forme de tore en pierre sculpté et couronnant le haut de cet escalier. Sur la photo ci-dessous on voit nettement les arêtes de la sculpture, n’en croyant pas mes yeux je vérifie que ces arêtes sont en fait dans des plans, et sont donc des cercles de Villarceau. Manque de courage, et de savoir où rechercher si cette sculpture villarceau-ique était un hasard ou si les sculpteurs connaissaient ces cercles, j’ai depuis abandonné l’idée de connaître la réponse. Mais pour ce qui est de ces cercles, et des questions et des résultats de géométrie qu’ils ont engendré ultérieurement, je n’ai jamais manqué d’inclure cette photo, et un texte plus ou moins long pour l’accompagner, dans tous mes livres de géométrie où Villarceau pouvait intervenir assez naturellement
(2).

Figure 3 : L’escalier d’accès au musée de l’Œuvre Notre-Dame, à Strasbourg. Le premier palier (en bas) est fait de cercles concentriques (parallèles du tore). Le deuxième palier (en haut) est plus intéressant. Tout d’abord, comme l’autre, il est horizontal, contrairement à ce qu’un effet de perspective de cette photo prise par en-dessous peut laisser croire (on s’en convaincra en considérant que les colonnes reliant un palier à l’autre sont forcément de même taille). Ensuite, il est composé de cercles de Villarceau : à droite, en médaillon, les trois cercles de Villarceau représentés par l’architecte de l’escalier, Thomas Uhlberger – ce sont des cercles non sécants, enlacés, appartenant à la même famille. Contrairement à ce que la photo laisse paraître, ces cercles sont assez petits dans la réalité – le diamètre des tores ne dépasse guère 70 cm (photo Michel Pfeiffer, Pour la Science, n° 292, février 2002)
Arrivons-en à des choses plus sérieuses… Les cercles de Villarceau s’obtiennent en coupant un tore (de révolution, à cela près quelconque, i.e. les deux rayons qui le déterminent, à une isométrie de l’espace près, étant quelconques) par des plans dessinés en coupe sur la figure 2. Cette section plane du tore se compose de deux cercles, au lieu d’être vulgairement une courbe plane, de degré quatre comme le tore l’est lui-même. C’est cette séparation en deux cercles, certes sécants, qui est le phénomène tout à fait inattendu. La révolution autour de l’axe fournit ainsi deux familles à un paramètre de cercles situés sur le tore, en quelque sorte « obliques ». Présupposant le lecteur de nature aussi paresseuse que moi, mais empreint de curiosité facile, voici maintenant d’abord les propriétés principales, plus ou moins aussi inattendues, de ces cercles. Nous reviendrons plus bas sur les preuves variées de ce phénomène. Bien réaliser qu’il y a deux familles différentes, continues et à un paramètre de ces cercles (les amateurs de quadriques pourront penser aux deux familles de génératrices des paraboloïdes hyperboliques et hyperboloïdes).
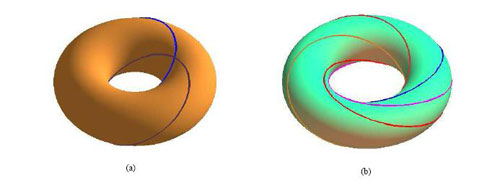
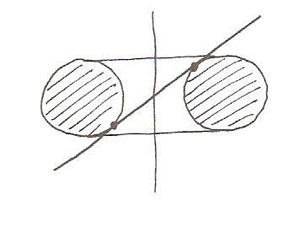
Figure 4 : Une des deux familles des cercles de Villarceau (à dr.). La figure (a) à gauche représente les deux cercles de Villarceau issus de la coupe par un plan bitangent, définissant chacun deux familles. La rotation autour du tore du cercle supérieur bleu clair en (a), ou la rotation du plan bitangent, donne la famille de cercles représentée en (b), à gauche. Il s’agit d’une des deux familles de cercles de Villarceau. On constate que le cercle inférieur bleu foncé en (a) ne coïncide avec aucun des cercles en (b) : il appartient à la deuxième famille. Les deux familles sont différentes car, à la différence des cercles méridiens, il n’y pas invariance (retour à la même position) par rotation à 180° : le retour à la même position se fait par rotation complète à 360° et définit deux familles de cercles.
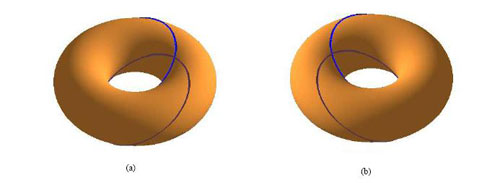
Figure 4bis (ci-dessous) : Pas d’invariance par rotation du plan bitangent à 180° (la position n’est pas la même).(images Lionel Garnier, Université de Bourgogne, Revue électronique francophone d’informatique graphique, 2008)
Style de cet article
Notre désir est de plaire au lecteur, qu’il puisse trouver une certaine joie géométrique, et ne s’enfoncer plus dans le terreau des démonstrations que si cela lui plaît vraiment. En d’autres termes nous préférons énoncer sans démonstration des propriétés géométriques, très visibles le plus souvent, à l’exception notable de la querelle de la géométrie dite « moderne ».
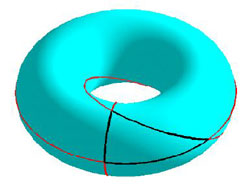
Figure 5 : Triangle rectangle 3D à bords circulaires, sur un tore, dont les bords sont un arc de méridien, un arc de parallèle et un arc de cercle de Villarceau (image Lionel Garnier, Université de Bourgogne, Revue électronique francophone d’informatique graphique, 2008)
Première propriété des cercles de Villarceau : l’enlacement. Bien remarquer d’abord que dans tout ce qui suit, sauf mention explicite du contraire, le tore considéré est quelconque. Alors on a tout ceci : deux cercles distincts de familles opposées se rencontrent toujours en deux points distincts. Par contre, le comportement de deux cercles distincts de la même famille est beaucoup plus subtil. Non seulement ils ne se rencontrent pas, mais surtout ils sont toujours enlacés. Certes c’est évident sur les figures pour la non-rencontre, et en fait démontré de façon simple (laissée au lecteur), mais la question de l’enlacement est d’un tout ordre de difficulté. Nous laissons le lecteur définir mathématiquement ce que sont deux courbes fermées simples de l’espace enlacées. L’histoire est ici intéressante, à notre connaissance ce fut Gauss le premier qui s’occupa de ces questions d’enlacement, et ainsi que de la théorie des noeuds tant que nous y sommes. L’idée est celle, typique des mathématiques, associer à toute paire de courbes (fermées simples toujours) un invariant, appelé nombre d’enlacement de ces deux courbes, invariant auquel on demande d’être nul si les deux courbes sont séparables – s’il est non nul, alors les deux courbes ne sont pas séparables, elles sont enlacées
(3).
Deuxième propriété des cercles de Villarceau : la loxodromie. Une propriété, propre à tous ces cercles, est celle-ci : tout cercle de Villarceau est une
loxodromie du tore. Rappelons, si nécessaire, qu’une loxodromie sur la Terre, sur une surface de révolution, en un sens plus mathématique est une courbe qui coupe tous les méridiens (et donc aussi bien tous les parallèles) sous un angle constant. Cette notion a pas mal disparu à notre époque, avec les centrales à inertie pour la navigation maritime ou aérienne, mais surtout de nos jours avec le GPS. Mais avant ces moyens de naviguer, tant sur mer que dans les airs, les loxodromies étaient fondamentales. En effet, par définition en quelque sorte, quand on navigue « à cap constant », on fait en sorte que la boussole marque toujours le même cap, c'est-à-dire le même angle avec le méridien magnétique
(4). On notera que les loxodromies d’un tore ne sont des cercles de Villarceau que pour cette (« une ») valeur.
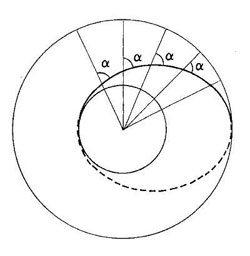
Figure 6 : Propriété de loxodromie. Le cercle de Villarceau (qui apparaît comme un ovale dans cette vue perspective de dessus) coupe chacun des méridiens avec le même angle, fonction uniquement des caractéristiques R et r du tore (figure Marcel Berger, Géométrie, tome 2, Cédic Fernand Nathan, 1979).
L’historique complet des cercles de Villarceau est mal connu, je n’ai pas de référence : il semble que par exemple cette propriété de loxodromie était connue dès 1881. Qui le premier a découvert le premier cette propriété loxodromique ? Je suis preneur d’autres références. Aussi, je n’ai aucune idée sur la façon dont Villarceau a découvert les cercles éponymes. Sa note de 1848 de moins d’une demi-page dans les Compte-rendus de l’Académie des sciences est seulement un calcul ultra-sec et rapide. L’article de la même année dans les Nouvelles annales de mathématiques ne dit rien de plus, sauf l’extension au cas des surfaces de révolution engendrée par une conique quelconque, d’écriture toute aussi foudroyante.
Propriétés des cercles de Villarceau : mieux que loxodromie, la parataxie
On peut relire cette propriété loxodromique ainsi : tous les plans méridiens, c’est à dire les plans passant par l’axe du tore, coupent un cercle de Villarceau sous le même angle. On dit que les cercles de Villarceau sont des hélices du tore. Là non plus, on ne sait pas qui le premier a découvert cette propriété et quand. Elle appartient au domaine dit de la parataxie.
Cette propriété généralise à tout nombre réel α le fait banal que tout plan contenant l’axe d’un cercle coupe ce cercle sous un angle droit. En outre toute sphère contenant un cercle coupe l’axe du cercle toujours sous un angle droit. C’est la figure particulière de deux cercles formant un anneau orthogonal. Chaque sphère contenant l’un coupe l’autre à angle droit. Plus généralement un couple de cercles se trouve être paratactique quand toute sphère contenant l’un coupe l’autre sous un angle constant, et alors réciproquement, – i.e. cette condition est symétrique : toute sphère passant par le second cercle coupe encore le premier sous un angle constant et qui est le même. Le résultat ici est : toute paire de cercles de Villarceau de la même famille est paratactique (pour un angle qui dépend de la paire).
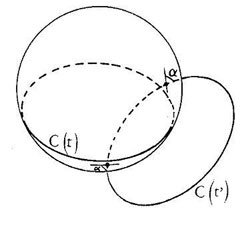
Figure 7 : Propriété de parataxie. Toute sphère contenant un cercle de Villarceau coupe un autre cercle de Villarceau de la même famille sous le même angle α de loxodromie (figure Marcel Berger, Géométrie, tome 2, Cédic Fernand Nathan, 1979).
Un mot bref sur la parataxie : on la trouve exposée avec le bon langage conceptuel chez Félix Klein et l’école allemande de géométrie dès 1900
(5).
A contrario, l’école française de géométrie « classique », en perte de vitesse notoire entre 1850 et 1950, a maintenu, notamment pour la parataxie, un enseignement et des ouvrages didactiques de « style » plus ou moins ancien, voir par exemple Hadamard, Dontot
(6), etc. J’ai eu l’occasion de narrer ce « trou » mathématique français
(7)…
Et des démonstrations ? la naïve mais hard
La démonstration originale de Villarceau était analytique ; elle est hyper-facile si l’on connaît le résultat, car on trouve à l’oeil quel est le rayon et le centre de ces cercles, donc leur équation dans le plan de section, et on vérifie que l’équation du quatrième degré de cette section se décompose bien en le produit des équations de ces deux cercles.
La preuve analytique est développée dans l’encadré ci-dessous. Puis, dans la partie suivante, nous donnerons une preuve qui a eu un succès considérable, encore de nos jours, car introduisant plusieurs nouveaux concepts, à savoir la complexification d’un espace ou d’un plan ordinaires, puis l’adjonction de points à l’infini
(8).
Équations cartésienne et paramétriques du tore et de ses cercles de Villarceau
Pour les lecteurs cartésiens donnons néanmoins quelques équations dont ils sont friands (on commencera par les coordonnées dites toriques, justement).
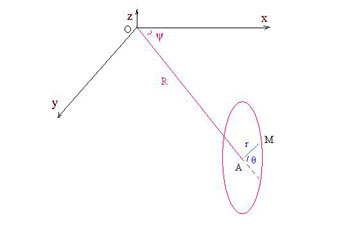
Un point M du tore est paramétré par les angles ψ et θ comme suit : x = (R + rcosθ) cosψ y = (R + rcosθ) sinψ z = rsinθ Pour rester en pures coordonnées cartésiennes, on projette M sur l’axe OA en un point m (non représenté) de coordonnées (x,y,0). L’équation du tore s’écrit AM² = r², soit (Om – OA)² + mM² = r², soit :
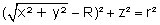
On retrouve cette équation en utilisant les coordonnées toriques ci-dessus. L’équation la plus générale, prenant en compte l’autre partie du tore, symétrique, par rapport à O, s’écrit :
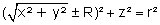
On élimine les radicaux comme suit :
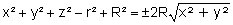
d’où l’équation cartésienne du tore, du 4° degré :
(x² + y² + z² + R² - r²)2 = 4R² (x² + y²)
On peut retrouver les deux équations ci-dessus avec le paramétrage du tore en ψ et θ donné ci-avant.
@@@@@@@
Partons maintenant à la recherche des cercles de Villarceau, même si c’est plus facile quand on sait qu’ils existent et qu’on connaît leurs centres respectifs et leur rayon ! Par souci de simplification, la tangence en MT dans un plan (x,z) s’exprime par un angle α entre le plan bitangent et le plan parallèle principal du tore tel que (voir figure 2bis pour la trace du plan bitangent) : sinα = r/R. Dans le plan (x,z), le point MT de contact a pour coordonnées (OMcosα, OMsinα) ; il vérifie donc l’équation : xsinα = zcosα, soit 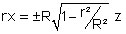 (le signe
(le signe 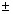 rappelle que dans une coupe (x,z) donnée, il y a deux plans bitangents, symétriques par rapport à l’axe des x. La bitangence s’exprime donc par r²x² = (R² - r²) z². Le premier cercle de Villarceau relatif à cette configuration a pour centre le point (0, r, 0), l’autre (0, -r, 0). Montrons qu’il s’agit bien d’un cercle, de rayon R, i.e. vérifiant l’équation x² + (y-r)² + z² = R² (en fait le cercle de Villarceau va être l’intersection d’une sphère avec le plan bitangent). Pour ceci, paramétrons y comme suit y = r + Rt. L’équation de la sphère ci-dessus donne x² + z² = R² (1 – t²) Quand on y associe la coupe par le plan bitangent, on obtient
rappelle que dans une coupe (x,z) donnée, il y a deux plans bitangents, symétriques par rapport à l’axe des x. La bitangence s’exprime donc par r²x² = (R² - r²) z². Le premier cercle de Villarceau relatif à cette configuration a pour centre le point (0, r, 0), l’autre (0, -r, 0). Montrons qu’il s’agit bien d’un cercle, de rayon R, i.e. vérifiant l’équation x² + (y-r)² + z² = R² (en fait le cercle de Villarceau va être l’intersection d’une sphère avec le plan bitangent). Pour ceci, paramétrons y comme suit y = r + Rt. L’équation de la sphère ci-dessus donne x² + z² = R² (1 – t²) Quand on y associe la coupe par le plan bitangent, on obtient
x²[1 + r²/(R² – r²)]= R² (1–t²) x² = (R² – r²) (1–t²)
Or, l’équation caractéristique du tore est :
f(x) = (x² + y² + z² + R² - r²)2 – 4R² (x² + y²) f(x) = [(x² + z²) + (r+ Rt)² + R² - r²)]2 – 4R² [x² + (r + Rt)²] f(x) = [R²(1-t²) + r² + R²t² + 2Rrt + R² - r²]2 – 4R² [x² + (r +Rt)²] f(x) = 4R² [(R+rt)² - x² - (r +Rt)²]
En reportant la valeur de x pour le plan bitangent ci-dessus:
f(x) = 4R² [(R+rt)² - (R² – r²) (1–t²) - (r +Rt)²]
équation riche de dix termes dont on vérifiera qu’ils s’annulent deux à deux. Le point en question appartient bien au tore. L’intersection de la « sphère de Villarceau » de centre (0,r,0) et de rayon R avec le plan bitangent donne une figure dont tous les points (paramétrés par t) appartiennent au tore. L’intersection d’une sphère et d’un plan sécants étant un cercle, tous ces points représentent donc un cercle sur le tore : c’est le cercle de Villarceau.
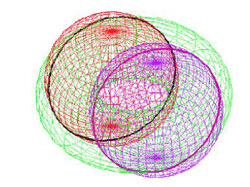
Figure 8 : Les cercles de Villarceau peuvent aussi être vus comme l’intersection des deux « sphères de Villarceau » avec le tore. Ces sphères sont symétriques par rapport à l’axe vertical du tore, leur centre est à une distance r (petit rayon du tore) du point central, de part et d’autre ; leur rayon est R (grand rayon du tore) (image Lionel Garnier, B. Belbis, S. Foufou, Université de Bourgogne, Revue électronique francophone d’informatique graphique, n°3, 2009)
La Démonstration de géométrie « pure » et vraiment éclairante
C’est ici pour moi une occasion assez unique d’expliquer le vocable géométrie moderne, sa gloire et ses méfaits. Voici comment les choses étaient présentées quand j’étais en classes préparatoires au milieu des années 1950. Et personne n’y trouvait rien à redire, à tout le moins dans les cercles scientifiques, dont je reparlerai. Voici le verbatim, patience si vous ne comprenez pas même simplement les objets en jeu.
Il faut d’abord voir que dans un plan euclidien, quand on le double en utilisant deux nombres complexes comme coordonnées, et que l’on ajoute des points à l’infini, dans cet espace (de dimension réelle quatre) l’extension d’un cercle devient une courbe qui contient toujours deux points à l’infini appelés « points cycliques », ceci parce que l’équation d’un cercle commence toujours par x
2+ y
2 +…, ainsi dans cet espace
doublement généralisé, deux cercles en position générique ont toujours quatre points en commun : en coordonnées (x,y) étendues en (x, y, z), mais à ne considérer qu’à un scalaire près, pour avoir des points à l’infini (x,y,0), nos points cycliques s’écrivent (1,
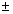
i ,0), où
i est le nombre complexe classique (i
2 = -1).
On se place maintenant dans le domaine de la géométrie d’un espace de dimension 3 qui soit à la fois complexe et possède des points à l’infini (il est donc de dimension réelle six). Notre tore est algébrique (c'est-à-dire un objet défini par un polynôme) et de degré 4, donc toute section plane sera aussi algébrique et de degré 4. Mais le tore contient, de façon double, l’ombilicale, à savoir les points à l’infini définis par x² + y² + z² = 0 (voir plus bas, figure 9), ceci parce que l’on a une surface de révolution et avec des méridiennes circulaires. La section du tore par notre plan candidat à Villarceau contient quatre points doubles, deux pour les points de contact (ils ne sont pas à l’infini ni complexes eux !) et deux autres qui sont les points d’intersection de cette courbe ombilicale double avec le plan considéré. Or la géométrie algébrique nous dit qu’une courbe de degré quatre et qui possède quatre points doubles est forcément dégénérée en une paire de coniques, des cercles évidemment ici. Et voilà pourquoi votre fille est muette
(9) !
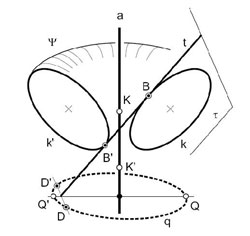
Figure 9 : Démonstration de géométrie projective. Dans cette figure, en partie doublement symbolique (car il y a des éléments imaginaires et des éléments à l’infini), Ψ désigne le tore, a est l’axe du tore, k et k’ désignent les deux cercles méridiens du plan frontal, B et B’ désignent les deux points de contact avec le tore du plan bitangent considéré, noté τ, t est la droite-trace du plan τ (comme en figure 2bis). Tous sont réels, mais maintenant, comme les méridiens sont des paires de cercles (k et k’) leurs points cycliques Q,Q’ (imaginaires et à l’infini) engendrent une courbe, comptée deux fois, notée q (toujours à l’infini et imaginaire, appelée ombilicale) et dessinée en pointillés gras pour aider cette vision impossible. Le plan considéré τ la coupe en deux points D, D’. Ces points sont des points doubles pour notre section, parce que l’ombilicale est décrite deux fois. (figure Anton Hirsch, Extension of the « Villarceau-Section » to Surfaces of Revolution with a Generating Conic, Journal for Geometry and Graphics Volume 6 (2002), No. 2).
Beaucoup de travaux de Poncelet, dès 1815, procèdent de façon analogue. Poncelet était un visionnaire, qui travaillait entièrement à l’aise dans l’espace projectif complexe, et ce sans aucun usage de coordonnées. Mais il n’en donnait aucune définition, aucune construction. Pas étonnant que l’Académie des sciences ait alors refusé ces travaux, comme « en dimension quatre », ou «romantiques ». En fait, pour notre cas du tore de l’espace, il s’agissait – bien pire – de la dimension (réelle) six !
Une définition correcte de ce qu’est l’espace projectif complexe dut attendre le deuxième demi-siècle, après 1850. À savoir ce que nous avons écrit plus haut, c’est l’ensemble des quadruplets (x,y,z,t) de nombres complexes, mais seulement définis à un multiple près. Les points à l’infini sont ceux de la forme (x,y,z,0). Dans la démonstration ci-dessus on oublie bien sûr, c’est évident, de dire que l’on revient in fine dans l’espace réel, et non projectif. Quand on lit les textes de ces époques on ne sait jamais si on est dans le réel, dans le complexe, ou dans le projectif !
La démonstration ci-dessus est ce que l’on a appelé, en France jusqu’à bien récemment, disons 1950, de la «géométrie moderne ». La France a connu un retard mathématique énorme, surtout entre les deux guerres, dans tous les domaines – à part quelques rares exceptions qui ne furent pratiquement pas diffusées –, tandis que les choses était faites correctement en Allemagne, disons autour de Klein, dès 1900. Votre auteur avait fait ses délices, durant l’été 1944, du livre de Duporcq
(10) (avec bien sûr la douleur et la joie des exercices), que l’on recommandait à tous les taupins qui voulaient en faire un peu plus que le programme, et même en terminale pour les doués « accro » à la géométrie sans coordonnées. Ce n’est que plus tard qu’il en fit part, dans les années 1956 à Jean-Louis Koszul dont il était devenu le collègue à Strasbourg. Et de s’entendre dire « mais, Berger, rien n’est vraiment démontré dans ce bouquin ! » Ainsi perdis-je une certaine virginité…
En effet il faudrait le rendre solidement démontré, ce qui est facile à faire pour ce petit livre, mais est surtout rendu nécessaire pour corriger certains «résultats » de l’école italienne de géométrie algébrique du début du XXe siècle, obtenus de façon « moderne », et dont certains se sont avérés faux ! C’est toute la «Géométrie algébrique » (c’est à dire celle des objets définis exclusivement par des équations polynomiales), qu’il a fallu ainsi mettre sur pied à partir de la fin du XIXe siècle…
In fine deux questions : sont-ce des questions naturelles ?
Ce qui suit me semble une excellente illustration de la façon dont fonctionnent les grands mathématiciens. Ces questions tournent autour du fait qu’un tore comprend quatre familles (sous-entendu toujours à un paramètre continu) de cercles. Première question : peut-on trouver des surfaces ayant plus de quatre familles de cercles ? Deuxième question : quelles sont les surfaces ayant plusieurs familles de cercles, comment les caractériser ? On doit à Darboux dès 1880 un très bon texte sur la question. Mais il est difficile à lire, car on est en plein dans le flou de la géométrie « moderne », il faut s’accrocher à la lecture de Darboux pour savoir si on est dans le domaine complexe ou le réel. L’idée de Darboux, et qui marche, est qu’en tout point de notre surface, l’existence de cercles contenus dans la surface et passant par ce point implique de fortes restrictions sur la seconde forme fondamentale
(11) de la surface considérée. Ainsi, dix familles de cercles est un maximum – sauf pour les sphères qui ont évidemment une infinité de telles familles. Les surfaces ayant dix familles sont d’ailleurs complètement connues.
On trouve des surfaces dépendant seulement de cinq paramètres. Il est facile de voir que l’on ne peut pas avoir plus de six telles familles de cercles dans le réel – mais c’est dix dans le complexe. À notre connaissance il n’existe pas de production informatique de ces surfaces, quand les cinq paramètres sont tous différents, à six familles de cercles, qui proviennent, outre les Villarceau, du dédoublement des parallèles et des méridiens
(12). Pour le lecteur actif et porté sur les outils informatiques produisant des figures géométriques, etc., je suis preneur de figures pour des surfaces à six familles réelles.
En tout cas, il nous semble que ce mémoire de Darboux laisse ouvertes de nombreuses questions, telles que classer, si c’est possible, les surfaces ayant des familles de cercles en nombre moins que dix...
Digression sur les cyclides, celles de Dupin et les autres
Quand deux des cinq paramètres sont égaux, ces cyclides sont appelées cyclides de Dupin. Une caractérisation en est que ce sont les seules surfaces dont les deux surfaces nappes focales se réduisent en fait toutes deux à des courbes, donc une double dégénérescence, sont les cyclides de Dupin.
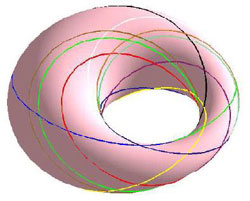
Figure 10 : Cyclide de Dupin. Décrites en 1820 par le mathématicien et homme politique français Charles Dupin, les cyclides de Dupin sont les images d’un tore de révolution par inversion (l’inversion de centre O et de puissance k associe à un point M un point M’ tel que OM’ = k OM/OM², la notation en gras étant prise pour les vecteurs). La cyclide de Dupin la plus commune est celle ci-dessus, formant un croissant qui se referme. On y a représenté les cercles de Villarceau, images de ceux du tore (l’image d’un cercle par une inversion est un cercle) (images Lionel Garnier, Université de Bourgogne, Revue électronique francophone d’informatique graphique, 2008)
Rappelons quelques notions : localement, les normales à une surface enveloppent deux surfaces, dites nappes focales. Les deux points de contact sur une normale sont les deux centres des courbures principales au point considéré. Les courbures principales sont celles des lignes de courbure, à savoir les courbes intégrales des deux directions principales, qui sont à leur tour les directions propres de la seconde forme fondamentale, et les centres de courbure sont aux distances 1/r et 1/r’ sur la normale, où r et r’ sont les valeurs propres de cette seconde forme fondamentale. Bien faire attention, voir la figure, que ces valeurs propres, non nulles certes, ont un signe une fois la surface orientée ; dans le cas « convexe » elles sont de même signe – mais elles peuvent être de signes opposés dans le cas d’un col de montagne, ou encore typiquement pour un paraboloïde hyperbolique.
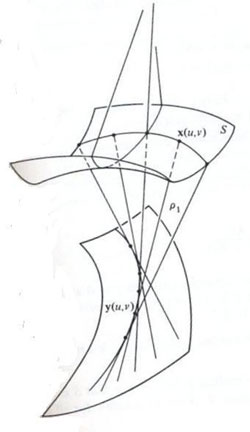
Figure 11 : Construction d’une nappe focale suivant les normales à une surface S. Quand on considère l’ensemble des normales à une surface (la normale en un point est la perpendiculaire au plan tangent en ce point),cet ensemble peut être vu comme l’ensemble des rayons lumineux d’un appareil d’optique. À part les sphères dont les normales convergent en un point, toute optique est toujours imparfaite. Les nappes focales sont là où se concentrent les rayons lumineux (et ça y brûle !). Les deux points de concentration de lumière, sur une normale, décrivent en général deux surfaces, dont les points de contact sont différents, ce qui définit l’astigmatisme de cette optique (tels malheureusement que le plus souvent nos yeux). Pour trouver ces surfaces focales, il fondamental de remarquer que, lorsqu’on considère les normales à la surface le long d’une courbe quelconque, on obtient une surface réglée. Mais si la courbe est une ligne de courbure, alors ces normales deviennent tangentes à une même courbe. Et réciproquement.
Si maintenant nos deux nappes focales sont dégénérées toutes deux en une courbe, et non une surface, alors les normales le long d’une ligne de courbure passeront par un point fixe, et les points correspondant de la surface formeront un cercle, et il y aura en outre une sphère tangente à la surface tout le long dudit cercle. Ainsi nos surfaces sont des doubles enveloppes de sphère ; pour le tore ce sont les sphères tangentes tout le long d’un méridien et celles tout le long d’un parallèle. À une transformation conforme près (des produits d’inversion) nous retrouvons nos tores
(13), ainsi que leurs Villarceau …
Mars 2010
L’auteur et le site BibNum remercient Lionel Garnier, de l’Université de Bourgogne, de les avoir autorisés à utiliser certaines de ses images.

(1) Villarceau (dont le prénom semble être Antoine-François et le patronyme complet Yvon Villarceau) était en fait un astronome (voir biographie). Une rue de Paris porte son nom à Paris (XVI° arrondissement).
(2) Voir par exemple Berger, Géométrie, section 10.12, ou Berger, L’échelle de Jacob, p. 121.
(3) On trouvera dans Berger-Gostiaux, sections 7.4, la définition de ce nombre. Le lecteur intéressé pourra calculer cet invariant pour deux cercles de Villarceau, à défaut seulement prouver qu’il est non nul.
(4) On sait que l’orthodromie (suivre un grand cercle de la Terre, en bateau ou en avion) est la navigation la plus courte, mais elle oblige à changer de cap en permanence. La loxodromie est une navigation plus aisée (on conserve le même cap), mais le chemin décrit est plus long.
(5) On trouvera cet exposé, i.e. dans le bon langage, algébrique en particulier, dans les sections 10.12, 18.9 et 20.7 de Berger, Géométrie. On ne comprend pas vraiment ce qui se passe sans trois concepts essentiels pour la géométrie des cercles et des sphères de l’espace : l’espace de toutes les sphères, les coordonnées penta-sphériques, le groupe conforme de la sphère, et vient ensuite l’idée de passer par projection stéréographique de l’espace ordinaire à la sphère de dimension trois, qui a l’avantage d’être compacte.
(6) Jacques Hadamard, Leçons de Géométrie élémentaire, Armand Colin 1932 ; René Dontot, Étude élémentaire de la parataxie et des cyclides, Vuibert 1945.
(7) Marcel Berger, Cinq siècles de mathématiques en France, ADPF (Association pour la Diffusion de la pensée française), 2005.
(8) On trouvera aussi une approche des cercles de Villarceau, informelle, par rotation autour de l’axe des plans de coupe du tore, depuis le plan vertical jusqu’au plan vertical en passant par le plan de bitangence, dans le blog d’Alexandre Moatti, « Les cercles du tore ».
(9) On trouvera dans Lebesgue une preuve de « géométrie moderne », à la fois plus rapide mais par contre plus dure à mettre en œuvre complètement pour les passages aller et retour du réel au complexe. À savoir ceci : on fait une inversion. On prend comme centre d’inversion un des points cycliques des cercles méridiens. Alors l’inverse du tore devient un cône de révolution, et le plan de section devient une sphère bitangente à ce cône, leur intersection est alors élémentairement vue comme se décomposant en deux cercles.
(10) Ernest Duporcq, Premiers principes de géométrie moderne l'usage des élèves de Mathématiques Spéciales et des candidats à la Licence et à l'Agrégation, Gauthiers Villars 1912 (réédition Jacques Gabay 1995).
(11) La seconde forme fondamentale d’une surface (en un point) est la forme quadratique qui donne, pour les plans passant par normale en ce point, la valeur de la courbure – en tant que courbe plane – de la section plane de la surface par un tel plan. Cette forme décrit comment la surface est située dans l’espace. Darboux montre que l’existence de beaucoup de sections qui sont des cercles détermine complètement la seconde forme fondamentale.
(12) Voir leur équation dans Berger, Géométrie, Sections 18.10 et 20.7.2, et dans Berger-Gostiaux, sections 10.6.8.2.4 et 10.2.3.
(13) En effet, on montre facilement alors que les deux courbes focales forment nécessairement une paire de coniques dites focales, c’est à dire que chacune d’entre elles est le lieu des points tels que le cône défini par ce point et s’appuyant sur l’autre conique soit un cône de révolution. Dans le cas du tore, ces deux coniques focales dégénèrent en un cercle et son axe (regardez les normales à un tore !).


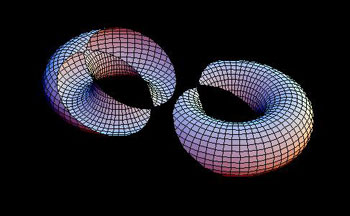








![]()
![]()
![]()
![]() (le signe
(le signe ![]() rappelle que dans une coupe (x,z) donnée, il y a deux plans bitangents, symétriques par rapport à l’axe des x. La bitangence s’exprime donc par r²x² = (R² - r²) z². Le premier cercle de Villarceau relatif à cette configuration a pour centre le point (0, r, 0), l’autre (0, -r, 0). Montrons qu’il s’agit bien d’un cercle, de rayon R, i.e. vérifiant l’équation x² + (y-r)² + z² = R² (en fait le cercle de Villarceau va être l’intersection d’une sphère avec le plan bitangent). Pour ceci, paramétrons y comme suit y = r + Rt. L’équation de la sphère ci-dessus donne x² + z² = R² (1 – t²) Quand on y associe la coupe par le plan bitangent, on obtient
rappelle que dans une coupe (x,z) donnée, il y a deux plans bitangents, symétriques par rapport à l’axe des x. La bitangence s’exprime donc par r²x² = (R² - r²) z². Le premier cercle de Villarceau relatif à cette configuration a pour centre le point (0, r, 0), l’autre (0, -r, 0). Montrons qu’il s’agit bien d’un cercle, de rayon R, i.e. vérifiant l’équation x² + (y-r)² + z² = R² (en fait le cercle de Villarceau va être l’intersection d’une sphère avec le plan bitangent). Pour ceci, paramétrons y comme suit y = r + Rt. L’équation de la sphère ci-dessus donne x² + z² = R² (1 – t²) Quand on y associe la coupe par le plan bitangent, on obtient




 http://fr.wikipedia.org/wiki/Cercles_de_Villarceau Les cercles de Villarceau sur Wikipedia.
http://fr.wikipedia.org/wiki/Cercles_de_Villarceau Les cercles de Villarceau sur Wikipedia.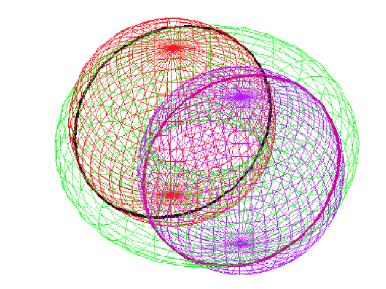 articles de Lionel Garnier, Université de Bourgogne, in Revue électronique francophone d’informatique graphique, article de 2008 (téléchargeable), et article de 2009, avec B. Belbis et S. Foufou (téléchargeable)
articles de Lionel Garnier, Université de Bourgogne, in Revue électronique francophone d’informatique graphique, article de 2008 (téléchargeable), et article de 2009, avec B. Belbis et S. Foufou (téléchargeable) Marcel Berger, Géométrie vivante, ou l’échelle de Jacob, Cassini 2009, ou Geometry revealed, or the Jacob staircase, Springer 2010
Marcel Berger, Géométrie vivante, ou l’échelle de Jacob, Cassini 2009, ou Geometry revealed, or the Jacob staircase, Springer 2010 Marcel Berger, Géométrie, CEDIC/ Fernand Nathan 1978 – épuisé en librairie, mais en cours de réimpression chez Cassini, ou Geometry, Springer 1987.
Marcel Berger, Géométrie, CEDIC/ Fernand Nathan 1978 – épuisé en librairie, mais en cours de réimpression chez Cassini, ou Geometry, Springer 1987. Berger & Gostiaux, Géométrie différentielle : variétés, courbes et surfaces, PUF 1992.
Berger & Gostiaux, Géométrie différentielle : variétés, courbes et surfaces, PUF 1992. Marcel Berger, Cinq siècles de mathématiques en France, ADPF (Association pour la Diffusion de la pensée française) 2005
Marcel Berger, Cinq siècles de mathématiques en France, ADPF (Association pour la Diffusion de la pensée française) 2005






