Luca Pacioli : la multiplication des multiplications

Figure 1 : Luca Pacioli (v. 1445-1517), ca 1495, tableau attribué à Jacopo de Barbari. Il est accompagné de son élève Guidobaldo, duc d’Urbino, et représenté avec ses principaux titres de gloire : la main sur un livre de géométrie, que certains reconnaissent comme sa traduction d’Euclide en latin ; à droite un gros volume qui est peut-être sa Summa de Arithmetica (sa Divina proportione, qui serait plus vraisemblable dans ce contexte de géométrie, n’est pas aussi volumineuse) ; deux polyèdres, celui de droite est un dodécaèdre régulier ; et une figure géométrique sur une ardoise, qui porte la mention EVCLIDES à l’extérieur de son cadre, et dans l’angle de laquelle on aperçoit sur la peinture originale une addition par écrit, et donc en nouveau calcul (Musée de Capodimonte, Naples | Wikimedia Commons)

Au xxi^e siècle, nous pratiquons la numération de position comme Monsieur Jourdain faisait de la prose, sans en être conscients. Et nous l’habillons de chiffres que nous appelons arabes – à tort, puisqu’ils sont d’origine indienne – tout aussi naturellement, sans nous poser de questions. Parce que c’est le moyen le plus pratique d’écrire les nombres. Et que nous n’avons donc pas de raison d’en changer.

Mais la numération de position et les chiffres arabes n’ont pas été adoptés parce qu’ils étaient pratiques. Ils sont entrés dans notre civilisation parce qu’un nouveau calcul venu d’Orient, beaucoup plus efficace, et qu’on réalisait dorénavant par écrit, nécessitait cette numération. Il permettait notamment d’effectuer une multiplication bien plus facilement qu’avec des jetons^[1].

C’est pour présenter ce nouveau calcul à ses contemporains italiens que Luca Pacioli a écrit son énorme ouvrage, publié en 1494. Son texte constitue bel et bien un summum – une summa comme il le dit en italien – en montrant tout ce qu’on peut tirer de la nouvelle technique. Léonard de Pise l’avait certes précédé, mais longtemps avant l’imprimerie, sous la forme d’un manuscrit au « tirage » par définition très restreint ; à une époque où le commerce et la banque étaient beaucoup mois développés ; et en latin de surcroît[2]. Tandis qu’en 1494, un tel traité tombait à pic dans un sol fertile, où la « demande » était bien plus forte.

Désireux de montrer tout ce que peut fournir le nouveau calcul, Pacioli a décrit huit (!) manières différentes d’effectuer une multiplication. Les six premières consistent en l’application d’une recette – pour nous d’un algorithme – et les deux dernières en l’utilisation de propriétés, en vue desquelles l’utilisateur choisit ses décompositions (et comme nous le verrons, celles de Pacioli ne sont pas les meilleures !). C’est le passage que nous avons retenu. Car c’est notamment pour réaliser ces multiplications qu’on a besoin de la numération de position.

Figure 2 : Page de garde de l’ouvrage de L. Pacioli (édition de Toscolano, 1523) (numérisation ETH Zurich)

 [Extrait 1] En pains d’épices (bericuocoli), ou en échiquier

[texte] Mettons que tu veux multiplier 9876 par 6789, avec autant de chiffres à l’un qu’à l’autre […]

La première impression que nous donne cette multiplication, c’est qu’elle est pareille à « la nôtre » ; et cela nous est confirmé par la description de son mode opératoire, qui suit parfaitement l’algorithme classique. Mais un détail retient ensuite l’attention : le texte mentionne la main, dont le rôle est de mémoriser les retenues plutôt que de les écrire en petit quelque part, comme on nous l’apprend à l’école. L’auteur dit de les mettre « dans la main », et il fait ainsi référence à une numération oubliée de nos jours, la numération digitale[3].

Plus précisément, les retenues sont dites une fois « tenues en mains », ce qui permet d’être certain qu’il s’agit de numération digitale – outre qu’on en a la confirmation par le tableau des mains, quelques pages plus loin –, et plusieurs autres fois simplement « tenues », certainement pour éviter la répétition, mais peut-être aussi parce que rien n’empêche de les garder en tête. On peut d’ores et déjà signaler que les mêmes termes apparaissent dans les procédés Colonna, Crocetta, Quadrilatero et Gelosia. Une autre différence que présente cette multiplication, vis-à-vis de celle que nous utilisons aujourd’hui, c’est que chaque chiffre multiplicateur y est barré après épuisement.

[Extrait 2] Tableau de la numération digitale

On saute dix folios plus loin – vingt pages en termes modernes – pour tomber sur une image célèbre, souvent reproduite mais pas toujours bien commentée, et qui prend ici tout son sens : comment montrer les unités, les dizaines, les centaines et les milliers sur les deux mains ? Donc jusqu’à 9999 si l’on utilise les deux mains. Il est vrai que le plus souvent les calculateurs n’avaient besoin d’aller que jusqu’à 99, et ne se servaient donc que d’une main.

Ce tableau illustre certes l’expression « dans la main » rencontrée dans l’extrait précédent – et qui réapparaîtra dans les suivants –, mais il montre surtout que les lecteurs de Pacioli savaient ce que signifiait « dans la main » : ces dessins n’apparaissent en effet que vingt pages après la description de la première multiplication, après quinze pages après la description de la huitième ; et uniquement comme un rappel accompagné d’un commentaire très succinct. Celui-ci ne comporte que quelques lignes, à la page qui précède le tableau, où l’auteur dit qu’elle permet de calculer « plus légèrement » (piu legiermente).

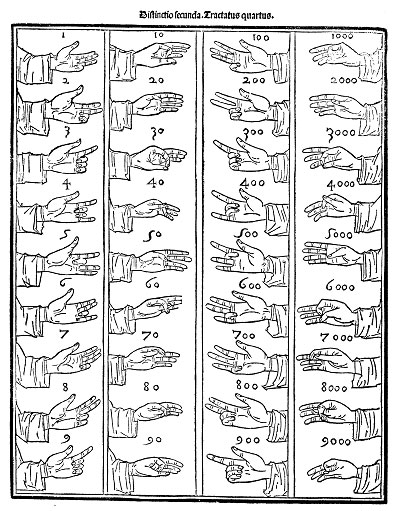
On rappellera que la plus ancienne description de la numération digitale, en latin et sans dessins, se trouve dans un ouvrage de Bède le Vénérable datant de 725 ; cela quand bien même cette manière de montrer les nombres était connue des Grecs et des Romains, et était donc pratiquée depuis mille ans au moins. C’est l’occasion de rappeler un souci permanent des historiens du calcul : avant l’imprimerie, et par souci d’économie, on n’écrivait pas ce que tout le monde savait. Alors quand un procédé – notamment une méthode de calcul – était connu de tous, parce que tous les enfants l’apprenaient, on n’en parlait pas dans les ouvrages… et l’historien moderne a beaucoup de peine à reconstituer son puzzle !

Par rapport à la description de Bède, le tableau de Pacioli reflète un changement qui est attesté dans d’autres textes de la Renaissance, et qui s’était donc généralisé à cette époque : c’est l’inversion des centaines et des milliers à la main droite : chez Pacioli les centaines se montrent avec les trois doigts mineurs (index, annulaire et auriculaire), tandis que chez Bède ces doigts servent à montrer les milliers ; et réciproquement.

 [Extrait 3] Châtelet

En italien, un castello est un château. Et le suffixe -ucio marque la mauvaise qualité, ou le mépris. Un castellucio est donc un vilain château, ou un château moche. Mais comme on ne voit pas pourquoi le procédé proposé ressemblerait à un château minable, nous préférons opter ici pour un simple diminutif.

[texte] D’abord on multiplie les milliers de l’un des nombres par tout l’autre nombre et on le met en tête. Ensuite on multiplie les centaines par l’autre […]

Cette méthode est très proche de la première (extrait 1) – c’est « la même chose à l’envers » –, mais elle n'est pas habituelle. Et un peu déroutante pour le lecteur moderne. Pacioli y pratique la preuve (Prova) par 7 (Per 7) : il réduit les deux facteurs modulo 7, trouve 6 dans les deux cas, puis fait le produit de ces deux 6 qu’il réduit à nouveau modulo 7, ce qui donne 1 ; les trois résultats intermédiaires (6, 6 et 1) sont écrits à droite des facteurs ; il réduit ensuite à son tour le résultat de la multiplication modulo 7, et trouve 1 qu’il écrit entre deux points – comme tous les nombres dans son texte – tout à droite, ce qui constitue la preuve espérée.

[Extrait 4] Colonne

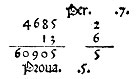
[texte] La troisième manière est dite multiplier en colonne ou aussi par tablette ; elle est utilisée le plus fréquemment quand on a deux nombres dont l’un est grand et l’autre relativement petit, qu’on peut calculer avec peine, comme par exemple 13 par 4685, où le plus petit se fait tout d’un trait, comme s’il était un seul chiffre. Dis-le, 13 par 5 fait 65, pose 5 et tiens 6. Ensuite 13 par 8 fait 104 et 6 que tu tenais fait 110 pose zéro à côté de 5 sous la règle et tiens 11 […]

Il s’agit à première vue – pour nous – d’une manière un peu ardue de multiplier, relevant en partie du calcul mental. Mais le verbe « tenir » (tieni, teniui) nous en détrompe immédiatement : Pacioli sous-entend de tenir dans la main, et donc de recourir ici aussi à la numération digitale. Du même coup, le procédé cesse d’être ardu pour nous : la mémoire intermédiaire, qui stocke les retenues, est organique et ne fatigue pas l’esprit.

Comme il est question de retenir 11 – certainement sur une seule main, mais le raisonnement resterait valable avec le recours à deux mains – on est renforcé dans l’idée qu’ici aussi Pacioli fait appel à la numération digitale, et selon le tableau reproduit comme notre extrait n° 2.

[Extrait 5] Petite croix, ou casier

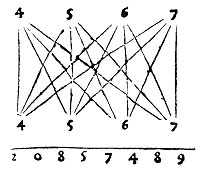
[texte] Et ainsi, si l’on avait à multiplier quatre chiffres par quatre chiffres comme par exemple 4567 par 4567, dispose-les un peu largement comme tu le vois, et commence avec les premiers [chiffres] et dis 7 par 7 fait 49, pose 9 et tiens 4, et ensuite vas aux deuxièmes. Et dis les croix 6 par 7, 42, et 6 par 7, 42, joints ensemble fait 84, et 4 que tu tenais fait 88, pose 8 et tiens 8 ; puis viens aux troisièmes, et tu diras 5 par 7, 35, et 5 par 7, 35, puis ceux du milieu seulement 6 par 6 fait 36, alors joins ensemble ces 3 multiplications, c’est-à-dire 35, 35 et 36, font 106 et 8 que d’abord tu tenais font 114, pose 4 et tiens 11. Ensuite viens aux derniers en croix avec les premiers, et dis 4 par 7, 28, et 4 par 7, 28, ensemble fait 56, et 11 que tu tenais fait 67 […]

C’est le procédé le plus remarquable dans la panoplie multiplicative de Pacioli. A première vue, il apparaît comme complètement tordu, et pas raisonnablement utilisable, même avec des nombres de grandeur raisonnable ; c’est ce qu’on en a pensé jusque tout récemment. Mais quand on connaît la numération digitale, et qu’on voit qu’elle fait partie intégrante du procédé, l’impression change du tout au tout : on voit c’est un moyen qui ne fatigue pas la tête, qui permet d’écrire le résultat progressivement – on a envie de dire goutte à goutte –, et qui est de ce fait le plus économe en papier de tous ceux présentés dans l’ouvrage !

Léonard de Pise avait exposé ce procédé en 1202 déjà, dans son Liber abaci rédigé en latin. Il appelait cette multiplication in cruce (en croix), et sa redoutable efficacité n’a été comprise que tout récemment – comme pour Pacioli –, à la lumière de la numération digitale redécouverte. C’est dire d’une part qu’il a été en usage très longtemps, mais surtout que sa présence chez Pacioli pourrait servir de preuve supplémentaire, si c’était nécessaire, que la numération digitale était encore d’actualité en Italie à la fin du xv^e siècle.

L’auteur avance progressivement. Il commence par appliquer sa crocetta aux multiplications 37×37 puis 456×456, qu’il développe sans reprendre son souffle. Et tout au long, il dit de « tenir » la retenue, en précisant parfois que cela se fait « dans les mains », ale mani ou ailleurs alemani. Il décortique ensuite 4567×4567 – c’est l’extrait que nous avons choisi – toujours d’une traite. Et c’est un des endroits où apparaît une fois de plus la preuve indiscutable du recours à la numération digitale. Parmi toutes ses retenues, on en rencontre d’abord une de 11, et une autre de 12. Or si l’on peut éventuellement comprendre jusqu’à 10 qu’il utilise notre système moderne, avec 5 sur une main et 5 sur l’autre – ce qui serait peu commode, car il devrait poser sa plume, et perdrait tout le bénéfice de l’écriture du résultat goutte à goutte –, toute hésitation est balayée par ces deux dernières retenues : elles ne sont possibles sur les mains qu’en numération digitale !

Et si cela ne suffisait pas... Il n’y a pas que les retenues dont Pacioli dit de les « tenir ». On monte à des nombres beaucoup plus élevés quand on regarde de près ses calculs, et notamment l’étape la plus longue de cette multiplication, qui débute à la septième ligne de notre extrait :

[…] dis 4 par 7, 28, et 4 par 7, 28, ensemble fait 56, et 11 que tu tenais fait 67 ; et ensuite en croix ceux du milieu, c'est-à-dire les troisièmes avec les deuxièmes, et dis 5 par 6, 30, et 5 par 6 etc.

Ce moment est particulièrement éclairant. A 56, l’auteur dit à son lecteur d'ajouter 11 « que tu tenais », ce qui fait 67. Il lui fait réaliser ensuite deux calculs qui totalisent 60, un nombre auquel il dit d’ajouter ces 67 « que tu avais » pour obtenir 127. C’est donc bien 67 que le calculateur devait retenir à ce stade. Et cela n’est possible dans la main qu’avec la numération digitale.

On voit aussi, quand il dit « pose 7 et tiens 12 », qu’il écrit le résultat de sa multiplication étape par étape. Et qu’il n’écrit que cela. En d’autres termes – et au contraire de tous les autres procédés décrits – celui-ci ne nécessite aucune notation intermédiaire. Le résultat apparaît goutte à goutte sous la plume du calculateur. Ce qui présente l’avantage supplémentaire – outre l’élégance du procédé – d’économiser du papier. Or le papier était très cher, à l’époque de Pacioli…

[Extrait 6] Quadrilatère

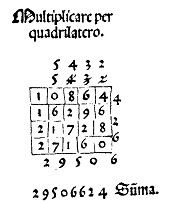
[texte] Comme tu le vois par exemple, mettons qu’on ait à multiplier 5432 par 5432. Commence par les premiers chiffres et dis 2 par 2 fait 4. Ce qu’écris dans le premier carré du quadrilatère. Et ensuite dis 2 par 3 fait 6, ce que mets dans le deuxième carré. Et ensuite dis 2 par 4 fait 8 et mets-le dans le troisième carré. Et ensuite dis 2 par 5 fait 10, et pose 10 c’est-à-dire toujours un chiffre par carré, le zéro dans le quatrième carré et le 1 dans le cinquième […]

Maintenant il faut rassembler ces multiplications, qu’il faut rassembler de cette manière : c’est-à-dire toujours en diagonale de coin à coin, et commencer par le premier carré. Et dis 4 et pose 4 en-dessous contre le quadrilatère ou à côté des susdits carrés. Et ensuite viens aux carrés suivants où tu vois 6, et dis 6 et 6 fait 12, pose 2 et tiens 1. Et ensuite viens à l’autre carré où il y a 8, et dis 8 et 1 que tu as tenu fait 9 et 9 qui suit dans l’autre carré fait 18 et 8 fait 26 et pose 6 et tiens 2. Et viens à l’autre carré où il y a 0, et dis 2 que tu as et 2 qui suit dans l’autre carré fait 4 et 2 dans l’autre fait 6 et pose 6 à côté des autres et viens à l’autre carré où il y a 6 et dis 6 et 7, 13, et 6, 19 et 1 fait 20, pose 0 et tiens 2, et viens au carré où il y a 1. Et dis 1 et 1, 2 et 1, 3 et 2 que tu tenais fait 5 et pose 5 à côté de l’autre. Et ensuite viens à l’autre carré où il y a 7 et dis 7 et 2, 9 et pose 9. Et ensuite viens au dernier carré où il y a 2 et pose 2 dans l’ordre avec l’autre. Et voilà finie notre multiplication qui fait en tout 29506624.

C’est le procédé que Léonard de Pise appelait l’échiquier. Et c’est une multiplication fortement apparentée aux deux premières, avec en plus une originalité : son addition finale, qui évite les décalages ou la présence de zéros.

On remarque qu’ici aussi, comme dans le procédé des pains d’épices (extrait n° 1), les chiffres du multiplicateur sont barrés après épuisement. Et comme dans la crocetta ci-dessus (extrait 5), le résultat apparaît goutte à goutte, mais seulement à la fin, et sans économie de papier.

C’est l’introduction qui pourrait nous poser un problème : la phrase où Pacioli dit que cette manière « ne nécessite pas de tenir en tête les dizaines » (non bisogno tenere amente le dicine) est étrange, car cette méthode nécessite bel et bien de retenir les dizaines ; et surtout, dire au lecteur de les retenir en tête est contradictoire vis-à-vis de tout ce que nous avons souligné précédemment concernant la numération digitale. Mais on devine ce que veut dire l’auteur, qui le fait maladroitement : les dizaines s’intègrent mécaniquement l’une après l’autre dans le produit élémentaire suivant, elles passent donc par la tête et en ressortent immédiatement, ce qui se fait comme un automatisme ; et cela ne constitue donc pas un véritable effort à fournir avec la tête.

[Extrait 7] Jalousie ou grillage

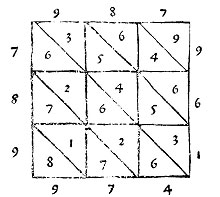
[texte] mettons que tu as à multiplier 987 par 987. Tu feras un carré, divise son côté en autant de parties qu’il y a de chiffres, soit ici 3. Et au-dessus de chaque partie pose un chiffre, et un sur le côté comme tu vois sur la figure dessinée ici. Et dis 7 par 7, 49 et tout cela sans tenir en tête les dizaines, mais fais en sorte de mettre un de ces chiffres, soit le nombre [le chiffre des unités] au-dessus de la diagonale du carré, et l’autre au-dessous soit les dizaines. Et ensuite dis pour l’autre 7 par 8, 56 et pose-le dans le carré suivant, le 6 au-dessus de la diagonale et le 5 au-dessous comme tu as fait dans l’autre […]

[ensuite, dans les rubans diagonaux du coin supérieur droit vers le coin inférieur gauche] additionne-les en diagonale en commençant par le premier, 9, et mets-les en face de leur file et pose 9. Et ensuite dis pour l’autre bande 6 et 4 et 6 font 16, et pose 6 à sa place et tiens un pour la dizaine et ensuite continues subséquemment et ce sera bien ; en faisant la preuve comme on l’a dit ci-dessus etc. La dite jalousie se fait d’une autre manière, c’est-à-dire dans l’autre sens. Comme déjà dit, ainsi que tu vois ici sur le dessin, en multipliant le tout on pose sans tenir en tête quoi que ce soit […]

[ici le résultat 987 × 987 = 974 169]

On admire d’abord l’introduction ! Et ensuite l’élégance du procédé, qui fait que certains élèves – c’est l’expérience des auteurs de ces lignes – demandent qu’on l’enseigne en lieu et place de celui qui figure au programme de toutes nos écoles !

La grande force de cette multiplication est l'absence de retenues lourdes, puisqu’on atteint rarement 2 dans les additions en diagonale, dans une jalousie de trois sur trois. Pacioli le voit bien, en insistant sur le fait que dans les multiplications élémentaires il n’est pas nécessaire de « tenir en tête les dizaines » (senza tenere amente le dicine), puisqu’on les écrit directement dans le carré correspondant. C’est sa façon de dire que le calculateur fait encore moins d’efforts que dans le procédé précédent, puisqu’ici les dizaines ne passent pas du tout par sa tête.

[Extrait 8] Repiego

On quitte ici les algorithmes – on en a vu six –, pour aborder une nouvelle catégorie de procédés… qui relèvent plutôt de la théorie que de la pratique. Mais comme on l’a dit, Pacioli voulait être complet ! Les deux procédés qu’il présente sont fondés sur la décomposition de l’un des facteurs, après quoi ils exploitent diverses propriétés.

Le premier est appelé repiego par notre auteur. Qui explique – un peu maladroitement – que le repiego d’un nombre est sa décomposition en un produit de deux autres nombres, qu’on appelle ses repieghi (le pluriel de repiego). Ce mot est certainement une image, comme pour le procédé qui suit. Et du seul fait qu’il l’explique, on peut tirer qu’il ne pensait pas que cette image serait évidente pour ses lecteurs. Mais qu’a-t-il voulu évoquer ? En italien actuel, un ripiego est une ressource, un moyen ou un remède ; et le verbe ripiegare signifie replier, ou émousser. Quel rapport avec la décomposition d’un nombre en produit de deux autres ? Nous laissons nos lecteurs imaginer une réponse, raison pour laquelle nous avons conservé le terme original dans notre traduction !

Pour appliquer le procédé du repiego, on commence par décomposer l’un des facteurs de la multiplication, et on applique ensuite la propriété selon laquelle pour multiplier A par B, si A a été préalablement décomposé en ab, on peut calculer d’abord aB, et multiplier ensuite le résultat par b :

si A = ab   AB = (aB)b

En termes modernes, après avoir fait la décomposition, on applique les propriétés d’associativité ou de commutativité de la multiplication. C’est ce qu’on voit dans l’exemple que donne Pacioli :

24 × 29 = 6 × 4 × 29 (décomposition) = 6 × (4 × 29) (associativité) = 6 × 116 = 696

ou :

24 × 29 = 4 × 6 × 29 (décomposition) = 4 × 29 × 6 (commutativité) = 116 × 6 = 696.

[Extrait 9] Décapitation

À l’heure actuelle, scapezzare signifie étêter ou écimer, et s’emploie en arboriculture. Le nom d’aschapezzo donné à cette multiplication pourrait donc évoquer une décapitation. Et à nouveau, on se demande quelle image Pacioli avait en tête…  La suite de son texte montre que cette multiplication est une sœur de la précédente, à ceci près qu’au lieu d’un fractionnement multiplicatif de l’un des facteurs, l’auteur pratique ici un fractionnement additif. Sa décapitation est donc en fait un découpage en morceaux !

Pour multiplier A par B, il décompose A en addendes, puis multiplie chacun de ces addendes par B :

si A = a + b + c + d   AB = aB + bB + cB + dB

Les propriétés invoquées cette fois sont la décomposition en somme, et la distributivité. On le voit dans son exemple :

24 × 42 = (4 + 6 + 5 + 9) × 42 (décomposition en somme)

= 4 × 42 + 6 × 42 + 5 × 42 + 9 × 42 (distributivité)

= 168 + 252 + 210 + 378 = 1008.

Pacioli ne donne pas ici l’impression d’être très habile, car cette méthode pourrait déboucher sur quelque chose de plus spectaculaire, et surtout de plus facile à calculer :

24 × 42 = (10 + 10 + 4) × 42 = 10 × 42 + 10 × 42 + 4 × 42 = 420 + 420 + 168 = 1008.

[Extrait 10] Les tabelles, ou tables de multiplication

C’est à elles que renvoie l’auteur quand il traite de la méthode du repiego. Mais comme elles peuvent également être utiles dans le procédé de la décapitation, il les fait apparaître après celle-ci.

Il est amusant de voir d’une part quels sont les produits qui lui semblent les plus utiles – il est visiblement fâché avec les facteurs 21 et 22 –, et d’analyser d’autre part sa manière très personnelle de répartir « géographiquement » les cases dans lesquelles il les présente. Dans les deux premières pages, ces cases constituent des groupes de deux grandes colonnes parallèles, du haut en bas de la page – le troisième groupe étant à cheval sur deux pages –, avec à chaque niveau une case à gauche où la progression des unités est à gauche, et une autre à droite où la progression des dizaines est au centre, le produit étant toujours à droite. Le cinquième groupe est consacré quant à lui aux carrés de 11 à 100… avec en bouche-trou, tout en bas à droite, les produits de 11 par les dizaines de 12 à 20.

Quant à la troisième page, l’auteur y a inséré dans une moitié gauche des produits qu’il regrettait certainement de n’avoir pas pu intégrer logiquement aux pages précédentes : les nombres de 12 à 20 multipliés par les nombres de 13 à 20. Puis il a profité de l’espace restant, dans la moitié droite, pour y ranger des produits utiles à Venise – le lieu d’édition de son ouvrage – pour calculer en monnaie locale : de 2 à 10 fois 24, 32 et 36 ; et enfin la conversion en sous et deniers de quelques gros montants en dinars.

En conclusion

Il était important pour Pacioli – et il est tout aussi important pour nous – de rendre hommage à tous ces procédés, qui ont joué un rôle unificateur fondamental. Car durant de nombreux siècles auparavant, l’art d’écrire un nombre et celui de calculer étaient deux activités indépendantes. On calculait physiquement à l’aide de cailloux puis de jetons, et on écrivait les nombres à l’aide de chiffres romains. Et cette façon d’écrire les nombres aurait pu régner encore très longtemps, car elle était efficace. Ce qui a incité à adopter la numération de position, ce n’est pas le fait qu’elle permettait d’écrire les nombres différemment, mais bien le fait qu’elle était nécessaire pour la pratique du nouveau calcul venu d’Orient. Les procédés de multiplication exposés par Pacioli ont donc constitué un maillon indispensable dans la chaîne qui explique la numération que nous pratiquons aujourd’hui.

(mars 2016)