Le Mémoire sur les conditions de résolubilité des équations par radicaux a été déposé par Évariste Galois à l’Académie des sciences en janvier 1831, soit un an avant sa mort à l’âge de vingt-et-un ans. Il s’agit de la troisième version des recherches de Galois à ce sujet : les deux premiers manuscrits, précédemment communiqués à l’Académie, avaient été perdus. Ce dernier travail n’a pas reçu l’approbation de l’Académie, malgré un rapport plutôt encourageant où Poisson et Lacroix invitaient le jeune mathématicien à poursuivre ses recherches en vue de parfaire ses résultats. C’est néanmoins à un autre thème de recherches, les fonctions elliptiques, que Galois a consacré les derniers mois de sa vie. Il est mort en duel en 1832, sans avoir complété son mémoire sur les équations. Celui-ci ne sera finalement publié qu’en 1846 dans le Journal de Liouville.

Figure 1 : Portrait d’Évariste Galois, dessiné par son frère.
Dans ce Mémoire, Évariste Galois a cherché une condition nécessaire et suffisante pour qu’une équation soit résoluble par radicaux, c’est-à-dire pour qu’il soit possible d’en exprimer les racines à l’aide d’opérations algébriques portant sur les coefficients. Au début du XIXe siècle, on savait résoudre les équations de degré 4 ou moins, en calculant explicitement leurs racines. En 1826, le mathématicien norvégien Abel était parvenu à démontrer un théorème dont on pressentait l’exactitude depuis les travaux de Lagrange : la résolution algébrique est impossible pour les équations de degré 5 ou plus
(1). Dans ce contexte, Galois ne cherche pas à obtenir une formule permettant de calculer les racines, mais un critère pour savoir si ce calcul est possible ou non.
Équations du second degré
Par exemple, toutes les équations du second degré (de la forme ax2 + bx + c = 0) sont résolubles algébriquement dans le corps des nombres complexes. Il faut pour cela calculer leur discriminant : Δ = b2 — 4ac.
Les deux racines sont ensuite données par la formule :
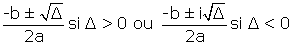
On voit ici que les racines se calculent à l’aide d’opérations algébriques portant sur les coefficients a, b et c de l’équation. Le critère donné par Galois dans son article ne permet pas d’obtenir ces formules ; il assure seulement que toutes les équations de degré deux sont résolubles dans le corps des nombres complexes.
@@@@@@@
1) Les « principes »
Le
Mémoire sur les conditions de résolubilité des équations par radicaux débute par l’exposition des principes sur lesquels repose l’exposé : la notion d’adjonction et les substitutions. Selon la définition qu’en donne Galois, adjoindre une quantité à une équation signifie qu’on la considère comme connue pour la résolution (cf. encadré ci-dessous) ; les fonctions rationnelles alors utilisées pour exprimer les racines sont des fonctions des coefficients de l’équation et de cette quantité. Cette notion, dont on trouve la trace dans les travaux antérieurs d’Abel, constitue une nouveauté par rapport aux recherches menées au XVIIIe siècle : Lagrange et Ruffini
(2) raisonnaient uniquement avec les nombres que l’on pouvait former à partir des coefficients de l’équation. Chez Galois, l’irréductibilité d’une équation est relative aux quantités que l’on y adjoint, ce qui implique que :
« Lorsque nous conviendrons de regarder ainsi comme connues de [sic] certaines quantités, nous dirons que nous les adjoignons à l’équation qu’il s’agit de résoudre (…) L’adjonction d’une quantité peut rendre réductible une équation irréductible. »
Adjoindre une quantité
Donnons un exemple pour éclaircir cette notion d’adjonction. Une équation de degré 2 de discriminant négatif n’admet pas de racine réelle (voir encadré précédent). On dit qu’elle est irréductible dans le corps des nombres réels. Par contre l’équation devient réductible si l’on se place dans le corps des nombres complexes, c’est-à-dire si l’on adjoint la quantité i, définie par i2 = -1. Les racines s’expriment alors en fonctions des coefficients de l’équation et de la quantité i.
La deuxième notion préliminaire introduite par Galois est celle de substitution, comme « passage d’une permutation à l’autre ». L’idée de lier l’étude des équations à celle des permutations de leurs racines remonte aux travaux de Lagrange et de Vandermonde
(3) publiés à la fin du XVIIIe siècle
(4). Il suffit de penser à un des rapports rédigé en 1813 par l’académicien Poinsot pour se convaincre que ce principe était encore considéré au début du XIXe siècle comme une piste féconde pour les recherches en théorie des équations :
« Les principes qui regardent ce problème [la résolution algébrique] résident essentiellement dans la théorie des combinaisons et celle des nombres. C’est ce que l’on peut démontrer par la nature des choses et, […] s’il est possible de l’avancer encore, ce n’est que par des idées du même genre et par quelques éléments nouveaux qui manquent encore à la théorie des permutations. »
(5)Les recherches de Galois s’inscrivent donc parfaitement dans les problématiques de son époque quant aux moyens à mettre en œuvre. Les définitions qu’il donne des termes « substitution » et « permutation » sont empruntées aux articles publiés par Cauchy en 1815
(6). Il faut préciser ici que la théorie des permutations était encore bien peu défrichée, puisque Abel et Galois étaient les deux seuls mathématiciens à avoir exploité les résultats obtenus par Cauchy. De plus, les articles de 1815 ne font qu’esquisser les contours d’une théorie à laquelle Cauchy ne donnera une forme plus aboutie qu’en 1844
(7). Ceci explique que Galois n’ait pas une parfaite maîtrise de ces notions : il semble bien connaître ces travaux, comme le montre l’allusion qu’il y fait ensuite dans la proposition VII, mais de nombreuses confusions entre les termes de « groupes de permutations » et de « groupes de substitutions » demeurent dans son mémoire. Ainsi, Galois définit le groupe d’une équation comme « groupe de permutations » des racines, tout en précisant ensuite que :
« dans le groupe de permutations dont il s’agit ici, la disposition des lettres n’est point à considérer, mais seulement les substitutions de lettres par lesquelles on passe d’une permutation à l’autre ».
Permutations et substitutions – exemple d’un groupe de substitutions
- Une permutation de n lettres distinctes est une liste ordonnée de ces lettres. Exemple : (1,2,3,4,5) et (2,5,3,1,4) sont des permutations de 5 lettres.
- Les substitutions sont les opérations qui consistent à passer d’une permutation à une autre. En 1844, Cauchy a introduit pour cela une notation en deux lignes. Exemple : la substitution 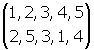 transforme 1 en 2, 2 en 5, 4 en 1 et 5 en 4.
transforme 1 en 2, 2 en 5, 4 en 1 et 5 en 4.
Si l’on s’en tient à la définition moderne d’un groupe, ce sont les substitutions de n lettres et non les permutations qui forment un groupe.
Ce que Galois appelle un « groupe de permutations », c’est l’ensemble qu’il note sous forme « matricielle » p. 422, qui n’est pas un groupe au sens moderne. La citation atteste en revanche qu’il s’intéresse également au (« vrai ») groupe que l’on peut construire à partir de ces permutations, bien que celui-ci ne soit pas explicité.
@@@@@@@
A titre d’exemple d’un groupe de substitutions au sens moderne du terme, le groupe S3 des substitutions de trois éléments 1, 2, 3 se compose des six substitutions suivantes : l’identité Id, la substitution circulaire s1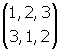 , la substitution circulaire s2
, la substitution circulaire s2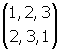 , la transposition t1
, la transposition t1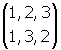 , la transposition t2
, la transposition t2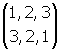 , la transposition t3
, la transposition t3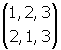 .
.
La table de ce groupe est la suivante :
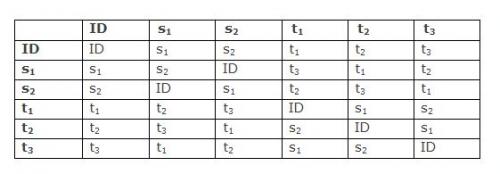
On peut aussi noter que Galois ne reprend pas la notation en deux lignes pour les substitutions introduite par Cauchy. L’obscurité du mémoire de Galois pour le lecteur contemporain est en grande partie due à l’utilisation approximative des notions de substitution et de permutation. Il devait en être de même pour les mathématiciens du début du XIXe siècle, peu habitués à en faire un usage abstrait : si Lagrange les avait utilisées dans ses recherches sur les équations, il s’agissait alors davantage d’un procédé calculatoire que d’un outil conceptuel.
L’exposé des « Principes » se termine par quatre lemmes relatifs à la théorie des équations. Le premier a pour énoncé :
Lemme I. « Une équation irréductible ne peut avoir aucune racine commune avec une équation rationnelle sans la diviser ».
Ce lemme signifie que si un polynôme irréductible P a une racine commune avec un autre polynôme f, alors f peut s’écrire : f(x) = P(x) × Q(x).
Il n’est peut-être pas inutile ici de donner un exemple en se plaçant dans le corps des nombres réels.
Le polynôme P(x) = x2 + 1 est irréductible dans R. Ses racines dans C sont i et – i.
Le polynôme f(x)= x3 - x2 + x - 1 n’est pas irréductible dans R (puisque 1 est racine). Dans C, ses racines sont 1,i et –i.
On peut écrire : f(x)= P(x) × (x-1)
Ce résultat n’est pas inédit, il avait déjà été démontré par Abel, dans un « Mémoire sur une classe particulière d’équations résolubles algébriquement » paru dans le Journal de Crelle en 1829.
Pour les second et troisième lemmes, Galois reprend l’idée fondamentale des fonctions semblables que Lagrange développe dans les « Réflexions sur la résolution algébrique des équations » de 1770 : il cherche une fonction V des racines prenant n! valeurs distinctes par permutations des racines. Cette fonction sera alors semblable à une fonction qui donne les n racines de l’équation de départ :
Lemme II. « Étant donné une équation quelconque, qui n’a pas de racines égales , dont les racines sont a,b,c,…, on peut toujours former une fonction V des racines, telle qu’aucune des valeurs que l’on obtient en permutant dans cette fonction les racines de toutes manières, ne soient égales. »
Lemme III. « la fonction V étant choisie comme il est indiqué dans l’article précédent, elle jouira de cette propriété, que toutes les racines de l’équation proposée s’exprimeront rationnellement en fonction de V ».
Expression rationnelle et résolvante
Une fonction rationnelle est le quotient de deux polynômes.
Au sens où l’entend Galois, dire que les racines peuvent s’exprimer rationnellement en fonction de V signifie que l’on peut écrire chaque racine xi sous la forme :
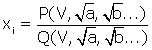 , où P et Q sont deux polynômes.
, où P et Q sont deux polynômes.
On peut donner comme suit l’exemple d’une résolvante : V(x,y) = x² + y², où x et y sont solutions d’une équation du second degré X² + PX + Q = 0, est invariante par les deux substitutions du groupe S2, Id et s substitution des racines. On peut dans ce cas montrer que V s’exprime rationnellement en fonction des coefficients de l’équation : V (x,y) = (x+y)² - 2xy = P² - 2Q.
Galois se place donc, là encore, dans un schéma de résolution conforme aux pratiques algébriques de son époque, qui consiste à passer par une étape intermédiaire en définissant une fonction résolvante.

Figure 2 : La fameuse « note XIII » de l’ouvrage de Lagrange sur les équations que Galois a étudiées alors qu’il était au lycée.
@@@@@@@
2) La théorie
Les recherches originales de Galois, ce qu’il appelle sa « théorie », ne débutent qu’après le rappel de ces principes trop connus selon lui pour qu’il soit nécessaire d’en fournir de nouvelles démonstrations.
De nombreuses démonstrations sont à peine esquissées, voire tout simplement absentes, du Mémoire sur les conditions de résolubilité des équations par radicaux. À ce propos, on entend souvent que Galois est mort trop jeune et trop précipitamment pour parfaire sa théorie.
Toutefois, il est très probable que l’absence des démonstrations de ces lemmes soit un choix et non une nécessité. En effet, dans la préface qu’il avait écrite pour le Mémoire, et qui n’a pas été publiée dans le Journal de Liouville, il explique qu’il est inutile de « reprendre dans ses éléments toute une théorie, sous le prétexte de la présenter sous une forme nécessaire à l’intelligence »
(8).
La proposition I définit le « groupe d’une équation » comme un groupe de permutations des racines :
« Soit une équation donnée dont a, b, c, … sont les m racines. Il y aura toujours un groupe de permutations des lettres a,b,c,… qui jouira de la proposition suivante :
1°. Que toute fonction des racines, invariable par les substitutions de ce groupe, soit rationnellement connue ;
2°. Réciproquement, que toute fonction des racines, déterminable rationnellement, soit invariable par les substitutions. »
La démonstration de Galois consiste à exhiber le « groupe » et à montrer qu’il vérifie les propriétés demandées. Il faut noter, cependant, que Galois ne cherche nullement à prouver qu’il s’agit bien là d’un groupe au sens moderne du terme : le groupe d’une équation est pour lui un ensemble organisé, c’est-à-dire qui peut être écrit sous forme de tableau, et non un ensemble fermé pour la multiplication.
Les propositions II et III établissent ensuite le lien entre le groupe de l’équation et les quantités adjointes : l’adjonction d’une nouvelle grandeur provoque un partage du groupe de l’équation en un certain nombre de groupes plus petits et comparables (ce sont, en langage moderne, des sous-groupes normaux du groupe de départ). On peut alors recommencer le raisonnement avec le nouveau groupe obtenu, et ainsi de suite. La démonstration de la proposition II est incomplète : en fait, la forme de la factorisation après adjonction d’une nouvelle quantité de l’équation dont la résolvante V est une racine n’est pas aussi « claire » que Galois l’affirme, et ce point sera l’objet de l’attention de nombreux successeurs de Galois. Quant à la proposition III, elle est énoncée sans démonstration.
Dans la proposition II, Galois affirme que si l’adjonction d’une racine r d’une équation auxiliaire rend réductible l’équation étudiée, alors le polynôme P dont la résolvante est racine se factorise en :
P(V) = f(V,r) × f(V,r’) × f(V,r’’)…, où r, r’, r’’, … sont les différentes racines de l’équation auxiliaire de la résolvante, et la fonction f toujours la même.
Toutefois, cette décomposition n’a rien d’une évidence puisque, après adjonction d’une quantité r, si l’on applique les résultats usuels de factorisation des polynômes, on obtient plutôt une décomposition de la forme :
P(V) = f(V,r) × f1(V,r) × f2(V,r)…, où les fonctions fi sont différentes, mais font intervenir les mêmes variables V et r.
Dans la proposition V du mémoire, Galois montre que l’équation initiale est résoluble par radicaux si, au terme du processus, on obtient un groupe qui ne contient plus qu’un seul élément :
« Pour résoudre une équation, il faut successivement abaisser son groupe jusqu’à ne contenir plus qu’une seule permutation ».
Exemple des propositions II et V appliquées à une équation du 4° degré particulière
On prend l’équation x4 – 5x² + 6 = 0 ; elle se factorise en (x² - 2)(x² - 3) = 0 et a pour racines ±√2 et ±√3. Il existe à l’origine un groupe de 4 substitutions permutant ces racines : Id, X (inversant √2 et √2, laissant fixe √3 et - √3), Y (inversant √3 et -√3, laissant fixe √2 et -√2), Z = XoY (inversant √2 et -√2, inversant √3 et -√3). Il s’agit du groupe de Galois particulier à cette équation.
En appliquant la proposition II, et en adjoignant successivement les quantités √2 et √3, on réduit progressivement le groupe de Galois (les mathématiciens disent aussi « dévisser » le groupe). Par exemple, dans le corps des rationnels auquel on adjoint √3 (ensemble des « entiers quadratiques » a + b√3, qu’on note Q[√3], il existe de nouvelles relations entre racines au sein de Q[v3], rendues possibles par cette extension de Q (par exemple 2√3 × √3 + √3 × (√3) = 3, polynôme des racines √3 et -√3, en gras, qui reste dans Q[√3]). Dans cette extension, les substitutions Y et Z ne préservent plus ce polynôme, tandis que X (inversion des racines √2 et -√2) le préserve encore : le groupe de Galois initial Id, X, Y, Z a été réduit à son sous-groupe Id, X. Quand on adjoint v2, dans le corps Q[√2,√3]) composé des nombres de type a + b √2 + c √3 + d √2 √3, la seule substitution qui conserve le polynôme est Id : pour reprendre l’expression de Galois, on a « abaissé » ainsi le groupe « jusqu’à ne contenir plus qu’une seule permutation » : l’équation est donc soluble par radicaux.
Cet exemple illustre la proposition II « Si l’on adjoint à une équation la racine r d’une équation auxiliaire irréductible 1° il arrivera de deux choses l’une : ou bien le groupe de l’équation ne sera pas changé ; ou bien il se partagera en p groupes appartenant chacun l’équation proposée quand on lui adjoint chacune des racines de l’équation auxiliaire », et la proposition V rappelée ci-dessus « Pour résoudre une équation, il faut successivement abaisser son groupe jusqu’à ne contenir plus qu’une seule »
Toutefois, plutôt que d’énoncer ce résultat sous la forme d’un théorème, Galois décrit de façon algorithmique le mécanisme qui relie le processus d’adjonction à celui de la décomposition du groupe.
Un tel procédé d’écriture est inhabituel au début du XIXe siècle, puisqu’il s’agit d’une narration où les résultats intermédiaires ne sont pas explicités, et non d’une preuve calculatoire. Ainsi, si la proposition V permet de comprendre pourquoi certaines équations seront résolubles et d’autres pas, elle ne dit pas comment on doit s’y prendre concrètement, à partir d’une équation particulière, pour répondre à la question. Selon les critères du début du XIXe siècle, où l’intérêt des mathématiques résidait encore avant tout dans leur applicabilité pratique à des phénomènes concrets, une telle conclusion n’était en aucun cas satisfaisante. C’est d’ailleurs, en substance, ce qu’écrit Poisson dans son rapport :
« [Le mémoire] ne renferme pas […] la condition de résolubilité des équations par radicaux [ …]. La condition de résolubilité, si elle existe, devrait être un caractère extérieur que l’on peut vérifier, à l’inspection des coefficients d’une équation donnée ou, tout au plus, en résolvant d’autres équations d’un degré moins élevé que celui de la proposée »
(9).
Dans les propositions VII et VIII, Galois applique les résultats précédents aux équations irréductibles de degré premier. La proposition VII énonce ainsi le critère dans le langage des groupes :
« Si une équation irréductible de degré premier est soluble par radicaux, le groupe de cette équation ne saurait contenir que des substitutions de la forme xk, xak+b, a et b étant des constantes. »
Enfin, le critère de résolubilité est traduit dans le langage traditionnel des équations dans la proposition VIII :
« Pour qu’une équation irréductible de degré premier soit soluble par radicaux, il faut et il suffit que deux quelconques de ces racines étant connues, les autres s’en déduisent rationnellement ».
Le groupe de résolution d’une équation
La notion de groupe apparaît dans le mémoire de Galois. Page 419, il précise que « si dans un groupe on a les substitutions S et T, on est sûr d’avoir la substitution ST ». Si cette notion est esquissée dans le travail de Galois, elle connaitra d’importants développements au cours du XIXe siècle, développements qui conduiront à une interprétation du Mémoire sur les conditions de résolubilité où le concept de groupe joue un rôle central.
Ainsi, cent ans plus tard, Gustave Verriest, dans un texte de 1934 intitulé Evariste Galois et la théorie des équations algébriques (10) , indique que Galois a permis de découvrir que « le nœud du problème réside non pas dans la recherche directe des grandeurs à adjoindre, mais dans l’étude de la nature du groupe de l’équation. ».
Verriest précise ensuite ce qui constitue, au début du XXe siècle, la représentation canonique du concept de groupe dans le cadre de la résolution des équations :
« Ce groupe exprime le degré d’indiscernabilité des racines : il caractérise donc non pas ce que nous savons des racines, mais ce que nous n’en savons pas (…) il se fait ainsi que deux équations de degrés différents, mais ayant des groupes semblables, se résolvent de la même façon. Ce n’est donc plus le degré d’une équation qui mesure la difficulté de la résoudre, mais c’est la nature de son groupe ».
@@@@@@@
3) Architecture et conception du Mémoire
Le Mémoire sur les conditions de résolubilité des équations par radicaux est rédigé de façon extrêmement concise ; certaines démonstrations sont absentes, d’autres sont incomplètes. On attribue souvent cet inachèvement aux circonstances tragiques de la vie de Galois et à sa mort prématurée, qui l’auraient empêché de mettre au propre ses recherches après la perte des premières versions. Pourtant, l’examen du manuscrit original montre que ce travail, bien qu’inachevé, a fait l’objet de nombreuses corrections et relectures. En outre, Galois l’a jugé suffisamment abouti pour le soumettre à l’Académie. Il s’agit donc d’un travail de recherche à part entière, non d’un résumé des résultats obtenus précédemment : si ce mémoire fut, un jour, dans les versions antérieures soumises à l’Académie, plus complet, les explications que l’on suppose manquantes aujourd’hui le sont seulement parce que Galois a délibérément décidé de ne pas les reproduire dans la dernière version, ou parce que lui-même ne disposait pas encore des démonstrations nécessaires. En faisant abstraction de l’impression d’inachèvement et des imprécisions de vocabulaire qui caractérisent l’ensemble du premier mémoire et donnent une impression uniforme d’obscurité, on peut constater que Galois a traité les trois parties de manières sensiblement différentes. Elles dévoilent la façon dont il concevait ses recherches.
Les « Principes » par lesquels débute le mémoire consistent en « quelques définitions et une suite de lemmes qui sont tous connus ». Les quatre premiers lemmes sont séparés du reste de l’exposé, et Galois n’a pas attaché d’importance à leur démonstration : ils font pour lui partie de la théorie classique des équations et non de celle qu’il veut établir.
Les propositions I à V forment le cœur du mémoire ; y est exposé ce que l’on qualifiera plus tard de « théorie de Galois ». Dans cette partie, Galois établit ainsi le principe de correspondance entre les équations et les groupes de substitutions. Ces propositions font l’objet de preuves abstraites, au sens où les résultats sont décrits en français et non écrits en langage mathématique et où ils sont enchaînés sans que les calculs dont ils résultent ou auxquels ils aboutissent ne soient explicités. Il s’agit de prévoir « la marche de l’analyse », pour reprendre une expression de Galois, c'est-à-dire de décrire quel doit être le déroulement du processus, et non de parcourir l’ensemble des opérations.
La concision de cette partie n’est pas due au manque de temps. En effet, on trouve dans les papiers de Galois une première version de la proposition I sur le groupe d’une équation datant très probablement de juin 1830, et dont la démonstration offre plus de détail que la version définitive. Il en va de même avec la proposition III, dont la version initiale, hachurée lors des corrections, est en fait une application de la proposition précédente aux équations de la forme « xp = a », avec lesquelles Galois a dû se familiariser par la lecture des Disquisitiones Arithmeticæ de Gauss. Dans la version finale du manuscrit, elle a été remplacée par un théorème beaucoup plus général, qui semble découler lui aussi de la proposition II mais qui est énoncé sans démonstration.
Le travail de relecture qu’a fait Galois semble donc plutôt destiné à aller à l’essentiel. De fait, le mémoire sur les conditions de résolubilité des équations offre un bel exemple de pensée mathématique en construction. Galois ne nous a pas laissé la généalogie de ses travaux, mais c’est très probablement en se familiarisant avec la théorie traditionnelle des équations, en apprenant à manipuler des substitutions et permutations à partir d’équations particulières, à la manière calculatoire traditionnelle de Lagrange ou d’Abel, qu’il a formulé ses premières idées sur le lien entre résolubilité et groupe de substitutions des racines. On trouve ainsi sur certains des brouillons conservés de nombreux calculs algébriques, parfois juxtaposés sur une même feuille avec des manipulations sur des permutations de nombres entiers : c’est par la pratique et l’entraînement, par l’immersion dans la théorie classique, en quelque sorte, que Galois est parvenu à ses premiers résultats. Cependant, aucun de ces calculs n’a été conservé lors de la rédaction définitive.

Figure 3 : Exemple de brouillon de Galois qui a été conservé (certains sont nettement plus explicites…)
Ces quelques exemples montrent que Galois ne cherche pas d’emblée à éviter les calculs, ni à se placer au plus grand degré de généralité possible. Les manipulations algébriques concrètes sur des cas particuliers d’équations font partie intégrante de son travail de recherche. Ce n’est qu’une fois qu’il a compris, par induction, quels sont les principes qui régissent ces calculs qu’il les fait disparaître. Comme Galois l’explique dans la préface que Liouville n’a pas reproduite
(11), ce ne sont que des « détails » sur lesquels « l’esprit n’a plus le temps de s’arrêter », qui restent à l’état de brouillons et sont finalement absents de la rédaction du mémoire, très épurée. Une fois acquise l’aisance nécessaire, il s’agit donc pour Galois d’extraire l’essence des calculs, en essayant de comprendre ce qui rend une équation résoluble. La formulation de la théorie générale se fait ainsi par des allers-retours permanents entre cette théorie et les cas particuliers qui en deviennent les applications.
La troisième partie du mémoire, composée des propositions VI à VIII, constitue une illustration de la théorie précédente dans le cas des équations irréductibles de degré premier (c'est-à-dire dont le degré est un nombre premier). Cette application bénéficie d’un traitement plus calculatoire, même si ce terme peut paraître surprenant s’agissant des mathématiques de Galois. En effet, les opérations n’y sont toujours pas effectuées, mais leur résultat apparaît dans le texte en langage algébrique et non en français. Par exemple, Galois prend la peine d’écrire le dernier groupe qui intervient dans la résolution des équations irréductibles de degré premier, ou d’exprimer les substitutions qu’il utilise : l’exposé est plus concret que celui des propositions I à V. Cependant, l’application n’a pas ici de visée pratique, puisque Galois ne fournit pas d’algorithme qui permettrait de décider si une équation donnée est résoluble par radicaux : le résultat final reste théorique. Ainsi, l’application aux équations de degré premier semble davantage destinée à éclairer les principes généraux selon lesquels les propositions I à V sont formulées — Galois a du reste conscience de ne pas être parvenu à exprimer ces principes avec toutes les précisions souhaitables — qu’à fournir un critère effectivement exploitable. Son indifférence vis-à-vis de la faisabilité pratique de son raisonnement apparaît d’ailleurs lorsqu’il donne, pour finir, l’exemple du degré 5 : il écrit le groupe de substitutions que doit avoir une telle équation pour être résoluble, au lieu de montrer comment décider de la résolubilité d’une équation particulière dont les coefficients numériques seraient fixés à l’avance.
@@@@@@@
On présente souvent le Mémoire sur les conditions de résolubilité des équations comme un texte prophétique, trop en avance sur son temps pour être accessible à l’entendement des contemporains. Il repose néanmoins sur des savoirs et savoir-faire familiers aux mathématiciens du début du XIXe siècle, puisqu’il s’appuie sur une tradition mathématique qui remonte à Lagrange et tente de faire jouer la dialectique théorie/applications si chère aux polytechniciens qui dominent alors le milieu mathématique parisien. Reconnaître que le Mémoire de Galois n’est pas inaccessible à ses contemporains et qu’il s’inscrit dans les problématiques de son époque ne signifie pas en nier la valeur mathématique ; cela consiste simplement à prendre au sérieux la valeur historique qu’a également ce document.

(1) Niels Henrik Abel, « Démonstration de l’impossibilité de la résolution algébrique des équations générales qui passent le quatrième degré »,
Journal de Crelle, t. 1, 1826. Joseph-Louis Lagrange, « Réflexions sur la théorie algébrique des équations »,
Mémoire de l’Académie royale des sciences et belles-lettres de Berlin, 1770, p. 134-215, 1771, p. 238-253.
(2) Paolo Ruffini (1765-1822) est un mathématicien italien qui a publié en 1799 un ouvrage où il démontrait que les équations du cinquième degré ne sont pas résolubles par radicaux. L’exactitude de la preuve qu’il proposait a fait l’objet d’une controverse parmi les mathématiciens contemporains.
(3) Alexandre Vandermonde (1735-1796) est un mathématicien français proche de Gaspard Monge, élu à l’Académie des sciences en 1771.
(4) Lagrange, op. cit.; A. Vandermonde, « Mémoire sur la résolution des équations »,
Histoire de l’Académie royale des sciences, avec les mémoires de mathématiques et de physique tirés des registres de cette Académie, Paris, 1774, p. 365-416.
(5) Procès-verbaux des séances de l’Académie des sciences, t. 5, séance du 27 décembre 1813, p. 294.
(6) Augustin-Louis, Cauchy, « Sur le nombre de valeurs qu’une fonction peut acquérir lorsqu’on y permute de toutes les manières possibles les quantités qu’elles renferment »,
Journal de l’École polytechnique, n° 10, 1815, p. 1-28 ; Augustin-Louis Cauchy, « Sur les fonctions qui ne peuvent obtenir que deux valeurs égales et de signes contraires par suite des transpositions opérées entre les variables qu’elles renferment »,
Journal de l’École polytechnique, n° 10, 1815, p. 29-112.
(7) Augustin-Louis Cauchy, « Mémoire sur les arrangements que l’on peut former avec des lettres données, et sur les permutations ou substitutions à l’aide desquelles on passe d’un arrangement à un autre »,
Exercices d’analyse et de physique mathématique, t. 3, 1844, p. 151-252.
(8) Évariste Galois, « Préface à deux mémoires d’analyse pure
(9) Procès-verbaux des séances de l’Académie, séance du 4 juillet 1831, t. 9, p. 660.
(10) Cité par Norbert Verdier,
Pour la science- les Génies de la science, Evariste Galois, février-mai 2003 (voir rubrique « Pour en savoir plus ».
(11) Cette préface figure dans l’édition intégrale des oeuvres de Galois : Evariste Galois,
Ecrits et mémoires mathématiques, édition critique intégrale des manuscrits et publications d’Evariste Galois par Robert Bourgne et Jean-Pierre Azra, Paris, Gauthier-Villars, 1962 (rééd. Jacques Gabay, 1997)
 Ce mémoire de 1830 est auréolé du halo de prestige et de mystère qui entoure Evariste Galois et sa courte vie.
Ce mémoire de 1830 est auréolé du halo de prestige et de mystère qui entoure Evariste Galois et sa courte vie.
![]()
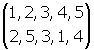 transforme 1 en 2, 2 en 5, 4 en 1 et 5 en 4.
transforme 1 en 2, 2 en 5, 4 en 1 et 5 en 4.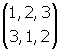 , la substitution circulaire s2
, la substitution circulaire s2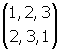 , la transposition t1
, la transposition t1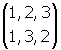 , la transposition t2
, la transposition t2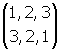 , la transposition t3
, la transposition t3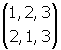 .
.
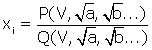 , où P et Q sont deux polynômes.
, où P et Q sont deux polynômes.


 Évariste Galois, Écrits et mémoires mathématiques, réédition Jacques Gabay, préface de Jean Dieudonné, 1997.
Évariste Galois, Écrits et mémoires mathématiques, réédition Jacques Gabay, préface de Jean Dieudonné, 1997. Gustave Verriest, Leçons sur la théorie des équations selon Galois, précédées d'une introduction à la théorie des groupes, 1939, suivi de Evariste Galois et la théorie des équations algébriques, 1934 ; réédition Jacques Gabay, 1997.
Gustave Verriest, Leçons sur la théorie des équations selon Galois, précédées d'une introduction à la théorie des groupes, 1939, suivi de Evariste Galois et la théorie des équations algébriques, 1934 ; réédition Jacques Gabay, 1997.










 Paul Dupuy, La Vie d’Évariste Galois, 1903, réédition
Paul Dupuy, La Vie d’Évariste Galois, 1903, réédition 

