La révolution quantique
Tandis que la révolution relativiste prit ses racines et son essor, tout à la fois, dans un seul article d’un seul auteur, Albert Einstein, la révolution quantique resta longtemps en gestation, larvée et se cherchant, indispensable depuis le tout début du XXe siècle mais d’abord déroutante et inintelligible, ne débouchant que dans les années 1920 – peut-être seulement, en vérité, dix ans après –, longtemps combattue pied à pied, avec acharnement et impétuosité, par une cohorte minoritaire mais prestigieuse – comprenant Louis de Broglie et Schrödinger, qui avaient tant œuvré pour elle, mais aussi le grand Einstein lui-même. La bataille décisive se livra en Belgique – est-il endroit mieux choisi pour une bataille décisive ? – dans un congrès Solvay, en 1927. Plutôt qu’à une bataille rangée, on assista à un duel, à un combat singulier. Il mit aux prises Albert Einstein et Niels Bohr (1885-1962), de Copenhague. L’enjeu était capital : il y allait de la vie ou de la mort de la théorie quantique, de son interprétation et donc de sa fondation en totalité.
Le texte BibNum : Une lettre d’Ehrenfest
Le texte choisi est la « petite chronique d’un grand événement ». Le grand événement, c’est le congrès Solvay de 1927, déjà mentionné. La petite chronique, c’est la relation qu’en fait Paul Ehrenfest, un des participants au congrès, sous forme de lettre
(1) à ses collègues Uhlenbeck et Goudsmit, qui ne participaient pas au congrès.

Figure 1 : Les participants au congrès Solvay de Bruxelles 1927. Au 1er rang, à partir du 2ème à gauche Planck, Marie Curie, Lorentz, Einstein, Langevin. Au 2ème rang, à partir de la droite, Bohr, Born, Louis de Broglie, Compton, Dirac. Au 3ème rang, 3ème à gauche, Ehrenfest. Au 3ème rang, à partir du 3ème à droite, Heisenberg, Pauli. Au centre du 3° rang, Schrödinger.
Paul Ehrenfest (1880-1933) est un physicien autrichien, élève de Boltzmann. Il est auteur de contributions importantes en mécanique quantique et en mécanique statistique. Il est professeur à l’université de Leyde (Pays-Bas) de 1912 jusqu’à son suicide (2) en 1933. C’était un ami d’Einstein ; à Leyde il jouera un rôle important dans la diffusion de la nouvelle physique en invitant les plus grands savants de l’époque à donner des cycles de conférences. George Uhlenbeck (1900-1988) et Samuel Goudsmit (1902-1978), tous deux néerlandais et tous deux élèves d’Ehrenfest, avaient découvert, peu de temps auparavant (en 1925), le spin de l’électron, en analysant les raies spectrales qu’émettent les atomes – leur structure fine. On peut s’étonner que le Comité Nobel ne les ait pas récompensés, pour une découverte aussi fondamentale en même temps qu’inattendue. Ernest Solvay (1838-1922), industriel belge, mit au point un nouveau procédé de fabrication du carbonate de sodium, dit « soude Solvay ». Il consacra une partie des bénéfices qu’il retira de son invention à financer des institutions et congrès scientifiques. À partir de 1911 se tinrent épisodiquement des Conseils Solvay, où se rencontraient une trentaine de physiciens ou chimistes, invités pour la circonstance, de toutes nationalités.
La discussion Bohr-Einstein
On sait que cette discussion du congrès Solvay de 1927, mainte fois relatée, trouve sa cause dans une interprétation différente qu’avait Einstein (et avec lui Schrödinger ou De Broglie) de la mécanique quantique. Pour lui, au contraire de Bohr, principe d’incertitude ou fonction d’onde ne pouvaient correspondre qu’à une description incomplète de la réalité physique, ce qu’il résumera plus tard dans une lettre à Max Born
(3), par la formule souvent citée : « En tout état de cause, je suis convaincu que, Lui, ne joue pas aux dés ».
La relation que fait Ehrenfest de cette discussion entre Bohr et Einstein prend, sur le ton de chronique qu’a sa lettre, un tour savoureux :
C’était pour moi un délice d’assister aux conversations entre Bohr et Einstein. Comme une partie d’échecs. Einstein sortant sans cesse de nouveaux exemples. Une sorte de perpetuum mobile de la deuxième espèce pour briser la RELATION D’INCERTITUDE. Bohr cherchant constamment à tirer d’un obscur nuage de fumées philosophiques les instruments pour démolir exemple après exemple. Einstein comme un diable dans sa boîte : jaillissant à nouveau chaque matin inentamé. C’était savoureux. Mais je suis presque sans réserve pro-Bohr contra-Einstein.
On dirait plutôt, aujourd’hui, des contre-exemples, puisqu’ils cherchaient à prendre en défaut la théorie embryonnaire avancée par Bohr. Le « mouvement perpétuel », vieux rêve d’une machine fonctionnant indéfiniment sans apport extérieur, est exclu par les lois de thermodynamique (celui dit « de deuxième espèce » violerait le « deuxième principe ») !
[Einstein] se conduit maintenant avec Bohr exactement comme les tenants de la simultanéité absolue se conduisaient avec lui.
La théorie de la relativité (restreinte) d’Einstein stipule que deux événements, simultanés dans un référentiel déterminé, apparaissent l’un après l’autre – ou l’autre après l’un, selon – dans d’autres référentiels. Certains physiciens combattaient la relativité en arguant que la simultanéité ne pouvait dépendre ainsi du point de vue : elle était absolument, pour eux, ou n’était pas.

Figure 2 : Niels Bohr et Albert Einstein en discussion, dans la maison de Paul Ehrenfest à Leyde (Pays-Bas), en 1925.
Les Interprétations successives de Bohr, de la relation d’incertitude au principe de complémentarité
Paul Ehrenfest poursuit ainsi sa chronique :
[Bohr] a poussé la relation d’incertitude au premier plan, mais en lui conférant une simplicité et une universalité merveilleuses. Quelque chose de ce genre : Ne considérez d’abord que la question de la LUMIÈRE. Alors de la seule CINÉMATIQUE DES ONDES [résulte] l’incertitude suivante
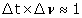
. Plus est courte la durée d’un signal d’onde, plus est grande l’incertitude sur sa fréquence. D’où, du fait des relations Planck Einstein
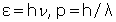
(moment), les « relations d’incertitude réciproques »
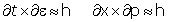
. Ainsi l’incertitude réciproque des données spatio-temporelles vis-à-vis des données dynamiques apparaît D’ABORD DANS LE DOMAINE DE LA LUMIÈRE.
La relation
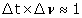
est parfaitement connue et assimilée en physique classique. Elle découle par voie naturelle d’une propriété mathématique de la transformation de Fourier. La constante de Planck
h caractérise le domaine quantique :
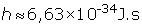
.
Relations d’incertitude ondulatoires
Une onde progressive lumineuse monochromatique est décrite (à une seule dimension d’espace) par une expression de la forme :
A cos (kx – ωt), avec ω = kc pour satisfaire l’équation de propagation (c vitesse de la lumière)
Une onde réelle superpose – d’où l’expression "paquet d’ondes" – un ensemble de tels termes : on multiplie par une fonction g(k) et on somme sur k.
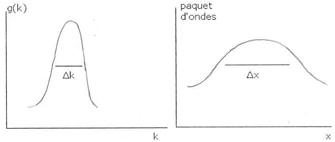
Si g(k) est prise comme l’indique la figure, le paquet d’ondes n’est appréciable – à t fixé – que dans un intervalle restreint de l’axe des x (constatation analogue en t à x fixé). Mais ∆x croît si ∆k décroît :
∆x. ∆k ≥ 1 (1)
De même, si l’on prend le second terme de cos (kx – ωt), on a :
∆ω. ∆t ≥ 1 (2)
Ce type d’inégalités – connu depuis longtemps comme propriété de la transformation de Fourier – acquiert en mécanique quantique une signification physique nouvelle car les paramètres k et ω sont reliés aux grandeurs impulsion p et énergie E : Sachant que k= ω/c = 2πv/c = 2π/λ, et que λ= h/p (relation de De Broglie), en remplaçant dans (1) ci-dessus, on a ∆x. ∆k ≥ h/2π = 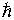 Sachant que E = hv (formule de Planck), en remplaçant dans (2) ci-dessus, on a ∆(2πv). ∆t ≥ 1 soit a ∆E. ∆t ≥
Sachant que E = hv (formule de Planck), en remplaçant dans (2) ci-dessus, on a ∆(2πv). ∆t ≥ 1 soit a ∆E. ∆t ≥ 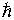
Puis le chroniqueur Ehrenfest explique comment Bohr passe de la lumière à la matière :
Voilà pour la lumière. Maintenant, des phénomènes tels que l’effet Compton
(4) en particulier montrent que dans une interaction entre lumière et matière en mouvement la LOI DE CONSERVATION vaut pour le vecteur d’impulsion. DONC il s’ensuit que pour de telles interactions, du fait de la loi de conservation (!!!!!!!!!!!), les relations d’incertitude supra passent de la lumière à la matière (!!!!!!! BRAVO BOHR !!!!!!!). Et pas des incertitudes d’un autre ordre qu’en optique, mais, merveille des merveilles, là encore de l’ordre de h (…) Et maintenant on peut en toute confiance laisser la relation d’incertitude envahir les moindres recoins de la physique grâce à la loi de conservation.
Une grandeur est conservée si elle garde constamment même valeur (éventuellement vectorielle) dans tout système isolé – c’est-à-dire, pour les collisions, même valeur dans l’état final que dans l’état initial. Ehrenfest emploie indifféremment « moment » (momentum) et « impulsion » pour la même grandeur vectorielle. En mécanique classique, l’impulsion ou moment se construit comme produit de la vitesse par la masse.
Enfin, Ehrenfest introduit le principe de « complémentarité » de Niels Bohr :
Somme toute, l’idée de « suivre en pensée la particule entre les instants d’observation » doit être rejetée au même titre que celle de « suivre un corpuscule de lumière à travers le champ d’onde entre son émission et son absorption » (j’espère ne pas pécher contre les conceptions de Bohr avec cette formulation). Dans l’article de Naturwissenschaften, vous verrez comment Bohr insiste sans cesse sur la « description complémentaire » de toutes les expériences. Bohr dit : Nous ne disposons pour l’instant que des mots et des concepts qui nous fournissent un tel mode de description complémentaire.
S’explicite ici le fondement de l’interprétation de Bohr – sans qu’Ehrenfest ait « péché » à son encontre –, que reprend depuis la mécanique quantique moderne : le corpuscule (photon ou particule matérielle) se manifeste en tant que tel lors de son émission puis de son absorption, et plus généralement dans tout processus de mesure de ses caractéristiques propres (position, ou impulsion,…) ; entre de telles observations directes, l’évolution du corpuscule se fait à travers son état quantique, de type ondulatoire (champ électromagnétique ou fonction d’onde), qui peut manifester quant à lui des effets d’interférence.
L’interprétation de Copenhague aujourd’hui
Bohr – on peut le dire sans faire injure à son illustre adversaire – sortit vainqueur de la confrontation, et entraîna sur ses positions l’immense majorité des physiciens. Copenhague se convertit en capitale scientifique du monde, où les plus grands noms venaient sacrifier sur l’autel de la dualité onde-corpuscules. On décora de l’épithète « orthodoxe », comme on ferait d’un Ordre honorifique, la mécanique quantique fondée sur l’ « interprétation de Copenhague ». Elle fut longtemps encore combattue, dans des escarmouches d’arrière-garde, comme illégitime, usurpatrice ou auto-contradictoire, alors même que s’accumulaient ses succès et qu’elle apportait une compréhension profonde de la physique atomique, puis de la physique nucléaire, enfin de la physique des particules. La mécanique quantique orthodoxe, telle qu’elle est, se montre partout en accord avec les données de l’observation et les mesures ; elle a enfanté des prédictions inouïes et hors du sens commun, qui ont pourtant été vérifiées et confirmées, en bonne et due forme, par l’expérience et l’expérimentation.
Pour un physicien de métier, le formalisme quantique n’a rien d’exceptionnel. Il est enseigné, sans difficulté majeure, dans nos Universités, aux étudiants de troisième ou quatrième année. Il faut seulement prendre garde à ce qu’il est très contraignant : dans telle situation, c’est l’application de telle règle théorique qui s’impose, et surtout pas une autre
(5). Cela se réduit à une exigence de rigueur et de discipline personnelle, sans plus.
La mécanique quantique est donc une théorie formelle et abstraite. Toutes les théories physiques sont formelles et abstraites, en ce qu’elles découlent de concepts et de principes qui ne se déduisent pas directement et mécaniquement des données expérimentales. Ainsi en va-t-il de la théorie relativiste, de la mécanique newtonienne, de la théorie de l’électromagnétisme, et même du principe d’Archimède ou de celui de l’hydrostatique, qui paraissent pourtant, par leurs effets, si proches de notre expérience quotidienne et concrète. La mécanique quantique a ceci de spécifique qu’elle manie systématiquement – délibérément, pourrait-on croire – des notions et des techniques que rien jusque-là n’avait pu nous rendre familières, et qu’elle s’adresse en outre – ceci explique sans doute cela – à un domaine où toute intuition anthropomorphe est a priori défaillante.
Pour le commun des physiciens mortels, la mécanique quantique ne pose pas de problème métaphysique : elle se présente comme une « bonne théorie », découlant de postulats clairs et parfaitement formulés, expliquant tous les résultats expérimentaux qui ressortissent à sa compétence, et permettant, aujourd’hui encore, d’en prédire de nouveaux.

(1) La traduction de la lettre en français est de Rémy Lambrechts.
(2) Paul Ehrenfest, signataire de cette lettre enthousiaste, est mort en 1933, à cinquante-trois ans. Sans doute était-il juif. Son fils, trisomique, était soigné en Allemagne. À l’avènement de Hitler, Paul Ehrenfest tua son fils et se suicida.
(3) Max Born (1882-1970), allemand, prix Nobel de physique 1956, apporta à l’édifice quantique une pierre angulaire en proposant l’interprétation probabiliste de la fonction d’onde.
(4) Arthur Compton (1892-1962), physicien américain, mit en évidence en 1922 la nature corpusculaire du photon en analysant les collisions de photons sur des électrons pratiquement libres – i.e. la diffusion de rayons X sur un bloc de graphite. Pour une explication de l’effet Compton, voir encadré hors-texte dans document BibNum (
analyse du texte de Röntgen sur les rayons X, 1896).
(5) Le formalisme de la relativité restreinte, quoique moins compliqué, nécessite lui aussi une attention particulière à chaque cas.




![]() Sachant que E = hv (formule de Planck), en remplaçant dans (2) ci-dessus, on a ∆(2πv). ∆t ≥ 1 soit a ∆E. ∆t ≥
Sachant que E = hv (formule de Planck), en remplaçant dans (2) ci-dessus, on a ∆(2πv). ∆t ≥ 1 soit a ∆E. ∆t ≥ ![]()

 Un film du congrès Solvay de 1927, 3 minutes de vidéo (film muet, commentaire voix-off en anglais) ; film pris pendant la pause par Irving Langmuir (qui sera prix Nobel de chimie en 1932), site FreeScienceLectures.
Un film du congrès Solvay de 1927, 3 minutes de vidéo (film muet, commentaire voix-off en anglais) ; film pris pendant la pause par Irving Langmuir (qui sera prix Nobel de chimie en 1932), site FreeScienceLectures. Bernard Diu, Traité de physique à l’usage des profanes, Odile Jacob 1997, réédition 2008.
Bernard Diu, Traité de physique à l’usage des profanes, Odile Jacob 1997, réédition 2008. Étienne Klein, Petit voyage dans le monde des quanta, Champs Flammarion 2004.
Étienne Klein, Petit voyage dans le monde des quanta, Champs Flammarion 2004.





