
Figure 1: Henri Poincaré (1854-1912), détail de la photo du premier Congrès Solvay en 1911 à Bruxelles.
En 1896, pour interpréter une expérience de Birkeland, Henri Poincaré détermine les trajectoires de rayons cathodiques dans le champ d’un pôle magnétique. Son article est examiné du point de vue d’un physicien des plasmas d’aujourd’hui. Poincaré fut-il un précurseur du confinement magnétique ?
Un norvégien à Paris
Vers la fin du XIXe siècle, les progrès des techniques du vide et des hautes tensions avaient permis d’expérimenter sur le passage du courant électrique à travers des gaz de plus en plus raréfiés. Cela avait conduit à la découverte, par William Crookes, des rayons cathodiques dont en 1896-97 J.J. Thomson devait révéler la nature : des faisceaux de particules chargées négativement, les électrons. Avant même que soit élucidée la nature des rayons cathodiques, le physicien norvégien Kristian Birkeland (1867-1917) qui travaillait à l’université de Christiania (aujourd’hui Oslo) reprenait à son compte des intuitions anciennes (Lomonossov) attribuant les aurores boréales à l’impact de particules issues du Soleil : n’y aurait-il pas une analogie entre ces objets et d’autres, hypothétiques, qui constitueraient les rayons cathodiques ?
À l’époque, les études de décharges électriques ou, comme on disait alors, du passage de l’électricité dans les gaz raréfiés étaient à la pointe de la recherche. Pour mettre ses idées à l’épreuve, Birkeland réalisa une série d’expériences dans lesquelles il faisait agir des champs magnétiques sur un faisceau de rayons cathodiques. La première en date, en même temps la plus simple, consiste à disposer l’un des pôles d’un barreau fortement aimanté près de l’extrémité du tube opposée à la cathode
(1). Birkeland constatait alors une concentration spectaculaire des rayons cathodiques au voisinage du pôle magnétique (figure 3). Plus tard il disposa une sphère métallique dissimulant un aimant, au milieu d’un caisson étanche où il pouvait faire un vide primaire. Une fois celui-ci obtenu, une électrode était portée à une haute tension négative. Birkeland parvint ainsi à obtenir des couronnes lumineuses entourant les pôles magnétiques. Reprenant un terme façonné aux temps élisabéthains par l’anglais William Gilbert, l’expérience fut baptisée « Terrella » (petite Terre en latin). D’abord strict objet de recherches, la terrella servit à des démonstrations publiques à partir de 1917, puis tomba dans un oubli dont elle fut tirée par le récent regain d’intérêt que suscite dans tous les pays le patrimoine culturel et scientifique.

Figure 2 : Kristian Birkeland (1867-1917), ca. 1900.
Birkeland avait reçu une solide formation de mathématicien avant de se tourner vers la physique théorique autant qu’expérimentale. Il obtint en 1892 une bourse qui lui permit de voyager à l’étranger. Il fit un séjour à Paris auprès de Poincaré, un autre à Genève. Il put ainsi nouer des relations utiles pour publier (en français !) dans les Comptes Rendus de l’Académie des Sciences de Paris et dans les Archives des Sciences Physiques et Naturelles de Genève. Il maintint le contact avec Henri Poincaré jusqu'au décès de celui-ci en 1912, lui communicant régulièrement ses résultats et les manuscrits de ses publications.
Poincaré eut ainsi la primeur des expériences de Birkeland sur les rayons cathodiques.
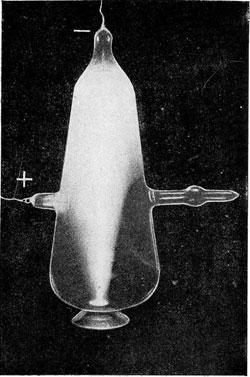
Figure 3 : Une expérience de Birkeland : focalisation de rayons cathodiques sous l’action du pôle d’un barreau aimanté disposé près de l’extrémité du tube opposée à la cathode (source de l’image : selon Carl Stormer, autre norvégien francophone, qui reproduit dans le texte de la conférence qu’il a donnée en 1923 à la Société Française de Physique, cette image a été publiée par Birkeland dans son mémoire « Expédition norvégienne 1899-1900 pour l'étude des aurores boréales », Videmhàbs Selskabet Schrifter, Christiania, 1899).
Un modèle
Pour expliquer la focalisation des rayons cathodiques, Poincaré
(2) se mit en devoir de résoudre les équations du mouvement d’une particule chargée dans le champ
H d’un pôle magnétique placé à l’origine des coordonnées. La source est une cathode très éloignée du pôle et perpendiculaire à l’axe de symétrie du dispositif expérimental.
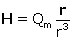
L’équation du mouvement, sous l’effet de la force magnétique, d’une particule de masse
m portant la charge
q est
(3) :
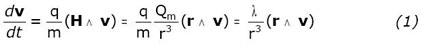
(où λ est une constante)
La force exercée par le champ sur une particule est orthogonale à la fois à la vitesse et aux lignes de champ. Dans ce problème simplifié, très académique, les trajectoires peuvent être déterminées par des méthodes purement analytiques.
Intégrales premières
Suivant une méthode qui a largement fait ses preuves en mécanique, on recherche des intégrales premières au moyen d’opérations judicieuses. Ainsi d’abord, en multipliant scalairement les deux membres de (1) par la vitesse v, on obtient un résultat nul, d’où :
v² = cte = V²
Ensuite, la multiplication scalaire des deux membres de (1) par r donne également un résultat nul
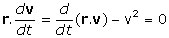
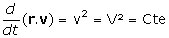
(r.v)=V2t+B
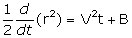
r² = V²t² + 2Bt + A (2)
(où A et B sont deux constantes)
Enfin en multipliant vectoriellement à gauche les deux membres de (1) par r il vient :
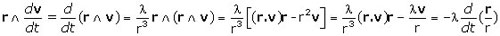
d'où :
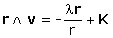 (3)
(3)
(où K est un vecteur constant)
En multipliant scalairement les deux membres de
(3) par
r, le résultat est toujours nul ce qui fournit
(4) :
λr = K.r (4)
La direction de r (soit r/r) fait donc un angle constant avec celle de K (le produit scalaire de ces deux vecteurs est constant, égal à λ) : les trajectoires sont donc situées sur un cône de révolution qui a pour sommet l’origine et dont l’axe a la direction du vecteur K. L’origine du cône est le pôle magnétique, vers lequel les trajectoires convergent donc, sans l’atteindre toutefois.
Ce cône est une surface de flux magnétique dont les génératrices sont les lignes de champ. L’accélération des particules est orthogonale aux lignes de champ comme à la vitesse (d’après (1)). La force magnétique a une composante le long de l’axe du cône et dirigée du pôle vers la source, quel que soit le signe des charges, ce que Poincaré indique ainsi :
Ce qui donne à cette observation son caractère paradoxal, c’est que les phénomènes ne changent pas quand on renverse les pôles de l’aimant.
Poincaré s’étonnait, puisque la dynamique d’une particule chargée dans des champs électromagnétiques dépend le plus souvent de son signe.
Détermination des constantes
Pour les composantes du vecteur K, on revient à la situation physique. Les particules sont issues d’une source éloignée du pôle magnétique. Dans l’exemple d’une électrode plane orthogonale à un axe des z qui passe par le pôle, la vitesse initiale est approximativement parallèle à cet axe. Il existe donc une asymptote à la trajectoire initiale, qui est parallèle à l’axe des z et repérée par
x = x0 , y = y0,
Près de cette asymptote, au départ de la cathode, la vitesse est principalement dirigée le long de l’axe des z :
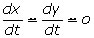
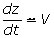
z=r
En reportant dans le système (3), équation par équation, on a
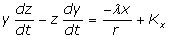
ce qui donne K
x=Vy
0 ; on obtient de la même manière K
y= - Vx
0 et K
z=λ.
Équations du cône de révolution
La représentation en ce cas est la suivante (O l’origine est le lieu du pôle magnétique, Oz l’axe du tube) :
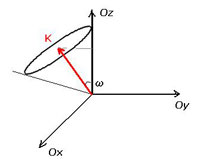
Figure 4 : Représentation du cône de convergence, support de certaines trajectoires. Le trait fin partant de l’extrémité de K vers l’axe Oz mesure la norme de la projection de K sur le plan Oxy (cf. ci-après).
L’équation (4) donne l’équation cartésienne d’un cône :
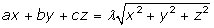
en y reportant les valeurs initiales ci-dessus :
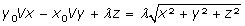
Le demi-angle au sommet du cône est donné par :
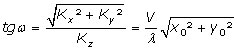 (5)
(5)
Contrairement à ce qu’indique Poincaré et avec lui les Comptes Rendus, cette valeur est bien celle de tgω et non celle de sinω : on n’est d’ailleurs pas dans le cas de petits angles où sin et tg peuvent être assimilés.
La relation (3) montre que la somme géométrique des vecteurs –λr/r et K est orthogonale à la direction de r (figure ci-dessous) :
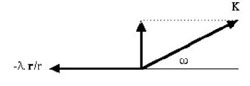
Figure 5 : Le demi-angle au sommet ω figure le cône autour du vecteur K.
Cherchons la distance minimale au pôle magnétique atteinte par la trajectoire. Elle obéit à d(r²)= 0, soit r.v = 0. En reportant sur la figure 5, on a :
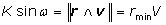
puisqu’à ce moment-là, r et v sont orthogonaux. Or, d’après la figure 4,
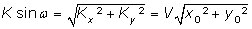
d'où 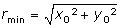
La particule chargée se rapproche du pôle magnétique jusqu’à cette distance minimale, puis elle s’en éloigne tout en restant sur le cône : c’est l’effet miroir magnétique.
En dérivant l’équation (2), on voit que cette distance minimale est atteinte en un temps tel que V2tmin = - B (B étant négatif). En reportant dans l’équation (2) à tmin, on a :
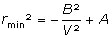
Or la constante A n’est autre que le carré de la distance r0 de la particule au pôle à l’instant t = 0. En identifiant les deux expressions de rmin, il vient :
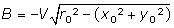
L’effet miroir magnétique tel que connu de nos jours
Les miroirs magnétiques sont des éléments importants de l’environnement de la Terre d’une part, et des dispositifs construits en vue la fusion nucléaire contrôlée d’autre part. Le champ magnétique créé par le dipôle terrestre piège des particules chargées en provenance du Soleil. Elles circulent d’une région polaire à l’autre entre deux miroirs magnétiques et forment les ceintures de radiations. Des perturbations du champ terrestre (orages magnétiques) provoquent des fuites de particules de grande énergie le long des lignes de force, phénomène à l’origine des aurores polaires.
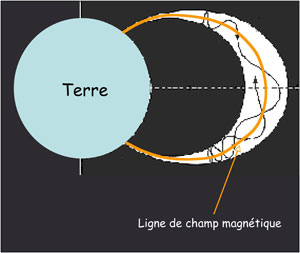
Figure 6 : Particules chargées dans le dipôle terrestre.
Pour la fusion nucléaire contrôlée, on a inventé des machines cylindriques à double miroir, mais cette filière n’a pas eu le succès escompté. Dans les machines toroïdales (5), le champ magnétique est inhomogène ce qui entraîne des effets miroir dont il est impératif de tenir compte.
Un peu de géométrie
La relation (3) et la figure 5 montrent que le produit vectoriel r∧v est un vecteur de grandeur constante. Il est orthogonal à la surface du cône. Dans une application de la surface du cône sur le plan tangent le long de l’axe des z (qui fournit un développement du cône) l’image de la trajectoire est déterminée par coordonnées polaires r, θ, où θ est l’angle entre les 2 vecteurs r et v d’origine le sommet S du cône (le pôle magnétique). On tire de (3) et de la figure 5 :
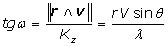
donc 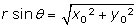
C’est, en coordonnées polaires r, θ, l’équation d’une droite D parallèle à l’axe des z. L’intersection I1 avec l’autre frontière du développement du cône est l’image de l’intersection de la trajectoire avec l’axe des z. Des développements successifs jusqu’à recouvrir complètement le demi-plan contenant D fournissent les images de toutes les intersections possibles de la trajectoire avec l’axe des z
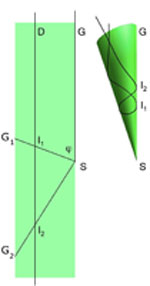
Figure 7 : Les intersections In de D avec les images Gn de G obtenues par les développements successifs du cône (figure de gauche) sont les images de toutes les intersections possibles de la trajectoire avec G axe des z (figure de droite).
La trajectoire se rapproche du pôle sans jamais l’atteindre pour s’en éloigner ensuite. La distance minimale d’approche est tout simplement égale à la distance à l’axe de symétrie du point d’émission sur la cathode.
Le pôle se comporte comme un miroir pour les particules, qui s’en rapprochent puis s’en éloignent. Cela s’explique aisément : le cône est une surface de flux magnétique dont les génératrices sont des lignes de champ. La force magnétique, orthogonale aux lignes de champ, a une composante le long de l’axe du cône, dirigée du pôle vers la source quel que soit le signe des charges, et qui ralentit les particules avant de les renvoyer.
Conditions de validité
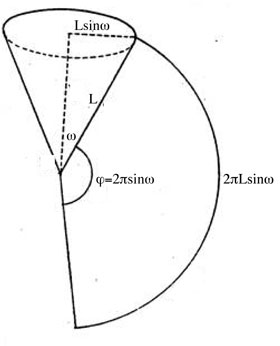
Soit φ = 2πsinω l’angle du développement total du cône. Les positions successives des intersections de la trajectoire avec l’axe des z sont alors distantes de l’origine de :
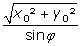 (point I1),
(point I1), 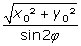 (point I2),
(point I2), 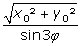 (point I3),…
(point I3),…
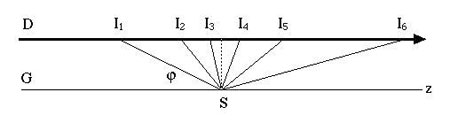
Figure 8 : (ceci correspond à une variante de la figure 7) Points de croisement de la trajectoire avec l’axe Oz. La distance du point I1 au pôle est donnée par la formule ci-dessus, sachant que la distance de S à la droite D est √(x0² +y0²), et φ est l’angle entre SI1 et G. De même, 2φ est l’angle entre SI2 et G. En fonction de la valeur initiale de φ, l’angle multiple de φ dépasse π/2 à partir d’un certain In. L’interprétation est la suivante : la trajectoire s’enroule autour du cône, coupant l’axe Oz en I1, puis I2, puis I3 en se rapprochant du pôle, l’approchant au plus près, puis s’éloignant (effet miroir) en I4, I5 tout en continuant à s’enrouler.
Figure 8bis (ci-dessous) : visualisation de l’angle de développement φ = 2πsinω d’un cône de demi-angle au sommet ω.
Il n’y a intersection que si les angles φ, 2φ, 3φ… sont inférieurs à π. Cette condition appliquée à φ impose a minima :
φ< π, soit sinω < ½ ou ω < π/6
ou encore, en revenant aux conditions initiales (formule (5))
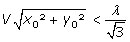
λ étant une constante (formule (1)) liée à la nature de la particule et à l’intensité du champ, cette condition exprime que la vitesse initiale de la particule et sa distance à l’axe ne doivent pas être trop importantes pour qu’ait lieu le piégeage dans le cône – ou confinement.
La notion de confinement magnétique de nos jours
Une voie vers la fusion contrôlée consiste à isoler de toute paroi qui pourrait le refroidir un plasma (gaz ionisé) ténu mais chaud (108 K) en l’insérant dans une configuration magnétique. Les particules chargées dont la trajectoire s’enroule autour des lignes de champ restent liées à celui-ci. Dans un “tokamak“ (ITER) un anneau de plasma est ainsi confiné par un champ très inhomogène dont la grandeur est une fonction décroissante de la distance à l’axe du tore.
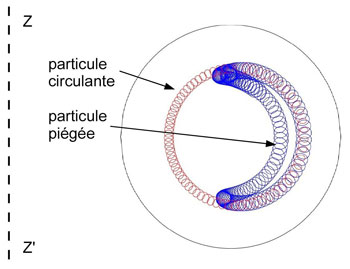
Figure 9 : Rabattements sur un plan méridien du tore de trajectoires de particules chargées confinées dans un tokamak. ZZ’ est l’axe vertical du tore. Une partie reste piégée dans les régions à champ faible et subit l’effet miroir magnétique. Les autres (circulantes) ont accès aux zones à champ fort tout en restant confinées.
Commentaires
Pour interpréter les expériences de Birkeland qui montrent une focalisation des rayons cathodiques lorsqu’on approche du tube le pôle d’un aimant, Poincaré avait porté son attention sur les intersections de la trajectoire avec l’axe des z dans le cas d’une cathode circulaire orthogonale à cet axe qui passe par son centre.
Mais, son article contient plus que ce qu’il recherchait.
Il montre que le pôle magnétique entraîne bien une focalisation partielle des particules mais surtout qu’il les renvoie et donc les confine dans les régions où le champ est faible : ainsi obtient-il au passage l’effet miroir magnétique (indépendant de la charge) sans s’y attarder ni reconnaître son caractère fondamental.
On remarque aussi que les calculs sont faits dans le cadre de la mécanique newtonienne (la relativité n’apparaîtra que dix ans plus tard). Mais, étant donné que la force magnétique sur une particule chargée ne travaille pas, la grandeur V de la vitesse est nécessairement invariante, de sorte que les résultats s’appliquent sans modifications à des objets relativistes.
L’analyse de Poincaré fait apparaître deux invariants du mouvement : la grandeur V de la vitesse et le demi-angle ω d’ouverture du cône. Or ω est relié à une grandeur bien connue des physiciens des plasmas d’aujourd’hui, le moment magnétique μ associé au mouvement de rotation de la particule transversalement au champ magnétique (on peut montrer que μ = ½ q λ tg
2ω, vérifiant ainsi son invariance
(6)).
À l’époque de cette note (1896), on ne connaissait pas l’électron et l’atomistique n’avait pas bonne presse dans la communauté scientifique française. Assimiler les rayons cathodiques à un flot de particules chargées était une hypothèse hardie. En résolvant un problème académique inspiré par les travaux de Birkeland, Poincaré faisait, en véritable précurseur, du confinement magnétique comme M. Jourdain de la prose, sans le savoir.
Octobre 2011

(1) Archives des sciences physiques et naturelles de Genève, t. I, 4e période, juin 1896
(2) H. Poincaré, « Remarques sur une expérience de M. Birkeland », C.R.A.S. T. CXXIII (1896) p. 530
(3) Poincaré ne faisait pas usage de notation vectorielle. Il écrivait toutes les composantes. L‘équation (1) ci-dessus correspond au système p.531 dans le texte de Poincaré.
(4) Poincaré écrit ceci en haut de page 532 sous la forme ax + by + cz = r.
(5) Comme par exemple le tokamak Tore Supra à l’Institut de recherche sur la fusion magnétique (IRFM) à Cadarache (Bouches-du-Rhône).
(6) Dans cette relation, λ et ω sont représentatifs de l’intensité du champ et des conditions initiales, respectivement. L’invariance de μ est ainsi exacte dans le cas traité par Poincaré, alors qu’elle n’est qu’approximative (adiabatique) dans les situations réelles, dipôle magnétique terrestre ou champs de confinement pour la fusion thermonucléaire contrôlée.




![]()
![]()
![]()
![]()
![]()
![]()
![]() (3)
(3)![]()
![]()

![]()
![]()
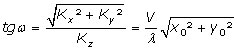 (5)
(5)
![]()
![]()
![]()
![]()
![]()

![]()
![]()

![]() (point I1),
(point I1), ![]() (point I2),
(point I2), ![]() (point I3),…
(point I3),…

![]()













