L’AUTEUR
Richard P. Feynman (1918-1988), professeur au prestigieux Cal’Tech
(Californian Institute of Technology), fut couronné en 1965 du prix Nobel de physique – qu’il partagea avec le physicien américain Julian Schwinger (1918-1994) et le physicien japonais Sin-Itiro Tomonaga (1906-1979) – pour ses travaux de pionnier en théorie quantique des champs. Universellement connu, de surcroît, pour l’intérêt ardent qu’il porta à l’enseignement de la physique, tout particulièrement envers les étudiants entrant à l’Université. Il publia en 1963 un ouvrage
(1) en tous points remarquable – trois tomes d’un format et d’une couleur inhabituels –, couvrant sur un ton très personnel, mais avec une vision résolument fondamentale, un large éventail de sujets.
PRÉSENTATION DU TEXTE
Aussitôt qu’avancé, le titre du chapitre – « Vecteurs » - est d’emblée précisé par la première phrase, puis page 7 :
In this chapter we introduce a subject that is technically known in physics as
symmetry in physical law (2) . Cette technique appelée le
calcul vectoriel fournit le titre de ce chapitre ; à proprement parler, cependant, c’est un chapitre sur la symétrie des lois physiques.
Suit en introduction une définition précise, reprise de Hermann Weyl, du concept de symétrie, pour application à la physique – où elle se confondra bientôt avec la notion d’« invariance ». Feynman s’en tient, pour l’essentiel, aux transformations – translations, rotations – que l’on qualifie de « passives » : l’objet d’étude demeure intouché et immuable ; c’est le repère que l’on déplace seulement – l’origine et les axes cartésiens permettant de le décrire. On envisage aussi parfois des transformations « actives » : fixé le repère, on transporte l’objet lui-même par translation ou rotation. Dans le premier cas – passif –, les propriétés de la réalité à étudier persistent intactes, à l’évidence ; mais les lois qui en rendent compte ? Conservent-elles la même expression dans le nouveau repère qui valait dans le précédent ? Feynman analyse longuement, de ce point de vue, les lois de Newton. Dans le second cas – actif –, les propriétés mêmes du système observé peuvent s’altérer au cours des manipulations qu’il subit – comme au cours d’une rotation celles d’une « horloge de grand-père » (p.4) :
Si une horloge à balancier se tient verticale, elle fonctionne correctement, mais si on la penche d’un certain angle, le balancier tombe sur le côté de l’armoire et tout s’arrête.
Cet examen méthodique et minutieux, détaillé et approfondi – près de six pages, sur les quinze que compte en tout le chapitre – de l’invariance des lois physiques par changement du repère de référence – examen centré sur l’exemple simple mais ô combien significatif ! des lois de Newton – aboutit à mettre en évidence « an accident of sorts, which is of extreme importance » : il dévoile en pleine lumière – vérité éblouissante et sacrée – l’origine ultime – alpha et oméga – et la propre raison d’être des vecteurs et des scalaires. « Behold ! » (p.6)
GRANDEUR VECTORIELLE, GRANDEUR SCALAIRE
Sont associés à une grandeur vectorielle « three numbers » – ses composantes. Toutefois :
No, not every three numbers form a vector !
La propriété spécifique des vecteurs s’énonce avec l’évidence d’un dogme : les trois composantes d’un vecteur (quelconque) se maintiennent inchangées dans toute translation des axes de référence ; dans une rotation, elles se transforment textuellement comme font les coordonnées d’un point (quelconque) de l’espace.
Le fait qu’une relation physique puisse être exprimée comme une équation vectorielle nous assure que la relation reste inchangée lors d’une simple rotation du système de coordonnées. C’est la raison pour laquelle les vecteurs sont si utiles en physique.
@@@@@@@
Une grandeur scalaire est caractérisée par un nombre unique – sa valeur – que n’affecte ni une translation ni une rotation du repère (p.13) :
Quelque chose de nouveau entre en jeu. Nous pouvons produire une nouvelle grandeur, une fonction de x, y et z, appelée fonction scalaire, une quantité qui n’a pas de direction mais qui reste la même dans les deux systèmes [de coordonnées]
Feynman prend l’exemple du scalaire égal au module d’un vecteur et insiste :
Cela ne dépend pas des axes, la réponse est la même pour tout ensemble d’axes. Nous avons ainsi un nouveau type de quantité, un nouvel invariant ou scalaire produit par un seul vecteur « élevé au carré ».
Á ce propos, affirmons avec force, contre les vents de croyances et les marées de dires que propage maint manuel de mathématiques, qu’un vecteur ne peut en aucun cas se réduire à une collection de scalaires parce qu’un vecteur a une direction (p.7) :
Il signifie trois nombres [x, y, z], mais en réalité il ne signifie pas qu’eux, parce que si nous utilisons un système de coordonnées différent, les trois nombres se transformeront en x’, y’, z’.
C’est là, sans nul doute, que réside la « substantifique moelle » de ce chapitre.
Feynman s’emploie ensuite, faisant preuve de la même « naïveté » – rien ne s’acquiert par évidence non-démontrée, sauf l’invariance des lois physiques –, à construire pierre à pierre et agencer pas à pas une « algèbre vectorielle » fondée sans compromis sur l’addition, la soustraction et le produit (scalaire). C’est à propos de cette troisième opération que Feynman développe les accents lyriques qui ont été cités naguère. Ainsi nous conduit-il à une sorte de point d’orgue, une expression valable pour « any vector whatsoever », mais qui n’épuise pas le sujet : « This discussion of vectors is by no means complete
(3) ».
@@@@@@@
Nous allons essayer à présent de prolonger et d’illustrer le travail de Feynman par des exemples pris dans les grandeurs (vectorielles et scalaires) de la physique moderne.
INVARIANCE PAR PARITÉ
Tant que nous n’avons pas quitté notre bon vieil espace à trois dimensions, ayons recours au pouvoir évocateur des « bipoints », alias « vecteurs géométriques »,

qui joignent un point M de l’espace à un autre point N – dans cet ordre. Effectuons sur ces objets – des longueurs, pour ce qui est de leurs dimensions physiques – une symétrie, ou réflexion, par rapport à un point fixe 0.
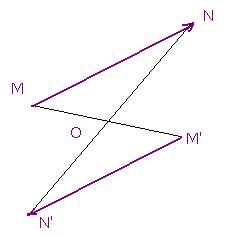
Aucun doute (figure ci-dessus) : le symétrique

d’un bipoint

lui est directement opposé :

= -

. Rappelons, s’il en était besoin, que

ni

ne renvoient à une quelconque « classe d’équivalence » ; l’un unit un point précis, M – dont M’ désigne l’unique symétrique par rapport à 0 – au point précis N – de symétrique N’.
Imaginons maintenant un mobile franchissant le point P avec

pour vitesse – grandeur vectorielle. Nous posons la question : comment se caractérise la situation symétrique de la précédente par rapport au point 0 fixe ? Que le point P soit transporté en son image P’ ne paraît pas soulever de difficulté. Mais la vitesse

?... Suivant en cela, à nouveau, Feynman, nous dessinons en P une flèche, chargée de représenter

. Elle prend évidemment pour origine le point P – position du mobile à cet instant. Sa direction emprunte aussi une véritable direction qui préexistait dans l’espace. Quant à son extrémité, elle ne saurait se situer à proprement parler dans l’espace que nous percevons, puisque la « longueur » de

se mesure en mètres par seconde – ou kilomètres à l’heure –, et non pas en mètres ou centimètres comme celles de l’espace et donc de la flèche. Qu’à cela ne tienne – entend-on de-ci de-là. Convenons d’un coefficient de transposition : tant de centimètres pour une flèche représentant tant de mètres par seconde de vitesse. Nous tracerons alors, à partir du point P’ symétrique de P, une flèche

opposée à

– comme

l’est à

.
Mais voilà que la physique – la Nature, à dire vrai – nous saisit au tournant, là même où nous voulions virer autour de la pointe de flèche comme nous aurions fait auprès d’un point de bon aloi. Pour ce qui est de la vitesse, rien à redire : la transformée de dans une réflexion lui est bien opposée. Elle n’est point seule à présenter ce comportement : toute une catégorie de grandeurs vectorielles – on les qualifie de « vraies » ou de « polaires » - changent de signe dans une symétrie réflexive par rapport à un point – transformation que l’on nomme « parité ». Outre la vitesse et l’accélération, les forces, l’impulsion, le champ électrique… se conduisent en vecteurs polaires, en « vrais » vecteurs.
Il existe néanmoins une autre classe de vecteurs, que l’on dit « axiaux » ou «
pseudovecteurs » - moment cinétique, champ magnétique, … - qui ne sont pas changés par parité. Ainsi, un champ magnétique

qui affecte le point P devient par parité

=

au point P’ symétrique de P. C’est pourquoi la prudence est recommandée dans la représentation d’une grandeur vectorielle – autre qu’un bipoint – par une « fléche ».
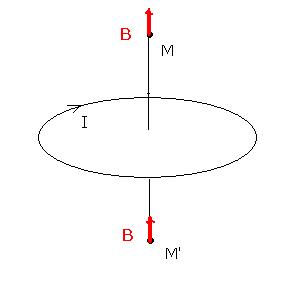
Le pseudo-vecteur champ magnétique
Le champ magnétique  est un exemple particulièrement important de pseudo-vecteur. La figure ci-dessous l’illustre : la spire parcourue par un courant crée un champ magnétique ; le plan de la spire est un plan de symétrie pour elle (situation inchangée) ; c’est un plan d’antisymétrie pour le champ magnétique (le champ en M’ n’est pas l’opposé du champ en M, c’est le même).
est un exemple particulièrement important de pseudo-vecteur. La figure ci-dessous l’illustre : la spire parcourue par un courant crée un champ magnétique ; le plan de la spire est un plan de symétrie pour elle (situation inchangée) ; c’est un plan d’antisymétrie pour le champ magnétique (le champ en M’ n’est pas l’opposé du champ en M, c’est le même).
Le champ électrique se comporte, lui, en « vrai » vecteur : il est proportionnel à la force qu’il induit (E = F/q) ; or, une force, comme la vitesse, l’accélération, sont de vrais vecteurs. On peut comprendre cette différence entre le champ magnétique pseudo-vecteur et le champ électrique par les équations de Maxwell, notamment : En effet, l’opérateur différentiel
En effet, l’opérateur différentiel se comporte comme un vrai vecteur, et le produit vectoriel de deux vrais vecteurs est, lui, un pseudo-vecteur : c’est pourquoi le champ
se comporte comme un vrai vecteur, et le produit vectoriel de deux vrais vecteurs est, lui, un pseudo-vecteur : c’est pourquoi le champ  en est un. On remarquera que la "force de Lorentz" qui agit sur une particule de charge q plongée dans un champ électromagnétique {
en est un. On remarquera que la "force de Lorentz" qui agit sur une particule de charge q plongée dans un champ électromagnétique { }, qui s’écrit
}, qui s’écrit

est bien, comme toute force, un vrai vecteur. La formule voit tous ses termes changer en leur opposé par parité (car le produit vectoriel d’un vrai vecteur, , par un pseudo-vecteur,
, par un pseudo-vecteur, , est un vrai vecteur).
, est un vrai vecteur).
@@@@@@@
Elles aussi, les grandeurs scalaires se divisent en deux groupes à l’égard de la parité : les « vrais scalaires » se transportent sans changement de P à son « image » P’ ; les « pseudoscalaires » sont changés par cette opération en leur opposé ; la température et la pression appartiennent au groupe des « vraies », l’hélicité – projection du moment cinétique d’une particule sur son impulsion – se comporte en « pseudo »
(4).
Invariance relativiste
La théorie einsteinienne de la Relativité (restreinte) trouve dans l’espace-temps de Minkowski une image géométrique commode : dans cet espace les « points », dénommés «
événements », associent un lieu de l’espace commun – trois coordonnées x, y, z – à une date – une coordonnée supplémentaire t, de temps. Des
translations, dans le temps comme dans l’espace, peuvent y être envisagées, ainsi que des «
transformations de Lorentz » généralisant les rotations de naguère. Les plus simples d’entre elles, dites «
transformations de Lorentz pures », combinent le temps avec une seule coordonnée d’espace
(5) dans un changement de référentiel (v
e : vitesse du référentiel R’ par rapport à R ; c : vitesse de la lumière dans le vide) :

Ces formules font aussitôt apparaître comme non-euclidien l’espace de Minkowski : c’est en effet la différence entre les carrés des coordonnées qu’elles conservent – la coordonnée de temps étant multipliée par c par raison de dimensions physiques –:
x’² - c²t’² = x² - c²t² est l’ « invariant relativiste ».
@@@@@@@
Malgré cette différence fondamentale avec l’espace euclidien à trois dimensions, un «
vecteur de Lorentz », ou « quadrivecteur », présente quatre composantes qui par définition se transforment, dans un changement de référentiel, comme les coordonnées d’un événement – simple traduction à quatre dimensions du résultat antérieur à trois. Par exemple, l’impulsion

et l’énergie E d’une particule ou d’un système forment ensemble un quadrivecteur : p
x, p
y, p
z, E/c. Dans la transformation de Lorentz pure écrite ci-dessus, ce quadrivecteur acquiert pour composantes p’
x, p’
y, p’
z, E’/c reliées aux précédentes selon :

Bien entendu, se construit sur le modèle des coordonnées le « carré scalaire » de ce quadrivecteur : si du carré véritable il a perdu le signe spécifique, il conserve du scalaire la propriété d’invariance :
p’² - E’²/c² = p² - E²/c²
A noter que le champ électrique

ni le champ magnétique

– trivecteurs pourtant sans tache et sans reproche – ne se prolongent, à la différence de l’impulsion, en des quadrivecteurs, mais bien en un tenseur (voir ci-après).
Les Grandeurs tensorielles
Un atome – nous prendrons celui d’hydrogène H pour prototype – apparaît de l’extérieur rigoureusement neutre, pour ce qui est de sa charge électrique globale. Il est pourtant constitué d’un noyau positif très compact – dimension de l’ordre du fermi, soit 10-15m – entouré d’une sorte de nuage électronique, négatif quant à lui. L’atome H comporte ainsi un proton pour noyau, au centre d’une sphère d’environ 1 angström de diamètre (10-10 m) dans laquelle les effets quantiques « délocalisent » l’unique électron de H. Les charges électriques du proton et de l’électron s’équilibrent exactement ; d’où la neutralité de l’atome d’hydrogène – et celle de tous les autres atomes, s’ils ne sont ionisés.
Cependant si, par des moyens extérieurs, l’on applique à l’atome H un
champ électrique 
, les forces électriques poussent le proton dans un sens – celui de

– et tirent l’électron en sens inverse. L’atome reste globalement neutre – sauf si l’électron en est arraché –, mais maintenant le centre du nuage électronique ne coïncide plus avec le noyau : survient dès lors un
moment dipolaire – que l’on schématise par deux charges ponctuelles opposées que sépare une courte distance.
Dipôles et moment dipolaire d’une molécule
En électromagnétisme, un dipôle est schématisé par un couple de deux charges opposées, - q et + q, que sépare une courte distance a (figure).

Un dipôle est caractérisé par son moment dipolaire, un vecteur  de valeur qa, dirigé suivant le segment joignant - q à + q. Certaines molécules portent un dipôle permanent, par suite d’une dissymétrie dans la répartition de leurs charges : le "nuage" électronique (charge négative) favorise l’un des atomes – qui en devient plus négatif qu’on ne s’y serait attendu – au détriment d’un autre – que la dérobade des électrons rend plus positif. Les chimistes enseignent ainsi que, dans la molécule HCl, le chlore se montre "électronégatif " et l’hydrogène "électropositif " ; la molécule présente un moment dipolaire permanent, dirigé de Cl (excès de charge négative) vers H (excès de charge positive). De même, dans H2O (molécule coudée en O), les électrons se concentrent préférentiellement autour de O – qui porte une charge négative excédentaire – et abandonnent partiellement les H, qu’ils laissent plus positifs, d’où là aussi un moment dipolaire. Des arguments analogues valent pour l’ammoniac NH3 (molécule pyramidale).À noter que CO2 ne présente aucun dipôle permanent : molécule linéaire O = C = O, symétrique par réflexion autour du centre de C. Un éventuel moment dipolaire (vrai vecteur) devrait être égal à son symétrique, c'est-à-dire à son opposé ; il ne peut que s’annuler, sauf si un champ électrique extérieur
de valeur qa, dirigé suivant le segment joignant - q à + q. Certaines molécules portent un dipôle permanent, par suite d’une dissymétrie dans la répartition de leurs charges : le "nuage" électronique (charge négative) favorise l’un des atomes – qui en devient plus négatif qu’on ne s’y serait attendu – au détriment d’un autre – que la dérobade des électrons rend plus positif. Les chimistes enseignent ainsi que, dans la molécule HCl, le chlore se montre "électronégatif " et l’hydrogène "électropositif " ; la molécule présente un moment dipolaire permanent, dirigé de Cl (excès de charge négative) vers H (excès de charge positive). De même, dans H2O (molécule coudée en O), les électrons se concentrent préférentiellement autour de O – qui porte une charge négative excédentaire – et abandonnent partiellement les H, qu’ils laissent plus positifs, d’où là aussi un moment dipolaire. Des arguments analogues valent pour l’ammoniac NH3 (molécule pyramidale).À noter que CO2 ne présente aucun dipôle permanent : molécule linéaire O = C = O, symétrique par réflexion autour du centre de C. Un éventuel moment dipolaire (vrai vecteur) devrait être égal à son symétrique, c'est-à-dire à son opposé ; il ne peut que s’annuler, sauf si un champ électrique extérieur  vient rompre cette symétrie.
vient rompre cette symétrie.
Dans sa situation initiale, l’atome H présente la symétrie sphérique. C’est dire que le vecteur moment dipolaire se dirige nécessairement suivant le champ qui l’induit, lui étant pratiquement proportionnel :


étant la « polarisabilité » de l’atome.
Cela compris, adressons-nous maintenant à une distribution de charge de symétrie moindre – disons, axiale – comme la molécule de CO2 (cf. encadré ci-dessus). Un champ électrique extérieur pointant selon l’alignement O = C = O induira un moment dipolaire – en détruisant, par son sens privilégié, la symétrie de parité. Indépendamment de cet effet, un champ électrique appliqué dans une direction perpendiculaire à la droite O = C = O produira lui aussi un moment dipolaire – suivant cette nouvelle direction.
Point n’est besoin de connaissances approfondies pour comprendre que les deux coefficients de proportionnalité

différeront le long de l’axe moléculaire ou selon l’une de ses perpendiculaires. Sans compter qu’un champ électrique

quelconque – on le décomposera suivant les deux lignes évoquées – donnera naissance à un vecteur moment dipolaire

qui s’écartera significativement du champ inducteur

qui s’écartera significativement du champ inducteur
Pour une molécule quelconque et des axes O
x, O
y, O
z quelconques, les composantes μ
x, μ
y, μ
z du vecteur moment dipolaire

induit par un champ électrique (de composantes E
x, E
y, E
z) revêtiront la forme générale :
μx =  xxEx +
xxEx +  xyEy +
xyEy +  xzEz μy =
xzEz μy =  yxEx +
yxEx +  yyEy +
yyEy +  yzEz μz =
yzEz μz =  zxEx +
zxEx +  zyEy +
zyEy +  zzEz
zzEz
Interviennent dans ces égalités les neuf composantes

ij d’un « tenseur du deuxième ordre
(6) » qui rend compte de la « polarisabilité » de la molécule choisie. Une translation des axes du repère cartésien n’affecte pas les composantes du tenseur. Une rotation du repère les transforme par application réitérée, sur les deux indices, des formules qui relient x,y,z – coordonnées d’un point de l’espace – à x’,y’,z’ – coordonnées du même point dans le nouveau repère.
Dans l’espace à quatre dimensions de Minkowski (cf. chapitre « Invariance relativiste »), on est convenu d’associer des lettres grecques – prises de préférence vers le milieu de l’alphabet – aux indices quadrivectoriels. Ainsi, l’impulsion énergie s’écrira pμ , avec pour μ les valeurs 0,1,2,3 : p0 = E/c, p1 = px, p2 = py, p3 = pz.
Existent ici, à l’instar de l’espace « ordinaire », des scalaires – dits « de Lorentz » –, des (quadri) vecteurs, des pseudoscalaires et des pseudovecteurs, et des tenseurs. La théorie relativiste de l’électromagnétisme présente les six composantes des champs électrique

et magnétique

comme constituant un tenseur antisymétrique d’ordre deux, F
μv. À raison de 4 possibilités pour chaque indice, on attend a priori 16 composantes pour un tenseur d’ordre deux. Ici, les 4 termes diagonaux F
μμ s’annulent par antisymétrie, et les 12 qui subsistent s’égalent 2 à 2 – ou plutôt s’opposent. Les 2 x 3 composantes des (tri) vecteurs

et

s’insèrent parfaitement dans ce cadre taillé à leur mesure.
Conclusion
Feynman dévoile ici avec brio et rigueur la raison d’être fondamentale des scalaires et des vecteurs : c’est de la symétrie-invariance des lois physiques dans les transformations de l’espace qu’ils tirent leur origine véritable. Une loi donnée peut s’exprimer par l’égalité entre deux scalaires, une autre par l’égalité entre deux vecteurs ; sont catégoriquement exclues, en revanche, toutes formules qui tenteraient d’équilibrer un scalaire et l’une des composantes d’un vecteur.
Ces idées théoriques connaissent d’importants développements dans de multiples directions – quelques-uns en ont été évoqués dans le présent commentaire
(7).

(1) The Feynman lectures on physics, R.P. Feynman, R.B. Leighton & M. Sands, Addison-Wesley éditeur (1963).
(2) C’est Feynman qui souligne.
(3) Un oubli surprenant, toutefois, de la part de Feynman : si le produit scalaire a.b peut être défini pour « any two vectors », en revanche la somme a+b est dépourvue de sens si a et b diffèrent en nature – en « dimensions physiques » – : on n’additionne pas une force et une vitesse.
(4) Si, après une première réflexion par rapport à un point fixe O, on en effectue une seconde – par rapport au même point O –, on rétablit par là la situation initiale. C’est pourquoi le facteur par quoi la parité multiplie une grandeur ne peut différer de 1 ou -1 – son carré vaut nécessairement un.
(5) Entre les trois premières coordonnées continuent d’opérer les rotations stricto sensu, si on les sollicite.
(6) Bien entendu, se rencontrent également des tenseurs d’ordre supérieur à deux.
(7) Remarquons que le mot ou la notion d’équipollence n’apparaissent à aucun endroit dans les arguments de Feynman. La définition des vecteurs comme classe d’équivalence, que l’on inculque aux élèves du second degré, est scientifiquement erronée et néfaste pédagogiquement.


![]() est un exemple particulièrement important de pseudo-vecteur. La figure ci-dessous l’illustre : la spire parcourue par un courant crée un champ magnétique ; le plan de la spire est un plan de symétrie pour elle (situation inchangée) ; c’est un plan d’antisymétrie pour le champ magnétique (le champ en M’ n’est pas l’opposé du champ en M, c’est le même).
est un exemple particulièrement important de pseudo-vecteur. La figure ci-dessous l’illustre : la spire parcourue par un courant crée un champ magnétique ; le plan de la spire est un plan de symétrie pour elle (situation inchangée) ; c’est un plan d’antisymétrie pour le champ magnétique (le champ en M’ n’est pas l’opposé du champ en M, c’est le même).
![]() En effet, l’opérateur différentiel
En effet, l’opérateur différentiel![]() se comporte comme un vrai vecteur, et le produit vectoriel de deux vrais vecteurs est, lui, un pseudo-vecteur : c’est pourquoi le champ
se comporte comme un vrai vecteur, et le produit vectoriel de deux vrais vecteurs est, lui, un pseudo-vecteur : c’est pourquoi le champ ![]() en est un. On remarquera que la "force de Lorentz" qui agit sur une particule de charge q plongée dans un champ électromagnétique {
en est un. On remarquera que la "force de Lorentz" qui agit sur une particule de charge q plongée dans un champ électromagnétique {![]() }, qui s’écrit
}, qui s’écrit![]()
![]() , par un pseudo-vecteur,
, par un pseudo-vecteur,![]() , est un vrai vecteur).
, est un vrai vecteur).


![]() de valeur qa, dirigé suivant le segment joignant - q à + q. Certaines molécules portent un dipôle permanent, par suite d’une dissymétrie dans la répartition de leurs charges : le "nuage" électronique (charge négative) favorise l’un des atomes – qui en devient plus négatif qu’on ne s’y serait attendu – au détriment d’un autre – que la dérobade des électrons rend plus positif. Les chimistes enseignent ainsi que, dans la molécule HCl, le chlore se montre "électronégatif " et l’hydrogène "électropositif " ; la molécule présente un moment dipolaire permanent, dirigé de Cl (excès de charge négative) vers H (excès de charge positive). De même, dans H2O (molécule coudée en O), les électrons se concentrent préférentiellement autour de O – qui porte une charge négative excédentaire – et abandonnent partiellement les H, qu’ils laissent plus positifs, d’où là aussi un moment dipolaire. Des arguments analogues valent pour l’ammoniac NH3 (molécule pyramidale).À noter que CO2 ne présente aucun dipôle permanent : molécule linéaire O = C = O, symétrique par réflexion autour du centre de C. Un éventuel moment dipolaire (vrai vecteur) devrait être égal à son symétrique, c'est-à-dire à son opposé ; il ne peut que s’annuler, sauf si un champ électrique extérieur
de valeur qa, dirigé suivant le segment joignant - q à + q. Certaines molécules portent un dipôle permanent, par suite d’une dissymétrie dans la répartition de leurs charges : le "nuage" électronique (charge négative) favorise l’un des atomes – qui en devient plus négatif qu’on ne s’y serait attendu – au détriment d’un autre – que la dérobade des électrons rend plus positif. Les chimistes enseignent ainsi que, dans la molécule HCl, le chlore se montre "électronégatif " et l’hydrogène "électropositif " ; la molécule présente un moment dipolaire permanent, dirigé de Cl (excès de charge négative) vers H (excès de charge positive). De même, dans H2O (molécule coudée en O), les électrons se concentrent préférentiellement autour de O – qui porte une charge négative excédentaire – et abandonnent partiellement les H, qu’ils laissent plus positifs, d’où là aussi un moment dipolaire. Des arguments analogues valent pour l’ammoniac NH3 (molécule pyramidale).À noter que CO2 ne présente aucun dipôle permanent : molécule linéaire O = C = O, symétrique par réflexion autour du centre de C. Un éventuel moment dipolaire (vrai vecteur) devrait être égal à son symétrique, c'est-à-dire à son opposé ; il ne peut que s’annuler, sauf si un champ électrique extérieur ![]() vient rompre cette symétrie.
vient rompre cette symétrie.![]() xxEx +
xxEx + ![]() xyEy +
xyEy + ![]() xzEz μy =
xzEz μy = ![]() yxEx +
yxEx + ![]() yyEy +
yyEy + ![]() yzEz μz =
yzEz μz = ![]() zxEx +
zxEx + ![]() zyEy +
zyEy + ![]() zzEz
zzEz
 Richard Feynman, Cours de physique, Dunod 1999 ; réédition de Bilingua Addison-Wesley ; 3 tomes en français Mécanique I, Électromagnétisme I, Électromagnétisme II.
Richard Feynman, Cours de physique, Dunod 1999 ; réédition de Bilingua Addison-Wesley ; 3 tomes en français Mécanique I, Électromagnétisme I, Électromagnétisme II. Richard Feynman, Leçons sur la physique, Odile Jacob 2007 ; extraits du Cours de Physique de Feynman.
Richard Feynman, Leçons sur la physique, Odile Jacob 2007 ; extraits du Cours de Physique de Feynman. Bernard Diu, Traité de physique à l’usage des profanes, Odile Jacob 1997, réédition 2008.
Bernard Diu, Traité de physique à l’usage des profanes, Odile Jacob 1997, réédition 2008.





