Au début du XIXe siècle, les machines à vapeur sont omniprésentes dans le monde industriel occidental et plus particulièrement en Angleterre. De nombreux ingénieurs tentent, de manière pratique, d’améliorer leur rendement, souvent très limité : il faut attendre Sadi Carnot en 1824 pour élaborer une vraie théorie scientifique de la chaleur et de son application aux machines thermiques (également appelées machines à feu). Nicolas Léonard Sadi Carnot (1796-1832), ancien élève de l’École Polytechnique, est à ce titre un des pionniers de la thermodynamique : il conçoit à 28 ans le cycle thermodynamique théorique idéal qui sert encore aujourd’hui de point de référence pour les machines thermiques, dit "cycle de Carnot". Sadi Carnot était le fils du physicien Lazare Carnot, dit "le grand Carnot" ; il convient de ne pas le confondre avec son neveu, Marie François Sadi Carnot (1837-1894), qui avait aussi le même prénom usuel Sadi, et qui fut président de la République française de 1887 jusqu’à son assassinat en 1894.

Figure 1 : Sadi Carnot (1796-1832). Son portrait en uniforme de polytechnicien, peint par Boilly en 1813.
Les machines à feu : un enjeu économique
Sadi Carnot veut percer à jour les secrets de la chaleur et de son utilisation dans les machines permettant de fournir de la puissance motrice. Il commence ses réflexions, plutôt philosophiques au début, par des constats de transformation de la chaleur en mouvement dans la nature. Il est véritablement le premier à envisager l’équivalence entre chaleur et mouvement et il est impressionné par cette puissance naturelle disponible qui ne demande qu’à être exploitée :
C’est dans cet immense réservoir que nous pouvons puiser la force mouvante nécessaire à nos besoins ; la nature, en nous offrant de toutes parts le combustible, nous a donné la faculté de faire naître en tous temps et en tous lieux la chaleur et la puissance motrice qui en est la suite. Développer cette puissance, l’approprier à notre usage, tel est l’objet des machines à feu.
Les enjeux économiques liés à l’augmentation du rendement des machines à feu constituent une des motivations principales de Sadi Carnot. La machine à vapeur a permis le développement des grandes puissances au XIXe siècle, et plus particulièrement de l’Angleterre. Sadi Carnot écrit en page 4 :
Enlever aujourd’hui à l’Angleterre ses machines à vapeur, ce serait lui ôter à la fois la houille et le fer ; ce serait tarir toutes ses sources de richesse, ruiner tous ses moyens de prospérité ; ce serait anéantir cette puissance colossale.
Les limites des machines à feu
Une des préoccupations principales de Sadi Carnot est de savoir s’il y a un maximum atteignable en termes de rendement pour transformer la chaleur en puissance motrice, ce qu’il évoque en page 6 :
On a souvent agité la question de savoir si la puissance motrice de la chaleur est limitée ou si elle est sans bornes.
Sa démarche est originale, car Carnot ne cherche pas seulement à améliorer les machines à vapeur, il cherche à trouver une théorie scientifique générale pour les machines à feu, tout comme s'était élaborée une théorie mécanique :
[…] il faut établir des raisonnements applicables, non seulement aux machines à vapeur, mais à toute machine à feu imaginable.
Chaleur, calorique, puissance motrice et travail
La chaleur est une énergie qui est échangée spontanément entre deux corps à températures différentes, de manière à atteindre un équilibre thermique. Mesurée en joules, elle est le résultat de la propagation de l’agitation thermique des particules de proche en proche au niveau microscopique. À l’époque de Sadi Carnot, les termes « chaleur » et « calorique » sont synonymes et se réfèrent à cette énergie qui était alors assimilée à une sorte de fluide s’écoulant des corps chauds vers les corps froids. Carnot utilise d’ailleurs ce principe du calorique dans ses Réflexions. La puissance motrice – terme utilisé par Sadi Carnot en 1824 – n’est pas une puissance au sens d’aujourd’hui, mais une énergie qui permet le mouvement, ce qui sera appelé « travail » et noté « W » (1). Sadi Carnot exprime en général cette grandeur en mètres cube d’eau élevés de 1 mètre de hauteur (soit par unité de 1 000 kilogrammes-mètres, unité de travail souvent utilisée au XIXe s.) ce qui correspond à un travail d’environ 10 000 Joules (W = M x g x h = 1000 kg * 10 m/s² * 1 m = 10 000 J).
On a longtemps pensé que les machines à vapeur « consommaient » du calorique tel un combustible mais Sadi Carnot met fin définitivement à cette hypothèse aux pages 9 et 10 en expliquant scientifiquement à partir de l’analyse simple d’une machine à vapeur que la chaleur n’est pas consommée mais simplement transportée d’une source chaude (le foyer où s’opère la combustion) vers une source froide (l’eau froide du condenseur) et que c’est ce transport qui génère une puissance motrice :
La production de puissance motrice est donc due dans les machines à vapeur, non à une consommation réelle du calorique, mais à son transport d’un corps chaud à un corps froid, c’est-à-dire à son rétablissement d’équilibre, équilibre supposé rompu par quelque cause que ce soit, par une action chimique, telle que la combustion, ou par toute autre.
La machine à vapeur apparaît au milieu du XVIIIe siècle, le premier brevet est déposé par James Watt (1736-1819) en 1769. C’est une machine thermique qui permet la transformation de la chaleur produite par la combustion du charbon en mouvement mécanique à l’aide de vapeur d’eau – en général pour faire tourner une roue. Du charbon est brûlé dans un foyer en contact avec une chaudière remplie d’eau. L’eau s’évapore et donne naissance à de la vapeur qui est envoyée dans un cylindre poussant un piston qui entraine une bielle permettant la rotation d’un volant d’inertie. La vapeur d’eau est ensuite condensée dans un condenseur dans lequel de l’eau froide circule, généralement issue d’un cours d’eau à proximité.

Figure 2 : La machine à vapeur de Watt (1769). On remarque le régulateur centrifuge (boules coulissant sur un axe vertical) qui permet d’assurer un fonctionnement régulier de la machine, indépendant des variations de la puissance sollicitée en sortie (Image Wikipedia, Hall d’entrée de l’École technique supérieure d’ingénierie industrielle à Madrid – Université polytechnique de Madrid)
La vapeur d’eau était certes le fluide le plus utilisé dans les machines à feu de l’époque, mais Sadi Carnot insiste tout au long de ses Réflexions sur le fait que n’importe quel autre élément peut être utilisé, on peut par exemple lire à la page 10 :
La vapeur d’eau est un moyen de réaliser cette puissance, mais elle n’est pas le seul : tous les corps de la nature peuvent être employés à cet usage ; tous sont susceptibles de changements de volume, de contractions, et de dilatations successives par des alternatives de chaleur et de froid (…) Un corps solide, une barre métallique, par exemple, alternativement chauffée et refroidie, augmente et diminue de longueur, et peut mouvoir des corps fixés à ses extrémités.
Une fois l’indépendance du vecteur démontrée, Sadi Carnot expose clairement la réversibilité des transformations mises en jeu ainsi que l’équivalence entre différence de température et puissance motrice :
Partout où il existe une différence de température, il peut y avoir production de puissance motrice. Réciproquement, partout où l’on peut consommer cette puissance, il est possible de faire naître une différence de température.
Il décrit ensuite dans les pages 17 et 18, les différentes transformations thermodynamiques qui se produisent dans une machine à vapeur. Écrit de manière plus moderne, voici les trois transformations:
1 – « Emprunter du calorique au corps A pour en former de la vapeur » : vaporisation isotherme de l’eau en vapeur d’eau à la température TA grâce à une source chaude (chaudière alimentée par le charbon). 2 – « La vapeur ayant été reçue dans une capacité extensible, tel qu'un cylindre muni d'un piston, augmenter le volume de cette capacité et par conséquent aussi celui de la vapeur. Ainsi raréfiée, elle descendra spontanément de température » : détente adiabatique (sans transfert thermique externe) de la vapeur dans un piston : abaissement de la température de TA à TB. 3 – « Condenser la vapeur en la mettant en contact avec le corps B (…) jusqu’à ce qu’elle soit entièrement liquéfiée » : liquéfaction isotherme de la vapeur en eau dans le condenseur à la température TB à l’aide d’une source froide (cours d’eau à proximité en général).
Une fois encore, Sadi Carnot tente ici de donner une description scientifique des différents phénomènes tout en restant compréhensible – en utilisant des mots simples et sans formules. Parallèlement, il fait référence à la pratique des machines – dont il tire sa théorie : le corps A correspond à la chaudière, le corps B (corps froid) correspond à « l'eau d'injection », tirée d'un cours d'eau à proximité, et permettant la condensation.
@@@@@@@
C’est à la page 22 qu’il formule sa principale proposition, qui donnera naissance au fameux cycle de Carnot :
Le maximum de puissance motrice résultant de l’emploi de la vapeur est aussi le maximum de puissance motrice réalisable par quelque moyen que ce soit.
On voit encore ici la volonté de Sadi Carnot d’élaborer une théorie des machines à feu la plus générale possible. Pour arriver à cette proposition, Carnot part du principe que le mouvement perpétuel est impossible, fait déjà approuvé depuis la fin du XVIIIe siècle par l’Académie des Sciences de Paris sous l’influence de Laplace. Cependant, il insiste sur l’impossibilité du mouvement perpétuel par quelque moyen que ce soit : un système utilisant la chaleur ou l’électricité, à l'instar d'un système mécanique, ne peut aboutir à un mouvement perpétuel et donc à une création de puissance motrice ex nihilo. Page 23, il formule la première condition à respecter pour obtenir le rendement maximal dans une machine à feu :
La condition nécessaire du maximum est donc qu’il ne se fasse dans les corps employés à réaliser la puissance motrice de la chaleur aucun changement de température qui ne soit dû à un changement de volume. Réciproquement, toutes les fois que cette condition sera remplie, le maximum sera atteint.
Autrement dit, deux corps ayant des températures différentes ne doivent jamais être mis en contact car la chaleur échangée lors de ce contact serait une perte pour la puissance motrice. Il faut donc réaliser des changements de température exclusivement par compression et par détente, ce qui implique de réaliser également des compressions et des détentes isothermes, guère possibles dans la pratique. Pour les démonstrations de ces propositions dans les pages 25, 26 et 27, Carnot fait usage de méthodes de calcul infinitésimal qui lui permettent d’effectuer des démonstrations par itérations et d’étendre les propositions à des cas plus généraux avec plusieurs corps.
@@@@@@@
Le père de Sadi Carnot, Lazare Carnot (1753-1823), grand mathématicien et physicien, est l’un des fondateurs de l’École polytechnique et a beaucoup travaillé sur les machines hydrauliques. Aussi, son fils n’hésite pas à comparer les machines hydrauliques étudiées par son père aux machines à feu en termes de rendement et de puissance maximale :
[…] on peut comparer avec assez de justesse la puissance motrice de la chaleur à celle d’une chute d’eau : toutes deux ont un maximum que l’on ne peut pas dépasser […]
Sadi Carnot tente de rapprocher la hauteur de la chute d’eau des machines hydrauliques avec la différence de température dans les machines thermiques. Il s’interroge sur l’éventuelle relation entre la chute du calorique et la puissance motrice en bas de la page 28 :
Dans la chute du calorique la puissance motrice augmente sans doute avec la différence de température entre le corps chaud et le corps froid ; mais nous ignorons si elle est proportionnelle à cette différence. Nous ignorons, par exemple, si la chute du calorique de 100° à 50° fournit plus ou moins de puissance que la chute de ce même calorique de 50° à 0°.
(2)À cette époque il n’existait pas encore de relation mathématique entre la puissance mécanique maximale théorique et la différence de température. Sadi Carnot essaye alors de faire des analogies avec les machines hydrauliques dans lesquelles la puissance motrice est proportionnelle à la hauteur de la chute d’eau, ce qui explique l'expression « chute du calorique
(3) ».
Le cycle de Carnot
Sadi Carnot présente alors une deuxième démonstration, plus rigoureuse, de sa proposition principale qui stipule que la puissance motrice produite par une machine thermique ne peut dépasser une certaine limite. Cette limite est exclusivement fixée par la différence de température entre la source chaude et la source froide et est indépendante du vecteur utilisé (vapeur, eau, alcool, etc.). Autrement dit, une machine thermique ne peut fournir du travail que si elle emprunte de la chaleur à une source chaude (ex : une chaudière) pour la rejeter vers une source froide (ex : un cours d’eau). Cela implique qu’une machine monotherme ne peut pas fournir de puissance mécanique ; cette proposition constitue la première énonciation du second principe de la thermodynamique (voir encadré de fin). Cette démonstration, faite à la page 18, repose sur un cycle thermodynamique idéal réalisé dans une machine idéale composée d’un piston dans un cylindre : la machine de Carnot représentée ci-dessous.
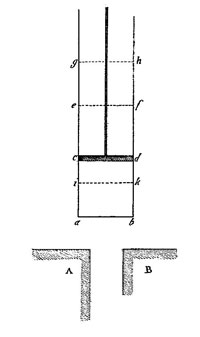
Figure 3 : La machine de Carnot (figure I de l’ouvrage, planche de figures à la fin). Un vaisseau cylindrique est muni d’un piston mobile, figuré là à la position ‘cd’, et qui peut bouger de haut en bas de manière à compresser ou à détendre le fluide élastique contenu dans le cylindre. Les deux corps ‘A’ et ‘B’ symboliquement représentés en bas du dessin sont deux corps isothermes où A représente la source chaude et B la source froide.
Les différentes transformations thermodynamiques effectuées dans cette machine idéale constituent le cycle de Carnot. Le cycle est composé de quatre transformations réversibles décrites à la page 33 qui peuvent être énoncées de la manière suivante:
1 – Détente isotherme à la température TA. A cette occasion, une quantité de chaleur QA > 0 est apportée au système (étape 2° de la page 33). 2 – Détente adiabatique réversible (isentropique, i.e. à entropie constante) où le fluide voit sa température diminuée de TA à TB sans échanger de chaleur avec l’extérieur (étape 3° de la page 33). 3 – Compression isotherme à la température TB. Cette compression s’accompagne du rejet d’une quantité de chaleur QB < 0 vers l’extérieur (étape 4° de la page 33). 4 – Compression adiabatique réversible (isentropique) où la température augmente de TB à TA sans échanger de chaleur avec l’extérieur (étape 5° de la page 33).
Concernant les cycles 2 et 4, Carnot ne manque pas de s'appuyer sur des «faits d'expérience qui prouvent le mieux le changement de température par la compression ou la dilatation » (comme par exemple la baisse du thermomètre sous une machine pneumatique où l'on fait le vide), en soulignant toutefois que :
Le changement de température occasionné dans les gaz par le changement de volume peut être regardé comme l'un des faits les plus importants de la physique, à cause des nombreuses conséquences qu'il entraîne, et en même temps comme l'un des plus difficiles à éclaircir et à mesurer par des expériences décisives.
De nos jours, ce fait d'expérience est bien connu : lorsqu'on comprime l'air dans une pompe à vélo, celle-ci chauffe ; lorsqu'on utilise une bombe aérosol, le fluide se dilate et refroidit le récipient.
@@@@@@@
Au final, ce cycle permet de générer une puissance motrice (autrement dit, un travail), égale à la somme des chaleurs échangées :
W= QA + QB
Ce cycle idéal ne suppose pas de fluide particulier et il permet de fournir le maximum théorique de puissance motrice car tous les changements de température sont exclusivement dus à des changements de volume (compression ou détente) : à aucun moment il n’y a échange de chaleur par contact ou perte par frottement. De plus, ce cycle est réversible : en effectuant les transformations dans l’autre sens et en apportant du travail mécanique, c’est le cycle de réfrigération (ou de chauffage) idéal, ce que Carnot explicite à la page 36 :
[…] le résultat des opérations inverses est la consommation de la puissance motrice produite, et le retour du calorique corps B au corps A […]
Le cycle de Carnot est passé relativement inaperçu lors de sa présentation orale à l’Académie des Sciences en 1824
(4), ainsi que dans l'ouvrage
Réflexions. Ce n’est que dix ans plus tard, en 1834, qu’Emile Clapeyron (1799-1864) portera un intérêt particulier aux
Réflexions de Sadi Carnot et en comprendra la portée. Clapeyron illustre alors le cycle de Carnot dans un diagramme qui porte aujourd’hui le nom de diagramme de Clapeyron dans lequel la pression est représentée en fonction du volume lors des transformations.
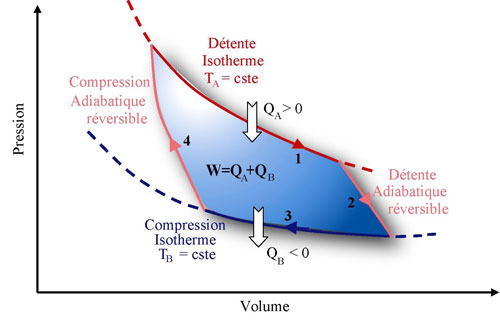
Figure 4 : Le cycle de Carnot dans le diagramme de Clapeyron (Pression/Volume). Le cycle est composé de 2 isothermes et de 2 adiabatiques réversibles : les notations de 1 à 4 correspondent aux notations ci-dessus. (diagramme B. Bradu)
Le second principe de la thermodynamique
Le second principe de la thermodynamique stipule que tous les processus physiques comme l’échange de chaleur sont des processus irréversibles. Une nouvelle variable thermodynamique est alors créée par Clausius (1822-1888) en 1850 suite à la lecture des Réflexions de Sadi Carnot, afin de rendre compte de l’irréversibilité des transformations thermodynamiques : l’entropie, notée « S ». C’est une grandeur extensive (elle est sommative) définie ainsi : sa variation lors d'une transformation réversible est égale à la quantité de chaleur apportée au système divisée par la température de ce même système :
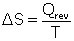 (1)
(1)
Toutes les transformations thermodynamiques réelles (donc irréversibles) génèrent de l’entropie à cause des phénomènes dissipatifs (friction, diffusion, réactions chimiques, etc.). L’entropie d’un système fermé ne peut alors qu’augmenter dans le temps. On peut en déduire la fameuse inégalité de Clausius qui formalise le second principe de la thermodynamique et qui est représenté dans l'inéquation :
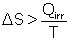 (2)
(2)
Pour la construction de machines thermiques, il faut comprendre, avec le second principe de la thermodynamique, que la génération d'entropie est un obstacle : l’entropie créée vient diminuer le rendement des machines. Autrement dit, il faut fabriquer des machines qui minimisent la création d'entropie, c'est-à-dire principalement les frictions et les transferts de chaleur ; ce que Sadi Carnot avait parfaitement compris lorsqu’il dit que la première règle à respecter pour concevoir une machine à feu efficace est d’éliminer tous les transferts de chaleur ayant une origine autre que la compression et la détente.
Sadi Carnot énonce en fait pour la première fois dans les Réflexions le deuxième principe de la thermodynamique, qui sera par la suite formalisé par Clausius avec l’entropie vingt-cinq ans plus tard. En appliquant le deuxième principe au cycle de Carnot, qui est basé sur des transformations idéales réversibles, on peut alors écrire l’égalité de Clausius-Carnot valable pour une machine de Carnot réversible ayant une source chaude à la température TA et une source froide à la température TB (l’entropie est conservée lors des transformations adiabatiques) :
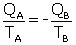 (3)
(3)
Le rendement de Carnot est égal au rapport entre la puissance motrice W et la puissance apportée au système QA (lors de l'étape 1, par exemple en chauffant de l'eau dans une machine à vapeur). Il dépend exclusivement du rapport entre les températures de la source froide et de la source chaude, indépendamment du vecteur :
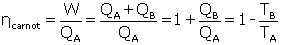 (4)
(4)
Ainsi, en utilisant de la vapeur d’eau à pression atmosphérique comme source chaude (100°C, soit 373 K) et l’eau d’un cours d’eau comme source froide (20°C, soit 293 K), l’équation (4) nous donne un rendement théorique maximum de :
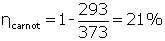 (5)
(5)
Toute machine thermique fonctionnant entre 100°C et 20°C ne peut donc pas dépasser 21 % de rendement. On peut voir dans l’équation (4) que le rendement de Carnot tend vers 100 % si la source froide est à 0 K, ce que la physique nous interdit (c’est une conséquence du troisième principe de la thermodynamique, formulé bien plus tard en 1904 par Walther Nernst, 1864-1941), il est donc impossible d’obtenir une machine thermique ayant un rendement de 100 %, même avec une machine de Carnot.
Une fois sa démonstration terminée, Sadi Carnot reformule sa proposition principale de manière encore plus générale à la page 38 :
La puissance motrice de la chaleur est indépendante des agents mis en œuvre pour la réaliser ; sa quantité est fixée uniquement par les températures des corps entre lesquels se fait, en dernier résultat, le transport du calorique.
C’est cette dernière proposition qui constitue véritablement le début de la thermodynamique moderne et son application aux machines thermiques. Tous les ingénieurs d’aujourd’hui travaillant sur des moteurs thermiques, des systèmes de chauffage ou des réfrigérateurs tentent de se rapprocher au plus près du cycle de Carnot pour obtenir un rendement maximal ; mais nous sommes encore très loin d’atteindre le cycle de Carnot de manière industrielle. On comprend facilement que plus la différence de température entre la source chaude et la source froide est importante, plus la machine est efficace – car le rendement de Carnot est plus élevé. À titre d’exemple, les systèmes de réfrigération utilisant de l’hélium liquide fonctionnent entre 300 K et 4,2 K : une machine de Carnot idéale consommerait, pour fournir une puissance de réfrigération de 1 W à 4,2 K, une puissance de 70 W à 300 K
(5); les meilleurs réfrigérateurs à hélium d’aujourd’hui consomment en fait 230 W de puissance électrique pour fournir 1 W de réfrigération à 4,2 K. Ceci représente à peine 30 % du cycle de Carnot, ce qui est principalement dû à la génération d’entropie causée par les frictions dans les machines tournantes (compresseurs et turbines) et par les pertes thermiques lors des transferts de chaleur (échangeurs de chaleur).

(1) C’est le physicien Coriolis (1792-1843) qui proposera en 1829, dans son
Calcul de l’effet des machines, la désignation de « travail », auparavant désigné sous des termes divers (quantité d’action, puissance, travail mécanique,…).
(2) Le "rendement de Carnot", concept qui sera introduit après lui, permet de répondre à cette question : le rendement de 100 à 50°C est de 1 – 323/373 = 0,134, le rendement de 50 à 0°C est de 1 – 273/323 = 0,155.
(3) Carnot semble penser que la "chute du calorique" entre un corps chaud et un corps froid, c’est-à-dire le transfert de chaleur d’un corps chaud vers un corps froid, permet de créer un travail. Comme le calorique était à l’époque considéré comme une sorte de fluide, l’analogie avec la chute d’eau était presque parfaite mais en fait erronée : la chaleur prélevée à la source chaude n’est pas égale à la chaleur rejetée à la source froide car pendant les transferts de chaleur (ou "chute du calorique"), de l’entropie est générée et le travail n’est pas créé par ce transfert de chaleur mais par la transformation de la chaleur même.
(4) Séance du 14 juin 1824, présentation par l'académicien Pierre-Simon Girard (1765-1835).
(5) Suivant la formule (3) ci-dessus, 70/300 ≈ 1/4,2.







![]() (1)
(1)![]() (2)
(2)![]() (3)
(3)![]() (4)
(4)![]() (5)
(5)
 Réflexions sur la puissance motrice du feu…, Bachelier 1824, réédition Jacques Gabay 2005
Réflexions sur la puissance motrice du feu…, Bachelier 1824, réédition Jacques Gabay 2005 J. Payen, « Une source de la pensée de Sadi Carnot », Archives internationales d'histoire des sciences, 1968, p. 15.
J. Payen, « Une source de la pensée de Sadi Carnot », Archives internationales d'histoire des sciences, 1968, p. 15. Sadi Carnot sur Wikipedia (labellisé "Article de qualité")
Sadi Carnot sur Wikipedia (labellisé "Article de qualité") Blog "La science pour tous" (B. Bradu) : La thermodynamique : Les bases & Thermodynamique : Principes et Applications
Blog "La science pour tous" (B. Bradu) : La thermodynamique : Les bases & Thermodynamique : Principes et Applications






