Le Carré magique du Pape Léon III
- INFORMATION
- ACTUALITÉ
- ANALYSE
- EN SAVOIR PLUS
- À TÉLÉCHARGER
Enchiridion Leonis Papæ Serinissimo Imperatori Carolo Magno (Enchiridion du pape Léon, envoyé à l’empereur Charlemagne)
ca 795
Un des premiers carrés magiques, qui figure dans l’Enchiridion du pape Léon III. Ce carré magique « papal » possède de nombreuses propriétés détaillées ici.
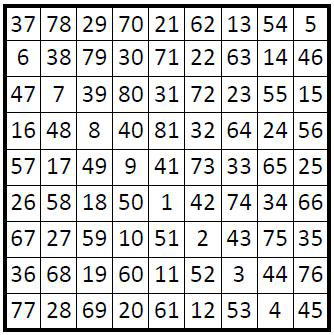
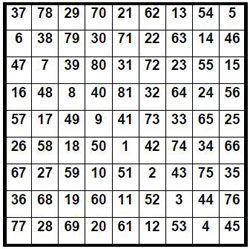
Le pape Léon III rédige vers 795 un opuscule, « l’Enchiridion », dans lequel on trouve une grille numérique insolite et sans aucun commentaire, qui s’avère être un carré magique normal d’ordre n = 9 et de constante magique M9 = 369.
On distingue dans ce carré magique de type associé, de nombreuses progressions arithmétiques, ainsi qu’un certain nombre de sous-carrés magiques, tandis que sa construction, par la Méthode du cheminement régulier, reste simple.
Prétendu mystérieux, ce carré magique se révèle, après décryptage, posséder de nombreuses propriétés inédites intéressantes et remarquables.
René Descombes est Ingénieur divisionnaire des Travaux Publics de l’État – Chef d’Arrondissement honoraire du Service de la Navigation du Rhin à Strasbourg, et auteur de plusieurs ouvrages scientifiques sur les carrés magiques.

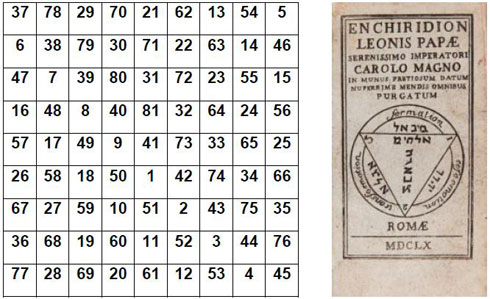
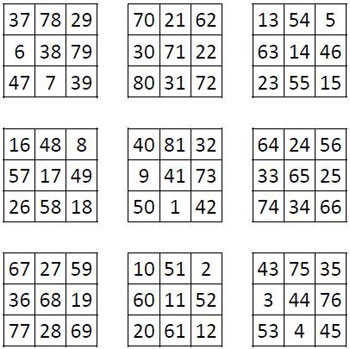
La grille numérique carrée ci-dessus se trouve telle quelle, sans aucun commentaire, dans un opuscule connu sous le nom d’Enchiridion du pape Léon, rédigé par Léon III. À vrai dire, on ne sait pas trop ce que vient faire ici ce carré magique normal, d’ordre n = 9, de constante magique(1) M9 = 369, à tel point que dans certaines éditions modernes de l’Enchiridion, cette grille numérique a été supprimée (édition de 1660 par exemple). Un genre de talisman ?
On retrouve ce carré magique dans l’ouvrage de Mouny (2), ainsi que dans les Curiosités et récréations mathématiques, de G. Boucheny, Larousse 1939, p. 130, de façon tout aussi insolite que dans l’Enchiridion, sans liaison aucune avec le texte du livre.
D’aucuns considèrent ainsi, mais de façon abusive, cette grille numérique comme très mystérieuse.
Un carré magique de type associé
Tout d’abord c’est un carré magique de type associé : la somme des termes complémentaires (3) est constante et égale à la constante de polarisation S (dénomination du général Cazalas, 1934), qui est elle-même égale à S = n2 + 1, soit S = 82 dans le cas qui nous occupe.
Dans le cas d’un carré magique d’ordre impair, ce qui est le cas du carré magique d’ordre n = 9 étudié, la case centrale est égale à la moitié de cette constante de polarisation, soit 41 ; c’est aussi le terme médian de la série des entiers « 1, 2, 3, . . . n2 », soit ici « 1, 2, 3 . . . 81 ». Dans ce cas particulier, cette case médiane, est égale à la demi somme des termes situés sur les médianes et les diagonales du carré central d’ordre n = 3 (qui est donc « magique » sur ses médianes et diagonales, M’3 = 123)
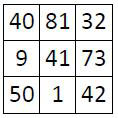
On peut d’ailleurs faire une remarque analogue à propos des grilles carrées centrées d’ordre n = 5 et n = 7, qui sont « magiques » sur leurs médianes et diagonales.
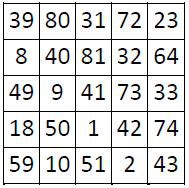
M’5 = 205
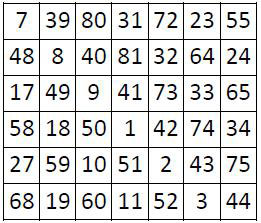
M’7 = 287
|
Le pape Léon III
Homme d’église de l’époque carolingienne, Léon III, né et décédé à Rome (750–816), fut pape de 795 à 816, soit pendant une vingtaine d’années. Ce fut un grand admirateur et ami de Charlemagne ; lorsque sa légitimité fut contestée, en 799, il se réfugia auprès de Charlemagne à Paderborn, en Saxe. Il le couronna empereur, à Noël 800, dans la basilique Saint-Pierre de Rome. Dans l’Enchiridion Leonis Papae, que l’on peut traduire Manuel du pape Léon, un « grimoire » rédigé vers 795, on trouve de mystérieuses oraisons, des invocations, des conjurations pour tous les maux et circonstances, des textes des rois antiques, ainsi que des formules pour déclencher les forces sacrées, des sceaux, des pentacles, des talismans… L’Enchiridion fut offert par Léon III à Charlemagne. Un exemplaire original en latin est conservé à la bibliothèque du Vatican à Rome. Précisons que Léon III n’était pas mathématicien !
Figure 1 : Une représentation supposée de Léon III, sur une mosaïque d’époque du Palais du Latran, à Rome (image WikiCommons).
Gerbert d’Aurillac (945 –1003) qui devint pape sous le nom de Sylvestre II (999 –1003), connu comme « Pape de l’an Mil », fut le seul pape mathématicien. Il favorisa l’introduction et l’essor en Occident de la numération de position, des tables d’opération et des chiffres dits arabes. Le zéro inventé aux Indes, et rapporté en Occident par les invasions arabes, trouva en lui un ardent défenseur : il tentera de l’imposer, mais ce n’est que vers le XIVème siècle que le monde occidental l’acceptera définitivement. Il a publié plusieurs ouvrages de mathématiques. |
Des progressions arithmétiques
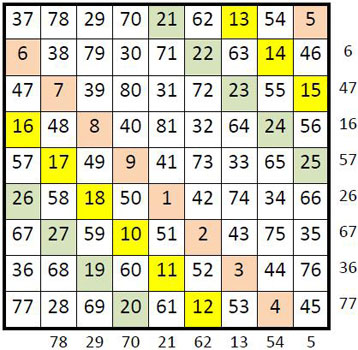
Dans les diagonales parallèles à la première diagonale (4), dans une diagonale sur deux (représentées sur fond parme ou jaune ci-dessous), tous les termes sont en progression arithmétique de raison r = 1. Dans les diagonales intermédiaires (sur fond blanc), ces progressions sont moins régulières, s’arrêtant en cours de route, et reprenant à partir d’un autre nombre.
Il n’y a apparemment pas d’ordonnancement bien défini.
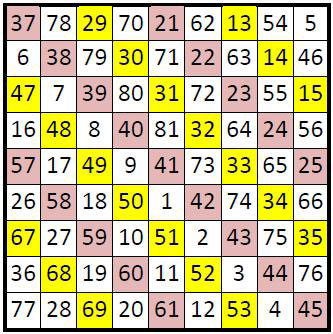
Parallèlement à la seconde diagonale, on peut faire les mêmes remarques : les termes, dans une diagonale sur deux, sont tous en progression arithmétique régulière de raison r = 9. Ces progressions sont interrompues dans les diagonales intermédiaires, pour reprendre à partir d’un autre nombre, mais toujours avec la même raison r = 9.
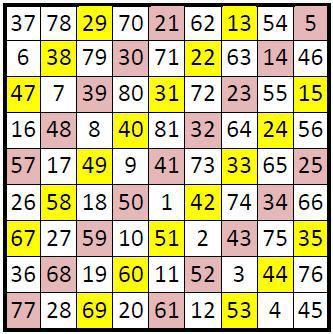
Des écarts réguliers
Considérons maintenant les termes dans les colonnes. On ne constate pas la présence de progression arithmétique dans la suite des termes, mais une certaine régularité dans la différence entre deux termes accolés verticalement, dans chaque colonne : ces différences figurent au droit de chaque colonne du carré magique ci-dessous.
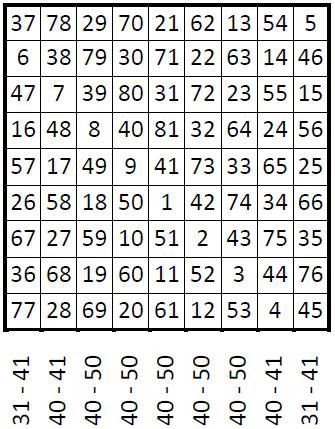
Si l’on considère alors les lignes, nous constatons, à défaut d’un enchaînement systématique, les mêmes différences entre deux nombres accolés, de colonne en colonne – soit une petite « famille » qui se réduit à quatre nombres : 32, 40, 41 & 49 (ci-dessous, en blanc, le carré magique ; les colonnes jaunes représentent la différence entre les deux nombres voisins horizontalement dans le carré).
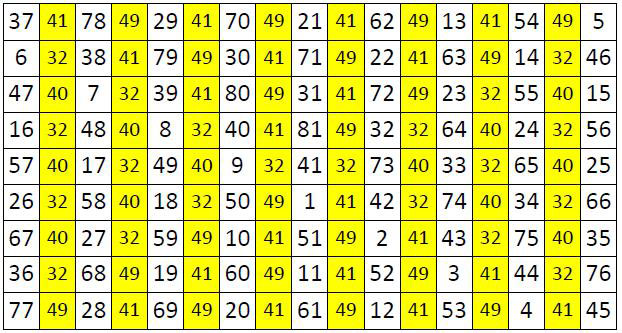
On peut encore remarquer que dans les colonnes, on assiste à une sorte de classement numérique des entiers : la première colonne est réservée aux entiers se terminant par 6 ou 7 ; la seconde par 7 ou 8 ; la troisième par 8 ou 9 ; la quatrième par zéro (avec la présence d’un 9) ; la cinquième aux neuf nombres qui se terminent par 1 ; la sixième par 2 (avec la présence d’un 3) ; la septième par 3 ou 4, la huitième par 4 ou 5 ; et enfin la neuvième par 5 ou 6.
La polymagie du carré magique papal
Dans le carré magique papal, les vingt alignements magiques (lignes, colonnes et diagonales) ne sont pas les seuls à assurer cette magie : il y a en effet un grand nombre N de combinaisons de la série des 81 premiers entiers de cette grille pris 9 à 9, dont la somme des termes est « magique », c’est-à-dire égale à M9 = 369. C’est ce que l’on nomme la « polymagie » d’un carré magique : la connaissance de ces nombreuses combinaisons magiques, et leur catalogue, est tributaire d’un logiciel ad hoc (récursif par exemple). Au-delà de n = 6, il est nécessaire de disposer d’un ordinateur ayant une capacité-mémoire très importante.
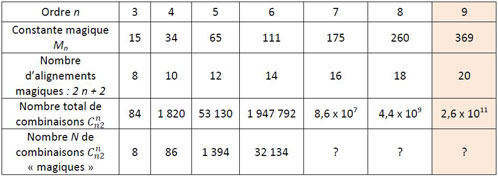
Compte-tenu de la progression rapide de N, on peut augurer que le carré magique papal compte un nombre impressionnant de combinaisons de neuf termes dont la somme est « magique ».
Le carré magique papal est autocomplémentaire
Rappelons que lorsque l’on remplace chaque terme d’un carré magique normal d’ordre n, par son complémentaire à n2 + 1, on obtient un carré magique, dit « complémentaire », qui a la même constante linéaire et les mêmes propriétés que le carré d’origine.
Et si ce « complémentaire » se superpose, après rotation(s), avec le carré d’origine, ce dernier est alors dit « autocomplémentaire ». On dit aussi de ces deux carrés magiques qu’ils sont jumeaux.
C’est précisément le cas du carré magique papal, avec n2 + 1 = 82 : le « complémentaire » coïncide après rotation de deux quarts de tour, avec le carré magique papal.
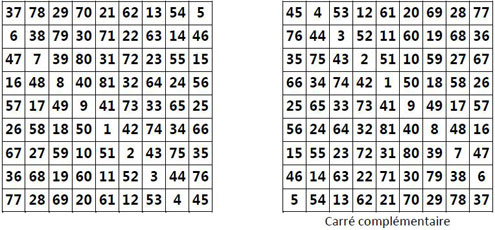
Ceci n’est pas une propriété générale des carrés magiques impairs construits en application de la Méthode par cheminement régulier (que nous détaillerons plus loin) : ces carrés magiques ne sont pas tous autocomplémentaires.
Mais on retrouve cependant certaines coïncidences. Ainsi dans l’exemple ci-dessous d’un carré magique normal d’ordre n = 5, de constante magique M5 = 65 :
-
Case-départ : n° 7 du carré naturel ;
-
Marche principale : une des 8 marches du cavalier aux échecs ;
-
Saut secondaire : on saute 2 cases parallèlement à la seconde diagonale, vers le haut et à droite (ex. à g. ci-dessous : 5 à 6, 10 à 11, 15 à 16, 20 à 21).
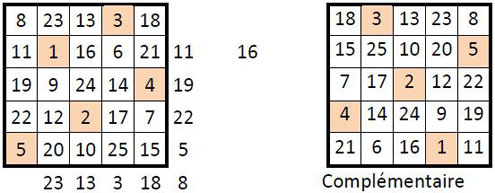
Dans le « Complémentaire », avec n2 + 1 = 26, on retrouve les alignements horizontaux inversés (ce qui correspond à une symétrie dont l’axe vertical se trouverait entre les deux grilles), mais les lignes correspondantes ont subi une permutation circulaire.
Remarquons que les termes des cycles successifs de n = 5, sont bien situés sur une permutation figurée dans les deux grilles (cases pochées – voir plus loin).
Des sous-carrés magiques
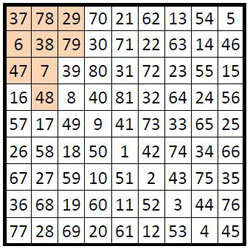
On peut aussi considérer ce carré magique d’ordre n = 9, de 81 cases, comme formé de neuf sous-carrés (5) d’ordre n = 3 de 9 cases, numérotés ci-dessous, de 1 à 9, tels qu’ils sont placés dans ce carré magique :
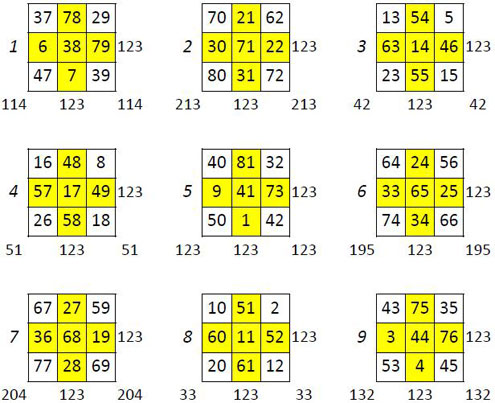
On observe alors les propriétés suivantes :
-
Les médianes ont toutes la même somme, S = 123, soit M9/3 ;
-
Les sommes des diagonales sont égales dans chaque sous-carré pris individuellement ;
-
Dans le sous-carré central, les sommes des médianes et des diagonales sont égales, S = 123.
@@@@@@@
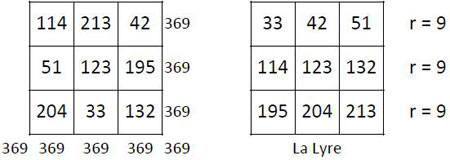
Maintenant, si l’on place les sommes des différentes diagonales de chaque sous-carré, dans une grille d’ordre n = 3 (ci-dessous), on forme un carré magique type associé, de constante magique M’3 = 369, et de constante de polarisation (6) S = 246, soit le double de la case centrale.
Dans la Lyre (7) correspondante, chaque ligne est en progression arithmétique de raison r = 9.
On peut naturellement faire la même manipulation avec les sommes des médianes, avec le même résultat.
Une construction mystérieuse ?
Dans son ouvrage Nouvelles découvertes sur les carrés Magiques (8), le colonel Guy-Claude Mouny écrit à propos du carré magique du pape Léon III :
Certes, nous n’avons pas découvert le mode de construction de [ce carré magique]… Comme les choses vont vite, nous sommes attentif à un long développement de M. Alain Becquart (que nous avions consulté) pour la construction de ce carré. Il la décrit comme simple, ce qui est vrai pour le montage numérique. Mais nous ne la reproduirons pas, car cela demanderait plusieurs pages. Nous restons à la disposition des lecteurs qui en voudraient copie.
Le colonel Mouny (1930-2007) n’est hélas plus là pour nous communiquer cette fameuse méthode de M. Alain Becquart pour la construction du carré magique du pape Léon III…
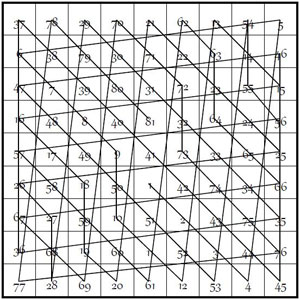
Voici néanmoins une méthode de construction de ce carré magique papal, très simple, et qui ne nécessite que quelques lignes d’explications :
-
On établit un cheminement régulier, parallèle à la première diagonale principale.
-
On part de la case numérotée « 1 », juste au-dessous de la case centrale (n° 50 du carré naturel correspondant), en procédant aux reports habituels lorsque l’on tombe en dehors de la grille, et l’on saute une case vers le bas en fin de cycle, après 9 sauts : soit dans ce premier cycle, après le 9, on poursuit par le 10, en sautant une case vers le bas.
-
On continue ce cheminement, toujours en observant le décalage d’une case vers le bas, tous les 9 sauts. On ne peut pas se tromper : on remplit ainsi une diagonale brisée après l’autre, dans toute la grille. Les cases pochées en couleurs ci-dessus représentent les trois premiers cycles de 9 sauts.
|
La Loubère, retour de Siam
Il s’agit de la « Méthode siamoise » rapportée par Simon de La Loubère (1642–1729), qui fut ambassadeur extraordinaire de Louis XIV auprès de Naraï, roi de Siam (Thaïlande actuelle), vers 1687–1688. Il consacre une soixantaine de pages aux carrés magiques dans le second volume de son ouvrage Du Royaume de Siam (1691) ; c’est lui qui introduisit en Occident le qualificatif de carré « magique ». La Loubère était, entre autres, mathématicien : il a laissé un ouvrage posthume De la résolution des équations, ou de l’extraction de leurs racines, publié en 1732. Il fut élu membre de l’Académie Française en 1693. Cependant on peut penser que la « Méthode siamoise », dite de Simon de La Loubère, ou « Méthode par cheminement régulier », était connue en Occident bien avant lui.
Figure 2 : S. de La Loubère, Du Royaume de Siam (1691), Tome 2, p. 300 (image Gallica BnF) |
Des permutations figurées
On constate immédiatement que les cycles ci-dessus, sur diagonales brisées, correspondent à des permutations figurées : ces neuf permutations figurées (1-9 en saumon, 10-18 en jaune,… 73-81 en bistre) remplissent toutes la grille.
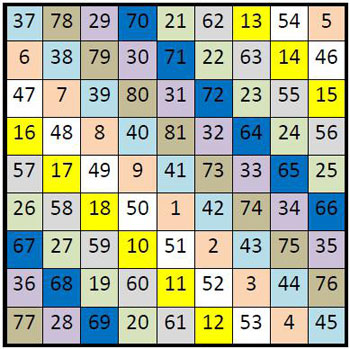
C’est une propriété générale des carrés magiques construits par la Méthode par cheminement régulier. Cependant, ces diagonales brisées ou ces permutations figurées, ne sont pas magiques : le carré magique normal papal n’est pas diabolique (9), ce qui serait un comble !
@@@@@@
Il existe de nombreuses variantes de cette méthode de construction d’un carré magique d’ordre impair. Au départ de l’une des cases de la grille d’ordre n = 9, on peut imaginer 4 marches principales diagonales, et 16 sauts secondaires en fin de cycle (10), soit : 81 x 4 x 16 = 5 184 carrés magiques de type papal.
Voici une application, qui conduit bien à un carré magique normal de type papal, M9 = 369 : case-départ n° 22 du carré naturel d’ordre n = 9 ; marche principale diagonale vers le haut et à gauche ; saut secondaire orthogonal : 2 cases à droite.
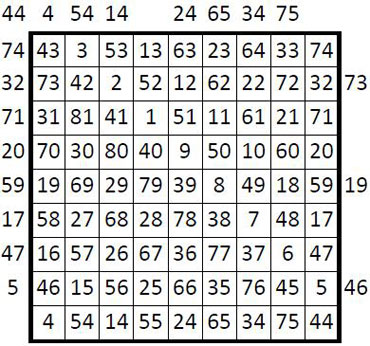
On peut envisager divers sauts secondaires orthogonaux, mais aussi diagonaux, l’ensemble atteignant ainsi au premier saut toutes les cases disponibles de la grille. Dans cette éventualité, on peut construire : 81 x 4 x 72 = 23 328 carrés magiques de ce type.
Une méthode très prolifique
La méthode dite « par cheminement régulier », applicable aux ordres impairs n > 3, compte-tenu des choix de la case-départ, de la marche principale, et du saut secondaire, peut être considérée comme très prolifique, même si elle ne donne pas toujours un carré magique, mais souvent un carré semi-magique, ou un carré avec une seule diagonale magique. Voici un exemple, d’ordre n = 5, un carré magique de constante magique M5 = 65, de type associé, S = 26 : on saute 2 cases vers le bas en fin de cycle.
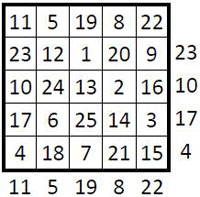
On dénombre les solutions comme suit : compte tenu du choix de la case-départ (25 choix), du cheminement (4 directions diagonales possible à partir de la case départ), et de toutes les possibilités de saut secondaire, dans les cases disponibles lors du premier saut secondaire, soit n2 – n = 20 cases, le nombre de solutions est alors, dans ce cas particulier N = 25 x 4 x 20 = 2 000.
@@@@@@
Voici un autre exemple d’application de la Méthode par cheminement régulier, pour un carré semi-magique normal d’ordre n = 7 :
-
Case départ : case centrale (n° 25 du carré naturel) ;
-
Marche principale : une des marches du cavalier aux échecs ;
-
Saut secondaire orthogonal : une case à gauche en fin de cycle (ex. ci-dessous de 7 à 8) (11) ;
-
Constante magique M7 = 175 ;
-
Lignes et colonnes sont magiques, mais seule la seconde diagonale l’est.
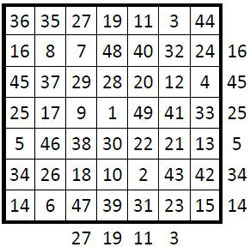
Ce cas particulier se dénombre ainsi : avec le choix de la case-départ parmi les n2 = 49 cases de la grille, le choix du cheminement dans l’une des 8 marches du cavalier, et le choix de l’un des 12 sauts secondaires orthogonaux possibles en fin de cycle, le nombre N de carrés magiques ou semi-magiques que l’on peut ainsi construire théoriquement est N = 49 x 8 x 12 = 4 704.
Un tapis magique
Soit le « tapis » ci-dessous, formé de quatre carrés magiques du Pape Léon III juxtaposés. Si l’on promène à l’intérieur de ce tapis une grille d’ordre n = 9 de 81 cases, on obtient toujours un carré magique ou semi-magique, avec souvent une seule diagonale magique.
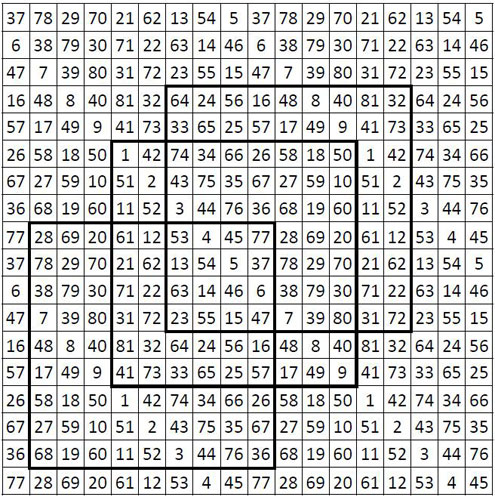
et encore des sous-carrés magiques !
Les sommes des termes des sous-carrés magiques d’ordre 3 forment elles-mêmes, ci-dessous, un carré magique d’ordre 3, de constante magique M’3 = 1107 (1107 = 3 x 369) et de type associé, de constante de polarisation S = 738 (738 = 3 x 246)

Dans les lignes de la lyre correspondante, ces sommes sont en progression arithmétique : r = 9.
Notons qu’avec les termes homologues des sous-carrés de 9 cases, on peut former 9 grilles numériques, lesquelles sont autant de carrés magiques de type associé, on de carrés semi magiques.
Un problème de pavage
On peut toujours paver une grille carrée d’ordre n, avec n polyminos d’ordre n, identiques ou bien différents.
Ainsi la grille d’ordre n = 9 du carré magique papal, peut être pavée de n = 9 polyminos d’ordre n = 9. Il existe de nombreuses solutions (il y a 1285 9-ominos, sans compter les rotations ni les symétries…) ; ci-dessous un exemple de pavage à symétrie centrale.

On peut également paver cette grille avec 27 triminos : une des solutions se déduit aisément de l’exemple ci-dessus.
@@@@@@
Mais peut-on paver la grille du carré magique papal avec 9 polyminos d’ordre n = 9 « magiques », c’est-à-dire dont la somme S des neuf termes soit égale à la constante magique de ce carré magique, soit S = M9 = 369 ? C’est un problème très difficile – peut-être insoluble ?
Est-ce plus facile avec 27 triminos de somme S = M9/3 = 123 ?
Un tracé remarquable
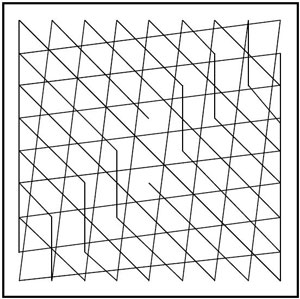
Voici à présent le tracé régulier remarquable du carré magique du pape Léon III, à symétrie centrale : la méthode de construction par cheminement apparait nettement.
La duplication du carré magique du pape Léon III – La Méthode des quatre carrés.
C’est une opération délicate qui exige beaucoup d’attention, qui passe par l’intermédiaire d’un carré auxiliaire, lequel n’est pas toujours facile à établir.
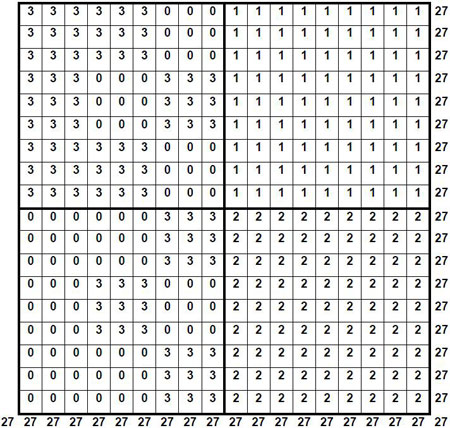
On prépare une grille d’ordre n = 18, de 324 cases, que l’on divise en quatre quadrants. On remplit cette grille avec la série « 0, 1, 2, 3 », en nombre égal dans chaque ligne et chaque colonne, de façon à avoir 3p = 27 (p étant la constante du carré papal, égale à 9) comme constante linéaire. Voici une solution ci-dessus, parmi d’autres.
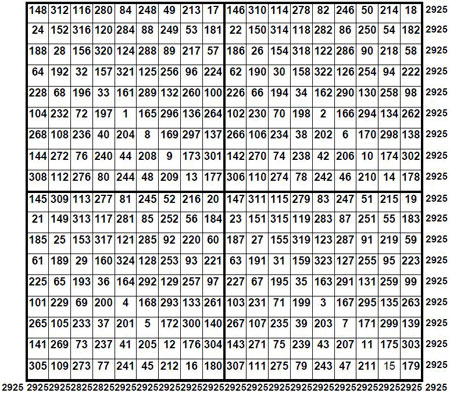
Explication de la duplication ci-dessus : dans une grille vierge d’ordre n = 18, on applique la relation opérationnelle : « 4 a + r – 3 », case par case : « a » étant le nombre donné par le carré papal, et « r » par le carré auxiliaire K. Ainsi la case en haut à gauche du duplicat est obtenue comme suit (12) : 4*37 + 3 – 3 = 148 ; la case en bas à droite est obtenue par 4*45 + 2 – 3 = 179 ; la 10e case de la première ligne du duplicat est obtenue par 4*37 (on reprend ici la case en haut à gauche du carré initial) + 1 – 3 = 146.
On obtient un carré magique normal d’ordre n = 18 et de constante magique M18 = 2 925, soit un duplicat du carré magique du pape Léon III. Il y a de nombreuses solutions pour le carré auxiliaire K, conduisant ainsi à un duplicat différent du carré papal.
Quelques propriétés du duplicat
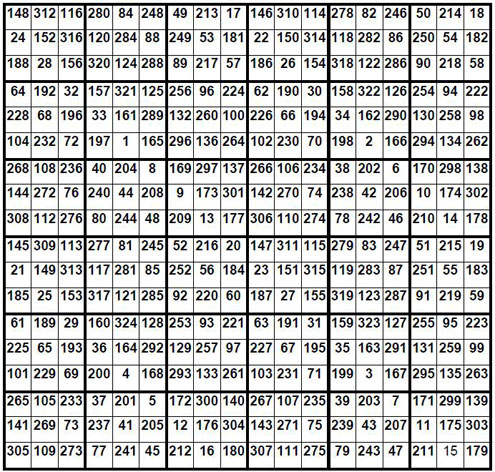
On divise ce duplicat en 6 x 6 = 36 sous-carrés d’ordre n = 3, de 9 cases (cf. ci-dessus ce découpage). Les sommes des 9 termes de chaque sous-carré forment alors un carré magique d’ordre n = 6, de constante linéaire M6 = 8 775, dans les lignes, les colonnes et les deux diagonales principales.
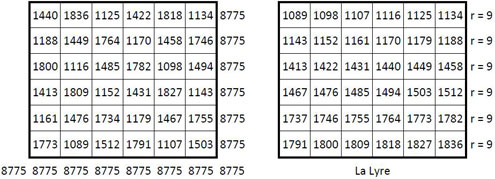
Dans la « Lyre » correspondant à ce carré magique, on constate que les termes sont en progression arithmétique régulière de raison r = 9 dans toutes les lignes. Dans les colonnes, on constate certaines différences Δ égales :
-
dans les termes des lignes 1/2, 3/4 et 5/6, deux à deux : Δ = 54 ;
-
dans les termes des lignes 2/3 et 4/5 : Δ = 270 ;
-
dans les termes des lignes 6/1 : Δ = 702
Toutes ces différences Δ sont des multiples de 9.
@@@@@@
On divise encore ce nouveau carré magique d’ordre n = 6 (à gauche ci-dessus), en sous-carrés de 4 cases, soit 3 x 3 = 9 sous-carrés d’ordre n = 2. Les sommes des termes de ces 9 sous-carrés forment à leur tour un carré semi-magique d’ordre 3, de constante linéaire M’3= 17 550 ; les deux diagonales principales ne sont pas magiques, mais leur somme est égale à 2 M’3 : 17 505 + 17 595 = 35 100.
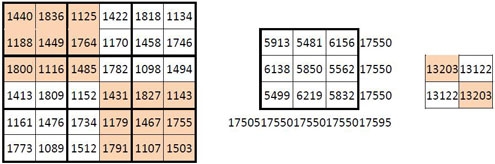
Remarquons encore que les quartiers opposés de ce carré magique d’ordre n = 6 ci-dessus, comme d’ailleurs les quartiers opposés du duplicat lui-même, ont même somme : 13 203 suivant la première diagonale principale, et 13 122 suivant la seconde (cf. petite grille ci-dessus à droite )
Le carré papal à la puissance deux ?...
On pourrait envisager de compléter ces manipulations par l’élévation au carré du carré papal, c’est-à-dire faire le produit du carré papal par lui-même. Et obtenir un carré magique d’ordre n = 81, de 6 561 cases, de constante magique M81 = 265 761, et rechercher alors les propriétés caractéristiques de ce carré papal à la puissance deux (13) !
…et la racine carrée d’un carré magique ?
On peut remarquer à ce sujet, que certains carrés magique normaux d’ordre n = 9, peuvent être considérés comme le produit de deux carrés magiques normaux d’ordre n = 3. Si ces deux carrés magiques normaux d’ordre n = 3 sont identiques, le produit d’ordre n = 9 correspond alors à l’élévation au carré du carré formateur.
Ceci ne semble pas être le cas du carré magique papal : peut-on à cet égard, pour le vérifier, extraire la racine carrée d’un carré magique : est-ce une opération possible ?
À titre documentaire, voici l’élévation au carré de deux formes identiques du Lo Shu : on obtient un carré magique normal d’ordre n = 9, et de constante magique M9 = 369.
On peut ainsi construire huit carrés magiques normaux d’ordre n = 9 différents (ci-dessous, application de la Méthode Kraitchik).
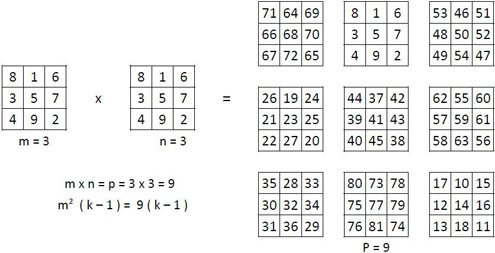
Chaque bloc d’ordre n = 3 de la grille-produit d’ordre n = 9, est issu du carré magique d’ordre m = 3, auquel on ajoute, à chaque terme, la quantité m2 (k – 1), k étant la valeur de la case correspondante dans le second carré magique d’ordre 3. Les valeurs des quantités m2 (k – 1) sont données dans le tableau ci-dessous.
Cette méthode dans un mode inverse, permettrait-elle, étant donné un carré magique normal d’ordre n = 9, d’en extraire la racine carrée, comme c’est possible par ailleurs pour tout nombre positif ?
Les mosaïques magiques du carré papal
Les mosaïques magiques ont été inventées par Bernard Gervais (14). On poche les cases paires, ou bien les cases impaires, les autres restant alors vierges. Voici les deux applications au carré magique du pape Léon III.
Apparait une belle symétrie centrale, à laquelle on ne s’attendait pas, avec une croix centrale bienvenue dans notre contexte (ci-dessous).
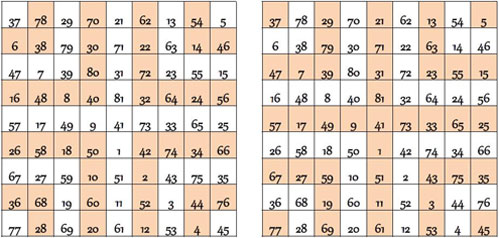
Remarquons que les mosaïques magiques de deux carrés magiques jumeaux ou complémentaires, sont identiques ou superposables. Application au carré magique papal qui est autocomplémentaire :
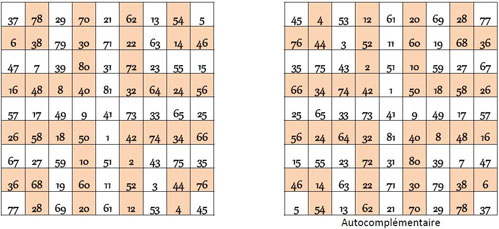
Voici un second exemple : des carrés magiques jumeaux complémentaires.
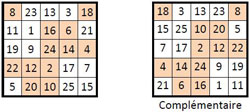
La « réduction » du carré magique papal
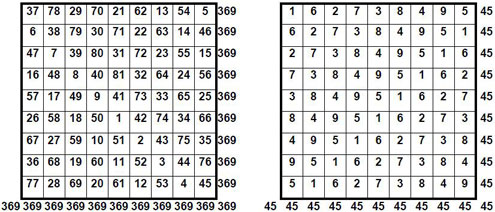
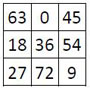
Considérons les restes ou résidus r de la division par 9 de chaque terme « N » de la grille papale : N = 9 d + r.
Cette division par 9 correspond par ailleurs à ce que les numérologues nomment la réduction d’un nombre, soit la recherche de sa racine numérique ou racine digitale : on additionne tous les chiffres du nombre en cause, et on recommence cette addition jusqu’à ce que l’on obtienne un seul chiffre. Exemple :
645 : 6 + 4 + 5 = 15 ; 1 + 5 = 6. 6 est la racine digitale de 645.
Ceci correspond bien aussi au reste r = 6, avec d = 71 dans la relation N = 9 d + r : 645 = (9 x 71 ) + 6
Appliquons donc cette réduction aux termes du carré magique papal : on obtient une curieuse grille « magique », de somme linéaire constante M’9 = 45 (ci-dessus). Et la relation suivante apparaît : 369 = ( 8 x 45 ) + 9
On ne retrouve pas cette propriété dans tous les carrés magiques : c’est l’une des propriétés spécifiques du carré magique du pape Léon III.
@@@@@@
Ainsi, le carré magique du pape Léon III, s’il demeure une énigme au sein de l’Enchiridion, n’a rien de mystérieux en lui-même, et n’en présente pas moins, après décryptage, des propriétés tout-à-fait intéressantes, sinon remarquables.

1. La constante magique est la somme commune à chacune des neuf lignes, neuf colonnes et deux diagonales.
2. Colonel Guy-Claude Mouny, Nouvelles découvertes sur les carrés magiques, Éditions des 3 Spirales, 2005.
3. Dans un carré magique de type associé, les termes complémentaires symétriques par rapport au centre de la grille, ont même somme S = n2 + 1. Ainsi par exemple 37 & 45, 38 & 44, etc.
4. On appelle première diagonale celle qui va du coin en haut à gauche au coin en bas à droite, et seconde diagonale celle qui va du coin en haut à droite au coin en bas à gauche.
5. Dans ce cas, un peu comme les sous-grilles d’un sudoku. La comparaison s’arrête là.
6. Rappelons que la constante de polarisation se définit comme la somme des termes complémentaires symétriques par rapport au centre de la grille.
7. On définit la lyre d’un carré magique comme le résultat du placement des termes en ordre croissant d’une ligne à l’autre, dans une grille de même ordre.
8. Op. cit.
9. Un carré magique est dit « diabolique » lorsqu’en sus des lignes, des colonnes et des deux diagonales principales, les diagonales brisées sont également magiques.
10. Par exemple, après le 9, on peut placer le 10 dans les 8 cases de la ligne du 9, ou les 8 cases de sa colonne.
11. Puisque la case où viendrait le 8 par marche du cavalier depuis le 7 est déjà prise par le 1.
12. Cette Méthode de duplication du carré magique, dite « Méthode des quatre carrés », est donnée et expliquée en détail dans René Descombes, Les Carrés magiques, Éditions Vuibert, 2ème édition, 2000 (494 p.), p. 359-361.
13. Appel aux amateurs courageux et entreprenants, qui pourront s’inspirer des méthodes pour faire le produit de deux carrés magiques, par celles décrites dans René Descombes, Les Carrés magiques, op. cit ., pp. 357-359.
14. Gervais a particulièrement étudié les mosaïques magiques d’ordre 5, dans son ouvrage Les carrés magiques de 5, Éditions Eyrolles, 1998, 195 pp.
À LIRE
 |
|
OUVRAGES
 |
|
 |
|
 |
|
 |
|
ENCHIRIDION DE LÉON III
![Enchiridion du pape Léon, envoyé comme un rare présent à l'empereur Charlemagne, édition en français, 1660 – exemplaire de la Bibliothèque municipale de Lyon (provenant de la Bibliothèque jésuite des Fontaines à Chantilly), numérisé par Google Books [NB : comme indiqué dans le texte, le carré magique situé dans l’ouvrage d’origine ne figure pas dans ses éditions post-Gutenberg]](/sites/default/files/en-richidion.jpg) |
|
leoniii-texte.pdf

leoniii-analyse.pdf







