Naissance de la théorie de l'information

Figure 1 : Léon Brillouin (1889-1969). Image American Institute of Physics.

Léon Brillouin dans le siècle

Léon Brillouin est un physicien franco-américain auteur de contributions majeures en physique du solide et en physique quantique (on lui doit le concept des "zones de Brillouin" qui caractérisent les volumes élémentaires dans les structures cristallines). Issu d'une famille scientifique, fils du physicien Marcel Brillouin (1), il entre à l'École normale supérieure en 1908. Il termine ses études à l'Institut de physique théorique de Munich dirigé par Arnold Sommerfeld. Il revient en France en 1913 et commence à travailler à sa thèse sur "la théorie des solides et quanta" qu'il terminera en 1920.

Comme la plupart des jeunes scientifiques du début du siècle, il a dû interrompre ses travaux à cause de la mobilisation de la Grande Guerre. Il participe après celle-ci à l'essor fantastique de la mécanique quantique. Il publie avec Heisenberg, Bohr et Jordan. Il fut un des représentants français au fameux congrès Solvay de 1927 réunissant Einstein, Bohr, Marie Curie et de nombreux autres (2), comme son père l’avait été au premier congrès Solvay, en 1911.

Juste avant la Seconde Guerre mondiale, il est nommé directeur de la radiodiffusion française en raison de ses compétences en propagation des ondes. Devant l'offensive allemande, il ordonne la destruction systématique du réseau. Risquant en retour d'être accusé de sabotage, il fuit le régime de Vichy fin 1940 pour émigrer aux États-Unis, où il entame sa carrière américaine. Il s'intègre parfaitement dans l'environnement stimulant de recherche qui y règne (Universités du Wisconsin, de Brown, d'Harvard, de Columbia). Malgré son statut d'expatrié, il est accueilli dans les services de recherche de guerre où il travaille sur différentes améliorations du radar.

Figure 2 : Claude Shannon (1916-2001). Image © Life Magazine, Alfred Eisenstaedt, 1951.

Outre-Atlantique, il est immédiatement séduit par la toute nouvelle théorie de l'information proposée en 1948 par le mathématicien Claude Shannon des laboratoires Bell. En bon physicien, il prend plaisir à reprendre et modeler la théorie selon ses propres recherches. Il publie en 1956, en anglais, Science and information theory, traduit en français en 1958 chez Masson sous le titre "La Science et la théorie de l'information" (3). Cet ouvrage étend largement les travaux de Shannon en direction de l’électronique et de la physique : Brillouin sera le premier à faire rigoureusement le lien entre l'entropie de Shannon (qui était surtout pour ce dernier une définition mathématique) et l'entropie statistique de Boltzmann, celle de la physique. Par ailleurs, Brillouin pose les bases d'une véritable "théorie de l'information" de la matière et des objets, étendue à d'autres domaines d'application que ceux sur lesquels Shannon avait travaillé – encodage ou traitement des symboles –, dans la science calculatoire elle-même, mais aussi dans d'autres branches de la science, comme la physique (avec un mode de résolution du démon de Maxwell) ou la biologie.

Le titre du livre – qui semble opposer "science" et "théorie" – donne la couleur de la contribution de Brillouin. Il s'en explique dans sa préface :

Le titre de ce livre a déconcerté quelques lecteurs ; son sens est double : théorie scientifique de l'information d'une part, mais aussi : application de la théorie de l'information à des problèmes de science pure. En somme action et réaction entre Science et Information. Ces deux aspects réciproques sont tous deux essentiels.

Le contexte historique

Replaçons-nous dans le contexte historique. L’humanité sort du plus grand conflit armé qu'elle a connu. Sous l’impulsion de l'effort de guerre des États-Unis, les nouvelles technologies de télécommunication explosent : invention du transistor (4), prolifération du téléphone grâce aux nouveaux commutateurs automatiques.

Le téléphone, la télévision, le radar n'étaient pas des concepts nouveaux en 1950. La surprise est venue d'un nouveau venu inattendu : l'ordinateur. Loin des automates humanoïdes du XVIIIème siècle et des robots se faisant passer pour des humains comme dans Métropolis (5), l'ordinateur est une machine sans forme.

Figure 3 : Le robot de Metropolis, le film de Fritz Lang (1927)

L’idée même que cet objet soit sans forme particulière et puisse même être dispersé au travers d’un réseau sous plusieurs formes indistinctes est une source de malaise dans un siècle où les objets, comme les avions, voitures, navires, fusées sont avant tout des formes et des symboles de modernité. En 1956, les voitures américaines arboraient de lourds ornements en chrome dont la seule destination était de rappeler les ailerons des nouveaux chasseurs a réaction de l’US Air Force, a l’époque le nec plus ultra de l’avant garde. Prenant le contre-pied de cette tendance, dans « The City and the Stars, » publié en 1956, Arthur C. Clarke (6) décrit un ordinateur surpuissant et omniprésente, la « calculatrice », qui est rassemblée dans une vaste salle dans un ensemble de cubes blancs et silencieux qui ne contiennent aucun élément mobile. Cette dernière idée prenait à contre-courant, aussi, le souvenir familier des machines à calculer mécaniques toutes vrombissantes de rouages mobiles, et préfigurait avec quarante ans d’avance les ordinateurs multi-processeurs refroidis au fréon et les mémoires flash qui remplacent maintenant les disques durs rotatifs.

Mais qu'une machine puisse ranger, traiter l'information plus vite et plus massivement que le cerveau humain, que son langage soit celui des mathématiques pures constituait une vraie révolution pour beaucoup. Si le début du siècle avait vu le triomphe sur la matière et l'énergie – dans les transports grâce au moteur à explosion et dans les télécommunications grâce à la maîtrise des ondes radios –, les années 1950 voyaient l'irruption des systèmes électroniques complexes et le retour en force des mathématiques à fin de les maîtriser. Longtemps réduites au rôle d'auxiliaire du savoir ou d'outil de fignolage de l’ingénieur mécanicien, les mathématiques repassaient brutalement sur le devant de la scène.

Définition scientifique de l'information

Brillouin passe du temps à définir l'information. Il évite de tomber dans le piège de la définition circulaire.

Tout d'abord, qu'est-ce que l'information? Le dictionnaire de Webster donne la définition: «Communication ou réception de renseignements. Faits, tout prêts à être communiqués, et que l'on doit distinguer de ceux relevant de la pensée ou de ceux incorporés dans une théorie ou un corps de doctrine. Données, faits nouveaux, renseignements, connaissances résultant de l'étude d'une observation ». On peut poser que l'information est le matériau brut et qu'elle consiste en une collection de données, tandis que la «connaissance », la science demandent une certaine réflexion, un effort de la pensée et l'organisation de cet ensemble de données par comparaison et classification. Ce n'est que dans une étape ultérieure que l'on parvient à la connaissance scientifique et à la formulation scientifique des lois.

La théorie de l'information ne s'intéresse pas au contenu, ni aux moyens de comprendre l'information. À ce niveau, Brillouin tourne le dos à la théorie de la programmation, qui avait pourtant bien avancé avec Turing. Pour ce dernier, la notion de contexte de l'information qui contient les mécanismes de compréhension de l'information prend aussi une part essentielle dans la compilation et la compression de l'information : sans le recours au contexte, et l'objet "programme", il serait impossible de comprendre le code-source d’une image et l’ordinateur ne pourrait pas afficher l’image sur l’écran (7). Cette vue n'est néanmoins pas contradictoire avec l'objectif central de Brillouin : éliminer tout facteur humain dans le concept d'information pour en faire une grandeur physique au même titre que la masse et la charge électrique.

Les méthodes de cette théorie peuvent être appliquées avec succès à divers problèmes concernant l'information : codage, télécommunication, machines à calculer mécaniques etc. ... Dans tous ces problèmes, on transforme véritablement l'information ou on la transmet d'un point à un autre et la présente théorie trouve son extrême utilité en posant les règles, en introduisant les limites exactes qui précisent dans quelles circonstances cela peut être fait ou non. Mais il est impossible de décrire le mécanisme de la pensée, impossible aussi, pour l'instant, de faire intervenir la valeur humaine de l'information. L'élimination de l'élément humain se présente comme très sérieuse limitation, mais elle correspond, en fait, au prix inévitable que comporte la fondation d'une doctrine scientifique. Les restrictions ainsi introduites permettent de donner une définition quantitative de l'information et de traiter l'information comme une grandeur mesurable. Cette définition ne permet pas, toutefois, de distinguer une information ayant une grande importance, d'une information secondaire n'ayant guère de valeur pour celui qui la reçoit.

Brillouin offre aussi une palette impressionnante du champ d’application de la théorie de l’information. Il mentionne les machines à calculer mécaniques, en fait les ordinateurs, thème qu’il développe davantage dans la suite de son livre. Le premier ordinateur, Univac, date de 1944, et la science informatique est à son plein essor. Dans le chapitre qu’il consacre aux machines à calculer, Brillouin, citant Poe, entrevoit les immenses perspectives de l’informatique :

(…) nous pouvons, sans difficulté, concevoir la possibilité de construire une pièce mécanique qui, prenant son point de départ dans les données de la question à résoudre, continuera ses mouvements régulièrement, progressivement, sans déviation aucune, vers la solution demandée (…) (8)

En proposant d’incorporer le calculateur au sein des circuits électroniques, lui attribuant une valeur « d’entropie négative » en théorie de l’information, il préfigure l’émergence de l’ère du tout numérique.

Figure 4 : Univac, le premier ordinateur commercial (mis en service en 1951)

Les mathématiques de l’information

Brillouin expose certaines des conséquences de la définition mathématique de l’information comme, notamment, l’additivité des logarithmes lorsque deux informations sont indépendantes (voir encadré ci-dessous). Récemment certains physiciens ont remis en question l’emploi du logarithme comme opérateur de mesure de l’information. Au niveau des particules élémentaires, ils proposeraient plutôt une représentation basée sur le carré des probabilités, plus commode à leur goût pour rendre visible l’information cachée dans les systèmes quantiques paradoxaux, comme ceux des photons intriqués du paradoxe EPR ; mais cette représentation quadratique n'a pas eu grand succès, il est vrai, en raison de son incapacité à passer à l’échelle macroscopique.

 

 

Brillouin expose dans son premier chapitre la relation entre l’information définie par Shannon et la probabilité :

Il pose le problème, comme on l’a dit, avant tout en physicien :

Il définit l’information I comme logarithme de la probabilité modulo une constante : I₁ = K Log(P₀/P₁) = K Log P₀. Soient deux problèmes indépendants, l’un avec P₀ solutions également probables, l’autre avec Q₀ solutions également probables. Le nombre d’états initiaux possibles (9) issus de ces deux séries de données est P₀Q₀. On a alors I = K Log (P₀Q₀) = K Log P₀ + K Log Q₀ = I (système p) + I (système q). L’indépendance des deux systèmes initiaux conduit aux probabilités multiplicatives et à l’additivité des quantités d’information. Brillouin donne pour l’information contenue l’exemple assez parlant de jeux de cartes : si l’on choisit une carte dans 32 cartes, et qu’on choisit la constante de manière adéquate pour l’écriture en système binaire, on peut écrire I = Log₂ P. Soir pour 32 cartes, I = Log₂ 32 = 5 bits. Il prend l’exemple de deux paquets de 32 cartes et d’une carte tirée indépendamment dans chacun des paquets, le nombre d’états est PQ = (2⁵)²= 2¹⁰. On a alors I = 10 bits. Ainsi, le choix d’une carte parmi 32 cartes peut se « coder » sur 5 bits ; le choix de deux cartes chacune dans deux paquets différents se code sur 10 bits. À noter que ce dernier problème est différent de celui d’une carte à choisir dans deux paquets rouge et bleu mélangés, problème qui se code sur 6 bits (les 5 bits de la carte et le bit de la couleur du paquet).

La physique de l’information et le démon de Maxwell

Brillouin souligne aussi, du point de vue de la physique, la relation entre entropie de Boltzmann et quantité d’information. Si Shannon a utilisé le terme entropie pour mesurer une quantité d’information, c’est simplement parce que les deux concepts coïncidaient dans leur définition mathématique (10). Il y a une grande distance entre considérer la statistique des mots dans un message et considérer celle des états atomiques d’un gaz : mais Brillouin la franchit et pousse la fusion des concepts jusqu’au bout. Pour lui, il n’y a pas de différence entre entropie physique et entropie de l’information : pour obtenir de l’information sur un système, il faut le mesurer, cette mesure augmente l’entropie de l’univers d’une quantité exactement égale à la quantité d’information obtenue. De cette manière, Brillouin établit une échelle absolue de la mesure de l’information et à cette fin crée une nouvelle grandeur : la néguentropie, ou entropie négative. Il pousse le raisonnement jusqu'à sa réciproque (l'information crée de l'entropie, mais l'entropie crée de l'information) : l’univers fournit de l’information sur lui-même à chaque fois qu’il crée de l’entropie, ce qu’il fait de manière permanente compte tenu du second principe.

Tout système physique est incomplètement défini. Nous connaissons seulement les valeurs de quelques variables macroscopiques et nous sommes incapables de définir les positions exactes ainsi que les vitesses de toutes les molécules intérieures au système. Nous ne possédons qu'une information limitée et partielle sur notre système et il nous manque la plus grande partie de l'information relative à sa structure intime. L'entropie mesure le manque d'information ; elle nous donne la quantité totale d'information qui fait défaut et qui est relative à la structure ultra­microscopique du système.

Cette façon de voir est exprimée par le principe de néguentropie de l'information qui se présente comme une généralisation immédiate du second principe de la thermodynamique puisque l'entropie et l'information doivent être étudiées de pair et ne peuvent être envisagées séparément. Le principe de néguentropie de l'information se trouve vérifié dans un grand nombre d'exemples variés, tirés de la physique théorique, dans son état actuel. Le point fondamental est de montrer que toute observation ou expérience effectuée sur un système physique conduit automatiquement à un accroissement de l'entropie du laboratoire. Il est alors possible de comparer la perte de néguentropie (accroissement de l'entropie du laboratoire) à la quantité d'information obtenue. Le rendement d'une expérience peut être défini comme le rapport de l'information obtenue à l'accroissement concomitant de l'entropie. Ce rendement est toujours inférieur à l'unité conformément au principe de Carnot généralisé.

Certains physiciens sont allés beaucoup plus loin, avec des succès très relatifs, il est vrai. John Archibald Wheeler a été jusqu’à comparer l’univers à un immense ordinateur programmé pour donner de l’information à l’ensemble de ses observateurs conscients. Il résume son modèle par sa célèbre phrase « it from bit (11) » que l’on peut traduire librement par « je calcule, donc je suis ». D’après lui, l’univers « invente » ses lois physiques à mesure qu’on les observe et qu’on les expérimente. Ces vues audacieuses n’ont à vrai dire suscité que peu d’échos dans la communauté scientifique, l’idée que la Nature calcule au lieu de réagir à des règles physiques ne semble plus faire recette. En fait, les éclairages nouveaux sur le fonctionnement du cerveau, l’objet de la Nature qui se rapproche le plus de l’ordinateur, ont montré que le premier n’est absolument pas organisé comme ce dernier avec ses processeurs, ses circuits et ses mémoires séparés. Le cerveau serait plutôt un objet contenant un câblage complexe mais mou, basé sur des fonctions purement analogiques. Donc, si nous ne sommes pas exactement des ordinateurs, pourquoi l’univers en serait-il un ?

Pour l’instant, les théoriciens s’en tiennent à une séparation assez stricte des aspects physiques de l’information utilisable, considérée comme une partie extrêmement faible de l’entropie de l’univers, principalement composée de sources de signaux aléatoires. Néanmoins, il est très intéressant de pousser les recherches au plus loin afin de connaître la nature exacte de la frontière entre l’information et l’entropie pure. A l’heure actuelle on commence à parler de « moles » d’information (6,02 x 10²³ bits, un petit peu moins de 2 à la puissance 79) grâce au progrès constant des capacités des mémoires. L’enjeu est de taille : saura-t-on un jour stocker de l’information dans chaque molécule d’un volume donné de gaz ? Pourra-t-on stocker dans la structure intime de la matière et de l’espace-temps ?

Pour arriver à cette conclusion, Brillouin se fonde sur sa résolution du paradoxe du « démon de Maxwell », qu’il développe dans son livre. Le paradoxe de Maxwell consiste à maintenir une cloison mobile entre un compartiment rempli de gaz chaud et un compartiment de gaz froid, un démon ne faisant passer dans le compartiment chaud que les molécules les plus énergétiques du compartiment froid et dans le compartiment froid que les molécules les moins énergétiques du compartiment chaud : il contribue ainsi, sans dépense de travail, à élever la température du compartiment chaud tout en abaissant la température du compartiment froid, ce qui est en contradiction avec le second principe de la thermodynamique.

 

 

 

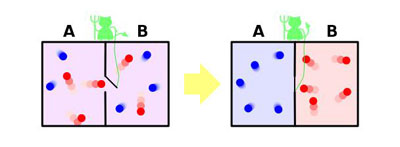
Léon Brillouin a « exorcisé le démon » (pour reprendre son expression, p. 159 de son ouvrage) justement en montrant que le tri des molécules nécessite en fait l’acquisition d’information sur le niveau d’énergie de chacune d’elles et que ce tri prélève de l’énergie en fonction de la néguentropie ainsi créée, ce qui rétablit la validité du second principe. La conséquence de la résolution du paradoxe de Maxwell est qu’il est possible de donner une valeur minimale de l’entropie développée pour collecter et stoker un bit d’information. Il s’agit de la constante de Boltzmann divisée par logarithme de deux, soit environ 2  10-23 joule par Kelvin. Au-dessous de cette valeur, le démon de Maxwell pourrait chauffer le compartiment chaud et refroidir le compartiment froid, ce qui violerait le second principe.

L’information dans la biologie

Pour terminer, Brillouin imagine les aspects prometteurs de la théorie de l’information. Il cite la biologie, mais insiste beaucoup sur la physique, notamment sur le démon de Maxwell. Brillouin est plus vague en ce qui concerne la biologie : sans doute est-ce dû à sa formation de physicien. Pourtant, la transmission de l'information du gène – le code génétique – est fondamentale dans l’organisation de la vie et avait déjà été découverte au moment où Brillouin écrit. Après les expériences de Fred Griffith en 1932, Oswald Avery montra en 1944 que l’ADN transmet les caractères héréditaires. Dans son livre « What is Life ? » publié en 1944, que Brillouin a lu, le physicien Erwin Schrödinger pouvait écrire : « La fibre chromosomique contient, chiffré dans une sorte de code miniature, tout le devenir d’un organisme, de son développement, de son fonctionnement ». Cette vision du physicien quantique, quinze ans avant le livre de Brillouin, avait été confirmée par la découverte de la double hélice par J. D. Watson et F. Crick en 1953.

On peut espérer que la théorie scientifique de l'information constitue le point de départ d'un nouveau et important chapitre de la recherche scientifique, plus particulièrement en physique et en biologie. Il est déjà acquis que cette nouvelle théorie permet de rassembler et de regrouper un très grand nombre de faits épars, spécialement sur les définitions et mesures essentielles de la physique. La théorie nouvelle présente aussi l'avantage de consolider la position de la thermodynamique statistique et d'éliminer un bon nombre de paradoxes, comme le démon de Maxwell.

Conclusion

La mise en théorie de l’information est une des révolutions qui ont permis l’émergence du tout-numérique. Nous vivons toujours cette révolution, et même si notre vie quotidienne a déjà été modifiée de manière radicale, nous n’en avons pas fait le tour- et il est encore difficile de prendre du recul sur ce sujet. Mais les effets positifs sont indéniables. D’aucuns voient dans l’ère de l’information et des télécommunications numériques la solution aux problèmes environnementaux que notre ère industrielle a posés a notre planète, eu égard à l’emploi massif de l’énergie fossile et au développement du transport de masse.

Brillouin apporte, quant à lui, une vision scientifique osée et des perspectives souvent justes, même de nos jours, avec cinquante ans de recul. Son ouvrage est plus qu’une simple vulgarisation de la théorie de Shannon, il prolonge la pensée de celui-ci et de ses précurseurs. Il offre une perspective sur toutes les réalisations modernes qui seront la conséquence de ces nouvelles mathématiques.

Le résultat est une vision forte, vivante, passionnante. Si certains des points développés par Brillouin restent toujours en suspens et si d’autres seront abandonnés en cours de route, sa vision restera néanmoins pour longtemps une source d’inspiration stimulante pour la recherche.

(1) Marcel Brillouin (1854-1948), normalien, était un mathématicien et physicien, membre de l’Académie des sciences, professeur au Collège de France à partir de 1900 (chaire de physique théorique).

(2) Sur le congrès de Solvay de 1927 et le principe de complémentarité de Bohr qui y fut discuté, voir texte BibNum (lettre de Paul Ehrenfest)

(3) Léon Brillouin est mentionné en tête de l’ouvrage comme « Professeur honoraire au Collège de France, Membre de la National Academy of Sciences (Washington, U.S.A.).

(4) Les premiers transistors sont conçus en 1947 aux laboratoires de la Bell Telephone par trois chercheurs qui reçurent le prix Nobel de physique en 1956.

(5) Métropolis est un roman (1926) de science-fiction de l’allemande Thea von Harbou, adapté au cinéma muet en 1927 par Fritz Lang.

(6) Arthur Clarke (1917-2008) est un auteur et inventeur britannique, qui a aussi écrit "2001, L'Odyssée de l'espace" (1968).

(7) Au-delà de la théorie de l'information, c'est la "théorie de la complexité" qui a été ouverte par les travaux de Turing, puis ceux de Kolmogorov, sur la programmation.

(8) Edgar Poe, Le Joueur d’échecs de Maelzel (1836) in Œuvres complètes, (cité par Brillouin dans son ouvrage, page 262)

(9) N’oublions pas, pour bien comprendre la façon dont Brillouin pose son sujet, que c’est un physicien quantique. Rappelons aussi la définition par Boltzmann de l'entropie comme proportionnelle au logarithme du nombre Z d'états microscopiques du système S = k log Z, où k est la constante de Boltzmann.

(10) Léon Brillouin rend hommage à plusieurs reprises dans son ouvrage aux travaux précurseurs de Léo Szilard, physicien comme lui [L. Szilard, Z. Physik, 53, 840 (1929)] ; l’ouvrage de Shannon et Weaver date de 1940 [The mathematical theory of information, University of Illinois Press].

(11) J.A. Wheeler (1911-2008), physicien théoricien américain, a collaboré avec Einstein à Princeton sur la recherche d'une théorie physique unifiée. Avec son allégorie "it from bit", il émet l'hypothèse que les lois de la physique dériveraient toutes, en dernier ressort, de la théorie de l'information binaire.