Le Livre Premier de La Géométrie de Descartes

La Géométrie est le troisième et dernier essai du fameux Discours de la Méthode publié à Leyde en 1637 par René Descartes ; c’est le seul ouvrage de mathématiques qu’il ait publié, mais c’est aussi le plus important, car il a eu une répercussion mondiale conduisant notamment à la numérisation de la physique et, par là, à la maîtrise de l’univers rationnel qui est aujourd’hui la nôtre.

Figure 1 : Discours de la méthode (1637). La partie « Discours » proprement dite est suivie de trois « essais de cette Méthode ».  Curieusement, l’édition raisonnée des œuvres de Descartes, celle du philosophe Victor Cousin en 1826, a séparé le « Discours » initial des trois essais qui en sont pourtant partie intégrante (dans l’édition Cousin, l’un est dans le tome I des œuvres complètes, les autres dans le tome V).

 

Réputé, à juste titre, comme le premier écho publié de la naissance de la géométrie analytique, ce traité de cent-dix-sept pages avait en fait pour but caché de donner une méthode générale de résolution des équations algébriques, c’est-à-dire de la forme P(x) = 0, où P est un polynôme arbitraire et x l’inconnue (réelle par définition). Sa lecture est difficile ; mais l’auteur lui-même précisait en exergue :

Iusques icy i’ay tasché de me rendre intelligible a tout le monde, mais pour ce traité ie crains, qu’il ne pourra estre leu que par ceux, qui sçauent desia ce qui est dans les livres de Geometrie (1)

Sa première phrase est essentielle pour la compréhension du Traité tout entier :

Tous les problèmes de géométrie se peuvent facilement réduire à tels termes, qu'il n'est besoin par après que de connaître la longueur de quelques lignes droites, pour les construire.

Elle signifie, dans notre langage, que tout problème géométrique peut être résolu par des traitements numériques.

Il appliquera cette phrase à la recherche d’une construction géométrique de lignes (segments) de longueurs égales aux racines d’une équation algébrique donnée que l’on désire résoudre, en commençant naturellement par celles que nous a léguées l’Antiquité.

Résoudre géométriquement les équations de degrés 1 et 2

Ce Livre donne donc d'abord ses constructions géométriques élémentaires concernant le produit et le quotient de deux nombres, ainsi que la racine carrée d'un nombre à partir de segments donnés, qui peuvent s'obtenir à la règle et au compas. Même sur ces questions très simples, il se montre novateur par rapport à ses prédécesseurs, Viète y compris.

Produit et quotient sont ainsi présentés comme de simples applications de ce que nous appelons théorème de Thalès : il suffit de lire sur sa figure (figure 1) une égalité de rapports du type a/b = c/d pour comprendre que poser l’un de ces nombres égal à 1 (d par exemple) permet d’en déduire des relations telles que a = b.c et c = a/b. Du coup, on peut désormais donner une résolution géométrique de l’équation du premier degré la plus générale, mais aussi, entre autres, une construction des valeurs d’une fonction polynôme, ou homographique etc.

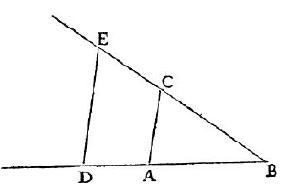
Figure 2 : « Soit par exemple AB l'unité, et qu'il faille multiplier BD par BC, je n'ai qu'à joindre les points A et C, puis tirer DE parallèle à CA, et BE est le produit de cette multiplication » (application du théorème de Thalès BC/BA = BE/BD).

 

On doit noter au passage que le fait de prendre à sa guise une longueur comme unité, si banal aujourd’hui, était pour l’époque une innovation d’une abstraction inouïe !

La construction de la racine carrée, dans cette même page, est exactement la même qu’aujourd’hui : avec les notations de sa figure, on dispose en effet de l’égalité GI² = GH.

Figure 3 : « Ou s’il faut tracer la racine carrée de GH, je lui ajoute en ligne droite FG qui est l’unité, et divisant FH en deux parties égales au point K ; du centre K je trace le cercle FIH puis élevant du point G une ligne droite jusqu’à I à angle droit FH, c’est GI la racine cherchée ». On vérifie facilement, en posant GH = a dont on cherche la racine carrée : FH = 1+ a (« FG qui est l'unité »), KI = KF = (1+a)/2 (K est le centre du cercle), puis en écrivant KI² = KG² + GI², on a GI² = [(1+a)/2]² - [(1+a)/2 – 1]² = a ; donc GI est bien la racine cherchée.

 

 

Descartes décrit ensuite les préceptes à suivre dans sa géométrie à l'occasion d'un passage majeur (p. 298 à 302), où il explique qu'il faut « nommer » les différentes grandeurs géométriques d'une figure, les classer en connues et inconnues, mettre en équation et résoudre ces équations.

Ainsi voulant résoudre quelque problème, on doit d'abord le considérer comme déjà fait, et donner des noms à toutes les lignes, qui semblent nécessaires pour le construire, aussi bien à celles qui sont inconnues qu'aux autres. Puis, sans considérer aucune différence entre ces lignes connues, on doit parcourir la difficulté […] jusqu'à ce qu'on ait trouvé moyen d'exprimer une même quantité en deux façons : ce qui se nomme une Équation : car les termes de l'une de ces deux façons sont égaux à ceux de l'autre. Et on doit trouver autant de telles Équations qu'on a supposé de lignes, qui étaient inconnues. Ou bien s'il ne s'en trouve pas tant […], cela témoigne que [la question] n'est pas entièrement déterminée.

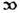
Arrêtons-nous un instant sur les égalités du haut de la page 300 : le signe spécial cartésien , fait de deux lettres « o » minuscules accolées dont celle de gauche a perdu la moitié de sa matière – d’un coup de burin de l’imprimeur –, équivaut au moderne « = ».

Descartes applique aussitôt constructions et règles ainsi introduites aux problèmes liés aux équations du second degré, faisant même au passage nettement mieux qu'Euclide, qui avait traité le même sujet mais de façon plus lourde et désordonnée.

Cela est clair sur les figures des pages 302 et 303. La première s’applique au cas où l’équation du second degré n’a qu’une racine, forcément positive, car dans ce texte, Descartes ignore – volontairement – les nombres négatifs. Cette racine est respectivement la longueur MO ou la longueur MP, selon que la somme des deux racines est positive ou négative. Sur la seconde figure, les longueurs MQ et MR sont les deux racines, positives, d’une équation. Chaque fois, les justifications de ces faits reposent sur la notion élémentaire de puissance par rapport à un cercle.

Figure 4 : « Car si j'ai par exemple z² = az + bb, je fais le triangle rectangle NLM, dont le côté LM est égal à b racine carrée de la quantité connue bb, et l'autre [côté] LN est ½a, la moitié de l'autre quantité connue […] puis prolongeant MN la base de ce triangle jusqu'à O, en sorte qu' NO soit égale à NL, la toute OM est z la ligne cherchée. Et elle s'exprime en cette sorte z = ½a + √(¼aa + bb).» C'est bien la solution connue par le discriminant de l'équation du second degré z² = az + bb, ce qu'on vérifie facilement avec la valeur de z donnée par Descartes.

Le problème de Pappus : naissance de la géométrie analytique

La fin du Premier Livre introduit le problème de Pappus dont il a été déjà parlé. Surprenante aux yeux d'un contemporain, cette partie est pourtant essentielle pour les deux raisons déjà indiquées : légitimation de la géométrie analytique par l'exposé d'une solution neuve à un défi ancien, et mise au point d'un atelier fournissant à la demande des courbes de plus en plus complexes car définies par des équations de degré de plus en plus élevé, mais néanmoins introduites à partir d'une préoccupation géométrique, justification aujourd'hui incongrue mais qui était nécessaire pour l'époque, où le statut de l’algèbre était encore considéré comme mineur (presque un amusement de chercheurs arabes des environs de l’an mil) par rapport à la science reine : la géométrie.

C'est là qu'arrivent enfin, presque incidemment pourrait-on dire (p. 310), x et y, l'abscisse et l'ordonnée, qu'on retrouvera plus loin (par exemple p. 321, non reproduite ici, et plus généralement dans tout le Traité) :

Que le segment de la ligne AB, qui est entre les points A et V, soit nommé x et que BC soit nommé y et que toutes les autres lignes données soient prolongées, jusqu'à ce qu'elles coupent ces deux, aussi prolongées qu'il est besoin, et si elles ne leur sont point parallèles.

Si essentielles que ces « coordonnées cartésiennes » nous paraissent aujourd'hui, elles ne sont pourtant pour Descartes que des outils, comme sa méthode des coefficients indéterminés (p. 347 du Livre Second), ou sa « Parabole cartésienne», nécessaire pour résoudre le sixième degré par sa méthode (innovation du Livre Troisième).

Croire que l’invention de cette géométrie cartésienne se résume à l'invention des axes de coordonnées, si extraordinaire qu'elle soit – et Descartes le sait –, est donc une erreur grave ; c'est confondre le moyen et la fin. L'auteur, au moins dans ce passage initiatique, ne considère les coordonnées x et y fixant un point variable que comme deux longueurs privilégiées, à partir desquelles il se fait fort de déterminer tous les autres éléments géométriques de la figure. D'une certaine manière, on peut retrouver là un souci de classification, voire d'automatisation, nous ramenant au Discours de la Méthode, mais il n'y est pas fait explicitement allusion.

En ce qui concerne le problème de Pappus lui-même, dont l'examen minutieux peut être évité par un lecteur non spécialiste malgré son importance capitale dans l'élaboration de la révolution cartésienne, un moderne ferait évidemment plus court. Sans doute se dispenserait-il de reproduire, en tout cas in extenso, la traduction latine du texte grec original.

 

Pappus d'Alexandrie a vécu à la fin du IIIe et au début du IVe siècle après J.-C. Son œuvre majeure est une Collection mathématique, compilation en huit livres, sans doute rédigée vers 320. Parfois enrichie de contributions originales, elle nous est incomplètement parvenue (manquent le premier livre et le début du second) mais reste un document précieux, souvent unique, pour les travaux de mathématiciens antérieurs comme Aristée, Euclide, Archimède ou Apollonius, dont certains écrits sont perdus en tout ou partie. Descartes nous dit en marge : « Je cite plutôt la version latine que le texte grec afin que chacun l'entende plus aisément ». Il s’agit de la fameuse édition latine de Commandin (Pappi Alexandrini Mathematicae Collectiones, Pise, 1588), que Descartes reproduit avec quelques lapsus. En voici une traduction littérale de la partie essentielle ; Descartes fournira lui-même en français un résumé partiel (p. 306) :

En langage moderne, le problème de Pappus, « proposé en trois (ou quatre) lignes droites » s’énonce comme suit. Ces lignes, au nombre de trois ou quatre, sont supposées « données en position », c'est-à-dire connues par quelque moyen ; par exemple, on possède, pour chacune d'elles, un couple de points distincts, ou un point et sa direction. Étant donné un rapport (« proportion », ou « raison ») ρ, il est demandé de trouver les points du plan tels que le « rectangle », c’est-à-dire le produit des distances de ce point aux deux premières soit égal au produit par ρ du carré de la distance (2) à la troisième (ou au produit par ρ du produit des deux dernières, s'il y a quatre droites en tout). Avec des notations modernes, la signification de ce problème peut s’exprimer ainsi : rechercher les points vérifiant, selon le cas, une relation du type D(1).D(2) = ρ.D(3)² ou D(1).D(2) = ρ.D(3).D(4), où D(i) désigne la distance à la droite de numéro i.

Un moderne pourrait, par exemple, commencer par établir un lemme proche de ceci : étant donnés un repère xOy, une droite ∆ et un angle φ, la distance CC', séparant un point variable C de coordonnées x et y du point C' de ∆ tel que CC' et cette droite fassent entre elles l'angle φ, s'exprime par la valeur absolue |ax+by+c| d'une expression du type ax+by+c, où a, b et c sont indépendants de la position du point mobile C. (Ce lemme n'est autre qu'un corollaire facile du théorème selon lequel l'équation d'une droite est un polynôme du premier degré en x et y).

Descartes ne le dit pas, mais il l’applique. Dès lors il devient évident qu'un lieu de Pappus « à quatre droites » est une conique qui a une équation de la forme

Cet exemple est celui sur lequel Descartes s'étend longuement – avant d'y revenir au Second Livre dans un premier calcul cartésien éblouissant prouvant ses dires, montrant comment substituer des manipulations de nombres à des raisonnements purement géométriques de type euclidien.

Sous la plume de Descartes : des courbes de degré arbitraire

Dans le prolongement du problème initial de Pappus, Descartes introduit les lieux à 2n droites, et leurs variantes à 2n-1 droites :

Et ainsi cette question se peut étendre à tout autre nombre de lignes. Puis à cause qu'il y a toujours une infinité de divers points qui peuvent satisfaire à ce qui est ici demandé, il est aussi requis de connaître, et de tracer la ligne, dans laquelle ils doivent tous se trouver.

Ces lieux sont reconnus de la même manière comme étant ce que l'on appelle aujourd'hui des courbes algébriques de degré n, définies par des équation de la forme F(x,y) = 0, où F est un polynôme de degré n (que, réciproquement, toute courbe de ce genre admette une définition à la Pappus est un problème difficile, dont la solution est négative, et que Descartes ne se pose pas). Le problème de Pappus peut s'étendre en effet à une famille de 2n droites, sous la forme D(1).D(2)…D(n) = ρ.D(n+1).D(n+2)…D(2n), ou à une famille de 2n-1 droites, avec cette fois-ci D(1).D(2)…D(n) = ρ.D(n+1).D(n+2)…D(2n-1) pour n ≥ 3 (le cas n = 2 étant spécial pour Descartes comme on vient de le voir).

Les positions des solutions d'un tel problème de Pappus constituent une courbe (ou ligne, ou lieu géométrique) formée d'une infinité d'éléments (de points) qu'il n'est donc pas question d'obtenir tous (puisqu'on n'en pourra jamais tracer qu'un nombre fini). Descartes demandant de « connaître » (ou encore « trouver » ou « tracer ») une telle courbe, il faut comprendre qu’il considérera son problème comme résolu quand il saura trouver une infinité de points par où elle passe, c’est-à-dire déterminer (par résolution d'équations algébriques) tous les points du lieu situés sur une droite arbitraire dont seule la direction est imposée (en effet, les droites d’un plan dont la direction est donnée forme une famille dont la réunion est le plan tout entier : connaître les points situés sur ces droites, revient bien à connaître tous les points de la courbe). Techniquement, cela reviendra, pour toute valeur du paramètre y, à pouvoir résoudre en l'inconnue x l'équation F(x,y) = 0 qui donne les abscisses des points de la courbe d'ordonnée y, par des constructions géométriques comme celles qu'il a données plus haut et qu'il complétera dans le Livre Troisième.

Soient quatre droites D1, D2, D3, D4 d'équations respectives x=a, x=-a, y=0 et y=x (voir figure ci-dessous). Si l'on note Di la distance d'un point M à la droite Di, on peut rechercher le lieu des points M tels que D1.D2=√2.D3.D4 On a D1 = |x-a|, D2 = |x+a|, D3 = |y| et D4 = 1/√2.|x-y| (pour cette dernière distance, le calcul est assez simple en remarquant que le point x,y se projette orthogonalement sur la droite x = y en suivant une droite de pente – 1) Le lieu des points M est donc donné par |x²-a²|=|y(y-x)|, soit x² - a² = y² - yx, ou x² - a² = xy – y² Il y a deux coniques solutions, toutes de centre O, passant toutes deux par les quatre points (a,0), (a,a), (-a,0), (-a,-a) : l'hyperbole équilatère d'équation x²+xy-y²=a², passant en outre par les points (2a,-a) et (2a,3a) l'ellipse d'équation x²-xy+y²=a², passant en outre par les points (0,a) et (0,-a).

L’invention de la géométrie analytique

Descartes affirme page 307, à ce moment-là sans preuve (voir le Livre Second), que si le problème de Pappus est en trois, quatre ou cinq droites (à la seule exception du cas de cinq droites parallèles), on peut construire point par point le lieu étudié par les moyens ordinaires, c'est-à-dire à la règle et au compas (le problème est alors plan).

Et premièrement, j'ai connu que cette question n'étant proposée qu'en trois, ou quatre, ou cinq lignes, on peut toujours trouver les points cherchés par la Géométrie simple ; c'est-à-dire en ne faisant que de la règle et du compas.

Pour un nombre de droites plus élevé, il faut recourir à des courbes plus élaborées : c’est justement pour pouvoir en disposer qu’il va introduire les coordonnées qui portent aujourd’hui son nom.

Il montre en page 309 et suivantes comment mettre en équation le problème de Pappus en quatre droites (celui en trois droites s'en déduira sans difficulté), a priori dans un cas particulier (rapport ρ égal à 1), mais « prendre quelque autre proportion donnée » ne changerait pratiquement rien à cette étude.

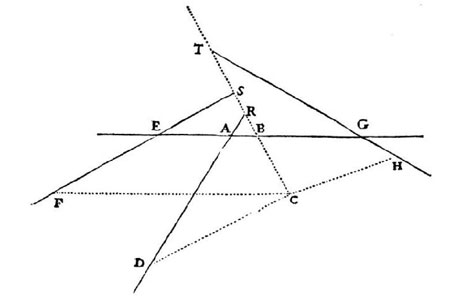
Figure 5 : Présentation par Descartes du problème de Pappus à quatre droites AB, AD, EF, GH.

 

Il commence donc par prendre quatre droites D(1) = AB, D(2) = SEF, D(3) = RAD et D(4) = TGH, qui sont, avec les points AEG, les seuls éléments fixes de la configuration, les droites CBRST, CF, CD et CH étant variables tout en gardant des directions fixes, les points B, F, D, H, S, R et T décrivant respectivement des parties des droites D(1), D(2), D(3), D(4), D(2), D(3) et D(4), le point C enfin étant astreint pour sa part à décrire le lieu géométrique étudié.

Pour cette mise en équation, il ramène les calculs de toutes les longueurs dont il a besoin à deux d’entre elles, à savoir x = AB et y = BC. Par rapport à nos coordonnées usuelles, on peut noter que A est l’origine du repère et que D(1) = AB est l’axe des abscisses. L’axe des ordonnées n’est pas tracé sur les figures des pages 309 et 311 : mais il serait facile à dessiner comme étant la parallèle à CBRST (de direction connue) issue du point A.

Ainsi notre géomètre et ses « neveux » – vous et moi – disposent-ils, pour la première fois dans l'histoire, d'objets d'étude – et d'outils pour un algorithme fondamental de résolution des équations algébriques – aussi complexes qu'on le désire, ayant une définition « à l'ancienne » leur assurant un lien solide avec les maîtres de l'Antiquité qui, en dehors de quelques cas spéciaux inventés pour les besoins de la cause (courbes trisectrices par exemples) n'avaient dans leur besace qu'une famille assez courte, essentiellement limitée aux sections coniques.

Le saut quantitatif et qualitatif est considérable. Par exemple, grâce à ces outils pleinement originaux, pour la première fois seront résolues in fine les équations de degrés cinq et six. L'auteur est donc légitimement et visiblement fier de son travail, lorsqu'il annonce, pour clore ce Livre, qu'il doit maintenant établir les propriétés des nouveaux êtres qu'il vient d'engendrer par sa découverte, ce qu’il fera dans le Second et le Troisième livre de La Géométrie.