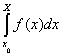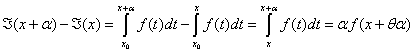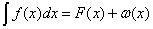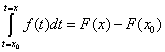Cauchy, une nouvelle conception du calcul intégral
- INFORMATION
- ACTUALITÉ
- ANALYSE
- EN SAVOIR PLUS
- À TÉLÉCHARGER
« Calcul intégral », Leçons 21 à 26 (p. 122-156), Résumé des leçons données à l’École Royale polytechnique sur le calcul infinitésimal, Paris, Impr. Royale, 1823.
1823
Dans ses cours à l’École polytechnique, Cauchy donne une définition de l’intégrale comme limite des sommes (dites de Cauchy) de calcul d’aire sous la courbe, calcule les intégrales d’un certain nombre de fonctions, et donne diverses propriétés algébriques des intégrales telles qu’il les a définies.
Dans ses cours à l’École polytechnique, Cauchy donne une définition de l’intégrale comme limite des sommes (dites de Cauchy), qui correspondent aux rectangles situés sous la courbe et qui approchent celle-ci en limite. À l’aide de cette limite de sommes, habilement calculées de plusieurs manières (sommes arithmétiques, géométriques), il retrouve les fonctions primitives d’un certain nombre de fonctions.
Mais l’originalité de son approche tient dans tout ce qu’il fait dire à l’intégrale définie : c’est un objet additif, l’inversion de ses bornes inverse son signe, c’est-à-dire un certain nombre de propriétés algébriques de l’intégrale définie. Il définit aussi la famille de primitives d’une fonction continue, à une constante additive près.
Il étend aussi sa nouvelle approche aux intégrales à borne (supérieure ou inférieure, ou les deux) infinie, et aux intégrales définies singulières, avec des points de discontinuité (en nombre fini) de la fonction initiale.
Riemann ou Lebesgue poursuivront ce type de travaux, et donneront des définitions beaucoup plus générales de la notion d’intégrale. Même si le collectif Bourbaki éreintera plus tard Cauchy (« sa démonstration, qui deviendrait correcte si elle s’appuyait sur le théorème de continuité uniforme des fonctions continues dans un intervalle fermé, est dénuée de toute valeur faute de cette notion » – Bourbaki 1969) : cette appréciation, sévère et juste en toute rigueur mathématique à la lumière de nos connaissances actuelles, ne serait-elle pas néanmoins injuste ? Car Cauchy, dans ses cours des années 1820 – d’ailleurs peu accessibles à ses étudiants ! – changea la façon de concevoir l’intégrale et la théorie de l’intégration.
Après avoir complété une maitrise en mathématiques et un doctorat en philosophie des mathématiques, Jean-Philippe Villeneuve a commencé, en 2007, à enseigner les mathématiques au Cégep de Rimouski (QC, Canada). Ses recherches portent sur l’histoire des mathématiques (principalement l’analyse au XIXe siècle), le calcul différentiel et intégral, et l’impact de la généralisation sur le développement des connaissances mathématiques. Il a écrit des articles pour le site CultureMath et pour la revue Tangente. Il est chroniqueur pour le Bulletin de l’Association mathématique du Québec.

Augustin Louis Cauchy (1789-1857) publia deux livres importants sur le calcul différentiel et intégral dans les années 1820 : le Cours d’analyse en 1821 et le Résumé des Leçons données à l’École Royale Polytechnique sur le calcul infinitésimal en 1823.

Le premier est un cours préliminaire au calcul différentiel et intégral (calcul infinitésimal) dans lequel Cauchy présente les définitions de fonction, de continuité, de limite « intuitive » et de convergence de séries. En fait, il y introduit une nouvelle notion de limite qui lui permet de définir la continuité d’une fonction, de résoudre le problème des infinitésimaux (ces quantités qui étaient parfois considérées comme nulles, parfois comme infiniment petites) et de présenter la première définition de la convergence d’une série qui est indépendante des critères de convergence : une série est convergente si et seulement si la suite des sommes partielles converge. De plus, il présente ce qui est maintenant appelé « suites de Cauchy » et démontre que si une suite converge, alors elle est de Cauchy. Il promet de revenir avec une démonstration de la convergence (si une suite est de Cauchy alors elle converge), mais il ne le fera pas. On sait aujourd’hui que, pour ce faire, il faut utiliser la propriété de complétude des nombres réels (une suite croissante et bornée de nombres réels converge dans les nombres réels – ou bien : tout ensemble borné de nombres réels admet une borne supérieure).
@@@@@@@
Le second livre résume les cours qu’il donna à l’École Royale Polytechnique. Il devait être publié en deux volumes, mais un seul fut produit. Le Résumé se compose de quarante Leçons divisées également entre le calcul différentiel et le calcul intégral. C’est le calcul intégral qui nous intéresse ici, parce qu’il comporte beaucoup d’innovations. En effet, avant les travaux de Cauchy, il n’existait aucune technique uniforme pour un calcul d’aire sous la courbe y = f(x), et l’intégrale était définie comme l’opération inverse de la dérivée.
Cauchy démontre que la fonction d’aire d’une fonction continue f(x) est une primitive de f(x). L’idée d’utiliser la fonction d’aire pour résoudre le problème de la recherche de primitives vient de Lagrange et de son traité (1) de 1796, mais Lagrange ne produit pas une technique uniforme permettant de calculer l’aire sous la courbe. Cauchy le fait.
Il démontre que, dans le contexte des fonctions continues, l’intégrale définie permet de résoudre le problème de la recherche de primitives. De plus, l’intégrale indéfinie peut être utilisée afin de calculer l’aire sous une courbe lorsque la fonction est continue. Ces liens entre l’intégrale définie et l’intégrale indéfinie s’appellent « le théorème fondamental du calcul ».
|
Rappel de quelques définitions, en liaison avec le texte de Cauchy
Cauchy distingua l’intégrale définie de l’intégrale indéfinie. L’intégrale définie représente la limite des « sommes de Cauchy (2) » et permet de calculer l’aire de la surface comprise entre une courbe et l’intervalle en abscisse [a, b]. L’intégrale définie est donc un nombre réel et devient une fonction, dite fonction d’aire, lorsque l’extrémité b de l’intervalle d’intégration devient une variable. L’intégrale indéfinie est l’opération inverse de la dérivée et elle est obtenue par l’inversion des formules de dérivation :
L’intégrale indéfinie d’une fonction f(x) produit donc une fonction F(x), dite antidérivée, qui est aussi une primitive de f(x) : une fonction F(x) est une primitive de f(x) si F’(x) = f(x). L’antidérivée d’une fonction f(x) est donc une primitive mais il existe des fonctions qui ont une primitive et qui n’ont pas d’antidérivée. En 1835, Louville (3) démontre qu’il y a des fonctions continues qui n’ont pas d’antidérivée. C’est le cas de f(x)=e-x2, dont la seule primitive est
Ainsi la primitive ne s’exprime pas nécessairement comme une expression analytique, et donc la fonction f(x) peut ne pas avoir d’antidérivée qui s’exprime sous forme de fonction.
|
@@@@@@@
Le calcul intégral débute avec la Leçon 21 et se termine avec la Leçon 40. Les Leçons qui nous intéressent sont les Leçons 21 à 26. Cauchy commence en force ces Leçons en présentant une technique uniforme (les sommes de Cauchy) pour calculer l’aire sous la courbe et en démontant que ces sommes convergent vers l’intégrale définie lorsque la fonction est continue (Leçon 21). Il donne ensuite quelques propriétés de l’intégrale définie (Leçon 22), propose une interprétation géométrique de cette intégrale définie (Leçon 23), présente deux généralisations de l’intégrale définie (Leçons 24 et 25) et démontre finalement le théorème fondamental du calcul pour les fonctions continues (Leçon 26). Présentons donc ces résultats.
Leçon 21 – l’intégrale définie comme limite des sommes de Cauchy d’une fonction continue
L’objectif de la Leçon 21 (Intégrales définies) est d’introduire les sommes dites de Cauchy et de démontrer que si la fonction est continue, alors ces sommes convergent vers un nombre réel, appelé l’intégrale définie. Au début de la leçon, Cauchy écrit :
Supposons que, la fonction y = f(x), étant continue par rapport à la variable x entre deux limites finies x = x0 et x = X, on désigne par x1, x2, …, xn-1 de nouvelles valeurs de x interposées entre ces limites, et qui aillent toujours en croissant ou en décroissant depuis la première limite jusqu’à la seconde. On pourra se servir de ces valeurs pour diviser la différence X – x0 en éléments
(1) x1 – x0, x2 – x1, x3 – x2, …, X – xn-1,
qui seront tous de même signe. Cela posé, concevons que l’on multiplie chaque élément par la valeur de f(x) correspondante à l’origine de ce même élément, savoir l’élément x1 – x0 par f(x0), l’élément x2 – x1 par f(x1), …, enfin l’élément X – xn-1 par f(xn-1); et soit
(2) S = (x1 – x0)f(x0) + (x2 – x1)f(x1) + … + (X – xn-1)f(xn-1)
la somme des produits ainsi obtenus.
L’expression (1) s’appelle maintenant une partition de l’intervalle d’intégration [x0, X] selon la notation de Cauchy, et l’expression (2), une somme de Cauchy. En termes contemporains, soit une fonction f(x) définie sur l’intervalle [a, b], avec a < b et soit {a = x0, …, xn = b}, une partition de l’intervalle. Alors la somme de Cauchy SC(f, P) = 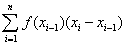
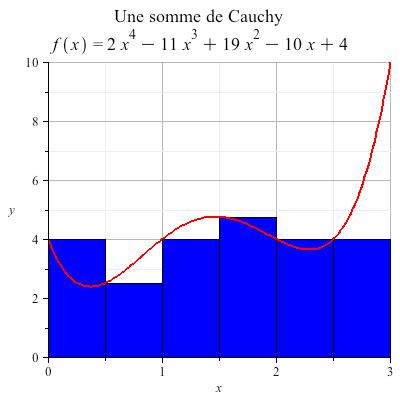
Figure 1 : Calcul d’une somme de Cauchy pour la fonction affichée. Les rectangles bleus s’alignent sur la valeur de gauche des sous-intervalles : f(0) = 4 (premier rectangle) ; f(0,5) = 2,5 (deuxième rectangle) ; f(1) = 4 ; f(1,5) = 4,75 ; f(2) = 4 ; jusqu’à f(2,5) = 4 (sixième rectangle). La courbe polynomiale figure en rouge, elle croise à chaque abscisse marquée les rectangles en leur coin gauche (par construction). On a f(3)=10, mais le rectangle correspondant n’est pas tracé, car ce rectangle ne se retrouve pas dans la somme de gauche (de toute façon, sa base aurait été nulle). On peut calculer la somme de Cauchy avec ce découpage : elle vaut 0,5*(4+2,5+4+4,75+4+4) = 11,625. La surface sous la courbe rouge vaut, par calcul de la primitive : 12,45.
Le reste de la Leçon 21 porte sur la démonstration selon laquelle les sommes de Cauchy d’une fonction continue convergent vers un nombre réel, nommé l’intégrale définie. En fait, Cauchy démontre plutôt que les sommes de Cauchy d’une fonction uniformément continue forment une suite de Cauchy, donc sont convergentes dans les nombres réels.
Cauchy commence la démonstration en se donnant une partition P et en montrant qu’il existe un nombre réel θ compris entre 0 et 1 tel que la somme de Cauchy (x1 – x0)f(x0) + (x2 – x1)f(x1) + … + (xn – xn-1)f(xn-1) soit égale à (xn – x0)f(x0 + θ (xn – x0)).
Pour démontrer l’existence de θ, il affirme utiliser un théorème sur les moyennes (Cours d’analyse, p. 16) et un argument similaire à la démonstration du théorème des accroissements finis (Leçon 7 du Résumé, p. 44). Il utilise en fait le théorème des valeurs intermédiaires.
@@@@@@@
Cauchy se donne ensuite un raffinement Q de la partition P. Il écrit :
Pour passer du mode de division que nous venons de considérer à un autre dans lequel les valeurs numériques des éléments X – x0 soient encore plus petites, il suffira de partager chacune des expressions (1) x1 – x0, x2 – x1, x3 – x2, …, X – xn-1, en de nouveaux éléments.
Soit donc Q, un raffinement de P, c’est-à-dire une partition qui sous-divise au moins un des sous-intervalles de P. Considérons le raffinement du premier sous-intervalle de P : x0 = y0, y1, …, yk = x1. Alors, en utilisant le même argument qu’au paragraphe précédent, il existe un nombre θ0 entre 0 et 1 tel que, sur l’intervalle [x0, x1],
(y1 – y0)f(y0) + … +(yk – yk-1)f(yk-1) = (x1 – x0)f(x0 + θ0(x1 – x0))
En répétant l’argument aux autres sous-intervalles de P, la nouvelle somme de Cauchy devient :
SC(f, Q) = (x1 – x0)f(x0 + θ0(x1 – x0)) + … + (xn – xn-1)f(xn-1 + θn-1(xn – xn-1)),
où {θi} sont des nombres compris entre 0 et 1. Cauchy utilise alors la continuité de la fonction sur [xi, xi-1] pour affirmer qu’il existe un εi-1 tel que f(xi-1 + θi-1(xi – xi-1)) = f(xi-1) ± εi-1. La somme de Cauchy sur la partition Q devient alors :
SC(f, Q) = (x1 – x0)f(x0 + θ0(x1 – x0)) + … + (xn – xn-1)f(xn-1 + θn-1(xn – xn-1)).
SC(f, Q) = (x1 – x0)(f(x0) ± ε0) + … + (xn – xn-1)(f(xn-1) ± εn-1).
En développant l’expression et en appliquant le théorème des moyennes (± (x1 – x0)ε0 ± … ± (xn – xn-1)εn-1 = (xn – x0)ε, où ε est une moyenne (4)), la somme devient :
SC(f, Q) = (x1 – x0)f(x0) + … + (xn – xn-1)f(xn-1) ± (x1 – x0)ε0 ± … ± (xn – xn-1)εn-1.
SC(f, Q) = SC(f, P) ± (x1 – x0)ε0 ± … ± (xn – xn-1)εn-1.
SC(f, Q) = SC(f, P) ± (xn – x0)ε.
Ainsi |SC(f, Q) – SC(f, P)| < (xn – x0)ε, donc la suite forme 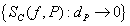 une suite de Cauchy lorsque le pas de la partition
une suite de Cauchy lorsque le pas de la partition 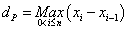 tend vers 0 (en prenant par exemple ε = 1/n, on a (xn – x0)ε ≤ n*dp*1/n = dp). Cauchy écrit :
tend vers 0 (en prenant par exemple ε = 1/n, on a (xn – x0)ε ≤ n*dp*1/n = dp). Cauchy écrit :
il résulte des équations [SC(f, P)] et [SC(f, Q)] comparées entre elles qu’on n’altérera pas sensiblement la valeur de S calculée pour un mode de division dans lequel les éléments de la différence X – x0 ont des valeurs numériques très petites, si l’on passe à un second mode dans lequel chacun de ces éléments se trouve subdivisé en plusieurs autres.
Il en conclut :
Donc, lorsque les éléments de la différence X – x0 deviennent infiniment petits, le mode de division n’a plus sur la valeur de S qu’une influence insensible; et, si l’on fait décroître indéfiniment les valeurs numériques de ces éléments, en augmentant leur nombre, la valeur de S finira par être sensiblement constante ou, en d’autres termes, elle finira par atteindre une certaine limite qui dépendra uniquement de la forme de la fonction f(x) et des valeurs extrêmes x0, X attribuées à la variable x. Cette limite est ce qu’on appelle une intégrale définie.
L’intégrale définie d’une fonction continue est donc la limite des sommes de Cauchy. Celui-ci propose ensuite des notations et choisit 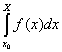 , en indiquant « la première de ces notations, imaginée par M. Fourier, est la plus simple ».
, en indiquant « la première de ces notations, imaginée par M. Fourier, est la plus simple ».
Leçon 22 – L’intégrale définie
À la Leçon 22 (Formules pour déterminer des valeurs exactes ou approchées des intégrales définies), Cauchy résume la leçon précédente en présentant l’intégrale définie comme la limite des sommes de « gauche ». Il généralise ces sommes de Cauchy en permettant à la fonction d’être évaluée en n’importe quelle valeur du sous-intervalle :
SC(f, P) = 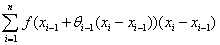
Il utilise cette généralisation uniquement pour retrouver les sommes de gauche (θi = 0, ∀i) et pour définir les sommes de droite (θi = 1, ∀i) :
SC(f, P) = 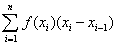 .
.
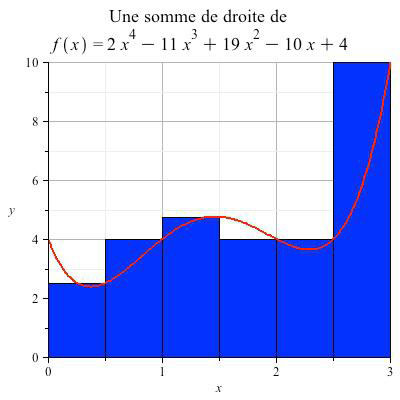
Figure 2 : Somme « de droite » de Cauchy pour la fonction de la figure 1. Les rectangles bleus s’alignent sur la valeur de droite de chaque intervalle. La courbe polynomiale figure en rouge, elle croise à chaque abscisse marquée les rectangles en leur coin droit (par construction). La somme de Cauchy « de gauche » (fig. 1) valait 11,625, cette somme « de droite » vaut 14,625. L’aire de la surface sous la courbe rouge vaut toujours 12,45. Pour obtenir une meilleure approximation, il faut augmenter le nombre de sous-intervalles (n). Lorsque n = 100, les approximations deviennent 12,3625 et 12,5424
À partir des sommes de droite et de la permutation des éléments de la partition, il obtient la valeur des sommes de gauche, multipliée par un signe négatif. Il en conclut que la permutation des extrémités de l’intervalle d’intégration introduit un négatif dans l’intégrale définie :
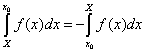
Il remplace ensuite les éléments de la partition par des suites arithmétiques ou géométriques :
On emploie fréquemment les formules [sommes de gauche] et [sommes de droite] dans la recherche des valeurs approchées des intégrales définies. Pour plus de simplicité, on suppose ordinairement que les quantités x0, x1, …, xn-1, X comprises dans ces formules sont en progression arithmétique […] On pourrait supposer encore que les quantités x0, x1, …, xn-1, X forment une progression géométrique dont la raison diffère très peu de l’unité.
Dans le premier cas (progression arithmétique), la partition est {x0, x0 + i, x0 + 2i, ..., x0 + ni = X} avec 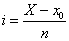 , et les sommes de gauche et de droite deviennent :
, et les sommes de gauche et de droite deviennent :
SC(f, P) = 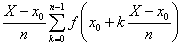 (A)
(A)
SC(f, P) = 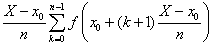
Dans le second cas (progression géométrique de raison légèrement supérieure à 1), la partition est {x0, x0(1 + α), x0(1 + α)2, ..., x0(1 + α)n = X} avec 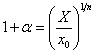 et les sommes de gauche et de droite deviennent :
et les sommes de gauche et de droite deviennent :
SC(f, P) 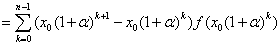
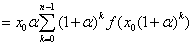 (G)
(G)
et
SC(f, P) 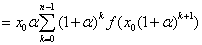
Ces deux formules par partition lui permettent de calculer non seulement des valeurs approchées de l’intégrale 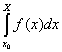 , mais aussi sa valeur exacte, en tant que limite limS des sommes de Cauchy.
, mais aussi sa valeur exacte, en tant que limite limS des sommes de Cauchy.
|
Exemples de calculs faits par Cauchy
Développons ici, en gardant ses notations, un des calculs que Cauchy mentionne sans le faire. Pour la fonction f(x) = x, on prend i = (X – x0)/n le pas de la progression arithmétique, et on applique la formule (7) de Cauchy des sommes de gauche (correspondant à (A) ci-dessus) :
En l’appliquant à f(x) = x, on écrit : S = i [nx0 + (1+2 +…+(n-1))i] = i (nx0 +n(n-1)/2*i) En remplaçant n par (X - x0)/i : S = (X - x0) x0 + ½(X - x0) (X - x0 - i) = (X - x0) (X + x0 – i)/2 Ce qui amène à la formule donnée par Cauchy pour limS :
On retrouve le troisième terme en appliquant la suite géométrique, par la formule (G) ci-dessus :
Donc, qu’on le calcule par la formule arithmétique (A) ou géométrique (G), on trouve pour l’intégrale de la fonction f(x)=x, par la limite des sommes de Cauchy mesurant l’aire des rectangles, la valeur bien connue ½ (X² - x0²). @@@@@@@ Cauchy donne aussi l’exemple de la fonction exponentielle de base A : f(x) = Ax. La formule (7) ou (A) ci-dessus donne : S = En mettant en évidence et en utilisant la formule de la somme des n premiers termes d’une série géométrique, on obtient
Pour calculer cette limite quand i → 0, on applique la règle de l’Hôpital (5) :
Ainsi S = |
Cauchy calcule ainsi la valeur exacte de l’intégrale de certaines fonctions : la fonction identité, des fonctions exponentielles (encadré ci-dessus), des fonctions puissances et la fonction 1/x. Il démontre aussi d’autres propriétés des intégrales :
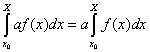
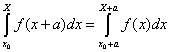
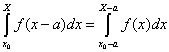
Il conclut la Leçon 22 avec la version intégrale du théorème des accroissements finis (équation (19) Leçon 22, p. 131). Soit une fonction f(x) continue sur [x0, X]. Alors il existe 0 ≤ θ ≤ 1 tel que
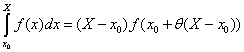 .
.
Il n’en présente pas de démonstration : il affirme que le théorème sur les moyennes appliqué à une somme de Cauchy calculée en utilisant la partition triviale [x0, X] donne SC = 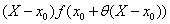 (équation (4) de la Leçon 21) et que la SC peut être tout simplement remplacée par l’intégrale. Il ajoute que si la fonction est croissante ou décroissante et que la partition forme une suite arithmétique, alors l’intégrale définie sera coincée entre les sommes de gauche et les sommes de droite, dont la différence sera d’au maximum
(équation (4) de la Leçon 21) et que la SC peut être tout simplement remplacée par l’intégrale. Il ajoute que si la fonction est croissante ou décroissante et que la partition forme une suite arithmétique, alors l’intégrale définie sera coincée entre les sommes de gauche et les sommes de droite, dont la différence sera d’au maximum
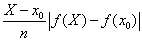
Leçon 23 – Propriétés algébriques de l’intégrale définie – Interprétation géométrique de l’intégrale définie
Il présente d’autres propriétés à la Leçon 23, intitulée :
Décomposition d’une intégrale définie en plusieurs autres. Intégrales définies imaginaires. Représentation géométrique des intégrales définies réelles. Décomposition de la fonction sous le signe en deux facteurs dont l’un conserve toujours le même signe.
Ces propriétés sont :
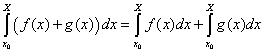
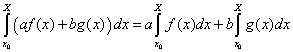
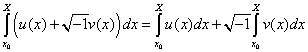

La dernière propriété sera utilisée dans la démonstration du théorème fondamental du calcul.
Il donne aussi une interprétation géométrique de l’intégrale définie :
Concevons à présent que, la limite X étant supérieure à x0, et la fonction f(x) étant positive depuis x = x0 jusqu’à x = X, x, y, désignent des coordonnées rectangulaires, et A la surface comprise d’une part entre l’axe des x et la courbe y = f(x), d’autre part entre les ordonnées f(x0), f(X).
Pour calculer cette aire, Cauchy utilise un argument géométrique qui revient à affirmer la version intégrale du théorème des accroissements finis. Il écrit :
[L’aire] sera donc équivalente à un rectangle construit sur une ordonnée moyenne représentée par une expression de la forme f(x0 + θ(X – x0)); en sorte qu’on aura A = (X – x0)f(x0 + θ(X – x0)), θ désignant un nombre inférieur à l’unité.
Autrement dit : .
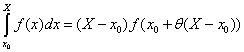
![Figure 3 : La version en calcul intégral du théorème des accroissements finis. L’aire sous la courbe de la fonction f(x) = x3 + 2 entre x = 1 et x = 2 vaut 5,75 et elle est équivalente à l’aire du rectangle dont la base est l’intervalle [1,2] et la hauteur 5,75. Cette hauteur est atteinte lorsque la fonction f(x) est évaluée en x = ½ (30)⅓.](/sites/default/files/figure-3_10.jpg)
Il poursuit en appliquant le même argument à chacun des sous-intervalles d’une partition de l’intervalle [x0, X]. Il obtient une somme de rectangles de bases (xi – xi-1) et de hauteurs f(xi-1 + θi(xi – xi-1)), avec une liste θ0, …, θn–1 de nombres positifs inférieurs à l’unité, d’où
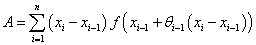
En passant à la limite, il obtint l’intégrale définie, c’est-à-dire que l’aire sous la courbe y = f(x) peut se calculer en utilisant l’intégrale définie (6) :
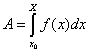
Or, cette aire deviendra une fonction lorsque X deviendra une variable. Elle sera aussi une primitive de f(x). Ce sera le théorème fondamental du calcul.
Leçons 24 et 25 – Les intégrales à borne infinie, et les intégrales définies singulières (discontinuité)
La Leçon 24 (Des intégrales définies dont les valeurs sont infinies ou indéterminées. Valeurs principales des intégrales indéterminées) et la Leçon 25 (Intégrales définies singulières) ont comme objectif de généraliser l’intégrale aux fonctions continues définies sur un intervalle infini et aux fonctions continues par morceaux. Au début de la Leçon 24, Cauchy écrit :
Dans les leçons précédentes, nous avons démontré plusieurs propriétés remarquables de l’intégrale définie
(1)
mais en supposant : 1- que les limites x0, X étaient des quantités finies, 2- que la fonction f(x) demeurait finie et continue entre ces mêmes limites. Lorsque les valeurs extrêmes x0, X deviennent infinis, ou lorsque la fonction f(x) ne reste pas finie et continue depuis x = x0 jusqu’à x = X, on ne peut plus affirmer que la quantité désignée par [SC] dans les leçons précédentes ait une limite fixe, et par suite on ne voit plus quel sens on doit attacher à la notation (1) qui servait à représenter généralement la limite de [SC].
Ces deux généralisations sont basées sur la même technique : l’intervalle d’intégration est tronqué afin d’obtenir une fonction continue sur un intervalle fini, la fonction est intégrée sur cet intervalle, puis on passe à la limite sur l’intervalle. Si la limite existe, alors la fonction est intégrable. La limite est donc utilisée afin d’étendre la validité de l’intégrale au-delà des fonctions continues sur un intervalle fini. De façon plus détaillée, Cauchy introduit, à la Leçon 24, les valeurs principales et les valeurs générales de l’intégrale. Soit ε > 0, soient x1, …, xm, les discontinuités de la fonction f(x) et soient μ, ν, μ1, ν1, …, μm, νm des constantes positives arbitraires. Alors les valeurs générales de l’intégrale sont :
(12) 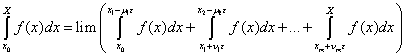
(13) 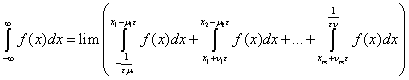
En posant les μi, νi comme étant égaux à 1, on obtient les valeurs principales :
(15) 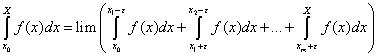
(16) 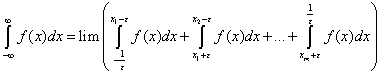
Le critère de validité est présenté à la Leçon 25 comme un théorème (p. 149-150) qui stipule que si la différence entre les valeurs générales et les valeurs principales tend vers 0, alors la fonction est intégrable.
Leçon 26 – Le théorème fondamental du calcul
Finalement, la Leçon 26 (Intégrales indéfinies) porte sur ce qui est maintenant appelé le théorème fondamental du calcul. Ce théorème permet de lier l’intégrale définie à l’intégrale indéfinie et vice versa (7). L’intégrale définie se calcule comme la limite des sommes de Cauchy d’une fonction f(x) continue et représente l’aire sous la courbe. L’intégrale indéfinie est l’opération inverse de la dérivée et permet de trouver une primitive de la fonction f(x). Or, l’intégrale définie peut être utilisée pour trouver une primitive (donc pour résoudre le problème de la recherche de primitives) et l’intégrale indéfinie peut être utilisée pour calculer l’aire sous la courbe. Ces liens reposent sur la fonction d’aire : 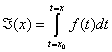 , où x est une variable (8).
, où x est une variable (8).
Cauchy démontre que si f(x) est continue, alors ℑ(x) est continue, dérivable et est une primitive de f(x). Pour ce faire, il utilise la version intégrale du théorème des accroissements finis (la formule (19) de 22e Leçon) et une propriété des intégrales. Il écrit :
Il suit des équations
(2)
et ℑ(x0) = 0,
et
(3)
que, si la fonction f(x) est finie et continue dans le voisinage d’une valeur particulière attribuée à la variable x, la nouvelle fonction ℑ(x) sera non seulement finie, mais encore continue dans le voisinage de cette valeur, puisqu’à un accroissement infiniment petit de x correspondra un accroissement infiniment petit de ℑ(x).
En divisant l’équation (3) par α, Cauchy obtient :
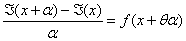
Comme la fonction est continue en x, ℑ’(x) = f(x), lorsque α tend vers 0. Ainsi l’intégrale définie permet de résoudre le problème de la recherche de primitives, car 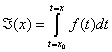 est une primitive de f(x).
est une primitive de f(x).
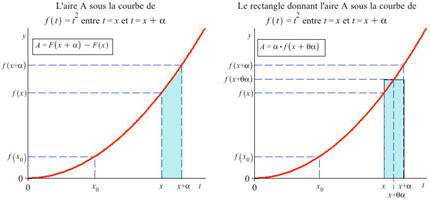
Figure 4 : Interprétation graphique de l’équation (3) : Deux représentations équivalentes de l’aire sous la courbe d’une fonction f(t) entre t = x et t = x + α. L’aire peut être calculée à l’aide de la fonction d’aire A = F(x+α) – F(x). La figure de gauche représente ce calcul. Or, par la version « en calcul intégral » du théorème des accroissements finis, cette aire A est la même que l’aire d’un rectangle dont la base est α et la hauteur f(x + Θα), pour un certain . Ce rectangle est représenté sur la figure droite.
@@@@@@@
Cauchy présente ensuite deux problèmes et leurs solutions :
Problème I : Trouver la forme de la fonction ω(x) telle que ω’(x) = 0.
Problème II : Trouver la valeur générale de y propre à vérifier l’équation dy = f(x)dx.
La solution de Cauchy au problème I est qu’une fonction dont la dérivée est nulle est constante par morceaux. Quant à la solution au problème II, Cauchy affirme que si y = F(x) est une solution particulière (valeur particulière) de l’équation dy = f(x)dx ou y’ = F’(x) = f(x), alors F(x) + ω(x), avec ω’(x) = 0 est la solution générale (valeur générale de l’équation). F(x) peut être trouvée par l’intégrale indéfinie, donc par inversion des formules de dérivation, c’est-à-dire qu’elle est l’antidérivée (9) de f(x). Or, si f(x) est continue, alors , calculée comme la limite des sommes de Cauchy, est aussi une primitive. Ceci avait été démontré en introduction de la leçon. Ainsi, la valeur générale devient :
avec ω’(x) = 0.
Cauchy démontre de plus que les primitives de f(x) ne différent entre elles que d’une constante. Il écrit :
Cette valeur générale de y, qui comprend, comme cas particulier, l’intégrale
et qui conserve la même forme, quelle que soit l’origine x0 de cette intégrale, est représentée dans le calcul par la simple notation
, et reçoit le nom d’intégrale indéfinie.
Si F(x) est une primitive non triviale d’une fonction continue f(x), alors cette primitive donne l’intégrale indéfinie et cette primitive permet de calculer l’intégrale définie. Il conclut :
Il résulte des équations
(15)
(17)
(18)
que, étant donnée une valeur particulière de F(x) de y, propre à vérifier la formule dy = f(x)dx, on peut en déduire : 1° la valeur de l’intégrale indéfinie
; 2° celles des deux intégrales définies
,
, dans le cas où les fonctions f(x), F(x) restent continues entre les limites de ces deux intégrales.
Lorsque l’intégrale indéfinie permet de trouver une primitive, cette primitive permet de calculer l’aire sous la courbe.
Cauchy, quels apports ?
Finalement, les innovations de Cauchy furent : 1°) d’introduire l’intégrale définie comme technique uniforme pour calculer l’aire sous une courbe ; 2°) d’utiliser l’intégrale définie pour résoudre le problème de la recherche de primitives et de démontrer que toute fonction continue est intégrable et que toute fonction continue a une primitive. Pour y arriver, Cauchy a introduit les notions de limite et de suites de Cauchy, mais le plus important fut la propriété de continuité de la fonction. Il généralisa son intégrale définie aux fonctions continues par morceaux, donc aux fonctions n’ayant qu’un nombre fini de discontinuités.
La suite des recherches sur l’intégrale de Cauchy passera par l’étude des fonctions discontinues ayant une infinité de discontinuités et par la caractérisation de l’ensemble de ces discontinuités. Dirichlet posa une conjecture en 1829 (« une fonction est intégrable si et seulement si l’ensemble de ses discontinuités est nulle part dense (10) ») et Lipschitz présenta en 1864 une démonstration dans un cas spécifique (11).
Cauchy ouvrit donc une nouvelle voie de recherche sur l’intégration, jusqu’aux travaux de Riemann (12) en 1854. Riemann définit l’intégrale dans toute sa généralité, comme la convergence des sommes de Riemann d’une fonction arbitraire, et changea la façon de définir l’intégrabilité d’une fonction, en caractérisant non plus l’ensemble des discontinuités de la fonction mais son comportement. Il s’intéressa ainsi aux fonctions bornées (et non plus aux fonctions discontinues) et démontra l’équivalence entre deux conditions d’intégrabilité. En 1875, Darboux (13) reprit les recherches de Riemann et introduisit une nouvelle façon de définir l’intégrale : à l’aide des sommes supérieures et inférieures. Il démontra que ces sommes convergent toujours lorsque la fonction est bornée et définit qu’une fonction est intégrable si ces deux limites sont égales. Il démontra le théorème fondamental du calcul pour ces fonctions intégrables. Et puis viendra Lebesgue (14), qui proposa de partitionner l’image de la fonction au lieu de son domaine et d’introduire les fonctions mesurables : comme les ouvrages de Cauchy en 1821, son article de 1901 changea la façon de concevoir l’intégrale et la théorie de l’intégration.
(octobre 2014)

1. Théorie des fonctions analytiques, contenant les principes du calcul différentiel, dégagés de toute considération d'infiniment petits et d'évanouissans de limites ou de fluxions, et réduits à l'analyse algébrique des quantités finies, Impr. de la République Paris, 1796.
2. Il ne faut pas confondre les sommes de Cauchy avec les suites de Cauchy. Les sommes de Cauchy sont une façon d’approximer l’aire sous la courbe d’une fonction alors qu’une suite de Cauchy est une suite de nombres réels {ai} telle que la différence entre les termes de la suite tend vers 0.
3. Liouville, Joseph, 1835, « Mémoire sur l’intégration d’une classe de fonctions transcendantes », Journal für die reine und angewandte Mathematik, 13, p. 93-118.
4. C’est là que Cauchy utilise la continuité uniforme, car εi-1 ne doit pas dépendre de xi-1 sur l’intervalle [xi, xi-1] pour que ε puisse tendre vers 0.
5. Règle énoncée en 1696 par Guillaume de L’Hôpital (1661-1704) : si f et g sont deux fonctions définies sur [a, b], dérivables en a, s'annulant en a et telles que le quotient f’(a)/g’(a) soit défini, alors lim (x → a+) [f(x)/g(x)] = f’(a)/g’(a). C’est un cas particulier de la formule de Taylor des développements limités.
6. Cauchy ne porte pas attention aux variables muettes. On écrit maintenant A(x) = 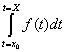 .
.
7. Le théorème fondamental du calcul peut maintenant être vu comme une solution aux problèmes d’inversion des opérateurs « intégrale » et « dérivée » : Sous quelles conditions, l’intégrale est-elle l’inverse à droite ou l’inverse à gauche de la dérivée ? L’analyse fonctionnelle a été développée au début du XXe siècle et c’est pourquoi le théorème fondamental du calcul se présente, dans les travaux de Cauchy, comme le lien entre l’intégrale définie et l’intégrale indéfinie.
8. Cauchy, comme souvent, n’utilise pas correctement la variable muette, car il écrit plutôt 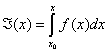 . La notation a été changée.
. La notation a été changée.
9. L’antidérivée d’une fonction f(x) est calculée par l’intégrale indéfinie. Elle est, lorsqu’elle existe, une primitive de f(x). Il y a des fonctions qui ont des primitives et qui n’ont pas des antidérivées. C’est un résultat de Louville (cf. premier encadré).
10. Dirichlet, P. G. Lejeune, 1829, « Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données, » Journal für die reine und angewandte Mathematik, 4, p. 157-169.
11. Lipschitz, Rudolf, 1864, «Recherches sur le développement en séries trigonométrique des fonctions arbitraires d’une variable et principalement de celles qui, dans un intervalle fini, admettent une infinité de maxima et de minima, » Acta Mathematica, 1913 (36) p. 281-294.
12. Riemann, Bernhard, 1854, « La possibilité de représenter une fonction par une série trigonométrique » Bulletin des sciences mathématiques et astronomique, Tome V, 1873, p. 225-279 (prononcé lors de son Habilitation en 1854, publié en allemand en 1867 et traduit en français par Gaston Darboux en 1873).
13. Darboux, Gaston, 1875, « Mémoire sur la théorie des fonctions discontinues, » Annales scientifiques de l’École normale supérieure (2) 4, p. 57-112.
14. Lebesgue, Henri, 1901, « Sur une généralisation de l’intégrale définie », Comptes rendus hebdomadaires des séances de l’Académie des sciences, 132, p. 1025-1028.
LIVRES
 |
Belhoste, Bruno, Cauchy, 1789-1857 : un mathématicien légitimiste au XIXe siècle, préface de Jean Dhombres, Paris, Belin (1985). |
 |
|
 |
|
 |
|
ARTICLES SUR INTERNET
 |
|
 |
|
ŒUVRES DE CAUCHY SUR INTERNET
![Résumé des Leçons données à l’École royale polytechnique sur le calcul infinitésimal, Paris, Impr. Royale (1823) [dont est extrait le texte BibNum] (Gallica)](/sites/default/files/resume-des-lecons-donnees.jpg) |
|
 |
|
cauchy-texte.pdf

cauchy-analyse.pdf



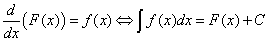
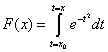
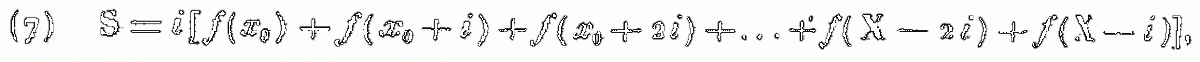
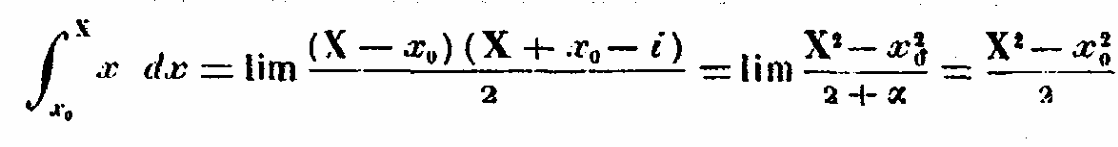
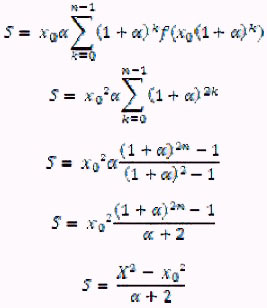
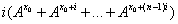
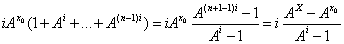
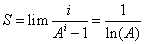
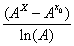 .
.