Méthode pour la recherche du minimum et du maximum

Méthode pour la recherche du minimum et du maximum.

Auteur :

Pierre de Fermat (1601-1665)

Auteurs de l'analyse: Jacques Bair, Valérie Henry

Publication :

Œuvres de Fermat, publiées par les soins de MM. Paul Tannery et Charles Henry, Gauthier-Villars, 1896 (Tome troisième, extrait pp. 121-123)

Année de publication :

1636

Nombre de pages :

Résumé :

Ce document nous permet de comprendre comment au XVII° siècle, bien avant la notion de fonction, de dérivée, de calcul infinitésimal ou différentiel, on pouvait appréhender les notions de « minimum et de maximum ».

Source de numérisation :

BnF (Gallica)

Les infiniment petits selon Fermat : prémisses de la notion de dérivée

Jacques Bair
Professeur ordinaire à l’Université de Liège (Belgique)

Valérie Henry
Chargée de cours aux Facultés Universitaires Notre-Dame de la Paix à Namur (Belgique) et à l’Université du Luxembourg

LA MÉTHODE ET LES QUESTIONS QU’ELLE SOULÈVE

Le texte sélectionné de Fermat a trait à la recherche d’une valeur, notée a, d’une variable x susceptible de procurer un maximum (ou un minimum) d’une fonction f:x → f(x). La méthode (1), qui semble avoir été mise au point aux alentours de 1629, est d’abord présentée dans le texte original de façon littéraire, puis détaillée plus analytiquement sur un exemple (2), à savoir celui pour lequel la fonction f livre la valeur du produit AE×EC lorsque l’on cherche « à partager AC (fig. 91 du texte) en E, de sorte que AE×EC soit maximum ».

La méthode de Fermat

Rappelons que, pour un segment (figure ci-dessous), Fermat présente ainsi sa méthode pour trouver le maximum de AE×EC :

« Posons AC = b ; soit a un des segments, l’autre sera b – a, et le produit dont on doit trouver le maximum : ba – a². Soit maintenant a + e le premier segment de b, le second sera b – a – e, et le produit des segments : ba – a² + be – 2ae – e².
Il doit être adégalé au précédent : ba – a²
Supprimant les termes communs : be ae + e²
Divisant tous les termes : b 2a + e
Supprimez e : b = 2a
Pour résoudre le problème, il faut donc prendre la moitié de b. »

Si l’on reprend ce qui précède, les étapes à suivre pour déterminer la valeur a recherchée sont les suivantes :

1) « adégaler » f(a) et f(a + e), ce qui est noté dans l’exemple à l’aide du signe
2) supprimer les termes semblables figurant dans les deux membres de cette adégalité
3) diviser les deux membres de l’adégalité restante par e
4) supprimer les termes qui contiennent encore e tout en transformant l’adégalité obtenue en une égalité.

D’après Fermat lui-même, « il est impossible de donner une méthode plus générale » et « cette méthode ne trompe jamais, et peut s’étendre à nombre de questions très belles », par exemple, pour trouver « les centres de gravité de figures terminées par des lignes droites et courbes, aussi bien que ceux de solides », mais aussi, et surtout, pour déterminer « des tangentes des lignes courbes », ainsi qu’il est montré dans la fin de l’extrait pour une parabole : « nous ramenons à la méthode précédente l’invention des tangentes en des points donnés à des courbes quelconques. »

Une autre application par Fermat de sa méthode : la recherche de tangentes

Voici une présentation, un peu adaptée (3), du texte de Fermat sur cette question.

Dans le plan rapporté à un repère orthogonal, considérons la parabole d’équation x = y². Sur celle-ci se trouve un point B par lequel on cherche à mener la tangente à la courbe ; cette tangente va rencontrer l’axe des abscisses en E. Notons C le point situé sur l’axe horizontal à la même abscisse, notée d, que B et désignons par a la longueur EC : a est l’inconnue de notre problème (4). Choisissons encore sur l’axe des abscisses un point I entre l’origine O du plan et C, notons e la longueur IC. Construisons enfin les points D et D’ qui se trouvent sur la droite verticale passant par I ainsi que, respectivement, sur la tangente recherchée et sur la parabole : on a donc, en vertu de l’équation de la parabole, d – e = (D’I)² et d = (BC)² .

La figure ci-dessous représente la situation étudiée.

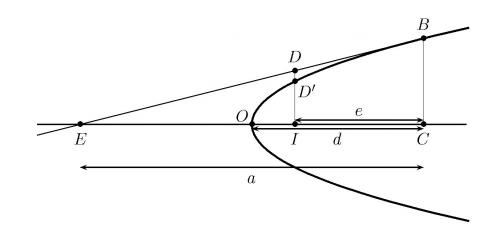
Comme la parabole est située sous la tangente, on a DI > D’I.

Or, le théorème de Thalès permet d’écrire . En vertu de ce qui précède, on peut donc écrire ou encore avec nos notations , ce qui est équivalent à . Il suffit alors de suivre fidèlement la démarche de Fermat, puisque quand e se rapproche de 0, le point D’ se rapproche du point D :

- adégaler les deux membres de l’inégalité précédente : d(a-e)² a²(d-e) (ce qui revient à adégaler DI et D’I)
- supprimer les termes semblables dans les deux membres de l’adégalité : de² - 2ade -a²e
- diviser les deux membres de l’adégalité restante par e : de-2ad - a²
- supprimer le terme qui contient encore e et transformer l’adégalité en égalité, ce qui permet d’écrire a=2d.

La présentation algorithmique en quatre étapes soulève à tout le moins ces deux questions :

a) Que représente e ? Est-ce un nombre non nul par lequel on peut diviser les deux membres d’une adégalité ce qui est préconisé au point 3) ci-dessus, ou est-ce zéro comme il est admis en fin de raisonnement au point 4).

b) Qu’est en réalité une « adégalité » et que signifie précisément le signe

Nous allons tenter d’apporter des réponses, en langage moderne, à ces deux questions.

LA QUANTITÉ e

La méthode de Fermat consiste finalement à poser e= 0 dans l’expression

qui est ensuite égalée à zéro. En d’autres termes, le nombre a recherché annule la dérivée de f : ce résultat est connu de nos jours sous le nom de Théorème de Fermat (pour les maximums). Dans cette optique, le symbole e désigne donc une variable tendant vers 0. Il convient toutefois de constater que le raisonnement de Fermat n’est qu’un prélude à cette présentation contemporaine, puisque, notamment

- la notation fonctionnelle désormais classique f(x) n’a été introduite qu’au dix-huitième siècle par Euler (5);

- le concept de dérivée a été découvert essentiellement par Newton et Leibniz (en 1684 pour ce dernier), avant d’être exploré et développé en particulier par Lagrange, et enfin seulement défini en termes d’une limite notamment par Cauchy.

Notons que le raisonnement de Fermat n’était pas encore bien compris au milieu du dix-septième siècle. C’est ce qui poussa Huygens à présenter, à l’Académie des Sciences et plus de 30 ans après Fermat (soit précisément en 1667 (6) ), une communication dans laquelle il expliquait la méthode du savant toulousain ; il y mentionnait que e est une « quantité infiniment petite », en utilisant pour la première fois d’ailleurs les mots « infiniment petit ». Ceci montre une nouvelle fois à quel point l’œuvre de Fermat était profonde et novatrice, puisque le concept d’infiniment petit ne fut véritablement introduit de façon pragmatique que dans les travaux de Leibniz et de ses successeurs sur les fondements de l’analyse mathématique. Contestés et abandonnés par les mathématiciens dès le début du dix-neuvième siècle, car supposer leur existence soulevait des objections de nature ontologique et entraînait des contradictions logiques, les infiniment petits furent néanmoins remis à l’honneur dans la seconde moitié du siècle dernier par le logicien Abraham Robinson (1918-1974). Celui-ci en prouva l’existence dans le contexte des nombres hyperréels, ce qui donna naissance à l’analyse non standard, une nouvelle façon de concevoir l’analyse mathématique. Il est désormais acquis, de manière incontestable, que l’ensemble des nombres réels peut être étendu en un ensemble de nombres hyperréels au sein duquel existent des nombres infiniment petits en ce sens qu’ils sont non nuls mais en valeur absolue inférieurs à tout réel positif.

Les nombres hyperréels – l’analyse non standard

Les nombres hyperréels forment un corps algébrique totalement ordonné dont celui des réels est un sous-corps : ainsi, tout nombre réel est hyperréel et l’on peut additionner, soustraire, multiplier et diviser entre eux des nombres hyperréels avec les mêmes règles algébriques en vigueur dans les nombres réels (à condition, bien sûr, de ne pas diviser par zéro). De plus, il existe des nombres hyperréels non réels : ils sont dits « non standards », les réels étant qualifiés de « standards ». De façon plus précise, les nombres hyperréels sont répartis selon trois « ordres de grandeur » :

a) des nombres infiniment petits, c’est-à-dire des nombres dont la valeur absolue est inférieure à tout nombre réel positif ; le seul réel infiniment petit est 0 (7).
b) des nombres infiniment grands, c’est-à-dire des nombres hyperréels dont la valeur absolue est supérieure à tout nombre réel positif ; ce sont encore les inverses d’infiniment petits non nuls ;
c) des nombres appréciables, c’est-à-dire des nombres hyperréels compris (au sens large) entre deux réels non nuls.

De façon imagée, il est possible de visualiser tous les nombres hyperréels en partant d’une classique droite numérique représentant les réels : les infiniment petits forment le « halo » de 0 apparaissant sous la forme d’un phylactère dessiné au dessus du point représentatif de 0 (8) , les appréciables sont dessinés dans le halo d’un réel non nul (9), tandis que les infiniment grands positifs (igp en abrégé) et les infiniment grands négatifs (ign en abrégé) se trouvent respectivement à l’extrême droite ou l’extrême gauche sur l’axe numérique (10) :

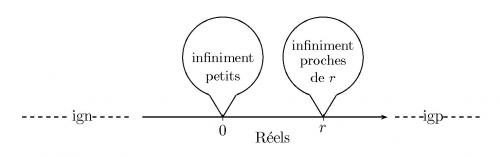
De plus, tout hyperréel x qui n’est pas infiniment grand est infiniment proche d’un réel en ce sens que la différence entre x et ce réel est infiniment petite : ce réel, qui est unique, est appelé la partie standard de x et est noté st (x). Les règles régissant le passage à la partie standard sont classiques et assez naturelles : par exemple pour des hyperréels x et y non infiniment grands, st (x + y) = st (x) + st (y), st (x × y) = st (x) × st (y), mais x < y entraîne st (x) = st (y).

L’analyse infinitésimale peut être avantageusement et aisément développée dans ce contexte : on est alors en présence de ce que l’on appelle l’ « analyse non standard ». Par exemple, un fonction f est dite continue en un réel a dès que, pour x infiniment proche de a, f(x) (11) est infiniment proche de f(a) ; ou encore, f est dérivable en a si, pour tout « infiniment petit » non nul e, est limité et de partie standard indépendante de e : cette partie standard vaut alors le nombre dérivé f'(a).

Interprétons dès lors la méthode de Fermat dans le contexte des nombres hyperréels et cherchons, comme le savant toulousain, à maximiser la fonction f définie par f(x) = b x –x² .

Considérons un infiniment petit non nul ε et admettons que f(a) est le maximum, supposé strict (12), cherché. On doit dès lors avoir

f(a+ε)< f(a)

et l’on en déduit

si ε>0 ,mais si ε<0.
Un passage par la partie standard livre
si ε>0 et si si ε<0.

D’où la conclusion résultant de la définition du nombre dérivé en analyse non standard

La dernière ligne du raisonnement formulé par Fermat sur son exemple, à savoir : « supprimez e : b=2a » s’explique très aisément en analyse non standard. En effet, les nombres hyperréels 2a+e et b sont infiniment proches l’un de l’autre si e désigne un infiniment petit ; leurs parties réellement observables, c’est-à-dire leurs parties standards, valant respectivement 2a et b, sont donc égales. La transformation du signe

d’adégalité en égalité correspond à un « retour naturel » de l’ensemble des hyperréels à celui des réels grâce à un passage par les parties standards.

L’ADÉGALITÉ

La méthode de Fermat repose fondamentalement sur le concept d’adégalité, symbolisé par le signe

. Il s’agit, en reprenant les termes de l’auteur dans un autre extrait de ses oeuvres, de « cette sorte de comparaison adaequalitem comme Diophante l’appelle » ou encore d’une « comparaison feinte » dans la mesure où les deux nombres comparés sont « comme s’ils étaient égaux, quoi qu’en fait ils ne le soient point » (13) . La traduction anglaise du mot latin adeaqualitas est souvent approximate equality, termes auxquels certains préfèrent pseudoequality.

L’interprétation du signe

n’est pas aussi simple qu’il n’y paraît, même en analyse non standard. De fait, on pourrait a priori penser traduire ce symbole par « est infiniment proche de », car cela expliquerait bien le premier usage du signe dans l’exemple, à savoir « be

2 a e + e² ». Toutefois, cela ne permet pas de justifier la suite du raisonnement, soit « b

2a+e »; en effet, si deux nombres hyperréels sont infiniment proches l’un de l’autre, il n’en va pas nécessairement de même pour leurs quotients par un même infiniment petit : par exemple, si ε désigne un infiniment petit positif, ε et ε² sont infiniment proches l’un de l’autre, alors que 1 n’est évidemment pas infiniment proche de e.

Si, dans l’exemple, l’on regarde les deux lignes dans lesquelles intervient le signe

, on s’aperçoit qu’elles font intervenir soit deux hyperréels infiniment petits, à savoir be et 2 a e + e², soit deux appréciables (14), à savoir b et 2a+e ; on pourrait donc penser à traduire ce symbole par « est du même ordre de grandeur que » (15) . Cette tentative ne permet toutefois pas d’expliquer l’égalité ultime « b=2a » ; effectivement, on peut exhiber des infiniment petits, tels que ε et 2ε + ε² par exemple, qui ont donc même ordre de grandeur, dont les quotients par e sont appréciables et ont dès lors également le même ordre de grandeur tout en ayant des parties standards égales aux deux réels distincts 1 et 2.

Une explication rigoureuse du raisonnement de Fermat peut être donnée en « juxtaposant » en quelque sorte les deux relations « être infiniment proche de » et « être de même ordre de grandeur que ». De façon plus précise, on peut utilement faire appel à la notion suivante : pour deux hyperréels x et y arbitraires et un hyperréel infiniment petit positif quelconque ε, on a x

y si et xy seulement si la différence x-y est telle que le quotient

est appréciable. Avec cette définition, reprenons le raisonnement de Fermat pour résoudre son exemple. On a bien, pour e=ε infiniment petit, « be

2a e + e² » puisque

est appréciable. De plus, la mention « b

2a + e » signifie alors que

est appréciable, ce qui ne peut se produire que lorsque les deux réels b et 2a coïncident (16), d’où « b=2a ».

CONCLUSION

L’analyse précédente montre que la théorie sur les extrema de Fermat préfigure assurément les développements ultérieurs de l’analyse mathématique, de ses débuts au dixseptième siècle avec ses fondateurs Newton et Leibniz, jusqu’à ses développements les plus récents avec l’avènement de l’analyse non standard.

En effet, la méthode de Fermat a été développée avant la naissance des notions fondamentales de l’analyse mathématique, c'estàdire avant l’apparition pragmatique des infiniment petits, et avant même l’introduction de la notion générale de fonction et, bien sûr, de celle de dérivée.

Cet épisode de l’histoire des mathématiques montre également une certaine évolution dans la rigueur des développements. La méthode de Fermat a d’abord été décrite de manière technique, avant d’être justifiée en utilisant des théories plus générales (17), mais aussi plus abstraites (18).

La naissance de l’analyse non standard a remis à l’honneur, et cette fois avec toute la rigueur exigée aujourd’hui, l’importance des infiniment petits dans les problèmes locaux étudiés en analyse mathématique. Mais le prix à payer pour un retour aux idées intuitives et efficaces de Fermat tout en se conformant aux exigences contemporaines de rigueur est une sophistication de l’outil mathématique : la démonstration rigoureuse de l’existence d’infiniment petits reste assez abstraite et fait appel à des théories relativement compliquées de logique mathématique (19). Il est toutefois possible, dans une introduction à l’analyse mathématique, d’exploiter efficacement les infiniment petits sans recourir à des techniques évoluées de logique (20).

Ainsi, on peut désormais interpréter le raisonnement de Fermat à l’aide de théories rigoureuses et récentes tout en conservant les intuitions initiales du savant.

(1) En fait, Fermat présente plusieurs méthodes différentes pour résoudre ce problème ; nous analysons ici uniquement celle qui se trouve au début du chapitre intitulé « Méthode pour la recherche du maximum et du minimum » (aux pages 121 à 156 de la référence consultée).
(2) Dans ses Œuvres, Fermat illustre sa méthode par plusieurs exemples semblables ; celui-ci est le premier d’entre eux et le plus simple.
(3) De manière à mieux expliquer le raisonnement de Fermat, nous modifions légèrement la figure originale en changeant l’orientation de la parabole (afin de caractériser celleci par une équation simple) et révisons également quelque peu les notations de Fermat : en fait, par rapport à la figure initiale, nous échangeons les lettre D et O, puisque le sommet de notre parabole est l’origine O du plan.
(4) En effet, la connaissance de a entraîne celle de E, et la tangente recherchée, qui est la droite passant par B et E, peut alors être tracée.
(5) L. Euler (1707 – 1783) a précisé la notion générale de fonction et, à l’instar de Clairaut A. (1713 – 1765), a utilisé la notation f(x) pour désigner l’image par une fonction f d’un nombre x : elle lui semblait en effet mieux adaptée que celle initialement introduite J. Bernoulli (1667 – 1748), à savoir f_x ou même φ_x.
(6) C. Huygens, Œuvres complètes, Martinus Nijhoff, La Haye, (1940), Tome 20.
(7) En effet, un réel non nul est tel que sa valeur absolue n’est pas inférieure, par exemple, à sa moitié.
(8) Les nombres infiniment petits non nuls ne figurent pas sur la droite numérique réelle, mais il est possible de les imaginer dans l’oculaire d’un « microscope infiniment puissant » qui permettrait de « distinguer » le réel 0 des différents éléments de son halo.
(9) Ils peuvent être envisagés à l’aide d’un « microscope infiniment puissant » centré sur n’importe quel réel non nul.
(10) Les infiniment grands peuvent être conçus virtuellement en recourant à des « télescopes infiniment puissants » dirigés vers l’extrême droite (pour les igp) ou l’extrême gauche (pour les ign) de la classique droite numérique réelle.
(11) En réalité, il s’agit de l’image de x par ce que l’on appelle l’ « extension naturelle » de f, cette fonction au sein des hyperréels jouissant exactement des mêmes propriétés que f dans les réels.
(12) Le cas des inégalités larges se traite semblablement.
(13) Œuvres de Fermat, Tome troisième, Traductions par M. Paul Tannery, Paris, GauthierVillars et Fils, imprimeurslibraires, M DCCC XCVI, p. 126. Dans le texte BibNum luimême, Fermat indique « on adégalera, pour parler comme Diophante,… ».
(14) Un hyperréel est dit appréciable lorsqu’il coïncide avec un réel non nul ou bien est infiniment proche d’un réel non nul.
(15) Rappelons qu’au sein des nombres hyperréels, on distingue trois ordres de grandeur : les nombres infiniment petits, les nombres appréciables et les nombres infiniment grands.
(16) En effet, si b diffère de 2a, l’expression (b 2a)/e est infiniment grande.
(17) Il est aujourd’hui prouvé que le « théorème de Fermat (pour les maximums) » s’applique non seulement aux
fonctions polynomiales (considérées par le savant) mais aussi à des fonctions bien plus générales.
(18) Comme la définition en epsilon – èta du concept de limite ou le recours aux nombres hyperréels.
(19) Plus spécialement, la théorie des modèles.
(20) Voir l’onglet « Pour en savoir plus » du texte BibNum.