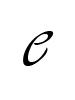La démonstration de la transcendance de e

Contexte historique

Quand Hermite publie en 1873 son mémoire, la démonstration par Liouville de l’existence de nombres transcendants remonte à moins de trente ans (1). La théorie de l’irrationalité est bien maîtrisée, grâce à l’outil fondamental constitué par le développement en fractions continues. Euler avait développé cette théorie et explicité un certain nombre de tels développements, comme celui du nombre e en 1737. C’est la théorie des fractions continues qui permet à Johann Heinrich Lambert (1728-1777) de démontrer en 1761 l’irrationalité du nombre Pi — ses recherches sont explicitement motivées par la question de la quadrature du cercle, mais il ne prétend pas la résoudre et se contente d’une magnifique démonstration de l’irrationalité de quantités circulaires et logarithmiques (2). Une autre approche de l’irrationalité est enseignée par Joseph Fourier (3) dans ses cours à l’École polytechnique en 1815 pour le nombre e, utilisant le développement de Taylor de la fonction exponentielle – cette méthode a été développée par Liouville trente ans avant qu’il n’exhibe les premiers exemples de nombres transcendants : par la méthode de Fourier, Liouville démontre l’irrationalité de e², puis il montre que ce nombre n’est pas quadratique, c'est-à-dire qu’il n’est pas solution d’une équation du second degré à coefficients rationnels. D’une certaine manière, on peut voir la démonstration de Hermite en 1873 comme une vaste généralisation de celles de Fourier et Liouville : au lieu d’approcher la fonction exponentielle par des polynômes, obtenus en tronquant le développement de la fonction exponentielle, Hermite va considérer des approximations par des fractions rationnelles.

C’est seulement un an après la publication du mémoire de Hermite que Georg Cantor introduira des arguments différents pour démontrer l’existence de nombres transcendants, basés sur sa théorie de l’infini. L’approche de Cantor connaîtra d’autres développements, conduisant à la théorie métrique de l’approximation diophantienne, dans laquelle on s'intéresse au comportement, du point de vue de l'approximation par des nombres rationnels, de "presque tous les nombres" (au sens de la mesure de Lebesgue – cela revient en quelque sorte à se demander ce qui se passe pour un nombre "pris au hasard").

Figure 1 :Un portrait de Charles Hermite (1822-1901) jeune, sur l’édition de ses œuvres complètes. Ces œuvres ont été éditées sous l’auspice de l’Académie des sciences, de 1905 à 1917, par son gendre Émile Picard, mathématicien, secrétaire perpétuel de l’Académie (cliché Alain Juhel).

- Irrationalité de e : L. Euler (1737) - Irrationalité de e^r pour r nombre rationnel non nul, de log s pour s rationnel positif, de la tangente d'un nombre rationnel non nul, ce qui donne notamment l'irrationalité du nombre Pi : J.H. Lambert (1761) - Démonstration de l'irrationalité de e par J. Fourier (1815), de e² par J. Liouville (1840) ; e² n'est pas quadratique. - Existence de nombres transcendants par J. Liouville (1844, 1852) - Le problème de la quadrature du cercle reste posé (les résultats de Wantzel sur les nombres constructibles datent de 1837).

Le mémoire de Hermite en 1873

Le résumé du texte de Hermite fait par le Dr Felix Müller (4) de Berlin dans le Jahrbuch der Mathematik (JFM 05.0248.01) est instructif. Il présente un problème qui peut être considéré comme une généralisation de la question de l’approximation diophantienne simultanée de nombres réels ou complexes : étant données des fonctions analytiques, on veut les approcher simultanément par des fractions rationnelles, ayant toutes le même dénominateur. L’approximation ici signifie que les développements de Taylor à l’origine auront les mêmes premiers termes. Müller poursuit en expliquant comment l’algèbre linéaire permet de s’assurer de l’existence d’une solution, sous des conditions naturelles concernant la qualité de l’approximation désirée, puis indique que l’auteur (Hermite) donne une solution explicite à ce problème dans le cas où les fonctions analytiques considérées sont des exponentielles. Dans ce résumé, Müller n’indique pas le résultat fondamental de l’article, qui est le fait que le nombre e est transcendant. Il est vrai que cet énoncé n’est formulé par Hermite qu’après 5 pages d’introduction (texte p. 22):

Je vais maintenant tenter d’aller plus loin à l’égard du nombre e, en établissant l’impossibilité d’une relation de la forme

N+ e^a N₁ + e^b N₂ +…+ e^h N_n =0,

a, b, …, h étant des nombres entiers, ainsi que les coefficients N, N1, …, Nn.

Avant de formuler cet énoncé, il a indiqué comment il allait procéder, et mis en lumière que cela lui fournissait aisément une nouvelle démonstration du résultat de Lambert, selon lequel l’exponentielle d’un nombre rationnel non nul est un nombre irrationnel. L’approche de Hermite est novatrice, même s’il fait preuve, dans une lettre datée de 1873 adressée à Borchardt (5), d’une modestie exemplaire :

Tout ce que je puis, c’est de refaire ce qu’a déjà fait Lambert, seulement d’une autre manière.

La manière est en effet bien différente, et la voie ouverte par Hermite conduit à des énoncés que la méthode de Lambert ne permet pas d’atteindre. Pour sa démonstration de l’irrationalité de l’exponentielle d’un nombre rationnel non nul, Hermite approxime la fonction exponentielle par une fraction rationnelle. L’existence de polynômes A et B, de degrés contrôlés tels que les développements de Taylor à l’origine des deux fonctions ez et A(z)/ B(z) aient les mêmes premiers termes, est facile à établir (voir encadré ci-après). Le premier tour de force de Hermite est de donner des formules explicites pour de tels polynômes. L’irrationalité de ea quand a est un nombre rationnel non nul découle facilement de ces formules, en utilisant un critère d’irrationalité très simple : soit x un nombre réel ; on suppose que pour tout 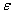> 0, il existe deux nombres entiers p et q avec q > 0 tels que 0 <|qx-p| < 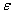. Alors x est irrationnel.

Figure 2 : Cour d’honneur de la Sorbonne (à gauche) et médaillon consacré à Charles Hermite, au-dessus d’une des portes (à droite). Hermite y fut titulaire de la chaire d’algèbre de 1871 à 1898 (cliché Alain Juhel).

 

Comme nous l’avons dit, après ce brillant début, Hermite annonce son intention d’aller plus loin en montrant que le nombre e ne vérifie aucune relation polynomiale – autrement dit le nombre e est transcendant. Il s’agit donc de montrer que les puissances consécutives de e sont des nombres linéairement indépendants sur le corps Q des nombres rationnels. Le critère d’indépendance linéaire que va utiliser Hermite est simple : soient x₁,…,x_n des nombres réels ; par définition, dire que les nombres 1,x1,…,x_n sont linéairement indépendants sur Q signifie que si a₀, a₁,…, a_n sont des nombres entiers non tous nuls, alors le nombre :

L = a₀+a₁x₁+…+a_nx_n

n’est pas nul. Pour cela, on cherche à approcher simultanément les nombres x₁,…,x_n par des nombres rationnels : si on montre l’existence de nombres entiers rationnels b₀, b₁,…, b_n tels que les quantités
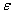_i = b₀x_i - b_i (i=1,…n) et R = a₁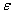₁+…+a_n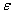n vérifient 0<|R|<1, alors L 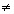0. Cela résulte de l’observation que le nombre

A= a₀b₀+a₁b₁+…+a_nb_n

est un entier rationnel satisfaisant b₀L= A+R.

Pour Hermite, les xi sont des puissances entières de e. Afin de les approcher simultanément par des nombres rationnels, Hermite recherche des approximations simultanées, par des fractions rationnelles, des puissances entières de la fonction exponentielle, puis substitue z = 1 dans ses formules analytiques.

Ainsi, une étape essentielle de la démonstration d’Hermite consiste à expliciter des fractions rationnelles, ayant le même dénominateur, qui approchent les fonctions exponentielles. La solution qu’il apporte à ce problème original est admirable : ce qu’il obtient est le premier exemple de ce qu’on appelle maintenant approximants de Padé, du nom de son disciple Henri Eugène Padé (1863-1953), qui développera systématiquement la théorie de l’approximation de fonctions analytiques par des fractions rationnelles. Les formules intégrales que produit Hermite sont maintenant classiques, elles ont de multiples applications.

Une fois que Hermite dispose de ces approximations par des fractions rationnelles et qu’il substitue z = 1 dans ces formules de façon à exhiber des approximations numériques, il lui reste une étape qui lui demande encore des efforts : dans le critère d’indépendance linéaire que nous avons énoncé, il est crucial de vérifier que le reste R n’est pas nul (6). On lit dans le texte (p. 77):

… on ne peut, en général, admettre que le déterminant proposé s’annule,…

Mais une autre voie conduira à une démonstration plus rigoureuse…

Ainsi Hermite n’arrive pas à démontrer que son déterminant n’est pas nul : cela lui suffirait pour conclure, mais il y a là une vraie difficulté. Pour la contourner, il lui faut développer de nouveaux arguments pour lesquels il cite le travail de Liouville en 1844, où l’existence de nombres transcendants a été démontrée.

IMPACT DU MÉMOIRE DE HERMITE

Je ne me hasarderai point à la recherche d’une démonstration de la transcendance du nombre . Que d’autres tentent l’entreprise. Nul ne serait plus heureux que moi de leur succès. Mais, croyez m’en, mon cher ami, il ne laissera pas que de leur en coûter quelques efforts.

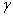
Avec le recul du temps, on peut considérer que toutes les idées nécessaires pour parvenir à ce résultat étaient pourtant en germe dans le mémoire de Hermite. 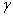Cependant, il ne faut pas oublier qu’il a quand même fallu près de dix ans pour que la méthode de Hermite soit généralisée de façon à s’adapter au nombre , et plus généralement à la démonstration du théorème de Hermite-Lindemann : si est un nombre algébrique non nul, alors e est un nombre transcendant. 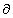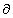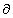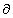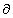De façon équivalente, si est un nombre algébrique non nul et si log est une détermination quelconque (7) (mais non nulle au cas où = 1) du logarithme de , alors log est un nombre transcendant.

Cet énoncé a été encore généralisé par Lindemann et Weierstrass en un résultat d’indépendance algébrique pour des valeurs de la fonction exponentielle en des points algébriques linéairement indépendants. La recherche de simplifications des démonstrations de Hermite et Lindemann occupera de brillants mathématiciens comme Adolf Hurwitz (1859-1919), Paul Gordan (1837-1912), David Hilbert (1862-1943) : en 1932, Henri Lebesgue fera une analyse pertinente de leurs apports respectifs. On peut maintenant donner des démonstrations très courtes de la transcendance de e (comme par exemple celle qui est donnée en annexe) et de , mais on ne comprendra vraiment ce qui se passe qu’en se référant au texte de Hermite.

Figure 3 : Charles Hermite (1822-1901), en 1887. Hermite était ancien élève de l’École polytechnique. Il avait épousé la soeur du mathématicien Joseph Bertrand (1822-1900), secrétaire perpétuel de l’Académie des sciences de 1874 à sa mort, et sa fille épousera le mathématicien Émile Picard (1856-1941), secrétaire perpétuel de l’Académie des sciences de 1917 à sa mort.

La méthode de Hermite, Lindemann et Weierstrass a été enrichie par les travaux de C.L. Siegel en 1929, avant que A.O. Gelfond et Th. Schneider ne démontrent la transcendance de nombres de la forme ab ou de la forme log a₁ / log a₂ pour a, b, a₁, a₂ nombres algébriques, résolvant ainsi le septième des problèmes de Hilbert (anticipé par Euler qui avait suggéré un tel énoncé – voir la fin de l’Introductio in Analysin Infinitorum (8)). La théorie des nombres transcendants s’est considérablement développée au XXè siècle, donnant lieu à de nombreuses applications, notamment par ses liens avec d’autres questions diophantiennes (approximation, géométrie, équations). D’une certaine manière, on peut considérer que toutes les méthodes de transcendance qui ont été développées après Hermite ont leurs racines dans son mémoire fondamental de 1873 : les idées essentielles s’y trouvent. Les outils élaborés ensuite font appel à de nombreuses branches des mathématiques, mais la stratégie de base est celle qui a été proposée par Hermite.

Mais la découverte d’Hermite qui surpasse toutes les autres, c’est la démonstration de la transcendance du nombre e, démonstration qui, à peine modifiée, entraîne la transcendance du nombre , c’est-à-dire l’impossibilité du fameux problème de la quadrature du cercle… … sa méthode sera admirée tant que des hommes existeront capables de comprendre la notion de nombre.

CONCLUSION

(1) Cette démonstration date de 1844 (voir texte BibNum correspondant).

(3) Cette démonstration de Fourier a été reprise par Janot de Stainville en 1812, voir le texte BibNum correspondant.

(4) Félix Müller (1843-1928) était un mathématicien et historien des mathématiques allemand.

(5) Karl Wilhelm Borchardt (1817-1880) était un mathématicien allemand, éditeur du Journal de Crelle à partir de 1856. La lettre de Hermite à Borchardt paraît dans cette revue lors du n°76, en 1873 (pp. 342-344) ; elle peut être vue en ligne dans la bibliothèque numérique de l’université de Göttingen.

(6) En effet, même si la démonstration conduit au fait que |R| < 1, on doit aussi vérifier R ≠ 0, car sinon la relation b₀L = A + R ne permet pas de conclure.

(7) Un nombre complexe t est un logarithme d'un nombre complexe non nul z si e^t = z. Tout nombre complexe non nul z admet une infinité de logarithmes, si l'un est t, les autres sont de la forme t + 2ik avec k entier rationnel (positif, négatif ou nul). Comme e⁰ =1, le seul nombre admettant t = 0 comme logarithme est z = 1.

(8) On peut se référer à http://www.math.dartmouth.edu/~euler/pages/E101.html pour ce texte.