Tout taupin connaît ou doit connaître la démonstration de l’irrationalité de e. En revanche, les circuits de transmission de sa démonstration fondée sur le développement de e en série est méconnu. C’est une étrange histoire, où l’on croise, entre autres, un répétiteur un peu fou de l’École polytechnique, un célèbre Baron et un certain Liouville.
STAINVILLE , POINSOT , FOURIER ET E
Nicolas Dominique Marie Janot de Stainville (1783-1828) est un polytechnicien de la promotion 1802. Dès 1810, il avait été nommé répétiteur adjoint à l’École polytechnique. Au moment, où paraissent ses Mélanges d'analyse algébrique et de géométrie, en 1815, Stainville passe une période difficile :
« En 1815 des raisons d’économie déterminèrent son excellence le ministre d’état de l’intérieur à supprimer deux places de répétiteurs adjoints, par suite de cette suppression Mr de Stainville demeurera sans traitement mais il n’en continue pas moins à remplir les mêmes fonctions avec le titre d’adjoint honoraire » [Janot de Stainville, Archives de l’École polytechnique AEP].
Stainville multiplie, en cette période, les tentatives pour avoir une stabilité professionnelle. Il explique, dans une lettre non datée expédiée « à son excellence le ministre secrétaire d’état de l’intérieur » :
« Les malheurs de la révolution ayant détruit mon patrimoine j’ai du chercher toutes mes refsources [sic] dans mes talents dans mes talents. Je me suis voué constamment à l’étude des sciences
(1) et au pénible exercice de l’enseignement. » [Janot de Stainville, AEP].
Il appuie ses demandes en insistant sur ses origines familiales — une famille vouée à la cause royale — et sur des appuis scientifiques venus des savants de premier ordre d’alors : Poinsot, Ampère, Delambre, Lacroix, Prony, etc. Il est reconduit dans ses activités de répétiteur.
Les Mélanges d'analyse algébrique et de géométrie de Stainville [Stainville, 1815], qui rendent hommage en préambule à Delambre, commencent par un avertissement dans lequel il explique ses intentions. L’ouvrage comprend une « table abrégée des matières », présentant « les principaux articles qu’il renferme » : des centaines d’articles fruits de lectures (Legendre, Lacroix, Laplace et Euler principalement) et de conseils de Poinsot, pour quelques uns.
C’est le cas de la note 232. Dès le début de sa note, Stainville annonce l’objectif :
« Après avoir trouvé une valeur approchée du nombre e, il est bon de le considérer en lui-même, et de faire voir que non seulement il est compris entre 2 et 3, mais qu’aucune fraction rationnelle comprise entre ces deux nombres ne peut le représenter ». [Ibid.]
Il articule sa démonstration en deux parties. Son premier travail consiste à encadrer e entre 2 et 3 en partant du développement de e:
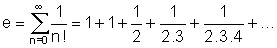
Il remarque d’abord que e est plus grand que 2 puisque la somme des deux premiers termes vaut 2 et tous les autres termes sont positifs. Ensuite, il majore le terme général par 1/22, autrement dit :
e est plus petit que
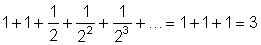
(en effet la série géométrique de premier terme ½ et de raison ½ vaut 1).
Dans un second temps, Stainville établit l’irrationalité en procédant ainsi :
« Je dis en second lieu, qu’aucune fraction rationnelle ne peut le représenter, car si une fraction irréductible m/n lui était égale, on aurait
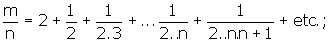
mais si on multiplie les deux membres de cette équation par le produit 1.2..n de la suite naturelle des nombres, jusqu’à celui qui indique le dénominateur de la fraction qui se trouve dans le premier membre, on aura
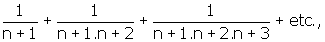
Comme précédemment, la dernière série est majorée par :
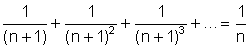
Il en déduit le raisonnement suivant :
« le premier membre est un nombre entier, il s’ensuivrait que si à un nombre entier on ajoutait une fraction moindre que 1/n, le résultat serait un nombre entier, ce qui est absurde ; donc il est également absurde de supposer que le nombre e soit rationnel, donc il est irrationnel. » [Ibid.]
Ensuite, Stainville explicite l’origine de la note dans un nota bene : « Cette démonstration m’a été communiquée par M.Poinsot, qui m’a dit la tenir de M. Fourier. » [Ibid.] Cette démonstration de l’irrationalité de e par le développement en série de l’exponentielle aurait donc été transmise par Poinsot, via cet ouvrage de 1815 de Stainville, sans doute peu diffusé (2). Nous ignorons dans quelle circonstance Fourier a donné cette démonstration. Il paraît peu probable qu’elle ait été publiée. Y a-t-il des traces écrites ou Fourier l’a-t-il seulement communiqué oralement (3) ?
Dans son dernier article paru dans les
Annales de Gergonne intitulé « Démonstration d’un point de calcul algébrique très important et très remarquable, et des principales conséquences qui en résultent » [Stainville, 1818-1819], Stainville mentionne : « La série du premier membre est, comme l’on sait, un nombre incommensurable, compris entre 2 et 3 : c’est la base du système de logarithmes népériens » [
Ibid., 239]. Dans une note de bas de page, pour des détails sur la démonstration, il renvoie à un autre article paru dans le même tome des
Annales. L’article en question est dû à Jean, Jacques Bret
(4), « professeur à la faculté des sciences de Grenoble, Chevalier de l’Ordre royal de la Légion d’honneur ». Dans cet article [Bret, 1818-1819], l’auteur développe une « théorie générale des fractions continues » et démontre qu’effectivement e ne peut pas être rationnel [Ibid., 50], « incommensurable » comme on le disait plus fréquemment à l’époque. Curieusement, Stainville ne fait pas allusion à la démonstration qu’il a publiée mais à une démonstration de Bret ; cette démonstration n’est pas celle de Fourier, c’est une démonstration qui repose sur la preuve historique de Euler, à base de fractions continues.
Gergonne critique les considérations « longue[s] et laborieuse[s] » [Gergonne, 1818-1819] de Bret et fait référence au mémoire de Stainville, à deux reprises, en 1818-1819 [Ibid.] et en 1822-1823 [Gergonne, 1822-1823]. C’est la dernière référence à Stainville dans un journal mathématique : il est interné depuis plusieurs années — après avoir été exclu de l’Ecole polytechnique en 1821 pour cause d’aliénation mentale — à l’asile de Charenton où il décède en 1828.
LES EXTENSIONS DE LIOUVILLE
Liouville, dans ses travaux autour de l’irrationalité dans les années 1840, ne cite ni Fourier ni Stainville. Il se contente de préciser en préambule de son premier article sur le sujet en 1840 : « Le nombre e, base des logarithmes népériens, n’a pas une valeur rationnelle. » [Liouville, 1840a, 192]
Liouville étend l’irrationalité de e de la manière suivante :
« e ne peut pas être racine d'une équation du second degré à coefficients rationnels, en sorte que l'on ne peut pas avoir a e + b/e = c, a étant un entier positif et b, c, des entiers positifs ou négatifs. » [Ibid.].
Dit autrement, Liouville, dans sa courte note montre que e n'est pas quadratique. Pour ce faire, il utilise les développements de l'exponentielle :
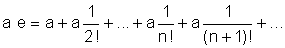 (1)
(1)
Or
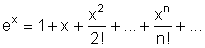
appliquée à x = -1 donne :
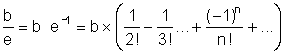 (2)
(2)
En ajoutant (1) et (2), et en multipliant par n!, l’équation ae + b/e = c devient :
a/(n+1) (1+1/(n+2) + ...) + (-1)n+1 b/(n+1) (1 - 1/(n+2) + ...) = n!c – a(n! +n!/2! + n!/3!….+n!/n!) - b (n!/2! -n!/3! + …. (-1)n n!/n!)
Le second membre de l'équation est effectivement un nombre entier relatif que Liouville nomme µ:
a/(n+1) (1+1/(n+2) + ...) + (-1)n+1 b /(n+1) (1 - 1/(n+2) + ...) = µ
Il poursuit en affirmant: « On peut toujours faire en sorte que le facteur +/- b/(n+1) soit positif » en explicitant : « il suffira de supposer n pair si b est < 0 et n impair si b est > 0. » [Liouville, 1840a]. En effet, le signe de b est en fait (1)n+1 ce qui légitime les affirmations de Liouville.
Il effectue ensuite un passage à la limite :
« en prenant de plus n très grand, l'équation que nous venons d'écrire conduira dès lors à une absurdité ; car son premier membre étant essentiellement positif et très petit, sera compris entre 0 et 1, et ne pourra pas être égal à un entier µ. Donc, etc. » [Ibid.]
Le texte de Liouville mérite quelques explications supplémentaires
(5) afin de justifier pourquoi la limite du membre de gauche est nulle. La justification de l'affirmation de Liouville réside dans le fait que la série (1+1/(n+2) + ...) qui est plus exactement la série (1+1/(n+2) + 1/(n+2)(n+3) + ….) est une série positive vérifiant le critère de d'Alembert
(6), elle est donc, de ce fait, convergente. Il en résulte que son terme général a/(n+1) (1+1/(n+2) + ...) tend vers 0 quand n tend vers l'infini. De même la série (1 - 1/(n+2) + 1/(n+2)(n+3)...) est absolument convergente
(7), d'où la conclusion de Liouville, démontrant ainsi que l’équation ae = b/e = c conduit à une absurdité, donc que e n’est pas un nombre quadratique.
En utilisant la même trame, plus technique tout de même, Liouville ouvre le cahier de juin 1840 de son Journal, en prolongeant son résultat à e²:
« On peut étendre au carré du nombre e le théorème que nous avons démontré dans le dernier cahier de ce Journal; en d'autres termes, on peut prouver que l'équation a e2 + b e-2 = c est impossible, a désignant un entier positif, et b, c, des entiers positifs, nuls ou négatifs. » [Liouville, 1840b, 193].
Dans ces notes de Liouville, nous retrouvons une stratégie
(8) qui intervient à chaque fois dans les démonstrations élémentaires de transcendance : une quantité strictement positive est égale, d’une part, à un entier (µ dans l’exemple ci-dessus); d’autre part cette quantité tend vers 0 quand n croît. Il en résulte qu'au bout d'un certain rang, elle est comprise strictement entre 0 et 1, et ne peut donc être entière : on est conduit à une absurdité. Après ces travaux autour de l’irrationalité de e, Liouville abandonne ce champ d’études pendant quelques années. Il y revient dès 1844 avec le succès que l’on sait, c’est-à-dire sa découverte de nombres transcendants : « ses » nombres dit aujourd’hui de Liouville
(9).

BIBLIOGRAPHIE CONTEMPORAINE DE STAINVILLE
Bret, Jean, Jacques 1818-1819. Théorie générale des fractions continues, Annales de Mathématiques Pures et Appliquées, 9 (1818-1819), 37-51.
Gergonne, Joseph-Diaz 1818-1819. « Recherches sur les fractions continues », Annales de Mathématiques Pures et Appliquées, 9 (1818-1819), 261-270. 1822-1823. « Extension et démonstration nouvelle du théorème de M. de Stainville, présentée à la page 229 du IXe volume du présent recueil », Annales de Mathématiques Pures et Appliquées, 13 (1822-1823), 270-276.
Liouville, Joseph 1840a, « Sur l'irrationalité du nombre e = 2,718 … », Journal de Mathématiques Pures et Appliquées , I, 5 (1840), 192. 1840b. « Addition à la note sur l'irrationalité du nombre e », Journal de Mathématiques Pures et Appliquées, I, 5 (1840), 193-194.
(Janot de) Stainville Nicolas Dominique Marie 1809. Recueil de problêmes résolus par des considérations purement géométriques, Courcier. 1815. Mélanges d'analyse algébrique et de géométrie, Paris, Veuve Courcier, 1815. 1818-1819. « Démonstration d’un point de calcul algébrique très important et très remarquable, et des principales conséquences qui en résultent », Annales de Mathématiques Pures et Appliquées, 9 (1818-1819), 229-240.
(1) Dès 1809, Stainville avait, en effet, fait paraître chez Courcier son
Recueil de problèmes résolus par des considérations purement géométriques [Stainville, 1809].
(2) Il ne se trouve, en France, que dans 3 bibliothèques, à Grenoble, à la Bibliothèque Sainte-Geneviève et à la BNF. Cependant, il a traversé la Manche puisque, Giovanni Percij, dans une lettre à Talbot, datée du 31 octobre 1823 et faisant partie du fonds Talbot au Fox Talbot Museum, précise que l'ouvrage de Stainville appartient à la bibliothèque de la
« London Residence of the Feildings », 31, Sackville Street, à Londres. Stainville bénéficiait-il des réseaux royalistes installés à Londres ? Nous possédons un exemplaire de l’ouvrage de Stainville.
(3) Nous avons contacté Louis Charbonneau (UQAM, Quebec) qui a consacré de nombreux travaux à Fourier depuis sa thèse en 1976 (
L’œuvre mathématique de Joseph Fourier, EHESS, 1976) et que nous remercions pour les points de vue échangées autour de l’œuvre de Fourier. A sa connaissance, il n’existe aucune trace écrite de Fourier sur ce sujet.
(4) Professeur de mathématiques transcendantes au lycée puis à l’Université de Grenoble, Jean, Jacques Bret fait partie de cette première génération de polytechniciens (promotion 1800) qui opte pour l’enseignement. Il publie de nombreux articles dans les
Annales de Gergonne et dans le
Journal de l’Ecole polytechnique.
(5) L'article a sûrement été composé pour tenir en une page afin d'achever le cahier de mai 1840.
(6) Si une série positive de terme général u
n est telle que le rapport de deux termes consécutifs u
n+1/u
n tend vers un nombre strictement inférieur strictement à 1 alors elle est convergente. Si la limite obtenue est strictement supérieure à 1, elle est divergente. Si elle vaut 1, on ne peut pas conclure.
(7) Si une série de terme général u
n est telle que la série de terme général « valeur absolue de u
n » converge, on dit que la série est « absolument convergente ». On démontre que l’absolue convergence entraîne la convergence.
(8) Nous remercions François Gramain, Michel Serfati & Michel Waldschmidt pour les échanges à propos des démonstrations élémentaires de transcendance lors de la journée de séminaire de Michel Serfati (consacrée à la transcendance), à l’Institut Henri Poincaré, le 17 novembre 2004.
(9) voir article Bibnum correspondant.
 Dans ce court texte de trois pages, Stainville nous redonne une démonstration lumineuse du caractère irrationnel de e, la base des logarithmes népériens.
Dans ce court texte de trois pages, Stainville nous redonne une démonstration lumineuse du caractère irrationnel de e, la base des logarithmes népériens.![]()
![]()
![]()
![]()
![]()
![]() (1)
(1)![]()
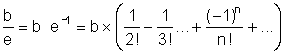 (2)
(2)








