La mécanique classique et la théorie de la relativité

L’histoire de la relativité générale ne comporte pas de trace de contributions de scientifiques français. Est-ce à dire qu’ils sont complètement passés à côté de ce pilier de la physique contemporaine ? Au contraire, mais peut-être ont-ils eu le tort d’avoir eu raison trop tôt, comme en atteste la contribution de Painlevé, entre autres, dont tout l’intérêt n’a été compris que dans les années 2000 !

La relativité générale et l’académie des sciences (1921-1924)

Einstein publie ses équations définitives en novembre 1915, en plein conflit mondial, alors qu’il est professeur à Berlin. Inutile de dire que dans ces conditions, l’Académie des Sciences, d’ailleurs mobilisée pour l’effort de guerre, se soucie peu de cette publication.

La situation va commencer à changer en 1921, d’une part du fait que Herman Weyl, grand mathématicien reconnu, consacre une partie de son ouvrage « Zeit-Raum-Materie » à la relativité générale, traduit en français en 1922 sous le titre « Temps-Espace-Matière » [1] et d’autre part parce qu’Einstein est récompensé par le prix Nobel (mais pas pour la relativité générale).

Vis-à-vis de cette nouvelle théorie, l’Académie des Sciences va montrer une grande défiance (Le Roux [2], [3]), qui va cependant évoluer dans le temps. Paul Langevin, convaincu que le temps de la réconciliation était venu, du moins entre scientifiques, est le premier en novembre 1921 ([4]) à prendre la défense de la théorie de la relativité générale. Un débat assez vif, mais non stérile, se développe, avec 12 contributions sur la relativité générale en 1921, 19 en 1922 et 9 en 1923. Langevin, ambassadeur compétent et efficace, continuera à créer progressivement un courant favorable aux idées d’Einstein au sein de l’Académie.

Dans ce contexte, Paul Painlevé se propose, dans un premier compte rendu à l’Académie des Sciences le 24 Octobre 1921 ([5]), de faire un état des lieux et de comparer les deux théories, celle de Newton et celle d’Einstein. Ce premier article, assez critique, mais constructif, est une annonce du travail qu’il va présenter de manière plus détaillée dans un deuxième article, peu de temps après, le 14 novembre 1921 ([6]). Il en fera un troisième en mai 1922 ([7]), après un débat avec Einstein et ses collègues, au Collège de France, pendant la visite d’Einstein à Paris (30 Mars-7 avril 1922). Rappelé par sa carrière politique, il se retirera du débat après le 1^er Mai 1922. Sa contribution se sera faite sur une période limitée à 6 mois.

Il a été qualifié de piètre relativiste. S’il est vrai qu’il n’avait pas accepté certains fondements de la théorie, cela ne le dessert pas, car en tant que mathématicien il en avait compris le mode d’emploi et, libre de toute contrainte, il bouscule les limites conceptuelles existantes à l’époque, au point qu’il sera totalement incompris de ses contemporains et que lui-même, quelque peu dépassé, ne saura en assumer l’héritage.

Au-delà de certains aspects polémiques, la contribution de Painlevé comporte plusieurs propositions originales.

Un formalisme géométrique de la gravitation newtonienne d’où émerge un temps physique

Pour le problème du champ gravitationnel à l’extérieur d’un corps matériel unique à symétrie sphérique, afin de permettre une comparaison efficace de la gravitation newtonienne et de la gravitation relativiste, comme cette dernière est une théorie géométrique de la gravitation, Painlevé propose un formalisme également géométrique mais strictement spatial (sans référence au temps) pour la gravitation newtonienne. Ainsi dans son article de novembre 1921, il indique :

Il suit de là, comme on voit, qu’on peut donner à la théorie de la gravitation newtonienne la forme suivante (principe de la moindre action) : Les trajectoires du point P sont les géodésiques du ds² 

ds² = (U+h) (dx²+ dy² + dz²)              (h constante arbitraire)

où U est une fonction de x, y, z qui s’annule à l’infini dont le ΔU est nul à l’extérieur de la sphère S et est égal à une constante négative dans S.

U est le potentiel newtonien et h une constante. On remarque que cette équation, purement spatiale, sans facteur temps, décrit le ds² euclidien affecté du facteur conforme (U+h).

Ce facteur joue ici le rôle d’une jauge au sens où H. Weyl le définit à cette époque. En effet, si l’on définit souvent la géométrie spatiale de la trajectoire (plane) en coordonnées polaires par l’équation r(φ), on peut aussi la définir de manière paramétrique r(λ) et φ(λ) où λ est le paramètre affin de cette trajectoire. Comme l’équation r(φ) suffit à définir la courbe spatiale, le paramètre λ est libre et Painlevé peut y appliquer (U+h), comme jauge ce qui rend λ proportionnel au temps propre τ d’un corps réel décrivant cette trajectoire. On peut montrer que dans ce cas ne dépendant pas du temps où l’énergie est conservée, sous réserve de poser τ = iλ, où i² = -1, cette formulation unifiée pourtant strictement spatiale, donne le même résultat spatial (des coniques) et temporel (τ = t) que celui de la mécanique newtonienne qui nécessite deux équations dont l’une dépend du temps universel newtonien t (loi des aires).

Trois propriétés remarquables s’en déduisent

1. Le formalisme est unifié : Une seule équation décrit la géodésique au lieu de deux.

En formalisme newtonien, où le temps est universel et indépendant de l’espace, deux équations sont nécessaires pour décrire le mouvement géodésique : celle qui décrit la géométrie spatiale (une conique qui peut être dégénérée) et celle qui décrit le mouvement géodésique sur cette courbe spatiale (loi des aires). Une seule équation est nécessaire dans le formalisme géométrique proposé par Painlevé.

2. Le concept capital d’un temps (propre) émergeant des équations strictement spatiales.

Cette contribution est remarquable. Ce temps, qui ne fait pas référence au temps universel newtonien, émerge de la physique puisque c’est l’application du facteur conforme (U+h) sur le paramètre affin, agissant en tant que jauge associée au champ gravitationnel, qui le détermine. Ce paramètre affin, temps propre d’un observateur décrivant la géodésique déterminée par la gravitation, en est le paramètre dynamique. C’est une avancée majeure dans la compréhension de la nature du temps en physique. Le débat philosophique de la primauté de deux concepts parmi ceux de temps, d’espace et de mouvement, qui sont liés par une relation, trouve ici une solution semblable à celle que la relativité proposera. La méthode de Painlevé imposant à la mécanique classique des habits relativistes, pour comparer les deux théories, jette un pont formel entre elles, qui en révèle certains caractères communs.

3. Ce temps propre apparaît comme « imaginaire » dans les équations, confortant la forme relativiste.

En effet, dans l’équation unifiée le temps apparaît naturellement (avec un facteur i) par rapport à l’espace (i² = -1). Ceci montre que quand on veut unifier le temps et l’espace dans les équations, ces deux concepts se différencient par cette propriété, comme en relativité.

Généralisation de ce formalisme à la relativité générale

Painlevé généralise ce formalisme à la relativité générale ([7]) en l’adaptant à un espace non euclidien, la métrique spatiale euclidienne étant remplacée par une métrique spatiale non euclidienne. Sa généralisation sera incorrecte, ce qui montre que la théorie newtonienne et la théorie einsteinienne sont différentes. La phénoménologie relativiste inclut un auto-couplage entre la masse active et la masse passive d’un corps et impose une vitesse finie constante à la lumière¹, impliquant que le ds² contienne la coordonnée temporelle et converge, localement, vers celui de la relativité restreinte, propriétés absentes en mécanique classique. Mais ces deux théories sont équivalentes (pour cette solution) pour les géodésiques suivies par la lumière, du fait qu’elle échappe à ces différences. Cette équivalence signifie que la structure causale est identique.

La forme relativiste de Painlevé

Dès son premier article, Painlevé propose une forme nouvelle de métrique alternative à celle proposée par Schwarzschild :

Cette hypothèse admise, les einsteiniens parviennent au ds² (quatre variables) aujourd’hui célèbre, dont les géodésiques définissent dans leur théorie le mouvement du point gravitant, à savoir

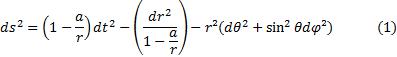
Mais ce ds² n’est pas le seul qui réponde à toutes les conditions einsteiniennes. Il en est une infinité d’autres dépendant de deux fonctions de r et le choix de la formule (1) entre toutes ces formules est purement arbitraire. Parmi ces formules il en est d’aussi simples que la formule (1) et qui entraînent exactement les mêmes vérifications. Telles que celle-ci² :

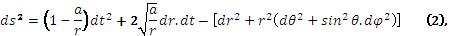
où a désigne une constante arbitraire que déterminera la masse du centre matériel O.

Painlevé établit la première forme de métrique à ce problème, non singulière sur l’horizon (aucune valeur de r ≠ 0 ne rend l’expression infinie) ! La singularité sur « l’horizon » de la forme de Schwarzschild donnait bien du souci aux relativistes qui cherchaient à l’éluder en la considérant comme un artefact mathématique. Eddington déclarait même que la nature ne pouvait pas permettre une telle monstruosité. La forme proposée par Painlevé est la première, dans l’histoire de la relativité, qui, à la différence de celle de la forme de Schwarzschild, est non singulière sur l’horizon. Painlevé expliquera dans le deuxième article comment il établit cette équation.

La solution de Painlevé, dont le terme non quadratique (celui qui contient dr.dt) invoque une orientation de l’espace-temps, ne sera pas comprise par ses contemporains alors que, dans ce type de coordonnées sphériques, cette orientation est impliquée par le caractère «unidirectionnel » du franchissement de l’horizon

Il est vrai qu’à l’époque, la singularité sur l’horizon dans la forme de Schwarzschild semblait le désigner comme une barrière infranchissable et le souci d’Einstein et des relativistes était plutôt de prouver son impossibilité physique, comme nous le verrons.

Si la forme de Painlevé avait été comprise, cela aurait ouvert, tout grand, les portes à l’approche moderne de la solution. Mais manifestement ce concept d’orientation de l’espace-temps était trop innovant, même pour son auteur qui n’a pas su bien le défendre.

La méthode utilisée par Painlevé pour construire sa forme de métrique

En tant que mathématicien, Painlevé a bien compris comment on doit dériver une équation conforme à la relativité générale. Il part donc d’une forme générique à symétrie spatiale sphérique qu’il va contraindre par l’équation d’Einstein.

En vertu des postulats précédents, si on adopte le repérage des observateurs de S, à savoir les coordonnées polaires de l’espace de centre O et le temps ordinaire, ce ds² doit être de la forme³ :

Quelles que soient d’ailleurs les fonctions A, B, C, D de r que l’expérience nous conduirait à adopter, il serait toujours possible de former des conditions invariantes auxquelles devraient satisfaire les coefficients de ds² quand on y remplace r, θ, φ et t en fonction de 4 variables entièrement quelconques.

Painlevé va contraindre sa forme générale par l’équation d’Einstein pour obtenir une solution relativiste :

Mais Einstein veut a priori que ces conditions invariantes soient des dérivées partielles du deuxième ordre d’une forme spéciale, qui s’inspirent à la fois des théories de la gravité newtonienne en coordonnées curvilignes, et de la théorie de la courbure des surfaces ordinaires.

Ce sont ces restrictions capitales et non le truisme pur et simple de l’invariance, qui parmi les ds² de la forme (3) ne laissent subsister que les suivants :

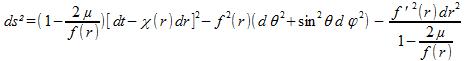
où µ est une constante et où f(r) et χ(r) sont deux fonctions arbitraires de r telles seulement que χ(r) tende vers zéro et f '(r) (toujours positif) tende vers 1 lorsque r tend vers l’infini.

Painlevé propose la forme la plus générale de solution au problème posé

Cette dernière équation donne la forme relativiste la plus générale de la solution au problème du champ extérieur à une masse à symétrie sphérique. En effet, quelles que soient les fonctions f(r) et χ(r), elles satisfont identiquement l’équation d’Einstein.

On peut observer que si on pose χ(r) = 0 et f(r) = r, soit f '(r) = 1, on obtient la forme de Schwarzschild et que si on pose χ(r)= (2M/r)^1/2(1-2M/r)^-1 et f (r) = r, cette forme générique donne la solution que Painlevé avait proposée dans son article d’octobre 1921, ce qui montre que cette dernière équation est correcte et génère au moins ces cas particuliers.

Painlevé déduit donc directement de considérations de symétrie et des équations d’Einstein une classe de solutions dont certaines non singulières sur l’horizon, et ceci plus de 10 ans avant Lemaître. C’est un élément totalement méconnu dont il faut lui rendre justice.

Les débats au Collège de France avec Einstein au printemps 1922

En novembre 1921, Painlevé écrit à Einstein pour lui présenter ses critiques et sa solution et l’inviter à en débattre avec lui et ses collègues de l’Académie des Sciences. Dans une lettre du 7 décembre, Einstein répond aux critiques mais ayant des engagements explique qu’il ne peut pas se rendre à Paris rapidement⁴.

Il viendra au printemps 1922 et fera une série de conférences-débats du 31 mars au 7 avril. Charles Nordmann fera un compte-rendu des discussions : « Einstein expose et discute sa théorie » publié dans la Revue des Deux Mondes [8].

Charles Nordmann commence par souligner que la prestation d’Einstein au Collège de France, à l’invitation de Paul Langevin, a été un évènement sans précédent. Aux États-Unis, à Londres, en Italie où Einstein avait été reçu dans les mois précédents, il s’était contenté de faire un exposé ex cathedra sous forme d’un monologue non contradictoire.

Figure 3 : (à g.) Couverture de L’Illustration du samedi 1^er avril 1922 lors de la visite d’Einstein à Paris, avril 1922 ; (à dr.) Paul Langevin et Einstein au cours de cette visite.

L’estime d’Einstein pour l’école scientifique française brillamment représentée par Langevin et ses amis, dont Painlevé, est réciproque. À témoin, un groupe d’académiciens, dont Painlevé, militaient au sein de l’Académie des Sciences pour proposer à Einstein un poste de correspondant qui allait être vacant prochainement, au grand dam d’un membre influent de l’Académie qui estimait qu’il était hors de question d’offrir cela à « celui qui a détruit la mécanique ».

À Paris, Einstein fera l’effort de s’exprimer en français et adoptera une attitude résolument dialectique, argumentera de manière contradictoire avec ses interlocuteurs, les laissera débattre entre eux, sous son arbitrage, dans le souci d’aller au fond des choses et de pas laisser de zone d’ombre.

La séance d’ouverture le 30 mars se déroulera devant un public nombreux et enthousiaste, le Collège de France ayant largement ouvert ses portes aux hommes de sciences mais aussi à des étudiants.

Figure 4 : La foule se pressant aux portes du Collège de France pour assister à une conférence d’Einstein. À droite de la grille, on devine Painlevé filtrant les entrées (image Gallica BnF)

D’autres séances plus techniques suivront devant un public plus restreint mais plus spécialisé dans le domaine et s’apparenteront plutôt à des groupes de travail⁵. C’est ainsi qu’il faut considérer les discussions avec Painlevé, en présence notamment de H. Becquerel, M. Brillouin, E. Cartan, T. De Donder, J. Hadamard, P. Langevin et C. Nordmann.

Figure 5 : Einstein et Painlevé (dessins L’Illustration à gauche, Lucien Jonas à droite).

Le problème de l’horizon dans la solution du corps unique à symétrie sphérique

Figure 6 : Einstein exposant le problème de l’horizon devant une audience restreinte attentive. Painlevé est assis à côté de l’extrémité gauche du tableau.

Voici des extraits de la narration que fait Charles Nordmann de cette réunion de travail en cercle restreint :

C’est Monsieur Hadamard qui est professeur de mécanique céleste au Collège de France qui ouvre le débat avec une question relative à la formule avec laquelle Einstein exprime la nouvelle loi de la gravitation universelle. Dans cette formule, en utilisant la forme simple que Schwarzschild lui a donnée et qui répond aux besoins pratiques de l’astronomie, il existe un certain terme qui intrigue Monsieur Hadamard, du fait que le dénominateur de ce terme peut devenir nul, ceci signifiant que ce terme devient infini et que cette formule devient singulière et, du moins, on peut se demander quel peut bien être cette signification physique et comment cela pourrait-il se produire dans la nature. Ce n’est pas le cas du Soleil mais ce serait peut-être le cas d’une étoile qui pourrait être beaucoup plus massive que lui.

Einstein ne cache pas le fait que cette question profonde est quelque chose qu’il trouve très embarrassant et il confirme que, si ce terme peut effectivement devenir nul quelque part dans l’univers, ce serait un désastre inimaginable pour la théorie et qu’il serait difficile de dire a priori ce qui pourrait advenir du point de vue physique car cette formule cesserait d’être valable. Ce serait une catastrophe qu’Einstein, en plaisantant, appelle la « catastrophe d’Hadamard » et dans ce cas on se demande quels pourraient bien en être les effets physiques.

Charles Nordmann intervient alors pour donner quelques précisions sur des étoiles très massives connues, comme Bételgeuse dont le diamètre vaut 300 Soleils⁶ mais qui est loin de satisfaire au critère redouté⁷. Il signale que, selon les travaux de l’astronome anglais Eddington : quand la masse d’une étoile a tendance à s’accroître de plus en plus, du fait de l’attraction gravitationnelle, la température intérieure de cette étoile croît de façon importante et le rayonnement produit tend à la faire exploser. En conséquence, il semble qu’il soit dans la nature des choses qu’une limite insurmontable soit atteinte dans l’accroissement de la masse d’une étoile ce qui devrait nous protéger contre la « catastrophe d’Hadamard » qui ne devrait jamais se produire parce que les conditions d’existence de telles étoiles ne pourraient jamais être satisfaites.

Einstein répondit qu’il n’était pas entièrement rassuré par ces calculs qui impliquent différentes hypothèses. Il préférait s’appuyer sur d’autres moyens pour échapper aux inconvénients de la catastrophe d’Hadamard représentés dans cette théorie.

Effectivement dans la session suivante, le 7 avril, il apporta le résultat d’un calcul qu’il avait fait concernant ce point particulier qui montre que si le volume s’accroît indéfiniment sans accroître la densité, ce qui serait le cas pour une sphère d’eau, la pression au centre de la masse deviendrait infinie, et cela arriverait bien avant que les conditions de la catastrophe d’Hadamard soient remplies.

Dans ces conditions conformément à la théorie de la relativité générale, les horloges se figent et plus rien ne peut se produire, ce serait la « mort » et en conséquence tout changement capable d’apporter la catastrophe d’Hadamard deviendrait impossible.

Monsieur Hadamard, dans ces conditions se déclara lui-même satisfait et pensait qu’il était impossible que cette catastrophe si redoutée se produise.

Painlevé saisit cette occasion pour demander à Einstein des éclaircissements sur d’autres conséquences de sa théorie en particulier sur les grandeurs mesurables physiques comme les distances au Soleil. Un débat contradictoire brillant et animé digne d’une compétition sportive s’ensuivit sur la signification physique des équations. Brillouin incapable de s’exprimer dans ce tumulte s’empare alors du tableau et, craie à la main, y inscrit ses propres contributions, restaurant l’attention d’un public haletant et quelque peu perturbé !...

Einstein, qui écoutait silencieusement, indifférent au tumulte, demanda poliment la parole. Ceci détendit l’atmosphère, et le silence revenu, il ne lui fallut que quelques minutes, pour convaincre les intervenants et réduire les principales objections...

Figure 7 : Banquet à la maison des polytechniciens en l’honneur d’Einstein, lors de sa visite d’avril 1922. On reconnaît Langevin, à droite d’Einstein, et Marie Curie, qui tourne la tête à l’objectif (photo droits réservés ESPCI)⁸.

La solution de Painlevé ignorée

On voit que l’enthousiasme des participants a généré une certaine confusion dans ces débats, et que les problèmes sur l’horizon, que la forme de Painlevé permettait de supprimer, n’ont pas été traités en profondeur, mais éludés au motif que la formation d’un horizon n’était pas possible physiquement.

Cette forme, dont le terme non quadratique implique une orientation de l’espace-temps, nécessaire dans ce type de coordonnées, pour être non singulière sur l’horizon puisque celui-ci se comporte comme une membrane unidirectionnelle (peut être franchi dans le sens entrant mais pas sortant), n’a pas été comprise à l’époque. Elle offre pourtant une description naturelle de la solution du champ du corps unique à symétrie sphérique, et en révèle les symétries profondes et certains attributs qu’elle partage avec la mécanique newtonienne sans s’y confondre pour autant. À ce titre, la forme de Painlevé peut être considérée comme une passerelle entre la mécanique classique et la relativité générale.

Cette opportunité a été manquée et la forme remarquable de Painlevé sera mise aux oubliettes de l’histoire pour 80 ans environ. 

Les débats à l’Académie des sciences

Comme nous l’avons indiqué, l’Académie des Sciences avait ignoré la relativité générale jusqu’en 1921, année où Einstein obtient le prix Nobel de physique qui lui sera remis en 1922. Si ce prix ne lui est pas attribué pour la relativité générale, ce qui montre que cette théorie était loin d’être acceptée à l’époque, cela lui confère une notoriété que l’Académie des Sciences ne peut ignorer.

De par sa constitution, l’Académie des Sciences est une institution plutôt conservatrice. Certains membres de l’Académie, parmi les plus influents, sont très hostiles à la théorie de la relativité générale qu’ils considèrent comme destructrice de la mécanique classique. Ce courant, dont Jean Le Roux, auteur d’une multitude de notes visant à disqualifier la théorie d’Einstein, est le membre le plus actif, est majoritaire surtout au début. Mais on verra apparaître rapidement un courant, animé par M. Brillouin, de scientifiques séduits par cette approche nouvelle et constructive de la gravitation permettant d’explorer autrement l’univers.

La contribution de Painlevé débutant octobre 1921, consécutive à une critique très virulente par M. Le Roux de la relativité générale, avait pour objet de « modérer » le débat puisqu’il se proposait de faire une étude critique comparative des deux théories à l’usage de ses collègues assez désemparés par cette nouvelle théorie. Si, de par sa formation, il lui était difficile d’être vraiment objectif, c’était une tentative estimable et qui comme nous l’avons vu s’est révélé hautement constructive. Elle a pu servir de pivot aux réactions qui ont suivi.

La controverse menée par Le Roux

La controverse, nourrie, peut être illustrée par quelques exemples d’échanges assez vifs entre les chefs de file des deux camps. Pour donner le ton, citons le début du premier article de Jean Le Roux (1863-1929, professeur à la faculté des sciences de Rennes) en mai 1921 ([2]) :

On a considéré comme une confirmation éclatante de la théorie de la relativité la découverte d’une loi de la gravitation susceptible d’expliquer le mouvement du périhélie de Mercure.

Une critique judicieuse constate que ce résultat a bien été obtenu à propos de la théorie de la relativité, mais qu’il n’en est pas une conséquence et ne constitue même pas un argument en sa faveur.

Le Roux poursuivra sa critique destructrice dans de nombreux autres articles, par exemple en novembre 1922 ([3]) :

Les résultats fournis par la théorie de la gravitation d’Einstein ont semblé, au premier abord, concorder remarquablement avec l’observation particulièrement dans le cas du mouvement séculaire du périhélie de Mercure. Cependant, pour arriver à cette conclusion, on est obligé d’admettre que les perturbations dues aux actions mutuelles des planètes conservent dans la théorie d’Einstein les mêmes valeurs que dans la mécanique classique. Si l’on supprime les perturbations, la concordance disparaît. Or il arrive que l’hypothèse fondamentale d’Einstein est incompatible avec l’existence des actions mutuelles et des perturbations telles qu’on les considère dans la mécanique classique.

Et concluant son article ainsi :

La confrontation avec l’expérience dans le cas particulier du mouvement de Mercure donne lieu aux constatations suivantes. L’avance séculaire constatée est de 574''. La théorie de Newton qui entraîne les perturbations, fournit une explication satisfaisante jusqu’à une limite maxima de 536'', avec un résidu minimum inexpliqué de 38''. Dans la théorie d’Einstein, le mouvement déduit du ds² calculé par Schwarzschild donnerait pour Mercure une avance séculaire de 42''9. Mais, comme cette théorie exclut les perturbations dues aux actions mutuelles, il subsiste un résidu inexpliqué de 531''.

Tel est le résultat brutal....

En attendant, on doit constater que la théorie d’Einstein, dans son état actuel, ne permet ni d’expliquer ni de prévoir, même avec l’approximation la plus grossière, le mouvement séculaire de Mercure.

Le Roux écrira pire dans d’autres articles⁹, mais déjà à ce niveau ses déclarations lui valent une réponse cinglante, argumentée de Marcel Brillouin en novembre 1922 ([10]) :

Tout le monde sait que la théorie de la gravitation d’Einstein comprend comme première approximation celle de Newton. La Note de M. Le Roux montre qu’il est néanmoins utile de le rappeler. Les dix potentiels d’Einstein g_μν contiennent non seulement les coordonnées x_µ du point de l’espace autour duquel ils définissent le ds², mais aussi contrairement à la singulière affirmation de M. Le Roux (P. 810, lignes 21-27), les coordonnées ξ de tous les points singuliers de l’espace, c’est-à-dire de tous les points où se trouve une masse attirante, fixe ou mobile, ainsi que la grandeur de chacune de ces masses. Lorsque ces masses sont mobiles, sous leurs seules influences mutuelles, on est obligé d’étudier à la fois les mouvements de toutes ces masses, c’est-à-dire de traiter le problème des n corps soit sous sa forme rigoureuse, lorsqu’on saura former exactement les g_μν d’un espace contenant n corps mobiles, en fonction des quatre coordonnées ξ de chacun de ces corps, soit approximativement à la façon du problème des perturbations. Au premier ordre, à cause de la grandeur de la vitesse de la lumière, le seul potentiel qui diffère de celui d’un espace euclidien est le coefficient de dt², g₄₄, qui à cet ordre d’approximation, obéit à l’équation de Poisson, se forme comme en théorie newtonienne et fournit toutes les perturbations classiques.

Les critiques, de M. Le Roux, sont dépourvues de tout fondement.

Cette joute oratoire durera jusqu’au début de 1924, où le rapport de force va s’équilibrer et où la position de M. Le Roux commence à ressembler de plus en plus à un combat d’arrière-garde stérile. Painlevé, repris par son activité politique, avait pris une position plus neutre et s’était retiré du débat après son article du 1^er Mai 1922, consécutif à la visite d’Einstein au Collège de France.

Les contributions remarquables qui ont émergé de ce débat

Indépendamment des contributions innovantes de Painlevé qui ont été décrites dans ce document, d’autres contributions ont montré l’excellence de la communauté scientifique française.

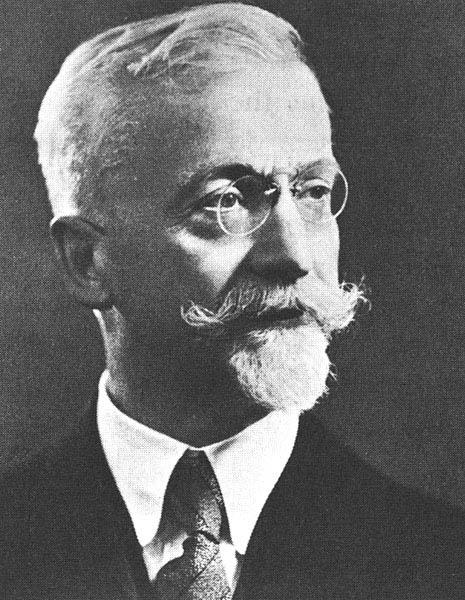
Figure 8 : Le mathématicien Élie Cartan (1869-1951), qui apporta d’importantes contributions à la relativité (photo WikiCommons).

Élie Cartan, dans une note du 27 mars 1922 « Sur les espaces conformes généralisés et l’Univers optique » ([11]), définit les directions principales nulles d’un espace-temps. Après avoir rappelé les propriétés d’un espace conforme, Cartan écrit : 

Le cas n = 4 est particulièrement important. Nous pouvons convenir d’appeler Univers optique d’Einstein l’espace conforme généralisé normal défini en annulant le ds² de l’Univers d’Einstein. C’est conformément aux propriétés géométriques de cet Univers optique que se fait la propagation de la lumière. La courbure de rotation de cet Univers est définie en chaque point par dix quantités scalaires, ou encore par une forme quadratique ternaire à coefficients complexes, qu’un changement du système de référence transforme par une substitution orthogonale. Au point de vue géométrique la propriété suivante mérite d’être signalée. Il existe en chaque point A quatre directions optiques (c’est-à-dire annulant le ds²) privilégiées. Elles sont caractérisées par la propriété que si AA' est l’une d’elles, elle se conserve par le déplacement associé à un parallélogramme élémentaire admettant comme côté AA' et une autre direction optique quelconque issue de A. Dans le cas d’une seule masse attirante (ds² de Schwarzschild), ces quatre directions optiques privilégiées se réduisent à deux (doubles) : Les deux rayons lumineux qui leur correspondent iraient au centre d’attraction ou en viendraient.

L’article de Maurice Sauger (avril 1922, [12]) « Sur une coïncidence remarquable dans la théorie de la relativité » est intéressant à plusieurs titres. D’une part il peut permettre de comprendre ce qui a inspiré Painlevé dans l’élaboration de sa forme originale, même si ici Sauger se réfère à la forme de Schwarzschild. D’autre part, il permet de comprendre les liens entre cette solution et l’espace-temps de Minkowski et donne une interprétation claire de la phénoménologie des décalages spectraux radiaux tels qu’on les établit formellement, dont certains résultats peuvent paraître paradoxaux. L’auteur construit très simplement la forme de Schwarzschild à partir de la relativité restreinte et de la mécanique newtonienne en notant simplement que la vitesse v d’un corps tombant en chute libre depuis l’infini vaut v = -(2GM/r)^1/2, par rapport à un observateur à l’infini.

L’article de Jean Chazy (mai 1922, [13]) « Sur les vérifications astronomiques de la théorie de la relativité » est le premier à établir rigoureusement la forme de la métrique de Schwarzschild avec constante cosmologique en partant de l’équation d’Einstein avec constante cosmologique, au lieu de celle sans constante cosmologique de laquelle partait Schwarzschild. C’est une contribution très originale, totalement oubliée, exposant une solution qui sera retrouvée par Lemaître dix ans plus tard.

Qu’est-il advenu de ces contributions remarquables ?

Toutes ces contributions innovantes et fondamentales résultant du débat dialectique qui s’est déroulé à cette période sont tombées dans l’oubli. Manifestement, leur importance ne s’est pas imposée aux différents intervenants, sans doute du fait qu’elles résultaient plus de travaux formels inspirés par le sujet que d’une compréhension profonde de la physique qu’elles sous-tendaient. Il est clair qu’à cette époque, même chez les esprits les plus brillants comme Einstein, la perception des implications de la théorie de la relativité générale était loin d’être claire, comme en témoigne un certain manque de considération à la proposition de Painlevé, qui permettait pourtant de résoudre formellement le problème de la singularité sur l’horizon se posant à la relativité générale. Ainsi va la science, mais il est dommage que cette opportunité pour la communauté scientifique française de valoriser son talent dans cette discipline n’ait pas pu être concrétisée. Cela aurait sans doute changé le cours de leur participation au développement de cette théorie et lui aurait donné une place significative dans la construction de ce pilier de la science du XX^e siècle.

Conclusion

Painlevé reconnaît que si l’approche d’Einstein le séduisait par son « audace », il n’était pas prêt pour autant à abandonner tout l’édifice de la mécanique classique au profit de la relativité générale. Sa méthode heuristique de géométrisation de la mécanique newtonienne pour jeter un pont entre les deux théories se révèle d’une grande efficacité comme nous l’avons souligné, puisqu’elle va bien au-delà de l’objectif fixé en refondant le concept de temps en mécanique newtonienne !

S’il n’était pas convaincu par l’approche d’Einstein, c’est pourtant lui qui a fait voler en éclats certaines barrières qui emprisonnaient les arguments des physiciens relativistes. S’il n’était pas non plus un relativiste émérite, il était néanmoins bon mathématicien et avait assimilé le « mode d’emploi » de la relativité, comme sa contribution le montre.

Ce détachement vis-à-vis de la théorie lui a permis d’aborder plus facilement que les physiciens relativistes le problème et de proposer, sans état d’âme, des solutions qu’ils s’interdisaient au motif de contraintes mal maîtrisées qu’ils s’imposaient. Les contributions brillantes de ses collègues de l’Académie des Sciences s’inscrivent sans doute dans ce même contexte.

A ce titre le problème de l’horizon est édifiant, puisque la forme établie par Painlevé montre que c’est un faux problème – alors qu’Einstein, dans ses conférences au Collège de France, invoque des arguments périphériques visant à montrer que ce cas ne peut pas physiquement se produire.

Ceci atteste d’une complémentarité entre les théoriciens « découvreurs de théories » et les théoriciens défricheurs de ces théories découvertes, les deux domaines demandant des qualités différentes. Le bon développement de la science appelle une coopération harmonieuse des deux.

(avril 2014)

Références de l’article

• [1] Weyl H. : (1922), Temps, espace, matière (traduite de l’édition 4 de Zeit, Raum, Materie de H. Weyl par G. Juvet et R.Leroy), Librairie scientifique A. Blanchard, Paris.

• [2] Le Roux J. (1921) « Sur la théorie de la relativité et le mouvement séculaire du périhélie de Mercure », C.R.A.S., Note T.172 1227-1230.

• [3] Le Roux J. (1922) « Sur la gravitation dans la mécanique classique et dans la théorie d’Einstein », C.R.A.S., Note T.175 809-811.

• [4] Langevin P. (1921), « Sur la théorie de relativité et l’expérience de M. Sagnac », C.R.A.S., Note T.173, 831-834.

• [5] Painlevé P. (1921a) « La mécanique classique & la théorie de la relativité », C.R.A.S., T. 173, 677-680.

• [6] Painlevé P. (1921b), « La gravitation dans la Mécanique de Newton et dans la Mécanique d’Einstein », C.R.A.S., T.173, 873-887.

• [7] Painlevé P. (1922), « La théorie classique et la théorie einsteinienne de la gravitation », C.R.A.S., T.174, 1137-1143.

• [8] Nordmann C. (1922), « Einstein expose et discute sa théorie », Revue des deux mondes, tome IX, p. 129-166.

• [9] Société Astronomique de France: Bulletin et revue mensuelle, avril 1922.

• [10] Brillouin M. (1922), « Gravitation einsteinienne et gravitation newtonienne; à propos d’une récente note de M. Le Roux », C.R.A.S., Note T.175 923.

• [11] Cartan E. (1922), « Sur les espaces conformes généralisés et l’Univers optique », C.R.A.S., Note T.174 857-860.

• [12] Sauger M. (1922), Sur une coïncidence remarquable dans la théorie de la relativité, C.R.A.S., Note T.174 1002-1003.

• [13] Chazy J. (1922), « Sur les vérifications astronomiques de la théorie de la relativité », C.R.A.S., Note T.174 1157-1160.

• [14] Gullstrand A. (1922), “Allgemeine Lösung des statischen Einkörper-problems in der Einsteinchen Gravitations theorie“, Arkiv.Mat.Astron.Fys. 16(8), 1-15.

• [15] Eisenstaedt J. (1982), „Histoire et Singularités de la Solution de Schwarzschild (1915-1923)“, Archive for History of Exact Sciences, Vol 27, Nb 2, pp. 157-198.

• [16] Martel K. & Poisson E. (2000): “Regular coordinate systems for Schwarzschild and other spherical spacetimes”, ArXiv.gr-qc/0001069 v4 18 Oct 2000.

• [17] Hamilton A. & Lisle J. (2006):“ The river model of black holes“. ArXiv: gr-qc/0411060v2, 31 Aug. 2006.

• [18] Moatti A. (2007), Einstein: Un siècle contre lui, Ed. Odile Jacob.