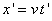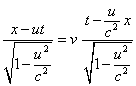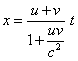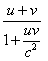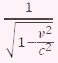De l’électrodynamique des corps en mouvement

Figure 1 : Albert Einstein (1879 – 1955), alors à l’Office des brevets de Berne, ca. 1905 (Image WikiCommons, ETH-Bibliothek Zürich, cc-by-sa 3.0).

 

Un article qui marque son temps

Nous sommes en juin 1905. L’expert technique de troisième classe à l’office des brevets de Berne s’apprête à publier un article historique à plus d’un titre : véritable rupture par rapport aux travaux antérieurs et contribution décisive au regard des développements ultérieurs. Dans une lettre (1) à son ami Conrad Habicht, l’un des membres de l’académie Olympia (2), Albert Einstein écrit à propos de son travail :

Il s’agit d’une électrodynamique des corps en mouvement qui repose sur une modification de la théorie de l’espace et du temps. La partie cinématique vous intéressera sûrement. 

Le temps d’un article, Einstein unifie en une théorie-cadre bouleversante des concepts familiers que l’on croyait inexorablement séparés. En quoi cet acte peut-il être qualifié de révolutionnaire ? Pour répondre à cette question, nous nous proposons d’analyser en détail la partie cinématique, qu’Einstein lui-même considérait comme son apport le plus important.

 

 

La physique pré-relativiste

Einstein ne décrit pas les tentatives antérieures pour expliquer l’ensemble des phénomènes électromagnétiques connus, car sa démarche est originale et indépendante. Il est néanmoins important pour saisir les particularités de son approche de résumer les conclusions auxquelles étaient parvenus ses prédécesseurs.

 

 

Figure 2 : Sur cette photo du congrès Solvay de 1911 apparaissent les deux principales figures de la physique pré-relativiste : Lorentz (quatrième assis à partir de la gauche) et Poincaré (assis au premier plan et discutant avec Marie Curie). Einstein et Langevin sont debout à droite. Lieu : hôtel Métropole, Bruxelles ; photo Wikimedia Commons).

 

En 1905, avant Einstein donc, la théorie la plus probante pour expliquer l’ensemble des faits connus dans le domaine de l’optique et de l’électromagnétisme est la dynamique de l’électron déformable de Lorentz (élaborée entre 1892 et 1904), complétée par Poincaré (entre 1900 et 1905).

La lumière étant alors vue comme une onde électromagnétique qui se propage dans un milieu, appelé éther, immobile entre les étoiles, – qu’elle ne fait que traverser, à la manière du son pour l’air –, Lorentz construit sa théorie microscopique de l’électromagnétisme en s’inspirant de la théorie ondulatoire de Fresnel, avec l’éther associé. Pour rendre compte des expériences ou observations connues, il lui est nécessaire d’attribuer à l’éther diverses propriétés additionnelles permettant d’expliquer par des effets de compensation l’apparente constance de la vitesse de la lumière. Pour justifier l’absence d’écarts en v/c, Lorentz introduit un temps local, que Poincaré interprète physiquement comme le temps valable en un point donné d’un référentiel en mouvement rectiligne uniforme par rapport à l’éther, et en ce point uniquement – les horloges comobiles distantes étant impossibles à synchroniser, compte tenu du procédé utilisé (3). Pour justifier l’absence d’écarts en v²/c² (résultat négatif de l’expérience de Michelson et Morley), il faut supposer que tous les corps subissent dans le sens de leur mouvement à travers l’éther une compression physique causée par une force spéciale, que Poincaré précise.

Dans ce cadre, les lois de l’électromagnétisme gardent la même forme dans tout référentiel inertiel (4) par application des transformations de Lorentz (1904), permettant de passer d’un référentiel à l’autre. Elles garantissent la validité du principe de relativité (5) pour les interactions électromagnétiques – l’appellation « principe de relativité » étant due à Poincaré. Ce dernier pense avoir fait le tour du sujet avec son mémoire (6) de 1905, comme il l’indique en 1909 dans une lettre à Gaston Darboux destinée à énumérer ses principales contributions à la physique en vue de l’attribution d’un éventuel prix Nobel (7) :

J’ai publié dans les Rendiconti un article où j’expose la théorie de Lorentz sur la Dynamique de l’Électron, et où je crois avoir réussi à écarter les dernières difficultés et à lui donner une parfaite cohérence.

Malgré la confiance exprimée par Poincaré, les problèmes qui se posaient à l’électrodynamique étaient loin d’être résolus en profondeur.

 

 

L’annus mirabilis 1905

L’article ici commenté est le quatrième publié par Einstein en 1905 par ordre chronologique. Cette année exceptionnelle pour la physique est marquée par cinq articles qui apportent chacun une solution novatrice à un problème fondamental de l’époque :

1. Explication de l’effet photoélectrique par le quantum de lumière (mars) ;

2. Thèse de doctorat « Sur une nouvelle détermination des dimensions moléculaires » (avril) ;

3. Explication du mouvement brownien (mai) ;

4. Premier article sur la relativité restreinte (juin) ;

5. Second article sur la relativité restreinte (septembre).

Avec ces publications, Einstein propose une nouvelle théorie de l’espace et du temps ; il introduit l’équivalence masse-énergie, explique l’effet photoélectrique en supposant que la lumière est composée de grains d’énergie (baptisés plus tard « photons ») et prouve la réalité des atomes en estimant leur taille à partir des fluctuations observées sur des particules en suspension dans un liquide.

 

 

Figure 3 : Incipit de l’article de juin 1905 ici analysé.

 

Pourquoi le titre « sur l’électrodynamique des corps en mouvement » ?

Pour un lecteur d’aujourd’hui, le titre peut surprendre quand on sait qu’il s’agit de fonder une nouvelle théorie de l’espace et du temps. En réalité, le sujet de l’article s’inscrit dans le contexte de l’époque : quelle théorie dynamique adopter pour englober l’ensemble des phénomènes électromagnétiques et optiques connus ? Le titre se réfère donc au problème plus qu’à la solution. Il est important de noter toutefois que la mention « corps en mouvement » renvoie davantage chez Einstein à une théorie macroscopique (qui ne se limite pas au comportement des électrons) que, par exemple, les articles de Poincaré qui s’intitulent invariablement « dynamique de l’électron » en référence à la théorie microscopique de l’électron déformable de Lorentz.

 

Le plan de l’article

Le plan de l’article est clair et concis. Une première nouveauté audacieuse qui tranche avec tous les travaux précédents est la décomposition en deux parties, l’une cinématique (description du mouvement selon le référentiel considéré), l’autre dynamique (liens entre les forces et le mouvement), la deuxième partie étant dérivée de la première. Tous les physiciens en pointe parlaient de dynamique sans remettre en cause le cadre cinématique newtonien (caractérisé par un espace et un temps « évidemment » séparés).

La partie cinématique est développée comme suit :

1. Définition de la simultanéité ;

2. Sur la relativité des longueurs et des temps ;

3. Théorie de la transformation des coordonnées et du temps d'un système stationnaire à un autre qui se déplace à une vitesse uniforme relativement au premier ;

4. Signification physique des équations obtenues pour les corps rigides et les horloges en mouvement ;

5. Théorème d'addition des vitesses.

 

L’introduction

Einstein commence par exposer certaines difficultés propres à l’électrodynamique de son époque.

Il est connu que si nous appliquons l'électrodynamique de Maxwell, telle que nous la concevons aujourd'hui, aux corps en mouvement, nous sommes conduits à une asymétrie qui ne s'accorde pas avec les phénomènes observés.

La première anomalie qu’Einstein considère comme un vrai problème est l’incapacité des équations de Maxwell à rendre compte de la symétrie du phénomène (expérience de Faraday), selon qu’on l’observe depuis l’aimant ou le conducteur, en mouvement l’un par rapport à l’autre. Un même phénomène devrait s’expliquer d’une façon unique.

 

 

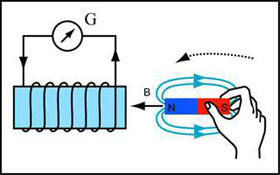
Une asymétrie théorique embarrassante     Imaginons un aimant en mouvement qui traverse une boucle conductrice à la vitesse v.     Figure 4 : L'induction électromagnétique. En approchant un aimant permanent d'une bobine connectée à un galvanomètre, l'aiguille de l'instrument dévie (©Ilarion Pavel, article BibNum sur Tesla).   Du point de vue de la boucle conductrice, l’aimant dans son mouvement produit un champ magnétique variable B. Selon la loi de Faraday, une force électromotrice liée à la variation de flux magnétique (dΦ/dt) apparaît : un champ électrique E est induit à l’intérieur de la boucle conductrice, la force électrique qE agit sur les particules de charge q, et un courant électrique apparaît dans la boucle conductrice. Du point de vue de l’aimant, c’est la boucle conductrice qui se déplace (en sens inverse) à la vitesse v. Dans ce cas, ce n’est plus la force électrique mais la force magnétique dite de Lorentz qv×B (où B est le champ magnétique créé par l’aimant) qui agit sur les particules de charge q et crée ainsi un courant électrique dans la boucle conductrice. L’électrodynamique de Maxwell-Lorentz fournit donc deux interprétations différentes du courant induit (en termes de force électrique ou de force magnétique) alors que celui-ci ne dépend que du mouvement relatif de l’aimant et du conducteur. Ce constat était connu avant Einstein, mais la plupart des physiciens acceptaient cette asymétrie en l’attribuant à des effets du mouvement des corps (aimant ou conducteur) à travers l’éther qui seraient précisés ultérieurement.

 

 

Einstein sait déjà que l’électromagnétisme de Maxwell ne suffit pas à décrire la réalité physique puisque, dès son article de mars, il propose une explication de l’effet photoélectrique fondée sur l’hypothèse corpusculaire pour la lumière – ce qui signifie que la théorie de l’onde électromagnétique ne permet pas à elle seule de « sauver les phénomènes ».

Des exemples similaires, tout comme l'essai infructueux de confirmer le mouvement de la Terre relativement au « médium de la lumière », nous amènent à la supposition que non seulement en mécanique, mais aussi en électrodynamique, aucune propriété des faits observés ne correspond au concept de repos absolu ; et que dans tous les systèmes de coordonnées où les équations de la mécanique sont vraies, les équations électrodynamiques et optiques équivalentes sont également vraies, comme il a été déjà montré par l'approximation au premier ordre des grandeurs.

Après avoir relevé des problèmes de cohérence interne de la théorie en vigueur, Einstein mentionne les résultats négatifs des expériences réalisées afin de détecter d’éventuels écarts dans la vitesse de la lumière. L’expression « medium de lumière » désigne l’éther, le milieu supposé de propagation de la lumière. Einstein ne cite pas expressément les expériences concernées : les trois principales sont celle de l’aberration des étoiles (expérience d’Arago de 1810) (8), celle de Fizeau sur la vitesse de la lumière dans un tube d’eau en mouvement et celle de Michelson et Morley (années 1880) – même si cette dernière semble avoir joué un rôle mineur dans le travail d’Einstein.

 

 

Figure 5 : François Arago (1786 - 1853), Hippolyte Fizeau (1819 – 1896), Albert Michelson (1852 – 1931). Trois physiciens ayant fourni des résultats expérimentaux cruciaux pour la future relativité restreinte.

 

Einstein propose d’étendre à l’électromagnétisme le principe de relativité valable pour la mécanique. Il précise que cela n’a été montré théoriquement jusqu’ici que par l’approximation au premier ordre (en v/c, où v est la vitesse du corps en mouvement) des grandeurs. Dans la traduction française de Maurice Solovine (qui date des années 1920), Einstein indique dans une note qu’il n’avait pas connaissance, lors de la rédaction de son article, de la publication de Lorentz de 1904.

Dans le texte qui suit, nous élevons cette conjecture au rang de postulat (que nous appellerons dorénavant « principe de relativité ») et introduisons un autre postulat — qui au premier regard est incompatible avec le premier — que la lumière se propage dans l'espace vide, à une vitesse c indépendante de l'état de mouvement du corps émetteur.

D’entrée, Einstein pose ainsi deux postulats : le principe de relativité et la constance de la vitesse de la lumière dans le vide, indépendamment du mouvement de la source. Le premier postulat est une extension à l’électromagnétisme du principe de relativité déjà énoncé par Galilée pour la mécanique. Le terme « principe de relativité » est dû à Poincaré en 1904 mais ce dernier, quoique conscient de son importance, l’énonce comme une conjecture (qui pourrait se révéler fausse un jour), et non comme un axiome premier.

Le second postulat ne se limite pas, comme ce passage pourrait le laisser croire, à l’indépendance de la vitesse de la lumière vis-à-vis de celle de la source : ce fait, qui caractérise simplement la propriété ondulatoire, était connu depuis les expériences d’Arago en 1810 et faisait partie de la théorie ondulatoire de Fresnel. Il s’agit bien, comme Einstein le précise au paragraphe 2 de son article, d’un constat qui reste valable quel que soit le référentiel inertiel considéré, ce qui est beaucoup plus surprenant. Comme l’indique Einstein, le maintien de ces deux principes conjoints paraît impossible, car la vitesse de la lumière mesurée devrait dépendre de la vitesse de l’observateur, en vertu de la loi d’additivité des vitesses bien connue. Einstein propose de fonder pourtant sa cinématique sur ces deux principes apparemment contradictoires, démarche d’une grande hardiesse. Mais il ne s’arrête pas là :

Il sera démontré que l'introduction d'un « éther luminifère » est superflu, puisque selon les conceptions que nous développerons, nous n'introduirons ni un « espace absolument au repos » muni de propriétés spéciales et ni n'associerons un vecteur-vitesse à un point où des phénomènes électromagnétiques se déroulent.

Einstein est ici le premier à proposer une théorie cohérente qui abandonne toute idée d’éther (9), c'est-à-dire d’un milieu de propagation pour la lumière. Cela revient à rejeter deux présupposés : la lumière n’a pas besoin d’un support matériel pour se propager (contrairement au son), et sa vitesse de propagation n’est pas valable uniquement par rapport au référentiel privilégié que serait l’éther. Cette affirmation est fondamentale, car elle se démarque radicalement du point de vue des meilleurs théoriciens de l’époque, au premier chef desquels Lorentz et Poincaré, qui cherchaient à préciser la nature des interactions entre la matière et l’éther pour expliquer certains phénomènes électromagnétiques. Poincaré voyait certes dans l’éther avant tout une convention commode : mais il indiquait qu’il fallait à tout prix la conserver, compte tenu des avantages qu’il lui attribuait.

 

 

Définition de la simultanéité (paragraphe 1)

Ce paragraphe est l’un des plus novateurs de cet article. Einstein y discute de questions qui pourraient paraître anodines voire enfantines, tant elles semblent basiques. Et pourtant, le nœud du problème à résoudre est bien là, autour du concept de temps. Einstein écrira dans un autre important article (10) de 1907 :

Mais, de façon surprenante, il se révéla en fait que, pour surmonter la difficulté […], il était seulement nécessaire d’appréhender le concept de temps avec suffisamment d’acuité.

Revenons à l’article de 1905. Einstein fournit d’abord une définition importante pour la suite de son article :

Supposons un système de coordonnées dans lequel les équations newtoniennes sont vraies. Pour distinguer ce système d'un autre qui sera introduit plus tard, et pour rendre cette notion plus claire, nous l'appellerons le « système stationnaire ».

Il appelle « système stationnaire » un référentiel inertiel, c'est-à-dire dans lequel la loi d’inertie s’applique (tout corps persévère dans un mouvement rectiligne uniforme s’il n’est soumis à aucune force). Comme par la suite il examinera les mouvements relatifs entre référentiels, le référentiel dit « stationnaire » désignera un référentiel inertiel quelconque. Les guillemets sont là pour nous rappeler que ce système choisi comme « au repos » ne possède aucun statut privilégié.

Il indique alors que le problème de la détermination du temps se ramène à la notion d’événements simultanés.

Nous devons prendre en considération le fait que nos conceptions, où le temps joue un rôle, portent toujours sur des évènements simultanés. Par exemple, si nous disons « qu'un train arrive ici à 7 heures », cela signifie « que la petite aiguille de ma montre qui pointe exactement le 7 et que l'arrivée du train sont des évènements simultanés ».

La solution la plus simple pour mesurer le temps d’un événement est de disposer d’une horloge à l’endroit précis où se produit l’événement pour éliminer les incertitudes d’une observation à distance. Mais si nous voulons parler correctement de l’événement qui se produit en A à l’instant t_A et de de l’événement qui se produit en B à l’instant t_B, les horloges disposées aux points A et B doivent être synchronisées entre elles. Einstein décrit donc un procédé pour y parvenir, qui est basé sur un échange de signaux lumineux entre A et B.

Nous avons jusqu'à maintenant un « temps A » et un « temps B », mais aucun « temps » commun à A et B. Ce dernier temps (c'est-à-dire le temps commun) peut être défini, si nous posons par définition que le « temps » requis par la lumière pour aller de A à B est équivalent au « temps » pris par la lumière pour aller de B à A. Par exemple, un rayon lumineux part de A au « temps A », t_A, en direction de B, est réfléchi de B au « temps B », t_B, et revient à A au « temps A », t'_A. Par définition, les deux horloges sont synchronisées si

 

t_B – t_A = t’_A - t_B

 

L’hypothèse cruciale ici est la constance de la vitesse de la lumière dans les deux sens, conformément au deuxième postulat. Einstein peut dès lors préciser ce qu’il entend par le « temps d’un événement » :

Le « temps » d'un évènement est l'indication simultanée d'une horloge au repos située à l'endroit de l'évènement, qui est synchronisée avec une certaine horloge au repos dans tous les cas de détermination du temps.

La définition opérationnelle du temps est donc basée sur l’établissement d’un réseau d’horloges synchronisées dans un référentiel inertiel donné.

En accord avec l'expérience, nous ferons donc l'hypothèse que la grandeur 2 AB / (t’_A - t_A) est une constante universelle (la vitesse de la lumière dans l'espace vide).

C’est la première fois ici qu’Einstein parle de « constance universelle » pour la vitesse de la lumière, la synchronisation des horloges reposant sur cette invariance dans tout référentiel inertiel.

 

 

@@@@@@@

 

 

Figure 6 : Buste de 1909 d'Henri Poincaré (par Joseph Cartier), situé dans le hall principal de l'École polytechnique à Palaiseau (collections BCX Bibliothèque de l'École)(image WikiCommons, auteur A. Moatti cc-by-sa 3.0).

 

Il est important de comparer les approches de Poincaré et d’Einstein à propos de la synchronisation des horloges. Poincaré est le premier à proposer (dès 1900) un procédé similaire à celui d’Einstein pour régler à distance deux horloges dans un référentiel inertiel. Celui-ci consiste aussi à supposer la constance de la vitesse de la lumière dans les deux sens ; mais l’analogie s’arrête là. Considérons nos deux horloges placées aux points A et B d’un référentiel ℜ en mouvement par rapport à l’éther (qui existe bel et bien selon Poincaré). Nous n’avons aucun moyen connu pour estimer la vitesse de ℜ par rapport à l’éther. Nous choisissons par convention de considérer que la vitesse d’un signal lumineux partant de A (dans le sens du mouvement) serait identique à celle d’un signal partant de B (en sens contraire). Hors, selon Poincaré, cette convention, pour commode qu’elle soit, ne correspond pas à la réalité : la loi d’additivité des vitesses classique nous indique que, vue de ℜ, la vitesse du signal partant de A va se trouver diminuée de la vitesse (inconnue) de ℜ par rapport à l’éther, de même celle du signal issu de B va se trouver augmentée. Comme le procédé ne tient pas compte de ces différences, les deux horloges aux points A et B seront désynchronisées d’une certaine quantité (11), bien que nous ne puissions pas nous en apercevoir. Poincaré parle du temps local en A et du temps local en B. La vitesse de la lumière apparaîtra identique dans les deux sens, uniquement parce que nous sommes contraints d’utiliser le temps local, autrement dit parce que nous mesurons le temps à l’aide d’horloges au « réglage défectueux » selon les propres termes (12) de Poincaré. Pour résumer, Poincaré raisonne toujours dans un cadre cinématique newtonien (avec un espace et un temps absolus, et une constance seulement apparente pour la vitesse de la lumière) ; alors qu’Einstein s’apprête à bouleverser ce cadre avec des conséquences nouvelles stupéfiantes, comme la suite de l’article le révèle.

 

 

Sur la relativité des longueurs et des temps (paragraphe 2)

Einstein revient sur les deux postulats de départ de sa cinématique qu’il reformule plus précisément. Tout d’abord le principe de relativité :

Les lois selon lesquelles l'état des systèmes physiques se transforme sont indépendantes de la façon dont ces changements sont rapportés dans deux systèmes de coordonnées (systèmes qui sont en mouvement rectiligne uniforme l'un par rapport à l'autre).

Il s’agit d’une réaffirmation du principe déjà énoncé par Galilée 300 ans plus tôt, qu’il généralise à toute la physique. Poincaré, rappelons-le, avait souligné (davantage qu’aucun de ses contemporains) l’importance de ce principe avant Einstein : mais il n’en fit jamais un principe opératoire, générateur de conséquences cinématiques nouvelles. Pour lui, l’impossibilité de mettre en évidence tout mouvement par rapport à l’éther devait être expliqué en partant de la dynamique, en liaison avec les interactions physiques (électromagnétiques ou autres) alors que pour Einstein, il s’agit d’un axiome premier de sa théorie, sans lequel tout l’édifice s’écroule. Max Planck saisit très tôt l’originalité de la démarche d’Einstein. Dès 1910, il écrit à l’adresse du Conseil de l’Université de Prague :

Si, comme je l’attends, la théorie d’Einstein est confirmée, on le tiendra pour le Copernic du vingtième siècle (13).

Einstein explicite ensuite rigoureusement le principe d’invariance de la vitesse de la lumière (dans le vide) :

Chaque rayon lumineux se déplace dans un système de coordonnées « stationnaire » à la même vitesse c, la vitesse étant indépendante de la condition que ce rayon lumineux soit émis par un corps au repos ou en mouvement.

Ici, Einstein précise que la lumière se propage à une vitesse constante quel que soit le référentiel inertiel (« stationnaire ») considéré. C’est cette invariance qui est novatrice, et non l’indépendance vis-à-vis de la vitesse de la source (qui peut s’expliquer de manière simple par le caractère ondulatoire de la lumière). Ce principe a choqué ou interloqué certains physiciens de l’époque, car Einstein posait comme postulat un résultat qu’ils s’évertuaient à expliquer depuis des décennies ! Ne s’agissait-il pas là d’un procédé artificiel, d’une convention de plus ? La réponse est négative, car se donner ce principe, c’est admettre en fait que nous vivons dans un espace à quatre dimensions entremêlées (à cause de l’existence d’une vitesse limite) plutôt que dans celui à la géométrie purement spatiale qui nous semble si familier. Comme nous le verrons plus loin, la structure particulière de notre univers peut être dérivée en substituant au principe de constance de la vitesse de la lumière des principes d’invariance plus généraux (isotropie de l’espace notamment), où aucune référence à certains types de signaux n’apparaît. L’édifice einsteinien n’en apparaît que plus fortifié.

Avant même d’en déduire les transformations de Lorentz, Einstein met en évidence de façon essentiellement qualitative deux résultats très importants de sa cinématique nouvelle : la contraction des longueurs et la relativité de la simultanéité.

 

La contraction des longueurs (qualitative)

Einstein explique le procédé à utiliser pour mesurer la longueur d’une tige rigide, soit lorsque celle-ci est au repos dans le référentiel considéré, soit lorsque celle-ci est en mouvement.

L'observateur pourvu de la règle à mesurer se déplace avec la tige à mesurer et mesure sa longueur en superposant la règle sur la tige, comme si l'observateur, la règle à mesurer et la tige étaient au repos.

Einstein insiste sur le fait que la longueur de la tige dans le référentiel considéré en mouvement est identique à celle dans le référentiel « au repos » si elle est mesurée par un observateur comobile avec la tige, constat qui n’est que l’expression du principe de relativité.

Selon le principe de relativité, la longueur trouvée par l'opération a), que nous appelons la « longueur de la tige dans le système en mouvement », est égale à la longueur ℓ de la tige dans le système stationnaire.

Einstein décrit ensuite le procédé pour mesurer la longueur de la tige en mouvement depuis le référentiel « au repos » :

L'observateur détermine à quels points du système stationnaire se trouvent les extrémités de la tige à mesurer au temps t, se servant des horloges placées dans le système stationnaire.

L’opération ci-dessus n’est possible que parce que les horloges du système « au repos » ont été préalablement synchronisées. Einstein annonce alors le résultat qu’il prédira quantitativement plus loin à partir de ses deux postulats :

Cette longueur est à calculer en s'appuyant sur nos deux principes, et nous découvrirons qu'elle diffère de ℓ.

La contraction des longueurs est un effet de perspective, puisque pour un observateur comobile avec la tige, la longueur n’est pas altérée. Remarquons que pour Poincaré et Lorentz, qui raisonnent dans un cadre cinématique classique, la contraction des longueurs est une compression physique causée par une force spéciale exercée sur les corps en mouvement par rapport à l’éther. Comme tous les instruments sont comprimés de la même façon, aucune compression n’est constatée par un observateur comobile avec la tige mobile, constat ici identique à celui d’Einstein, même si l’explication n’a rien à voir.

 

 

La relativité de la simultanéité

Supposons de plus que deux horloges synchronisées avec des horloges dans le système stationnaire sont fixées aux extrémités A et B d'une tige, c'est-à-dire que les temps des horloges correspondent aux « temps du système stationnaire » aux points où elles arrivent ; ces horloges sont donc « synchronisées dans le système stationnaire ».

Que se passe-t-il si nous échangeons des signaux lumineux entre les points A et B (trajet de A vers B puis de B vers A) d’une tige en mouvement ?

Prenant en compte le principe de la constance de la vitesse de la lumière, nous avons t_B – t_A = r_AB / (c – v) et t’_A – t_B = r_AB / (c + v)

où r_AB est la longueur de la tige en mouvement, mesurée dans le système stationnaire.

Le début de l’extrait ci-dessus est capital : les formules précédentes sont en effet obtenues sur la base de la constance de la vitesse de la lumière (deuxième postulat). C’est de cette invariance contre-intuitive qu’Einstein dérive la relativité de la simultanéité. Les formules telles quelles peuvent être trompeuses si l’on pense à tort qu’elles sont exprimées dans le référentiel « en mouvement », auquel cas elles signifieraient qu’il y a une différence de vitesse dans les deux sens (14), conformément à la théorie de l’éther défendue par Poincaré et Lorentz.

Mais la première expression est bien obtenue dans le référentiel au repos en posant que la vitesse de la lumière est c dans les deux sens : c (t_B – t_A) = r_AB + v (t_B – t_A). Cette égalité exprime les deux façons de calculer la longueur parcourue dans le référentiel au repos : c’est la distance franchie par le rayon lumineux pour une durée (t_B – t_A) et une vitesse c inchangée ; et c’est aussi la longueur de la tige augmentée de la distance supplémentaire à parcourir du fait que la tige s’est déplacée à la vitesse v pendant l’intervalle de temps (t_B – t_A).

Nous en concluons que nous ne pouvons pas attacher une signification absolue au concept de simultanéité. Dès lors, deux évènements qui sont simultanés lorsque observés d'un système ne seront pas simultanés lorsque observés d'un système en mouvement relativement au premier.

Il est important de comprendre que, pour Einstein, la relativité de la simultanéité est une conséquence directe de l’invariance de la vitesse de la lumière tandis que, pour Poincaré, la vitesse ne se conservant pas, elle résulte du réglage défectueux des horloges qui sont nécessairement désynchronisées. Pour Poincaré, le caractère non absolu de la simultanéité n’a rien de relativiste, il s’agit d’un simple artefact des opérations de mesure (15).

 

Théorie de la transformation des coordonnées et du temps d'un système stationnaire à un autre qui se déplace à une vitesse uniforme relativement au premier (paragraphe 3)

Dans ce paragraphe, Einstein déduit les fameuses transformations de Lorentz, qui permettent de passer des cordonnées d’un événement exprimées dans un référentiel inertiel à celles exprimées dans un autre référentiel, en mouvement rectiligne uniforme par rapport au premier.

Ici, la véritable nouveauté est que ces transformations sont démontrées à partir des deux postulats de la nouvelle cinématique – tandis que Lorentz et Poincaré les avait construites (16) ad hoc pour laisser invariantes les équations de Maxwell. Chez Einstein, elles ont une portée beaucoup plus générale car elles ne sont pas spécialement rattachées aux lois de l’électromagnétisme. La démonstration qu’utilise Einstein dans cet article est assez laborieuse ; d’ailleurs, dès 1907 dans son article de synthèse sur la relativité restreinte, il optera pour une démonstration beaucoup plus compacte basée sur la propagation des ondes lumineuses sphériques dont l’équation x² + y² + z² = c²t² doit rester inchangée d’un référentiel à l’autre.

Einstein connaissait-il à l’avance les formules qu’il déduit (17) ? L’utilisation d’un facteur d’échelle (noté φ(v) dans les formules) au choix quelque peu arbitraire pourrait le laisser croire : mais il est très possible qu’il ait d’abord par tâtonnements obtenu les bonnes équations et ensuite élaboré son raisonnement déductif. Il n’y aurait rien là d’inhabituel : Galilée en 1632 faisait déjà remarquer (18) que la démonstration se trouve grandement facilitée si l’on a à l’avance une idée suffisamment précise de ce que l’on cherche ! Ajoutons que le terme « transformations de Lorentz » est dû à Poincaré dans son article de 1905 « Sur la dynamique de l’électron ».

Enfin, dernier point important : comme nous l’avons déjà évoqué, il est possible de dériver les transformations de Lorentz en remplaçant le principe de constance de la vitesse de la lumière par d’autres principes plus généraux de symétrie ou d’invariance (19). Pour un physicien relativiste, la vitesse de la lumière est avant tout une constante structurelle dont la valeur coïncide avec la vitesse des particules de masse nulle (en l’occurrence les photons).

 

La signification physique des équations obtenues pour les corps rigides et les horloges en mouvement (paragraphe 4)

Nous arrivons au paragraphe certainement le plus révolutionnaire de cet article, du point de vue de la physique. Notons d’abord que le titre est déjà très novateur : on ne trouve rien de comparable dans les travaux antérieurs. Einstein commence par décrire quantitativement la contraction des longueurs qu’il avait annoncée précédemment.

Alors que les dimensions en y et z de la sphère (ou de n'importe quel autre solide) ne semblent pas modifiées par le mouvement, la dimension en x est raccourcie selon le rapport ; le raccourcissement est d'autant plus grand que la vitesse v est grande.

Einstein rappelle qu’il s’agit d’un effet observé uniquement selon l’axe des x et fournit la valeur du taux de contraction, d’autant plus élevée que la vitesse du corps est proche de celle de la lumière.

Il est évident que des résultats semblables sont vrais pour des corps au repos dans un système stationnaire, lorsqu'ils sont observés depuis un système en mouvement rectiligne uniforme.

Einstein fait remarquer ici que l’effet est réciproque : en ce sens que si l’on imagine la tige dans le référentiel « au repos », telle que mesurée depuis un référentiel en mouvement rectiligne uniforme, le résultat est identique. Ce raccourcissement n’est qu’un effet de perspective pour Einstein puisqu’il n’est observé qu’à partir d’un référentiel dans lequel la tige est en mouvement, jamais par un observateur comobile avec la tige. Rappelons que chez Lorentz et Poincaré, la contraction des longueurs est très différente du point de vue physique, car il s’agit d’un effet dynamique correspondant à une compression effective.

Einstein passe alors aux effets temporels, beaucoup plus surprenants et, qui plus est, inédits.

Soit une horloge immobile dans le système stationnaire qui donne le temps t, et qui donne le temps τ lorsqu'immobile dans un système en mouvement. Supposons qu'elle se trouve à l'origine du système en mouvement k et réglée pour donner le temps τ. À quelle cadence avance cette horloge, lorsqu'observée du système stationnaire ?

La question ci-dessus est déjà novatrice : personne n’avait osé cette interrogation étonnante voire saugrenue. Nous savons que nous devons comparer notre horloge considérée en mouvement avec un réseau d’horloges synchronisées dans le système « au repos ». Si nous supposons que l’horloge en mouvement est synchronisée avec une horloge qu’elle croise au temps 0, quel temps τ indiquera-t-elle au moment où elle croisera une horloge du système « au repos » marquant le temps t ?

 

 

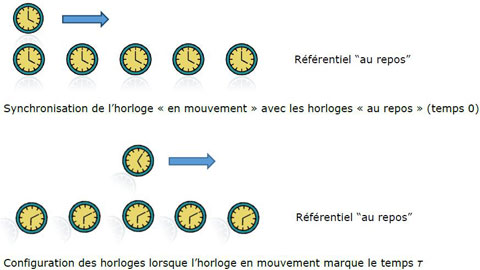
Figure 7

 

La réponse à la question ci-dessus est donnée par la transformation de Lorentz (équation donnant τ en fonction de t et de x) :

 

 

 

 

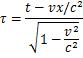
En remarquant que x = vt, Einstein en déduit que le temps τ marqué par l’horloge en mouvement (temps écoulé depuis sa synchronisation avec les horloges « au repos ») est inférieur à celui marqué par l’horloge croisée (nous aurions « évidemment » τ = t avec la cinématique classique) :

 

 

 

 

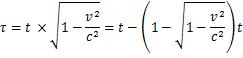
Or l’expression 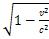 est équivalente, en se limitant au second ordre en v/c, à :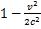

Einstein déduit que le décalage relatif en fréquence de l’horloge en mouvement (par rapport aux horloges « au repos ») est donné par :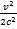

Donc, l'horloge retarde de  secondes (lorsqu'observée du système stationnaire) par seconde ou, en négligeant les approximations du quatrième ordre et supérieurs,  secondes.

Remarquons que l’effet est réciproque : en effet, nous pouvons faire le même raisonnement en observant depuis le référentiel en mouvement (qui devient « stationnaire ») une horloge en mouvement de l’autre référentiel qui est alors considéré « en mouvement ». Nous constaterons à nouveau que l’horloge en mouvement croise les horloges synchronisées entre elles du système « stationnaire » en indiquant un retard vis-à-vis du temps marqué par l’horloge croisée.

Il n’y rien là de contradictoire puisque dans les deux situations inversées nous ne mesurons pas la même chose : il n’y a pas d’ailleurs de symétrie dans les deux cas pour l’opération de mesure puisqu’il nous faut toujours dans un référentiel une horloge en mouvement et dans l’autre « stationnaire » un réseau d’horloges « immobiles » synchronisées entre elles, devant lesquelles passe l’horloge en mouvement. Ce phénomène qu’Einstein est le premier à inférer (20) est appelé dilatation des durées impropres : la cadence d’une horloge lorsqu’observée du système stationnaire apparaît toujours ralentie (étant entendu que nous raisonnons ici avec des référentiels inertiels). Autrement dit, l’intervalle de temps entre deux événements mesuré par un observateur extérieur (appelé impropre) est toujours supérieur à l’intervalle de temps propre (c'est-à-dire mesuré par un observateur pour lequel les deux événements se produisent au même endroit).

Ce phénomène se traduit donc par un décalage des fréquences vers le rouge lorsque celles-ci sont observées depuis le système stationnaire. Le phénomène fut constaté pour la première fois en 1938 grâce à l’expérience d’Ives et Stilwell. Ce décalage apparent des fréquences est un effet de perspective puisque la fréquence de l’horloge considérée en mouvement n’est jamais altérée par le mouvement : un observateur comobile avec l’horloge ne constatera aucune modification du rythme de l’horloge (en vertu d’ailleurs du principe de relativité).

Cela dit, l’effet le plus révolutionnaire est encore à venir et Einstein en souligne l’importance sans tarder.

De ceci découlent des conséquences remarquables.

Malgré la mise en relief par Einstein, cette partie de son article est souvent ignorée par les commentateurs (21) bien qu’elle soit sûrement la plus novatrice au niveau des conséquences physiques.

Supposons qu'en deux points A et B de K, lorsqu'observées depuis le système stationnaire, se trouvent deux horloges synchronisées. Supposons que l'horloge en A est mise en mouvement à la vitesse v sur une ligne qui rejoint B, alors lorsqu'elle arrive à B, les deux ne seront plus synchronisées, mais l'horloge qui s'est déplacée de A à B aura un retard sur l'horloge toujours demeurée en B de la quantité tv²/2c² secondes (en négligeant les approximations du quatrième ordre et supérieurs), où t est le temps pris pour accomplir le déplacement de A à B.

Einstein reprend donc son expérience de pensée précédente (celle de la dilatation des durées impropres) en imaginant cette fois-ci qu’une horloge est d’abord « mise en mouvement à la vitesse v », donc accélérée depuis le repos dans le système stationnaire jusqu’à la vitesse v. Dans ces conditions, il prédit un retard pour l’horloge mise en mouvement lorsqu’elle atteindra l’horloge restée immobile en B dans le référentiel stationnaire. Ici, la comparaison porte sur les temps cumulés enregistrés par les horloges respectives et non plus sur une différence apparente de rythmes. Le résultat est encore plus spectaculaire si l’on imagine un aller-retour pour l’horloge mise en mouvement.

Si nous faisons l'hypothèse que le résultat obtenu pour une ligne polygonale est également vrai pour une ligne courbe, nous obtenons le théorème suivant : si à A, il y a deux horloges synchronisées et si nous déplaçons l'une d'elles à une vitesse constante selon une courbe fermée qui revient à A, le déplacement étant complété en t secondes, alors à son arrivée à A, cette dernière retardera de tv²/2c² secondes sur l'horloge immobile.

Ce paragraphe superbe contient l’une des prédictions les plus étonnantes et contre-intuitives de la relativité : on peut l’appeler au choix désynchronisation des horloges parfaites ou multiplicité des temps propres. La version la plus spectaculaire de cette expérience est connue sous l’expression « paradoxe des jumeaux ». Deux horloges parfaites (c'est-à-dire au rythme identique et ne se déréglant jamais), initialement parfaitement synchronisées, vont pourtant se décaler en fonction des trajectoires qu’elles suivent dans l’espace à quatre dimensions. Cela signifie que chaque observateur emporte avec lui son temps propre (le temps indiqué par une horloge parfaite qui lui est attachée) et qu’en général ces durées propres sont discordantes. Nous sommes tous des êtres désynchronisés ! Dès 1911, lors d’une conférence à Zurich, Einstein utilise une description plus imagée de cette prédiction troublante :

Si nous placions un organisme vivant dans une boîte […] on pourrait s'arranger pour que cet organisme, après un temps de vol aussi long que voulu, puisse retourner à son endroit d'origine, à peine altéré, tandis que les organismes correspondants, qui sont restés dans leur position initiale auraient depuis longtemps cédé la place à de nouvelles générations. Car pour l'organisme en mouvement, la grande durée du voyage était un court instant, à condition que le mouvement ait été effectué quasiment à la vitesse de la lumière (22).

Peu de temps après, lors d’une conférence à Bologne, le physicien français Paul Langevin utilisera un scénario (23) à la Jules Verne – un voyage en boulet –, l’effet étant cette fois-ci observable en comparant l’âge d’êtres humains voyageurs avec l’âge de ceux restés sur Terre.

 

 

Figure 8 : texte de Langevin, p.50 (réf. en NbdP)

 

 

Einstein/Langevin ou le paradoxe introuvable   Il est intéressant de noter qu’Einstein n’a vu à juste titre aucun paradoxe dans la situation décrite pour une horloge décrivant une courbe fermée. Cet effet « remarquable » suscitera pourtant de nombreuses discussions souvent confuses dans les décennies qui suivront. Au contraire, la conclusion d’Einstein sur le retard réel de l’horloge voyageuse à son retour suit une ligne de raisonnement très fluide. Il commence par prédire l’effet réciproque de dilatation des durées observé lorsqu’on raisonne avec deux référentiels inertiels (qui sont en mouvement rectiligne uniforme l’un par rapport à l’autre). Dans ce cas il est impossible conformément au principe de relativité de savoir laquelle des deux horloges retarde effectivement (Einstein se contente d’ailleurs de comparer les rythmes relatifs des horloges). Ensuite, il met en mouvement l’une des horloges dans le référentiel inertiel où elle était immobile avec l’autre horloge. Dans ce cas, la symétrie est rompue et le retard constaté est nécessairement celui de l’horloge en mouvement. Langevin dans son exposition initiale du « paradoxe » des jumeaux (en fait un voyage en boulet) ne parle pas non plus de paradoxe (donc de contradiction logique). Le terme (tout comme celui de « jumeaux ») est venu plus tard par d’autres auteurs qui ont cru voir une incohérence en supposant à tort une symétrie parfaite entre chaque horloge – ou jumeau. C’est avec le formalisme de Minkowski que l’effet prédit par Einstein peut être expliqué « naturellement » dans le cas de mouvements tout à fait quelconques pour chacune des horloges : à chaque ligne d’univers son temps propre. Les lignes d’univers dans l’exemple donné par Einstein étant distinctes, les temps cumulés respectifs ne concorderont pas.

 

Cette prédiction d’Einstein que personne n’avait imaginée avant lui (qui est indépendante de toute convention de synchronisation) est certainement la conséquence la plus importante de cet article de 1905. La multiplicité des temps propres est une caractéristique essentielle de la relativité restreinte. C’est aussi l’aspect le plus difficile à faire comprendre aux néophytes. Comment deux horloges supposées parfaites et idéalement synchronisées peuvent-elles finir par se décaler ? Rappelons que chaque observateur muni de son horloge ne constatera aucun dérèglement de l’horloge : le rythme de l’horloge n’est pas altéré par son mouvement. D’où vient donc le décalage prédit ?

L’effet est chrono-géométrique : ce ne sont pas les horloges qui se dérèglent mais les « longueurs » temporelles qui ne se conservent pas lors de nos déplacements, contrairement au cadre cinématique classique. L’existence d’une vitesse limite (donc absolue) implique la multiplicité des durées propres et est une conséquence directe de la simplicité structurelle de notre univers : elle est inévitable si l’on suppose la validité de certains principes d’invariance très généraux. Cette chrono-géométrie (géométrie à quatre dimensions inséparables) sera formalisée plus précisément par Minkowski dans son célèbre article (24) de 1908. On lui doit notamment les termes de « temps propre », « ligne d’univers » ou « cône de lumière ».

 

 

Figure 9 : Hermann Minkowski (1864 - 1909). Mathématicien qui fut le professeur d’Einstein, il apporta une contribution essentielle à la relativité restreinte en fournissant le formalisme adéquat en connexion avec la théorie physique.

 

Cette prédiction d’Einstein a-t-elle été vérifiée ? La réponse est : oui, assurément. En 1971, les américains Joseph Hafele et Richard Keating firent voler deux avions de lignes en sens contraire pour un tour complet autour de la Terre (au niveau de l’équateur) qui impliquait plusieurs escales. Chaque avion emportait quatre horloges atomiques de haute précision, et les temps indiqués par les horloges embarquées purent être comparés aux horloges de référence au sol. À leur retour le temps cumulé (nombre de cycles) enregistré par chaque horloge embarquée fut soigneusement répertorié. Un écart fut bel et bien mesuré, qui contenait outre l’effet prédit par la relativité restreinte (et énoncé par Einstein dans l’article ici commenté), un effet comparable prédit par la relativité générale, dû à la gravitation donc à la différence d’altitude entre les horloges embarquées et celles au sol (25). Notons que l’expérience initiale de Hafele et Keating a été répétée depuis à plusieurs reprises, avec des précisions améliorées, les résultats étant toujours conformes aux prédictions de la théorie d’Einstein. Aujourd’hui, l’exactitude des horloges est telle que l’effet peut être observé pour des vitesses voisines de 10 m/s, c'est-à-dire la vitesse d’un cycliste.

 

 

Figure 10 : Les physiciens américains Joseph Hafele et Richard Keating à bord d’un avion de ligne, avec leurs horloges atomiques au césium (revue Time Magazine, 18 octobre 1971)

 

Il est important de bien distinguer les deux phénomènes inférés de façon inédite par Einstein dans cet article de 1905 : la dilatation des durées impropres et la multiplicité des temps propres. Le premier consiste à mesurer depuis un référentiel inertiel la fréquence d’un processus physique périodique attaché à un corps en mouvement rectiligne uniforme ; le second à comparer les durées propres enregistrées par deux corps en mouvement quelconque l’un par rapport à l’autre. Très rares sont les auteurs qui font la distinction : seule la dilatation des durées impropres est généralement présentée (qualifiée d’apparente), ce qui rend difficilement compréhensible le second phénomène qui se traduit par un résidu temporel « absolu ». En fait, c’est le second effet qui est le plus général et qui devrait donc avoir la priorité des enseignants et vulgarisateurs, tandis que le premier constitue une expérience idéalisée et restrictive entre deux référentiels inertiels.

Einstein indique que son résultat est valable si l’on fait « l'hypothèse que le résultat obtenu pour une ligne polygonale est également vrai pour une ligne courbe ».  En effet, il ne donne pas la façon de procéder pour étudier de manière précise le phénomène dans le cas d’une courbe fermée quelconque, même si son approximation est exacte. La formalisation de Minkowski donnera les outils pour analyser n’importe quel type de mouvement : la relativité restreinte permet d’étudier tous les mouvements possibles (des rotations par exemple), car il s’agit d’une nouvelle cinématique tout à fait générale. Le terme « restreinte » signifie seulement que le principe de relativité n’est valable dans cette théorie que pour les référentiels inertiels. D’ailleurs la pratique théorique moderne de la relativité restreinte ne fait que rarement mention des référentiels inertiels (26).

Einstein fait une prédiction complémentaire :

En s'appuyant sur ce résultat, nous concluons qu'une horloge à balancier placée à l'équateur doit être plus lente par une très petite quantité qu'une autre identique placée à l'un des pôles, les autres conditions étant identiques.

La précision « les autres conditions étant identiques » prend ici tout son sens car Einstein ne savait pas à l’époque qu’un effet similaire de décalage des horloges était à l’œuvre pour la gravitation (il prédira cette conséquence dès 1907). Nous savons aujourd’hui que les deux effets (cinématique et gravitationnel) s’annulent à la surface de l’ellipsoïde terrestre en rotation, de sorte que les horloges distantes immobiles ne se décalent pas.

Signalons qu’une technologie disponible sur notre smartphone nécessite impérativement la prise en compte du décalage prédit par Einstein : la localisation par GPS. Notre localisation sur le globe via notre smartphone est tributaire de la connaissance de la position des satellites GPS, mais aussi de l’instant d’émission du signal vers la Terre (qui sert à déterminer la distance entre le smartphone et le satellite). Le satellite se déplaçant à 14000 km/h environ, le temps indiqué par l’horloge atomique embarquée est nécessairement décalé par rapport aux horloges au sol : il doit donc être corrigé, faute de quoi la position calculée serait inutilisable. Du fait de la désynchronisation cinématique des horloges parfaites, les horloges à bord des satellites GPS retardent par rapport aux horloges au sol et nous avons vu que ce n’est pas un effet apparent : si les horloges étaient ramenées au sol et comparées à leurs congénères, le décalage serait bien présent (27).
 

 

D’autres effets ?

Einstein prédit deux autres effets inédits dans son article. Ils figurent dans la partie dynamique qui n’est pas notre sujet mais nous ne devons en dire un mot car ils sont en fait d’origine cinématique (conséquences uniquement du mouvement). D’une part il établit la formule relativiste pour l’effet Doppler qui inclut l’effet Doppler transverse : celui-ci correspond au cas où la source se déplace perpendiculairement à l’axe d’observation. L’effet est nul en physique classique (pas d’éloignement ni de rapprochement) tandis que le terme résiduel correspond en relativité à la dilatation des durées impropres. D’autre part, il détermine la formule pour l’aberration relativiste qui décrit le phénomène bien connu mais se traduit aussi par des effets inédits.

 

 

Théorème d'addition des vitesses (paragraphe 5)

Einstein termine la partie cinématique en établissant la formule de composition des vitesses relativiste qui généralise l’additivité classique. Cette formule donne par exemple par rapport au système « stationnaire » la vitesse résultante pour un projectile émis par un corps en mouvement (qui n’est plus une simple addition). Einstein tient à interpréter physiquement cette formule.

De cette égalité, il découle que la combinaison de deux vitesses, chacune étant plus petite que c, donne une vitesse toujours plus petite que c.

Il est également évident que la vitesse de la lumière c ne peut être modifiée en lui ajoutant une valeur plus petite.

 

Une démonstration éclair de la composition des vitesses     Nous allons démontrer la loi de compositions des vitesses relativiste dans un cas très simple. Supposons qu’un train se déplace à la vitesse u sur sa voie rectiligne et qu’un voyageur se meut dans le train vers l’avant à la vitesse v (les deux mouvements s’effectuent donc selon le même axe). Si nous raisonnons dans un référentiel attaché au train, les coordonnées du voyageur (longueur parcourue x’ au bout du temps t’) sont données par l’équation :         Utilisons la transformation de Lorentz pour exprimer ces coordonnées en fonction de celles x et t mesurées dans un référentiel attaché à la voie:         On en déduit :         La vitesse du voyageur par rapport au sol (ou à la voie) n’est donc plus u+v mais :         La formule ci-dessus redonne la valeur classique en première approximation (pour des vitesses u et v faibles devant c). On remarquera, dans cette formule, que toute vitesse v composée avec c (u = c) redonne c (vitesse limite). Et que d’ailleurs la formule est bornée supérieurement par c (pour des vitesses inférieures à c).

 

Les deux remarques précédentes sont certes déjà la conséquence du deuxième postulat de la cinématique einsteinienne (invariance de c) ; mais l’important ici pour Einstein est de préciser la signification physique de cette composition des vitesses et la cohérence de l’ensemble. Poincaré a également établi cette même formule en 1905 ; mais il ne l’associe pas à une cinématique générale : elle est censée s’appliquer uniquement aux vitesses instantanées des électrons puisqu’elle sous-tend sa dynamique, le cadre cinématique étant toujours celui de la physique classique. Deux formules mathématiques identiques certes, mais avec une signification physique radicalement différente pour leurs auteurs.

Einstein remarque ensuite sans faire de démonstration :

Nous observons qu'une telle transformation parallèle forme (comme il se doit) un groupe.

Les propriétés de groupe sont aussi établies par Poincaré en 1905 dans son mémoire de Palerme ainsi que d’autres éléments mathématiques importants (par exemple le fait que les transformations de Lorentz sont équivalentes à une rotation dans un espace à quatre dimensions), qu’il n’interprète pas physiquement comme la base de la future chrono-géométrie de l’espace-temps révélée par Minkowski.

Einstein conclut en rappelant l’articulation de son article et la logique originale de son approche :

Nous avons déduit la cinématique qui correspond à nos deux principes fondamentaux pour les lois qui nous sont nécessaires, et nous passons maintenant à leur application en électrodynamique.

Cette phase que nous venons de commenter est spécifique à la démarche einsteinienne puisqu’il est le seul à proposer une solution basée sur une remise en cause profonde de l’espace et du temps en général.

La table qui suit récapitule les principaux éléments physiques constitutifs de la relativité restreinte tels qu’ils apparaissent chez Einstein en 1905, en nous limitant à la partie cinématique. Nous indiquons si ces éléments se retrouvent chez Poincaré et sous quelle forme.

 

 

	Einstein	Poincaré
Principe de relativité	Axiome premier (principe opératoire)	Conjecture (contrainte à appliquer à toute interaction physique)
Invariance de la vitesse de la lumière	Postulat de la nouvelle cinématique (constance structurelle)	Constance seulement apparente (variations compensées par d’autres effets)
Existence d’une vitesse limite	Conséquence de la nouvelle cinématique	Impossibilité dynamique (augmentation de la masse avec la vitesse)
Nouveau cadre cinématique	Einstein est le premier à proposer un nouveau cadre cinématique	Poincaré garde l’ancien
Pas d’espace absolu	Rejet de tout référentiel inertiel privilégié	L’éther reste le référentiel privilégié pour l’électromagnétisme, même si aucun mouvement par rapport à l’éther n’est détectable
Pas de temps absolu	Autant de temps que de référentiels inertiels Chaque voyageur emporte avec lui son temps propre : rejet du temps universel unique	Tous les temps mesurés sont apparents sauf au repos par rapport à l’éther. Le temps qui s’écoule réellement est absolu (comme chez Newton)
Pas de simultanéité absolue	Conséquence de la nouvelle cinématique (simultanéité relative à un référentiel inertiel donné)	Artefact des opérations de mesure (réglage défectueux des horloges)
Pas d’éther	Abandon de l’éther	Maintien de l’éther comme milieu de propagation de la lumière doté de propriétés spécifiques
Transformations de Lorentz	Dérivées des deux postulats de la nouvelle cinématique	Construites ad hoc pour laisser invariantes les lois de l’électromagnétisme
Composition relativiste des vitesses	Formule générale applicable à la nouvelle cinématique	Formule applicable uniquement aux vitesses instantanées des électrons
Contraction des longueurs	Effet de perspective (conséquence purement cinématique)	Effet dynamique (compression physique)
Dilatation des durées impropres	Einstein est le premier à prédire cet effet	Effet absent chez Poincaré
Multiplicité des temps propres	Einstein est le premier à prédire cet effet	Effet absent chez Poincaré
Effet Doppler transverse	Einstein est le premier à prédire cet effet	Effet absent chez Poincaré
Aberration relativiste	Einstein est le premier à prédire cet effet	Effet absent chez Poincaré

 

 

La table précédente montre de façon frappante le fossé énorme qui sépare l’approche d’Einstein de celle de Poincaré, la révolution conceptuelle autour du temps ayant échappé à tous les prédécesseurs d’Einstein.

 

Remerciements à besso

Pour finir, Einstein tient à témoigner sa gratitude à son ami le plus proche et quasi contemporain Michele Besso (1873-1955), qui lui servit de caisse de résonance pour ses réflexions sur la relativité :

En terminant, je tiens à souligner que mon ami et collègue M. Besso m'a prêté son concours pendant que je travaillais au problème discuté ici, et que je lui suis redevable de suggestions précieuses.

 

 

Figure 10 : Einstein et Besso, ca 1925 (image bibliothèque numérique ILCE)

 

Quelles sont les suggestions précieuses qu’évoque Einstein ? Nous pouvons nous en faire une idée intéressante par les propos que tient Einstein lors d’une conférence à Kyoto en décembre 1922, où il se remémore certains épisodes ayant précédé l’élaboration de sa théorie :

Cette invariance de la vitesse de la lumière était toutefois en conflit avec la règle d’addition des vitesses bien connue en mécanique. J’éprouvais une grande difficulté à comprendre pourquoi ces deux faits se contredisaient mutuellement. J’avais passé presque une année en considérations infructueuses, espérant parvenir à modifier l’idée de Lorentz, mais je fus bien obligé de reconnaître que ce problème n’était pas du tout évident. Par bonheur, un de mes amis berlinois [Michele Besso] vint à mon secours. Ce fut vraiment une très belle journée, ce jour où je lui rendis visite ; je commençai par lui expliquer : « J’ai rencontré récemment un problème que je ne parviens pas à résoudre et je viens en débattre avec toi. » Après avoir examiné avec lui pas mal de possibilités, je parvins soudain à cerner le problème. Le lendemain, je revins le voir et, sans prendre le temps de le saluer, je lui dis : « Merci. J’ai entièrement résolu le problème. » Ma solution résidait dans le concept même de temps, c'est-à-dire dans le fait que le temps n’est pas défini de manière absolue, mais qu’il existe une relation indissociable entre le temps et la vitesse d’un signal. Si l’on comprenait cela, on pouvait résoudre l’extraordinaire difficulté précédente. Cinq semaines après avoir reconnu ce fait, la théorie actuelle de la relativité restreinte était achevée (28).

Ces réminiscences d’Einstein signifient-elles que le travail de 1905 n’est que le résultat d’un éclair de génie ? Einstein a bien sûr subi des influences et s’est nourri de lectures diverses avant de pouvoir cerner le problème ; mais il n’en est pas moins vrai que sa démarche est largement indépendante (29) et se démarque nettement de ses prédécesseurs, car lui seul a su exploiter une perspective réellement novatrice. Laissons Einstein lui-même nous livrer sa propre appréciation de son travail, avec un recul salutaire:

Ce qui était nouveau dans ce mémoire, c'est d'avoir découvert le fait que la portée de la transformation de Lorentz transcendait sa connexion avec les équations de Maxwell et mettait en cause la nature de l'espace et du temps en général. Ce qui était également nouveau, c'est que l'invariance de Lorentz est une condition générale pour toute théorie physique (30) .

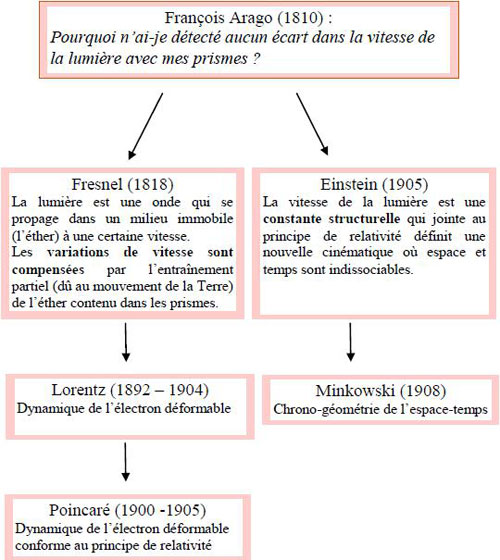
Un moyen d’y voir plus clair est de dessiner un schéma sur les deux approches principales concurrentes pour expliquer l’ensemble des phénomènes électromagnétiques connus (optiques inclus).

 

Deux réponses très différentes à une même question

 

 

Le premier indice en faveur de la future relativité restreinte remonte à l’expérience (31) de François Arago conduite en 1810. Arago cherche à détecter des écarts dans la vitesse de la lumière, notamment selon que la Terre se dirige vers les étoiles visées ou qu’elle s’en éloigne.

Arago a l’idée ingénieuse d’utiliser des prismes pour repérer ces éventuelles variations, la déviation des rayons lumineux devant être d’autant plus marquée que la vitesse incidente est plus grande. Or les prismes ne révèlent aucun écart, contre toute attente. Arago finit par se tourner vers son protégé Augustin Fresnel, qui parvient à expliquer les observations à l’aide d’une double hypothèse basée sur l’éther (voir l’encadré). Ce modèle de l’éther sera repris par Lorentz et Poincaré en y incorporant le comportement des électrons. L’idée astucieuse de la compensation (qui explique la constance apparente de la vitesse de la lumière) due à Fresnel fera école via le temps local (des horloges mal réglées) et la compression physique des corps en mouvement à travers l’éther.

Avec sa solution inédite, Einstein reprend le problème à zéro et remonte en quelque sorte à la question d’Arago posée à Fresnel : il propose une solution qui n’a rien à voir avec celle de Fresnel, une solution de son cru, plus simple et plus novatrice à la fois. À la lecture de son article de 1905, tout particulièrement les passages consacrés à sa définition du temps ou aux conséquences temporelles nouvelles, on ne peut s’empêcher de citer Arthur Koestler (32) :

Tout acte créateur – dans la Science, l’art ou la religion – implique le retour à un niveau primitif, l’innocence nouvelle d’une perception délivrée de la cataracte des croyances établies.

 

 

@@@@@@@

 

 

Une exclusivité d’Einstein : la dilatation des durées     Il est fréquent de lire (y compris dans des encyclopédies en ligne) que Larmor en 1900 puis, indépendamment Lorentz en 1904 auraient introduit la dilatation des durées dans leurs équations. Cette façon de présenter l’histoire est fâcheusement trompeuse car métonymique. Nous entendons par là l’habitude consistant à utiliser un mot désignant un nouveau phénomène physique pour évoquer l’usage d’une simple grandeur mathématique auxiliaire : en l’occurrence Ce dernier terme apparaît effectivement dans les formules de transformations de coordonnées proposées par Larmor (1900) puis Lorentz (1904) ; mais elles ne furent jamais jusqu’à Einstein considérées comme l’expression d’une nouvelle cinématique. Poincaré interprète physiquement à sa façon le temps (appelé « local ») t’ = t – vx/c2 mais ignore le terme qui, suite aux travaux d’Einstein, sera associé au phénomène physique de dilatation des durées. Pourtant il n’est pas rare de trouver sous la plume d’auteurs même récents, l’idée selon laquelle la dilatation des durées serait chez Poincaré ou Lorentz un phénomène d’origine dynamique de manière analogue à la contraction des longueurs : tous les corps subiraient lors de leur mouvement un « ralentissement » temporel en plus de la compression physique déjà supposée par les deux physiciens. Il est important de comprendre qu’il s’agit d’une extension de la théorie de Lorentz-Poincaré pour tenter de la rendre compatible avec les nouveaux effets prédits par Einstein. Une telle approche est-elle envisageable et surtout cohérente ? Comment expliquer par la dynamique (donc par l’intermédiaire d’une force spéciale exercée par l’éther) un phénomène aussi général que la multiplicité des temps propres qui impliquerait que tout processus physique périodique (une horloge à pendule aussi bien qu’une horloge atomique par exemple) serait ralenti identiquement lors de son passage à travers l’éther ? Est-il possible de rendre compte d’un effet chrono-géométrique (tel que le « paradoxe » des jumeaux) en partant de la dynamique ? La révolution conceptuelle autour du temps instaurée par Einstein a révélé en fait les limites de l’approche dynamique de Lorentz-Poincaré, impuissante à expliquer ces effets temporels dans toute leur généralité. Ce n’est donc pas un hasard si aucun physicien pré-relativiste n’a anticipé de tels changements (33).

 

 

Une approche fructueuse

Même si elle rencontra une forte résistance, la solution proposée par Einstein, grâce à son efficacité et sa simplicité, sera adoptée rapidement par certains physiciens, le plus célèbre d’entre eux étant Max Planck, qui fut le premier à publier un article sur la relativité après Einstein en 1906. Dès 1907, Max von Laue (membre de l’équipe de Planck) démontre que la formule connue de la théorie de l’éther de Fresnel donnant la vitesse de la lumière traversant un tube d’eau en mouvement (expérience de Fizeau) peut être retrouvée en première approximation par la relativité restreinte (34). Nous avons déjà indiqué que Paul Langevin est le premier physicien français à soutenir l’approche d’Einstein. Minkowski, qui fait partie de l’équipe du mathématicien David Hilbert publie un article capital en 1908 qui formalise l’espace-temps. Enfin Einstein lui-même publie en 1905 un autre article fameux (très court) où il dérive l’équivalence masse-énergie du principe de relativité. Puis, dès 1907, il énonce le principe d’équivalence locale entre gravitation et accélération dans un autre article mémorable (35), première étape importante sur la longue route qui le mènera à la relativité générale.

 

 

Figure 11 : Max von Laue (1879 - 1960), Max Planck (1858 – 1947), Paul Langevin (1872 - 1946). Trois physiciens de premier ordre qui soutinrent très tôt la théorie d’Einstein.

 

 

Révolution ou « pas » ?

Certains auteurs préfèrent parler de « pas » plutôt que de « révolution » pour qualifier l’originalité du travail d’Einstein. En fait, si l’on s’intéresse aux grands principes, on peut effectivement voir dans la démarche d’Einstein un prolongement splendide d’idées initiées par Galilée (construire la physique sur des principes d’invariance), donc une avancée majeure qui s’inscrit dans une certaine continuité. En revanche nous sommes incontestablement en présence d’une révolution conceptuelle autour du temps si l’on examine les conséquences physiques, si éloignées de notre expérience ordinaire et que l’on peut qualifier d’ « extraordinaires ».

Finalement, après avoir commenté cet article crucial de 1905, si riche et si original, une conclusion s’impose : la relativité restreinte, en tant que nouvelle théorie de l’espace et du temps, naît avec ce papier magistral, qui n’a rien perdu de sa fraîcheur.

Petite ironie de l’histoire des sciences : si nous voulons vraiment comprendre la relativité restreinte et sa genèse, nous devons accepter de perdre notre temps, c'est-à-dire de jeter aux oubliettes ce temps universel unique qui était jusqu’à Einstein une évidence immémoriale.

 

(Novembre 2014)

 

 

 

 

 

 

---