Euler et le parcours du cavalier dans une grille rectangulaire

Dans un Mémoire de 1759, intitulé « Solution d’une question curieuse qui parait soumise à aucune analyse », Leonhard Euler étudie essentiellement le parcours du cavalier des échecs dans l’échiquier de 64 cases. Il aborde sommairement le parcours du cavalier dans une grille rectangulaire, dans une seule et unique page que nous nous proposons de commenter et de développer (texte BibNum).

 

 

Le parcours du cavalier – Généralités – Propriétés.

Rappelons que le parcours du cavalier dans une grille carrée, rectangulaire ou cruciforme, peut être « ouvert » lorsque sa première case et sa dernière ne peuvent pas être jointes par un saut du cavalier. Dans ce cas, le parcours du cavalier ne peut être suivi que dans un sens ou dans l’autre.

Ce parcours est dit « fermé » ou « rentrant » dans le cas contraire : le parcours du cavalier peut être suivi, dans un sens ou dans l’autre, à partir d’une case quelconque du circuit.

Un parcours fermé du cavalier dans une grille carrée, est dit « symétrique », lorsque la différence de deux nombres complémentaires, c’est-à-dire diagonalement opposés, est constante Euler en donne un exemple dans l’échiquier de 36 cases,  précisément, au bas de la page 336, dernière figure : la différence constante des nombres complémentaires est ainsi de 18.

 

 

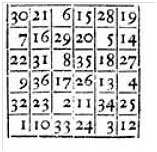
Un parcours ouvert ou fermé du cavalier dans une grille carrée, est dit « de type associé », lorsque les cases complémentaires ont une somme constante. Dans l’exemple ci-dessous, une grille d’ordre n = 7 de 49 cases, la somme constante est égale à  S = 50, soit S = n² + 1. La case centrale est alors égale à la demi-somme constante.

 

 

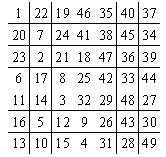
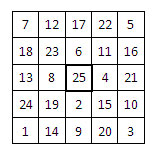
Il n’y a pas de parcours magique du cavalier dans l’échiquier de 64 cases – c’est-à-dire un parcours dont la grille constitue un carré magique[1]. On compte cependant 108 parcours semi-magiques dans l’échiquier de 64 cases. Le plus petit parcours magique interne du cavalier, a été annoncé le 25 mars 2003 par Awani Kunar, de Lucknow (Inde), dans une grille d’ordre n = 12 de 144 cases. Cependant, on trouve un parcours magique du cavalier, tout-à-fait particulier,  dans une grille d’ordre n = 5 de 25 cases !

Marche principale du cavalier : 2 pas à droite, un pas vers le haut.

Marche secondaire (à 5, 10, etc.) : 2 pas vers le haut.

Il faut préciser que ce parcours du cavalier ne se circonscrit pas dans les limites de la grille : lorsque le parcours déborde, il faut le réintégrer dans la grille, selon la technique habituelle.

 

 

P. 336 (et haut de page 337) du mémoire d’Euler 1759 (extrait du texte BibNum), sur le parcours du cavalier dans un rectangle (sujet auquel nous nous attachons plus particulièrement dans la suite).

 

 

 

 

Le parcours du cavalier dans la grille rectangulaire : La méthode d’Euler

Leonhard Euler donne une dizaine de parcours du cavalier dans des grilles rectangulaires de diverses tailles. À cette occasion il ne précise pas de façon explicite sa méthode de construction. Cependant, dans son Mémoire,  il expose, plutôt qu’une méthode, un procédé de construction du parcours du cavalier dans l’échiquier, en annonçant que cette technique est applicable aux grilles rectangulaires et cruciformes.

Leonhard Euler nous dit lui-même qu’il a été conduit à appliquer cette technique, à la suite d’une idée toute particulière qui lui a été donnée par un certain M. Bertrand de Genève : il s’agit du mathématicien Louis Bertrand (1731-1812).

Voici donc cette idée, qui n’apparait elle-même pas directement dans le Mémoire d’Euler, mais que l’on peut déduire de ses exemples : Si à l’intérieur d’un trajet, il se trouve quelque(s) case(s), [différente(s)de l’avant-dernière case], qui  puisse(nt) être reliée(s) par un saut du cavalier, alors on dispose d’un autre trajet, susceptible de débloquer le parcours en cours.

 

 

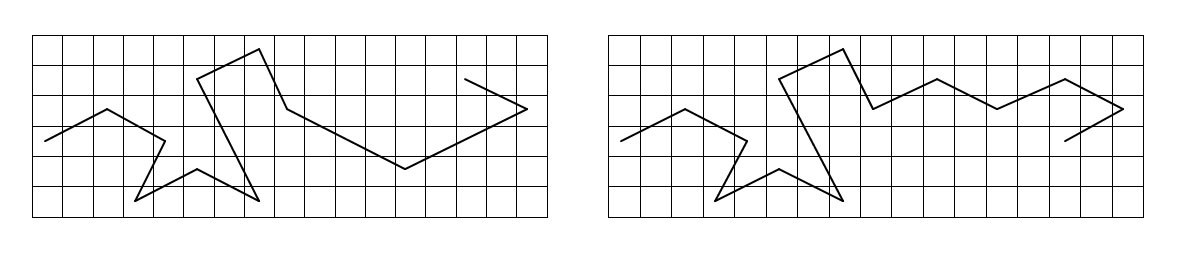
Voici ci-dessus une illustration de cette idée simple.

En effet, lorsque la dernière case du trajet en cours ne permet pas de joindre une case restée vide par un saut du cavalier, il y a blocage. L’idée de M. Bertrand, en conservant en partie le trajet qui précède,  permet de déplacer la case finale de ce trajet, et ainsi, soit immédiatement, soit après plusieurs tentatives, de rejoindre alors l’une des cases encore vierge, qui sera intégrée au parcours en question. De proche en proche, on arrivera ainsi à parcourir toute la grille. La « méthode » qui en résulte est applicable, répétons-le, à toute grille carrée, rectangulaire ou cruciforme.

Leonhard Euler applique systématiquement cette technique très simple en apparence, avec constance, négligeant parfois d’autres possibilités plus simples : c’est ce qui apparait notamment dans les exemples de parcours dans diverses grilles rectangulaires donnés par Euler (à partir de §42, p. 336).

 

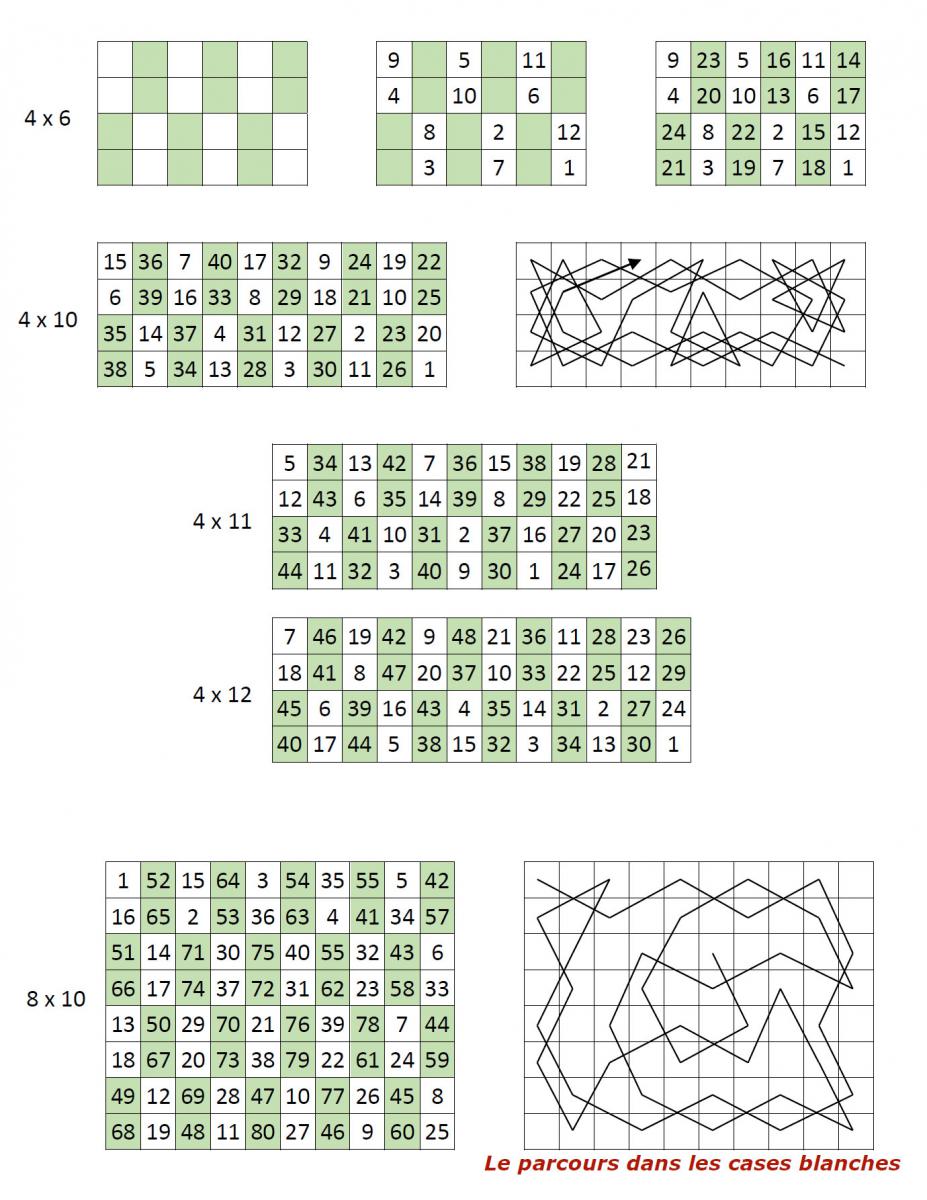
La Méthode de la Grille

Cette méthode était largement connue bien avant Leonhard Euler[2].

 

 

 

 

 

 

La méthode s’applique à l’origine au demi-échiquier, une grille rectangulaire 4 x 8. On poche la grille comme indiqué ci-dessus. On remplit tout d’abord les cases  blanches par un parcours du cavalier, soit la grille centrale ci-dessus ; puis on remplit les cases pochées. Elle s’étend aux grilles rectangulaires paires dont un côté est égal à 4 ou un multiple de 4. Mais pour les grilles carrées de 4 x 4 ou de 8 x 8 (grille carrée), cela semble impossible !

Voici quelques autres exemples d’application de la méthode :

 

La Méthode de Moivre (1722)

La « Méthode de Moivre », connue aussi sous le nom de « Méthode des bordures », semble apparaitre pour la première fois dans les Récréations mathématiques et physiques, de Jacques Ozanam (Paris, 1724, 4 vol.).

On sélectionne une couronne, ou une bordure, de largeur 2 cases, que l’on remplit avec un parcours du cavalier, en tournant toujours dans le même sens. On n’entre dans la grille centrale rectangulaire que lorsque l’on y est contraint, pour revenir aussitôt dans la couronne. Celle-ci remplie, on passe au parcours du cavalier dans la grille centrale. La méthode de Moivre est « réputée applicable à toutes grilles carrées ou rectangulaires, de tous ordres[3] ».

Cependant on observe quelques restrictions. On sait d’expérience que la grille centrale rectangulaire d’ordre 3 x 5 et 3 x 6 ne peut pas être parcourue par la cavalier ; ainsi la méthode de Moivre ne peut-elle pas s’appliquer aux grilles d’ordre 7 x 9 et 7 x 10 (c’est-à-dire 3 x 5 et 3 x 6 entourées d’une bordure de 2 x 2).

Voici un exemple d’application du parcours du cavalier dans une grille rectangulaire d’ordre 7 x 13 de 91 cases : un parcours ouvert.

 

 

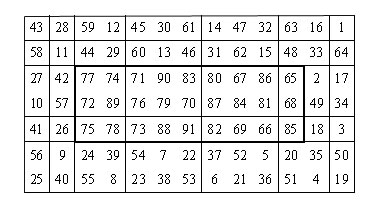
Si la couronne peut être assez facilement remplie par un parcours du cavalier, la grille rectangulaire centrale,  lorsqu’une ou deux  cases sont  déjà occupées, s’avère souvent plus difficile, sinon impossible à remplir.

 

 

Un cas particulier : absence de grille centrale.

Dans toutes les grilles qui ont un côté n = 4, la grille centrale disparait.

Après divers essais, on observe que la méthode de Moivre est applicable à toutes grilles mixtes d’ordre  4 x 5, 4 x 7, 4 x 9 . . . , à l’exclusion des grilles paires 4 x 6, 4 x 8, 4 x 10 . . .

Exemples : la case-départ et la case finale sont côte à côte.

 

 

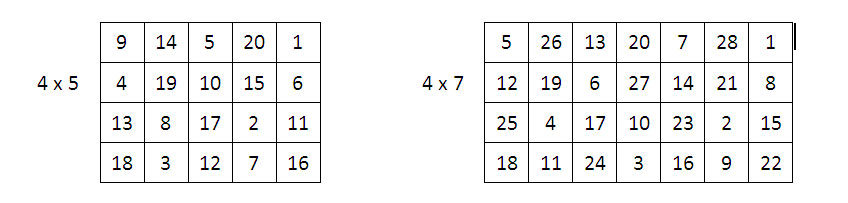
D’ailleurs, il semble bien que la Méthode de Moivre ne s’applique pas, en général,  aux grilles rectangulaires  paires : nous n’avons pas réussi à placer un parcours du cavalier, en application de la Méthode de Moivre, dans une grille rectangulaire paire. Mais cela ne veut pas dire que le parcours du cavalier est exclu des grilles paires !

Voici un bel exemple d’un parcours ouvert du cavalier dans  une grille rectangulaire paire d’ordre 10 x 12, réalisé par Arsène Durupt[4] :

 

 

Page 332 du Mémoire d’Euler.

Dans la grille carrée ci-contre, d’ordre n = 5, la grille centrale est réduite à une seule case centrale, qui correspond à la case finale.

 

 

 

Page 336 du Mémoire d’Euler.

Dans cet exemple, une grille rectangulaire d’ordre 4 x 7,  la grille centrale a disparu. La case-départ et la case finale sont côte-à-côte.

 

 

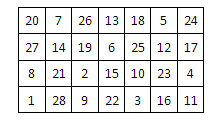
Dans les deux grilles ci-dessus, le parcours du cavalier selon la Méthode de Moivre, est bien visible dans la couronne  de deux cases de largeur (dans le 2^e cas, la grille centrale a disparu, mais le parcours en couronne est bien visible).

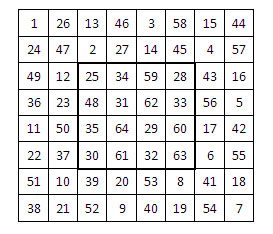
On trouve également parmi les manuscrits de Leonhard Euler à propos du parcours du cavalier, publiés par Jacques Sésiano (p. 42, fig. 39), un parcours ouvert du cavalier dans l’échiquier de 64 cases, construit en grande partie par la Méthode de Moivre (ci-dessous). Mais Euler fait plusieurs incursions dans la grille centrale (à partir de 25), avant de retourner dans la couronne. Peut-on éviter ces incursions intempestives ?

 

Le cavalier, à l’origine du rectangle magique

À ce jour, en 2015, on ne connait pas de parcours magique du cavalier dans une grille rectangulaire[5]. Ce qui ne veut pas dire que ce parcours magique n’existe pas  dans une grille rectangulaire d’ordre élevé. On peut dire que c’est un problème qui n’a pas encore trouvé de solution. Le parcours du cavalier est cependant à l’origine de la construction de la grille rectangulaire magique.

Un  parcours du cavalier dans le rectangle primaire

Rappelons que le parcours du cavalier peut se développer dans toute grille carrée, ou rectangulaire d’ordre impair, pair ou mixte, à l’exclusion des rectangles d’ordre 3 x 5 et 3 x 6 : Euler le précise lui-même dans son Mémoire :

Si la largeur contient 3 cases, & la longueur 5 ou 6, il est impossible de les parcourir [p. 336]

Cela étant, on se propose alors de rendre magique, par diverses manipulations,  la grille numérique rectangulaire contenant ce parcours, lorsque c’est possible.

La magie dans les rectangles mixtes n’étant pas possible, il nous reste à étudier le parcours du cavalier dans un rectangle primaire d’ordre impair et pair.

Dans ces conditions, la construction d’un rectangle magique comprend donc en principe deux phases :

1. La construction du parcours du cavalier remplissant toute la grille rectangulaire, comme rectangle primaire (phase abordée précédemment) ;

2. La construction du rectangle magique proprement dite.

 

 

Le parcours du cavalier dans un rectangle primaire d’ordre impair

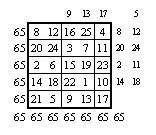
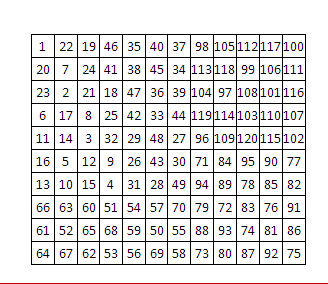
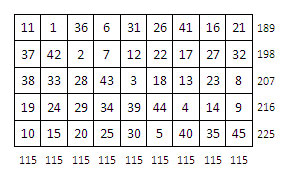
1^er exemple : rectangle 5 x 9.

Le parcours du cavalier, la case-départ étant fixée dans une case d’angle,  en utilisant une marche uniforme du cavalier, remplit toute la grille (avec la possibilité d’en sortir, suivant les règles habituelles), et celle-ci est immédiatement exploitable.

 

 

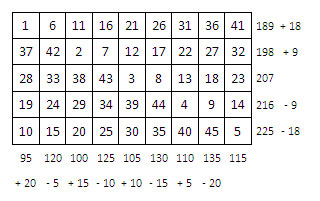
Rétablissons la magie des colonnes (somme 115) – hors parcours de cavalier :

 

 

Et celle des lignes (somme 207) :

 

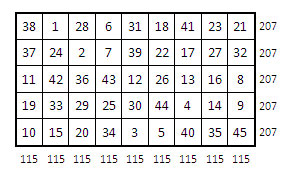
Voici d’autres parcours du cavalier dans un rectangle d’ordre impair, susceptibles d’être utilisés comme rectangle primaire pour la construction d’un rectangle magique :

 

 

 

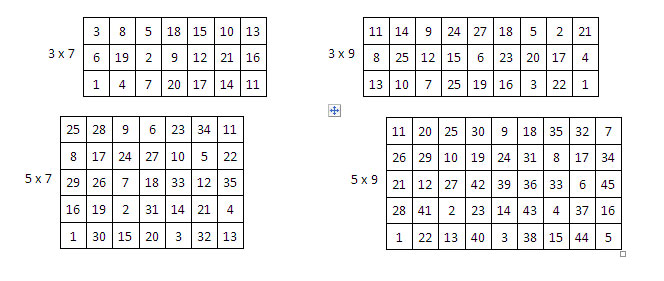
Le parcours du cavalier dans un rectangle primaire d’ordre pair

Le premier parcours du cavalier dans un rectangle d’ordre pair qui nous vient à l’esprit, est le demi-échiquier : un rectangle 4 x 8. Le cavalier peut en effet parcourir de façon indépendante les deux demi-grilles de l’échiquier de 64 cases.

Voici, par Leonard Euler (in Sesiano, p.66, fig. 75) un parcours du cavalier dans l’échiquier, de façon indépendante dans les deux demi-échiquiers. C’est un parcours fermé ou rentrant, présentant la curieuse propriété suivante : la différence des nombres complémentaires est constante, et égale à  D = 32.

 

 

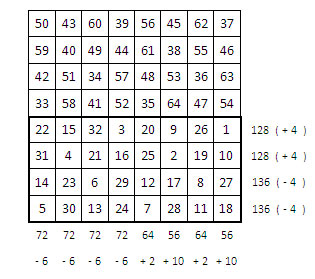
Peut-on considérer ce  rectangle  comme « rectangle primaire », et rendre  magiques ses colonnes et ses lignes ? Les constantes magiques rectangulaires étant  alors 66 pour les colonnes et 132 pour les lignes.

Rétablissement de la magie à la fois dans colonnes et dans les lignes :

 

 

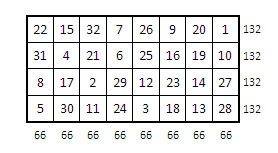
Rappelons à ce sujet, avec Euler, que le parcours du cavalier peut être rentrant ou fermé dans toute grille carrée ou rectangulaire dont le nombre de cases est pair, sous réserve qu’il n’y ait pas moins  de 5 cases sur un côté :

Jusqu’ici les routes rentrantes en elles-mêmes ne peuvent pas avoir lieu ; mais, donnant 5 cases à la largeur, et 6 à la longueur, on pourra aussi remplir cette condition, de même que dans tous les autres rectangles, dont le nombre de cases est pair, pourvu qu’il n’y ait pas moins de 5 cases dans un côté [§43, p. 336]

Le plus petit parcours rentrant du cavalier se trouve ainsi dans la grille rectangulaire 5 x 6 :

 

 

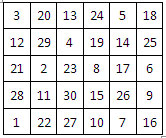
Voici un autre exemple de parcours du cavalier dans un rectangle d’ordre 4 x 6, donné également par Euler (in Sésiano, p.115, fig. 166) :

 

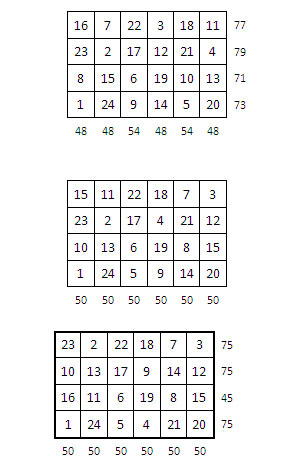
Si le principe de ces méthodes, inspirées de la Méthode du Dr Planck, est simple, le rétablissement de la magie dans les colonnes et les lignes, peut conduire à des essais  infructueux parfois relativement nombreux, ce qui peut rebuter quelque peu l’amateur. La patience est donc de rigueur !

 

 

Propriétés du rectangle magique

Nous éloignant d’Euler et de la marche du cavalier, saisissons l’occasion qui se présente d’offrir quelques propriétés du rectangle magique, bien négligé dans la littérature des figures magiques !

 

La construction d’un cube magique 

il s’agit d’un cas particulier du rectangle magique normal d’ordre 3 x 9. Voici l’une des solutions de ce rectangle magique normal  d’ordre  3 x 9 :

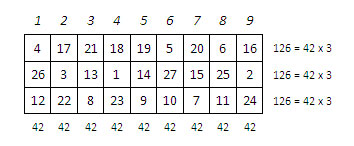
On peut permuter certaines colonnes (ainsi que les lignes) sans altérer la magie de ce rectangle magique. Ainsi, en regroupant 3 par 3 les colonnes  (1, 4, 7), (2,  5, 8) et (3, 6, 9), on obtient le rectangle magique ci-après, qui peut être décomposés en trois carrés magiques  ou semi-magiques d’ordre n = 3, lesquels,  superposés, forment un cube magique normal d’ordre n = 3, de constante magique  42 :

 

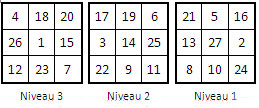
Voici ci-dessous les 15 coupes réglementaires de ce cube magique normal : 9 coupes orthogonales et 6 coupes diagonales, soit au total 120 alignements de 3 nombres (3 lignes, 3 colonnes, 2 diagonales, le tout multiplié par 15 grilles). On compte 88 alignements magiques (ceux où apparaît la somme 42), 2 carrés magiques et 6 carrés semi-magiques.

 

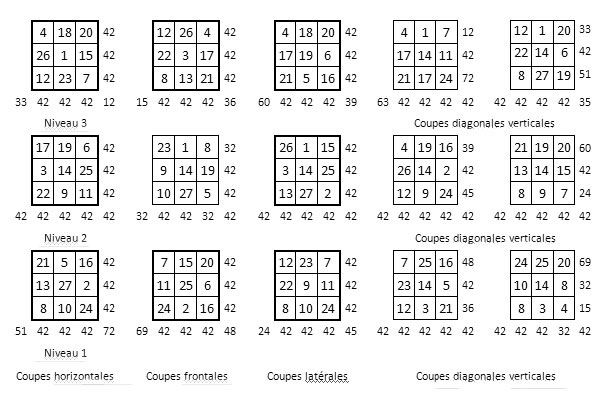
On peut penser que, suivant les mêmes errements, on peut construire  un cube magique d’ordre n = 4, n = 5, n = 6 . . . avec pour base un rectangle magique d’ordre  4 x 16, 5 x 25, 6 x 36…

 

 

 

 

 

 Le produit de deux rectangles magiques normaux

 

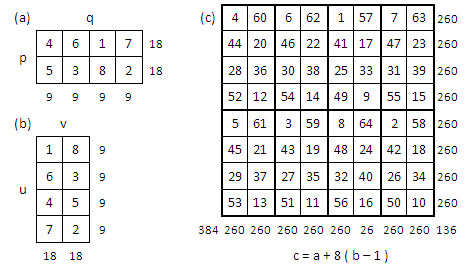
On se propose d’effectuer le produit des deux rectangles magiques normaux de 4 x 2 ci-dessus, et d’examiner les propriétés particulières du résultat de cette opération ; une idée tirée des recherches de Simon Falconoras et fils[6].

Rappelons que dans un rectangle magique, le nombre de cases sur chaque côté doit être de même parité ; il n’y a pas de rectangle magique « mixte ».

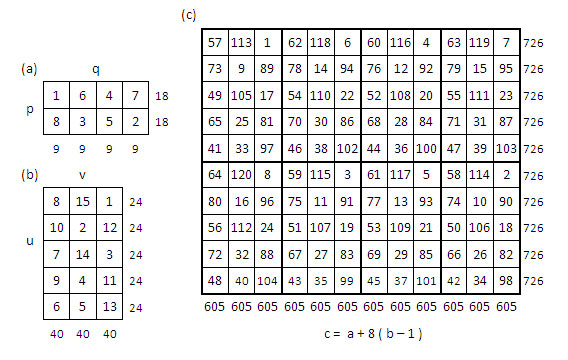
Soit « a » un terme du rectangle magique « p q », « b » un terme du rectangle magique « uv » et « c »  le nombre de la grille « produit » issu de la manipulation décrite ci-dessous, en fonction de « a » et « b ».

 

Première solution  (figure ci-dessus) : On applique la relation :

c = a + pq (b – 1), avec   p q = 8,

soit   c = a + 8 (b – 1) dans les conditions suivantes :

• L’implantation du chiffre « a » dans la grille « pq » correspond à l’implantation du sous-rectangle de 8 cases dans la grille « produit » ;
• L’implantation du chiffre « b » dans la grille « uv », correspond à l’implantation du nombre « c » dans le sous-rectangle défini ci-dessus.

Expl. b = 1 en uv=(1,1), donc c = a, on place chacun des chiffres du rectangle pq, 4, 6, 1, etc. au coin supérieur gauche (1,1) de chacun des 8 sous-rectangles définis en encadré gras dans la grille produit ; b = 8 en uv=(1,2), donc c = a + 56, on place chacun des chiffres c issu des a du rectangle pq, soit 60, 62, 57… à la place (1,2) de chacun des 8 sous-rectangles définis en encadré gras dans la grille produit) ; etc.

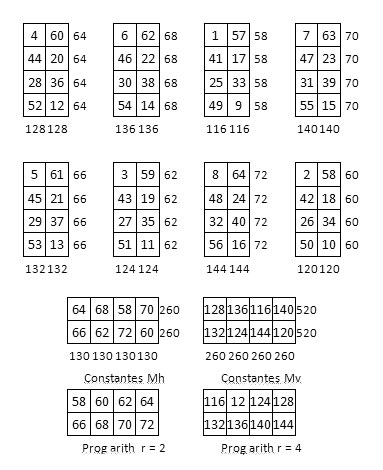
On obtient un carré semi-magique normal, de constante linéaire M₈ = 260.

 

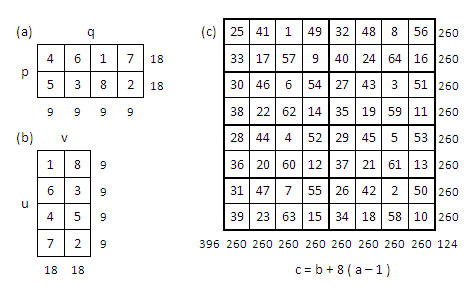
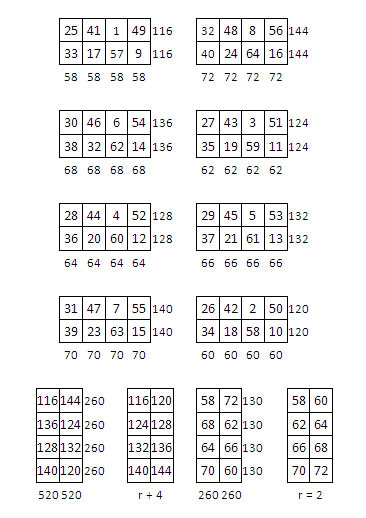
 Deuxième solution : On applique la relation « symétrique » : c = b + uv (a – 1), avec uv = 8,  soit  c = b + 8 (a – 1), dans des conditions analogues aux précédentes, mutatis mutandis.

Expl. a = 1 en pq=(1,3), donc c = b, on place chacun des chiffres du rectangle uv, 1, 8, 6, etc. à la place (1,3) de chacun des 8 sous-rectangles définis en encadré gras dans la grille produit ; b = 2 en pq=(2,4), donc c = b + 8, on place chacun des chiffres c issu des b du rectangle uv, soit 9, 16, 14… à la place (2,4), de chacun des 8 sous-rectangles définis en encadré gras dans la grille produit) ; etc.

On obtient un carré semi-magique normal de constante magique M₈ = 260, différent du précédent.

 

 

Cependant, on observe que les mêmes sommes des termes des sous-rectangles se retrouvent dans les deux carrés magiques. On remarque aussi que ces sommes  sont,  dans chaque grille carrée, en progression arithmétique, de raison r = 8  (grilles ci-dessous).

 

 

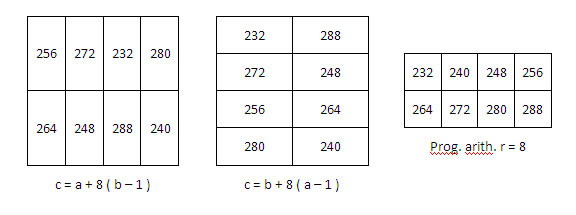
Propriétés du carré semi magique « produit »

Première solution : Les sous-rectangles sont des rectangles magiques, et leurs constantes magiques forment elles-mêmes des rectangles magiques, dont les termes sont en progression arithmétique.

 

 

Deuxième solution. On observe des propriétés analogues aux précédentes :

 

 

Second exemple – Première solution.

Voici un autre exemple de produit de deux rectangles magiques, tiré  du site de Simon Falconoras, « Loi de composition des rectangles magiques » :

 

 

 

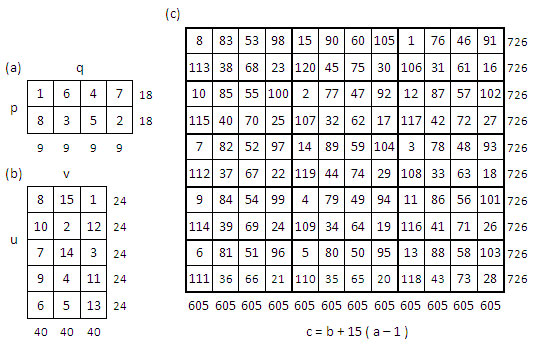
On applique la relation c = b + uv (a – 1) [solution 2 de l’exemple précédent], avec uv = 5 x 3 = 15, soit : c = b + 15 (a – 1). On obtient un rectangle magique  normal d’ordre 12 x 10, de constante horizontale  Mh = 726, et de constante verticale Mv = 605.

 

Second exemple – Seconde solution.

Mais ce qui n’apparait pas clairement, semble-t-il,  pas chez Simon Falconoras, c’est, comme on l’a vu précédemment, qu’une autre solution, avec les mêmes rectangles magiques « pq » et « uv » peut être obtenue, en appliquant la relation  « symétrique » : c = a + pq ( b – 1), soit avec pq = 8  : c = a + 8(b – 1).

Voici cette seconde solution : un rectangle magique normal de mêmes constantes magiques Mh et Mv que le précédent.

 

Propriétés des rectangles « produits »

Les sommes des termes des sous-rectangles forment des rectangles magiques, en progression arithmétique :

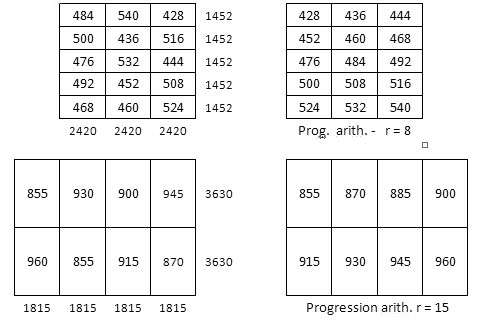
Les sous-rectangles sont des rectangles magiques, dont les constantes forment elles-mêmes des rectangles magiques en progression arithmétique.

 

Première solution

 

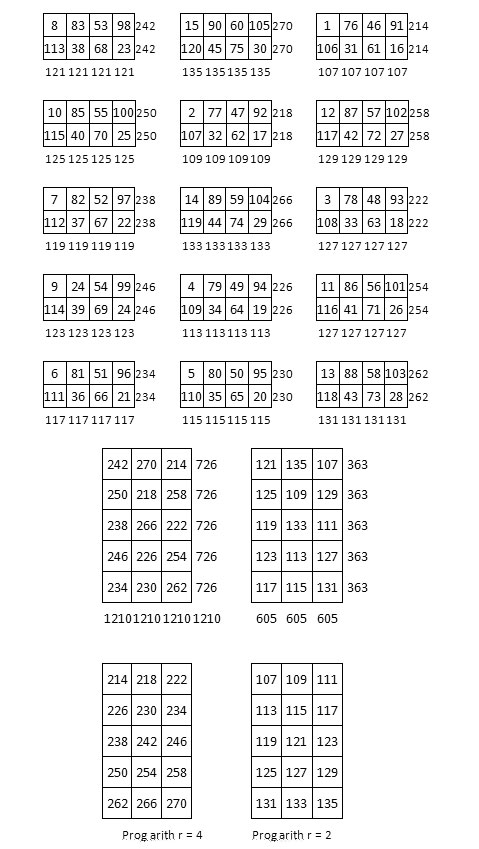
Deuxième solution

 

 

 

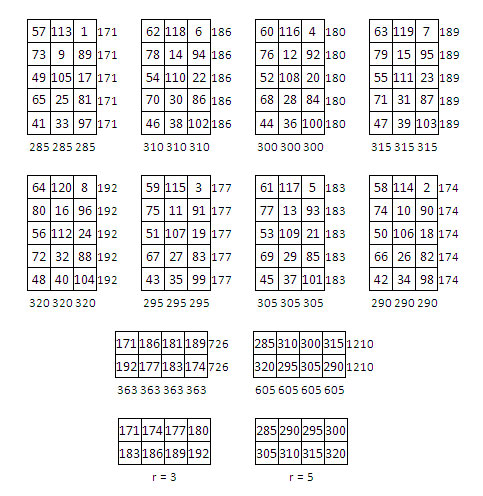
Ainsi  observe-t-on que le produit de deux rectangles magiques de même ordre (premier exemple, 2 ´ 4 par 4 ´ 2, tous deux d’ordre pair, à huit cases) conduit à un carré semi-magique normal ; tandis que le produit de deux rectangles magiques d’ordres différents conduit à un rectangle magique normal (deuxième exemple, 2 ´ 4 par 5 ´ 3, le premier d’ordre pair, le second d’ordre impair), et l’on a dans chaque cas au moins deux solutions à disposition.

On peut dire en effet  « au moins », car peut-être y a-t-il d’autres méthodes  et  manipulations pour effectuer le produit de deux rectangles magiques ?

On peut aussi constater que ces carrés semi-magiques et ces rectangles « produits » sont dotés de propriétés remarquables.

 

 

De curieux rectangles magiques !

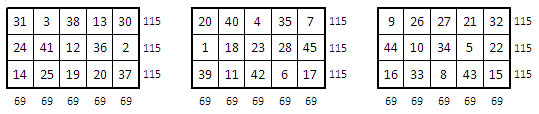
On prépare trois grilles rectangulaires identiques, susceptibles  d’être magiques : par exemple trois grilles 3 x 5 de 15 cases.

 

 

On se propose alors de remplir ces grilles avec la suite des entiers couvrant ces trois grilles, soit depuis 1 jusqu’à  3 x 15 = 45 dans l’exemple ci-dessus, de telle manière que ces trois grilles soient magiques, avec les mêmes constantes magiques dans les lignes et les colonnes.

Une idée comme  une autre !  Exemple : tous les nombres de 1 à 45 sont bien représentés.

 

 

D’après la terminologie anglo-saxonne, on nomme cet ensemble « 3-dimensional magic rectangle »,  soit  « rectangle magique tridimensionnel ». On pourrait dire aussi que ce sont là trois grilles complémentaires.                                                                    

Voici d’autres exemples, émanant du japonais Mitsutoshi Nakamura 2004/2005 (Kagoschima, Japon) :

 

Trois grilles 5 x 7, 35 cases ; un remplissage avec les entiers de 1 à  3 x 35 = 105.

 

 

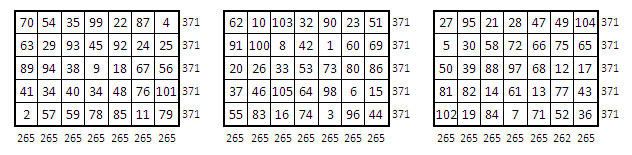
Trois grilles 5 x 11, 55 cases : un remplissage avec les entiers de 1 à 3 x 55 = 165

 

 

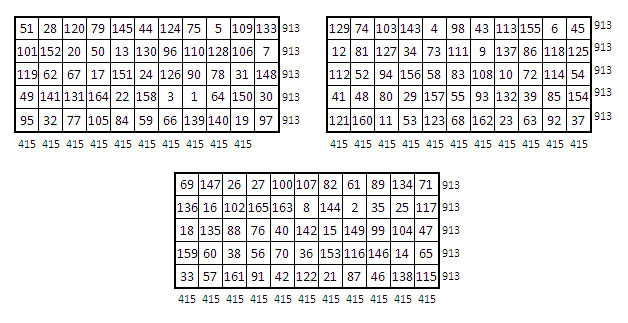
Trois grilles 5 x 13, 65 cases : un remplissage avec les entiers de 1 à 3 x 65 = 195

 

 

 

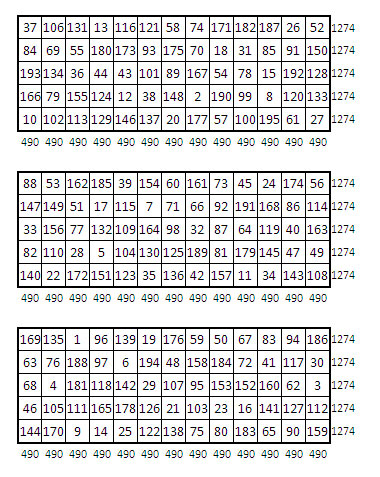
Calcul des constantes magiques associées

Soit  m : nombre de lignes ; n : nombre total de colonnes (somme des colonnes des trois grilles)

Les relations suivantes donnent les constates magiques :

  Constante magique des lignes :          M_m =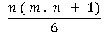

 

  Constante magique des colonnes :    M_n =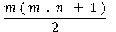

On pourra faire l’application numérique avec les (m, n) ce chacun des exemples ci-dessus.

 

@@@@@@@

 

En conclusion, le décryptage de la page intéressant le parcours du cavalier dans une grille rectangulaire du Mémoire  de Leonhard Euler de 1759, nous permet d’aborder des sujets proches, qui restent dans le cadre des préoccupations du savant bâlois.

 

 

 

(septembre 2015)