Textes fondateurs de la science
analysés par les scientifiques d´aujourd´hui
analysés par les scientifiques d´aujourd´hui
Einstein et les lentilles gravitationnelles
- INFORMATION
- ACTUALITÉ
- ANALYSE
- EN SAVOIR PLUS
- À TÉLÉCHARGER
Einstein et les lentilles gravitationnelles
Auteur : Albert Einstein (1879-1955) - Physicien allemand
Auteur de l'analyse :
Pierre Spagnou - Ingénieur chez Thales Air Systems, auteur scientifique, enseignant à l’ISEP (Institut supérieur d’électronique de Paris)
Publication :
“Lens-Like Action of a Star by the Deviation of Light in the Gravitational Field”, Science, New Series, Vol. 84, No. 2188 (Dec. 4, 1936), p. 506-507.
Année de publication :
1936
Nombre de Pages :
2
Résumé :
L’article d’Einstein sur les effets de lentille entre deux étoiles (anneau, images doubles, amplification de la lumière) constitue le point de départ d’un nouveau chapitre de l’astronomie qui restera longtemps théorique avant de faire quarante ans plus tard l’objet d’observations diverses et fructueuses.
Source de la numérisation :
American Association for the Advancement of Science.
Mise en ligne :
mars 2013
Très courte, la publication d’Einstein de 1936 consacrée aux effets de lentilles entre étoiles sera le point de départ d’un pan entier de l’astronomie dont les premières observations concrètes débutent en 1979. On peut presque qualifier cette note d’article de « science-fiction », car les effets décrits par son auteur ne seront observables que très longtemps après sa disparition ! C’est en fait un trio hétéroclite de trois personnages hors normes Mandl – Einstein – Zwicky qui donnera le coup d’envoi de l’étude (qui restera longtemps purement théorique) des lentilles gravitationnelles, phénomènes étonnants aujourd’hui exploités aussi bien pour la recherche de la matière noire que pour la détection d’exoplanètes.
Pierre Spagnou est ingénieur et auteur d’ouvrages de culture scientifique, notamment De la relativité au GPS – Quand Einstein s’invite dans votre voiture, aux éditions Ellipses. Il enseigne l’histoire des sciences à l’ISEP (Institut Supérieur d’Electronique de Paris) depuis 2012.
Einstein et les lentilles gravitationnelles
Pierre Spagnou - Ingénieur chez Thales Air Systems, auteur scientifique, enseignant à l’ISEP (Institut supérieur d’électronique de Paris)
Figure 1 : Albert Einstein pendant une conférence à Vienne en 1921 (photo Wikimedia Commons)
Une histoire de courbure
L’article futuriste d’Einstein « Lens-Like Action Of a Star by the Deviation of Light in the Gravitational Field », publié en 1936 dans la revue Science, est singulier à plus d’un titre et occupe une place à part dans l’histoire de la physique. Il s’agit d’une publication très courte (elle tient en gros sur une page) qui est devenue sur le tard l’un des articles les plus cités. En outre, son auteur n’a accepté à l’époque de l’écrire qu’à reculons en cédant à la pression intense mais sympathique d’un scientifique amateur, ingénieur un peu fantasque intimement persuadé de l’intérêt du sujet.
Ici le résumé pourrait être simplement : petit article, grands effets…
Pour bien comprendre le contenu de ce papier historique (car anticipant d’un demi-siècle les débuts d’un nouveau champ entier de l’astronomie), il est nécessaire tout d’abord de narrer succinctement les travaux qui l’ont précédé sur un thème similaire.
Dès 1704, Newton suggère dans le cadre de sa théorie corpusculaire de la lumière qu’un rayon lumineux pourrait être dévié par l’effet de la gravité. Toutefois il faut attendre 1804 (un siècle plus tard) pour que l’allemand Johann Soldner (astronome à l’observatoire de Berlin) calcule la déflexion prédite par la physique newtonienne pour un rayon lumineux frôlant le Soleil. L’angle de déflexion trouvé est de 0,84 seconde d’arc. La prédiction en physique newtonienne est obtenue en faisant l’hypothèse de particules de lumière de masse non nulle, la valeur de la masse n’important pas (car elle se simplifie dans les équations).
En 1907 (encore un siècle plus tard), c’est au tour d’Einstein de s’attaquer au sujet dans le cadre de ses réflexions relativistes (il ignorait les travaux antérieurs de Soldner, qui de toute façon s’étaient faits dans un cadre conceptuel très différent). Le principe d’équivalence lui permet dès cette année-là de prédire sans la calculer la déviation des rayons lumineux par la gravité. Il revient au problème en 1911 et calcule l’angle de déflexion pour un rayon de lumière rasant le Soleil. Son raisonnement s’effectuant toujours dans un espace plat (il n’a pas encore compris qu’il lui faudrait abandonner la géométrie euclidienne), il trouve sans le savoir la même valeur que Soldner (en fait 0,83 seconde d’arc).
Einstein se rend compte très tôt de l’intérêt d’observer les éclipses totales de soleil pour mesurer la valeur prédite (en comparant les positions des étoiles très proches du disque solaire lors de l’éclipse avec leurs nouvelles positions en dehors de l’éclipse). Il presse donc les astronomes pour qu’ils organisent des campagnes d’observations d’éclipses dans le monde dès que possible. Une tentative (qui aurait en fait consisté à comparer les mesures avec une valeur théorique erronée !) a lieu en 1914 à destination de la péninsule de Crimée en Russie mais échoue car entre temps la première guerre mondiale est déclarée.
En 1915, Einstein reprend les calculs dans le cadre de sa monumentale théorie de la relativité générale, désormais achevée. Il réalise alors son erreur : la nouvelle valeur prédite est égale à deux fois la valeur newtonienne, soit 1,74 seconde d’arc. La cause de cette différence est précisément la courbure de l’espace-temps propre à la relativité générale. Notons également que le résultat s’applique à des particules de masse nulle, ce qui était impensable en physique newtonienne.
Finalement, la première campagne d’observations d’une éclipse est réalisée par Eddington en 1919 à partir de trois ensembles de mesures (Sobral avec petit et grand télescope ainsi que l’île de Principe).
C’est le petit télescope de Sobral qui fournit les mesures de meilleure qualité car les observations à Principe sont gênées par des nuages – d’autre part des problèmes techniques entachent les mesures du grand télescope de Sobral. Eddington présente les résultats séparément pour ne pas fausser les données. La valeur mesurée à Sobral (petit télescope) est 1,98 ± 0,12 seconde d’arc et les observations confirment donc la valeur prédite par Einstein (1,74 seconde d’arc) avec une marge de 20%.
L’annonce retentissante faite par Eddington le 6 novembre 1919 à la Royal Society de Londres immortalise donc le Soleil comme la première lentille gravitationnelle découverte (en tant que déformation de l’espace-temps).
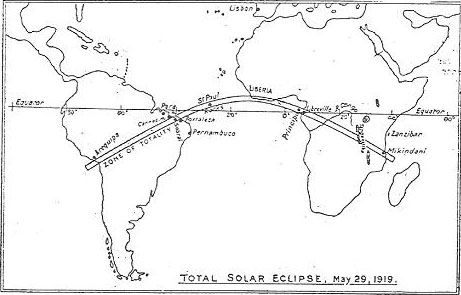
Figure 2 : Parcours de l’éclipse solaire de mai 1919 (image revue Nature, 1919, n°102).Cette ’expédition frappe les esprits parce que c’est une équipe de savants anglais (de la Royal Astronomical Society) qui vérifie la théorie d’un savant allemand, Einstein, et ce juste après la fin de la Première Guerre mondiale.
Figure 2bis : Principe d’observation de la déflexion de rayons lumineux frôlant la surface du soleil (schéma issu de l’ouvrage d’Eddington, 1920) : la trajectoire de la lumière issue de l’étoile P (considérée à l’infini) est courbée au voisinage du Soleil et, atteignant la Terre en E, semble provenir de P’.
Cependant une lentille gravitationnelle peut entraîner des effets bien plus extraordinaires que le simple décalage en position des étoiles et révéler la présence d’objets indétectables par d’autres moyens. Dès 1912, alors qu’il luttait encore pour élaborer sa future théorie de la gravitation, Einstein établit les équations décrivant les propriétés de lentille gravitationnelle d’une étoile. On a retrouvé des pages manuscrites écrites de sa main mais non publiées. Il déduit correctement qu’un étoile agirait comme une lentille en amplifiant la lumière émise par une étoile en arrière plan ou même, dans certains cas, en produisant une image double de la source unique. Il ne publie pas ces résultats ; il utilise encore à cette époque la mauvaise valeur pour la courbure des rayons lumineux. Le sujet tombe dans l’oubli mais ce ne fut en fait qu’une… éclipse.
Eddington entrevit certains de ces effets bizarres (principalement le dédoublement d’une source lumineuse) dans son ouvrage de vulgarisation de 1920 Space, Time and Gravitation (1).
En 1924, Orest Chwolson mentionna également dans un très court article (2) sans calculs, ne faisant pas appel à la relativité générale, la possibilité d’observer de tels effets et fut même le premier à évoquer l’éventualité de la formation d’un anneau lumineux par effet de lentille sur une source d’arrière plan.
Figure 3 : Le physicien russe Orest Kvholson (1852-1934).
L’article de 1936
C’est en 1936, à la demande pressante et répétée d’un ingénieur électricien tchèque, Rudi Mandl, passionné par le sujet, qu’Einstein reprit ses calculs de départ (ou en tout cas réétudia le problème) sans apparemment se rappeler ses premiers travaux non publiés de 1912 ! Dès le début, Einstein tient à souligner l’origine particulière de cet article.
Some time ago, R. W. Mandl paid me a visit and asked me to publish the results of a little calculation, which I had made at his request. This note complies with his wish.
Einstein envoya en complément à l’éditeur de Science une note précisant que ladite publication était de peu de valeur (les effets étant quasi inobservables) mais qu’elle avait le mérite d’avoir rendu heureux Rudi Mandl. Il est utile de nous attarder sur la façon dont Mandl parvint à « arracher » une courte publication à Einstein après avoir tenté en vain de se faire publier ou de convaincre d’autres scientifiques de reprendre ses idées dans un article.
Après avoir directement discuté avec le Science Service, une institution consacrée à la vulgarisation de la science (basée à Washington), Mandl parvint à obtenir une entrevue avec Einstein à Princeton le 17 avril 1936. Ses idées consistaient principalement à tester la relativité générale en observant des éclipses d’étoiles. Mandl était en outre convaincu que les phénomènes d’amplification de la lumière associés à ces lentilles gravitationnelles avaient eu un impact sur l’histoire de l’évolution des espèces sur Terre et pouvaient expliquer la disparition brutale des dinosaures. Une partie de ses idées pouvait donc être qualifiée de fantasque. Néanmoins ses affirmations sur les observations astronomiques éventuelles liées aux lentilles méritaient considération pour Einstein (au moins au départ), d’autant qu’il avait lui-même déjà réfléchi au sujet dès 1912, comme nous l’avons vu.
Après plusieurs échanges épistolaires avec Mandl, Einstein en vint néanmoins à la conclusion que les conséquences envisagées étaient inobservables et ne méritaient pas un article. Mandl était dans l’impasse car aucun des autres scientifiques qu’il avait contactés n’avait soutenu sa démarche. Il écrit à nouveau à Einstein en mai 1936.
In the last days I undertook desperate attempts to publish the results of my researches together with your formulas and I heard, without exception, the question: “Well, if Mr. Einstein appreciates your results why doesn’t he publish them himself ?” Hence it seems to depend on you to make the results accessible to the scientific world (3).
Mandl recontacte le Science Service qui s’enquiert auprès d’Einstein le 16 septembre des suites données aux propositions de Mandl. Finalement Einstein décide de publier un petite note qui paraîtra dans Science le 4 décembre 1936.
Figure 4 : La lettre du 16 septembre 1936 de l’éditeur du Science Service à Einstein (EA 17-039, © Einstein Archives, The Hebrew University Jerusalem ; cité par Renn & Sauer (4)).
Comme nous allons le détailler, Einstein décrit uniquement l’effet de lentille produit par une étoile sur une autre plus distante (ce que nous rangeons aujourd’hui dans les exemples de microlentilles), y compris la formation d’un anneau de lumière, aujourd’hui dénommé « anneau d’Einstein ». Il ne semble pas avoir eu connaissance des travaux antérieurs de Chwolson.
The light coming from a star A traverses the gravitational field of another star B, whose radius is R0.
Einstein décrit en fait trois phénomènes distincts dans l’ordre qui suit : 1. la formation d’un anneau de lumière correspondant à la déformation d’une étoile-source par une étoile-lentille ; 2. la formation de deux étoiles copies d’une étoile-source unique ; 3. l’amplification de la lumière de l’étoile-source par l’étoile-lentille.
@@@@@@@
Commençons par l’anneau de lumière.
According to the general theory of relativity, let α0 be the deviation of the light ray passing the star B at a distance R0 from its center.
Le diagramme illustrant le raisonnement est en fait fourni dans une lettre de Mandl à Einstein peu après leur entrevue à Princeton.
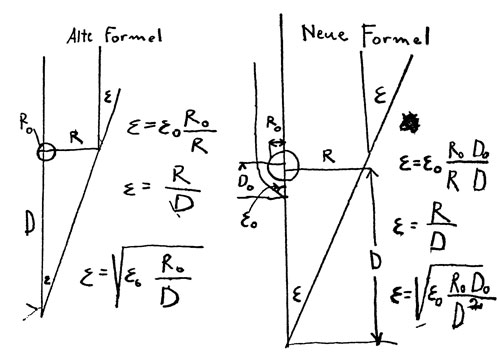
Figure 5 : Dessins de Mandl (EA 17-028, © Einstein Archives)
Dans la figure qui précède, c’est le diagramme de gauche qui est correct. Einstein fit remarquer à Mandl dans une lettre datant du 23 avril 1936 que celui de droite était erroné. Il ne redonne pas la formule pour l’angle de déflexion pour un rayon de lumière frôlant une masse sphérique qu’il avait obtenue en 1915. Ne se perdant pas en démonstrations, il se borne à fournir les résultats des calculs réalisés.
L’angle est déterminé en raisonnant dans un espace-temps muni d’une métrique de Schwarzschild – on trouve
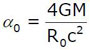
où G est la constante de gravitation universelle, c la vitesse de la lumière et M la masse de la lentille considérée (pour Einstein une étoile simple). Einstein donne la formule pour le rayon β de l’anneau de lumière et ajoute immédiatement :
Of course, there is no hope of observing this phenomenon directly.
Il en fournit peu après la raison principale.
The angle β will defy the resolving power of our instruments.
En effet, cet angle (qui sera appelé plus tard rayon d’Einstein) est proportionnel à α0 et au rayon de la lentille et ne peut qu’être extrêmement faible compte tenu du rayon et de la masse de l’étoile. En revanche, comme Zwicky le remarquera, les perspectives s’améliorent nettement (quoique hors de portée pour les instruments de l’époque) si la lentille utilisée est supposée être une galaxie au lieu d’une étoile.
Einstein conclut correctement que le seul effet éventuellement observable serait l’augmentation de luminosité causée par la lentille ; et parmi les cas d’étoiles simples décrits par Einstein, c’est bien le phénomène d’amplification de la lumière qui est aujourd’hui mesurable. Les anneaux ou les dédoublements n’ont à ce jour jamais été détectés dans le cas où seules des étoiles simples interviennent.
@@@@@@@
Einstein s’intéresse ensuite au cas d’images dédoublées, correspondant à un très léger défaut d’alignement entre l’observateur et les deux sources.
Then the observer will see A as two point-like light-sources, which are deviated from the true geometrical position of A by the angle β, approximately.
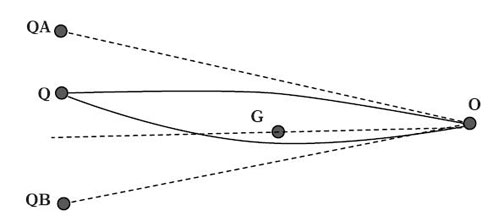
Figure 6 : La galaxie G située dans l’axe de visée défléchit, compte tenu de sa masse, les rayons lumineux suivant les lois de la relativité générale. Les rayons issus du quasar Q peuvent atteindre l’observateur O par plusieurs chemins optiques, formant par exemple deux images QA et QB. Le principe du mirage gravitationnel en astrophysique est très similaire à celui du mirage optique en astronomie (arc-en-ciel, relèvement et aplatissement du Soleil à l’horizon au crépuscule, etc.) : la principale différence est que le mirage gravitationnel ne dépend pas de la longueur d’onde (image extraite de A. Moatti, Les Indispensables astronomiques et astrophysiques pour tous, Odile Jacob, 2009).
Enfin, Einstein décrit brièvement en le quantifiant l’effet d’amplification de la lumière causé par la lentille sur la source lointaine.
The apparent brightness of A will be increased by the lens-like action of the gravitational field of B in the ratio q.
En effet, le corps intermédiaire (la « lentille ») focalise les rayons de la source lointaine exactement comme une loupe focalise les rayons du Soleil sur la zone particulière d’une feuille de papier qui vient alors à s’enflammer. Einstein montre que cette amplification est proportionnelle à la racine carrée de la distance de la lentille à l’observateur et qu’il faudrait un alignement quasi-parfait pour que l’effet soit mesurable (autrement dit que les positions observées de A et B coïncident).
Even in the most favorable cases the length l is only a few light-seconds, and x must be small compared with this, if an appreciable increase of the apparent brightness of A is to be produced by the lens-like action of B.
Il conclut que les chances d’observer un tel phénomène sont très minces :
Therefore, there is no great chance of observing this phenomenon.
Néanmoins il est important de souligner que, contrairement à l’anneau ou aux images doubles, il n’exclut pas totalement la possibilité d’observations futures.
Il avait déjà clairement souligné la différence entre les deux cas dans une lettre envoyée à Mandl avant la publication.
In any case there may well be more chance to occasionally observe this intensification effect than the “halo effect” with which we have dealt earlier. But the probability that we can get so precisely into the connecting line of the centers of two stars at very different distances is rather low, even lower the probability that the phenomenon, lasting in general only a few hours, happens to be observed (5).
Cette dernière remarque a aujourd’hui une résonance particulière car le type d’observation décrit correspond à la méthode de détection des exoplanètes par microlentille gravitationnelle (la première découverte remonte à 2003, soit près de 70 ans après l’article d’Einstein).
Einstein conclut en indiquant un aspect contre-intuitif du phénomène d’amplification, le fait qu’il augmente avec la distance de la lentille à l’observateur.
This apparent amplification of q by the lens-like action of the star B is a most curious effect […] since with increasing distance D of the observer not only does it not decrease, but even increases proportionally to √D.
Einstein a estimé très peu vraisemblable la détection de ce phénomène car il ignorait les dimensions colossales de l’univers observable et a restreint son analyse aux étoiles de la Voie Lactée (les galaxies lentilles pouvant être en fait distantes de plusieurs milliards d’années-lumière).
Il a également sous-estimé les capacités technologiques d’un futur certes lointain (des télescopes au sol plus puissants organisés éventuellement en réseaux, des télescopes spatiaux, le stockage et l’analyse automatique des données par des moyens informatiques, l’amélioration considérable des capteurs de lumière…) qui allaient permettre beaucoup plus tard des observations détaillées de ce « most curious effect ». En outre, il ne se doutait pas de la motivation qui allait naître pour la recherche de la matière noire (manquante) dans les galaxies et des potentialités offertes par les lentilles gravitationnelles en tant qu’outil cosmologique d’un genre nouveau. Cela revenait néanmoins à naviguer en quasi science-fiction.
Une autre raison a pu jouer : Einstein s’est peut-être habitué à l’idée que les effets propres à la relativité (générale surtout) resteraient infimes et sans application pratique, ce en quoi il se trompait. La théorie de la relativité générale a dépassé de loin tout ce que son auteur aurait pu espérer ou même rêvé en termes de tests expérimentaux. Pour preuve de cette attitude d’Einstein vis-à-vis des vérifications éventuelles, rappelons ses propos sur l’importance de la cohérence interne de la théorie :
L’importance de la théorie de la relativité générale n’est pas à rechercher dans la confirmation expérimentale de certains effets très faibles, mais bien plutôt dans la simplicité de ses fondements et sa cohérence interne.
Citons également ses réflexions amusantes (6) de 1948 (à destination de son assistant Ernst Strauss) sur la détection de la première lentille gravitationnelle de l’histoire de l’humanité :
Pendant l’éclipse de 1919, Planck est resté debout toute la nuit pour voir si elle allait confirmer la déviation de la lumière dans le champ gravitationnel solaire. S’il avait vraiment compris la façon dont la théorie de la relativité générale explique l’équivalence de la masse inerte et de la masse gravitationnelle, il serait allé se coucher comme moi.
La réaction de Zwicky
Figure 7 : Fritz Zwicky (1898-1974), discutant peut-être de l’anneau d’Einstein ?
En 1936, l’astrophysicien Fritz Zwicky lit l’article d’Einstein et est également sollicité sur ce sujet par un collègue qui avait été approché par le tenace Rudi Mandl. L’article semble avoir été un déclic pour Zwicky, physicien toujours prompt à s’aventurer sur des terrains inexplorés, qui se rend compte rapidement que les galaxies (ou même des amas de galaxies) pourraient être de meilleures lentilles que les étoiles uniques envisagées par Einstein et permettre ainsi de peser la matière noire (manquante) qu’il pensait avoir identifiée au sein d’un amas de galaxies. Il estime la taille et la luminosité d’un anneau d’Einstein créé par l’effet de lentille causé sur une galaxie d’arrière plan par une autre galaxie plus proche de nous. Zwicky fait clairement référence à Einstein et Mandl dès son premier article (7) :
Einstein recently published some calculations concerning a suggestion made by R.W. Mandl, namely, that a star may act as a “gravitational lens” for light coming from another star which lies closely enough on the line of sight behind. As Einstein remarks the chance to observe this effect for stars is extremely small.
Zwicky publie donc deux papiers en 1937 dans le Journal Physical Review et soutient avec force que l’effet de lentille entre galaxies permettrait plusieurs avancées :
1. Sonder des zones de l’univers inaccessibles en amplifiant la lumière de galaxies lointaines ; 2. Tester plus en détail la relativité générale ; 3. Permettre une détermination plus directe de la masse des galaxies.
Il ajoute que si ses estimations sur les masses des galaxies étaient correctes, la probabilité d’observer des galaxies agissant en tant que lentilles gravitationnelles était une quasi-certitude.
@@@@@@@
La différence des analyses d’Einstein et Zwicky à propos de l’observabilité du phénomène est frappante – ils écrivent pourtant pratiquement au même moment. Avec le recul, on peut dire que Zwicky avait vu juste sur les possibilités à venir (mais avec un excès d’optimisme pour le futur proche) tandis qu’Einstein avait correctement estimé l’infaisabilité pratique jusqu’à un horizon de plusieurs décennies (mais avec un excès de pessimisme sur les capacités à long terme). Dans ce cas, le véritable visionnaire fut donc Zwicky, à ceci près qu’il ne faut pas oublier que le déclencheur a été incontestablement l’article de 1936 d’Einstein qui a permis de déverrouiller les esprits.
Premières observations de lentilles gravitationnelles : un grand saut dans le futur
Il fallut attendre 1979, soit 42 ans après les prédictions de Zwicky et 60 ans après la campagne d’observations de l’éclipse de 1919, pour que les astronomes détectent enfin une lentille gravitationnelle autre que le Soleil, en l’occurrence le premier quasar double (ou jumeau).
Les quasars (Quasi-Stellar Objects) sont parmi les objets les plus énergétiques de l’univers. Ils sont incroyablement lumineux bien qu’ils soient distants de plusieurs milliards d’années-lumière. Le premier fut détecté en 1963. Nous savons aujourd’hui qu’ils sont alimentés par un trou noir géant en leur centre.
Revenons aux lentilles et raisonnons à la Zwicky : si une galaxie se trouve entre la Terre et le quasar, nous avons affaire à une super-lentille qui pèse au bas mot des milliards de fois la masse du Soleil ! Si le quasar se trouve par chance parfaitement aligné par rapport à la ligne de visée, l’image du quasar est déformée par la galaxie en un anneau qui entoure la galaxie de façon fictive. C’est le fameux anneau d’Einstein. Si le quasar est légèrement décalé, on aura une image multiple : deux ou quatre copies identiques du même quasar.
En 1979, le quasar double QSO 0957+561 est découvert par Walsh, Carswell et Weymann. D’abord observé comme une source radio unique, il apparaît sous la forme de deux objets A et B distincts dans le domaine optique. Ces deux sources exhibent le même décalage spectral qui correspond à une distance identique de 8 milliards d’années-lumière. En outre, les deux sources ont la même image spectrale, ce qui avec la détection de la galaxie intercalée (distante de quelques milliards d’années-lumière, et jouant le rôle de lentille) confirme l’existence d’un dédoublement.
On a découvert en outre plus tard un fait étonnant : comme les rayons lumineux engendrant chacune des deux sources suivent des trajectoires de longueur différente et traversent des régions au potentiel gravitationnel différent, l’image A du quasar atteint la Terre 14 mois plus tard que l’image B (8). On a donc une sorte de « paradoxe » des jumeaux : deux copies identiques d’une même source avec un âge différent !
Figure 8 : Quasar double Q0957+561 A+B. Les deux images A et B du quasar sont séparées de 6’’ d’arc. Le quasar se situe à une distance de 7,8 milliards d'années-lumière, alors que la galaxie lentille est à 3,7 milliards d'années-lumière.
On connaît aujourd’hui plus de 100 000 quasars dont une petite fraction seulement est susceptible de subir un effet de lentille au cas où une galaxie s’interpose – notons que certaines de ces configurations peuvent être fugaces, compte tenu du mouvement des galaxies. On a identifié une centaine de cas de quasars doubles, triples ou quadruples. Un exemple de quasar quadruple est donné ci-après.
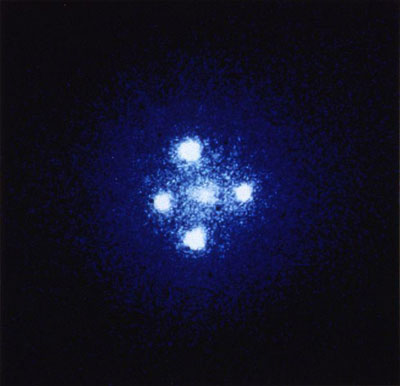
u>Figure 9 : Croix d'Einstein (QSO 2237+0305). L’observation de ce quasar situé à 8 milliards d’années-lumière se fait par déflexion à travers une galaxie-lentille située 20 fois moins loin, à 400 millions d’années-lumière (Photographie ESA, prise par le télescope américain Hubble).
Le premier anneau d’Einstein fut observé en 1987. Un exemple superbe d’anneau presque complet (photographié par le télescope spatial Hubble) est fourni ci-dessous.
Figure 10 : Anneau d'Einstein créé par la galaxie intermédiaire LRG 3-75. L’alignement entre les deux galaxies est ici si parfait que l’image de la galaxie d’arrière plan ébauche la forme d’un cercle (on dit parfois « image en fer-à-cheval »).
Si l’on résume les principaux phénomènes de lentilles gravitationnelles observés à ce jour dans le ciel, on peut lister : 1. Les images de quasars déformés par des galaxies ; 2. Les images de quasars déformés par des microlentilles (trous noirs, objets compacts, étoiles…) ; 3. Des anneaux d’Einstein correspondant à des galaxies d’arrière-plan déformées ; 4. Des arcs lumineux géants correspondant à des galaxies d’arrière plan déformées.
Conformément à ce qu’avait envisagé Zwicky très tôt, les lentilles gravitationnelles sont devenues un outil cosmologique précieux pour déterminer la masse des galaxies, étudier de façon plus détaillée des galaxies lointaines et analyser la distribution de la matière noire dans l’univers.
Une nouvelle méthode de détection des exoplanètes
Une dernière avancée a été permise par l’exploitation des microlentilles gravitationnelles. Celles-ci correspondent aux cas envisagés par Einstein dans son article de 1936, à savoir que l’effet de lentille est ici produit par une simple étoile éventuellement entourée de planètes qui agit sur la lumière en provenance d’une étoile plus distante. On exploite le phénomène d’amplification de la lumière qu’Einstein estimait quasi-indétectable à la fin de son article : « there is no great chance of observing this phenomenon ». La planète agit elle aussi par effet de lentille et est à l’origine d’un pic d’amplification qu’il s’agit de repérer et qui s’ajoute à l’effet engendré par son étoile.
La technique des microlentilles gravitationnelles n’est pas limitée en distance comme Einstein le remarque judicieusement à la fin de son article : l’étoile-lentille passe en général devant une étoile-source située non loin du Centre galactique, soit à environ 25 000 années-lumière de la Terre. L’effet étant purement géométrique, il est possible de détecter des planètes de masse même inférieure à celle de la Terre autour de l’étoile-lentille. La première exoplanète (9) détectée par cette technique (OGLE-2003-BLG-235) date de 2003 (il s’agissait d’une planète de masse comparable à Jupiter), 67 ans donc après l’article d’Einstein.
Cette méthode permet de détecter des planètes à la fois peu massives et lointaines mais a l’inconvénient de s’appuyer sur des alignements non reproductibles. Cette technique aurait sans doute laissé Einstein pantois car elle exploite l’effet de microlentille engendré par un objet minuscule, la planète orbitant l’étoile, donc un sous-cas de celui décrit dans son article, très difficile à imaginer à l’époque.
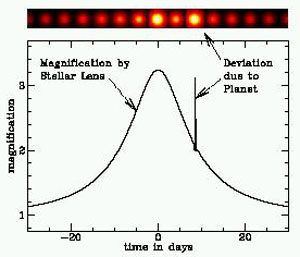
Figure 11 : Effet de microlentille gravitationnelle pour la détection d’exoplanètes. L’étoile centrale joue le rôle de lentille gravitationnelle pour l’observation d’une autre étoile (à droite). Lorsqu’elle passe au voisinage de l’alignement, la planète orbitant autour de l’étoile centrale (une des planètes figurant en rouge ou bleu)) agit elle aussi par effet de lentille et est à l’origine d’un pic d’amplification qui s’ajoute à l’effet engendré par son étoile. Figure 11 bis, ci-dessous : À droite du pic gaussien crée par l’étoile centrale, on voit apparaître un pic créé par la planète orbitante.
L’article d’Einstein illustre un cas particulièrement frappant de prédiction vérifiée très longtemps après qu’elle fut énoncée et confirme au passage le remarquable pouvoir de prédiction de la relativité générale. En matière de relativité, il faut souvent faire preuve de patience avant d’observer des effets qui paraissent au départ infimes et sans intérêt pratique. Par exemple, Einstein fut le premier à prédire en 1905 la désynchronisation des horloges parfaites (un phénomène radicalement nouveau) dans son article fondateur de la relativité restreinte « Sur l’électrodynamique des corps en mouvement » : mais il faudra attendre 1971 (donc 66 ans plus tard !) pour que Hafele et Keating vérifient cet effet lors de leur fameuse expérience d’horloges atomiques embarquées à bord d’avions de ligne. Là encore, la prise en compte de cet effet qui pouvait paraître insignifiant s’est révélée par la suite cruciale pour le fonctionnement du GPS qui équipe nos smartphones.
En 1936, Einstein invente en quelque sorte le télescope gravitationnel (10), sans en soupçonner les potentialités encore enfouies dans un lointain futur défiant l’imagination. Il fait ainsi écho à nouveau à l’œuvre de Newton, par un détour singulier, déflexion de sa propre pensée qui aura ici été provoquée par l’intervention heureuse d’un scientifique amateur, Rudi Mandl, à la fois perspicace, opiniâtre et visionnaire.
Mars 2013
(1) On trouvera une analyse (faite du point de vue la philosophie des sciences) du chapitre XII de cet ouvrage par Ph. Stamenkkovic, « La nature des choses selon Eddington, ou la physique dérivée de la géométrie », BibNum, février 2012.
(2) Chwolson, O (1924). "Über eine mögliche Form fiktiver Doppelsterne", Astronomische Nachrichten, 221 (20): 329–330 (en ligne NASA Astrophys. Data Systems). La conclusion de ce court article mentionne “ […] der Stern A von einem Ring umgeben erscheinen » (l’étoile A peut apparaître comme entourée d’un anneau).
(3) Mandl à Einstein, 21 May 1936, Einstein Archives 17038.
(4) Jürgen Renn & Tilman Sauer “Eclipses of the Stars – Mandl, Einstein, and the Early History of Gravitational Lensing” (paru dans ouvrage collectif, cf. onglet « Pour en savoir plus »; pre-print en ligne).
(5) Einstein à Mandl, 12 May 1936, Einstein Archives 17034 &35.
(6) Ces deux citations d’Einstein sont extraites du livre de Jean-Claude Boudenot, Comment Einstein a changé le monde, EDP Sciences (2005), page 108 pour la première, page 116 pour la seconde.
(7) F. Zwicky, Nebulae as Gravitational Lenses, Physical Review, 51, 290 (1937).
(8) Ce décalage est en fait la somme de deux termes : l’un géométrique qui est dû à la différence de longueur des trajets pour aller de la source à l’observateur ; l’autre gravitationnel (effet Einstein) qui est dû à la différence entre les potentiels gravitationnels des zones traversées par chacun des trajets.
(9) Planètes en orbite autour d’autres étoiles que le Soleil.
(10) Auquel le nom de Zwicky doit être associé : il a entrevu bon nombre de potentialités du concept.
OUVRAGES
Evalyn Gates, Einstein’s telescope - The Hunt for Dark Matter and Dark Energy in the Universe, WW Norton & Co, 2010
Pierre Spagnou, De la relativité au GPS : Quand Einstein s'invite dans votre voiture, Ellipses, 2012.
Jean Eisenstaedt, Einstein et la relativité générale. Les chemins de l'espace-temps, CNRS Éditions, 2007.
ARTICLE
Jürgen Renn & Tilman Sauer, “Eclipses of the Stars : Mandl, Einstein, and the Early History of Gravitational Lensing”, in Abhay Ashtekar, Robert Cohen, Don Howard, Jürgen Renn, Sahotra Sarkar, Abner Shimony (eds.), Petra Schröter (ed. ass.), Revisiting the Foundations of Relativistic Physics – Festschrift in Honour of John Stachel, Boston Studies in the Philosophy of Science: Kluwer Academic Publishers (version pré-print PDF sur le site du Max Planck Institut)
Einstein-analyse.pdf
>> Téléchargez l'analyse de Pierre Spagnou
Einstein et les lentilles gravitationnelles - Version PDF (590.66 Ko)
société des amis de la bibliothèque de l'X