La découverte de Neptune (1846)

Figure 1 : Urbain Le Verrier (1811-1877) juste après la découverte de Neptune, portrait par Charles Daverdoing. ©Bibliothèque de l’Observatoire de Paris

La planète Uranus a été découverte en 1781 par William Herschel (1738-1822). Cette découverte a eu un grand retentissement et a donné lieu à de nombreuses observations de la position de cette planète. On a également réalisé qu’elle avait été déjà observée une vingtaine de fois avant Herschel : on l’avait prise alors pour une étoile fixe. L’observation la plus ancienne, due à l’anglais John Flamsteed (1646-1719), remonte à 1690.

Alexis Bouvard en 1821, la première idée d’une nouvelle planète ?

Dans son célèbre traité, la Mécanique céleste, Pierre-Simon Laplace (1749-1829) donne l’expression mathématique des perturbations exercées par les planètes les unes sur les autres en raison de leur attraction gravitationnelle. Il s’agit ensuite de faire les calculs numériques permettant, à partir de ces expressions, de calculer la position des planètes au cours du temps, c’est-à-dire d’en établir des tables. Ceci entre dans les attributions du Bureau de longitudes, créé par la Convention en 1795. Sous la direction de Laplace, le travail est réparti par le Bureau entre trois astronomes confirmés : Jean-Baptiste Delambre (1749-1822), Alexis Bouvard (1767-1843) et Johann Karl Burckhardt (1773-1825). C’est à Bouvard, élève de Laplace, qu’échoit en 1821 la tâche la plus ingrate : le calcul des tables prédisant le mouvement des trois grosses planètes, Jupiter, Saturne et Uranus. Les tables de Jupiter et de Saturne sont calculées sans difficulté particulière, mais de gros problèmes surgissent pour Uranus. Après avoir tenu compte des perturbations exercées par les autres planètes, Bouvard ne parvient pas à trouver des éléments permettant de représenter le mouvement d’Uranus pendant toute la période où il a été observé. Une solution paraît possible en n’utilisant que les nombreuses positions d’Uranus mesurées de sa découverte en 1781 à 1821, mais il est alors impossible de rendre compte des positions anciennes, les écarts dépassant la minute de degré, une quantité qui paraît bien supérieure aux erreurs d’observation. À l’inverse, si l’on utilise les positions mesurées entre 1690 et 1781, les positions plus récentes sont très mal représentées par les tables. Avouant son impuissance, Bouvard écrit dans l’introduction de ses Tables d’Uranus de 1821, qu’il doit

laisser aux temps à venir le soin de faire connaître si la difficulté de conclure [concilier] les deux systèmes [celui qui représente les positions avant 1781 ou celui qui en rend compte après cette date] tient réellement à l’inexactitude des observations anciennes, ou si elle dépend de quelque action étrangère ou inaperçue, qui aurait agi sur la planète.

Après la publication des tables de Bouvard, qu’il avait finalement établies en n’utilisant que les observations récentes (entre 1781 et 1821), de nouveaux écarts se manifestent et ne font que croître au cours du temps, si bien qu’il devient impossible d’attribuer les discordances aux erreurs d’observation. Après la mort d’Alexis Bouvard en 1843, son neveu Eugène est chargé par le Bureau des Longitudes d’établir de nouvelles tables de la planète. Il les présente à l’Académie le 1er septembre 1845, mais elles ne seront jamais publiées. Il remarque à ce propos :

Les discordances entre les observations et la théorie me portent à croire qu’il y a beaucoup de vraisemblance dans l’idée émise par mon oncle sur l’existence d’une autre planète troublant Uranus.

@@@@@@@

C’est donc, semble-t-il, Alexis Bouvard qui a imaginé le premier que les anomalies du mouvement d’Uranus pourraient provenir de l’action gravitationnelle d’une nouvelle « planète troublante » ; d’autres prétendront plus tard qu’ils ont eu les premiers la même idée. Quoi qu’il en soit, elle est dans l’air et se répand rapidement dans le monde scientifique et même dans le grand public, à l’étranger comme en France. Par exemple, le célèbre astronome et mathématicien allemand Friedrich Wilhelm Bessel (1784-1846), qui dès 1830 avait insisté sur l’existence possible de « masses troublantes », en fait le sujet d’une conférence publique en 1840.

1845 : l’entrée en lice de Le Verrier, à l’instigation d’Arago

François Arago (1786-1853), qui est responsable de l’Observatoire de Paris, souhaite évidemment que le problème d’Uranus y soit traité. Mais Alexis Bouvard est mort ; Arago n’a pas grande confiance en Eugène Bouvard et ne voit personne d’autre à l’Observatoire qui soit capable d’aborder un problème aussi difficile. Au cours de l’été 1845, il demande à un jeune astronome extérieur à l’Observatoire, Urbain J.J. Le Verrier (1811-1877), de s’y attaquer, car il le croit capable de le résoudre. Le Verrier est alors répétiteur à l’École polytechnique et s’est fait remarquer par des travaux de mécanique céleste sur la stabilité du système solaire, qui témoignent d’une grande maîtrise. Il fait à ce moment des recherches non moins intéressantes sur l’orbite des comètes, mais il les abandonne pour se consacrer à Uranus. Dès lors, les choses iront très vite, car sa puissance de travail est considérable.

Les relations entre ces deux astronomes polytechniciens ont été fort mouvementées. En 1845, comme indiqué, Arago suggère à Le Verrier ce travail de recherche sur les perturbations d’Uranus – comme il avait suggéré à Fresnel de travailler sur l’expérience des fentes de Young – les deux suggestions s’avéreront fructueuses ! Le Verrier rend hommage à son « maître » dans une première note aux Comptes-rendus de l’Académie, en 1845 : Dans le courant de l’été dernier [1845], M. Arago voulut bien me représenter que l’importance de cette question imposait à chaque astronome le devoir de concourir, autant qu’il était en lui, à en éclaircir quelque point. J’abandonnai donc pour m’occuper d’Uranus, les recherches que j’avais entreprises sur les comètes (…) Arago, secrétaire perpétuel de l’Académie des sciences, valorisera la découverte de Le Verrier. On connaît sa fameuse phrase : « M. Le Verrier a aperçu le nouvel astre sans avoir besoin de jeter un seul regard vers le ciel ; il l’a vu au bout de sa plume » (Note aux Comptes Rendus de l’Académie des sciences, 1846, vol.23, p. 659-662). Il défendra Le Verrier contre Libri, qui voulait démontrer que la planète avait été découverte avant Le Verrier (voir plus avant).

 

 

Mais les relations entre les deux hommes n’allaient pas tarder à se dégrader. Dès 1847, auréolé de sa découverte, Le Verrier cherche, avec l’appui de Guizot, ministre de Louis-Philippe, à remplacer Arago à la tête de l’Observatoire. Pendant la II° République de 1848, Arago étant ministre, Le Verrier ravale ses ambitions. En 1854, après la mort d’Arago, Le Verrier, très en faveur auprès de Napoléon III, est nommé directeur de l’Observatoire. Il prendra le contre-pied de toutes les décisions de son prédécesseur Arago, que ce soit dans le choix des télescopes à installer, ou en supprimant la salle qu’Arago consacrait à ses conférences « d’astronomie populaire ». En règle générale, Le Verrier se comportera comme un dictateur à la tête de l’Observatoire, se faisant l’ennemi du personnel qui obtiendra sa démission en 1870, jusqu’à ce qu’il soit réinstallé en 1873 suite à la mort accidentelle de son successeur, Charles Delaunay (1796-1872). En tout état de cause, il est clair que le passage de Le Verrier à l’Observatoire entre 1854 et 1872 a mis fin à un certain nombre de pistes de recherche fructueuses en astronomie lancées par Arago ; Le Verrier n’en lança pas d’autres, d’ailleurs. Cependant il réorganisa l’astronomie française qui en avait grand besoin, le Bureau des Longitudes dont elle dépendait précédemment l’ayant laissé dans une certaine anarchie.

Le Verrier examine scrupuleusement toutes les observations disponibles jusqu’en 1845, notamment celles qui ont été faites récemment à l’Observatoire de Paris, que lui a communiquées Arago et qu’il trouve excellentes, et celles faites à Greenwich que lui a envoyées Airy. Il révise aussi soigneusement les calculs d’Alexis Bouvard (il semble n’avoir pas considéré ceux de son neveu Eugène Bouvard). Il découvre que certains termes y ont été négligés à tort, et y trouve plusieurs erreurs : il doit donc refaire en partie les calculs.

Malheureusement, en examinant avec une grande attention le préambule très concis des Tables d’Uranus, j’y découvris plusieurs causes d’erreurs, dont il était impossible d’apprécier avec justesse l’influence (…). Doit-on attribuer ce désaccord à ce que la théorie n’est pas suffisamment précise ? Ou bien cette théorie n’a-t-elle pas été comparée aux observations avec assez d’exactitude, dans le travail de base qui a servi aux Tables actuelles ? Enfin, se pourrait-il qu’Uranus fût soumis à d’autres influences que celles qui résultent des actions du Soleil, de Jupiter et de Saturne ? (…) En 1831, par exemple, le lieu calculé s’éloigne du lieu observé de 188’’, dont 140’’ environ ne sauraient être expliquées si l’on n’admet pas une autre influence que celles du Soleil, de Jupiter et de Saturne.

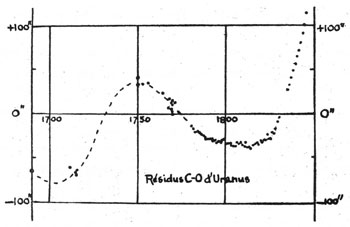
Figure 3 : Un exemple d’écarts entre les longitudes calculées C et les longitudes observées O d’Uranus de 1690 à 1845. Ici, les longitudes calculées, qui tiennent compte des perturbations par Jupiter et Saturne, sont celles de Bouvard dont la théorie, corrigée par Le Verrier, n’utilise que des observations de 1781 à 1821. Comme on le voit, les écarts varient de ± 100 secondes d’arc. Mais cette solution n’est pas nécessairement la bonne, car on aurait pu utiliser aussi les observations antérieures à 1781 pour calculer l’orbite d’Uranus. Calculs et dessin par André Danjon (L’Astronomie, Bulletin de la Société astronomique de France, 1946, p. 255-278).

De manière rigoureuse et méthodique, Le Verrier exclut un certain nombre d’autres hypothèses, comme celles d’une modification de la théorie, ou celle de l’action d’une comète (son thème de recherche antérieur):

Je ne m’arrêterai pas à cette idée que les lois de la gravitation pourraient cesser d’être rigoureuses, à la grande distance à laquelle Uranus est situé du Soleil. Ce n’est pas la première fois que, pour expliquer des inégalités dont on n’avait pu se rendre compte, on s’en est pris au principe de la gravitation universelle. Mais on sait aussi que ces hypothèses ont toujours été anéanties par un examen plus approfondi des faits (…) Je ne saurais croire davantage à la résistance de l’éther ; résistance dont on a à peine entrevu des traces dans le mouvement des corps de la densité la plus faible (…) Les inégalités particulières d’Uranus seraient-elles dues à un gros satellite qui accompagnerait la planète ? Les oscillations qui se manifesteraient dans la marche d’Uranus affecteraient alors une très courte période ; et c’est précisément le contraire qui résulte des observations (…) Serait-ce donc une comète qui, tombant sur Uranus, aurait, à une certaine époque, changé brusquement la grandeur et la direction de son mouvement ? (…) Mais alors, la période de 1781 à 1820 pourrait se lier naturellement, soit à la série des observations antérieures, soit à la série des observations postérieures, et ne serait incompatible qu’avec l’une d’elles. Or c’est ce qui n’a pas lieu (…) Il ne nous reste ainsi d’autre hypothèse à essayer que celle d’un corps agissant d’une manière continue sur Uranus, changeant son mouvement d’une manière très lente. Ce corps, d’après ce que nous connaissons de la constitution de notre système solaire, ne saurait être qu’une planète, encore ignorée.

Il entreprend alors de localiser la planète troublante. Le problème est tout à fait nouveau : jusqu’alors, on avait déterminé la position de chaque planète en tenant compte des perturbations exercées par les autres, dont la position est connue par l’observation. Il s’agit maintenant de déterminer la position d’une planète sur laquelle on ne sait rien à partir des perturbations qu’elle exerce : c’est ce qu’en mathématiques on appelle le problème inverse. Il est à la fois difficile et complexe, car il y a beaucoup d’inconnues à déterminer :

Si l’on pouvait déterminer, à chaque époque, la variation des perturbations dues à l’action de la masse inconnue, on en déduirait la direction dans laquelle tombe Uranus, par suite de l’action de ce corps troublant (…) Mais le problème est loin de se présenter aussi simplement. Les expressions numériques des perturbations ne pourraient se conclure immédiatement des observations, que si l’on connaissait les valeurs rigoureuses des éléments de l’ellipse décrite par Uranus autour du Soleil ; et ces éléments, à leur tour, ne peuvent se déterminer exactement, si l’on ne connaît pas la quantité des perturbations. On le voit, il est impossible de scinder en deux parties distinctes la recherche des éléments d’Uranus et celle des éléments du corps qui le trouble. (…) J’ai renversé le problème qu’on s’est, jusqu’ici, proposé (…) Au lieu d’avoir à mesurer l’action d’une planète déterminée, j’ai dû partir des inégalités reconnues dans Uranus, pour en déduire les éléments de l’orbite de la planète perturbatrice dans le ciel, et montrer que son action rendait parfaitement compte des inégalités apparentes d’Uranus.

Aussi Le Verrier simplifie-t-il dès le départ le problème en négligeant l’inclinaison de son orbite et en supposant connue la distance au Soleil de la planète troublante :

(…) les orbites de Jupiter, Saturne et Uranus étant fort peu inclinées à l’écliptique, on peut admettre, dans une première approximation, qu’il en est de même pour la planète cherchée. (…)

Mise en évidence en 1772, cette loi montre que l’on peut représenter approximativement la distance des planètes au Soleil par la relation empirique suivante :

a = 0,4 + 0,3 2^n-1

où a est le demi-grand axe de l’orbite exprimé en unités astronomiques (demi-grand axe de l’orbite terrestre, soit 1,496 108 km), et n un des nombres entiers consécutifs. Voici comment elle représente les distances des planètes au Soleil :

 

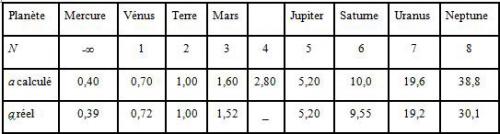
La lacune pour n = 4 a incité les astronomes à rechercher la planète qui aurait dû occuper cette place. Ces recherches furent couronnées de succès lorsque Piazzi découvrit en 1801 la petite planète Cérès, pour laquelle a = 2,77. Depuis cette époque, on a trouvé des milliers de petites planètes, ou astéroïdes, gravitant entre Mars et Jupiter. On constate un assez bon accord entre la loi de Titius-Bode et la réalité, sauf pour Neptune (qui n’était pas encore découvert à l’époque où la loi a été énoncée). On ne sait toujours pas s’il faut ou non lui attribuer une signification physique.

@@@@@@@

Voici déjà deux inconnues de moins. Mais il en reste encore beaucoup : en effet, les éléments de l’orbite d’Uranus sont eux-mêmes mal déterminés puisqu’on ne peut pas trouver de solution rendant compte de toutes les observations. L’hypothèse de la planète troublante ne change rien à cet état de choses. Bien sûr, on peut supposer connue l’orbite d’Uranus, en tenant compte des perturbations par les autres planètes que la planète troublante, et établir les écarts entre les positions calculées et les positions observées pour mettre en évidence l’effet de celle-ci : un exemple est montré Figure 2. Mais il est impossible d’obtenir ainsi la solution du problème puisque d’autres orbites sont possibles pour Uranus.

Deux étapes dans l’approche calculatoire de Le Verrier

Le Verrier est donc obligé de déterminer à la fois les éléments de l’orbite d’Uranus et de celle de la nouvelle planète, soit 12 inconnues (voir la Figure 3). Il en a déjà fixé deux, et en fixe encore deux autres pour Uranus pour lequel il suppose connus, comme pour la nouvelle planète, le demi-grand axe et l’inclinaison de l’orbite :

Il ne reste plus que 8 inconnues, auxquelles il faut ajouter la masse de la planète troublante. Nous ne pouvons pas ici entrer dans le détail des solutions des équations correspondantes (1). La première note aux Comptes rendus de l’Académie des sciences (séance du 1er juin 1846) donne des considérations complémentaires. Il y indique à 10 degrés près la position que sera susceptible d’occuper dans le ciel la planète troublante le 1er janvier 1847 :

Je prouve encore qu’il n’y a qu’une solution possible, et que, plus on s’éloigne de cette solution, et plus les écarts de la théorie, par rapport aux observations, deviennent considérables. Occupons-nous enfin de la position de la planète dans le ciel (…) je me bornerai à faire connaître l’expression de la longitude au 1er janvier 1847. C’est le but le plus important de mon travail ; c’est le résultat qui devra servir de point de départ aux observateurs pour découvrir le nouvel astre. (…) en assignant 325 degrés de longitude héliocentrique à la planète, au 1er janvier 1847, on ne commet pas une erreur de 10 degrés.

de présenter un extrait à l’Académie doit être considéré comme une ébauche d’une théorie qui commence.

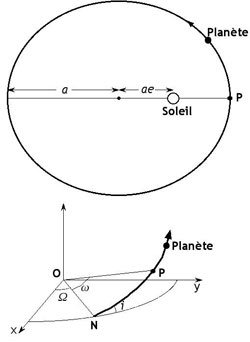
Figure 4 : Les paramètres de l’orbite d’une planète. En haut, l’orbite vue du Nord. P est le périhélie, a le demi grand axe et e l’excentricité. En bas, une portion de l’orbite dans l’espace. i est l’inclinaison de l’orbite par rapport au plan de référence xOy, Ω la longitude du nœud ascendant N par rapport à la direction Ox et ω la longitude du périastre P par rapport à N, dans le plan de l’orbite. Schéma de l’auteur.

Cependant, certains restent sceptiques : Airy écrit le 26 juin à Le Verrier pour lui demander des éclaircissements, tout en lui envoyant des observations faites à Greenwich dont Le Verrier va se servir. Il l’en remercie et donne à Airy les explications demandées, lui proposant même de lui communiquer les éléments de l’orbite de la planète troublante s’il veut en entreprendre la recherche. Airy est très impressionné, et dès lors son scepticisme tombe ; mais, curieusement, il décline l’offre de Le Verrier.

@@@@@@@

Malgré la nouveauté du problème et de grandes difficultés mathématiques, Le Verrier ne mettra pas plus de trois mois pour préciser les éléments de l’orbite de la planète troublante, pour donner sa masse et même un ordre de grandeur du diamètre apparent qu’elle devrait présenter si on venait à la découvrir. Dans sa note du 31 août 1846, la deuxième que nous reproduisons, il explique en détail sa méthode et donne les éléments qu’il prédit pour la nouvelle planète, avec une précision d’ailleurs totalement illusoire. Dans le tableau qui suit, nous comparons leur valeur aux données actuelles :

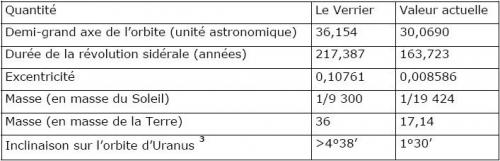
Le demi-grand axe de l’orbite a été un peu modifié par rapport à l’hypothèse initiale, où, suivant la loi de Titius-Bode, il avait été pris arbitrairement comme le double de celui de l’orbite d’Uranus, soit 38 unités astronomiques ; mais l’excentricité adoptée par Le Verrier est importante, si bien que la distance de Neptune à Uranus pendant la période considérée n’est pas beaucoup plus grande que sa vraie valeur. Le Verrier précise alors la position comme suit :

[La] longitude vraie diffère peu de 325 degrés, valeur qui résultait de mes premières recherches. La détermination actuelle est fondée sur des données plus nombreuses et plus précises ; elle place le nouvel astre à 5 degrés environ à l’Est de l’étoile δ du Capricorne.

Il indique aussi des valeurs approximatives pour le diamètre apparent et l’éclat de la planète. Enfin, il examine les positions observées d’Uranus sur la période 1781-1846 à la lumière de sa nouvelle théorie :

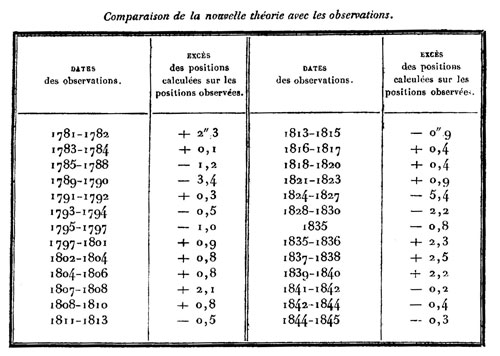
Figure 5 : Tableau p. 437 du second article de Le Verrier. Celui-ci reprend les observations d’Uranus à la lumière de sa nouvelle théorie. Au lieu des ± 100’’ d’écart observés auparavant (figure 1), on ne trouve plus que ± 5’’ d’écart.

Sur les indications de Le Verrier, la planète est observée à Berlin

Peu après avoir dévoilé à l’Académie des sciences, le 31 août 1846, les éléments de la planète et le lieu où on devrait la trouver, Le Verrier écrit à plusieurs astronomes étrangers qu’il sait disposer d’instruments puissants et surtout de bonnes cartes du Ciel qui n’existent pas à l’Observatoire de Paris. D’ailleurs, malgré les efforts d’Arago, on ne découvrira pas la planète à Paris. L’un de ces astronomes étrangers est Johann-Gottfried Galle (1812-1910), de l’Observatoire de Berlin. Le Verrier lui écrit le 18 septembre, la lettre arrive le 23 septembre, et dès la nuit qui suit Galle découvre la planète troublante. Le 25 septembre, Galle écrit en français à Le Verrier, qui ne connaît pas l’allemand :

Monsieur, La planète, dont vous nous avez signalé la position, réellement existe. Le même jour où j’ai reçu votre lettre, je trouvais une étoile de 8^me grandeur, qui n’étoit pas inscrite dans l’excellente carte Hora XXI (dessinée par M. le Dr Bremiker) de la collection des cartes célestes publiée par l’Académie de Berlin. L’observation du jour suivant décida que c’était la planète cherchée. Nous l’avons comparée, Mr. Encke et moi, par la grande lunette de Fraunhofer [objectif de 23 cm de diamètre] avec une étoile de 9^me grandeur […].

Figure 6 : Début de la lettre du 25 septembre 1846 de Galle à Le Verrier annonçant la découverte de Neptune. ©Bibliothèque de l’Observatoire de Paris.

Peu après l’annonce de la découverte, la planète est vue à Paris par Le Verrier et à l’étranger par plusieurs astronomes (3), qui lui écrivent pour le féliciter. Dans son enthousiasme, Le Verrier écrit dans une note du 5 octobre 1846 :

Ce succès doit nous laisser espérer, qu’après trente ou quarante années d’observations de la nouvelle planète, on pourra l’employer, à son tour, à la découverte de celle qui la suit, dans l’ordre des distances au Soleil. Ainsi de suite : on tombera malheureusement bientôt sur des astres invisibles, à cause de leur immense distance au Soleil, mais dont les orbites finiront, dans la suite des siècles, par être tracées avec une grande exactitude au moyen de la théorie des inégalités séculaires.

Son vœu ne s’est pas exaucé comme il l’avait prévu : on a bien trouvé dans le système solaire d’autres astres plus éloignés que Neptune, comme Pluton, mais ils sont trop loin et trop peu massifs pour exercer une influence appréciable sur l’orbite de cette planète, et ils n’ont été découverts que par des recherches systématiques.

Un déluge de félicitations va pleuvoir sur Le Verrier, mais ce sont certainement celles de ses collègues qui le touchent le plus. Il devient instantanément célèbre, et les honneurs affluent : il est promu officier de la Légion d’honneur alors qu’il n’était chevalier que depuis quatre mois (Galle est nommé chevalier), entre au Bureau des longitudes comme membre adjoint, et est nommé à la chaire de Mécanique céleste de la Faculté des sciences de Paris, créée à cette occasion.

 

Figure 7 : L’astronome allemand Johann Gottfried Galle (1812-1910)

Le roi Louis-Philippe I^er nomme Le Verrier précepteur pour l’astronomie de son petit-fils Louis-Philippe d’Orléans. La Royal Society of London lui décerne la prestigieuse médaille Copley, puis l’inscrit parmi ses membres étrangers, comme le feront aussi d’autres sociétés savantes. De nombreuses caricatures sont publiées, au relent souvent nationaliste (Fig. 6). Le ministre de l’Instruction publique, Salvandy, commande son buste au célèbre sculpteur Pradier et en fait hommage à Madame Le Verrier, avec l’instruction de le placer au collège de Saint-Lô, la ville natale de Le Verrier (il se trouve maintenant dans la mairie de cette ville).

Figure 8 : Caricatures de Cham sur la découverte de la nouvelle planète, parues le 7 novembre 1846. Elles sont dirigées contre son concurrent anglais Adams, les légendes sont : (en haut à gauche) M. Adams cherchant la planète de M. Leverrier ; (en haut à droite) M. Adams découvrant la planète dans le rapport de M. Leverrier ; (en bas, de gauche à droite) L’Angleterre prenant possession de la nouvelle planète ; Suite des découvertes de M. Leverrier ; Suite des découvertes de M. Adams. ©Bibliothèque de l’Observatoire de Paris.

Quelques divergences ultérieures

Cependant, quelques voix discordantes se font entendre. Louis-François Wartmann (1793-1864), un astronome amateur de Genève, avait observé (ou cru observer) en 1831 un objet pourvu comme Neptune d’un mouvement lent rétrograde. L’identification de cet objet à la planète troublante est une proposition du fameux Guglielmo Libri (1803-1869), membre de l’Académie des sciences, qui est l’ennemi d’Arago : il veut minimiser la découverte de Le Verrier en insinuant que la planète a déjà été découverte. Lors de la séance suivante, le 19 octobre 1846, Arago fera justice de cette insinuation. La presse quotidienne se fera cependant, jusqu’à la fin de 1846, l’écho de propos semblables à ceux de Libri.

On voit aussi apparaître d’autres critiques plus sérieuses, au fur et à mesure que l’on réalise que l’orbite réelle de la nouvelle planète diffère de façon importante de celle prédite par Le Verrier (Figure 7). Il est vrai que Le Verrier avait donné les éléments de la planète avec une précision trompeuse, alors qu’ils étaient par la force des choses assez incertains. Dans son enthousiasme, il avait fixé à leur valeur des limites exagérément étroites : 35 à 38 unités astronomiques pour le demi-grand axe de l’orbite, par exemple, alors que les observations montrent qu’il ne vaut que 30 unités, et 207 à 233 ans pour la période sidérale qui n’est que 164 ans. Par ailleurs, la découverte dès le 10 octobre 1846 par l’astronome amateur anglais William Lassell (1799-1880), possesseur d’un télescope de 60 cm d’ouverture, d’un satellite de Neptune, Triton, permet d’obtenir la masse de la planète en appliquant les lois de la gravitation universelle à l’orbite du satellite, à condition de connaître sa distance. Après quelques mois d’observation, Lassell trouve pour Triton une période d’un peu moins de 6 jours et détermine l’orbite de ce satellite, d’où il peut déduire la masse de Neptune : il trouve 20 fois celle de la Terre en utilisant la distance donnée par Le Verrier, alors que ce dernier avait annoncé 36 (elle n’est que 17,2 fois celle de la Terre en prenant la valeur actuelle de cette distance). Au vu de cette importante différence, l’astronome américain Benjamin Peirce (1809-1880) n’hésite pas à affirmer que dans ces conditions la découverte de Galle avait été purement fortuite. Il est vrai que Peirce s’était lui-même trompé en discutant les observations de Lassell, dont il avait déduit que Triton tournait en 21 jours ; la masse de Neptune aurait alors été beaucoup trop faible pour que cette planète pût exercer sur Uranus une action importante.

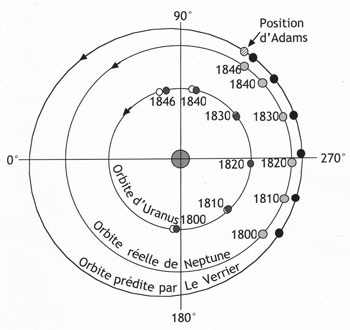
Figure 9 : Les orbites d’Uranus et de Neptune (les axes repèrent les longitudes vues du Soleil). Sur le cercle intérieur, la position d’Uranus de 1840 à 1846 est indiquée pour différentes dates par des cercles gris foncé ; les cercles blancs représentent schématiquement les positions qu’Uranus aurait dû occuper en l’absence de perturbation par Neptune (l’écart avec les positions réelles est très exagéré dans la figure). L’orbite de Neptune, telle que connue actuellement, est également tracée, avec sa position pour les mêmes dates (cercles médian). Neptune, située plus loin du Soleil, tourne moins vite qu’Uranus : son attraction a donc accéléré Uranus avant la conjonction de 1821, et l’a retardé ensuite, comme on le constate sur la figure. L’orbite de Neptune calculée par Le Verrier est indiquée, avec les positions toujours pour les mêmes dates (cercles noirs). Vue de la Terre, la position calculée pour la date de la découverte (23 septembre 1846) est située 1 degré en arrière de la position réelle. L’orbite de Neptune calculée par Adams est assez voisine de celle de Le Verrier pour la période considérée, mais sa direction pour la date de la découverte (cercle hachuré) est plus de 2° en avant de la position réelle. Schéma de l’auteur.

À dire vrai, la seule quantité qui soit assez bien déterminée par l’étude des perturbations est l’intensité de la force perturbatrice exercée par Neptune sur Uranus à l’époque de la conjonction des deux planètes, c’est-à-dire le moment où elles sont les plus rapprochées l’une de l’autre, soit en 1821 (figure 5). D’après la loi de la gravitation universelle, elle est proportionnelle à la masse de Neptune et inversement proportionnelle au carré de la distance qui la sépare d’Uranus. La Figure 7 montre que la distance entre Uranus et Neptune prédite par Le Verrier pour cette époque n’est pas très différente de la distance réelle : elle est seulement un peu trop grande, ce qui est à peu près compensé – pour la force de gravitation – par la masse exagérée qu’il assigne à la planète (Figure 8). Le Verrier ayant prédit un demi-grand axe trop grand, son orbite est exagérément excentrique alors qu’elle est en fait presque circulaire. Finalement, toutes les critiques seront vite oubliées devant l’immense succès qu’est la découverte de Neptune.

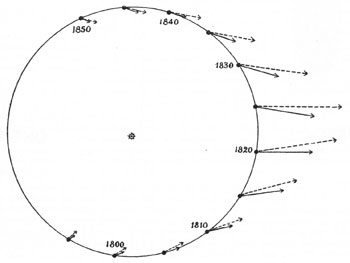
Figure 10 : Comparaison de la force perturbatrice exercée sur Uranus à différentes époques par Neptune, réelle (flèches en traits pleins) et estimée par Le Verrier (flèches en traits pointillés). On constate que la force perturbatrice correspondant aux éléments prédits par Le Verrier est sensiblement correcte en direction (encore que la date de la conjonction entre Uranus et Neptune soit trop tardive d’un an et demi), mais surestimée en intensité. D’après Danjon (L’Astronomie, Bulletin de la Société astronomique de France, 1946, p. 255-278).

Astronomie & nationalisme ?

Comme l’idée de l’existence d’une planète qui troublerait le mouvement d’Uranus était dans l’air bien avant l’intervention de Le Verrier, il ne faut pas s’étonner que plusieurs astronomes aient essayé comme lui de prédire sa position par le calcul. Dès avant 1840, Bessel avait chargé son élève Friedrich Wilhelm Flemming (1812-1840) de rassembler et de réduire les observations d’Uranus pour les comparer aux tables. Mais la mort prématurée de Flemming et la longue maladie qui devait emporter Bessel en 1846, n’ont pas permis à ce projet de réussir. Sinon, il est très probable que Bessel, dont le talent était immense, aurait résolu le problème, peut-être même avant Le Verrier.

Figure 11 : L’astronome anglais John Couch Adams (1819-1892)

Un autre concurrent, lui, avait abouti en Angleterre : John Couch Adams (1819-1892) (4) : voir la Figure 7. Il n’est pas de notre propos de rappeler les controverses passionnées sur la priorité de la découverte de Neptune, controverses où le nationalisme a joué un grand rôle. Ce n’est que récemment qu’elles se sont apaisées, et que l’on a reconnu des deux côtés de la Manche la priorité de Le Verrier. Si Adams n’a pas été le premier, c’est que sa timidité ne lui a pas permis de convaincre à temps le tout puissant Airy, et que lorsque la recherche a enfin été décidée à Cambridge, elle n’a pas été menée avec beaucoup d’intelligence. La concurrence n’a pas empêché Le Verrier et Adams d’établir et de conserver jusqu’à la fin de leur vie une grande estime mutuelle et des relations cordiales.