Rœmer et la vitesse de la lumière

Une histoire de satellites

Galilée, découvreur des quatre principaux satellites de Jupiter, a le premier proposé d'utiliser leur mouvement comme une horloge naturelle et universelle permettant de se repérer en longitude (cf. encadré). Cette méthode était censée résoudre la question du repérage des longitudes en mer, question cruciale à l'ère de la navigation transocéanique (1). Grâce à Huygens qui venait en 1657 de mettre au point son horloge à balancier (2), l'étude des éclipses des satellites joviens a été reprise en 1664 par Jean-Dominique Cassini (1625-1712) pour en dresser des tables plus précises et ainsi réaliser des cartes géographiques moins défectueuses ; Cassini exposa à cette fin sa méthode de détermination des différences de longitudes sur Terre par observation simultanée d'une même éclipse en deux lieux.

En 1667, année où débuta la construction de l'Observatoire de Paris, les astronomes de l'Académie – Auzout, Picard, Huygens et Roberval – élaborèrent de vastes programmes d'observations et de recherches, avec, parmi ceux-ci, la détermination – par la méthode de Cassini – de la différence de longitude entre l'observatoire de Paris et l'observatoire disparu de Tycho Brahe à Hveen, au Danemark (Observatoire d'Uraniborg). L'expédition à Uraniborg était nécessaire afin de pouvoir utiliser correctement les anciennes observations de Tycho Brahe, mais également d'Hipparque et de Ptolémée (3). Jean Picard fut chargé de cette mission tandis que Cassini restait à Paris pour observer dans le même temps les immersions d'octobre 1671 à janvier 1672.

Les quatre satellites galiléens de Jupiter (Io, Europe, Ganymède et Callisto), dont les orbites sont quasi équatoriales et coplanaires, présentent des phénomènes d'éclipses lorsqu'ils passent dans le cône d'ombre de la planète – on parle d'occultation lorsqu'ils passent derrière Jupiter - pour un observateur terrestre. Ces éclipses durent plus de deux heures pour Io. Selon les positions relatives de la Terre et de Jupiter, on ne peut observer, sur une période donnée, que l'immersion, c'est-à-dire l'entrée du satellite dans l'ombre de Jupiter, ou l'émersion, c'est-à-dire la sortie du satellite de l'ombre de Jupiter, mais pas les deux phénomènes ensemble, l'un étant toujours caché par la présence de Jupiter dans l'axe de visée.

 

 

 

 

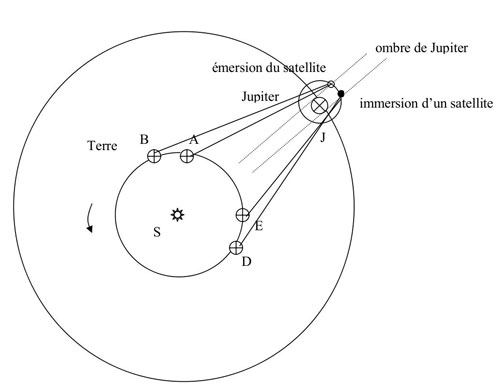
Les instants des éclipses (immersion ou émersion) étant calculés dans les éphémérides en temps vrai (temps solaire) du lieu de référence (Observatoire de Paris par exemple), on observe en un autre lieu l'un de ces phénomènes, repéré en temps vrai local. La différence de temps entre ces deux instants donne l'écart entre les deux échelles de temps vrai, c'est-à-dire la différence de longitude (4), à raison de 4 minutes par degré, qui représente la vitesse angulaire de rotation de la Terre. Simple dans son principe, cette méthode souffre de nombreuses difficultés, comme la faible fréquence du phénomène (206 révolutions de Io par an mais 150 seulement utilisables du fait de la présence du Soleil lors de la conjonction de Jupiter), l'heure (il doit faite nuit et Jupiter doit être visible dans le ciel du lieu dont on veut déterminer la longitude), les conditions météorologiques et la précision de l'observation. L'ensemble de ces conditions diminue substantiellement le nombre d'éclipses utilisables.

Picard arriva à Copenhague le 24 août 1671 puis partit pour Hveen le 6 septembre, « accompagné de Mons. Erasme Bartholin et d'un jeune Danois nommé Olaüs Rœmer que Mons. B. m'avoit fait connaître, et qui, étant ensuite venu en France avec moi, fut nommé membre de l'académie des sciences, où il a donné plusieurs marques de son rare génie et de son esprit. », écrit-il dans son Voyage d'Uranibourg, ou observations astronomiques faites au Dannemark (5).

Ce jeune astronome danois, Olaüs Christensen Rœmer (6) naquit à Aarhus le 25 septembre 1644. Il commença ses études de sciences exactes à l'Université de Copenhague en 1662. Immédiatement après, il devint assistant d'Erasmus Bartholin, professeur de mathématiques et de médecine. Rœmer se familiarisa avec l'astronomie grâce au travail que lui avait confié le roi du Danemark – Christian V – qui consistait à réviser et recopier les observations de Tycho Brahe, dont le roi venait d'acheter le manuscrit auprès du fils de Kepler. Bartholin devait d'ailleurs en assurer l'édition.

Rœmer assista donc Picard lors des observations des éclipses faites par ce dernier pour déterminer la différence de longitude entre Paris et Hveen. Une attaque de scorbut força Picard à revenir à Copenhague, laissant le soin à Rœmer et à l'un des compagnons de Picard de poursuivre les observations. Malgré la difficulté de la tâche, ses résultats furent d'une grande précision, ce qui accrut l'estime de Picard pour le jeune astronome. Il le ramena finalement avec lui à Paris au cours de l'été 1672. Rœmer fut logé à l'Observatoire et prit dès lors une part active au travail de l'Académie royale des sciences. Il continua entre autres avec Picard les observations des satellites de Jupiter et participa à la détermination de la parallaxe de Mars.

Jean Picard (dit l'abbé Picard) est né le 21 juillet 1620 à La Flèche et mort le 12 juillet 1682 à Paris. On sait très peu de choses sur ses jeunes années. Disciple de Galilée et de Gassendi – il remplacera Gassendi au poste d'astronomie au collège de France en 1655 –, il a beaucoup contribué à perfectionner les instruments d'optique de son temps et fait progresser l'astronomie de précision. Mais il s'est surtout rendu célèbre en mesurant le rayon de la Terre de façon précise. Dès 1666, la question de la mesure de la terre est au programme dans la toute nouvelle Académie des Sciences créée par Colbert, dont il fut l'un des 21 premiers membres. Entre 1668 et 1670, Picard mesure par la méthode de la triangulation – mise au point un siècle plus tôt par Gemma Frisius – la longueur d'un arc du méridien de Paris sous-tendu par un angle de un degré, entre Malvoisine (au sud de Paris) et Sourdon (à 20 km au sud d'Amiens). Cette mesure de l'arc de méridien demeure une première mondiale en terme de géodésie. Cette opération est à l'origine de la nouvelle carte de France ordonnée par Colbert et également de la controverse sur la forme de la Terre. Ses mesures l'ont conduit à un résultat de « 57 060 toises pour un grand cercle de la Terre », ce qui donne un rayon terrestre d'environ 6 372 km. Ses mesures seront compilées dans son livre La mesure de la Terre publié en 1671. La même année, Picard part au Danemark pour mesurer la différence de longitude entre Paris et l'observatoire d'Uraniborg de Tycho Brahe, sur l'île de Hven. Il en reviendra avec Ole Rœmer, pour le plus grand bénéfice de l'Académie des Sciences, de l'Observatoire et de la science en général.

Lorsque Cassini établit ses tables, il se rendit compte que les périodes des satellites comportaient des écarts par rapport à une régularité supposée découler des lois de Kepler. Outre une première irrégularité – ou inégalité – due à l'excentricité de l'orbite de la Terre et de Jupiter, Cassini en repéra une seconde en août 1675. Quelle en était la cause ?

L'explication de la seconde inégalité fut proposée en premier par Cassini lui-même en termes de « mouvement successif de la lumière », c'est-à-dire en supposant une vitesse de la lumière finie. Cette inégalité « paroît, dit-il, venir de ce que la lumière emploie quelque temps à venir du satellite jusqu'à nous, et qu'elle met environ dix à onze minutes à parcourir un espace égal au demi-diamètre de l'orbite terrestre (7)». Mais Cassini va délaisser cette hypothèse et laisser à Rœmer la gloire de cette découverte (8). C'est donc le 7 décembre 1676 que Rœmer présente le résultat de ses travaux à la communauté scientifique dans le Journal des Sçavans. La lecture de ce mémoire très concis – il ne fait que deux pages – est facile et convainc de la justesse de l'hypothèse de Rœmer. Mais en seconde lecture, il laisse un sentiment d'insatisfaction tant les calculs sont peu détaillés, comme nous allons le voir.

Il rappelle tout d'abord que les savants n'ont pas encore proposé d'expérience probante pour montrer que la vitesse de la lumière est finie : et pour cause, la plupart pensent que son mouvement est instantané.

Il y a longtemps que les philosophes sont en peine de décider par quelque expérience, si l'action de la lumière se porte dans un instant à quelque distance que ce soit, ou si elle demande du temps.

Rappelons néanmoins que Galilée fut le premier à essayer de mesurer directement cette vitesse ; il rapporte la méthode employée dans ses Discours concernant deux sciences nouvelles, publiés en 1638. Mais le résultat est négatif, et il peut seulement en déduire que la propagation de la lumière est sinon instantanée, du moins extrêmement rapide – bien supérieure en tout cas à celle du son. Descartes proposa de se tourner alors vers les phénomènes astronomiques, et en particulier les éclipses de Lune. En effet, si la lumière met du temps pour parcourir la distance Terre-Lune, une éclipse sera visible sur Terre un instant après le moment calculé où le Soleil, la Terre et la Lune sont alignés. Il supposa que la lumière parcourt l'aller-retour Terre-Lune en environ une heure. Mais pas même un décalage d'une demi-minute n'est décelable lors de l'éclipse. Il en conclut que l'infinité de la vitesse était établie (9), ce qui corroborait ses a priori mais plaçait dans le même temps un obstacle à l'acceptation de l'hypothèse de Rœmer (10).

Dans son analyse, Rœmer utilise les observations du premier satellite, Io, effectuées au cours des huit années écoulées (11). Une lettre de Rœmer à Huygens révèle que sa théorie du retardement de la lumière se fondait exclusivement sur des observations faites soit par Picard, soit par lui-même et ce dernier, et qu'il n'a pas utilisé les nombreuses observations réalisées par Cassini à cette époque.

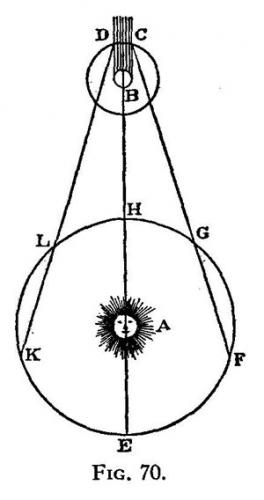
Figure 1: Schéma accompagnant le mémoire de Rœmer. Les immersions sont observées quand la Terre se rapproche de Jupiter, allant de F vers G. Les émersions sont observées quand la Terre s'éloigne de Jupiter, allant de L vers K.

Tout comme Cassini, Rœmer a été amené à constater que la durée de révolution du satellite était plus courte quand on la mesurait à partir d'une série d'immersions qu'à partir d'une série d'émersions, et cela indépendamment de la position de Jupiter sur son orbite :

Il est manifeste que si la lumière demande du temps pour traverser la distance LK, le satellite sera vu plus tard de retour en D, qu'il n'aurait été si la Terre était demeurée en K, de sorte que la révolution de ce satellite, ainsi observée par les émersions, sera retardée d'autant de temps que la lumière aura passé pour aller de L en K, et qu'au contraire […] les révolutions des immersions paraîtront autant raccourcies, que celles des émersions avaient paru allongées.

Rœmer propose que ces inégalités soient imputées au fait que « la lumière demande du temps » pour traverser l'intervalle supplémentaire LK due au mouvement de la Terre pendant les révolutions du satellite. Si, comme il le propose à titre d'hypothèse au début du mémoire, la lumière mettait une seconde pour franchir le diamètre de la Terre, alors la différence de temps serait

de près d'un demi quart d'heure entre deux révolutions du premier Satellite, dont l'une aurait été observé en FG, & l'autre en KL, au lieu qu'on n'y remarque aucune différence sensible.

Plutôt que d'en conclure à une vitesse infinie, comme l'a déduit Descartes de l'analyse qu'il avait faite de l'étude d'une éclipse de Lune, Rœmer propose d'augmenter le nombre de révolutions observées, le cumul permettant l'obtention d'un temps parfaitement mesurable (12). Il arrive donc au résultat crucial que la lumière met 22 minutes pour traverser le diamètre de l'orbite terrestre, et donc que la lumière a un « mouvement successif », et non instantané (13). Mais à aucun moment, pourtant, il ne livre une valeur numérique de cette vitesse. Pourquoi ? En parcourant la littérature, on constate que plusieurs raisons sont invoquées : parce que l'importance de la démonstration résidait uniquement dans le fait que la vitesse était finie, ou que le diamètre de l'orbite terrestre n'étant connu qu'avec une grande imprécision il s'avérait inutile d'en tirer une valeur de la vitesse de la lumière, ou encore parce que la vitesse lui semblait inconcevablement grande. Peu importe la vraie raison, le fait est que Rœmer n'a jamais proposé une valeur de la vitesse de la lumière, dans le sens où nous l'entendons maintenant (14)!

Les bases de calcul de Rœmer

Nous avons relevé que Rœmer ne donne aucun indice sur la provenance des valeurs qu'il cite. Ce fait est patent quand il écrit que pendant

42 heures et demi, que le Satellite emploie à peu près à faire chaque révolution, la distance entre la Terre & Jupiter dans l'un & l'autre quadrature varie tout au moins de 210 diamètres de la Terre [...]

Comment Rœmer sait-il qu'en 42 ½ heures la Terre se déplace sur son orbite d'« au moins 210 » diamètres terrestres ? Pour arriver à ce résultat, Rœmer a bien dû partir de la distance Terre-Soleil, et il est possible de dérouler le calcul à l'envers, comme l'a fait l'historien des sciences Albert Van Helden (15). Reprenons son analyse. Si la Terre parcourt sur son orbite 210 diamètres terrestres en 42 h ½, alors sa vitesse est de 43 314 diamètres terrestres par an, et donc la circonférence de son orbite, qu'elle parcourt en un an, est de 43 314 diamètres terrestres. Par conséquent, la distance Terre-Soleil est de 43 314 / 2π, soit 6 894 diamètres terrestres, ou 13 787 rayons terrestres. L'angle sous-tendu par le rayon de la Terre mesuré depuis le centre du Soleil, appelé parallaxe horizontale du Soleil, est alors égal à

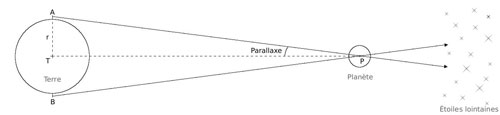
Figure 2 : Schéma représentant la parallaxe horizontale du Soleil. C'est l'angle sous lequel, placé au centre du Soleil, un observateur verrait le rayon de la Terre, le segment reliant le centre des deux astres étant perpendiculaire au rayon terrestre. La parallaxe horizontale du Soleil vaut 8,794″.

On peut donc conclure qu'il a effectué ses calculs avec une valeur de la parallaxe d'environ 15'', valeur proposée plus tôt par l'astronome belge G. Wendelin (1635) et les astronomes anglais J. Horrocks (1638) et T. Streete (1661) (16). Ce n'était pas la valeur retenue par Cassini et Richer à partir de la mesure de la parallaxe de Mars – mesure réalisée grâce aux observations effectuées à Paris et à Cayenne auxquelles Rœmer avait participé – puisque Cassini en tira une parallaxe de 9,5'' (beaucoup plus proche de la réalité connue aujourd'hui). En rapportant que la Terre se déplace d'« au moins 210 » de son diamètre en 42 ½ heures, Roemer nous permet de reconstituer le cheminement de son calcul et surtout la donnée initiale grâce à laquelle il a pu aboutir à ce résultat, à savoir sa valeur de la parallaxe solaire.

En définitive, Rœmer avait-il la possibilité de calculer la vitesse de la lumière (ce qu'il n'a pas fait, rappelons-le) ? Oui, pour peu qu'il eût eu la valeur du rayon terrestre. Or, il écrit au début de son mémoire que la grandeur du diamètre de la Terre est de 3 000 lieues environ, soit 6 675 km (cf. encadré Picard, ci-dessus). La distance Terre-Soleil ayant été évaluée à 13 787 rayons terrestres, et la lumière franchissant le double de cette distance en 22 minutes, cela nous mène à une vitesse de 139 437 km/s : cette valeur est effectivement largement sous-estimée par rapport à la valeur « moderne ».

Réception et distorsion des travaux de Rœmer par ses contemporains

J. D. Cassini, qui dans un premier temps avait soutenu l'hypothèse de la vitesse finie de la lumière pour expliquer les inégalités du premier satellite de Jupiter, s'y opposa ensuite notamment parce qu'il apparaissait que ce phénomène n'était pas présent pour les trois autres satellites joviens. « […] l'on n'est pas certain, écrivit-il, que cette inégalité de temps ne soit pas produite ou par l'excentricité du Satellite, ou par l'irrégularité de son mouvement, ou par quelqu'autre cause jusques ici inconnuë, dont on pourra s'éclaircir avec le temps (17). »

Fontenelle, qui lui aussi était séduit par l'hypothèse de Rœmer, s'en détourna ensuite puisque « Il paroît donc qu'il faut renoncer, quoique peut-être avec regret, à l'ingénieuse & séduisante hypothêse de la propagation successive de la lumière... A quoi tient-il que nous ne tombions pas dans de grandes erreurs! Si Jupiter n'eût qu'un Satellite, & si son excentricité à l'égard du Soleil eût été moindre, & ces deux choses-là étoient fort possibles, nous serions tenus sûrs que la lumière traversoit en 14' l'Orbe de la Terre (18). »

Il y eut donc une certaine résistance à cette nouvelle idée en France, mais il n'en fut pas de même à l'étranger. Le mémoire de Rœmer fut traduit en anglais dans les Philosophical Transactions en 1677 (19). Newton, Molyneux, Flamsteed ou encore Halley acceptèrent immédiatement la conclusion de Rœmer. Dans la première édition de ses Principia en 1687, Newton utilisa d'ailleurs la valeur de 22 minutes rapportée par Rœmer. Dans la première édition de son ouvrage Opticks, en 1704, il utilisa une valeur plus faible de 16 minutes, de même que dans les éditions successives des Principia, sûrement à la suite de ses propres calculs. Compte tenu du fait que Newton prit une valeur de la parallaxe solaire proche de 10'', cela mène au bout du compte au bon ordre de grandeur de la vitesse de la lumière.

Hooke fut le seul à ne pas partager l'avis de ses compatriotes. Il continua à soutenir le mouvement instantané de la lumière car « [...] supposing this may prove it to be temporary, and not instantaneous, yet we find that 'tis so exceeding swift that 'tis beyond imagination (20)».

Huygens, en Hollande, eut connaissance du mémoire de Rœmer par l'intermédiaire de la traduction anglaise, et il lui envoya immédiatement une lettre lui demandant plus d'informations. De fait, ce sera Huygens qui le premier présentera un calcul plus explicite de la vitesse de la lumière, dans son livre Traité de la lumière, lu devant l'Académie des Sciences en 1678 et publié finalement en 1690. Il est utile pour notre propos de reproduire le passage dans lequel Huygens déroule son calcul (cf. illustration 3 pour la référence au schéma):

Que si l'on considère la vaste étendue du diamètre KL [diamètre de l'orbite terrestre], qui selon moi est de quelque 24 mille diamètres de la Terre, l'on connaîtra l'extrême vitesse de la lumière [suivent divers calculs non reproduits ici]. Mais le Son, comme j'ai dit ci-devant, ne fait que 180 toises dans le même temps d'une seconde : donc la vitesse de la lumière est plus de six cent mille fois plus grande que celle du son : ce qui pourtant est tout autre chose que d'être momentanée, puisqu'il y a la même différence que d'une chose finie à une infinie. Or le mouvement successif de la lumière étant confirmé de cette manière, il s'ensuit, comme j'ai déjà dit, qu'il s'étend par des ondes sphériques, ainsi que le mouvement du son (21).

Huygens en arrive donc au résultat que la vitesse de la lumière est 600 000 fois plus grande que celle du son – soit de l'ordre de 200 000 km/s. C'est mieux – mais encore une fois nous voyons qu'à cette époque, ce ne sont pas les valeurs numériques absolues qui intéressent les savants, ce sont plutôt les rapports entre grandeurs de même nature.

Finalement, la découverte de Rœmer n'a été universellement admise que lors de la découverte par Bradley de l'aberration des étoiles en 1729 (22). Bradley eut le privilège de démontrer d'un coup deux hypothèses fondamentales, à savoir l'héliocentrisme et le mouvement successif de la lumière.

Distorsion ultérieure des travaux de Rœmer

Il nous faut maintenant aborder un dernier point important. En recherchant des informations sur internet à propos de Rœmer et la vitesse de la lumière, nous ne pouvons qu'être surpris à la lecture des valeurs de la vitesse de la lumière que l'on prête à Rœmer, valeurs variant dans un large intervalle. Un coup d'œil dans la littérature contemporaine nous confronte à ce même problème (23). Le physicien polonais Andrzej Wroblewski s'est amusé à recenser les différentes valeurs imputées à Rœmer – essentiellement dans la littérature anglo-saxonne –, ainsi que la date de sa « découverte » (24). Le résultat est édifiant. Comment et quand cette distorsion de l'histoire est-elle apparue ? C. Boyer, dans son article Early estimates of the velocity of light, a justement porté son attention sur la dispersion des valeurs de la vitesse créditées à Rœmer – ainsi que pour le temps de trajet entre le Soleil et la Terre – dans les ouvrages d'histoire des sciences, d'astronomie, de physique ou d'optique dans la période 1850-1940. Le constat était déjà identique à celui de Wroblewski. Qu'en est-il de la période plus proche de celle de la publication de Rœmer ? Déjà Fontenelle pensait bien faire en écrivant dans son Histoire de l'Académie Royale des Sciences qu' « il suit des observations de M. Roëmer que la lumière dans une seconde de temps fait 48 203 lieues communes de France, et 377/1141 parties d'une de ces lieues. »

Il en est de même de Priestley ou de l'article « Lumière » de l'Encyclopédie de Diderot et d'Alembert (25). Une telle ambiguïté sur la façon dont les auteurs ont rapporté la découverte de Rœmer a initié cette dérive que l'on constate encore à l'heure actuelle. Dans un livre du mathématicien français Joseph Bertrand, publié en 1869 et intitulé L'Académie des Sciences et les Académiciens de 1666 à 1793, nous pouvons lire que « Rœmer, en effet, a mesuré le premier la vitesse de la lumière, à laquelle Picard, par une voie toute différente, avait touché de si près (26)», sans d'ailleurs que Bertrand s'explique sur cette méthode de Picard.

Dans le volume 8 des Œuvres Complètes de Christiaan Huygens, publié en 1899, on peut lire en note à la correspondance entre Rœmer et Huygens : « […] Römer […] célèbre par la première détermination de la vitesse de la lumière (27). » Les lettres échangées entre ces deux savants étant en latin, on peut considérer que certains lecteurs n'ont retenu que cette phrase sans avoir pu lire le contenu des lettres. Les glissements de sens se logent dans ce type de phrase qui sont de signification claire dans l'esprit de leur auteur, mais ne le sont plus pour un lecteur non initié. Dans un article très détaillé sur Rœmer paru en 1913, l'historienne danoise Kirstine Meyer écrit « Jusqu'à ce jour, tout le monde a su qu'Ole Rœmer avait découvert le ''retardement'' de la lumière et mesuré le premier sa vitesse de propagation ; mais les observations sur lesquelles se basait sa découverte avaient disparu (28).» Effectivement, K. Meyer a étudié des manuscrits retrouvés de Rœmer, mais ces documents ne contiennent pas non plus de calcul explicite de la vitesse de la lumière. On peut lui accorder le fait que l'opinion commune attribuait ce calcul à Rœmer, comme on l'a vu plus haut, mais elle ne revient malheureusement pas sur cette affirmation dans son article pour lever le doute. L'ambiguïté est encore plus profonde par la réunion de cause à effet de la découverte du « retardement » de la lumière et celui de mesure de la vitesse de propagation. Ce genre d'ambiguïté se retrouve même sur la plaque commémorative scellée sur le mur nord du bâtiment Perrault de l'Observatoire de Paris, où il est inscrit « L'astronome danois Olaus Römer 1644-1710 a découvert la vitesse de propagation de la lumière à l'Observatoire de Paris en 1676 (29).»

Figure 3 : Plaque commémorative dédiée à Rœmer scellée sur le mur nord du bâtiment Perrault de l'Observatoire de Paris.

On peut comprendre qu'une personne, en voulant s'informer, ait repris une information erronée parmi toute cette littérature secondaire et l'ait transmise, et que cette distorsion se soit imposée à l'instar de la pomme de Newton ou de la baignoire d'Archimède (30). Nous ne pouvons pas contrôler chaque source, et nous sommes bien obligés de faire confiance. Mais il est maintenant aisé, grâce aux programmes de numérisation, d'avoir accès directement aux sources qui, il y a seulement quelques années, étaient difficilement consultables. Pourtant, force est de constater que l'erreur commise à propos de Rœmer et de son prétendu calcul de la vitesse de la lumière perdure. Laissons le mot de la fin à C. Boyer :

Such a state of affairs can not but impress one with the need of exercising caution in the history of science in citations of numerical values as well as of dates of events (31).

(1) Malheureusement, cette méthode n'a jamais pu être employée efficacement faute d'un dispositif approprié à l'observation.

(2) Avec cette horloge de Huygens, on commençait à avoir une mesure plus précise et plus stable du temps, ce qui permettait aux savants en divers points de l'Europe de noter puis de comparer l'instant où un événement était observé.

(3) I. B. Cohen, Rœmer and the first determination of the velocity of light, Isis, vol. 31, n°2, 1940, pp. 327-372.

(4) La latitude n'entre pas ici en considération : compte tenu de son éloignement, le phénomène est observé au même moment sur un méridien donné.

(5) Jean Picard, Voyage d'Uranibourg, ou observations astronomiques faites au Dannemark, Paris, 1680.

(6) Son prénom et nom peuvent s'orthographier de différentes manières Ole / Olus / Olaüs et Römer / Roëmer / Rœmer / Rømer.

(7) Cité dans I. B. Cohen, op. cit., p. 345.

(8) Cassini va d'ailleurs reconnaître plus tard la primauté de cette découverte à Rœmer. La question de savoir si ce fut Cassini ou bien Rœmer l'initiateur de cette explication a été arbitré en faveur de ce dernier par K. M. Pedersen (K. Pedersen & R. Taton, La vie et l'oeuvre de Rœmer in Rœmer et la vitesse de la lumière, Vrin, pp. 113-128, 1978) mais un manuscrit de Cassini retrouvé par Laurence Bobis et James Lequeux (L. Bobis, J. Lequeux, Cassini, Romer and the velocity of light, Journal of Astronomical History and Heritage, 11(2), pp. 97-105 (2008)) prouverait en fait le contraire.

(9) Carl B. Boyer, Early estimates of the velocity of light, Isis, vol. 33, n°1 (1941), pp. 24-40.

(10) Bien que Rœmer soit un cartésien convaincu, il s'opposera à l'opinion de Descartes quant à la vitesse de la lumière.

(11) K. Meyer a retrouvé en 1913 un manuscrit de Rœmer à la Bibliothèque de l'Université de Copenhague où sont consignées les données des éclipses qu'il a utilisées. Il en recense plus de soixante-dix.

(12) Voir à ce sujet l'article de J. H. Shea, Ole Romer, the speed of light, the apparent period of Io, the Doppler effect and the dynamics of Earth and Jupiter, Am. J. Phs, 66 (7), pp. 561-569, July 1998.

(13) Il ne reste pas de preuve de la façon dont Rœmer a obtenu cette valeur de 22 minutes.

(14) Dans son livre de notes Adversaria, conservé à la Royal Library à Copenhague, Rœmer écrit que la lumière met une minute pour franchir 1 091 diamètres terrestres.

(15) A. Van Helden, Rœmer's speed of light, Journal for the History of Astronomy, 14, n°40, 1983, pp. 137-141.

(16) Albert Van Helden, Measuring the universe, University Of Chicago Press, 1985.

(17) Cité dans I. B. Cohen, op. cit., p. 347.

(18) Cité dans I. B. Cohen, op. cit., p. 349.

(19) Le mémoire parut dans le vol XII, n°136, du 25 juillet 1677.

(20)Robert Hooke, Lectures on light, in The posthumous works of Robert Hooke, London, 1690, p. 78.

(21) Christiaan Huygens, Traité de la lumière, P. Vander, Leide, 1690. Ed. Dunod, 1992, p. 56.

(22) James Bradley, Letter to Edmond Halley giving an account of new discovered motion of the fix'd stars, Phil. Trans., vol. 35, n°406, pp. 637-661, 1729.

(23) Quelques exemples : Simon Singh, L'histoire du Big Bang, JC Lattes, 2005, p. 96 ; Hans Breuer, Atlas de la physique, Le Livre de Poche, 1997, p. 165 ; Colin Ronan, Histoire mondiale des sciences, Seuil, 1988, p.497; Bernard Maitte, La lumière, Seuil, 1981, p. 96 ; Isaac Asimov, La conquête du savoir, Marabout, 1982, p. 227 ; Marie-Antoinette Tonnelat, in Encyclopédie Universalis, article Lumière (tome 14), p. 41...

(24) Andrzej Wroblewski, de Mora Luminis : A spectacle in two acts with a prologue and an epilogue, Am. J. Phys., 53 (7), July 1985, pp. 620-630.

(25) C. Boyer, Op. cit., pp. 30 & 34.

(26) J. Bertrand, L'Académie des Sciences et les Académiciens de 1666 à 1793, J. Hetzel, Paris, 1869, p. 29.

(27) Œuvres Complètes de Christiaan Huygens, Société Hollandaise des Sciences (22 vol., La Haye, 1888-1950). La citation est tirée du vol. 8, note 1 de la page 30.

(28) Kirstine Meyer, Rœmer, Dansk Biografisk Leksikon, 20, (Copenhagen, 1941), pp. 392-400.

(29) Il est pourtant précisé dans le premier numéro du Magazine de l'Observatoire de Paris du printemps 2005, à propos de cette plaque, que le résultat des travaux de Rœmer conclut à la finitude de la vitesse de la lumière. Sage précision...

(30) Sven Ortoli & Nicolas Witkowski, La baignoire d'Archimède, Seuil, 1998

(31) C. Boyer, op. cit., p. 29.