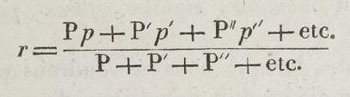Figure 1: Louis Poinsot, gravure de Boilly. Jules Boilly (1796-1874) est un peintre et lithographe spécialisé dans la gravure de personnalités, dont les membres de l’Institut (P.S. Girard, J.D. Cassini, Alexis Bouvard). Il était le fils d’un peintre plus renommé, Léopold Boilly (1761-1845), auteur de peintures de genre et de portraits, notamment de Sadi Carnot.
I - Préliminaires
En 1803, Louis Poinsot publia un traité de statique, à caractère révolutionnaire puisqu’il posait clairement le sujet non seulement en termes de forces mais aussi en terme de « couples » (c’est son expression), c’est-à-dire des paires de forces non colinéaires égales en amplitude et en direction mais en sens opposés. Plus tard, il adapta cette notion pour induire en dynamique une relation nouvelle entre mouvement linéaire et mouvement de rotation. Le présent article résume ces développements et examine leur réception, qui fut lente parmi ses contemporains mathématiciens et quasi inexistante parmi les « historiens » de la mécanique plus tard.
1. Les organisations
Un beau jour, lors des années révolutionnaires II ou III, période à présent plus connue sous le nom d’année 1794, un adolescent orphelin, étudiant au collège Louis le Grand à Paris, tomba sur un prospectus annonçant la création d’une nouvelle institution d’enseignement supérieur. Intrigué, il se porta candidat et fut accepté, ce qui détermina la suite de sa longue carrière.
Cette institution constituait un des deux projets du gouvernement français pour résoudre l’une des crises sociales causées par cinq années de révolution et de ruptures. La purge de l'aristocratie et des classes dirigeantes, et la fermeture de toutes les universités et écoles d'ingénieurs en 1793, avaient laissé en ruines la formation des classes professionnelles à tous les âges de la vie. Une partie de la solution passait par la création de deux grandes institutions d'enseignement supérieur, chacune couvrant un certain nombre de disciplines. Des savants éminents dans diverses matières y sont nommés professeurs, et 400 étudiants sont intégrés dans chacun des deux établissements, choisis par diverses organisations et dignitaires à travers le pays. Après 12 mois d’éducation fast-food, les diplômés retourneraient alors dans leur région d'origine et y créeraient des programmes d'enseignement et des institutions similaires.
Chacun de ces deux projets était absurde, et voué à l'échec : les deux institutions ont capoté un an ou deux après leur création, lors de l'hiver 1794-1795. Mais les circonstances de ces échecs sont différentes. L’École normale était principalement orientée vers les sciences humaines, et un peu vers les mathématiques ; elle a rapidement disparu, mais les versions publiées des cours qui y furent donnés auront une grande influence. L'École Centrale des Travaux Publics couvrait les sciences et en particulier le génie civil et militaire ; elle aurait pu connaître la même destinée, mais ses fondateurs se sont vite rendu compte de l’absurdité du projet et l’ont rapidement transformé en une organisation différente, l'École polytechnique [Langins 1987].
Des examinateurs d’admission et de sortie complétèrent alors le personnel enseignant – professeurs et répétiteurs –, sachant que la stratégie de sélection d’étudiants les plus compétents possible était maintenue ; le recrutement annuel fut cependant réduit de 400 élèves à environ 100-150. Le cours intensif de 12 mois fut remplacé par un cursus plus complet de trois années. On ne tentait plus d’enseigner tout ; au contraire, les élèves recevaient une formation de base dans de nombreuses techniques – et, après obtention du diplôme, suivaient alors une formation plus poussée en sciences de l'ingénieur dans l'une des écoles militaires ou civiles qui existaient déjà et avaient rapidement rouvert leurs portes après la fermeture totale. Les diplômés poursuivaient alors normalement leur carrière dans un Corps d’ingénieurs, dans l'armée ou dans la marine
(1).
Une conséquence de la création de l'École polytechnique fut totalement inattendue : dès le début et pendant les 25 années suivantes, parmi ses diplômés (dits « polytechniciens »), l’on trouva des douzaines de personnalités qui, plus tard, firent de brillantes carrières en tant que professeurs soit au sein de l’École elle-même et/ou dans un Corps, et/ou dans ce qui s’appellera « Université » – organisation d’écoles et d’instituts d’enseignement supérieur, créée par un décret impérial
(2) de 1808. Intéressons-nous à l'un de ces polytechniciens.
2. Louis Poinsot
Poinsot écrivait peu et ne lisait guère, il aimait la méditation (3).
Notre orphelin, Louis Poinsot (1777-1859), illustre en effet bon nombre de ces caractéristiques. Il était l'un des 400 élèves d'origine, comme l’étaient les futurs ingénieurs Barnabé Brisson et Charles Cagniard-Latour, les mathématiciens Louis-Benjamin Francœur et M.-A. Lancret, et les physiciens Jean-Baptiste Biot et Etienne Malus.
Après obtention de son diplôme en 1797, Poinsot passe par l’École des ponts et chaussées pour deux années supplémentaires. Sa performance y fut si lamentable (1 point sur 12 en menuiserie, par exemple) qu'il ne fut pas recruté dans le Corps éponyme
(4). Il fut en fait employé dans divers établissements d'enseignement parisiens : il enseigna notamment à l'École polytechnique dans les années 1810, et y fut examinateur d'admission pour une dizaine d’années à partir de 1816. Un de ses collègues, dans le sens le plus restrictif du terme, fut S.-D. Poisson : étudiant à Polytechnique de 1797 à 1800, il y est immédiatement nommé à un poste et devient professeur, puis examinateur de sortie de 1809 à sa mort, en 1840. Il écrivit :
Si Poinsot se présentait á l'École polytechnique, ma conscience ne me permettrait pas de l'y admettre
(5).

Figure 2 : Siméon-Denis Poisson (1781-1840), paronyme mais ennemi juré de Poinsot.
Poisson comme Poinsot ont également participé à l’institution universitaire
(6). En sus de son enseignement à la Faculté des sciences de Paris, Poisson est nommé au Conseil d'administration de l'Université en 1830. Poinsot enseigna dans diverses écoles parisiennes et, en 1809, est nommé Inspecteur général à l’Université (statut à peu près équivalent à celui d’examinateur de sortie de l'École polytechnique). En 1840, il remplace Poisson au Conseil – en estimant qu’il aurait dû obtenir le poste dix ans plus tôt, à la place de Poisson. Nous retrouverons ce sens très limité de la notion de fraternité dans leurs approches respectives de la mécanique.
Parmi d’autres postes et honneurs, Poinsot succède à Lagrange, pas moins, dans la classe scientifique de l'Institut de France en 1813, et à Gaspard Riche de Prony au Bureau des longitudes en 1842
(7). Alors plus en vue, il est élu à la Chambre des Pairs en 1846 (dans sa 70e année) et au Sénat six ans plus tard.
Sa carrière de professeur est quelque peu intermittente : peut-être avait-il hérité de ses parents tôt disparus (son père avait été un marchand prospère) – en tant que célibataire, il n’avait pas de dépenses à caractère familial. Sa production scientifique est également assez faible, surtout en comparaison de ses contemporains prolifiques comme Poisson ; mais elle est de haute qualité, et couvre de nombreuses branches des mathématiques – principalement la statique et la dynamique, mais aussi le calcul différentiel et intégral, les théories des équations et des fonctions, la théorie des nombres et enfin un peu de topologie alors en gestation.
Son début de carrière de chercheur fut également assez original : au lieu d'articles dans des revues telles que celle de l'École polytechnique, il commença à 26 ans par un manuel, Éléments de statique, volume de 267 pages publié par Calixte Voland en 1803. Il produisit des éditions revues de cet ouvrage jusqu'à une neuvième édition en 1848, principalement en y reproduisant certains de ses articles ultérieurs de dynamique, mais aussi en reprenant quelque peu le texte principal. Notre attention se porte sur sa principale innovation, la théorie du couple, qui a révolutionné l’idée de force en mécanique. Nous rappelons plusieurs des théorèmes majeurs de cette théorie, présentée dans la première édition de son livre, ainsi que leur accueil mitigé parmi ses contemporains à l'École polytechnique et ailleurs. Nous évoquons aussi le manque d'attention accordée à ses théories par les historiens de la mécanique.
3. La présentation traditionnelle de la composition des forces
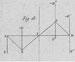
Poinsot commence son ouvrage par la spécification de la force comme « cause quelconque de mouvement » [§1]. Elle est représentée en amplitude (rationnelle ou irrationnelle), en direction et en sens par une ligne droite continue. Le théorème fondamental sur la composition des forces stipule que si deux forces coplanaires et non parallèles P et Q agissent en un point A, alors leur force résultante peut être représentée par la diagonale passant par A du parallélogramme dont les côtés représentent P et Q pris au sommet A.
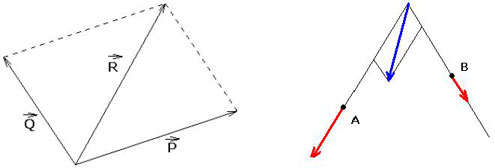
Figure 3 : Composition de deux forces P et Q s’appliquant en un même point (règle du parallélogramme, à g.) ; Si les deux forces agissent à des points différents, alors le sommet définissant ce parallélogramme est le point d'intersection des droites soutenant P et Q (à dr.)
Si les deux forces sont inégales, parallèles et de même sens – auquel cas le parallélogramme ci-dessus ne peut être construit –, P agissant en A et Q agissant en B, alors la résultante est (P + Q) agissant au point C (situé entre A et B) où les moments de P et Q s’équilibrent, c'est-à-dire :
P x CA = Q x CB
Si P et Q prennent des sens opposés, alors le théorème s’applique à (P - Q).
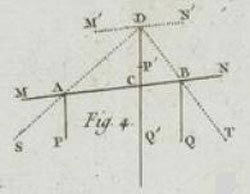
Figure 4 : Figure 4, §19 de Poinsot.
Tous ces résultats peuvent être étendus à un nombre fini de forces ; on le démontre en considérant chaque force supplémentaire une par une (ou deux par deux en trois dimensions) et en la rapportant à la résultante de toutes les forces précédentes. La théorie en dimension trois traite de trois forces agissant dans l'espace au point A et établit la résultante comme diagonale tirée de A du parallélépipède correspondant. Chaque théorème de composition des forces peut être lu à l’inverse en termes de décomposition.
Le seul cas non couvert est celui où les deux forces sont égales en amplitude, co-planaires mais non concourantes, parallèles mais de sens opposé (figure ci-dessus). Généralement ce cas était considéré comme une anomalie ou passé sous silence, bien qu’il fût fort courant dans la vie ordinaire : mouvement d'une paire de manivelles sur un treuil ou une pompe à eau, ou action humaine de rotation d’un robinet. Dans ses
Principia, Isaac Newton fixa (ou maintint) le genre
(8) : après avoir décrété ses trois « axiomes, ou lois de la nature», il induisit immédiatement mais à tort la composition et la décomposition des forces comme «corollaires», sans exclure les forces parallèles quelles qu’elles soient. Poinsot polytechnicien avait entendu Prony expliquer cette approche traditionnelle, mais avec plus d'emphase sur la notion mécanique de
composition (des vitesses aussi bien que des forces, par exemple), et donc avec une distinction moins nette entre statique et dynamique [1801, ch. 1] – Prony traitait le cas des forces parallèles [p. 50-58], mais ne mentionnait pas explicitement l’
anomalie.
Comme Poinsot n'a rien laissé filtrer de ses motivations ni n’a inclus de remerciements à ses collègues dans son ouvrage, il a gardé secrètes les origines de sa vision brillante suivant laquelle le couple n’était pas une anomalie, mais une notion fondamentale pour la bonne compréhension de la statique.
II- La conception de la théorie dans le domaine de la statique et sa réception
On aura lieu de s’y convaincre que la considération des couples n’est pas celle d’un cas singulier, mais d’un élément essentiel qui manquait à la Mécanique (9).
4. Une innovation : le couple
Poinsot étudie des collections finies Cn de forces indépendamment des corps auxquels elles s’appliquent. Une ligne droite continue S représente chaque force, qui peut être appliquée à n'importe quel point le long de S ; les corps permettant cette forme d'action des forces sont souvent appelés « rigides » (Poinsot n’utilise pas le terme). La propriété principale est «l'équilibre», quand une force R de Cn est égale en amplitude mais de sens opposé à «l'effet» de toutes les autres, pour lesquelles sa propre opposée -R était la «résultante». L'équilibre se distingue du repos, caractérisé par l'absence de forces agissant sur le corps [1803, § 1-10].
La première tâche de Poinsot est de fixer des «axiomes » concernant les forces P et Q : si elles agissent en un point, avec des amplitudes égales, dans la même direction, mais en sens opposé, comme une « paire nulle » (c’est nous qui introduisons ce terme), alors elles sont en équilibre :
Il est évident que deux forces égales et contraires appliquées à un même point sont en équilibre [§12].
Si elles agissent dans le même sens mais avec des amplitudes différentes, alors elles ont P + Q comme résultante ([§16], dans des éditions ultérieures présenté comme « l’axiome fondamental ») ; si Q est de sens inverse, alors la résultante est P – Q [§17].

Figure 5 : Axiome, §16.
Il établit aussi le cas standard de plusieurs forces non parallèles agissant en un point, qui utilise le parallélogramme (resp. parallélépipède) résultant en deux (resp. trois) dimensions [art. 33-36]. Pour trouver la résultante de forces parallèles et de même sens, P au point A et Q au point B, Poinsot les équilibre avec une force coplanaire R agissant sur A le long d’une certaine direction du triangle ∠PRQ. Si P = Q, alors la direction est la bissectrice de l’angle. Pour spécifier R, Poinsot suppose que l'état de Cn n'a pas été affecté si l'on y ajoute une paire de forces opposées. Il ajoute donc une paire de forces opposées M en A le long de BA et N en B le long de AB :
Appliquez à volonté aux deux points A et B, deux forces M et N, égales et contraires, et qui agissent dans le sens de la droite AB.
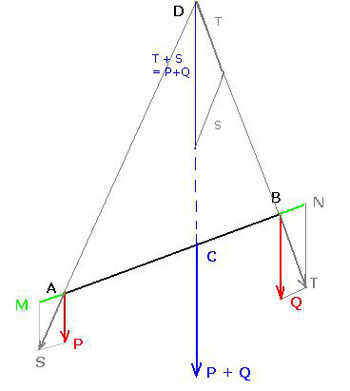
Figure 6 : Explicitation de la figure 4 ci-dessus (et figure 4 de Poinsot). On construit au point D la résultante T+S, qui est égale à P+Q. Le point d’application de cette résultante P+Q est le point C situé sur AB et donné par cette direction. Par la loi des triangles semblables, on écrit facilement : BC/DC = N/Q et AC/DC = M/P, et l’on déduit puisque M= N :P x BC = Q x AC.
Poinsot indique que la résultante de P et M est S et celle de Q et N est T. Les deux droites supports des forces S et T se rencontrent en un point D. Appliquées provisoirement en D, leur résultante prend une amplitude S + T, égale à P + Q, et un sens parallèle à celui de P et de Q. Sa droite support est dirigée vers un point C sur AB, tel que le rapport AC/BC est l’inverse du rapport P/Q :
Le point C d’application de la résultante de deux forces parallèles P et Q qui agissent aux extrémités d’une droite inflexible AB, partage cette droite dans la raison réciproque de P à Q : de sorte que l’on a : P : Q :: BC : AC [§23]
Pour deux forces parallèles et de sens opposé, la figure ci-dessus peut être vue comme indiquant Q comme résultante (P – R) de P et R, avec B situé sur une extension de AC [§24]. Ce cas s’extrapole bien évidemment au cas de deux forces égales et de sens opposé. Mais alors la résultante, d’amplitude nulle, s’applique à une distance infinie de A et de B : la théorie est mise en défaut.
Supposons que les deux forces P et R soient égales, la résultante Q sera zéro, et la distance AB de son point d’application sera, par la proportion ci-dessus, Rx AC/0, c'est-à-dire, infinie [§26].
Poinsot introduit alors le « couple » de forces (
P,
–P), représenté par deux lignes parallèles et la ligne coplanaire entre A et
P et B et
–P située à angle droit de leur direction commune. AB est son « bras » et
P × AB son « moment », indépendant de toute méthode de mesure ; son « axe » est situé sur la normale au plan des deux forces et son sens à déterminer par convention
(10).
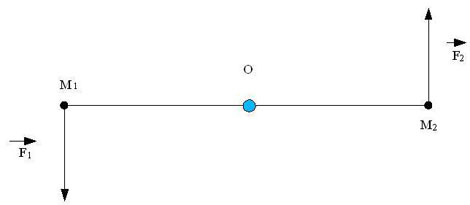
Figure 7 : Couple de deux forces opposées agissant sur le bras M1M2 (WikiCommons auteur ZweiStein) Si l’on note F l’amplitude commune de ces forces, d la distance OM1 (égale à OM2), le « moment » est représenté par un vecteur normal au plan de la figure et d’amplitude 2dF.

Il s’agit bien d’une « nouvelle cause de mouvement, qui est en quelque sorte d’une nature particulière » [§47], insiste Poinsot :
[…] cette action ne peut être contrebalancée par celle d’aucune simple force appliquée comme on voudra au même corps ; et que par conséquent l’effort d’un couple ne peut être comparé d’aucune manière à une simple force.
Les propriétés de cette nouvelle notion sont explicitées en près de 20 pages. Une propriété majeure en est la « translation », analogue à la translation de forces. Pour déplacer un couple de AB vers un bras parallèle et égal CD, dans le même plan ou dans un autre, il faut ajouter deux couples nuls de même amplitude sur CD (cf. figure 8) : (P’ en C,–P’ en D) et (P’’ en D, –P’’ en C), chacun agissant perpendiculairement à CD.
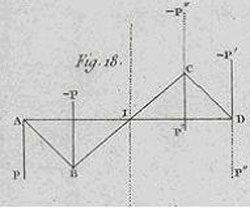
Figure 8 : figure 18, §48 de Poinsot. Translation d’un couple. La résultante de P (en A) et P’’ (en D), soit P + P’’ (en I milieu de AD), annule celle de –P (en B) et –P’’ (en C), soit –P–P’’ (en I milieu de BC), laissant le couple (P’,–P’) agissant avec le bras CD en lieu et place du couple (P,–P) agissant avec le bras AB.
La preuve est aussi valable si CD est coplanaire avec AB, faisant un angle avec AB, et donc pour tout CD à bras égal [§49-51].
5. Couples et moments
Jusque là, Poinsot avait traité des couples en termes de relations entre forces ou entre bras de levier. À présent, il se tourne vers la multiplication et étudie le « moment » d'un couple, défini comme le produit de son « intensité » et d’une longueur idoine, le long de son bras, dans un sens anti-horaire déterminé par l'orientation [§50-51].
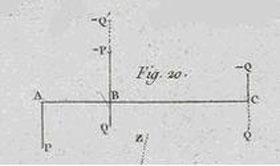
Figure 9 : Poinsot, figure 20, §50 : « Un couple quelconque (P, -P) appliqué sur un bras de levier AB peut être changé en un autre (Q, -Q) de même sens, appliqué sur un bras de levier BC, pourvu qu’on ait P x AB = Q x AC, c'est-à-dire pourvu que les moments de ces couples soient égaux. »
Il utilise encore le terme moment pour désigner ce qui est de nos jours souvent appelé le « couple » d'une ou de plusieurs forces parallèles
P par rapport à un point O choisi sur une droite perpendiculaire à leur direction commune : à savoir le produit de chacune de ces forces
P par sa distance à O [par exemple §80]
(11). Le contexte indique clairement quelle acception du terme moment est en jeu :
Les produits Pp, P’p’, etc. sont ce que l’on nomme ordinairement les moments des forces ; mais on n’attache pas au mot de moment d’autre idée que celle d’un simple produit, qui résulte de deux nombres dont l’un exprime la force et l’autre sa distance à un point : au lieu que le moment est pour nous la mesure d’une force particulière, c'est-à-dire de l’énergie du couple qui provient de la force lorsqu’on la transporte parallèlement à elle-même au point que l’on considère […] Au reste, lorsque nous ne voudrons parler que du simple produit numérique d’une force par sa distance à un point, à un axe perpendiculaire à sa direction, ou à un plan parallèle à sa direction, nous dirons aussi le moment de la force par rapport au point, à l’axe, ou au plan parallèle : et cela n’introduira aucune équivoque dans le discours, puisque l’on pourra entendre, si l’on veut, par ce produit, le moment du couple qui naîtra de la force transportée parallèlement à elle-même au point, ou sur l’axe, ou dans le plan parallèle [§79]
Quant à la composition d'une paire de couples, s'ils sont dans le même plan ou dans des plans parallèles, alors leur résultante est leur somme ou leur différence selon que leur sens de rotation est le même ou non :
§54.Tant de couples que l’on voudra, situés dans un même plan ou dans des plans parallèles, se composent toujours en un seul, dont le moment est égal à la somme des moments des couples composants, ou égal à leur différence, lorsqu’il y a des couples de sens inverse.
Si les deux couples ne sont pas parallèles, leurs moments peuvent être représentés par une paire de droites formant un angle égal à celui de leurs normales associées, car :
Au lieu de déterminer la position d’un couple par celle de son plan, on peut aussi la déterminer par la direction d’une droite quelconque perpendiculaire à ce plan, et que l’on pourra nommer l’axe du couple [§60]
Le couple résultant est alors représenté par la diagonale du parallélogramme correspondant. Réciproquement, et de manière non univoque, un couple peut être décomposé en une paire de couples suivant les mêmes conditions [§54-56, 60-61]. Les mêmes résultats à partir d’un parallélépipède sont valables pour trois couples dans l’espace [§64-65]. L’analogie de la composition des moments avec celle des forces s’avère forte.
Pour un ensemble de forces
Pr, Poinsot définit la force résultante
F et le moment résultant
C par rapport à un point A donné
(12) :
F = Σr Pr et C= Σr Pr x pr
Si l’ensemble de forces Pr est en équilibre, alors F = C = 0. S’il n’est pas en équilibre, alors la résultante F agit à une distance r de A donnée par C/F :
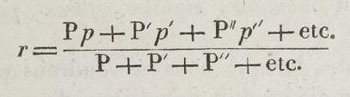
Le chapitre suivant, relativement court, concerne la détermination du centre de gravité d'un ensemble de forces, à un moment où la force de gravité commence à être prise en considération dans la théorie [ch. 3]
(13). Cette partie, dans laquelle Poinsot détermine le centre de gravité d’un certain nombre de corps simples, n’est pas spécialement originale – la notion de couple n’y intervient pas.
6. Quelles (non-) réactions en France à l'origine ?
L'ingénieuse Statique de M. Poinsot, fondée en grande partie sur la considération des couples, est donc un élégant tour de force qui restera comme un modèle de conception neuve et d'exposition correcte, mais qui ne pouvait avoir de succès durable dans l'enseignement, parce que les commençants, qui se font assez bien l'idée d'une force, auraient besoin d'une instruction beaucoup plus étendue, pour se faire une idée nette d'un couple. Hippolyte Sonnet [1867, 320]
Même si un peu répétitif et pédant par endroits, l’ouvrage est une réalisation remarquable de son jeune auteur, sur le plan scientifique comme sur le plan littéraire, et il connaît rapidement un certain succès. Dans le journal officiel Moniteur universel, “J.” (s’agit-il de J.-B. Biot ?) est bref mais positif. Une recension à la fois longue et élogieuse émane de Poullet de Lisle [1803] ; après une courte période passée en 1796-1797 à Polytechnique, puis à l’école des Ponts, Lisle avait suivi un parcours atypique similaire à Poinsot – professeur en institution et inspecteur à l’Université ; en 1810, il avait même publié une traduction des formidables Disquisitiones arithmeticae de Gauss (1801) portant sur la théorie des nombres.
Poinsot avait aligné son livre sur les besoins de l'École polytechnique en indiquant les parties qui n'étaient pas nécessaires pour les examens d'entrée. Il en donna un exemplaire à l'École, qui lui fit la courtoise de l’achat d'un deuxième exemplaire
(14). Grâce en particulier à l'importance de la mécanique dans les programmes de Polytechnique et des autres écoles d'ingénieurs, il y avait alors une publication en nombre de manuels et de traités de mécanique en français. Cependant, la résonance de la nouvelle théorie de Poinsot fut étonnamment faible.
Commençons avec Prony, père fondateur de la mécanique à l'École Polytechnique – qui donc avait enseigné la mécanique à Poinsot –, ainsi que directeur de l’École des ponts et chaussées où Poinsot n’avait pas brillé. Il inclut à l’occasion la notion de couple dans ses livres sur la mécanique postérieurs à celui de Poinsot [1809, leçons 27-28; 1810, 96-100, 150-166]. Son ouvrage antérieur, en 1800, avait été préfacé par Francœur, comme Poinsot un polytechnicien de la première promotion ; mais même dans la dernière édition de cet ouvrage [1825], il n'est fait aucune mention des couples.

Figure 10 : Louis-Benjamin Francœur (1773-1849, X1794), professeur d’algèbre à la Faculté des sciences de Paris (image L'Illustration, journal universel, 29 décembre 1849).
Lagrange, professeur fondateur de l'analyse mathématique à l’École polytechnique, ne mentionne pas la théorie dans le premier volume de la deuxième édition de sa Mécanique analytique, publié en 1811. Ceci est particulièrement curieux, puisque deux ou trois ans auparavant, il en avait explicitement fait l'éloge dans une lettre
(15) adressée au directeur général de l’Université nouvellement formée, en support d’un éventuel recrutement de Poinsot (
cf. ci-dessus).
Quant à Poisson, dans son cours de mécanique à l'École polytechnique [1810], et surtout dans son grand
Traité en deux volumes [1811] de l'année suivante, il mentionne de fait les forces parallèles. Cependant, il traite principalement le cas de forces de même sens ; pour les forces de sens opposé, il ne parle pas de
couple mais se contente de mentionner l’anomalie [1811, vol. 1, 42-46]. La deuxième édition pourtant largement augmentée du
Traité ne faisait toujours pas place aux couples [1833, vol. 1, 13, 90-106]
(16). Vraisemblablement, Poisson avait considéré cette théorie comme irrecevable, tout comme son auteur.
Hachette quant à lui fut étonnamment peu réceptif à la théorie de Poinsot. Depuis la création de Polytechnique, il avait secondé Gaspard Monge, l'un de ses fondateurs, qui y professait la géométrie descriptive ; il y avait lui-même instauré un cours de machines en 1806. Monge avait déjà publié un manuel de statique en 1778, dont Hachette avait fait une nouvelle édition en 1810, révisée en 1826. Dans son «Avertissement», il salue le livre de Poinsot mais réserve son admiration à Poisson [Monge 1826, vi, vii] ; en ce qui concerne les couples de Poinsot, Hachette ne modifie pas les présentations traditionnelles de Monge du parallélogramme des forces dans le chapitre introductif sur la composition [p. 13-17] et fait remarquer que la preuve de la relation entre forces et lignes droites était très semblable à celle de Poinsot [p. 28]. Ce n'est que dans les dernières pages [p. 46-50] du chapitre qu’il évoque les couples et donne une référence générale à la théorie de Poinsot, mais simplement comme un moyen de traiter «un cas particulier du parallélogramme des forces» !
Biot, polytechnicien de la promotion originelle comme Poinsot, avait très tôt assuré sa propre nomination comme professeur de physique au Collège de France en 1801. Deux ans plus tard, il fait l'éloge du livre de Poinsot à la classe scientifique de l'Institut. Vers la fin des années 1820, sa charge d’examinateur de sortie à l'école militaire de Saint-Cyr l’incita à concevoir un manuel élémentaire de statique. Il n’y fait aucune mention de la théorie de Poinsot mais, quelqu'un s'étant étonné de ce silence, Biot y ajouta quelques louanges et de toutes fraîches pages juste avant la publication du livre
(17) ! [15]
Plusieurs auteurs polytechniciens traitaient de mécanique, en particulier celle des applications et de l'ingénierie. Principalement connectée à la dynamique, en particulier avec la notion d’échange de forces vives et de «travail» (comme G.-G. Coriolis désignera la grandeur force x distance), la statique sera éclipsée, de sorte que la théorie de Poinsot joua un rôle mineur, voire aucun rôle. Cependant, sachant que l’évocation de couples pouvait équivaloir à celle de torsion, l'absence (ou presque) des couples dans ces textes est quelque peu surprenante. Poinsot avait consacré son dernier chapitre, substantiel, aux machines simples, concluant avec la (pas si simple) balance de Roberval [1803, ch. 4], en utilisant les couples en tant que de besoin ; mais il n'a pas été imité par ses confères ingénieurs. Les cours de géométrie et de mécanique de Charles Dupin au Conservatoire ne contiennent qu'un bref passage dans le chapitre sur les forces parallèles, sans mention du «couple» [1826, 73-74]. Les cours de «mécanique industrielle» de J.-V. Poncelet à Metz (où il était en poste en tant qu'officier de l'Armée) en disent peu, même sur les forces parallèles, dans son résumé des types et caractéristiques fondamentaux des forces [1829, art. 47-69] ; l'édition posthume considérablement augmentée [1870] n'est pas plus instructive dans son introduction de 140 pages portant sur les «principes fondamentaux». Le traité de Coriolis [1829], Calcul de l'effet des machines, est focalisé sur la dynamique et ignore en grande partie la statique ; il en va de même pour les conférences de Claude Navier [1833] à l’École des Ponts et chaussées sur les applications de la mécanique, dans lequel résistance des matériaux, stabilité des constructions et hydraulique tiennent le devant de la scène. En outre, un dictionnaire des mathématiques, conçu par des polytechniciens, explique la composition des forces, mais omet le couple [Montferrier 1840, 53-55].
Parmi les occasions de promotion de la théorie de Poinsot, il en est une importante et précoce qui fut manquée lorsque Delambre, secrétaire perpétuel de la classe scientifique de l'Institut, fit en 1809 à l'Empereur un rapport sur les progrès réalisés dans les sciences physiques depuis 1789 : Poinsot y est mentionné deux fois en passant, mais à propos d'autres contributions à la mécanique [Delambre 1810, 16, 119].
7. Une reconnaissance progressive des couples au niveau international
Cette conception qu’il a introduite depuis longtemps dans la Mécanique, et qui a été d’abord repoussée par quelques géomètres, a fini par obtenir un assentiment unanime […] J. M. C. Duhamel, à propos la théorie des couples de Poinsot [1845, préface]
Peu à peu, les partisans de la théorie de Poinsot prévalurent sur ceux qui la critiquaient ou qui l’ignoraient. Duhamel cité ci-dessus était bien placé pour le savoir : il était élève polytechnicien de 1814 à 1816 quand Poinsot y enseignait – cette citation provient de son propre cours de mécanique 30 ans plus tard, dans lequel il présente le couple [1845, 51-64, 155-163]. Son collègue professeur à Polytechnique J.C.F Sturm était tout aussi appréciateur [1861, vol. 1, 18-28; vol. 2, 1-8].
Poinsot publia de nouvelles éditions de son livre en 1811, 1821 (500 exemplaires), 1824 (2000), 1830 (2000), 1834 (3000), 1837, 1842 et 1848 ; des éditions posthumes sont publiées en 1861, 1873 et 1877. Certaines traductions de ces différentes éditions parurent : en allemand en 1828, 1831 et 1887 ; en russe, en 1842 et 1898 ; en norvégien, en 1844, et le premier chapitre en anglais en 1847. Ainsi, sa théorie a-t-elle été bien répandue, mais les générations qui suivirent l’apprirent-elles ? La réception internationale de la théorie de Poinsot dans la recherche comme dans l’enseignement fait partie de l’histoire, en grande partie à écrire, de la mécanique et de son enseignement au XIX
e siècle; quelques exemples en sont donnés dans la suite de cet article
(18).
Bien que l'index de la Société royale de Londres au XIX
e siècle ne recense que huit articles de mécanique portant spécifiquement sur les couples [Royal Society 1909, 99], la théorie de Poinsot a conduit à un certain nombre de recherches à partir de la fin des années 1830. En particulier, le mathématicien allemand Möbius utilise les couples dans sa théorie [1837] de «points zéro». L’approche de Poinsot a également joué un rôle dans le développement de méthodes graphiques en statique
(19).

Figure 11 : Le mathématicien allemand August Ferdinand Möbius (1790-1868), utilisateur précoce de la théorie des couples de Poinsot.
III– Quelques réflexions rétrospectives sur l’œuvre de poinsot
8. Les théories duales de Poinsot
Le livre de Poinsot est encore l'une des meilleures sources pour apprendre sa théorie des couples. Pour une utilisation contemporaine, il suffit de le compléter par les avancées des algèbres vectorielle et linéaire, qui en fait commençaient lentement à se développer, surtout à partir des années 1840 – la mécanique étant d’ailleurs l'un de leurs stimuli.
Bien que l’analogie entre couples et rotation ait joué un rôle important dans le développement par Poinsot de ses théories, il y a néanmoins une différence de statut entre sa théorie des couples et ses travaux de dynamique sur la rotation. Sa théorie des couples était révolutionnaire parce qu'il avait réfuté l’idée habituelle selon laquelle la statique était la science de l'équilibre des forces : il a montré que c’était la science de l'équilibre des forces et des couples, qui ne se réduisent pas à des forces. Ainsi, il a obligé mécaniciens (et historiens) à changer d'avis sur un point fondamental, ce qui n’est jamais facile pour l’être humain.
Récapitulatif sur la notion de couple en mécanique
Nous proposons de synthétiser par les étapes suivantes la notion de couple : - Un vecteur est un segment de droite continu et orienté. - Deux vecteurs sont parallèles s’ils sont coplanaires, ne coïncidant pas, et agissant dans la même direction (pas nécessairement le même sens). - Deux vecteurs forment un couple s’ils sont parallèles, d’amplitude égale, mais agissant en sens opposé, et ayant quelque moyen d’interaction mutuelle faisant intervenir leur distance (par exemple « le bras »). Ainsi, par exemple, la configuration de deux véhicules roulant sur des files parallèles en sens opposé ne saurait être représentée par un couple – puisque aucun bras n’agit. - Des vecteurs peuvent représenter des forces rectilinéaires ou de rotation, avec des amplitudes représentées par des nombres réels positifs. - Un couple statique de forces rectilinéaires ne résulte pas en une force, car sa résultante n’est pas rectilinéaire. - Un couple dynamique de rotations circulaires ne résulte pas en une rotation car sa résultante n’est pas un mouvement circulaire mais rectilinéaire (20). - Ainsi, ni les forces rectilinéaires, ni les rotations circulaires ne constituent un « groupe fermé ». - Ce sont des résultats duaux : on peut remplacer « forces rectilinéaires » par « rotations circulaires » ci-dessus, et vice-versa. - Si l’on prend deux couples statiques, égaux en amplitude avec des axes parallèles et de sens opposés. On ne peut les composer en un couple statique, puisque chacun d’eux peut être déplacé parallèlement à lui-même pour annuler l’autre.
Cette formulation de la propriété de couple a cours en mécanique ; mais les couples ont été utilisés dans d'autres parties de la physique. Un des premiers cas est l'étude par Biot, au début des années 1820, du nouveau sujet qu’était l'électromagnétisme : il utilise quelques « forces » similaires à des couples agissant aux deux pôles d'un élément magnétique et aux extrémités d'un élément électrique [Biot 1821]. En revanche Ampère, créateur de l'électrodynamique, suppose que l'action entre deux éléments infinitésimaux électriques se produit directement le long de la ligne les joignant – de même pour ce qui est de l'action électromagnétique entre un aimant et un fil [1826, 123-124]. Plus tard, l'enthousiasme de J.J.Thomson pour la notion de tourbillon, prolongée au-delà de la mécanique vers les théories de l'éther et de la matière, se traduira par l’utilisation des couples ; à partir des années 1910, ils feront aussi leur apparition dans certaines théories de la mécanique quantique, à l’appui notamment de la notion quantique de spin [Borrelli 2011, art. 16-18].
9. Poinsot « géomètre » de la mécanique
Les théorisations de Poinsot en mécanique ont toujours été fondées sur des préoccupations géométriques et spatiales. Comme P.-S. Girard le fait remarquer dans son étude [1835, 436-437], Poinsot abhorrait les théories mathématiques, dominées par des symboles : « on ne voit guère que les calculs sans aucune belle image de la rotation du corps » – c’est ainsi qu’il jugeait ce type de théories [1834, 3]. Dans une double allusion au symbolisme mathématique et à la bien-aimée (?) École polytechnique, surnommée l’X par ses anciens élèves, il soulignait non sans humour que « Cauchy a[vait] une diarrhée d’X» [Laffitte 1886, 148].
Dans une note [1851b] portant sur le pendule de Foucault, Poinsot admettait que la variation de la vitesse angulaire par rapport à la Terre pouvait varier, mais il émettait l’hypothèse que ce mouvement était « un phénomène purement géométrique», non gouverné « par les principes de la dynamique » – la tâche principale était selon lui de concevoir un support pour le pendule qui fixerait exactement le plan dans lequel son mouvement avait lieu. Sans doute là est-il allé trop loin.
Même si certaines puissantes théories à prédominance géométrique se sont développées en mécanique, le saint évangile reconnu de longue date était l'analyse mathématique, avec certaines algèbres associées. L'éminent physicien mathématique Émile Mathieu (1835-1890), polytechnicien de la promotion 1854, constitue un symbole caractéristique de l’approche déplorée par Poinsot :
Quand on a à résoudre un problème de Mécanique, on peut le faire en employant des considérations géométriques, ou l’on peut se servir exc1usivement de raisonnements analytiques. Le géomètre [sic] doit savoir démontrer toutes les propriétés élémentaires de la Mécanique à la fois des deux manières; mais, quand il s’agit de questions difficiles et qui exigent de longs calculs, il a presque toujours avantage à n’employer que l’Analyse. Cette méthode permet aussi, quand on ne peut résoudre une question exactement, de juger mieux ce que l’on néglige et d’obtenir toute la précision que l’on désire. Les raisonnements géométriques et mécaniques ont souvent l’avantage d’être plus faciles pour les esprits qui ne sont pas très familiarisés avec l’Analyse; ils sont aussi quelquefois pour tous plus intuitifs. Mais, pour ceux qui sont versés dans l’Analyse, il y a un certain intérêt à traiter toutes les questions d’une manière plus uniforme et en s’appuyant sur un nombre beaucoup moindre de principes [1873, v].
10. La figure de Poinsot dans l’histoire
Poinsot lui-même se montra capable de contributions à la mécanique analytique, en style algébrique, dans son autre article [1806b], publié dans le
Journal de l'École Polytechnique, qu’il reproduisit à partir de la 6
e édition (1834) de son ouvrage
Éléments de statique. Il y aborde un sujet mécanique d’une manière qui ne lui est pas habituelle, mais qui était à la mode parmi ses collègues. Un principe majeur de la mécanique analytique de Lagrange était le principe des vitesses virtuelles, suivant lequel un ensemble de corps soumis à un système de forces est en équilibre si et seulement si la somme algébrique du produit de ces forces et de leurs déplacements était nul. Beaucoup de controverses avaient entouré la formulation de ce principe, mettant en doute le caractère général des notions de
force, de
corps, d’
équilibre. Ce principe était-il un axiome, ou pouvait-il être prouvé – et si oui, comment ? Nombre d'efforts y furent consacrés, notamment à Polytechnique : Joseph Fourier, un des premiers enseignants de l’École, avait publié un essai important sur le sujet [1798]; tout comme l’avait fait A.-M. Ampère, dans le même volume du
Journal [1806] que l’article de Poinsot. Fort éloigné de son approche géométrique, Poinsot évite d’utiliser le principe pour caractériser l’état d'équilibre, en traitant les forces comme des gradients de potentiels ; il espérait obtenir le principe comme un théorème
(21).
Le point historiographique, c'est que cet article
atypique [1806b] de Poinsot a plus attiré l'attention des historiens que n'importe laquelle de ses autres contributions à la mécanique
(22) ! Les mathématiciens ont mis du temps à admettre la nécessité d'une théorie des couples, nombre d’entr’eux ne virent pas l’intérêt de celle de Poinsot. Mais les historiens ont été glaciaux : la quasi-totalité des histoires générales de la mécanique qui couvrent cette période mentionnent au plus l'une de ses contributions (généralement le couple, et le plus souvent brièvement).
Ernst Mach [1883] a par exemple fait quelques mentions louangeuses mais fort brèves de Poinsot. Lorsque la traduction française de l’ouvrage de Mach est publiée en 1903, Pierre Duhem cite l'une de ces mentions dans une longue recension [1903a]. Sa propre histoire de la mécanique paraît cette année-là [1903b] : Duhem s’y montre plus intéressé par les manifestations de la mécanique dans la physique que par la mécanique elle-même, et ne mentionne pas du tout Poinsot
(23). À nouveau, dans le volume de la grande
Encyklopädie der Wissenschaften mathematischen consacré à la mécanique [1901], Aurel Voss avait peu à dire sur les couples ou la rotation dans son recensement «des principes de la mécanique rationnelle». Cependant, Paul Stäckel a fort valablement traité Poinsot dans son étude analogue de la « dynamique élémentaire » [1905]. Le directeur de ce projet était Klein, dont le propre ouvrage de 600 pages sur l'histoire des mathématiques au XIX
e siècle contenait une phrase sur Poinsot, relative à son influence sur Möbius [Klein 1926, 119] ; cependant Klein accorde à Poinsot une page entière dans son étude sur la géométrie [1932, 32]
(24).
Parmi les moins connus quoique meilleurs historiens de la mécanique, Moritz Rühlmann met en parallèle, dans ses cours d’histoire, quelques pages de Poinsot avec d’autres de Poisson, jouant sur leur inimitié pour passer d’un texte à l’autre [1881, 299-304, 304-308]. Aux États-Unis, David Ray fait comme Rühlmann, mentionnant favorablement Poinsot sur plusieurs pages avant de retourner à Poisson (mais laissant de côté leur inimitié) [Ray 1910, 117-120] ; tandis que Woodward inclut une page chaleureuse sur Poinsot dans une étude excellente et concise du développement de la physique mathématique au XIXe siècle [1900, 136]. Les cours habituellement admirables d’Émile Jouguet sur la mécanique, reposant sur des sources originales, présentent simplement une brève mention des couples [1909, 240].
La seule reconnaissance historique substantielle de la notion de couple émane du philosophe Eugen Dühring [1873, 424-449], qui fait une présentation laudative du plaidoyer épistémologique de Poinsot sur l’indépendance des deux notions de couple et de moment d’une force. Dühring a été influencé par le philosophe positiviste Auguste Comte, lui aussi polytechnicien ; Poinsot avait été l'un de ses professeurs et sera présenté plus tard comme l’ « un des saints du Positivisme » [Laffitte 1886, 146], probablement en raison de sa pratique d’un style géométrique plus qu’algébrique.
Parmi les histoires générales plus récentes, René Dugas utilise, dans ses 600 pages, la peu compréhensible tournure de « mouvement à la Poinsot », en relation avec le pendule de Foucault [1957, 382]. Clifford Truesdell omet Poinsot de son recueil d'essais [1968] portant sur l'histoire de la mécanique – il accorde une grande attention à Euler (pour lequel certaines actions de type couple ne se produisent que dans certains contextes impliquant la torsion) – sur l'histoire du moment angulaire au XVIIIe siècle, ainsi que sur les formulations récentes de la mécanique rationnelle. Istvan Szabo est muet sur les couples dans sa longue histoire [1977], bien qu’il y décrive des situations de moment tournant ou de spin.

Figure 12 : Louis Poinsot, La Théorie générale de l’équilibre et du mouvement des systèmes, rééditions Librairie philosophique Vrin, 1975, 2000.
11. Réhabiliter Poinsot
Ce silence assourdissant et durable à propos de Poinsot est stupéfiant, surtout en ce qui concerne la statique. Un historien généraliste de la mécanique voudra-t-il rappeler l'importance de ses innovations ?
De fait, les thèmes abordés ici ouvrent quelques axes de recherche. Tout d'abord, élargir la discussion sur la propriété de couple pour y inclure les autres théories physiques utilisant cette notion. D'autre part, mettre en lumière les théories de la physique (en particulier en mécanique, y compris en ingénierie) qui mettent l'accent sur l’espace et la géométrie plutôt que sur l'analyse mathématique, en utilisant notamment les rotations (pas nécessairement circulaires) telles qu’étudiées par Poinsot et par d'autres. Troisièmement, étendre la période historique du présent article. Une histoire d’importance pourrait alors être écrite sur, par exemple, « Le rôle des théories spatiales et géométriques en physique mathématique, de Louis Poinsot (1803) à Albert Einstein (1905), avec une référence particulière aux couples et aux rotations ».
Janvier 2013
(l’auteur remercie pour leurs commentaires avisés Niccolò Guicciardini, Thomas Archibald, Alex Craik et Alexandre Moatti)
(traduction française Alexandre Moatti)
Bibliographie
Acloque, P. 1981. Oscillations et stabilité selon Foucault ..., Paris (CNRS).
Aczel, A. D. 2003. Pendulum: Léon Foucault and the triumph of science, New York (Simon and Schuster).
Altmann, S. and Ortiz, E. 2005. (Eds.), Olinde Rodrigues and his circle: mathematicians and social utopias in France, Providence R. I. (American Mathematical Society).
Ampère, A.-M. 1806. ‘Démonstration générale du principe des vitesses virtuelles …’, J. École polyt., (1)6, cah. 13, 247-269.
Ampère, A.-M. 1826. Mémoire sur la théorie mathématique des phénomènes électro-dynamiques …, Paris (Méquignon-Marvis); also Mém. Acad. Sci., 6 (1823: publ. 1827), 177-388. [Various reprints.]
Bailhache, P. 1975. (Ed. & comm.), Louis Poinsot, La théorie générale de l’équilibre et du mouvement des systèmes, Paris (Vrin).
Bertrand, J. L. F. 1864. ‘Des progrès de la mécanique’, Rev. deux mondes, 51, 96-115. [Réimpr. in L. Foucault, Recueil des travaux scientifiques, vol. 1, Paris (Gauthier-Villars), 1878, v-xxviii].
Bertrand, J. L. F. 1872. [Recension de Poinsot Statique, 11e ed. (1873)], J. sav., 405-420 (cited here). Aussi in 11e ed. (1873), ix-xxviii.
Bertrand, J. L. F. 1890. ‘Éloge historique de Louis Poinsot’, Rev. gén. sci. pures appl., 1, 753-762. Aussi in Eloges académiques, Paris (Hachette), 1-27; and in Mém. Acad. Sci., 45 (1899), lxvii-xcv.
Binet, J. P. M. 1813. ‘Mémoire sur la théorie des axes conjugués et les momens d’inertie des corps’, J. École polyt., (1)9, cah. 16, 41-67.
Binet, J. P. M. 1815. ‘Mémoire sur la composition des forces et sur la composition des momens’, J. École polyt., (1)10, cah. 17, 321-348.
Biot, J. B. 1821. ‘Sur l’aimantation imprimé aux métaux par l’électricité en mouvement’, J. sav., 221-235.
Biot, J. B. 1829. Notions élémentaires de statique …, Paris (Bachelier).
Borrelli, A. 2011. ‘Angular momentum between physics and mathematics’, in K.-H. Schlote and M. Schneider (eds.), Mathematics meets physics, Frankfurt/Main (Harri Deutsch), 395–440.
Caparrini, S. 2007. ‘Euler’s influence on the birth of vector mechanics’, in R. E. Bradley and C. E. Sandifer (eds.), Leonhard Euler : life, work and legacy, Amsterdam (Elsevier), 459-477.
Capecchi, D. 2012. History of virtual work laws: a history of mechanics prospective, Basel (Birkhäuser).
Coriolis, G. G. 1829. Du calcul de l’effet des machines …, Paris (Carilian-Goeury). de Freycinet, C. 1858. Traité de mécanique rationnelle comprenant la statique comme cas particulier de la mécanique avec figures intercalées dans le texte, vol. 1, Paris (Mallet-Bachelier).
de Prony, G. C. F. M. Riche 1800. ‘Mécanique philosophique ...’, J. École polyt., (1)3, cah. 8bis, vii + 479 pp. Also as a book, Paris (Imprimerie de la République).
de Prony, G. C. F. M. Riche 1809. Sommaire des leçons sur le mouvement des corps solides …, Paris (Gueffier).
de Prony, G. C. F. M. Riche 1810. Leçons de mécanique analytique, données à l’Ecole Polytechnique, vol. 1, Paris (École Nationale des Ponts et Chaussées). [Réimpr. 1815.]
Delambre, J. B. J. 1810. Rapport historique sur les progrès des sciences mathématiques depuis 1789 …, octavo ed., Paris (Imprimerie Impériale). [Repr. Paris (Belin), 1989. Index in Hist. math., 3(1976), 321-324.]
Duchayla, C. D. M. Blanquet 1804. ‘Démonstration du parallélogramme des forces’, Bull. sci. Soc. Philom. Paris, 242-243. Also Corr. Ecole Polyt. 1 ,(1804-08), 83-84.
Dugas, R. 1957. A history of mechanics, New York (Central). [orig. 1950.]
Duhamel, J. M. C. 1845, 1846. Cours de mécanique de l’École polytechnique, 2 pts., Paris (Mallet-Bachelier).
Duhem, P. 1903a. [Review of E. Mach, La Mécanique (1903)], Bull. sci. math., (1)27, 261-283.
Duhem, P. 1903b. L’évolution de la mécanique, Paris (Joanin). [trad. Angl. Alphen aan den Rijn (Sijthoff and Noordhoff), 1980.]
Dühring, E. C. 1873. Kritische Geschichte der allgemeinen Prinzipien der Mechanik, 1st ed., Berlin (Grieben).
Dupin, C, 1826. Géométrie et méchanique des arts et métiers et des beaux-arts, vol. 2, Paris (Bachelier).
Euler, L. 1793. ‘Methodus facilis omnium virium moments respectu axis cuiuscunque determinandi’, Nova acta Acad. Petropolitanae, 7 (1789), 205-214. [Repr. in Opera omnia, ser. 2, vol. 9, 399-406.]
Fourcy, A. L. 1828. Histoire de l’École polytechnique, Paris (École polytechnique). [Repr. Paris (Belin), 1987.]
Fourier, J. B. J. 1798. ‘Mémoire sur la statique …’, J. École polyt., (1)2, cah. 5, 20-60. [Réimpr. in Oeuvres, vol. 2, 475-521.]
Francoeur, L. B. 1825. Traité de mécanique élémentaire …, 5e ed., Paris (Bachelier). [1e ed. 1800.]
Gardner, H. J. and Wilson, R. J. 1993. ‘Thomas Archer Hirst - mathematician Xtravagant IV. Queenwood, France and Italy’, Amer. math. monthly, 100, 723-731.
Girard, P. S. 1835. Recension de [Poinsot 1834], J. sav., 423-437.
Grattan-Guinness, I. 1990. Convolutions in French mathematics, 1800-1840. From the calculus and mechanics to mathematical analysis and mathematical physics, 3 vols., Basel (Birkhäuser) and Berlin (Deutscher Verlag der Wissenschaften).
Grattan-Guinness, I. 1994. Companion encyclopaedia of the history and philosophy of the mathematical sciences, 2 vols., London (Routledge), [Repr. Baltimore (Johns Hopkins University Press), 2003.]
Gray, J. J. 1990. ‘Möbius’s geometrical mechanics’, in J. Fauvel, R. Flood and R. Wilson (eds.), Möbius and his band: Mathematics and astronomy in nineteenth-century Germany, Oxford (Oxford University Press), 78-103.
Hamel, G. 1909. ‘Über die Grundlagen der Mechanik’, Math. Ann., 60, 350-397.
Hayward, R. B. 1858. ‘On a direct method of estimating velocities, accelerations, and all similar quantities with respect to axes moveable in any manner in space, with applications’, Trans. Cambridge Phil. Soc. 10, 1-20.
Hennenberg, L. 1903. ‘Die graphische Statik der starren Körper’, in Encyklopädie der mathematischen Wissenschaften, vol. 4, pt. 1, 345-434 (article IV5).
Hentschel, K. 1988. ‘Die Korrespondenz Duhem — Mach: zur “Modellbeladenheit” von Wissenschaftsgeschichte’, Annals of science, 45, S. 73-91.
Hulin-Jung, N. 1989. L’organisation de l’enseignement des sciences: la voie ouverte par le second Empire, Paris (Comité des Travaux Historiques et Scientifiques).
Jouguet, E. 1909. Lectures de mécanique. La mécanique enseignée par les auteurs originaux, vol. 2, Paris (Gauthier-Villars).
Klein, C. F. 1926. Vorlesungen über die Entwicklung der Mathematik im 19. Jahrhundert, pt. 1, Berlin (Springer). [Repr. New York (Chelsea), n.d.]
Klein, C. F. 1932. Elementary mathematics from an advanced standpoint, vol. 2, New York (Macmillan). [German original 1926.]
Laffitte, F. 1886. ‘Relations d’Auguste Comte avec L. Poinsot’, Rev. occid. phil. soc. et polit., 16, 145-157.
Lagrange, J. L. 1811. Mécanique analytique, 2nd ed., vol. 1, Paris (Courcier). [Réimpr. (ed. J. L. F. Bertrand), Paris (Mallet-Bachelier), 1853; and in Oeuvres, vol. 11.]
Langins, J. 1987. La République avait besoin de savants, Paris (Belin).
Laplace, P. S. 1798. ‘Sur la détermination d’un plan … dans le mouvement d’un système de corps …’, J. Ecole Polyt., (1)2, cah. 5, 155-159. [Réimpr. in Oeuvres, vol. 14, 3-7.]
Lindt, R. 1904. ‘Das Prinzip der virtuellen Geschwindigkeiten. Seine Beweise und die Unmöglichkeit seiner Umkehrung bei Verwendung des Begriffes “Gleichgewicht eines Massensystems”’, Abhand. Gesch. Math., 18, 145-195.
Lützen, J. 1990. Joseph Liouville 1809-1882, New York (Springer). Mach, E. 1883. Die Mechanik in ihrer Entwicklung historisch-kritisch dargestellt, 1e ed. Leipzig (Brockhaus). [Later eds. to 9th (1933). Various translations.].
Martinez, A. 2009. Kinematics, Baltimore (Johns Hopkins University Press). Mawhin, J. 1994. ‘The centennial celebration of Poincaré and Lyapunov in ordinary differential equations’, Rend. del Circolo Mat. Palermo, (2)34, Suppl., 9-46.
Mathieu, E. 1878. Mécanique analytique, Paris (Gauthier-Villars) Möbius, A. F. 1837. Lehrbuch der Statik, 2 pts., Leipzig (Göschen).
Monge, G. 1826. Traité élémentaire de statique …, 6th ed. (ed. J. N. P. Hachette), Paris (Bachelier).
Montferrier, A. A. V., Sarrazin de 1840. (Ed.) Dictionnaire des sciences mathématiques pures et appliquées, par une société des anciens élèves de l’École polytechnique, vol. 2, Paris (Dénain).
Navier, C. L. M. H. 1833. Résumé des leçons données à l’École des Ponts et Chaussées, sur l’application de la mécanique à l’établissement des constructions et des machines, pt. 1, 2e ed., Paris (Carilian-Goeury).
Newton, I. 1687. Principia mathematica. [Edition utilisée: Principia mathematica, Berkeley (University of California Press), 1934.]
Olson, R. 1975. Scottish philosophy and British physics, 1750-1880. A study in the foundations of the Victorian scientific style, Princeton (Princeton University Press).
Poinsot, L. 1803, 1811. Éléments de statique …, 1st ed., 2nd ed. Paris (Calixte Volland).
Poinsot, L. 1806a. ‘Sur la composition des momens et la composition des aires’, J. École polyt., (1)6, cah. 13, 182-205. [Réimpr. in Statique, 3rd ed. (1821)-10th ed. (1861).]
Poinsot, L. 1806b. ‘Théorie générale de l’équilibre et du mouvement des systèmes’, J. Ecole Polyt., (1)6, cah. 13, 206-241. [Réimpr. in Statique, 6th ed. (1834)-10th ed. (1861); also in [Bailhache 1975], 33-95.]
Poinsot, L. 1814. [Report on Binet 1815], in Procès-verbaux des séances de l’Académie des Sciences tenues depuis la fondation [in 1795] jusqu’au mois d’août, 1835, vol. 5, Hendaye (Observatoire), 1914, 355-357.
Poinsot, L. 1830. ‘Théorie et détermination de l’équateur du système solaire’, in Statique, 5e ed. [Réimpr. up to 10th ed. (1861)].
Poinsot, L. 1834. Théorie nouvelle de la rotation des corps …, Paris (Bachelier). [Réimpr. in Statique, 8th ed. (1842)-10th ed. (1861).]
Poinsot, L. 1838. ‘Note sur une certaine démonstration du principe des vitesses virtuelles qu’on trouve au cha[pire III. du livre 1er de la Mécanique céleste’, J. math. pures appl., (1)3, 244-248. [Réimpr. in [Bailhache 1975], 96-100.]
Poinsot, L. 1846. ‘Remarque sur un point fondamental de la Mécanique analytique de Lagrange’, J. math. pures appl., (1)11, 241-253. [Réimpr. in Lagrange Oeuvres, vol. 11, 445-456.]
Poinsot, L. 1851a. ‘Théorie nouvelle de la rotation des corps’, J. math. pures appl., (1)16, 9-129, 289-336 [cité ici]; aussi Conn. temps, (1854: publ. 1851), 3-134; aussi Paris (Bachelier), 1852.
Poinsot, L. 1851b. ‘Remarques sur l’ingénieuse expérience imaginée par M. Léon Foucault pour rendre sensible le mouvement de rotation de la Terre’, C. r. Acad. Sci., 32, 206-207.
Poinsot, L. 1852. ‘Théorie des cones circulaires roulants’, Conn. temps, (1855), 3-25; also Paris (Bachelier]; aussi in J. math. pures appl., (1)18 (1854),41-70.
Poinsot, L. 1855. ‘Précession des équinoxes’, Conn. temps, (1858), 1-56. Poinsot, L. 1857-1859. ‘Sur la percussion des corps’, J. math. pures appl., (2)2, 281-350; (2)4, 421-426. [English trans. in Phil. mag, (4)15(1858), 161-180, 263-290, 344-359; see also (4)18(1859), 241-259 and (4)19(1860),430-434.]
Poisson, S. D. 1810. Cours de mécanique, 2 vols., Paris (Perroneau). [Très rare.]
Poisson, S. D. 1811, 1833. Traité de mécanique, 2 vols., 1e ed., 2e ed., Paris (Courcier).
Poncelet, J. V. 1829. Cours de mécanique industrielle…, Metz (Thiel). [Réimpr. Bruxelles (Meline), 1839.]
Poncelet, J. V. 1870. Introduction à la mécanique industrielle, physique ou expérimentale, 3e ed. (ed. X. Kretz), Paris (Gauthier-Villars).
Pratt, J. H. 1842. The mathematical principles of mechanical philosophy and their application to elementary mechanics and architecture: but chiefly to the theory of universal gravitation, 2nd ed., Cambridge (Deighton).
Ray, D. H. 1910. A history of mechanics. A brief review of the chief contributions of the eminent masters of the science, a table of its development, a critique of the fundamental mechanical concepts, and a bibliography of the science, Lancaster, Pa. (Printing Press of the New Era Company).
Routh, E. J. 1860. An elementary treatise on the dynamics of a system of rigid bodies: with numerous examples, 1e ed., Cambridge (Cambridge University Press).
Routh, E. J. 1891. A treatise on analytical statics. With numerous examples, 1st ed., Cambridge (Macmillans). Royal Society 1909. The Royal Society catalogue of scienitfic papers, Subject index, vol. 2, Mechanics, London (Royal Society).
Rühlmann, M. 1881. Vorträge zur Geschichte der theoretischen Maschinenlehre und der damit in Zusammenhang stehenden mathematischen Wissenschaften, pt. 1, Braunschweig (Schwetschke).
Schoenflies, A. and Grübler, M. 1903. ‘Kinematik’, in Encyklopädie der mathematischen Wissenschaften, vol. 4, pt. 1, 190-278 (article IV3). Scholz, E. 1989. Symmetrie Gruppe Dualität, Basel (Birkhäuser) and Berlin, DDR (Deutscher Verlag der Wissenschaften).
Sédillot, L. P. E. A. 1870. ‘Les professeurs de mathématiques et de physique générale au Collège de France’, pt. 4, Bull. bibl. stor. sci. mat. fis., 3, 107-170.
Sonnet, H. 1867. Dictionnaire des mathématiques appliquées: comprenant les principales applications des mathématiques: à l’architecture, à l’arithmétique commerciale, à l’arpentage, à l’artillerie, aux assurances, à la balistique, à la banque; à la charpente, aux chemins de fer, à la cinématique, à la construction navale, à la cosmographie, à la coupe des pierres, au dessin linéaire, aux établissements de prévoyance, à la fortification, à la géodésie, à la géographie, à la géométrie descriptive, à l’horlogerie, à l’hydraulique, à l’hydrostatique, aux machines, à la mécanique générale, à la mécanique des gaz, à la navigation, aux ombres, à la perspective, à la population, aux probabilités, aux questions de bourse, à la topographie, aux travaux publics, aux voies de communication, etc., etc., et l’explication d’un grand nombre de termes techniques usités dans les applications, 1st ed., Paris (Hachette).
Stäckel, P. G. 1905. ‘Elementare Dynamik der Punktsysteme und starren Körper’, in Encyklopädie der mathematischen Wissenschaften, vol. 4, pt. 1, 435-684 (article IV 6).
Sturm, J. C. F. 1861. Cours de mécanique de l’École polytechnique, 2 vols. (ed. E. Prouhet), Paris (Bachelier).
Szabo, I. 1977. Geschichte der mechanischen Prinzipien und ihren wichtigsten Anwendungen, Basel (Birkhäuser).
Thomson, W. and Tait, P. G. 1879, 1883. Treatise on natural philosophy, 2nd ed., 2 vols., Cambridge (Cambridge University Press).
Timerding, H. C. E. F. 1902. ‘Geometrische Grundlegung der Mechanik eines starren Körpers’, in Encyklopädie der mathematischen Wissenschaften, vol. 4, pt. 1, 435-684 (article IV2).
Truesdell, C. A., III. 1968. Essays in the history of mechanics, Berlin (Springer).
Voss, A. E. 1901. ‘Die Prinzipien der rationellen Mechanik’, in Encyklopädie der mathematischen Wissenschaften, vol. 4, pt. 1, 3-121 (article IV 1).
Weisbach, J. 1855. Lehrbuch der Ingenieur- und Maschinenmechanik, 3rd ed., pt. 1, Braunschweig (Vieweg).
Whewell, W. 1819, 1847. An elementary treatise on mechanics, 1st ed., 7th ed., Cambridge (Deighton).
Whewell, W. 1833. Analytical statics, Cambridge (Deighton). Whewell, W. 1841. Mechanics of engineering …, Cambridge (Deighton). Whittaker, E. T. 1904. A treatise on the analytical dynamics of particles and rigid bodies, 1st ed., Cambridge (Cambridge University Press). [3e ed. 1927.]
Woodward, R. S. 1900. ‘The century's progress in applied mathematics: Presidential address’, Bull. Amer. Math. Soc., 8,133-163. Also in Science, new ser., 11, 41-51, 81-92. Ziegler, R. 1985. Die Geschichte der geometrischen Mechanik im 19. Jahrhundert: Eine historisch-systematische Untersuchung von Möbius und Plücker bis zu Klein und Lindemann, Stuttgart (Steiner).

(1) La littérature concernant l’École polytechnique est très substantielle. Sa première histoire [Fourcy 1829], écrite par son premier bibliothécaire, est encore très intéressante. Comme l’est le site actuel www.polytechnique.edu.
(2) L’Université avait en son sein une école normale à Paris, qui ne devait rien à l’école précédente éponyme. Mais la formation des scientifiques y fut insignifiante jusqu’au milieu du XIXe s. [Grattan-Guinness 1990] couvre le panel des institutions et des intervenants en France, ainsi que leur principaux axes de recherche en mathématiques et en mathématiques appliquées, depuis la fin du XVIIIe s. jusqu’à 1840 ; de nombreuses autres sources historiques y sont citées.
(3) Joseph Bertrand, introduction de la notice nécrologique de Poinsot [1890].
(4) Voir le dossier personnel de Poinsot, Archives Nationales, F14-23021.
(5) [Bertrand 1864, vii-viii]; pour en savoir plus sur cette entente cordiale autour de Poinsot, voir [Bertrand 1872, 413-420].
(6) Sur l’enseignement de la science à l’Université, voir [Hulin-Jung 1989]; Poisson et Poinsot y sont cités à plusieurs reprises.
(7) L’étude la plus significative sur Poinsot est [Bailache 1975], centrée sur ses contributions à la mécanique analytique (section 13). Un fonds important mais peu organisé existe à la Bibliothèque de l’Institut, doss. 948-965, 4738. La plupart de ces dossiers a trait aux mathématiques, mais les dossiers 949, 959 et 960 contiennent des documents relatifs à l’Université.
(8) Newton [1687, 13]. Je n’ai pas trouvé de discussion sur ces corollaires dans la littérature sur Newton, rarement même une quelconque mention. Une histoire systématique de la loi de (dé)composition des forces au cours des siècles serait nécessaire, notamment en ce qui concerne le sujet des forces parallèles.
(9) Louis Poinsot, Éléments de statique, 2e édition [1811], préface.
(10) Poinsot utilisait rarement le terme “axe” ou la convention relative au sens.
(11) Le terme de couple de torsion semble apparaître en mécanique dans les années 1880 ; je n’ai pu en trouver l’origine. Un autre synonyme, peut-être plus récent, est moment tournant.
(12) C’est nous qui utilisons le symbole Σ de sommation. Poinsot utilise ‘+’ en reconnaissant explicitement sa signification vectorielle [§76-77].
(13) On aurait pu attendre que Poinsot rejoignît le modeste choeurs de mécaniciens, tels qu’Euler ou Prony [1800, §116], qui préféraient parler de « centre d’inertie ».
(14) École polytechnique Archives, Conseil d’Instruction, minutes de la réunion du 7 vendémiaire an 12.
(15) Lagrange, lettre du 26 mars [1808? 1809?] au Grand-Maître de l’Université: « Il est auteur d’un excellent Traité de Statique fondée sur une théorie qui lui est propre, et des très beaux mémoires qui ont reçu l’approbation de l’Institut, et qui annonce des talens bien digne d’être encouragés » (Bibliothèque Nationale, mss. nouv. acq. 1305, no. 96).
(16) Voir la lettre sarcastique de 1813 à propos de Biot et de Poisson envoyée à Poinsot par son camarade polytechnicien et inspecteur de l’Université Charles Blanquet Duchayla [Grattan-Guinness 1990, 1328-1330]. L’unique production mathématique de Duchayla est une preuve élégante du parallélogramme des forces [1804].
(17) Voir particulièrement [Biot 1829, iv, 42-46]. Pour un commentaire, voir [Sédillot 1870, 161].
(18) [Stäckel 1905] énumère un bon nombre de monographies pertinentes et de manuels scolaires portant sur la mécanique.
(19) [Hennenberg 1903]; sur l’histoire de ces méthodes, voir [Scholz 1990, ch. 2].
(20) De la même manière que deux forces égales et opposées se traduisent par un couple de rotation, deux couples égaux et opposés se traduisent par une translation.
(21) Plus tard Poinsot [1846] fera remarquer, comme “point fondamental”, que l’équation exprimant le principe nécessitait un système de coordonnées orthogonales (à comparer avec [1803, art. 92]).
(22) Sur ce point, voir notamment [Lindt 1904], et [Bailache 1975] pour les manuscrits de Poinsot y afférents. Une histoire plus récente en est donnée dans [Capecchi 2012].
(23) Sur les contacts entre Mach et Duhem, voir [Hentschel 1988]. Les nombreux autres écrits de Duhem sur l’histoire de la mécanique couvrent des périodes antérieures à Poinsot.
(24) À la même époque que ces travaux, citons, quoi qu’elle n’ait pas de caractère historique, l’axiomatisation de la mécanique par Georg Hamel, dans l’approche métamathématique de son maître David Hilbert. Cependant, aucun couple n’y figure, même pas en conjonction avec le parallélogramme des forces … [Hamel 1909, 358].