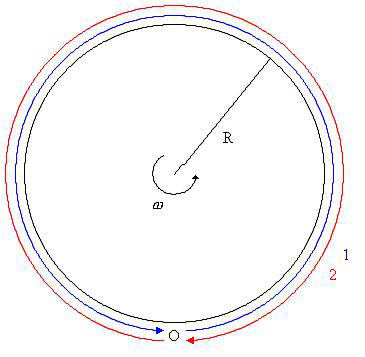
Figure 1 : Schéma de principe d’une expérience mettant en évidence l’effet Sagnac (deux signaux lumineux partant du point O au même instant et faisant en sens inverse à la même vitesse un tour complet d’un disque tournant) (image WikiCommons Didier Lauwaert)
L’EXPÉRIENCE DE SAGNAC : LE DERNIER TOUR DE L’ÉTHER
Contrairement à toutes les tentatives précédentes destinées à mettre en évidence des variations dans la vitesse de la lumière dues au mouvement de la Terre par rapport à l’éther (la plus célèbre étant celle de Michelson et Morley à la fin du XIXe siècle), l’expérience du physicien français Georges Sagnac (1869-1928) réalisée en 1913 se distingue par un résultat (enfin !) positif, et confirme ainsi une prédiction de la théorie de l’éther de Fresnel. Les deux notes de Sagnac publiées en 1913 dont il est ici question paraissent consacrer ce résultat important comme preuve solide de l’existence de l’éther, contre la relativité d’Einstein dont l’article fondateur date de 1905. Pourtant cette expérience va s’affirmer, au-delà des apparences, comme révélatrice d’un effet typiquement relativiste, avec à la clef des applications pratiques inattendues. À rebours des intentions de son auteur, l’expérience de Sagnac, prise dans toute sa généralité, est aujourd’hui l’une des plus emblématiques de la relativité restreinte dont elle constitue une éclatante confirmation.
LA LUMIÈRE, UNE ÉTRANGE AFFAIRE
L’histoire de l’étude des propriétés de la lumière est jalonnée de surprises et de rebondissements souvent déroutants. Quoiqu’omniprésente dans notre vie quotidienne, où elle nous apparaît comme une évidence, la lumière est l’un des phénomènes les plus extraordinaires et les plus riches qui aient été offerts à la sagacité des physiciens.
Dès l’Antiquité, deux hypothèses se font jour : l’une – corpusculaire (ou balistique) – imagine la lumière composée d’infimes projectiles dotés de vitesses caractéristiques ; l’autre – ondulatoire – interprète la lumière (par analogie avec le son pour l’air) sous forme d’une onde se propageant à travers un milieu emplissant la totalité de l’espace entre les étoiles, l’éther. Le premier scientifique de l’ère moderne (qui commence avec Galilée) à proposer une explication rationnelle est Huygens au XVIIe siècle avec sa remarquable théorie ondulatoire. Toutefois sa conception sera supplantée rapidement par la théorie corpusculaire de Newton qui fera autorité jusqu’au début du XIXe siècle. Newton imagine des particules de faible masse soumises à l’influence de la gravitation : on s’attend en conséquence à ce que la vitesse de la lumière varie en fonction de la taille des étoiles et de leur mouvement propre dans l’espace.
Les ennuis commencent avec la découverte de l’
aberration annuelle des étoiles par James Bradley en 1728. En cherchant la parallaxe (décalage apparent dans la position des étoiles selon l’angle d’observation depuis la Terre qui varie avec son mouvement autour du Soleil), Bradley tombe sur un phénomène inattendu qui s’avèrera une découverte-clef à plus d’un titre
(1) . Toutes les étoiles ont un mouvement apparent par rapport à la Terre (elles décrivent une ellipse) que l’on nommera
aberration (2) , car il s’agit d’un écart entre la position réelle et la position observée ; il s’agit d’un effet combiné de la vitesse de la lumière et de celle de la Terre, ne dépendant que du rapport V/c (avec V = 30 km/s). Bradley constate que le mouvement de la lumière est identique quelle que soit la distance et que l’aberration de toutes les étoiles se calcule
avec la même constante.
Cette conclusion ne fait pas l’unanimité car les données de l’époque n’excluent pas de petites variations de la vitesse de la lumière. Le physicien français François Arago en 1810 monte une expérience destinée à clarifier la question : est-il possible de déceler, conformément à la théorie corpusculaire, de faibles variations dans la vitesse de la lumière émise par les étoiles, ayant pour origine soit le mouvement des étoiles, soit les caractéristiques propres de ces astres (taille, densité…), soit enfin le mouvement de la Terre
(3) ? Arago a l’idée astucieuse d’utiliser des prismes pour amplifier l’effet de façon à le rendre mesurable. Il exploite une propriété prédite par la théorie corpusculaire newtonienne, à savoir que la déviation à travers le prisme du rayon de lumière incidente sera d’autant plus marquée que la vitesse d’entrée sera plus grande. Ceci s’explique par le fait que la composante normale de la vitesse incidente sera augmentée par la force de gravitation exercée par le milieu réfringent.
Que mesure donc Arago lors de ces expériences ? Le résultat sera clairement négatif : aucune déviation significative dans le prisme ne sera observée. Arago tentera de détecter des variations de deux façons : soit en examinant différentes étoiles, soit en captant la lumière de certaines étoiles le matin (desquelles la Terre, dans son mouvement autour du Soleil, se rapproche) et d’autres étoiles le soir (desquelles la Terre s’éloigne). Écoutons Arago lui-même raconter son ingénieuse expérience
(4):
On sait d'ailleurs que son mouvement [celui de la Terre] est dirigé vers les étoiles qui passent au méridien à 6 heures du matin et vers celles qui passent à 6 heures du soir, de telle sorte cependant qu'elle s'approche des premières et qu'elle s'éloigne au contraire des autres. La déviation, dans le premier cas, doit donc correspondre à la vitesse d’émission augmentée de sa 1/10000 partie, et, dans le second, à cette même vitesse diminuée de 1/10000 ; en sorte que les rayons d'une étoile qui passe au méridien à 6 heures du matin, doivent être moins fortement déviés que ceux d'une étoile qui passe à 6 heures du soir, d'une quantité égale à celle qu'occasionne 1/5000 de changement dans la vitesse totale.
Le chiffre ci-dessus de 1/10 000e correspond bien sûr au rapport de la vitesse de la Terre à celle de la lumière. Bien qu’un résultat négatif (la non-observation d’un effet attendu) soit frustrant pour l’expérimentateur, il est souvent riche d’enseignements. Arago était au départ un partisan convaincu de la théorie corpusculaire, mais comment concilier ses résultats avec cette théorie ? On s’attendrait à observer des variations aussi bien en fonction des caractéristiques (diamètre, densité, vitesse…) des étoiles sources que du mouvement de la Terre. Dans un premier temps, Arago n’a pas d’autre choix pour sauvegarder la théorie corpusculaire de supposer que nous recevons bel et bien des particules de lumière à des vitesses diverses mais que l’œil humain ne serait sensible qu’à une petite gamme de vitesses. Cette hypothèse ad hoc ne peut tenir la route longtemps et Arago se tourne en 1818 vers son protégé Augustin Fresnel, champion incontesté de la théorie ondulatoire de la lumière. Cette dernière explique sans peine l’indépendance de la vitesse de la lumière par rapport à la source émettrice (le cas est similaire pour l’onde sonore) si l’on suppose que l’espace entre les étoiles baigne dans un éther stationnaire. En revanche peut-elle expliquer que cette vitesse ne dépende aucunement de celle de l’observateur (la Terre) ?
Telle est la question ô combien stimulante posée à Fresnel. Celui-ci parvient à résoudre brillamment le problème en supposant que le résultat s’explique par des effets de compensation dus à l’utilisation de milieux réfringents (en l’occurrence les prismes). Pour cela, il lui faut arguer que l’éther contenu dans le prisme est partiellement entraîné par le mouvement de la Terre. Plus précisément, le mouvement du prisme entraînerait avec lui une quantité d’éther correspondant à l’excès d’éther contenu dans le prisme par rapport au vide. Fresnel suppose que la vitesse à laquelle l’éther dans le prisme est entraîné n’est ni nulle ni égale à la vitesse V de la Terre mais égale à :
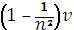
où n désigne l’indice de réfraction et V la vitesse de la Terre.
Fresnel parvient donc à expliquer pourquoi tous les phénomènes optiques observés sur Terre par des expériences de réfraction sont indépendants du mouvement terrestre si on se limite aux termes du premier ordre en V/c (donc si on néglige les termes d’ordre supérieur en V/c). Il prédira également des résultats similaires pour la propagation de la lumière à travers l’eau. Hippolyte Fizeau réalise le premier en 1851 une expérience utilisant des sources de lumière terrestre se propageant dans deux colonnes d’eau, l’une étant en mouvement. Les résultats confirment cet « entraînement partiel » de l’éther proposé par Fresnel. Léon Foucault quant à lui reprend en 1850 l’expérience d’Arago en comparant la propagation de la lumière à travers l’eau et l’air : la vitesse de la lumière est plus faible dans les liquides que dans l’air ou le vide. Ce résultat
(5) invalide la théorie corpusculaire de Newton qui prédisait le contraire.
@@@@@@@
Arrêtons-nous un instant en l’an 1860 : la théorie de l’éther de Fresnel est à cette date la plus complète et la plus cohérente pour expliquer l’ensemble des phénomènes optiques connus. Il y a bien eu une petite alerte avec l’aberration mais tout semble être rentré dans l’ordre.
Toutefois l’histoire est loin d’être achevée. Dans les années 1860, James Maxwell publie sa théorie de l’électromagnétisme dans laquelle la lumière apparaît comme un cas particulier d’onde électromagnétique voyageant toujours à la vitesse c dans l’éther, son milieu supposé de propagation. Maxwell envisage en 1879 de détecter des variations de vitesse de la lumière par un interféromètre terrestre. Cependant il juge les effets trop faibles à mesurer (car en V2/c2). L’idée est d’abandonner l’usage de milieux réfringents comme les prismes pour réaliser les mesures afin d’éviter les effets de compensation produits par l’entraînement partiel de l’éther. Le physicien américain Michelson (1852 – 1931), qui recevra le prix Nobel de physique en 1907, décide de relever le défi avec son collègue Morley. Si l’on sépare un faisceau lumineux en deux signaux parcourant la même longueur chacun en empruntant un bras perpendiculaire à l’autre, la physique classique prédit que la vitesse de la lumière le long de chacun des bras doit varier suivant la direction de la vitesse de la Terre dans son mouvement autour du Soleil, les deux signaux devant arriver en conséquence décalés au récepteur. Malgré de nombreuses reproductions de cette expérience, qui se poursuivront jusqu'au début du XXe siècle, les résultats resteront toujours négatifs. Était-il encore possible de sauver la théorie ondulatoire de Fresnel ?
Le physicien irlandais Fitzgerald est le premier en 1889 à proposer une solution dans le cadre de la théorie de l’éther : l’idée de compensation fait son retour. Il fait l’hypothèse que tous les objets sont contractés dans le sens du mouvement à travers l’éther : grâce à cette astuce, les variations de vitesse sont compensées par le raccourcissement des bras de l’interféromètre dans la direction du mouvement. Toutefois c’est à Lorentz que revient d’avoir réalisé quelques années plus tard la première synthèse de cette idée (qu’il propose indépendamment de Fitzgerald) avec sa propre théorie microscopique de l’électromagnétisme (dans laquelle il décrit le comportement des électrons en cohérence avec la théorie de Maxwell). Lorentz ne s’arrête pas là et élabore les transformations de coordonnées (que Poincaré appellera « transformations de Lorentz ») qui permettent de garantir l’invariance des lois de l’électromagnétisme dans tous les référentiels inertiels. Poincaré s’efforcera de clarifier certains aspects de la théorie de Lorentz en lui donnant une forme qu’il pense achevée. Le fameux mémoire de Palerme de Poincaré (dont la version complète est soumise à l’éditeur quelques semaines après l’article révolutionnaire d’Einstein) constitue en fait le prolongement ultime des tentatives pour concilier la physique classique (basée sur les notions d’espace et de temps absolus) avec l’ensemble des phénomènes connus, même si le formalisme mathématique que Poincaré explore avec talent anticipe sur de nombreux points celui de la future relativité restreinte.
Voilà ce que Poincaré écrit en 1909 à propos de ses propres travaux
(6) :
J’ai publié dans les Rendiconti un article où j’expose la théorie de Lorentz sur la Dynamique de l’Électron, et où je crois avoir réussi à écarter les dernières difficultés et à lui donner une parfaite cohérence.
Tous les physiciens en pointe de cette époque (Poincaré compris) raisonnaient en termes de dynamique, donc cherchaient à expliquer la contraction des longueurs comme l’effet de forces d’un genre spécial exercées par l’éther sur les corps dans le sens de leur déplacement. Aucun physicien avant Einstein n’a écrit une ligne sur la dilatation des durées en tant que phénomène physique. Le temps t’ dans la transformation de Lorentz n’a jamais été compris en prenant en compte la dilatation des durées. Lorentz ne lui attribuait pas de sens physique.
En 1915, avec un recul salutaire, il écrit avec une grande lucidité
(7) :
La principale raison de mon échec [pour la découverte de la relativité restreinte] fut de m’être accroché à l’idée que seule la variable t pouvait être considérée comme le temps réel, et que mon temps local t’ ne devait être regardé que comme une simple grandeur mathématique auxiliaire. Dans la théorie d’Einstein au contraire, t’ joue le même rôle que t ; si nous voulons décrire un phénomène à l’aide de x’, y’, z’, t’ nous devons travailler avec ces variables comme nous le ferions avec x, y, z, t.

Figure 2: Albert Einstein (1879-1955) et Hendrik Lorentz (1853-1928). Même si le second était au seuil de la relativité, il ne franchit jamais le pas décisif, contrairement au premier (photographie de 1921 prise par le physicien Ehrenfest devant sa maison de Leyde, image WikiCommons).
Quant à Poincaré, il s’attache certes à définir le temps local introduit par Lorentz comme une grandeur physique mesurable mais il ignore complètement le facteur
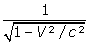
de dilatation des durées, de sorte que ce temps local
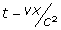
n’a rien à voir
(8) avec la relativité du temps. Il est vrai qu’expliquer la contraction des longueurs en termes de dynamique était possible – mais faire de même pour la dilatation des durées était une autre histoire : dans le cadre de la théorie de l’éther, comment comprendre que toutes les horloges en mouvement par rapport à l’éther puissent être ralenties par un effet mécanique ? Cet aspect a sûrement joué dans le blocage mental de l’époque : mais c’est un fait que ni Lorentz ni Poincaré n’ont jamais envisagé ce concept. Le seul à l’avoir effleuré est Larmor, mais il n’évoque jamais l’effet dans sa généralité ni comme applicable aux horloges en mouvement.
En dépit de ces données factuelles, certains physiciens, postérieurement aux publications d’Einstein, en s’appuyant de façon excessive sur des sources secondaires, ont construit une théorie physique
a posteriori, une sorte d’
uchronie scientifique, histoire parallèle de la physique qui n’a jamais existé. Cette théorie tantôt appelée théorie de Larmor-Lorentz ou théorie de Lorentz-Poincaré serait bâtie sur deux hypothèses fondamentales, la contraction des longueurs et la dilatation des durées tout en préservant le cadre classique de l’éther. Pourtant, comme nous l’avons souligné, aucun écrit sur la deuxième hypothèse n’existe
(9) avant l’article fondateur d’Einstein de 1905 «
Sur l’électrodynamique des corps en mouvement ».
Dans ce papier historique, le génial physicien renverse complètement la perspective en proposant une solution à la fois plus simple et plus radicale, capable de rendre compte de l’ensemble des phénomènes connus par son caractère universel : il « suffit » de changer le cadre cinématique qui était tenu comme allant de soi, c'est-à-dire la façon dont les coordonnées d’espace et de temps se transforment d’un référentiel à l’autre. Cette cinématique nouvelle naît de la fusion de deux axiomes apparemment incompatibles : la constance de la vitesse de la lumière dans tous les référentiels inertiels et le principe de relativité. Dans ce nouveau cadre applicable à toute théorie physique présente ou future, l’aspect le plus étonnant n’est plus la contraction des longueurs mais la relativité du temps car elle s’accompagne d’un effet absolu : la
désynchronisation des horloges parfaites (10). Cette conséquence inédite et révolutionnaire est prédite par Einstein dès son premier article de 1905 avec une facilité qui tranche singulièrement avec les hésitations de ses prédécesseurs. Autre nouveauté : Einstein se débarrasse tout simplement de l’éther qui devient une hypothèse superflue.
Laissons Einstein résumer lui-même peu de temps avant sa mort l’importance de sa contribution
(11) :
Ce qui était nouveau dans ce mémoire, c'est d'avoir découvert le fait que la portée de la transformation de Lorentz transcendait sa connexion avec les équations de Maxwell et mettait en cause la nature de l'espace et du temps en général. Ce qui était également nouveau, c'est que l'invariance de Lorentz est une condition générale pour toute théorie physique. Ce fut pour moi d'une importance particulière, car j'avais découvert déjà antérieurement que la théorie de Maxwell ne rendait pas raison de la microstructure du rayonnement (électromagnétique) et ne pouvait par conséquent prétendre à une validité universelle.
Qu’est-ce que la désynchronisation des horloges parfaites ?
Considérons deux horloges au départ immobiles H et H0 au point O dans un référentiel inertiel, et parfaitement synchronisées. Supposons que nous faisions parcourir à l’horloge H une courbe fermée quelconque qui part de O pour revenir en O et que nous constations à son retour au point O que l’horloge H retarde par rapport à l’horloge H0. Quelle peut en être la cause ? Le physicien classique avec son temps absolu n’a qu’une solution à proposer : l’horloge déplacée (ou chacune des deux) s’est déréglée, donc n’a pas mesuré correctement le temps écoulé, d’où l’écart à l’arrivée. En revanche pour le physicien relativiste, il existe une autre solution : chacune des horloges a continué à fonctionner parfaitement (battant la seconde imperturbablement) mais les durées réellement écoulées sont différentes dans chacun de leurs référentiels.

À chaque ligne d’univers (12) son temps propre : voilà une conséquence capitale de la relativité. Par temps propre, il faut entendre le temps mesuré par une horloge parfaite attachée à un observateur donné. La notion de temps propre est essentielle (13) en relativité car elle correspond à l’élément de distance spatio-temporel invariant d’un référentiel inertiel à l’autre. En relativité, ni les longueurs ni les durées ne se conservent d’un référentiel inertiel à l’autre mais un mélange des deux (introduit formellement par Minkowski dans son célèbre article (14) de 1908). À ceux que ces nouveaux concepts rebutent, on peut retourner la question : pourquoi devrions-nous vivre dans un univers dans lequel longueurs et durées ne changent pas d’un référentiel à l’autre ? On peut parfaitement imaginer des univers à la structure géométrique telle que ces grandeurs ne se conservent plus : il se trouve que nous vivons dans l’un de ces univers logiquement possibles.
Et la lumière tourna
Tel est le contexte au moment où, en 1913, Georges Sagnac s’apprête à réaliser son expérience. Il n’est pas le premier physicien à avoir anticipé l’effet qu’il cherche à mesurer, c'est-à-dire le décalage temporel dans la réception de signaux lumineux parcourant en sens inverse un circuit fermé.
Sir Oliver Lodge (1851-1940) envisage en 1893, dans le cadre de la théorie de l’éther, la détection du mouvement de rotation de la Terre autour de son axe à l’aide d’un hypothétique interféromètre d’un kilomètre carré ; puis en 1897 il anticipe le résultat de l’expérience de Sagnac en raisonnant avec un petit interféromètre qui serait mis en rotation. Michelson en 1904 étudie également la possibilité de mettre en évidence la rotation de la Terre en utilisant un interféromètre. C’est en 1925 que Michelson et Gale parviendront effectivement à mesurer l’effet prédit grâce à un interféromètre optique aux dimensions impressionnantes.

Figure 3: Sir Oliver Lodge (caricature par Leslie Ward, parue dans Vanity Fair du 4 février 1904, WikiCommons). Un exemple de dilatation des longueurs dans cette caricature ?
L’étudiant allemand Frank Haress, durant son travail de thèse en 1911, est tombé par hasard sur le phénomène en étudiant les effets de réfraction de la lumière à travers des prismes, toujours dans le cadre de la théorie de Fresnel. Pour des raisons de commodité, il avait disposé les prismes en anneau et animé l’ensemble d’un mouvement de rotation. Il constata sans pouvoir l’expliquer le déplacement des franges d’interférence. Involontairement, Haress contribua à démontrer que l’effet Sagnac était observé même en présence de milieux réfringents (que la lumière traverse à une vitesse inférieure à c).
Enfin Georges Sagnac lui-même prédit l’effet en 1911 avec la théorie de l’éther. Cette même année, Max Von Laue précise que la relativité restreinte rend compte également du phénomène après avoir dès 1907 démontré
(15) que cette théorie permet de retrouver en première approximation les prédictions de Fresnel pour l’entraînement partiel de l’éther.
@@@@@@@
Nous sommes prêts à présent pour analyser les deux notes publiées par Sagnac en 1913 comme compte-rendu de son expérience réussie. Nous nous focaliserons principalement sur la première note qui contient les aspects essentiels pour la discussion.
Sagnac dans cette première note intitulée « L’éther lumineux démontré par l’effet de vent relatif d’éther dans un interféromètre en rotation uniforme » commence logiquement par exposer le principe de la méthode utilisée :
Les deux faisceaux interférents, réfléchis par quatre miroirs placés au bord du plateau tournant, sont superposés en sens inverses sur un même circuit horizontal entourant une certaine aire S.
Les conditions sont ici clairement posées : on fait parcourir à deux signaux lumineux un circuit fermé identique mais en sens inverse dont on observe les interférences à leur point de rencontre (le récepteur étant une plaque photographique qui enregistre les franges d’interférence). Le schéma détaillé de ce circuit fermé est fourni dans la deuxième note.
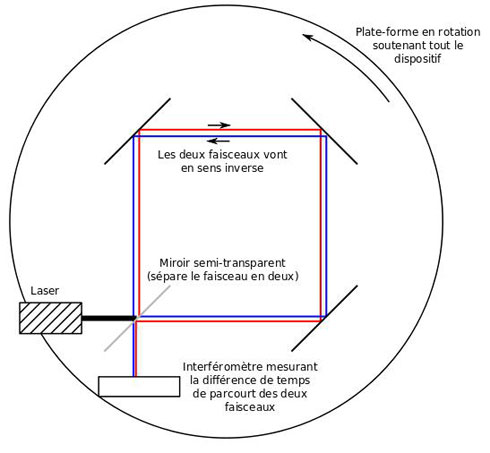
Figure 4 : Schéma de principe d’un interféromètre de Sagnac optique (image WikiCommons auteur Didier Lauwaert) ; figure 4bis (ci-dessous) : schéma tel que figurant dans l’article de G. Sagnac.
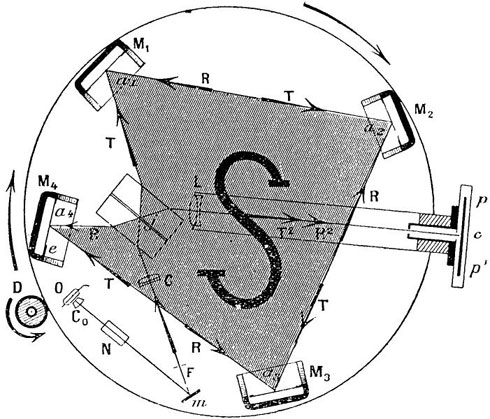
C’est le déplacement du centre d’interférence (c'est-à-dire du centre de la frange médiane qui correspond à l’intensité lumineuse maximale) qui est mesuré en comparant deux photographies distinctes, chacune correspondant à une rotation uniforme à même vitesse du plateau dans l’un des deux sens possibles.
Sagnac décrit ensuite l’effet prédit d’un point de vue théorique. Sur quelles hypothèses se base-t-il ? Qu’entend-il par effet tourbillonnaire optique ?
Dans un système en mouvement d’ensemble par rapport à l’éther, la durée de propagation entre deux points quelconques du système doit être altérée comme si le système était immobile et soumis à l’action d’un vent d’éther, dont la vitesse relative en chaque point du système serait égale et directement opposée à celle de ce point et qui emporterait les ondes lumineuses à la manière du vent de l’atmosphère emportant les ondes sonores.
Sagnac raisonne dans le cadre de la théorie de l’éther de Fresnel. L’onde lumineuse, à la manière du son pour l’air, se propage à travers l’éther (un milieu mystérieux dont la composition reste inconnue, contrairement à l’air), indépendamment du mouvement de la source émettrice. L’analogie avec l’onde sonore est permanente et guide l’argumentation. La vitesse de propagation de l’onde lumineuse devrait dépendre de la vitesse de l’observateur par rapport à l’éther, exactement comme pour le son par rapport à l’air. Si l’observateur se déplace en direction de la source à la vitesse Rω, il mesurera l’équivalent pour la lumière d’un vent pour l’air (soit c + Rω), tandis que s’il s’en éloigne, il mesurera c – Rω, d’où l’appellation vent d’éther. Cette terminologie était déjà en vigueur pour l’expérience de Michelson et Morley.
L’observation de l’effet optique d’un tel vent relatif d’éther constituera une preuve de l’éther, de même que l’observation de l’influence du vent relatif de l’atmosphère sur la vitesse du son dans un système en mouvement permettrait, à défaut d’autre effet sensible, de prouver l’existence de l’atmosphère entourant le système en mouvement.
Sagnac insiste ici sur l’analogie avec l’air : si la lumière se propage de façon similaire à l’onde sonore dans l’air, la détection du vent relatif d’éther devrait permettre de confirmer l’existence du milieu de propagation propre à la lumière. Nous reviendrons au calcul détaillé un peu plus loin.
Il mentionne ensuite une autre expérience réalisée par ses soins, mettant en jeu un circuit optique vertical : l’effet mesuré est nul à la précision des mesures près et permet d’exclure un entraînement de l’éther.
J’ai montré interférentiellement […] avec un circuit optique de 20m² de projection verticale, que l’entraînement de l’éther au voisinage du sol ne produit pas même une densité b de tourbillon d’éther de 1/1000 de radian par seconde.
Il prédit l’existence d’un effet dû la rotation de la Terre qui serait détectable à l’aide d’un circuit horizontal.
J’espère pouvoir déterminer si le petit effet tourbillonnaire optique correspondant existe ou non.
Mais Sagnac disparaît en 1928, et c’est Michelson et Gale en 1925 qui réussiront les premiers à mesurer cet effet à l’aide d’un interféromètre « géant ». Sagnac revient au sujet principal qui concerne le résultat obtenu avec un circuit optique de taille plus modeste que l’on met en rotation :
Il m’a été plus facile de trouver d’abord la preuve de l’éther en faisant tourner un petit circuit optique.
Il rappelle la valeur théorique prédite pour le paramètre z qui correspond au déplacement déjà mentionné du centre d’interférence entre deux photographies :
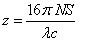
Où N est le nombre de tours par secondes du plateau tournant, S la surface du circuit fermé, λ la longueur d’onde utilisée, c la vitesse de la lumière (la notation de Sagnac est v0, encore courante à l’époque – nous avons remplacé par c).
La formule d’interférence de Sagnac
Comment obtient-on cette formule par la théorie de l’éther ? Dérivons la formule ci-dessus en raisonnant pour simplifier avec un disque tournant (celui de la figure 1), le cas se généralisant sans problème à un circuit fermé englobant une surface S quelconque. Nous avons donc deux signaux lumineux émis au même instant du point O (fixe sur le disque tournant) qui parcourent la circonférence par un jeu de miroirs pour revenir en O, chacun dans un sens. Bien qu’ils soient émis à partir du disque tournant, les signaux se propagent à la vitesse c par rapport à l’éther (laboratoire), conformément à la théorie de Fresnel. Par contre, par rapport au disque tournant, la vitesse de chacun des signaux est augmentée ou diminuée de celle du disque selon le sens de parcours (c’est la loi d’additivité des vitesses habituelle en physique classique). Le décalage temporel d’arrivée des signaux en O est donc donnée par :
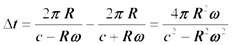
En remarquant que la vitesse de rotation du disque est faible devant c et que S = π R², nous obtenons :
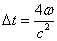
Le déphasage Δφ entre les deux faisceaux lumineux est ω ×Δt :
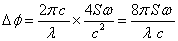
La valeur théorique fournie par Sagnac est le double de la précédente (qui est la valeur connue habituelle) parce que, rappelons-le, le déplacement du centre d’interférence est mesuré en comparant deux photographies correspondant à deux rotations en sens contraire de l’interféromètre tournant.
@@@@@@@
Une dernière précaution est signalée par Sagnac : il explique comment il s’est assuré que les déplacements des franges ne peuvent être imputés à une instabilité des pièces optiques pendant la rotation.
Cela montre que l’effet observé est bien dû à une différence de phase liée au mouvement de rotation du système.
Les résultats ayant confirmé la valeur prédite par la théorie de l’éther de Fresnel, Sagnac peut triomphalement annoncer que l’existence de l’éther est chose prouvée.
L’effet interférentiel observé est bien l’effet tourbillonnaire optique dû au mouvement du système par rapport à l’éther et manifeste directement l’existence de l’éther, support nécessaire des ondes lumineuses de Huygens et de Fresnel.
Il enfonce le clou en conclusion de sa deuxième note intitulée « Sur la preuve de la réalité de l’éther lumineux par l’expérience de l’interférographe tournant » :
Le résultat des mesures montre que, dans l’espace ambiant, la lumière se propage avec une vitesse V0, indépendante du mouvement d’ensemble de la source lumineuse O et du système optique. Cette propriété de l’espace caractérise expérimentalement l’éther lumineux.
Le résultat obtenu par Sagnac constituait un élément de preuve en faveur de la théorie de l’éther de Fresnel (ou de celle de Lorentz et Poincaré qui la prolongent avec l’électromagnétisme) : mais était-ce la seule explication possible ? Sagnac n’était pas sans savoir que la relativité restreinte, déjà âgée de 8 ans, ne pouvait être écartée de la discussion. L’un des plus proches collègues de Sagnac était d’ailleurs Langevin, l’un des rares physiciens français à soutenir résolument la théorie d’Einstein. L’honnêteté aurait ici commandé de laisser au moins ouverte la question de savoir si cet effet était interprétable dans le cadre relativiste. Cependant la forte conviction de Sagnac (celle du physicien expérimentateur trop heureux de conforter ses concepts familiers en lien direct avec les données sensibles) l’a sans doute précipité vers sa conclusion favorite au détriment d’une approche plus novatrice.
En tous les cas, à ce stade, nous pouvons énumérer quelques propriétés indubitables de l’effet Sagnac : - Il est conforme à la formule démontrée par Sagnac à l’aide de la théorie de l’éther. - Il ne dépend pas de la forme de la surface fermée. - Il ne dépend pas de la position du centre de la rotation. - Il ne dépend pas de la présence d’un milieu réfringent co-tournant sur le trajet du signal.
En fait, la relativité restreinte prédit l’effet Sagnac…
Quelle est la prédiction de la relativité restreinte pour l’effet Sagnac ? La réponse est importante puisque Sagnac a prétendu démontrer l’existence de l’éther, que la relativité a mis à la trappe.
Tout d’abord le raisonnement est identique à la théorie de l’éther si l’on se place dans le référentiel du laboratoire (qu’on peut considérer comme inertiel): dans les deux cas, la vitesse des signaux est égale à c (la différence est que la relativité ne présuppose pas l’existence d’un milieu de propagation pour la lumière). Il est facile de retrouver la prédiction obtenue avec la théorie de l’éther en se plaçant dans le référentiel du laboratoire où le disque tourne. Dans le laboratoire, le signal qui est émis dans le même sens que la rotation du disque doit parcourir une distance plus grande car le disque tourne légèrement pendant que le signal se propage. Le signal émis en sens inverse a quant à lui une distance plus courte à parcourir mais à la même vitesse, d’où le décalage temporel dans la réception des signaux. Faisons la démonstration détaillée à l’aide de la relativité.
Soient t+ et t- les durées des trajets de chacun des signaux mesurées dans le référentiel du laboratoire (en notant + le signal émis dans le même sens que la rotation du disque). Les longueurs parcourues par rapport au laboratoire sont :
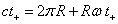
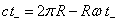
D’où
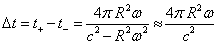
Les deux théories (éther et relativité) s’accordent donc quand on raisonne dans le référentiel du laboratoire. En revanche, comment la relativité décrit-elle la situation du point de vue du disque tournant ?
Le délai Sagnac mesuré par l’observateur en O est donné par :
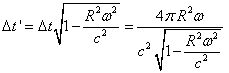
C’est bien cet intervalle de temps qui correspond au résultat de la mesure réalisée par Sagnac puisque le déphasage est mesuré par rapport au disque tournant. La valeur prédite par la relativité est légèrement différente de celle fournie par la théorie de l’éther : il y a un facteur de dilatation des durées à prendre en compte. Néanmoins, ce terme est négligeable en pratique et on peut donc considérer que les deux prédictions coïncident. Ce qui ne veut pas dire que les explications sont de même nature.
Contrairement à une idée assez répandue, l’origine relativiste du délai Sagnac n’est pas l’anisotropie (16) de la vitesse de la lumière dans le référentiel tournant (cette erreur d’interprétation provient du fait que l’on se croit autorisé à admettre l’anisotropie dans le référentiel tournant parce qu’il n’est pas inertiel) mais la structure particulière de notre espace-temps. Dans le référentiel tournant (17), les longueurs dépendent du sens du parcours et la vitesse de la lumière reste constante, contrairement à la physique classique.
@@@@@@@
Dans les années 1990, le physicien italien Franco Selleri a cru détecter un paradoxe
(18) (donc une contradiction logique) dans la relativité restreinte : selon lui, dans le cadre relativiste, les deux signaux ne se propageaient pas à la même vitesse par rapport au disque tournant (il supposait l’anisotropie, comme on le faisait en physique classique), ce qui paraissait admissible puisque le référentiel n’était pas inertiel. Le rapport entre les deux vitesses en sens contraire était différent de 1 et ne dépendait que de la quantité Rω/c car il supposait que les longueurs parcourues étaient identiques. En faisant tendre le rayon du disque vers l’infini et la vitesse angulaire ω vers zéro tout en maintenant la vitesse tangentielle Rω constante, le disque tournant devenait un référentiel inertiel dans lequel la condition d’isotropie de la vitesse de la lumière était violée, d’où le paradoxe. Ce raisonnement n’est pas valable puisqu’en réalité, les signaux dans le cadre relativiste minkowskien ont la même vitesse par rapport au disque tournant ; et nous allons voir à présent que l’originalité de l’effet Sagnac réside au contraire dans le fait qu’il est observé également pour des signaux ou objets quelconques parfaitement isotropes. Dès lors, le terme c
2 dans le délai Sagnac 4πR²ω/c² apparaîtra non plus comme le carré de la vitesse particulière d’un signal mais comme une
constante structurelle de notre univers.
L’universalité de l’effet Sagnac
Où en sommes-nous ? Nous avons constaté que la théorie de l’éther et la relativité restreinte étaient toutes deux capables de prédire l’effet observé avec des signaux lumineux mais différaient radicalement par l’explication fournie. Y a-t-il un moyen de les départager ? Les physiciens adorent faire varier les paramètres des expériences pour titiller leurs théories, et ce cas n’échappe pas à la règle. Que se passerait-il si au lieu de signaux lumineux, nous utilisions dans l’expérience de Sagnac des particules voire des objets macroscopiques parcourant la circonférence du disque tournant à une vitesse quelconque (mais identique) dans les deux sens ?
Faisons une expérience par la pensée qui nous sera fort utile et que nous appellerons le paradoxe des tortues.

Figure 5 : La « tortue – montre », un élément clé pour la compréhension de l'effet Sagnac universel
Revenons à notre disque tournant. Cette fois-ci, nous allons utiliser deux tortues au lieu des signaux lumineux. Pourquoi deux tortues ? Parce que nous voulons minimiser tout effet relativiste qui serait lié à leur vitesse. Ces deux tortues sont équipées de montres parfaites réglées toutes deux sur midi. Elles partent en sens contraire au même instant du point O fixe sur le disque tournant et font un tour complet à même vitesse V0.
Que pouvons-nous affirmer ? Tout d’abord chacune de nos tortues peut mesurer sa vitesse V0 tout au long du parcours et s’assurer que sa vitesse est constante et égale à V0. Elle peut également mesurer régulièrement la distance parcourue et s’assurer à l’arrivée qu’elle est bien égale à celle obtenue par sa comparse. Nous en déduisons que la durée de parcours pour chacune des tortues sera identique, par exemple 1 heure. Le temps indiqué sur chacune des montres à l’arrivée au point O sera donc 13h00.
Supposons que nos deux tortues ne parviennent pas au point O au même instant, ce qui signifie qu’un observateur en O verra une première tortue arriver et attendre l’autre pendant (par exemple) 10 minutes. Cela revient simplement à supposer que l’effet Sagnac mis en évidence pour les signaux lumineux serait observé aussi pour des objets quelconques.
Quelle conclusion pouvons-nous tirer ? Lorsque la deuxième tortue rejoint sa congénère au point O, quels sont les temps affichés par leurs montres respectives ?
La montre de la première tortue arrivée affichera 13h10 (puisqu’elle a attendu sa comparse pendant 10 minutes) tandis que l’autre indiquera 13h00. Les deux montres seront décalées de 10 minutes : c’est le phénomène de désynchronisation des horloges parfaites. Nous en déduisons que le délai Sagnac implique nécessairement la désynchronisation des horloges parfaites. Réciproquement, si ce phénomène de désynchronisation n’existait pas, nous ne pourrions pas observer un décalage dans l’arrivée de nos deux tortues (ou de deux objets quelconques).
Nous pouvons en conclure que toute théorie physique capable d’expliquer l’effet Sagnac universel (c'est-à-dire le décalage dans l’arrivée au point origine observé indépendamment de la vitesse et de la nature des signaux utilisés) doit aussi prendre en compte la désynchronisation des horloges parfaites.
En étendant l’expérience initiale de Sagnac à des objets ou signaux quelconques et de même vitesse par rapport au disque, nous avons un moyen de déterminer laquelle des deux théories (éther de Fresnel ou relativité) rend compte correctement du phénomène général.
@@@@@@@
Comparons à présent les deux théories quantitativement.
Dans le cadre de la théorie de Fresnel, le temps est absolu, donc les durées de parcours de chacun des objets voyageant en sens contraire à la vitesse V0 par rapport au disque seront identiques dans tous les référentiels : celui du laboratoire dans lequel le disque tourne, celui du disque tournant (émetteur-récepteur) et celui des objets parcourant le disque.
Voici les durées telles que prédites par la physique classique (donc la théorie de Fresnel) dans les différents référentiels à considérer :
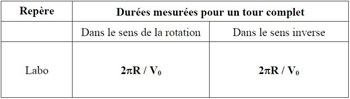
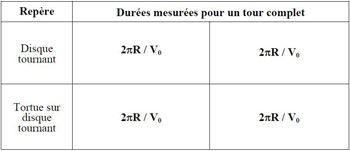
En physique classique, le délai Sagnac (différence entre les deux durées ci-dessus par rapport au disque tournant) est nul pour nos tortues (ou des objets quelconques) : elles reviennent donc à leur point de départ au même instant. Que deviennent ces durées avec la relativité restreinte ? Voici les nouvelles prédictions (19) :

Tableau tiré du livre de Pierre Spagnou, De la relativité au GPS, Ellipses, 2012
La différence entre les durées mesurées par rapport au disque tournant (indiquées dans la table ci-dessus) est le délai Sagnac, 4πR²ω/c² en première approximation, indépendant de la vitesse V0 par rapport au disque qui disparaît de la formule. Cependant les horloges attachées aux tortues mesurent quant à elles une durée identique (dernière ligne de la table ci-dessus) et sont donc désynchronisées lorsqu’on les compare au point O. Si l’on remplace nos tortues par des jumeaux, cela nous donne une variante du fameux paradoxe des jumeaux : à leur rencontre au point O, les deux jumeaux se retrouvent bel et bien avec des âges différents. Cela ne devrait pas surprendre : en relativité, la pluralité des temps propres est la règle et non l’exception.
Au-delà de ces prédictions théoriques, que nous enseigne l’observation ? L’effet Sagnac universel a-t-il été mesuré ? La possibilité de refaire l’expérience de Sagnac avec des électrons a été pour la première fois envisagée en 1935
(20) par Fernand Prunier (qui sera un anti-relativiste convaincu) dans le but de départager les théories classique et relativiste (l’effet devant être nul en physique non relativiste). La première mesure à l’aide d’un interféromètre à ondes de matière (les particules ayant un comportement quantique) fut réalisée en 1965 par Zimmerman et Mercereau avec des électrons supraconducteurs. Depuis, l’effet a été également observé avec des neutrons ou des atomes.
L’effet Sagnac universel est donc bien un phénomène naturel qui a été clairement établi avec des particules élémentaires ou des atomes.
Le décalage dans l’arrivée au point origine n’a pu jusqu’ici être mesuré directement avec des objets macroscopiques, car il faudrait être capable de mesurer des intervalles de temps extrêmement faibles (le comportement ondulatoire n’étant plus exploitable). Néanmoins on a pu mesurer la désynchronisation des horloges parfaites par une expérience assez similaire, réalisée par Hafele et Keating en 1971. Il s’agissait de faire voler l’un vers l’est, l’autre vers l’ouest, deux avions de ligne faisant un tour complet de la Terre au niveau de l’équateur et embarquant quatre horloges atomiques de haute précision. Le temps indiqué par les horloges à leur retour au point de départ fut comparé à celui fourni par les horloges de référence à la surface de la Terre. Les écarts mesurés montrèrent un bon accord avec les prédictions relativistes. Si l’on avait pu réaliser un voyage équatorial parfait, l’horloge partie vers l’est aurait retardé à l’arrivée de 207 nanosecondes par rapport aux horloges terrestres, tandis que celle partie vers l’ouest aurait avancé de 207 nanosecondes. Les valeurs mesurées furent légèrement inférieures du fait des écarts par rapport à la trajectoire équatoriale idéale.

Figure 6: Les physiciens Joseph Hafele (né en 1933) et Richard Keating à bord d’un avion de ligne, avec leurs horloges atomiques au césium (photo de la revue Popular Mechanics, janvier 1972)
La désynchronisation des horloges parfaites est aujourd’hui un phénomène clairement établi (qui plus est dans des circonstances voisines de celle de l’expérience de Sagnac), au même titre que l’effet Sagnac universel. Le paradoxe des jumeaux n’était donc pas une élucubration fantaisiste. Georges Sagnac, disparu en 1928, n’a jamais perçu la connexion étroite de ses propres observations avec l’une des conséquences les plus extraordinaires de la relativité restreinte, que son collègue Paul Langevin avait pourtant contribué à faire connaître à partir de 1911.
Une expérience sans intérêt pratique ?
Les réflexions précédentes n’étaient pas condamnées à rester abstraites et bien au contraire sont à l’origine d’outils technologiques de première importance.
L’étrangeté de l’effet Sagnac réside dans le fait qu’il ne dépend ni de la nature des signaux ou objets utilisés, ni de leur vitesse par rapport au référentiel tournant (pourvu qu’elle soit la même dans les deux sens et non nulle). Ceci signifie que la désynchronisation des horloges déplacées même très lentement à la surface de la Terre est inévitable,sauf à leur faire suivre un méridien ou une courbe par exemple en forme de huit
(21).
L’application la plus spectaculaire est le gyromètre (capteur de vitesse angulaire) : en effet si l’on fait parcourir dans les deux sens un circuit fermé à deux signaux à même vitesse, le déphasage mesuré nous donne une estimation de la vitesse de rotation du dispositif. Aujourd’hui l’un des composants courants d’une centrale inertielle
(22) (qui équipe notamment les avions de ligne) est le gyrolaser : les signaux sont deux faisceaux lumineux de lumière cohérente dont on mesure le déphasage. Couplés aux accéléromètres, les gyrolasers permettent de déterminer tous les déplacements et les changements d’orientation de l’appareil. Leur intérêt par rapport aux gyromètres classiques (conservateurs de cap) est qu’ils n’utilisent pas de pièces mécaniques en mouvement, d’où une usure moindre ; ils sont également peu sensibles aux chocs ou aux secousses.

Figure 7 : Exemple de gyrolaser fabriqué par la société Thales (source Thales Aerospace)
Il existe également des gyromètres à fibres optiques. La vitesse des signaux n’est plus c, mais est légèrement inférieure à cause de la réfraction : cela n’a pas d’impact sur l’effet Sagnac, comme déjà indiqué.
Des recherches sont en cours pour de futurs gyromètres utilisant des ondes de matière : on mesure alors le déphasage entre les deux paquets d’ondes associés à des atomes ou des particules (selon les lois de la physique quantique).
Un cas unique de phénomène à interprétations multiples… et fausses
L’effet Sagnac a donné lieu depuis l’expérience initiale de 1913 à un nombre considérable de publications proposant des interprétations très diverses du même phénomène. De nombreux papiers même récents prétendent fournir à partir d’hypothèses indépendantes un résultat identique (au moins en première approximation) à celui obtenu dans un cadre relativiste. Que valent ces interprétations ?
L’une des sources de confusion réside dans la croyance que la relativité du temps n’intervient dans l’effet Sagnac que par le facteur
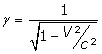
qui est négligeable en première approximation et que l’effet résiduel peut en conséquence s’obtenir par la physique classique. Autrement dit, l’on pense être autorisé à user d’un raisonnement post-newtonien, ce qui revient à traiter la prédiction relativiste comme
un simple correctif à un effet classique déjà existant. La pratique du raisonnement post-newtonien en relativité a une longue histoire
(23) mais expose à de sérieux risques d’erreur car il peut conduire à ignorer des effets purement relativistes
qui n’ont pas d’équivalent en physique classique, donc à ne pas comprendre des aspects essentiels de la relativité. L’effet Sagnac est une sorte de concentré de ces erreurs. Dans le cas des ondes de matière, il est parfois interprété comme l’effet d’une force de Coriolis appliquée à une particule de masse fictive
hν/c2, le déphasage constaté s’expliquant par la rencontre de deux ondes atomiques de vitesses différentes (par rapport au laboratoire) arrivant au même instant (contrairement au point de vue relativiste qui décrit deux ondes de même fréquence arrivant à des instants différents).
Il est intéressant de noter qu’un autre effet typiquement relativiste souffre d’erreurs de raisonnement analogues : l’
effet Einstein. Il s’agit du décalage des fréquences (tel que mesuré sur Terre) pour le spectre d’émission d’un atome distant placé dans un champ gravitationnel différent. Une interprétation courante dans les ouvrages de vulgarisation consiste à attribuer au photon une masse inertielle (donc gravitationnelle)
hν/c2 et d’en déduire que la fréquence du photon est modifiée car son énergie potentielle varierait avec la distance. Cette explication ne peut être correcte puisque nous savons que, d’après la relativité générale, c’est un effet de « contraction » du temps qui est à l’origine du phénomène,
les fréquences propres étant inchangées. Si l’explication non relativiste était correcte, nous devrions en fait observer un effet double
(24). L’origine relativiste a quant à elle été validée par des expériences comme celles de Hafele et Keating, déjà mentionnée.
Pour revenir à l’effet Sagnac, toutes les interprétations ne se valent pas car le déphasage observé est typiquement relativiste et ne doit donc pas être traité comme une approximation. Là encore, si les causes alléguées du phénomène n’ont pas de rapport avec la désynchronisation relativiste des horloges, l’effet devrait se cumuler avec celui prédit par la relativité, ce qui n’est pas le cas.
Toute interprétation non relativiste est en conséquence fausse
(25) et l’usage d’un tel raisonnement devrait être abandonné car il ne permet pas de comprendre correctement l’effet Sagnac dans toute sa généralité.
Au fil du temps, l’effet Sagnac a été un formidable révélateur des incompréhensions profondes dont la relativité pâtit encore aujourd’hui et son élucidation aura contribué largement à réaffirmer quelques vérités parfois oubliées : - L’effet Sagnac n’engendre aucun paradoxe (contradiction logique) en relativité restreinte. - L’effet Sagnac n’est en aucun cas une preuve d’anisotropie de la vitesse de la lumière qui entrerait en conflit avec la relativité restreinte. - La véritable originalité de l’effet tient dans ce qu’il est observé malgré l’isotropie parfaite en vitesse de signaux ou objets quelconques (par rapport au disque). - La relativité générale n’est pas utile pour expliquer l’effet Sagnac : il s’agit d’un effet purement cinématique (seul le mouvement entre en jeu) prédit par la relativité restreinte. - La relativité du temps (plus précisément la désynchronisation des horloges parfaites) est au cœur du phénomène. Toute explication de l’effet Sagnac ne passant pas par la cinématique de la relativité restreinte est
nécessairement erronée (26). Et on peut ajouter les éléments importants suivants : - La pluralité des temps propres est certainement le concept le plus important en relativité (restreinte et générale). - La relativité restreinte permet d’étudier n’importe quel type de mouvement, notamment les rotations. - La vitesse de la lumière est constante y compris dans les référentiels accélérés pourvu qu’elle soit mesurée à l’endroit où se trouve l’observateur.
@@@@@@@
Par une tendre ironie de l’histoire des sciences et un coup de théâtre final spectaculaire, la contribution la plus célèbre de Sagnac à la physique aura consisté à prouver le contraire de ce qui avait motivé son expérience initiale : il aura mis en lumière un phénomène purement relativiste qui s’explique entièrement dans le cadre de la relativité restreinte, le concept d’éther en tant que milieu de propagation de la lumière étant caduc.
Contresens est certainement le terme qui convient le mieux ici : contresens littéralement d’abord puisqu’il s’agit de faire voyager deux signaux en sens contraire ; contresens car au lieu de révéler une anisotropie de la vitesse de la lumière par rapport au disque tournant, le phénomène est observé identiquement pour des signaux ou objets quelconques et rigoureusement isotropes (en vitesse) ; contresens enfin car l’effet Sagnac, loin de signifier un retour en grâce des conceptions classiques, est au bout du compte une signature de la relativité du temps, le délai dans la réception des signaux correspondant exactement à la désynchronisation einsteinienne de deux horloges parfaites parcourant le disque en sens contraire.
À son insu, Georges Sagnac a donc réalisé en 1913 une superbe expérience à contresens, d’une richesse conceptuelle insoupçonnée et qui aujourd’hui est à classer parmi les plus représentatives de la relativité restreinte.
Octobre 2013

(1) L’aberration annuelle des étoiles est une magnifique preuve triple : 1°) Elle confirme le caractère fini de la vitesse de la lumière établi en 1676 par Römer (cf. texte et analyse BibNum par Francis Beaubois) tout en fournissant une première estimation fiable de cette vitesse (Bradley fournit une valeur pour le rapport v/c) ; 2°) Elle apporte la première preuve solide du mouvement de la Terre autour du Soleil (qui avait manqué à Galilée), validant ainsi l’héliocentrisme ; 3°) Elle montre que la vitesse de la lumière est indépendante du mouvement de la source mais aussi de celui de l’observateur, constatation qui s’avèrera cruciale pour la relativité restreinte.
(2) L’aberration traduit le fait suivant : la direction apparente d'une source lumineuse dépend de la vitesse de l’observateur, de même que la pluie qui, lorsque nous courons, semble nous arriver depuis une direction située vers l'avant de notre parapluie et non à sa verticale.
(3) Rappelons que, en physique classique, la loi d’additivité des vitesses nous indique que la vitesse de l’objet mesurée doit être diminuée de celle de l’observateur si ce dernier s’éloigne de la source ou augmentée dans le cas contraire.
(4) Citation extraite de son mémoire de 1810 (publié en 1853) dont on trouvera une analyse par James Lequeux, « Les expériences d’Arago sur la vitesse de la lumière (1810) », BibNum, septembre 2008.
(5) On trouvera une analyse de la thèse de Foucault décrivant son expérience de 1850 (qualifiée de cruciale par Arago) par Jean-Jacques Samueli « Foucault et la mesure de la vitesse de la lumière dans l’eau et dans l’air », BibNum, septembre 2009.
(6) Citation extraite de la lettre de Henri Poincaré à Gaston Darboux, Bibliothèque de l’Institut de France, Darboux Correspondance, MS 2720 (8-9).
(7) Lorentz, Théorie des électrons (deuxième édition de 1915, note 72).
(8) Le temps local chez Poincaré est le temps indiqué par l’une des horloges nécessairement mal réglées attachées à un référentiel inertiel en mouvement par rapport à l’éther. Ce temps est erroné par rapport au temps vrai car il est impossible selon Poincaré de synchroniser correctement les horloges entre elles, à cause de l’anisotropie de la vitesse de la lumière. Ce temps local permet d’expliquer l’échec des expériences optiques en V/c.
(9) Pour une analyse plus détaillée de ce fait historique insuffisamment connu, voir l’article de W. Rindler, « Einstein’s Priority in Recognising Time Dilation Physically », American Journal of Physics 38, 9 (1970) qui n’a rien perdu de son actualité.
(10) Cet effet est également appelé « paradoxe des jumeaux » sans qu’il y ait de contradiction logique : si l’on remplace les horloges par des jumeaux, les jumeaux se retrouvent avec des âges différents.
(11) Technische Rundschau, Berne, n° 20 du 6 mai 1955.
(12) Trajectoire pour aller d’un point A à un point B dans notre univers à 4 dimensions.
(13) Pour une justification plus détaillée de l’importance cruciale du temps propre en relativité, voir le chapitre 2 du livre de Jean Eisenstaedt, Einstein et la relativité générale, CNRS Editions (réed. 2013).
(14) « Die Grundgleichungen für die elektromagnetischen Vorgänge in bewegten Körpern », Königliche Gesellschaft der Wissenschaften zu Göttingen, mathematisch–physikalische Klasse, Nachrichten, 1908 : 53–111.
(15) On trouvera une analyse de l’article de Max von Laue de 1907 par Jean-Jacques Samueli et Alexandre Moatti, « L’entraînement partiel de l’éther et la relativité restreinte », BibNum, novembre 2010.
(16) L’anisotropie d’une grandeur physique est sa dépendance vis-à-vis de la direction.
(17) Voir l’article de G. Rizzi et A. Tartaglia, 1998, « Speed of Light on Rotating Platforms », Foundations of Physics 28, 1663 pour une démonstration détaillée. Dans le référentiel tournant, les longueurs parcourues ne correspondent plus à une courbe fermée (circonférence) mais à des hélices, lorsqu’on raisonne dans l’espace-temps de Minkowski.
(18) Voir l’article de G. Rizzi et A. Tartaglia, op. cit., pour une démystification du pseudo-paradoxe de Selleri.
(19) Pour une démonstration basée sur la formule de composition relativiste des vitesses, voir l’annexe A du livre de Pierre Spagnou, De la relativité au GPS, Ellipses (2012). Pour une démonstration par comparaison directe des temps propres, voir le chapitre 13 du livre d’Eric Gourgoulhon, Relativité restreinte, EDP sciences (2010).
(20) La note de Prunier intitulée « Sur une expérience de Sagnac qui serait faite avec des flux d’électrons » est présentée par Paul Langevin à l’Académie des Sciences en 1935. Langevin dans une note additionnelle confirme la différence entre les prédictions classique et relativiste pour une telle expérience.
(21) L’effet Sagnac est inexistant si l’on parcourt un méridien terrestre puisque que la vitesse dans le sens de la rotation ou en sens inverse est nulle. Si l’on parcourt une courbe en forme de huit, on annule l’effet puisque les deux termes correspondant à des trajectoires opposées par rapport au sens de la rotation terrestre se compensent.
(22) Une centrale inertielle est un système capable d'intégrer les mouvements d'un appareil (accélération et vitesse angulaire) afin d’estimer son orientation, sa vitesse et sa position à partir d’un point de référence connu (fourni par exemple par le GPS). Avec trois accéléromètres et trois gyromètres disposés sur trois axes, il est possible de déterminer la position et l’orientation dans l’espace de l’appareil de façon précise.
(23) Voir le livre de Jean Eisenstadt (op. cit.) pour une réflexion similaire sur les dangers du raisonnement post-newtonien en relativité générale (pages 361 – 362).
(24) Pour une analyse détaillée de cette erreur d’interprétation de l’effet Einstein, voir l’article de Okun, Selivanov et Telegdi, « Gravitation, photons, clocks », Physics 42 (10) 1045 – 1050 (1999).
(25) Pour une synthèse très complète des interprétations diverses de l’effet Sagnac (la plupart fausses), voir l’article de référence de Malykin « The Sagnac effect : correct and incorrect explanations », Physics 43 (12) 1229 – 1252 (2000). Il est intéressant de noter que Malykin semble sous-estimer le rôle crucial de la désynchronisation des horloges parfaites dans l’origine du phénomène, bien qu’il considère correctement l’effet Sagnac comme un effet purement cinématique de la relativité restreinte.
(26) La relativité générale est bien sûr utilisable (la relativité restreinte étant un cas limite) mais n’apporte rien de plus pour l’effet Sagnac, la gravitation n’ayant rien à voir avec le phénomène.


![]()





![]()
![]()
![]()
![]()
![]()
![]()
![]()
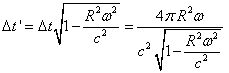






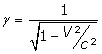 qui est négligeable en première approximation et que l’effet résiduel peut en conséquence s’obtenir par la physique classique. Autrement dit, l’on pense être autorisé à user d’un raisonnement post-newtonien, ce qui revient à traiter la prédiction relativiste comme un simple correctif à un effet classique déjà existant. La pratique du raisonnement post-newtonien en relativité a une longue histoire (23) mais expose à de sérieux risques d’erreur car il peut conduire à ignorer des effets purement relativistes qui n’ont pas d’équivalent en physique classique, donc à ne pas comprendre des aspects essentiels de la relativité. L’effet Sagnac est une sorte de concentré de ces erreurs. Dans le cas des ondes de matière, il est parfois interprété comme l’effet d’une force de Coriolis appliquée à une particule de masse fictive hν/c2, le déphasage constaté s’expliquant par la rencontre de deux ondes atomiques de vitesses différentes (par rapport au laboratoire) arrivant au même instant (contrairement au point de vue relativiste qui décrit deux ondes de même fréquence arrivant à des instants différents).
qui est négligeable en première approximation et que l’effet résiduel peut en conséquence s’obtenir par la physique classique. Autrement dit, l’on pense être autorisé à user d’un raisonnement post-newtonien, ce qui revient à traiter la prédiction relativiste comme un simple correctif à un effet classique déjà existant. La pratique du raisonnement post-newtonien en relativité a une longue histoire (23) mais expose à de sérieux risques d’erreur car il peut conduire à ignorer des effets purement relativistes qui n’ont pas d’équivalent en physique classique, donc à ne pas comprendre des aspects essentiels de la relativité. L’effet Sagnac est une sorte de concentré de ces erreurs. Dans le cas des ondes de matière, il est parfois interprété comme l’effet d’une force de Coriolis appliquée à une particule de masse fictive hν/c2, le déphasage constaté s’expliquant par la rencontre de deux ondes atomiques de vitesses différentes (par rapport au laboratoire) arrivant au même instant (contrairement au point de vue relativiste qui décrit deux ondes de même fréquence arrivant à des instants différents).



 Pour une explication détaillée de l’effet Sagnac dans le cadre de la relativité restreinte et la résolution du « pseudo-paradoxe » du physicien Selleri : G. Rizzi et A. Tartzaglia, “Speed of Light on Rotating Platforms”, Foundations of Physics 28, 1663 (1998) (lien PDF Arxiv)
Pour une explication détaillée de l’effet Sagnac dans le cadre de la relativité restreinte et la résolution du « pseudo-paradoxe » du physicien Selleri : G. Rizzi et A. Tartzaglia, “Speed of Light on Rotating Platforms”, Foundations of Physics 28, 1663 (1998) (lien PDF Arxiv) Pour une synthèse très complète des interprétations diverses (et souvent fausses) de l’effet Sagnac : Malykin, “The Sagnac effect: correct and incorrect explanations”, Physics 43 (12) 1229 – 1252 (2000) (présentation en ligne)
Pour une synthèse très complète des interprétations diverses (et souvent fausses) de l’effet Sagnac : Malykin, “The Sagnac effect: correct and incorrect explanations”, Physics 43 (12) 1229 – 1252 (2000) (présentation en ligne) Sur un autre phénomène purement relativiste, l’effet Einstein, sujet à des erreurs d’interprétation similaires à celles de l’effet Sagnac: Okun, Selivanov et Telegdi, “Gravitation, photons, clocks”, Physics 42 (10) 1045 – 1050 (1999) (disponible en ligne)
Sur un autre phénomène purement relativiste, l’effet Einstein, sujet à des erreurs d’interprétation similaires à celles de l’effet Sagnac: Okun, Selivanov et Telegdi, “Gravitation, photons, clocks”, Physics 42 (10) 1045 – 1050 (1999) (disponible en ligne) Sur Einstein en tant que « découvreur » unique de la relativité du temps : W. Rindler, “Einstein's Priority in Recognizing Time Dilation Physically”, American Journal of Physics 38 (1970) (PDF disponible en ligne).
Sur Einstein en tant que « découvreur » unique de la relativité du temps : W. Rindler, “Einstein's Priority in Recognizing Time Dilation Physically”, American Journal of Physics 38 (1970) (PDF disponible en ligne).




