L’héritage d’Henri Poincaré en physique

Je survolerai ici, de façon subjective et nécessairement superficielle, l’œuvre de Poincaré en physique et ses retombées au cours du siècle écoulé. Je mettrai en évidence quatre grandes idées toujours d’actualité, puis essayerai d’analyser ses conceptions de la physique.

Mais d’abord permettez-moi de vous dévoiler (partiellement) qui est « mon Poincaré » – plutôt ce qui m’a rapproché de lui… Mon premier contact fut la lecture de Science et méthode (1908) en Terminale. Puis vint un choix important de scolarité et, comme Poincaré, je choisis Polytechnique plutôt que l’ENS. Une grande partie de nos cours avait lieu… dans le prestigieux amphithéâtre Poincaré. Toujours à l’X, en 1954, l’exposition consacrée au centenaire de la naissance du savant me permit de prendre connaissance d’un certain nombre de documents et de photographies évocatrices[1] ; elle fut complétée par d’autres objets déposés par des élèves farceurs, comme à l’accoutumée[2]. Sortant de Polytechnique en 1954, je reçus la médaille Poincaré[3] assortie de ses travaux scientifiques en 11 gros volumes in-quarto dont la publication venait de s’achever – et qui occupent encore un rayon de ma bibliothèque[4].

Figure 1 : (ci-dessus) Appel en Une du Monde du 18 mai 1954, référant à la double page relatant le centenaire de la naissance de Poincaré, en double page (ci-dessous). La célébration du centenaire de la mort de Poincaré, en 2012, est loin d’avoir donné lieu à une couverture médiatique comparable.

@@@@@@@

Poincaré fait partie des savants, assez rares, qui ont beaucoup apporté à la fois à la physique et aux mathématiques. Les physiciens sont devenus de gros utilisateurs de mathématiques, ils en sont moins souvent des créateurs. Ces créateurs-là sont apparus par périodes :  en 1650 Descartes, Roberval, Pascal ; en 1800 Laplace, Ampère, Gauss, Poisson. Poincaré ouvre quant à lui une nouvelle période très riche en physique mathématique.

@@@@@@@

Poincaré lui-même analysé son œuvre scientifique en 1901[5] : il la classe en 7 parties, 3 de mathématiques, 2 de physique, une de philosophie des sciences, et une de cours et vulgarisation. Les 5 premières parties occupent chacune deux volumes de 600 à 700 pages, presque tout en français (avec cependant un peu d’allemand et d’anglais).

Parmi ses productions de physique qui nous intéressent ici, il distingue deux grandes parties[6], d’une part la mécanique analytique, la mécanique céleste et l’astrophysique, d’autre part la physique mathématique, qui couvre en fait une grande variété de travaux théoriques, y compris appliqués.  

Pour définir la physique mathématique, il insiste sur le fait que les mathématiques ne sont pas seulement un outil, mais qu’elles sont devenues le seul langage précis des physiciens ; la physique mathématique est ainsi une activité d’unification et de synthèse, justifiée par l’accord avec l’expérience. Elle constitue aussi une source d’inspiration pour les mathématiciens, physique et mathématiques se développant en parallèle. Ainsi, Poincaré résout-il par des méthodes physiques le problème de Dirichlet, et l’applique en même temps à l’électromagnétisme (champ intérieur à une cavité), l’acoustique (membranes vibrantes) ou la capillarité (surfaces de bulles de savon).

La théorie du chaos

Mais l’apport sans doute le plus important de Poincaré à la physique est la création d’une nouvelle discipline : par l’étude des systèmes dynamiques, il est l’initiateur de ce que nous appelons aujourd’hui le chaos déterministe, discipline toujours très active. On considère un problème dont les équations sont parfaitement connues, par exemple un problème de mécanique céleste, régi par les équations de Newton. La donnée exacte des conditions initiales permet en principe de prévoir toute la trajectoire – toute la suite du processus. C’était la conception de Laplace lorsqu’il avait étudié la mécanique céleste. Mais Poincaré montre comment la moindre déviation dans les conditions initiales, la moindre perturbation, la moindre erreur d’arrondi dans les calculs peuvent s’amplifier et empêcher toute prévision à long terme. Mathématiquement le processus est parfaitement déterministe ; physiquement, sur une durée suffisamment longue, il est « chaotique », imprévisible.

Ce phénomène se vérifie même pour des systèmes très simples. Poincaré l’a étudié sur le problème des 3 corps (Soleil, Jupiter, Terre). Actuellement on ne sait même pas si le système solaire est stable : un écart inférieur à 1 m, incontrôlable en pratique, modifie radicalement les trajectoires des planètes au bout de 10 millions d’années. L’idée que des équations exactes puissent donner naissance à une imprévisibilité était révolutionnaire à l’époque de Poincaré : ces travaux lui valurent le prix du roi Oscar II de Suède en 1889 avant même leur achèvement.

Après lui, ce genre de problème sera étudié par quelques mathématiciens, notamment russes, mais Poincaré était si novateur que les vrais développements n’ont commencé qu’après 1960. Les applications de la théorie du chaos sont aujourd’hui innombrables : physique, mécanique, géologie, finances, informatique, biologie, écologie, électrotechnique (réseaux). Elle est même passée dans le grand public, avec le fameux « effet papillon » tant ressassé (le battement d’ailes d’un papillon à Singapour peut provoquer un cyclone au Texas), et avec des bibelots décoratifs mobiles.

En dehors de la théorie du chaos déterministe, les techniques d’étude par Poincaré de ce problème sont devenues courantes dans d’autres branches de la physique. Il commence par identifier les trajectoires fermées périodiques ; elles sont exceptionnelles mais fournissent un squelette autour duquel on analyse les autres solutions. L’idée est couramment utilisée aujourd’hui : déterminer une fonction à partir de ses points singuliers, caractériser un solide par ses défauts, caractériser la lumière réfléchie par l’eau agitée d’une piscine en déterminant d’abord les points brillants, caractériser une image par ses contours.

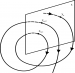
Poincaré étudie ensuite les trajectoires voisines d’une courbe fermée grâce à une « section de Poincaré », mesurant l’impact des trajectoires sur un plan. Il remplace ainsi un problème continu par un problème discret. La divergence des trajectoires devient un outil pour comprendre leur comportement.

Figure 2 : Section de Poincaré d’une trajectoire. Les sections de Poincaré sont des sous-espaces qui sont traversés par le système de manière récurrente et transverse (image université de Nice).

Ainsi, Poincaré a eu l’idée de chercher une description qualitative du phénomène : méthode quotidienne du théoricien lorsqu’il utilise des modèles physiques. Dans ce cadre, les trajectoires apparaissent comme des figures complexes dont la forme se reproduit par dilatation, préfiguration des notions de fractales, ou d’exposant critique dans les transitions de phase[7].

On trouve une autre idée nouvelle, celle de bifurcation ou d’invariance spontanément brisée, dans les travaux d’astronomie de Poincaré portant sur la forme des masses fluides en rotation : au-delà d’une certaine vitesse, il peut apparaître une infinité de formes stables différentes au lieu d’un ellipsoïde de révolution.

Le rôle des probabilités en physique

Une seconde idée-force acquise progressivement par Poincaré est le rôle central des probabilités en physique. Afin de pallier l’imprévisibilité dans un système déterministe mais chaotique, on considère un faisceau de trajectoires issues de points voisins, et on fait des prédictions probabilistes en estimant les marges d’erreur.

L’idée était déjà présente chez Laplace. On cite toujours sa fameuse phrase :

Nous devons donc envisager l’état présent de l’univers, comme l’effet de son état antérieur, et comme la cause de celui qui va suivre. Une intelligence qui, pour un instant donné, connaîtrait toutes les forces dont la nature est animée, et la situation respective des êtres qui la composent, si d’ailleurs elle était assez vaste pour soumettre ces données à l’analyse, embrasserait dans la même formule les mouvements des plus grands corps de l’univers et ceux du plus léger atome : rien ne serait incertain pour elle, et l’avenir comme le passé, serait présent à ses yeux[8].

Mais on oublie toujours que Laplace a mis ce texte au début de son Essai philosophique sur les probabilités, précisément afin d’introduire l’idée qu’une telle « intelligence » n’existe pas et que les probabilités sont donc indispensables à nos prévisions.

  Aujourd’hui, les probabilités sont devenues l’une des bases de toute la physique.  Dans deux grandes théories du xx^e siècle, on ne manipule que des probabilités : en mécanique statistique, où – comme son nom l’indique –  il est impossible de décrire des systèmes ayant de trop nombreux composants élémentaires ; en mécanique quantique, où il est impossible de décrire la nature avec les seuls concepts issus de la physique macroscopique, de sorte que les probabilités sont irréductiblement liées au formalisme et aux concepts quantiques. D’autre part, les probabilités sont aussi un outil majeur chez les expérimentateurs, par exemple pour l’analyse des gigantesques expériences du CERN en physique des particules. Il est devenu banal, ce que Poincaré soulignait déjà, que seule la répétition d’expériences peut fournir des résultats significatifs, mais comportant toujours certaines incertitudes.

Au début de sa carrière, Poincaré a émis des critiques sur la théorie cinétique des gaz, premier avatar de la mécanique statistique. Cependant, ses réticences proviennent en partie de l’état encore peu rigoureux de la théorie des probabilités :

[…] nous devons chercher à en approfondir les principes. Sous ce rapport je n’ai pu donner que des résultats bien incomplets[9] […]  

Mais bientôt, il donne une place prépondérante aux probabilités en physique, discutant longuement leurs fondements, leurs multiples aspects et leur signification. Il conçoit les vérités scientifiques comme des approximations probabilistes quoique perfectibles. Prévoir nécessite de généraliser ce qui a été observé, mais une telle extrapolation est en partie hasardeuse, donc nos affirmations scientifiques n’ont qu’une certaine probabilité d’être « vraies » :

Les faits prévus ne peuvent être que probables, mais la probabilité est souvent assez grande pour que pratiquement nous puissions nous en contenter[10].

Ainsi, la physique ne décrit-elle pas des objets en soi, mais fournit une image du monde dans notre esprit :

Les rapports véritables entre objets réels sont la seule réalité que nous puissions atteindre, et à seule condition, c’est qu’il y ait les mêmes rapports entre ces objets qu’entre les images que nous sommes forcés de mettre à leur place. Si ces rapports nous sont connus, qu’importe si nous jugeons commode de remplacer une image par une autre[11].

Ceci préfigure notre vision moderne de la mécanique quantique, la plus précise de nos théories, qui est pourtant probabiliste.

Figure 3 : H. Poincaré, La Science et l’Hypothèse, collection Bibliothèque de philosophie scientifique, Flammarion, 1902.

En 1912, Poincaré a même certaines prémonitions de la mécanique quantique. Il a découvert l’existence des fonctions propres et valeurs propres des opérateurs, un peu avant Ivar Fredholm (1866-1927). Il suggère alors l’existence d’objets élémentaires qui se comporteraient en résonateurs, avec des modes propres discrets, ce qui conduirait à la quantification des vibrations. (Cette idée, déjà connue pour les photons, préfigure la quantification, en 1925, des états électroniques et même la théorie purement phénoménologique de l’atome de Bohr 1913.) Il envisage aussi que les lois physiques pourraient changer :

Le clair génie de Newton avait bien vu (ou cru voir, nous commençons à nous le demander) que l'état d'un système mobile, ou plus généralement celui de l'univers, ne pouvait dépendre que de son état immédiatement antérieur, que toutes les variations dans la nature doivent se faire d'une manière continue […] Eh bien, c’est cette idée fondamentale qui est aujourd’hui en question : on se demande s’il ne faut pas introduire dans les lois naturelles des discontinuités, non pas apparentes, mais essentielles […][12]

Il se peut qu’un jour les lois statistiques remplacent les lois déterministes, mais on peut continuer à conserver celles-ci lorsque la probabilité avoisine l’unité.

Poincaré, la relativité et les groupes de transformations

Un troisième apport majeur de Poincaré concerne la relativité : Lorentz, voulant rendre compte de l’invariance des équations de Maxwell de l’électromagnétisme par changement de repère, avait commencé à voir qu’il fallait modifier l’espace-temps. Il l’avait fait au 1^er ordre en v/c (v, vitesse du repère). Poincaré lui suggéra de pousser au 2^e ordre, puis à tous les ordres. En 1905, il reprend lui-même la question du point de vue de la dynamique de l’électron[13]. Quelques mois avant l’article fondateur d’Einstein, il construit les équations du mouvement et établit leurs transformations par changement de référentiel galiléen. Plusieurs années auparavant, il avait montré que la vitesse de la lumière était invariante dans un tel changement[14]. Il généralise en même temps le « principe du mouvement relatif » qu’il avait inclus parmi les principes fondamentaux de la mécanique[15], en soulignant « l’impossibilité de démontrer le mouvement absolu » et en énonçant le « principe de relativité » :

Aucune expérience ne pourra jamais décider si un corps est en repos ou en mouvement absolu, soit par rapport à l’espace, soit même par rapport à l’éther[16].

Dans la brève mais riche note de 1905, Poincaré a déjà aussi l’intuition des ondes gravitationnelles : en considérant la force de gravitation exercée par un corps sur un autre, il suggère qu’elle est émise sous forme d’une onde gravifique (il souligne) et qu’elle se propage à la vitesse de la lumière.

Cette même note comporte également un apport personnel de Poincaré qui va imprégner toute la physique contemporaine, l’accent mis sur la nécessaire structure de groupe des transformations de la physique, comme les changements de repère d’espace et de temps (faire deux transformations successives équivaut à faire une seule transformation). Il clarifie ainsi les transformations de Lorentz, établit qu’on peut en faire un groupe – qu’il baptise groupe de Lorentz –, et en déduit la loi de composition relativiste des vitesses. Dans l’article de 1906, il défend cette idée avec force, en soulignant même la phrase :

Les transformations qui n’altèrent pas les équations du mouvement doivent              former un groupe.

Il généralise le groupe de Lorentz en incluant les translations et rotations, et introduit ainsi ce que nous appelons le « groupe de Poincaré », outil essentiel de la théorie de la relativité.

         L’importance des idées de groupe, de symétrie et d’invariance mises en avant par Poincaré n’a cessé de s’affirmer depuis, dans les directions les plus diverses. La théorie des groupes, qui avait déjà été introduite en cristallographie, dès la fin du xix^e siècle, a envahi la physique de la matière condensée, ordonnée ou non : par exemple en métallurgie, dans l’étude des matériaux nouveaux ou des transitions de phase. Le principe de Curie (« Lorsque certaines causes produisent certains effets, les éléments de symétrie des causes doivent se retrouver dans les effets produits », 1894) a dû être corrigé pour tenir compte de la structure de groupe des invariances. À l’échelle microscopique, on ne peut se passer de la théorie des groupes pour décrire les structures des atomes ou des molécules, ainsi que des noyaux. À plus petite échelle encore, les fondements mêmes de la physique des particules reposent sur des groupes de transformations entre objets de nature différente ainsi que sur le groupe de Poincaré.

@@@@@@@

Poincaré avait aussi souligné l’importance des lois de conservation. Cela lui a permis d’attribuer une quantité de mouvement à la lumière. Il est remarquable qu’un lien existe entre l’existence d’un groupe d’invariance et celle d’une loi de conservation. Il a été établi par Emmy Noether (1882-1935) en 1915. Celle-ci a par exemple montré que la conservation de la quantité de mouvement est conséquence de l’invariance par translation ; que la conservation de l’énergie est conséquence de l’invariance par changement d’origine du temps.

Figure 4 : La mathématicienne allemande Emmy Noether (1882-1935).

La sphère de Poincaré

Un quatrième héritage est la sphère de Poincaré, nouvelle représentation de la polarisation d’une onde lumineuse[17]. La représentation directe d’une polarisation linéaire est un vecteur perpendiculaire à la direction de propagation de l’onde. La représentation de Poincaré d’une polarisation arbitraire, totale ou partielle, d’un faisceau monochromatique se fait à l’aide de 3 paramètres, les coordonnées d’un point intérieur à une sphère abstraite. Mathématiquement, cette représentation repose sur l’équivalence entre un groupe (dit SU2) de matrices à deux dimensions et le groupe des rotations dans l’espace à 3 dimensions dans lequel la sphère est plongée.

Figures 5 et 5bis : (ci-dessus) Représentation par la sphère de Poincaré de la polarisation d’une onde lumineuse. Un point sur la sphère de rayon unité représente une polarisation totale (linéaire, circulaire ou elliptique), un point intérieur une polarisation partielle (image WikiCommons) ; (ci-dessous) Sphère de Bloch ou de Poincaré pour la représentation de l’état quantique d’un spin 1/2 (image WikiCommons, auteur J.-C. Benoist).

La sphère de Poincaré est aujourd’hui d’usage courant (souvent sous le nom de sphère de Bloch, figure 5bis) pour décrire le moment magnétique d’un électron (spin ½), ainsi que pour le calcul quantique : l’état d'un système à deux niveaux, tel qu'un spin ½, appelé qubit en théorie de l’information quantique, peut être représenté par un point intérieur à cette sphère.

@@@@@@@

Plus généralement, une idée-force de Poincaré, devenue commune, est l’existence de plusieurs formulations possibles de la réalité, qui sont mathématiquement équivalentes mais s’interprètent de façons différentes :

Les mathématiques fournissent la seule langue que le physicien puisse parler […] Il suffit de changer de langage pour apercevoir des généralisations qu’on n’avait pas d’abord soupçonnées[18].

Ainsi, en mécanique, les équations du mouvement de Newton équivalent au principe de moindre action. La mécanique quantique peut se formuler en termes d’ondes, de matrices, d’intégrales de chemin, de C*-algèbres : il est fructueux de passer de l’un à l’autre de ces concepts, suivant les circonstances.

Varia

Les autres travaux de Poincaré en physique sont nombreux et portent sur toutes sortes de sujets ; à l’inverse des précédents, les progrès de la physique leur ont ôté leur actualité. Je relèverai seulement qu’il n’a pas négligé – loin s’en faut – les applications de la physique :

• Au Bureau des Longitudes, pour la création du temps universel, il a considéré la synchronisation du temps sur Terre par utilisation de signaux lumineux (ceci fut à l’origine de son intérêt pour les travaux de Lorentz). Il fit aussi au Bureau divers apports sur la géodésie, la gravimétrie, les marées (décimalisation du temps et des angles…)
• La propagation des ondes électro-magnétiques, aux débuts de la Télégraphie sans fil[19] : étude de l’atténuation des signaux, de la propagation à travers l’atmosphère courbe.
• L’électrotechnique, avec la théorie des récepteurs téléphoniques, ou les commutateurs électromécaniques en télécommunications.

Figure 6 : Schéma d’un émetteur à arc, présenté par Poincaré dans son ouvrage La Théorie de Maxwell et les oscillations hertziennes. La Télégraphie sans fil (éd. Scientia, 1907) (schéma p.92, légendé « Transmetteur Marconi »).

@@@@@@@

Poincaré a beaucoup enseigné. Ses cours de physique ont porté sur tous les domaines (hydrodynamique, optique, électricité, capillarité, turbulence, thermodynamique, ondes, propagation chaleur), et manifestent une culture immense. Il a même inspiré Becquerel, en suggérant à celui-ci qu’il pouvait y avoir un lien entre la fluorescence (domaine d’excellence de la famille Becquerel) et les rayons X ; connaissant bien l’allemand, c’est lui qui fit connaître immédiatement à l’Académie des Sciences, au début de 1896, les travaux de Röntgen, dont il souligna l’importance[20].

@@@@@@@

Pourtant, bien qu’il ait ouvert de nouvelles voies, il a eu peu d’influence directe immédiate sur la physique française. Je ne lui ai trouvé aucun élève physicien connu. Il n’a d’ailleurs eu guère d’élèves non plus en mathématiques, supervisant quelques thèses, comme celles d’Émile Borel (1871-1956), ou de Louis Bachelier (1870-1946).

Pourquoi ?

• Peut-être était-il trop novateur ? Le chaos déterministe s’est développé 70 ans après ses travaux ;
• Son caractère, discret, l’a amené à parfois s’effacer : ce sont dans ses articles qu’ont été introduites les fonctions dites « Fuchsiennes » ou la transformation de « Lorentz ». On trouve souvent dans ses œuvres des suggestions qu’il ne mène pas à leur terme : dans son étude de l’équilibre d’une masse fluide en rotation, il laisse à d’autres le fait d’y voir l’origine de la Lune… ;
• Ou bien son peu d’impact immédiat serait-il lié à ses conceptions de la physique ?

La philosophie des sciences de Poincaré

À l’époque, l’idéologie dominante en France était empiriste, ou positiviste, basée sur les seuls faits. Mach ou Duhem attribuent à la théorie le seul rôle de classer les phénomènes, pas de les expliquer. On va même jusqu’à dévaloriser la physique théorique, « science allemande ». L’immense (45 vol.) et célèbre traité de physique d’Henri Bouasse (1866-1953), publié à partir de 1912, n’est qu’un gigantesque catalogue de phénomènes[21].

Ceci explique pourquoi la physique expérimentale domine alors en France (optique, radioactivité, Jean Perrin), et pourquoi les physiciens théoriciens sont si rares en France face à l’Allemagne (on peut les compter sur les doigts d’une main : Pierre Curie, Langevin, Brillouin, et plus tard Louis de Broglie) – seuls Langevin et Poincaré se sont intéressés à la relativité. C’est peut-être pourquoi Poincaré n’a pas fait école : assez isolé en France, il défend la théorie et son langage mathématique, en tant que source d’unification, et s’oppose au nominalisme :

Le savant doit ordonner ; on fait la science avec des faits comme une maison avec des pierres ; mais une accumulation de faits n’est pas plus une science qu’un tas de pierres n’est une maison[22].

Sa position est d’ailleurs comme souvent nuancée. Il s’oppose ainsi au scientisme :

Mais alors il n’y a plus des problèmes résolus et d’autres qui ne le sont pas ; il y a seulement des problèmes plus ou moins résolus, selon qu’ils le sont par une série de convergence plus ou moins rapide, ou régie par une loi plus ou moins harmonieuse[23].

La science est certes probabiliste, mais perfectible. Le progrès scientifique existe, et les théories sont justifiées par la réussite de l’action. Cette idée de progrès scientifique, souvent poussée à l’extrême à l’époque, reste aujourd’hui d’actualité face à une désaffection du public envers la science et à certains sociologues des sciences qui considèrent les affirmations scientifiques comme une seule question de pouvoir…

Nous avons rappelé le rôle majeur que Poincaré accorde aux mathématiques en tant que seul langage de la physique. Il souligne inversement, en particulier dans La Valeur de la Science, que la physique est une source majeure d’inspiration pour les mathématiciens. Cette symbiose, conduisant à des progrès parallèles, pourrait expliquer la « déraisonnable efficacité des mathématiques » en physique soulignée par Wigner.

Figure 7 : H. Poincaré, La Valeur de la Science, collection Bibliothèque de philosophie scientifique, Flammarion, 1905.

Timidité de Poincaré en certains sujets

Cependant, l’une des idées, pourtant fructueuse, de Poincaré l’a parfois inhibé. Nous avons rappelé ci-dessus l’importance qu’il accorde à l’existence d’explications théoriques mathématiquement équivalentes, mais fournissant des représentations humaines différentes de la réalité. Il est indifférent de choisir l’une ou l’autre de ces interprétations d’apparences différentes, pourvu qu’elle rende compte de l’expérience, et ce choix n’est affaire que de « commodité ». Ce mot de « commode » se retrouve souvent sous sa plume, par exemple lorsqu’il écrit :

[…] ces deux propositions « la Terre tourne » et « il est plus commode de supposer que la Terre tourne » ont un seul et même sens ; il n’y a rien de plus dans l’une que dans l’autre[24].

Il préconise aussi, dans La Valeur de la Science, de choisir les explications selon le « principe de moindre effort ».

Cette position l’a empêché d’éliminer, au contraire d’Einstein, l’éther et le temps absolu dans ses premiers travaux de 1905 sur la relativité. Il écrivait peu auparavant :

Peu nous importe que l’éther existe réellement, c’est l’affaire des métaphysiciens ; l’essentiel pour nous c’est que tout se passe comme s’il existait et que cette hypothèse est commode pour l’explication des phénomènes. Après tout, avons-nous d’autre raison de croire à l’existence des objets matériels ? Ce n’est là aussi qu’une hypothèse commode ; seulement elle ne cessera jamais de l’être, tandis qu’un jour viendra sans doute où l’éther sera rejeté comme inutile[25].

Ici, commode ne s’identifie pas, comme ailleurs chez Poincaré, à simple ou élégant, mais à traditionnel : Il lui est plus facile de penser en conservant, à côté du « temps apparent », un « temps réel », même inaccessible. Il est vrai que les principes de la physique étaient alors en crise (même celui de la conservation de l’énergie), de sorte qu’il était difficile de changer radicalement de mode de pensée. Néanmoins, quelques années plus tard, Poincaré se rallie à l’attitude d’Einstein :

         Quiconque parle de l’espace absolu emploie un mot vide de sens[26].

@@@@@@@

De même, Poincaré réfléchit (bien avant la relativité générale en 1915) sur les géométries euclidienne et non-euclidiennes :

Une géométrie ne peut pas être plus vraie qu’une autre ; elle peut seulement être plus commode. Or la géométrie euclidienne est et restera la plus commode[27] […]

Il écrit que le choix entre ces géométries n’est qu’affaire de « conventions » :

Une expérience, quelle qu’elle soit, comporte une interprétation dans l’hypothèse euclidienne, mais elle en comporte une également dans l’hypothèse non euclidienne[28]. 

Il imagine alors l’éventualité d’une découverte, pour des étoiles lointaines, de parallaxes qui signaleraient une déviation des rayons lumineux (anticipation des déviations aujourd’hui observées et expliquées par la relativité générale) :

Si la géométrie de Riemann est vraie, la parallaxe d’une étoile très éloignée sera négative. […] Si par impossible, on venait à découvrir des parallaxes négatives […], on aurait le choix entre deux conclusions : nous pourrions renoncer à la géométrie euclidienne ou bien modifier les lois de l’optique. […] Inutile d’ajouter que tout le monde regarderait cette seconde solution comme plus avantageuse, […] en d’autres termes la plus commode[29].

Ainsi, Poincaré aurait préféré, plutôt que renoncer à la géométrie traditionnelle d’Euclide, admettre que la lumière ne se propage pas en ligne droite dans l’espace euclidien. À l’inverse, Einstein aura en 1915 la témérité de modifier la géométrie de l’espace-temps, afin d’expliquer le comportement théorique des forces de gravitation par changement de repère – sans autre preuve expérimentale.

@@@@@@@

  Poincaré a eu aussi une position conservatrice sur la mécanique statistique naissante. Si les molécules d’un gaz enfermé dans un récipient sont initialement confinées dans une région intérieure à celui-ci, elles se répandent partout et ne se rassemblent jamais à nouveau dans la région initiale. Ceci est conforme à l’équation de Boltzmann, probabiliste et semi-empirique. Or Poincaré démontre que dans un système dynamique conservatif confiné, les trajectoires reviennent toujours près de leur point de départ au bout d’un temps appelé depuis « temps de récurrence de Poincaré ». Il contribue ainsi à opposer à la théorie cinétique le paradoxe de l’irréversibilité : les équations du mouvement des molécules, invariantes par renversement du temps, semblent en contradiction avec l’expansion irréversible du gaz :

Les phénomènes irréversibles […] ne sont pas explicables au moyen des équations de Lagrange[30].

Il estime donc qu’il existe deux physiques différentes, avec des principes différents : à notre échelle la matière est continue et obéit au principe de Carnot impliquant l’irréversibilité ; à l’échelle microscopique, les molécules obéissent aux lois de la mécanique – l’existence des atomes et molécules était d’ailleurs controversée à l’époque en raison de l’idéologie empiriste dominante, jusqu’à leur observation en 1908 par Jean Perrin.

Pourtant, aujourd’hui le paradoxe est élucidé, d’une part grâce à la probabilité extraordinairement faible des évolutions « remontant le temps », et d’autre part grâce à l’immensité du temps de récurrence de Poincaré (déjà pour 100 particules, il avoisine… l’âge de l’Univers). Il est surprenant que, face à ces deux propriétés résultant du grand nombre de molécules du gaz, Poincaré n’ait pas vu que des différences qualitatives peuvent émerger par changement d’échelle ou par augmentation de la complexité, et ce sans remettre en cause les lois microscopiques. Peut-être était-il trop mathématicien, car l’explication de l’irréversibilité macroscopique repose sur une approximation, justifiée par le grand nombre de constituants du gaz. Malgré tout, ses nombreux travaux sur la théorie cinétique montrent qu’il ne la rejetait pas, et espérait qu’elle pourrait être rendue rigoureuse. La mécanique statistique est effectivement devenue l’une des branches majeures de la physique théorique, et les « principes » de la thermodynamique n’en apparaissent plus que comme des conséquences[31].

@@@@@@@

Ces réserves ne doivent pas masquer l’énorme importance de l’apport de Poincaré en physique. Je cite pour mémoire les techniques mathématiques que nous lui devons et que nous utilisons quotidiennement. Par exemple, il a montré comment des séries asymptotiques issues de nos théories, qui sont pourtant divergentes en toute rigueur mathématique, peuvent fournir des approximations physiques. Ses théories des équations différentielles, des fonctions, de l’analyticité, ses approches géométriques sont si courantes que l’on ne connaît plus leur origine… En physique, j’ai souligné sa création de la théorie du chaos, son insistance sur l’importance des probabilités pour connaître les limites de nos prévisions, sur l’existence de groupes d’invariance sous-jacents aux phénomènes, sur l’intérêt de disposer de plusieurs descriptions mathématiquement équivalentes. Toutes ces conceptions imprègnent la science contemporaine.   

(juin 2017)

Figure 8 : Poincaré, été 1910 (archives Henri Poincaré)