Ce qui reste éternellement incompréhensible dans la nature, c'est qu'on puisse la comprendre (Albert Einstein) Je crois pouvoir affirmer que personne ne comprend la Mécanique Quantique (Richard Feynman)

Figure 1: John Stewart Bell (1928-1990). En 1964, Bell publia un article "On the Einstein-Podolsky-Rosen paradox" qui ouvrit une nouvelle vision sur la mécanique quantique et sa place dans le monde.
Depuis des millénaires, mais plus particulièrement depuis la Grèce vers 400 avant J.-C., les hommes ont essayé d’élaborer une description raisonnable de la Nature, utilisant maintes spéculations ; cette activité fut appelée philosophie naturelle. Puis, vers 1600, grâce d’abord à Kepler, Galilée, Descartes, mais de façon plus décisive sous l’influence d’Isaac Newton, une nouvelle discipline fut créée : la physique, description quantitative de la Nature fondée sur des mesures effectives. Le mot hollandais pour physicien est encore aujourd’hui « Natuurkundige », un sage de la nature. Aussi longtemps que les phénomènes étudiés étaient à échelle humaine, les deux disciplines ont assez bien cohabité. Elles constituaient deux approches distinctes, mais on ne se préoccupait guère de ce qui les distinguait.
Mais, plus récemment, de sérieux conflits sont apparus dans la description des phénomènes d’une part à l’échelle atomique et d’autre part à l’échelle cosmique. Ces conflits sont devenus particulièrement aigus dans le cas d’Albert Einstein lorsqu’il approcha de la vieillesse. À la fin du xixe siècle déjà, alors que tout semblait aller pour le mieux en physique, d’importants conflits étaient apparus, en particulier autour de la question du rayonnement du corps noir, pour lequel la physique de l’époque donnait des solutions allant à l’infini, ce qui posait problème. Max Planck, après une étude soigneuse des mesures du spectre du rayonnement du corps noir arriva à une équation qui s’adaptait remarquablement aux mesures ; il trouva alors le moyen d’« expliquer » sa formule suivant l’hypothèse d’un rayonnement absorbé et émis en petits paquets. Einstein ouvrit la boîte de Pandore de la mécanique quantique en inventant le photon : J.J. Thomson découvrit l’électron, mais Einstein inventa le photon. Newton avait pensé, vers 1700, que la lumière était, comme toute chose, constituée de particules. D’autres physiciens de cette époque, Christian Huygens en particulier, pensaient que la lumière était faite d’ondes. Ce désaccord resta une question philosophique, ouverte à la discussion, jusqu’à ce que Thomas Young démontrât, un siècle plus tard, en 1804, que la lumière donnait lieu à des phénomènes d’interférence.
Ceci régla la question pour le siècle suivant, jusqu’à ce qu’Einstein, pour expliquer l’effet photoélectrique et le rayonnement du corps noir, franchisse en 1905 l’étape décisive consistant à considérer la lumière à la fois comme particule et comme onde. Étant à l’époque jeune et hardi, il n’eut pas trop de scrupules pour avancer une telle hypothèse : sa priorité alors était de rendre compte des résultats expérimentaux.
Trente ans plus tard, Einstein trouva davantage de temps pour réfléchir aux étranges conséquences des théories qu’il avait contribué à enfanter. À ce moment, alors que la plupart des jeunes physiciens s’employaient à appliquer les nouvelles formules de la mécanique quantique pour rendre compte des résultats expérimentaux, Einstein s’occupait à en tester les fondements. En particulier, il fut un des premiers à comprendre que, dans certaines circonstances, la mécanique quantique violait localité et réalité, ce qu’il ne pouvait plus tolérer.
On appelle violation de la localité le fait que des changements arbitraires ayant lieu dans une région puissent être corrélés à des changements dans une autre région à peu près au même moment – alors qu’ils sont suffisamment éloignés dans l’espace pour qu’un signal lumineux ne puisse relier les deux événements pendant l’intervalle de temps donné. On appelle réalité le fait que, si un événement peut être décrit par certains paramètres, ils ne changent pas si l’événement est isolé. Les propriétés d'un système sont attribuables à ce système et ne peuvent changer que par interaction avec un autre système.
Einstein fut un des premiers à pleinement réaliser certaines propriétés non réelles et non locales de la mécanique quantique et à s’interroger sur ce sujet. Tout en reconnaissant que la mécanique quantique fournit toujours les réponses correctes lorsqu’on la confronte aux résultats expérimentaux à l’échelle atomique, il pensait que la solution n’était pas de la rejeter, mais de supposer qu’elle était incomplète et nécessitait des ajouts.
Là où la mécanique quantique semblait le plus bizarre, et en même temps le plus vulnérable, c’était au niveau des corrélations étranges pour lesquelles Erwin Schrödinger avait introduit le mot d’« intrication » (traduit de l’allemand
Einschränkung) en 1935. Schrödinger déclara que l’intrication était au cœur de l’étrangeté de la mécanique quantique ; c’est là qu’Einstein essaya de frapper dans le fameux « article EPR
(1) » qu’il publia avec Podolsky et Rosen, ses deux collaborateurs et étudiants qui apportèrent sans doute plus à l’anglais d’Einstein qu’à ses pensées les plus intimes.
Einstein lui-même ne fut jamais complètement satisfait du résultat. De fait, cet article fut une contribution remarquable à la philosophie naturelle, mais pas à la physique. Il spéculait que, étant donné que la mécanique quantique, telle qu’elle était, violait localité et réalité, et que la Nature devant être, par hypothèse, réaliste et locale, la mécanique quantique devait être incomplète
(2).
L’article EPR portait sur la position et le moment de deux particules identiques, émises par une particule au repos. En 1950, David Bohm
(3) donna une description plus succincte du même problème en recourant au spin de deux particules émises par une particule de spin zéro (le spin est le moment angulaire intrinsèque de la particule). La simplification vient de ce que les mesures de la position et du moment amènent à des variables continues, tandis que la mesure du spin d’une particule ne fournit qu’un nombre très limité de résultats : pour un électron les résultats sont +½ ou -½, pour un photon ce sont +1 ou -1.

Figure 2: David Bohm (1917-1992), physicien quantique américain (photo WikiCommons).
L’intrication est une propriété quantique suivant laquelle l’état de deux objets ne peut être décrit que globalement, sans pouvoir séparer un objet de l'autre, bien qu'ils puissent être spatialement séparés. Pour traduire cela dans le formalisme quantique, soit H1 (resp. H2) l’espace de Hilbert des états d’un objet quantique S1 (resp. S2) ; l’état du système S1 + S2 peut être décrit par un vecteur d’état de l’espace H1⊗H2. Certains de ces états peuvent être séparables (ou factorisables), c'est-à-dire s’écrire sous la forme d’un produit tensoriel entre un état de S1 et un état de S2. La plupart des autres états ne possèdent pas cette caractéristique, ils sont dits intriqués. Soit par exemple
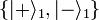 une base de l’espace H1 (resp.
une base de l’espace H1 (resp. 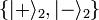 une base de l’espace H2). L’état Ψsep ci-dessous est séparable, se factorisant comme suit entre un état de H1 et un état de H2 :
une base de l’espace H2). L’état Ψsep ci-dessous est séparable, se factorisant comme suit entre un état de H1 et un état de H2 :
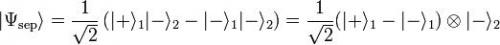
L’état Ψint ci-dessous n’est pas factorisable, il est intriqué :
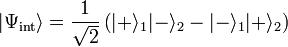
On montrera facilement, en raisonnant par l’absurde, qu’on ne peut trouver des coefficients tels que :
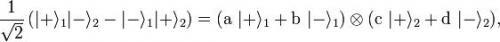
John Bell entre en scène
On en était là, lorsqu’en 1964, John Bell qui était comme Einstein un physicien théoricien tout en ayant comme lui une réelle vision expérimentale, eut l’idée que le caractère incomplet de la mécanique quantique pouvait être soumis à un test expérimental quantitatif, faisant ainsi passer le débat du domaine de la philosophie naturelle à celui de la physique
(4).
Trente ans séparent l’article EPR et l’article de John Bell, qui montrent l’importance du fossé entre les rêveries philosophiques et la mise en œuvre physique. Huit autres années passèrent avant la réalisation d’une expérience qui soumît ces idées à un test en laboratoire
(5). Les résultats de cette expérience ne furent pas encore complètement convaincants, et il fallut encore dix ans avant qu’un test pleinement convaincant ne fût mis au point
(6), bien que celui-ci présentât encore quelques points d’incertitude.
Il fut ainsi démontré que la réalité locale était incompatible avec la mécanique quantique. Il restait à déterminer toutefois ce qui, des contraintes de la réalité ou des contraintes de la localité, était violé par la mécanique quantique. Ces vingt dernières années, le grand nombre de tests qui ont été imaginés et réalisés semblent indiquer que les deux le sont (à la fois réalité et localité), et que de surcroît ce n’est pas seulement la localité classique (la structure de l’espace), mais aussi la structure du temps qui est violée.
Ce dernier point a été testé plus explicitement dans une récente expérience rendue publique en 2011
(7), où les références de fin d’article donnent une vue d’ensemble très à jour du développement du sujet sur les quarante-cinq dernières années, depuis le papier de John Bell en 1964.
Violation de la localité temporelle
Bell, et d’autres après lui, a surtout parlé de la non-localité de la mécanique quantique et des inégalités portant sur des objets intriqués séparés dans l’espace. On sait, depuis la théorie de la relativité restreinte, qu’espace et temps sont intimement liés et que la notion de simultanéité est purement relative à un observateur donné. Donc, pour deux particules A et B intriquées et séparées dans l’espace : savoir si la mesure de l’état de A arrive à l’observateur avant ou après la mesure de l’état de B dépend en fait de la vitesse de l’observateur par rapport à A ou à B – la notion suivant laquelle A influence B, ou l’inverse, n’a pas de sens. Mais en plus, on a pu établir des « inégalités de Bell » pour des objets intriqués non séparés dans l’espace ; ou même pour un seul objet, avec des mesures séparées seulement dans le temps. L’expérience de Fedrizzi et al. montre clairement que ces inégalités temporelles sont violées de manière plus importante encore que les violations locales usuelles (comme celles détaillées dans l’encadré ci-après).
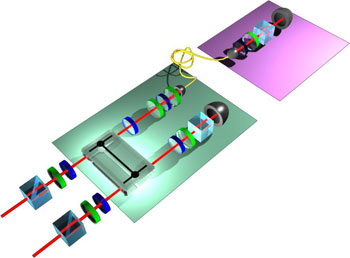
Figure 3 : Dispositif expérimental de violation temporelle des inégalités de Bell (schématisé sur son blog par Alessandro Fedrizzi, University of Queensland, Australie). Les deux mesures successives portent sur un seul et même photon. La première mesure est non-destructive, et faite avec un photon auxiliaire, par interférence à deux photons. La deuxième mesure sur le premier photon est faite dans la foulée, et de manière plus classique.
@@@@@@@
Je n’ai pas l’intention de faire ici un cours de mécanique quantique, mais je voudrais essayer d’expliquer ce qu’il en est de ces mesures. Je commencerai par un exemple non réaliste.
La plupart des gens sont plus à l’aise avec les couleurs qu’avec les nombres. Les photons blancs peuvent être considérés comme formés de couleurs complémentaires, rouge-cyan, jaune-violet, magenta-vert, orange-indigo, ces couleurs étant disposées sur un cercle de couleurs. Pour observer une couleur, nous disposons d’un détecteur de couleur, et nous supposons que chaque détecteur de couleur ne décèle que les couleurs complémentaires (le détecteur rouge-cyan ne verra que les photons rouge ou cyan, etc.). On commence avec les photons blancs qui se décomposent en deux photons de couleurs complémentaires ; mais, selon le choix de détecteur utilisé, ce seront telles couleurs complémentaires ou telles autres qui seront observées.
Or la mécanique quantique dicte que si l’on place deux détecteurs identiques à des points opposés pour détecter chaque photon depuis la décomposition d’un photon "blanc", la réponse sera toujours donnée par des couleurs complémentaires : rouge-cyan ou cyan-rouge, mais jamais rouge-rouge ou cyan-cyan. Jusqu’ici tout va bien. Mais si l’on place un détecteur rouge-cyan d’un côté et un détecteur jaune-violet de l’autre, alors la mécanique quantique détermine certaines probabilités pour l’apparition du rouge dans un détecteur et du jaune dans le détecteur opposé, et ces probabilités défient toute explication raisonnable.
Cependant, la physique ne se fait pas avec des couleurs, mais avec des nombres. Or, pour représenter le schéma de couleurs présenté ci-dessus, des nombres ordinaires ne conviennent pas, il faut des nombres complexes : ceux-ci peuvent être représentés sur un cercle, de telle sorte qu’à chaque point du cercle on puisse associer le point opposé, si bien que la somme soit égale à zéro. On obtient ainsi un schéma numérique que la mécanique quantique peut utiliser.
La quantité la plus facile à mesurer est le spin de l’électron ou du photon, qui, dûment mesuré, ne peut prendre que deux valeurs : (+1) ou (-1). Pour représenter complètement l’état de telles particules, on doit leur assigner des valeurs qui sont une combinaison de (+1) et de (-1) :
état (p)= a × (+1) + b × (-1)
où a et b sont des nombres complexes. Cela peut être représenté par un point sur un cercle, où a et b sont les projections sur les axes x et y. La mécanique quantique spécifie que les valeurs de a et de b déterminent la probabilité de trouver un électron ou un photon dans un état (+1) ou (-1). Le détecteur peut être représenté lui aussi par un point sur le cercle. C’est lorsque les deux détecteurs séparés sont représentés par différentes positions sur le cercle, et notamment quand un détecteur fait les mesures dans la position du cercle à 0° (point de coordonnées (0,1)), et l’autre détecteur dans la position du cercle à 45° que la prévision classique se trouve le plus clairement en contradiction avec les résultats expérimentaux, qui s’accordent parfaitement avec les prévisions de la mécanique quantique.
Illustration d’une inégalité de Bell
Cherchons à simplifier l’article de Bell en donnant un exemple simple d’application d’inégalité de Bell, avec des particules de spin ½. Soient deux particules 1 & 2, qui forment une paire EPR se propageant dans des directions contraires et dont on mesure les corrélations de spin suivant trois axes situés dans le plan des détecteurs, les axes a, b et c. S’il existait un paramètre caché, suivant sa valeur les paires EPR se diviseraient en huit classes :
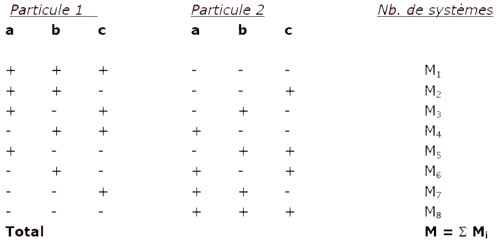
(la première ligne signifie que l’on mesure un spin positif sur les trois axes pour la particule 1 ; s’agissant d’un état intriqué, on mesure donc nécessairement un spin négatif sur les trois axes pour la particule 2 ; ainsi à chaque ligne) (P(a+, b+) étant la probabilité d’avoir pour la première particule une mesure de spin positive sur l’axe a , et pour la deuxième particule une mesure de spin positive suivant l’axe b), on a : P(a+, c+) ≤ P(a+, b+) + P(b+, c+) (1) (en effet ceci traduit M2 + M5 ≤ (M3 +M5) + (M2 +M6) Dans notre souci de simplification, prenons les trois axes a, b et c tels que b est la bissectrice de l’angle formé par a et c (figure):

Comme les deux particules sont intriquées, si la particule 2 se trouve dans l'état b+ alors la particule 1 se trouve dans l'état b-. Calculer la probabilité P(a+, b+) équivaut donc à déterminer la probabilité de mesurer dans l'état b- la particule 1, initialement dans l'état a+ ; d’après la théorie quantique, cette probabilité est proportionnelle au cosinus carré de la moitié de l’angle formé par a+ et b- (demi-droite opposée à celle représentée sur la figure en b) :
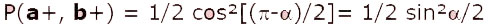
L’inégalité (1) donne ½sin²α ≤ ½sin²α/2 + ½sin²α/2, soit cos²α/2 ≤ ½. Cette inégalité est violée pour de nombreuses valeurs de α.
de la Philosophie naturelle à la Physique
Il existe ainsi une relation entre philosophie Naturelle et physique, mais elle est indirecte et ténue. La relation entre physique et technologie est directe et essentielle. Il n’est pas de progrès possible en physique sans progrès en technologie, et il n’est pas de progrès possible en technologie sans progrès en physique : elles forment un couple indissociable.
En 1964 l’article de John Bell donna un formidable élan au champ de l’intrication, à la fois dans le domaine théorique – avec le développement de méthodes efficaces pour le tester – et dans le domaine des mesures ; à la fois dans le champ de production de particules intriquées et dans celui de la détermination des propriétés de ces particules. Il y eut ces vingt dernières années des centaines d’articles scientifiques sur ce sujet, à une cadence toujours plus rapide, avec chaque semaine de nouveaux articles et des applications dans les champs de la communication et du développement des ordinateurs.
@@@@@@@
La mécanique quantique a donc résisté à ce jour à tous les assauts posés par les problèmes de l’intrication. Mais il reste des problèmes fondamentaux, aussi bien pour la mécanique quantique que pour la compréhension de l’intrication.
Pour ce qui est de la mécanique quantique, elle donne les bonnes réponses, jusqu’à la dixième décimale, pour tous les phénomènes à l’échelle atomique. Cependant il existe un problème quantitatif désastreux dans le calcul de l’énergie du vide, où la mécanique quantique donne un résultat qui est éloigné d’un facteur de 10 puissance cent si on le compare à la valeur mesurée ! Pour l’instant personne ne semble près de résoudre ce problème.
Un autre problème, plus difficile à définir, est le calcul de l’intrication. On comprend bien l’intrication de deux particules. L’intrication de plus de deux particules pose un problème sérieux, à la fois du point de vue théorique et du point de vue des mesures. On doit admettre que, si la mécanique quantique est correcte, l’énorme quantité de particules présentes dans l’univers est intriquée avec une quantité énorme d’autres particules. Cela pose un problème conceptuel qui a été complètement laissé de côté ; personne ne sait maintenant si ce problème peut révolutionner notre conception de l’espace et du temps, ou s’il vaut mieux l’ignorer, comme cela a été fait jusqu’à présent.
En sus de ce qui a déjà été discuté jusqu’ici, une autre caractéristique quantique en rapport avec l’intrication mérite d’être signalée. Il s’agit d’un problème de mesure, relatif au fait que le système à mesurer est microscopique (à l’échelle subatomique), alors que les appareils de mesure et les résultats de la mesure sont macroscopiques, à l’échelle humaine. Le sujet est connu sous le nom d’« effondrement de la fonction d’onde ». Comme nous l’avons vu dans le cas le plus simple, lorsque la mesure d’une particule ne peut conduire qu’à deux états (+1) et (-1), alors, selon la mécanique quantique, elle « existe » dans une combinaison de ces deux états, S = a × (+1) + b × (-1), où a et b sont des nombres complexes. Une mesure donnera (+1) ou (-1), mais jamais un mélange des deux, selon les probabilités déterminées par les valeurs de a et b. Nous avons vu que, lorsqu’un système intriqué est formé de deux parties identiques, A et B, alors pour mesurer B, il suffit de mesurer A, et on peut considérer que la mesure de A se traduit par la réduction du paquet d’onde de B en même temps que celle de A. Considérons maintenant une mesure normale : A est alors un appareil macroscopique complexe, et B une particule à l’échelle atomique. Mais là encore A doit être intriquée avec B pour permettre d’effectuer la mesure : alors, lorsque l’« aiguille » de A s’est fixée, la valeur de B est déterminée.
Il apparaît donc possible que les deux mystères de la mécanique quantique, sa « réalité non locale » et l’« effondrement de la fonction d’onde », soient étroitement liés. John Bell, dans son article, fit un pas crucial pour faire sortir ces problèmes du domaine de la philosophie naturelle pour les introduire dans celui de la physique, susceptible de mesures réelles.
Conclusion
L’article novateur de John Bell de 1964 a trouvé son importance, non pas en montrant la justesse de la mécanique quantique, mais en indiquant la possibilité de prouver expérimentalement, dans le cadre de notre conception actuelle de l’espace et du temps, que la mesure est par essence contextuelle et non-locale, indépendamment de la mécanique quantique, mais en accord avec celle-ci, et en désaccord avec Einstein.
Janvier 2012
(article traduit de l’anglais par Sylvie Taussig)

(1) Phys. Rev. 47, 777 (1935) A. Einstein, N. Rosen and B. Podolsky Voir le commentaire BibNum de cet article (F. Laloë, sept. 2010).
(2) Cette propriété de la mécanique quantique suivant laquelle les résultats de mesure en un endroit donné peuvent dépendre de mesures faites à un autre endroit suffisamment éloigné (tel qu’aucune transmission de signal ne soit possible entre les deux endroits) porte le nom de contextualité.
(3) D. Bohm, Quantum Theory (Princeton University Press, Princeton, NJ, 1951) p. 611-623.
(4) J.S. Bell, « On the Einstein Podolsky Rosen Paradox », Physics, Vol. 1, N°3, p. 195-200 (1964), texte BibNum; aussi J.S. Bell, Speakable and Unspeaskable in Quantum Mechanics, Cambridge University Press (1987).
(5) Phys. Rev. Lett. 28, 938 (1972) J.F. Clauser and S.J. Freedman.
(6) Phys. Rev. Lett. 47, 1804 (1982) A. Aspect, J. Dalibard and G. Roger.
(7) Phys. Re. Lett. 106, 200402 (2011) A. Fedrizzi et al.



 une base de l’espace H1 (resp.
une base de l’espace H1 (resp. ![]() une base de l’espace H2). L’état Ψsep ci-dessous est séparable, se factorisant comme suit entre un état de H1 et un état de H2 :
une base de l’espace H2). L’état Ψsep ci-dessous est séparable, se factorisant comme suit entre un état de H1 et un état de H2 :



![]()



 Blog "Mostly Quantum" d’Alessandro Fedrizzi, University of Queensland, Australie (co-auteur d’une des expériences décrites, de violation temporelle des inégalités de type Bell)
Blog "Mostly Quantum" d’Alessandro Fedrizzi, University of Queensland, Australie (co-auteur d’une des expériences décrites, de violation temporelle des inégalités de type Bell) chapitre 14, "États intriqués, paradoxe EPR et inégalités de Bell", extrait du Cours de mécanique quantique à l’École polytechnique, J.L. Basdevant & J. Dalibard (chapitre en ligne PDF) (cours complet PDF) (livre aux Éditions de l’École polytechnique)
chapitre 14, "États intriqués, paradoxe EPR et inégalités de Bell", extrait du Cours de mécanique quantique à l’École polytechnique, J.L. Basdevant & J. Dalibard (chapitre en ligne PDF) (cours complet PDF) (livre aux Éditions de l’École polytechnique)





