L’expérience cruciale de Hafele et Keating

L’expérience de Hafele et Keating réalisée en 1971 est souvent citée dans les présentations sur la relativité en étant associée à la « dilatation du temps », un terme confus (hélas fréquemment utilisé par les physiciens, encore en 2018) désignant un vaste ensemble disparate d’effets physiques[1]. Toutefois, sa réelle importance reste largement ignorée ou sous-estimée : elle peut en fait être qualifiée sans ambages de cruciale, sous de nombreux aspects – certains ayant même échappé à Hafele et Keating eux-mêmes. Son intérêt pédagogique et historique pour la relativité est immense, comme le démontre la lecture des trois articles ici commentés (2 de Hafele et Keating, 1 de Hafele seul).

 

Figure 1 : Joseph C. Hafele (1933-2014) et Richard E. Keating (1941-2006) avec « Mr. Clock » (quatre horloges atomiques qui occupaient deux sièges) Source : Time Magazine, 18 octobre 1971.

 

Les prédictions relativistes des écarts de temps pour des horloges embarquées

Intéressons-nous tout d’abord au premier article de Hafele et Keating, à propos de leur expérience de 1971, intitulé « Around-the-World Atomic Clocks : Predicted Relativistic Time Gains ». Ils y décrivent les prédictions théoriques pour les effets attendus, en commençant par situer leur démarche dans le contexte historique.

 

L’un des débats scientifiques les plus persistants de ce siècle est le « paradoxe » relativiste des horloges ou le « problème » relativiste des horloges, qui provient d’une soi-disant incohérence logique dans les différences de temps prédites entre des horloges voyageuses et des horloges de référence à l’issue d’un aller-retour. Ce débat théorique apparemment sans fin, qui a ressurgi récemment avec une nouvelle vigueur, appelle une résolution empirique convaincante à l’aide d’horloges macroscopiques.

 

D’emblée les deux auteurs établissent le lien entre leur expérience et le fameux « paradoxe » des jumeaux de Langevin (qu’on appelle également plus prosaïquement paradoxe ou problème des horloges). Leur expérience permet, comme nous le verrons, de trancher de façon non ambigüe l’existence ou non d’une différence d’âge au point de rencontre des deux jumeaux.

Le débat sans fin dont parlent les deux auteurs remonte à la conférence de Bologne donnée en 1911 (donc 60 ans plus tôt !) par Paul Langevin (1872-1946), principal défenseur de la relativité en France durant les premières décennies du xx^e siècle. Langevin n’a jamais évoqué de paradoxe ni mis en scène de jumeaux, mais seulement un voyage en boulet « façon Jules Verne » auquel prendraient part des humains. La notion de paradoxe date vraisemblablement du début des années 1920, avec l’écho que lui donne le philosophe Henri Bergson (1859-1941) dans son ouvrage Durée et simultanéité (1922), entièrement consacré à la relativité restreinte. C’est à Bergson que l’on doit l’évocation du « paradoxe » avec les jumeaux Paul (voyageur) et Pierre (resté sur Terre) ; il fournit sa propre interprétation (erronée) de la relativité restreinte qui va être reprise par une minorité de physiciens (dont Mendel Sachs, qui est l’initiateur de la réactivation de la polémique en 1971). Bergson soutient que la réciprocité étant parfaite entre les mouvements (« tout est relatif »), il ne peut y avoir de décalage entre les deux horloges réunies, contrairement à la prédiction[2] d’Einstein dans son article fondateur de 1905. Selon Bergson, les équations de la relativité restreinte sont correctes mais les temps qu’elle manipule sont fictifs et ne traduisent que le point de vue de chacun des jumeaux sur l’autre – la façon dont chacun des jumeaux se représente le temps de l’autre. Les effets observés seraient similaires à l’effet Doppler classique : un décalage de fréquence à distance qui n’implique aucune différence entre des temps cumulés.

 

Figure 2 : H. Bergson, Durée et simultanéité, Librairie Félix Alcan, 1922.

 

 

L’hypothèse de l’horloge

Bergson rejette une hypothèse implicite (mais essentielle) de la relativité : l’hypothèse de l’horloge, selon laquelle une horloge, quel que soit son mode de fonctionnement, qu’il s’agisse d’une clepsydre, d’une horloge à pendule ou d’une horloge atomique, mesure le temps propre[3] tel que prédit par la relativité (qui dépend pour la relativité restreinte de la vitesse instantanée dans le référentiel inertiel considéré). Le temps propre s’intègre le long de la ligne d’univers[4] de l’horloge.

Pour Bergson, la relativité ne décrit que des effets de perspective pour les longueurs ou pour les durées, de simples mirages à distance, tout rentrant dans l’ordre pour les horloges aux points de rencontre.

Il exprime[5] clairement son point de vue en 1924 :

 

Si  l’on  examine  attentivement les formules  de  Lorentz,  […] on  voit  que les  deux  années de  Paul  ne  sont  que des  années attribuées  à Paul  par le physicien  Pierre.  Le Paul qui vit dans un Temps plus lent que celui de Pierre est donc un être “fantasmatique”; c’est la vision que Pierre se donne de Paul quand il se conforme à ces règles de perspective que sont les formules de Lorentz.

 

Bergson refuse de considérer que le temps propre prédit par la relativité correspond au temps physique enregistré par l’horloge.

Le physicien américain Mendel Sachs (1927-2012) reprend ce point de vue dans un article[6] publié en cette même année 1971 ; la « nouvelle vigueur » à laquelle font référence Hafele et Keating est la polémique relancée par Sachs. Avant lui, un autre physicien, le Britannique Herbert Dingle (1890-1978), avait adopté la même posture, puis avait fini par reconnaître que la relativité devait incorporer l’hypothèse de l’horloge. Dingle en vint ensuite à rejeter carrément la théorie de la relativité elle-même, prétendant qu’elle était incohérente.

 

 

L’article de James Terrell

Le physicien James Terrell (1923-2009), dans sa réfutation claire des arguments de Sachs (voir la figure 3), évoque les raisonnements de Dingle et de Sachs, et conteste bien sûr la réciprocité entre mouvements quelconques. Terrell rappelle qu’un mouvement accéléré n’est pas équivalent à un mouvement inertiel (en l’absence de gravitation) : tout passager à bord d’un avion ou d’un train peut en témoigner ! On peut aussi ajouter qu’en relativité restreinte, la vitesse et la position sont relatives, mais l’accélération est absolue. En conséquence, les situations des jumeaux Paul et Pierre ne sont pas symétriques du point de vue physique (il n’y a donc aucun paradoxe au sens logique), et le fait que la relativité restreinte prédise un décalage entre les deux horloges à leur point de rencontre traduit simplement la dépendance du temps propre vis-à-vis de la ligne d’univers. En fait, cette caractéristique du temps propre est essentielle en relativité : c’est l’un des résultats incontournables de la relativité, qui peut même être qualifié de consubstantiel.

Autre erreur que souligne Terrell : croire que la relativité générale serait nécessaire pour traiter correctement le cas des deux jumeaux, car la relativité restreinte ne serait pas applicable à des mouvements accélérés. C’est une idée fausse et tenace (même de nos jours), qui n’est pas limitée aux néophytes, comme on peut s’en rendre compte en parcourant des ouvrages de vulgarisation actuels. En fait, la relativité restreinte permet d’étudier en détail le point de vue d’observateurs quelconques[7] (accélérés ou non) ; la relativité générale (dont la relativité restreinte constitue un cas limite) n’est requise que si les effets gravitationnels sont à prendre en compte.

Enfin, Sachs affirmant dans son article de 1971 qu’il n’existe aucune preuve directe de la désynchronisation des horloges parfaites, Terrell conteste ce constat en mentionnant notamment la fameuse expérience des muons cosmiques. Sur ce point, on ne peut donner complètement tort à Sachs, car avant Hafele et Keating, les vérifications de la désynchronisation étaient indirectes, ce qui laissait place à des interprétations alternatives. Certes, les résultats importants obtenus pour l’effet Doppler transverse ou le flux des muons cosmiques en fonction de l’altitude rendaient vraisemblable la réalité de la désynchronisation des horloges parfaites ; mais en physique, savoir repérer ce qui distingue un effet physique donné d’un autre effet est une nécessité si l’on veut accéder à une compréhension adéquate des phénomènes – d’autant que les physiciens ont pris la fâcheuse habitude en relativité d’amalgamer sous un terme plutôt confus « dilatation du temps » un ensemble hétéroclite d’effets physiques. Il s’agit là d’une dérive métonymique qui consiste à confondre les effets avec leur cause.

Les résultats obtenus par Hafele et Keating, qui constituent une preuve directe de l’effet recherché, furent d’ailleurs contestés par Sachs qui prétexta une stabilité douteuse des horloges atomiques embarquées (problème d’instrumentation) ainsi qu’une « remise en forme » des données par Hafele et Keating qui auraient cherché à les rendre conformes à la relativité (problème de méthodologie). Ces critiques n’ont pas résisté à l’analyse par des experts indépendants qui se sont penchés sur l’approche utilisée par Hafele et Keating et ont permis d’écarter les doutes exprimés par Sachs. En outre, d’autres expériences ont été menées depuis lors, avec des horloges sans cesse améliorées : toutes ont confirmé les prédictions relativistes. Anticipant la réaction de Sachs, Terrell indique avec lucidité dans son article que les résultats de l’expérience de Hafele et Keating (qui était alors en cours) avaient peu de chance de lui faire changer d’avis : « La longue histoire de cette controverse n’encourage pas cet espoir. »

 

Figure 3 : Première page de la réponse de James Terrell à l’article de Mendel Sachs (incluse dans les réponses diverses regroupées dans la publication « The clock ‘paradox’ - majority view ») Source : Physics Today, Vol. 25, Issue 1 (January 1972)

 

 

L’interprétation chronogéométrique

Rappelons quelle est l’interprétation standard de la relativité (on se limite ici à la cinématique), à l’aide de la figure ci-dessous.

 

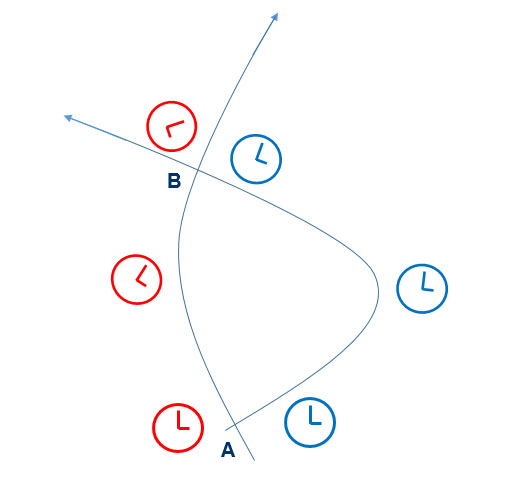
Figure 4 : Désynchronisation des horloges parfaites. Les deux horloges identiques sont synchronisées au départ (point A) mais ne le sont plus à leur point de rencontre (point B) à l’issue de leurs trajectoires respectives, chacune ayant enregistré un temps propre (cumulé) différent.

 

La principale difficulté en relativité est de raisonner entièrement avec une chronogéométrie, ce qui revient à laisser de côté notre espace et notre temps habituels en tant qu’entités séparées. Au niveau infinitésimal, il existe un élément de distance à 4 dimensions (mélange d’espace et de temps) qui se conserve. Ceci est la conséquence du principe de relativité et de l’existence d’une vitesse limite de propagation de l’information dans notre univers (constante structurelle de couplage c entre l’espace et le temps).

 

La relativité traite des durées cumulées enregistrées par les horloges (autrement dit les « temps propres ») comme des longueurs temporelles. Le temps propre mesuré par une horloge entre deux points de l’espace-temps ne dépend pas uniquement d’une date de début et d’une date de fin, mais de la trajectoire de l’objet (sa séquence d’événements) pour aller du point A au point B. Les expressions « l’horloge bat moins vite » ou « le temps s’écoule moins vite » ne devraient pas être employées car elles véhiculent l’idée fausse selon laquelle il existerait un flux temporel et que le rythme des horloges serait affecté. C’est le nombre de secondes qui varie d’une horloge à l’autre, et non la seconde qui se contracte ou se dilate. On peut regretter que de nombreux physiciens vulgarisateurs continuent à utiliser ces expressions, car elles sont une source de confusion pour les non-spécialistes. Notons que même Hafele et Keating y succombent à l’occasion, ce qui montre à quel point nous sommes prisonniers de notre langage. Rien ne devrait pourtant nous conduire à passer un pacte avec le sens commun, qui nous pousserait à revenir à d’anciens schémas de pensée.

 

@@@@@@@

 

Revenons à la figure 4. Chacune des horloges compte un nombre de cycles qui lui est propre, bien que les deux horloges soient parfaites et gardent un rythme identique (donc ne se dérèglent pas). Pour enfoncer le clou, nous ajouterons que la désynchronisation des horloges parfaites est un effet absolu. Notons que parmi toutes les trajectoires pour aller de A à B, il en existe une pour laquelle le temps propre est maximal : c’est celle correspondant à un mouvement inertiel, celui d’un corps libre de toute influence extérieure, qui se meut donc en ligne droite et à vitesse constante. Nous voyons que la situation décrite par la figure 4 est beaucoup plus générale que la présentation habituelle du pseudo-paradoxe des jumeaux. Le temps propre est a priori spécifique à la ligne d’univers considérée. On peut donc imaginer des scenarios très divers[8] : un voyageur parti de A en même temps que son comparse peut arriver après lui en B tout en ayant mesuré une durée propre plus courte ; les deux voyageurs partis ensemble de A peuvent arriver séparément en B tout en ayant enregistré chacun la même durée propre. Ce qui est contraire au sens commun certes – mais presque banal dans le cadre novateur de la chronogéométrie einsteinienne.

 

 

Le temps relativiste pour des tours du monde en avion

Dans leur premier article de 1972, Hafele et Keating, après avoir rappelé la longue histoire des controverses au sujet du pseudo-paradoxe des jumeaux, indiquent qu’un test équivalent à la situation des jumeaux est désormais réalisable :

 

Un test expérimental direct et simple de la prédiction relativiste avec des horloges atomiques transportables est désormais possible grâce à la stabilité sans précédent atteinte par ces horloges.

 

Les deux auteurs renvoient à la fin du paragraphe ci-dessus à un autre article (rédigé cette fois par Hafele seul) dans lequel la prédiction théorique est détaillée.

 

@@@@@@@

 

Il est fort instructif d’examiner cet article, « Relativistic Time for Terrestrial Circumnavigations », consacré par Joseph Hafele en 1972 à la prédiction théorique détaillée des effets mesurés lors de l’expérience historique conduite avec Richard Keating. Hafele souligne deux aspects importants : la dépendance de l’effet selon la direction du voyage (asymétrie intéressante à vérifier) et la faisabilité de l’expérience grâce à la qualité des horloges atomiques désormais disponibles. Rappelons que la première horloge atomique à fonctionner en continu date de 1955. Bien qu’Einstein eût été le premier à prédire l’effet de désynchronisation des horloges parfaites, cinématique d’abord (1905) puis gravitationnelle (1907), il n’a jamais envisagé sérieusement une vérification pratique à cause de l’imprécision trop grande des horloges durant la première moitié du vingtième siècle.

 

Le décalage temporel relativiste accumulé par une horloge durant un tour du globe dépend à la fois de la direction est ou ouest du voyage et de la vitesse de rotation de la Terre. Cette prédiction presque immédiate de la théorie semble avoir été ignorée jusqu’ici. En outre l’amplitude du décalage temporel attendu est amplifiée par la vitesse de rotation de la Terre de sorte qu’il devrait être détectable à l’aide d’horloges atomiques modernes embarquées dans des avions à réaction. En conséquence, j’ai suggéré un test expérimental de cette prédiction de la dépendance selon la direction du trajet. Le but de cet article est de présenter une description plus détaillée de ces effets relativistes et de discuter plus amplement de leurs implications.

 

Hafele décrit ensuite les conditions de l’expérience permettant de prédire l’effet relativiste :

 

Deux horloges similaires se trouvent initialement ensemble au repos à la surface de la Terre au niveau de l’équateur. Elles sont soigneusement vérifiées et comparées afin de s’assurer qu’elles conservent le même temps, c’est-à-dire qu’elles enregistrent le même nombre de « tics » sur de longues durées. Ensuite l’une des horloges est placée à bord d’un avion à réaction qui monte rapidement jusqu’à son altitude de croisière, effectue un tour complet sans escales autour de la Terre à cette altitude de croisière tout en maintenant une vitesse constante par rapport au sol, enfin descend rapidement jusqu’au point de départ où l’autre horloge est restée « au repos ». La question à considérer est celle-ci : Si les deux horloges indiquaient le même temps avant le vol, quels temps respectifs indiqueront-elles après le vol ?

 

Il précise ensuite un élément important sur lequel les deux auteurs reviendront avec insistance :

 

Nous supposerons que les horloges enregistrent le temps propre.

 

Il s’agit de l’hypothèse de l’horloge que nous avons déjà mentionnée. Leur expérience doit permettre de clore la polémique en montrant de façon directe que l’hypothèse en question est valide.

Hafele passe ensuite à la dérivation théorique de l’effet attendu dans le cadre de la relativité générale. Il choisit la métrique de Schwarzschild qui décrit la déformation spatio-temporelle engendrée par la masse sphérique de la Terre (en négligeant sa rotation). Si l’on note  le potentiel gravitationnel terrestre au point considéré, l’élément de métrique de l’espace-temps (distance entre deux événements « infiniment proches ») est donné par :

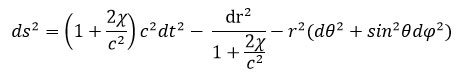Or le temps propre  enregistré par une horloge en mouvement quelconque dans l’espace-temps est ds/c, où c est la vitesse limite (qui coïncide avec celle de la lumière).

Hafele en déduit :

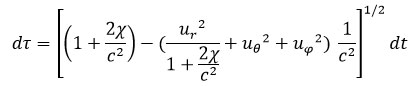où

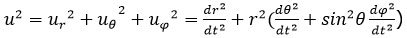
 u est le module de la vitesse-coordonnée, dt est l’élément infinitésimal du temps-coordonnée (temps qui serait mesuré par une horloge au point considéré en l’absence de champ gravitationnel ou par une horloge à l’infini).

Si nous tenons compte du fait que le potentiel gravitationnel terrestre est faible 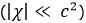 et que la vitesse de l’horloge (embarquée dans un avion) est également faible  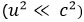, on peut approximer l’équation ci-dessus par :

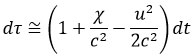Nous avons simplement négligé les termes d’ordre supérieur à .

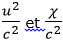Le temps propre cumulé enregistré par l’horloge embarquée sera donnée entre deux points A et B par :

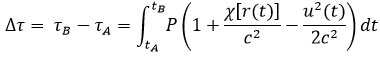Il suffit d’intégrer le temps propre le long du chemin parcouru P.

Hafele applique ensuite la formule ci-dessus aux horloges à la surface de la Terre et aux horloges embarquées.

Pour les horloges à la surface de la Terre, la vitesse  vaut Rω (où ω est la vitesse angulaire de la Terre et R son rayon) tandis que le potentiel X  vaut –GM/R (où G est la constante gravitationnelle et M la masse de la Terre). On obtient :

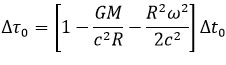Pour l’horloge embarquée (altitude h et vitesse par rapport au sol v ), la vitesse u vaut Rω + v tandis que le potentiel  vaut X –GM/(R+h). Hafele utilise un développement plus compliqué à partir de la loi de composition relativiste des vitesses. Le lecteur pourra se rendre compte que, à l’approximation considérée, la formule d’addition classique des vitesses suffit[9].

On obtient pour l’horloge embarquée :

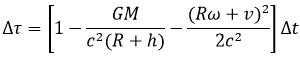Hafele remarque à juste titre que les intervalles de temps-coordonnée  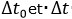sont égaux pour l’horloge embarquée et l’horloge au sol puisqu’elles partent du même point et arrivent au même point.

Le rapport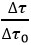  peut alors être approximé par :

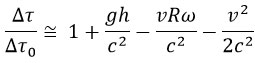où g = GM/R² est l’accélération de la gravité à l’équateur, la vitesse v étant comptée positivement pour le voyage vers l’est, négativement pour le voyage vers l’ouest.

Si l’on pose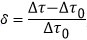 , la valeur prédite pour  est donnée par :

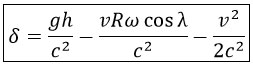
C’est l’écart temporel relatif entre l’horloge embarquée et l’horloge au sol. Le cosinus est un terme qui prend en compte la latitude pour le trajet de l’horloge embarquée (qui n’est pas limité à l’équateur). On a 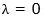  à l’équateur.

Hafele examine des cas concrets. Il remarque d’abord qu’une horloge à faible altitude enregistre moins de temps cumulé qu’une horloge identique à haute altitude. Il insiste ensuite sur une originalité de l’effet prédit par l’équation encadrée : le terme du premier ordre où intervient la vitesse de l’avion par rapport au sol dépend de la direction est ou ouest du voyage. Hafele donne quelques cas intéressants qui aident à saisir la situation (en supposant que l’altitude h soit nulle).

• Si le tour du globe a lieu vers l’ouest avec une vitesse par rapport au sol égale à –Rω, alors 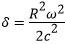. L’horloge embarquée avance à l’arrivée par rapport à l’horloge au sol.

• Si le tour du globe a lieu vers l’ouest avec une vitesse par rapport au sol égale à –2Rω, alors 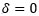. Il n’y a donc pas de décalage dans cet exemple entre l’horloge embarquée et l’horloge au sol.
• Si le tour du globe a lieu vers l’est, le terme  est toujours positif et l’horloge embarquée retarde à l’arrivée par rapport à l’horloge au sol.
• Pour des vitesses largement supérieures à Rω, la direction du voyage n’influe plus et l’horloge embarquée retarde par rapport aux horloges au sol quelle que soit la direction.

Notons que Hafele utilise les expressions « l’horloge bat plus vite » ou « l’horloge bat moins vite », ce qui, comme nous l’avons vu, est un léger abus de langage. Il évalue ensuite dans les conditions de l’expérience envisagée (altitude de 10 km, vitesse par rapport au sol voisine de 300 m/s, Rω autour de 1700 km/h) l’amplitude des effets prédits par rapport aux moyens de mesure :

 

Probablement le résultat le plus intéressant de cette étude est la prédiction selon laquelle les écarts relatifs qui peuvent être attendus avec les vitesses des avions à réaction commerciaux sont environ 10 fois plus grands que les fluctuations de fréquence (exprimées en écart-type) inhérentes aux horloges atomiques à césium.

 

L’écart relatif attendu  pour un voyage vers l’ouest est +2.1 10^-12 et vers l’est -1.0 10^-12.

 

Comme les fluctuations de fréquence relatives (exprimées en écart-type) pour des horloges à césium transportables se situent autour de 10^-13, ce qui est un ordre de grandeur en dessous des écarts prédits, le rapport signal sur bruit attendu est favorable et un test expérimental de cette dépendance directionnelle semble tout à fait réalisable.

 

Hafele souligne la portée cruciale du résultat par rapport au fameux « paradoxe » des horloges ou des jumeaux :

 

En même temps, une telle expérience permettrait de tester l’interprétation conventionnelle de la théorie, qui prédit que des horloges macroscopiques battent plus lentement lorsqu’elles se déplacent par rapport à un espace sans rotation. En d’autres termes, un tel test fournirait une résolution empirique du fameux paradoxe de l’horloge avec des horloges physiques macroscopiques.

 

Hafele indique aussi que l’expérience permettrait de valider l’hypothèse de l’horloge et de mettre ainsi un terme aux polémiques puisque que les prédictions relativistes seraient pour la première fois testées avec des horloges macroscopiques.

 

L’hypothèse ici, habituelle dans la théorie de la relativité, a été que toutes les horloges physiques macroscopiques, indépendamment de leur conception et de leur complexité, enregistrent le temps propre […]. Cette hypothèse de la théorie, qui semble solidement fondée sur le principe de relativité et le principe d’équivalence, reste néanmoins à établir par l’observation. Une telle tentative est désormais à notre portée.

 

Enfin, en annexe à son article, Hafele répond à un relecteur anonyme qui lui a signalé que la dépendance selon la direction de l’effet décrit est entièrement prédit par la relativité restreinte. Hafele répond fort justement que les termes cinématiques de la formule donnant l’écart relatif attendu  peuvent en effet être obtenus directement à partir de la relativité restreinte (métrique de Minkowski), mais souligne que la relativité générale est néanmoins le cadre adéquat pour l’effet complet puisqu’il y a un terme où intervient l’altitude (terme qui n’est pas prédit par la relativité restreinte).

Il est important de noter que la relativité restreinte et la relativité générale ne sont pas des théories complémentaires en ce sens que l’une (la relativité générale) prédirait uniquement les effets dus à la gravitation tandis que l’autre (la relativité restreinte) prédirait les effets purement cinématiques (liés au mouvement). Comme d’ailleurs Hafele le montre dans l’article que nous venons de commenter, la relativité générale permet de prédire précisément la désynchronisation aussi bien gravitationnelle que cinématique (en partant de la métrique de Schwarzschild). Si l’on néglige la masse de la Terre (donc si l’on ignore la gravitation), les prédictions de la relativité générale coïncident avec celles de la relativité restreinte, et dans ce cas on peut se contenter de raisonner à partir de la métrique de Minkowski. La relativité générale n’est pas une nouvelle théorie de la gravitation qui s’ajouterait à la relativité restreinte : elle est la meilleure théorie de l’espace, du temps et de la gravitation que nous possédions.

 

L’organisation de l’expérience

En 1971, Joseph Hafele est physicien à l’université de Washington (Saint-Louis, Missouri) et Richard Keating astrophysicien à l’Office of Naval Research. C’est Richard Keating qui obtient le financement par l’ONR, un modeste budget de 8000 dollars, dont plus de 7000 étaient attribués aux billets d’avion. Le financement (qui n’avait rien de luxueux) n’est pas pour autant acquis aisément. Cela est sans doute dû au fait que, pour la grande majorité des spécialistes, la réalité de la désynchronisation ne faisait pas de doute et avait été déjà validée par des expériences antérieures. Hafele et Keating étaient parfaitement conscients de l’importance de leur contribution et du caractère crucial du résultat à venir pour la physique, mais ils étaient un peu isolés. On peut voir là une situation un peu comparable à celle des ondes gravitationnelles : la première détection directe de ces ondes date de 2015 et constitue une confirmation majeure car, même si leur existence était jugée vraisemblable par les physiciens suite à des effets indirects mesurés sur la période de rotation des pulsars binaires (il y a plus de 40 ans, par Hulse et Taylor), la mesure de l’effet[10] du passage sur Terre d’une onde gravitationnelle était une première qu’il était crucial de valider.

Il y eut deux tours du monde équatoriaux d’une quarantaine d’heures avec des avions de ligne (comprenant des escales). Quatre sièges étaient réservés pour chaque vol car deux des sièges étaient occupés par « Mr. Clock », un ensemble de quatre horloges atomiques (fig. 1). Le contrôle des horloges devait être serré : il fallait s’assurer de leur bon état de fonctionnement d’autant que l’expérience se déroulait dans un avion commercial dans lequel voyageaient de nombreux passagers étrangers à celle-ci. Nos deux physiciens s’accordaient donc un maximum de 3 heures de sommeil durant le parcours.

 

Les écarts de temps prédits pour des horloges embarquées  

Pour la prédiction théorique, Hafele et Keating utilisent dans leur premier article de 1972 une dérivation simplifiée (courante) qui permet de calculer séparément les contributions cinématique et gravitationnelle. Il suffit de raisonner par rapport à un référentiel inertiel intermédiaire (le référentiel géocentrique qui suit la Terre dans son mouvement de chute libre autour du Soleil fait très bien l’affaire). On applique la formule approchée[11] de la relativité restreinte (vitesse par rapport au sol faible devant c) qui donne le rapport de la durée mesurée par l’horloge au sol à celle mesurée par l’horloge hypothétique du référentiel inertiel :

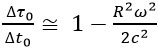De même, le rapport de la durée mesurée par l’horloge embarquée à celle mesurée par l’horloge hypothétique du référentiel inertiel est donné par :

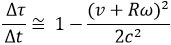On a utilisé l’addition classique pour les vitesses car elle est suffisante à l’approximation considérée. Ensuite, l’effet gravitationnel prédit par la relativité générale se traduit toujours par une avance pour l’horloge embarquée par rapport à l’horloge au sol :

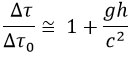
En remarquant que, puisque les horloges partent du même point et arrivent au même point, les durées dans le référentiel inertiel sont égales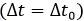 , on retrouve facilement la même formule que celle obtenue par la relativité générale pour le rapport 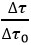 entre horloge embarquée et horloge au sol.

Dans une note, Hafele et Keating jugent utile de préciser :

 

Il est important de souligner que la relativité restreinte est censée décrire certains phénomènes physiques uniquement par rapport à des (ou du point de vue de) référentiels inertiels.

 

Hafele et Keating font ici erreur mais ils sont en bonne compagnie. Ils relayent une idée fausse tenace qui d’ailleurs est toujours en vogue en 2018. Rappelons-le une nouvelle fois : la relativité restreinte permet d’étudier complètement n’importe quel mouvement et le point de vue d’observateurs quelconques (accélérés ou non). Le cadre cinématique qu’elle propose est tout à fait universel. La relativité générale n’est requise que si l’on doit tenir compte d’effets gravitationnels.

Le voyage vers l’est (escales comprises) débuta le 4 octobre 1971 et dura 65 heures dont 41 heures de vol. Le voyage vers l’ouest (escales comprises) débuta le 13 octobre 1971 et dura 80 heures dont 49 heures de vol.  A partir des plans de vol (fournis par les pilotes), Hafele et Keating purent découper chaque trajet d’avion en intervalles, avec pour chacun une altitude et une vitesse par rapport au sol moyennes. Pour le vol vers l’est, 125 intervalles furent définis au total tandis que pour le vol vers l’ouest il y eut 108 intervalles. Pour chaque intervalle la formule donnant fut appliquée et le résultat final pour l’écart prédit s’obtint par simple sommation sur les différents intervalles.

 

 

Les écarts de temps mesurés pour des horloges embarquées

Dans leur deuxième article de 1972, « Around-the-World Atomic Clocks : Predicted Relativistic Time Gains », Hafele et Keating décrivent leur méthode pour obtenir des mesures suffisamment fiables et pouvoir les comparer aux valeurs théoriques. Ils annoncent d’emblée les conclusions tirées des résultats obtenus :

 

Comme attendu à partir des prédictions théoriques, les horloges embarquées perdirent du temps (vieillirent moins) lors du vol vers l’est et gagnèrent du temps (vieillirent davantage) lors du vol vers l’ouest.

 

Hafele et Keating firent voler quatre horloges atomiques pour le vol vers l’est et quatre autres horloges atomiques pour le vol vers l’ouest.

 

@@@@@@@

Voilà les résultats détaillés :

Figure 5 : Valeurs mesurées vs. valeurs théoriques (tableau original tiré de l'article de Hafele et Keating)

 

Dans la table précédente, les fourchettes pour les valeurs prédites ont été obtenues en tenant compte des incertitudes sur les plans de vol fournis par les pilotes. Les fourchettes pour les valeurs mesurées ont été obtenues simplement en calculant l’écart-type à partir des valeurs obtenues pour les quatre horloges.

Une première évaluation grossière (essentiellement qualitative) a été obtenue en moyennant les valeurs, ce qui permit déjà d’établir l’asymétrie entre le vol vers l’est et le vol vers l’ouest, comme le montre la figure ci-dessous : les horloges parties vers l’est retardaient tandis que les horloges parties vers l’ouest avançaient.

 

Figure 6 : Différences de temps moyennes pour les vols vers l'est et l'ouest. La comparaison entre horloges embarquées et horloges au sol n’était pas possible en vol (tableau original tiré de l'article de Hafele et Keating).

 

 

Un problème critique pour cette expérience est la capacité à repérer d’éventuels dysfonctionnements des horloges pouvant conduire à des écarts qui n’auraient rien de relativiste puisque liés à l’imperfection des horloges. Une première possibilité à envisager est une perturbation qui serait partagée par toutes les horloges embarquées. L’autre possibilité correspond au cas où l’une des horloges se dérègle, donc subit un saut de fréquence.

Pour y remédier, Hafele et Keating ont utilisé la méthode dite de « changements de rythme corrélés ». Ils ont comparé en continu les temps cumulés indiqués par les quatre horloges embarquées durant le vol de façon à détecter d’éventuels sauts aléatoires de fréquence (les horloges atomiques de l’époque en subissaient régulièrement dans une période de quelques jours, mais de manière aléatoire). Comme il y a très peu de chances que deux horloges subissent un saut au même moment, il est facile de repérer les sauts individuels. La comparaison des temps montra que, pour le vol vers l’est, l’horloge 120 changea de rythme trois fois, l’horloge 361 trois fois, l’horloge 408 deux fois, l’horloge 447 une fois. Pour le vol vers l’ouest, l’horloge 120 changea de rythme une fois, l’horloge 361 quatre fois ; il n’y eut aucun changement de rythme pour les horloges 447 et 408.

 

 

Ces données permirent de corriger les valeurs mesurées en rendant les horloges en quelque sorte parfaites a posteriori, et ainsi de comparer les temps indiqués par ces horloges avec les prédictions théoriques relativistes.

Hafele et Keating constatèrent donc que les horloges parties vers l’est retardaient par rapport aux horloges au sol d’environ 60 nanosecondes, tandis que celles parties vers l’ouest avançaient de près de 300 nanosecondes. Les résultats obtenus furent en accord avec les prédictions théoriques à 10% près.

 

 

La conclusion par Hafele et Keating de ce deuxième article de 1972 est limpide :

 

En tout cas, la discussion semble close quant à savoir si les horloges indiqueront le même temps après un aller-retour puisque nous avons trouvé que tel n’est pas le cas.

 

Nos jumeaux se retrouveront donc bel et bien avec un âge différent. Certains auteurs ont prétendu qu’une telle prédiction pourrait ne pas s’appliquer à des êtres humains, vivants et conscients, arguant que l’expérience n’a jamais été faite avec des humains. Il est facile de réfuter ce point de vue en remarquant que les rythmes biologiques fonctionnement essentiellement comme des horloges et que le temps propre cumulé pourrait être enregistré à partir du nombre de battements de cœur de chaque jumeau.

 

Importance de l’expérience par rapport aux précédentes

L’expérience de Hafele et Keating est beaucoup plus significative que les expériences vérifiant des décalages de fréquence à distance, qu’il s’agisse de l’effet Einstein (expérience de Pound et Rebka de 1960) ou de l’effet Doppler transverse (expérience d’Ives et Stilwell de 1938). Les décalages de fréquence entre points distants pouvaient être dérivés (via d’autres théories) sans supposer une différence entre temps propres cumulés, comme c’est déjà le cas pour l’effet Doppler classique. L’expérience des muons cosmiques (initialement due à Rossi et Hall en 1941) est également plus indirecte puisque les mesures concernent le flux de muons cosmiques reçus à une altitude donnée.

L’originalité de l’expérience de Hafele et Keating tient dans ce qu’elle est la première à mesurer des différences de temps propres cumulés. L’effet physique mesuré n’est pas du tout le même par exemple que pour l’effet Doppler transverse ou l’effet Einstein où l’on mesure la différence entre la fréquence reçue et la fréquence d’une onde émise depuis un point distant. Ici, on mesure des temps propres cumulés et la comparaison a lieu au même endroit ; les grandeurs mesurées et les conditions de l’expérience sont très différentes. Nombre de physiciens ont pris l’habitude d’amalgamer tous ces effets pourtant distincts sous la même appellation confuse « dilatation du temps », ce qui empêche de faire le distinguo. En fait, on peut voir dans la désynchronisation des horloges parfaites l’effet premier (purement relativiste) d’où découlent de nombreux effets secondaires tels que l’effet Doppler transverse, l’effet Einstein ou le flux des muons cosmiques à la surface de la Terre.

En résumé, l’expérience de Hafele et Keating est la première à montrer de façon directe (avec des horloges macroscopiques) que la multiplicité des temps propres est bien réelle et que le temps universel unique doit être abandonné.

 

 

Des expériences complémentaires de plus en plus précises

Pour ceux qui douteraient encore, ou qui feraient la fine bouche sur la précision des données obtenue par Hafele et Keating (prédictions théoriques vérifiées à 10% près), citons quelques autres expériences similaires conduites depuis (liste non exhaustive).

En 1975, l’expérience de Carroll Alley (Université du Maryland) fut conduite en se focalisant sur l’effet de désynchronisation gravitationnelle des horloges parfaites (en maîtrisant plus précisément les paramètres du vol). La valeur obtenue fut en accord avec la prédiction théorique à 1% près.

En 1996, pour fêter les 25 ans de l’expérience de Hafele et Keating, une horloge atomique fut embarquée par une équipe britannique du National Physical Laboratory (NPL) pour un aller-retour de Londres à Washington. A son retour elle avançait par rapport aux horloges au sol de 39 nanosecondes à 2 nanosecondes près, pour une prédiction théorique de 40 nanosecondes à quelques nanosecondes près.

En 2010, un tour complet autour de la Terre a été effectué (toujours sous l’égide du NPL) avec une horloge atomique : Londres – Los Angeles – Auckland – Hong-Kong – Londres. L’écart mesuré fut à l’arrivée de 230 nanosecondes à 20 nanosecondes près pour une valeur théorique de 246 nanosecondes à 3 nanosecondes près.

En 2018, il n’y a plus le moindre doute sur la réalité de ces écarts relativistes !

 

Une preuve décisive pour l’universalité de l’effet Sagnac

Bien qu’ils fussent pleinement conscients de l’intérêt de tester l’asymétrie dans les prédictions théoriques pour les vols vers l’est ou l’ouest, Hafele et Keating ne semblent pas avoir perçu la portée de leur résultat quant à l’universalité de l’effet Sagnac. L’effet Sagnac est le décalage temporel dans les arrivées de deux signaux ou objets quelconques faisant à contresens l’un de l’autre le tour complet d’un circuit fermé en rotation après avoir été expédiés par un émetteur-récepteur fixé sur le circuit.

Supposons que nous puissions effectuer les deux vols vers l’est et l’ouest dans des conditions strictement identiques : même vitesse par rapport au sol (dans les deux sens). Les deux vols partent en même temps du même point, chacun en sens contraire et reviennent au même point (où se trouve une autre horloge). Pour simplifier, nous supposerons que l’altitude est nulle pour nos horloges voyageuses.  Toutes les horloges sont parfaitement synchronisées au départ (au même endroit).

Observons la situation depuis le référentiel géocentrique, référentiel quasi inertiel qui suit la Terre dans sa chute libre autour du Soleil.

L’horloge partie vers l’est (dans le sens de rotation de la Terre) va plus vite que les horloges à la surface de la Terre. Selon la relativité restreinte, elle retardera à son arrivée par rapport à l’horloge au sol (effet de désynchronisation cinématique des horloges parfaites).

Le temps propre mesuré par l’horloge au sol pour le voyage vers l’est est donné par : 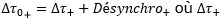  est le temps propre mesuré par l’horloge partie vers l’est,  Désynchro+ étant la valeur absolue de la désynchronisation.

L’horloge partie vers l’ouest va moins vite que les horloges à la surface de la Terre. Selon la relativité restreinte, elle avancera à son arrivée par rapport à l’horloge au sol (effet de désynchronisation cinématique des horloges parfaites).

Le temps propre 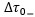 mesuré par l’horloge au sol pour le voyage vers l’ouest est donné par :  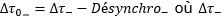  est le temps propre mesuré par l’horloge partie vers l’ouest,  Désynchro_ étant la valeur absolue de la désynchronisation.

Or les temps propres 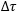+ et 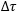_ sont égaux car la situation physique est identique pour les deux horloges voyageuses : même vitesse par rapport au sol et même longueur parcourue.

Le décalage temporel dans l’arrivée des deux horloges parties à contresens l’une de l’autre sera donc :

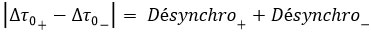
On retrouve ici le « délai Sagnac[12] », bien connu pour deux objets voyageant à contresens d’un disque en rotation (le raisonnement s’applique aussi à un circuit fermé quelconque en rotation). La relativité restreinte (seule ici la cinématique intervient) prédit le même délai quelle que soit la nature des entités utilisées pour le voyage (particules, ondes, corps macroscopiques…).

La relativité restreinte explique facilement cet effet Sagnac universel en tant que conséquence de la multiplicité des temps propres. Le délai temporel dans le retour au point de départ des deux objets partis à contresens correspond exactement à la désynchronisation cinématique de deux horloges qui seraient attachées aux objets. Sans cette désynchronisation, il ne pourrait pas y avoir d’effet Sagnac universel.

Chacune des horloges partie à contresens de l’autre enregistre le même temps propre cumulé (leur situation physique étant la même) pour revenir au point de départ mais celle partie vers l’ouest (dans le sens contraire de la rotation) arrive en premier et attend l’autre pendant une durée qui est égale précisément à la désynchronisation entre les deux horloges !

En vérifiant que la désynchronisation des horloges comporte bien un terme dépendant du sens du voyage de la façon prédite par la relativité, autrement dit en confirmant qu’il y a asymétrie dans la désynchronisation des horloges voyageuses par rapport à celles au sol selon le sens du parcours, Hafele et Keating ont apporté une preuve décisive en faveur de l’origine purement relativiste de l’effet Sagnac ainsi que de son universalité.

L’interprétation de l’effet Sagnac a fait l’objet de multiples controverses^[13] (peut-être encore davantage que le pseudo-paradoxe des jumeaux !). Il est d’autant plus important de se rappeler que Hafele et Keating ont apporté là un éclairage déterminant.

 

Une preuve décisive pour l’universalité de l’effet Einstein

L’effet Einstein est défini (si on se limite au cas des ondes électromagnétiques) comme le décalage entre la  fréquence d’une onde émise d’un point distant et la fréquence de l’onde reçue, lorsque les points de réception et d’émission correspondent à des potentiels gravitationnels différents. L’universalité de l’effet Einstein, c’est-à-dire le fait qu’il puisse être observé quelle que soit la nature des objets envoyés (ondes ou corps massifs) à une fréquence donnée du point A au point B où la fréquence reçue est mesurée, s’explique simplement en relativité générale comme la conséquence de la différence entre les temps propres cumulés aux points de réception et d’émission (le potentiel gravitationnel étant différent en ces points). D’autres théories peuvent a priori prédire le décalage de fréquence entre deux points distants sans l’imputer à une différence relativiste entre des temps propres cumulés.

Hafele et Keating ont pour la première fois montré sans ambiguïté la réalité de la désynchronisation gravitationnelle des horloges parfaites et ont donc apporté une preuve décisive en faveur de l’origine purement relativiste de l’effet Einstein^[14] ainsi que de son universalité.

 

Des applications pratiques

La désynchronisation des horloges parfaites (cinématique et gravitationnelle) mise en évidence par Hafele et Keating doit être prise en compte dans les systèmes de géolocalisation par satellites (tels que le système américain GPS ou le système européen GALILEO en cours de finalisation). La méthode de localisation est fondée sur l’estimation de la distance entre le récepteur GPS (au sol) et les satellites dont on reçoit le signal par ondes radio. Le satellite GPS orbitant à une altitude de 20200 km et à une vitesse d’environ 14000 km/h, l’horloge atomique à son bord est désynchronisée par rapport aux horloges au sol et les effets prédits par la relativité (similaires à ceux vérifiés par Hafele et Keating) sont impérativement à prendre en compte si l’on vise une précision de quelques mètres dans l’estimation de la position du récepteur GPS.

 

@@@@@@@

 

L’expérience de Hafele et Keating est cruciale à plus d’un titre :

• Elle confirme la validité de « l’hypothèse de l’horloge », selon laquelle les horloges, quel que soit leur mode de fonctionnement (clepsydres, sabliers, horloges à pendule, horloges atomiques…), mesurent le temps propre tel que prédit par la relativité ;
• Elle confirme la prédiction de la relativité restreinte concernant la désynchronisation cinématique des horloges parfaites (avec un terme dépendant de la direction du voyage);
• Elle confirme la prédiction de la relativité générale concernant la désynchronisation gravitationnelle des horloges parfaites ;
• Elle prouve l’origine purement relativiste de l’effet Sagnac (ainsi que son universalité) en éliminant certaines explications concurrentes ;
• Elle prouve l’origine purement relativiste de l’effet Einstein (ainsi que son universalité) en éliminant certaines explications concurrentes ;
• Elle prouve que le « paradoxe » des jumeaux n’en est pas un. La différence entre leurs âges à leur point de rencontre n’est que l’amplification d’un effet bien réel et omniprésent au gré de nos trajectoires respectives d’êtres humains, mais qui échappe à notre perception immédiate. Les résultats obtenus permettent de mettre un terme aux polémiques initiées principalement par Bergson et une minorité de physiciens qui niaient l’existence de l’effet mesuré en ne mentionnant que des temps fictifs qui ne seraient que des mirages. Le seul « vrai » mirage est le temps universel unique qu’il nous faut abandonner.
• L’aspect le plus important mis en lumière par Hafele et Keating est la multiplicité des temps propres, caractéristique incontournable de la chronogéométrie einsteinienne.

 

@@@@@@@

 

Le résultat obtenu par Joseph Hafele et Richard Keating en 1971 a des implications dont la richesse reste largement ignorée par les physiciens actuels, du fait d’un manque criant de compréhension des concepts relativistes et d’une confusion persistante entre certains effets physiques amalgamés sous la même appellation trompeuse « dilatation des temps ». L’expérience que ces scientifiques humbles et discrets ont réalisée avec sagacité il y a près d’un demi-siècle possède un intérêt pédagogique considérable, alors même que la révolution einsteinienne autour du temps (qui date pourtant de plus d’un siècle) n’a toujours pas imprégné en profondeur les esprits des physiciens[15]. En 2018, il est temps d’accorder la place qu’elle mérite à cette expérience de Hafele et Keating : celle de l’un des jalons les plus importants de l’histoire de la physique.

 

 

 (mars 2018)