Quand Joseph Bertrand accusait Coriolis de plagiat

Les documents que nous analysons habituellement sur ce site sont bien écrits, exacts et pédagogiques. Cependant, les exceptions sont aussi riches de leçons. Le document « Théorie des mouvements relatifs », publié en 1848 dans le Journal de l’École Polytechnique, 19, 149-154 par le jeune mathématicien Joseph Bertrand (1822-1900)[1], n’est pas vraiment correct scientifiquement, difficile à comprendre et teinté de préjugés. Toutefois, il est intéressant d’y jeter un coup d’œil, car ses erreurs ou ses faiblesses peuvent nous encourager à donner aux « mouvements relatifs » des explications plus précises, et à nous intéresser à des erreurs si tenaces dans les sciences, qu’elles sont aujourd’hui toujours présentes.

Malgré toutes ses faiblesses, l’intérêt principal du mémoire de Bertrand n’est peut-être pas scientifique, mais politique ; il a éveillé l’intérêt pour le mouvement relatif des systèmes rotatifs, qui a donné lieu quelques années plus tard à la fameuse expérience du pendule de Léon Foucault (1819-1868).

Ce qui retient le plus l’attention dans l’article de Bertrand, c’est son désir de discréditer un collègue. Il accuse le défunt Gaspard-Gustave Coriolis (1792-1843) de quasi-plagiat. Bertrand insinue qu’en échafaudant sa théorie sur la déviation du mouvement relatif, appelée aussi (par la suite) force de Coriolis, celui-ci aurait beaucoup emprunté au célèbre Alexis Clairaut (1713-1765) sans toutefois lui en faire crédit.

Figure 1 : Joseph Bertrand (1822-1900) était, à la fin des années 1840, une étoile montante de la communauté académique. Il a été admis à l’École Polytechnique à l’âge de 17 ans. Il a poursuivi son parcours à l’École des Mines qu’il a quittée en 1846 pour se concentrer sur les mathématiques et sur l’analyse des progrès de la physique générale (image Wikipédia).

1. Le mémoire de Coriolis de 1835

En 1835, dans son mémoire « Sur les équations du mouvement relatif des systèmes des corps » publié au Journal de l’École Polytechnique, 24^e Cahier, XV, p. 142-154[2], Coriolis indique que si un corps se trouvant à l’intérieur d’un système rotatif, à une distance R du centre de la rotation, se déplace à une vitesse V, relative à la rotation Ω, la force centrifuge ordinaire Ω²R ou, en notation vectorielle, -Ω×(Ω×R), devrait être complétée par une force supplémentaire 2ΩV ou, en notation vectorielle, -2Ω×V_r, que Coriolis appelle « force centrifuge composée » et que nous nommons « force de Coriolis ».

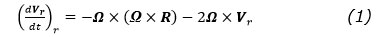
Cette « extension » de la force centrifuge est perpendiculaire au mouvement relatif V_r, dirigée vers la droite dans une rotation antihoraire (vers la gauche dans une rotation horaire)[3].

La force de Coriolis et la force centrifuge sont toutes deux des forces fictives ; elles ne possèdent pas d’origine physique comme la gravitation ou les forces magnétique ou électrique, et leur structure mathématique est bien différente. Toutes deux dépendent de la rotation Ω, mais la force centrifuge dépend également de la position R, et la force de Coriolis de la vitesse relative V_r. C’est peut-être pour cette raison qu’elles ont été perçues comme deux forces dont les origines sont indépendantes. Le fait que le mouvement inertiel et sans frottement sur la surface d’une planète en rotation puisse être décrit par la seule force de Coriolis peut avoir appuyé cette approche.

Le mémoire de 1835 de Coriolis constitue peut-être un des seuls textes qui établisse clairement que la force centrifuge et la force de Coriolis sont intrinsèquement liées. L’équation (1) n’exprime donc pas seulement une affinité mathématique entre les deux forces, mais aussi une affinité physique.

2. Coriolis ignoré

Le mémoire de Coriolis de 1835 semble ne pas avoir attiré beaucoup d’attention parmi les scientifiques de son temps. C’est peut-être, entre autres raisons, parce que sa « force centrifuge composée » 2ΩV n’a pas semblé être d’une importance cruciale. Pour la plupart des applications, elle s’élève à une faible fraction de la force centrifuge Ω²R. Plus généralement, elles sont égales quand

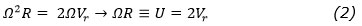
c’est-à-dire quand la vitesse relative V_r représente le double de la vitesse rotative U. Sur un manège où Ω = 2 rad/s (une révolution en 3,14 secondes), la force de Coriolis est plus forte que la force centrifuge uniquement dans un périmètre de 50 cm du centre de la rotation, pour un objet qui se déplace à 0,5 m/s.

Quand Coriolis publie son mémoire, Siméon Denis Poisson (1781-1840) travaillait – ou allait commencer à travailler – sur la déviation des grenades d’artillerie. Ces travaux débouchent en 1837 sur un mémoire intitulé « Extrait de la 1^ère partie d’un Mémoire sur le mouvement des projectiles dans l'air, en ayant égard à leur rotation et à l'influence du mouvement diurne de la Terre », Comptes Rendus des Séances de l'Académie des Sciences, 5, 660-667. 

Poisson ne semble pas avoir pris en compte l’étude de Coriolis, ou du moins ne s’y réfère pas dans ses travaux. Il est plus probable que Poisson se soit appuyé sur les travaux de Laplace (1749-1827), qui avait établi dans les années 1770 les équations complètes des mouvements sur une planète en rotation, et qui avait collaboré avec Friedrich Gauss (1777-1855) en 1803 pour donner une estimation de la déviation des objets en chute[4].

3. Le mémoire de Bertrand de 1848

Le mémoire de Bertrand débute par quelques pensées critiques :

Trop souvent, après avoir étudié la mécanique analytique, on croirait faire une chose inutile en cherchant à compléter l'étude de cette science par la lecture des travaux épars dont les prédécesseurs de Lagrange ont enrichi les recueils académiques du XVIII^e siècle. Je crois que cette tendance, malheureusement très-générale, est de nature à nuire aux progrès de la mécanique, et qu'elle a déjà produit de fâcheux résultats : la trop grande habitude de tout déduire des formules fait perdre jusqu'à un certain point le sentiment net et précis des vérités mécaniques considérées en elles-mêmes...[5]

Ces réflexions lui sont venues à la suite de la lecture de deux articles, écrits à un siècle d’intervalle. Le premier est le mémoire de Coriolis de 1835, le deuxième un mémoire rédigé par Alexis Clairaut. Ce dernier s’est intéressé en 1742 au problème du mouvement relatif dans un système rotatif, comme le montrent des passages de l’ouvrage « Sur quelques principes donnant la solution d'un grand nombre de problèmes », Mém. Acad. Sci. Berlin, pt. 1 (1742): 370-72.

À son grand étonnement, Bertrand aurait découvert que :

M. Coriolis […] s'est rencontré, sans le savoir, avec l'illustre Clairaut, qui […] avait résolu plusieurs problèmes, en faisant précisément usage du principe de M. Coriolis.

Mais ce principe qui, dans le Mémoire plus récent [celui de Coriolis] n'est démontré que par des calculs compliqués, semble à Clairaut tellement évident, qu'il néglige d'entrer dans le détail des raisonnements synthétiques qui l'y ont conduit, et se borne à en énoncer en quelques lignes le principe.

Figure 2 : Alexis Claude Clairaut (1713-1765), un scientifique majeur de son époque, a été crucial pour l’établissement de la validité des principes et résultats qu’Isaac Newton avait esquissés dans ses Principia. Il était l’un des membres éminents de l’expédition de 1736-1737 en Laponie pour mesurer la forme de la Terre et confirmer par là-même l’hypothèse de Newton selon laquelle elle est plus plate aux pôles (portrait gravé de Clairaut par Charles-Nicolas Cochin fils et Louis Jacques Cathelin, d'après un dessin de Carmontelle, Wikimedia Commons).

 Bertrand continue en ces termes :

Ainsi se trouvent mis en évidence, de la manière la plus nette, les avantages et les dangers que présentent en mécanique les raisonnements a priori : ils sont la plupart du temps plus rapides, toujours plus satisfaisants pour l’esprit ; mais Clairaut lui-même est exposé à s'y tromper.

Le but que je me propose ici est d'exposer avec détail la démonstration trop peu connue de Clairaut, de la rectifier en montrant pourquoi le théorème dont il est question ne s’applique qu'au principe des forces vives, et de faire voir enfin comment, en suivant les idées de Clairaut, on parvient sans aucun calcul à la notion des forces centrifuges composées, introduites par M. Coriolis dans son second Mémoire sur les mouvements relatifs.

4. Le mémoire de Clairaut de 1742

Dans le premier chapitre, intitulé « Pour trouver les Mouvements des systèmes de Corps entraînés avec les plans sur lesquels ils sont placés », Clairaut imagine un rectangle qui se déplace le long d’une trajectoire incurvée tandis que dans le même temps, un corps se déplace à l’intérieur du rectangle (figure 3).

Figure 3 : C’est ainsi que Clairaut a tenté de visualiser le mouvement relatif où le corps M se déplace le long de la courbe µ dans un rectangle FGHI qui glisse sur deux « rails » inclinés AB et CD à une vitesse égale sur les deux.

Clairaut envisage ensuite que les coins opposés G et I se déplacent à la même vitesse. Ceci s’est révélé être une erreur fatale : même en suivant une trajectoire incurvée, le rectangle ne pivote pas nécessairement. Le schéma en figure 4 illustre qu’un mouvement incliné n’implique pas nécessairement une rotation.

Figure 4 : représentation schématique de la différence entre mouvement de translation et de rotation. Un mouvement incurvé n’implique pas nécessairement une rotation (en bas à gauche). D’un autre côté, un mouvement de translation peut très bien induire une rotation (en bas à droite).

Bertrand identifie l’erreur de Clairaut, allant jusqu’à souligner la phrase clé : « [qu’on laissât] le plan FGHI se mouvoir uniformément et en ligne droite », qui exprimait une idée inexacte corrigée par Bertrand :

On sait, en effet, fort bien, qu'un système abandonné à lui-même ne se meut pas d'un mouvement rectiligne et uniforme ; c'est pour cette raison que la conclusion à laquelle parvient Clairaut n'est pas exacte[6].

Dans son Histoire de la mécanique (p. 354-57)[7], René Dugas exprime non seulement ses inquiétudes quant au modèle de Clairaut, estampillé comme étant « incomplet », mais ne se montre pas non plus enclin à suivre la version « corrigée » de Bertrand. Cependant, l’auteur de la présente n’est pas entièrement satisfait non plus de la version de Dugas. Nous essaierons ci-dessous d’expliquer la pensée de Bertrand en tenant compte de la version de Dugas.

5. Mouvement relatif soumis à rotation

Soit un système de coordonnées avec deux axes x et y et l’origine en M’, où se trouve également un objet M (figure 5) :

Figure 5 : Le système de coordonnées défini x, y avec l’origine en M’ et un point M situé à l’origine, libre de se déplacer dans toute direction.

Bertrand soumet ce système de coordonnées à une translation associée à une rotation, tandis que le point M se déplace de façon rectiligne dans une direction arbitraire. En premier lieu, nous considérerons uniquement la translation de l’origine de M’ à K, tandis que dans le même temps, M se déplace vers le point P à la même vitesse (figure 6).

Figure 6 : Le système de coordonnées se déplace de M’ à K par translation, tandis que l’objet M se déplace de façon rectiligne vers P, aux vitesses υ_a = υ_e.

Perçu depuis le cadre de référence du système de coordonnées, maintenant désigné par x’y’, le corps s’est déplacé légèrement vers l’arrière (figure 7) :

Figure 7 :  Perçu depuis le cadre de référence du système de coordonnées, le corps s’est déplacé légèrement vers l’arrière, soit vers la gauche de l’axe y, avec une vitesse relative υ_r.

En second lieu, faisons également pivoter, lors de la translation, le système de coordonnées avec une vitesse angulaire de ω rad/s (figure 8) :

Figure 8 : Lors de la translation, le système de coordonnées pivote également dans le sens anti-horaire à une vitesse angulaire ω.

Perçu depuis le système de coordonnées, le point M arrive à un endroit différent relatif au système de coordonnées, maintenant désigné par x’’, y’’ (figure 9) :

Figure 9 : Perçu depuis le cadre de référence du système de coordonnées, le corps s’est déplacé légèrement vers l’avant, soit vers la droite de l’axe y, avec une vitesse relative υ_r.

Le changement de position de la figure 7 à la figure 9 peut être compris comme le résultat d’une accélération horaire (rotative) a vers la droite sur une distance υ_rdt·ωdt (figure 10).

Figure 10 : Le mouvement relatif ur dans le système de coordonnées en rotation a résulté en une déviation horaire, soit une accélération couvrant une distance υ_rdt·ωdt.

La déviation, exprimée comme s’opérant sur une distance S, peut être formulée de deux façons :

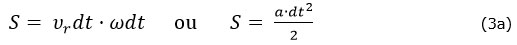
a étant l’accélération, ce qui donne

a = 2ω·υ_r                                                     (3b)

soit la version scalaire du terme de Coriolis.

6. avantages et inconvénients de la « dÉrivation simplifiée »

Plus tard au cours du XIX^e siècle, la dérivation de Bertrand se fait connaître sous le nom de « dérivation simplifiée » de la force de Coriolis. Ainsi perçue, nous la rencontrons le plus souvent sous cette configuration (figure 11) :

Figure 11 : Une version schématique de la dérivation de Bertrand : un corps M se déplace radialement à partir du centre de rotation M’, tandis que la plateforme sous-jacente (système de coordonnées) pivote dans le sens anti-horaire à un angle ωdt. Ceci aboutit à la déviation PK de ωdt·ν_rdt puis, pour finir, au terme 2ωv_r.

La dérivation de Bertrand est mathématiquement et physiquement correcte, et se retrouve dans de nombreux manuels populaires pour expliquer de façon intuitive la force de Coriolis. Il faut toutefois émettre quelques réserves à cette explication. La simplicité a un prix : il s’agit d’un cas particulier. Elle n’est valide qu’au centre, ou très près du centre de la rotation du manège. Ici, la distance avec le centre de rotation est dr ≈ 0, et la force centrifuge qui dépend de la distance est donc également ≈ 0.

Cette condition – la proximité avec le centre de rotation – est souvent ignorée des manuels. Les illustrations montrent un corps en mouvement qui commence son déplacement bien loin du centre de rotation. Ainsi, la version ci-dessous, bien qu’elle soit correcte géométriquement, est erronée du point de vue de la physique (figure 12) :

Figure 12 : application erronée de la dérivation « simplifiée » de la force de Coriolis selon Bertrand, loin du centre de rotation

Selon l’équation (1), en s’éloignant du centre de rotation et en augmentant la distance R,  la force centrifuge augmente, ce que l’on ne considère pas dans la figure 12.

7. La dérivation de Bertrand est-elle applicable à la terre en rotation ?

Jusqu’à présent, nous ne nous sommes intéressés qu’à un manège en rotation. Mais qu’en est-il de la Terre ? De nombreux manuels illustrent la force de Coriolis en représentant des ours blancs au Pôle nord qui marchent vers le sud. Cela est-il cohérent avec la dérivation de Bertrand ?

Oui et non. La force centrifuge est de zéro aux pôles, comme dans la dérivation de Bertrand. Mais, tandis qu’il s’agit du seul endroit où il est possible d’ignorer la force centrifuge dans la version de Bertrand, sur Terre, nous pouvons délaisser la composante horizontale de la force centrifuge, et ceci en tout lieu !

Les mathématiques de Bertrand ne couvrent pas cet aspect. Bien que la trajectoire d’un objet qui se déplace à la surface d’une planète en rotation puisse être décrite par le seul terme 2ΩV_r, la force centrifuge est tout de même présente. Cependant, en raison de la forme non-sphérique de la Terre (forme causée par la rotation), cette force est équilibrée par une composante gravitationnelle dirigée dans le sens opposé.

Nous espérons y revenir dans un article dédié, car c’était là un vif sujet de discussion à l’Académie à l’automne 1859.

8. Un test de tournesol pour l'effet Coriolis

Pour s’y retrouver parmi les différentes dérivations de la force de Coriolis, la règle suivante peut être utile : comme la force de Coriolis est perpendiculaire au mouvement, et d’une amplitude constante pour une vitesse constante, elle agit comme une « force centrale », et dévie ainsi tous les mouvements sur des trajectoires circulaires appelées « cercles d’inertie » (figure 13).

Figure 13 : En étant perpendiculaire au mouvement (V_r) d’un objet, la déviation de Coriolis va le propulser sur la trajectoire d’un « cercle d’inertie ». Son rayon ρ est calculé en considérant que 2ΩVr peut être perçu comme une force centripète V_r²/ρ.

Si, d’un point de vue mathématique ou conceptuel, la dérivation ne résulte pas en un mouvement circulaire, alors celle-ci est incomplète, inexacte ou erronée. Si, par exemple, une force centrifuge est également présente, la trajectoire sera une spirale d’Archimède qui n’aura cesse de s’élargir (figure 14).

Figure 14 : Agissant seule dans un manège en rotation horaire (zone verte), la force de Coriolis aurait idéalement conservé le corps en mouvement sur une trajectoire circulaire proche du centre de rotation (ligne rouge). Au lieu de cela, le corps va accélérer graduellement vers l’extérieur en raison de la force centrifuge (ligne bleue).

Mais que dire de la trajectoire incurvée M’P de la figure 11 ? Fait-elle partie d’un « cercle d’inertie » ou non ? Comme l’accélération que nous avons dérivée est 2ΩV_r et perpendiculaire (avec l’infinitésimal dr → 0), nous pouvons exprimer avec certitude que la trajectoire fait partie d’un « cercle d’inertie ».

Toutefois, ceci est une approche exclusivement logique et peu intuitive. Pour que l’on puisse établir de façon plus intuitive que la courbe fait partie d’un cercle, nous devons accepter deux compromis. Le premier est l’abandon du point de vue infinitésimal, comme étant contre-intuitif. Les différences doivent alors être interprétées comme des entités non-infinitésimales.

Mais la force centrifuge deviendrait alors apparente. Le compromis suivant est donc d’abandonner l’approche dynamique et physique, au profit d’une approche cinématique et géométrique, que nous présentons maintenant.

@@@@@@@

Notons tout d’abord que la déviation de l’objet en mouvement correspond au double de la direction, uniquement à cause de la rotation (figure 15).

Figure 15 : La tangente PM’’ mesure la direction de l’angle de déviation 2ωdt qui correspond au double du changement de direction dû à la rotation ωdt.

Lorsque l’angle de rotation a atteint les 90° (PM’ perpendiculaire à M’K), l’angle de déviation est de 180°, c’est-à-dire que PM’’ est parallèle à M’K.

La figure 16 ci-dessous ne constitue pas une preuve, mais représente plutôt une tentative pour fournir des arguments cinématiques et géométriques, afin de montrer que la trajectoire fait partie d’un cercle d’inertie dont le rayon correspond à la moitié de la grande plateforme rotative (cercle externe en figure 16).

Figure 16 : Sur la gauche, une réplique simplifiée de la figure 15 ; sur la droite, la même figure géométrique insérée dans le système de rotation complet. Quand ce système pivote à 90° (PM’ est perpendiculaire à M’K), la direction du mouvement dévié (le long de PM’’) est parallèle à sa direction originale (le long de M’K), et l’objet en mouvement a suivi un demi-cercle, soit la moitié d’un « cercle d’inertie ».

Une autre façon d’illustrer l’importance du concept de distance infinitésimale au centre de rotation est indiqué figure 17, où un objet se déplace sur un manège tournant. Supposons que la vitesse de rotation du manège soit d’un tour en 8 sec., soit Ω = 2p/8 = p/4 ; le rayon du manège étant de 2 m, et la vitesse du mobile 1 m/s. Sous des conditions « idéales », c’est-à-dire uniquement avec la force de Coriolis et sans force centrifuge, ceci conduirait, quelle que soit la position du mobile, à une trajectoire circulaire de rayon ρ = 2/p ≈ 0,6 m.

Sous des conditions normales, non idéales, où un objet se dirige en ligne droite sur le manège, passant au centre : hors le centre de rotation, s’exerce l’influence d’une force centrifuge, qui empêche la trajectoire d’être un « pur » cercle d’inertie, devenant ainsi une « boucle ». Cependant, au centre ou très près du centre, la courbure de la boucle correspond au rayon d’un cercle inertiel « idéal ».

Figure 17 : Un objet se déplace sur un manège tournant dans le sens trigonométrique, et passant au centre. Vue depuis un repère absolu, la trajectoire est une ligne droite ; vue dans le repère relatif du manège, c’est une boucle ; mais, à proximité du centre, la courbure de cette boucle est voisine de celle du cercle inertiel (ligne rouge pointillée), correspondant à la déviation « pure » de Coriolis, sans influence de la force centrifuge.

C’est une expérience populaire que de faire rouler une balle sur un manège tournant, en observant la déflection. En ayant la figure 17 en tête, les étudiants peuvent faire passer la balle par le centre du manège ou tout près, et ainsi observer les trajectoires circulaires quasi-inertielles qui en résultent. Notons que l’objet idél à faire rouler serait plutôt un palet de hockey qu’une balle ; ce à cause du moment angulaire d’une balle, due à l’auto-rotation, qui complique assez le mouvement.

9. Examen du mémoire de Bertrand par ses pairs

Comme Bertrand n’est pas encore membre de l’Institut à l’époque, son mémoire est revu par trois mathématiciens distingués : Augustin-Louis Cauchy (1789-1857), Gabriel Lamé (1795-1870) et Charles Combes (1801-1872). Dans leur « Rapport sur un mémoire de M.J. Bertrand concernant la théorie des mouvements relatifs », Comptes Rendus des Séances de l'Académie des Sciences, Paris, 27, 210-2013 du 21 juin 1848, ils approuvent les travaux de Bertrand, qu’ils jugent par ailleurs rédigés « dans un excellent esprit ».

Selon eux, bien qu’en soi le théorème ne soit pas nouveau, la nature des explications de Bertrand améliore la compréhension de son champ d’application, et de son utilité. Leur phrase suivante semble correspondre plus ou moins aux objectifs poursuivis par le projet BibNum :

Le fruit que M. Bertrand a tiré de la lecture des ouvrages des géomètres de la fin du XVII^e et de la première moitié du XVIII^e siècle, engagera sans doute les jeunes mathématiciens à étudier les œuvres, peut-être trop négligées aujourd'hui, de ces grands maîtres de la science.

Cependant, ils réfutent l’hypothèse selon laquelle Coriolis aurait plagié Clairaut : « Coriolis n’avait pas lu le mémoire de Clairaut », dont le raisonnement se trouve pris toutefois « en défaut ». Pour démontrer à quel point il est facile de suspecter un plagiat alors qu’il n’y en a pas, ils prennent pour exemple le Cours de Mécanique, un livre alors récent sur la mécanique de Jean-Baptiste-Charles-Joseph Bélanger (1790-1874), à propos du théorème de Coriolis :

Ainsi MM. Bertrand et Bélanger ont pu arriver au même résultat, à peu près en même temps, et par des méthodes semblables, sans qu'aucun d'eux eût connaissance des travaux de l'autre.

Or, Bertrand a présenté son mémoire le 21 juin 1847, alors que le livre de Bélanger était encore sous presse.

10. Les consÉquences du dÉbat de 1848

Joseph Bertrand a réalisé une analyse correcte de la déviation du mouvement relatif dans un système rotatif. Toutefois, cette analyse était incomplète dans la mesure où elle concernait un cas particulier (proximité du centre de rotation). Bertrand n’en a jamais saisi les implications plus profondes. Ce point est devenu manifeste quelque dix années plus tard, quand l’Académie consacre une grande partie ses travaux de l’automne 1859 sur le problème de la rotation de la Terre et ses effets sur les objets en mouvement. Polémiquant avec ses collègues académiciens, Bertrand maintient que la déviation de fonctionne que pour un mouvement nord-sud.

Cette position était alors appuyée par une explication populaire, mais erronée, nommée dérivation de Dove-Hadley. Elle avait été avancée par l’influent météorologue allemand Heinrich Dove (1803-1879), mais baptisée plus tard du nom du météorologue britannique George Hadley[8].

Le scientifique allemand balte Karl Ernst van Baer (1792-1876) créa une deuxième source de malentendu. En 1835, il tenta d’expliquer les sinuosités des rivières sibériennes s’écoulant du sud vers le nord comme une conséquence de la rotation terrestre[9]. Bertrand n’était pas le seul à commettre des erreurs.

L’expérience du pendule de Foucault de 1851, dans laquelle la déviation est indépendante de la direction du mouvement, aurait dû clarifier les choses. Mais certains scientifiques continuèrent à s’accrocher à leur point de vue erroné, tandis que d’autres changèrent d’avis sans vraiment comprendre pourquoi. Un argument fort pour nombre d’entre eux, paraît-il, était que la Seine et la Loire faisaient elles aussi beaucoup de méandres, mais s’écoulaient toutes deux de l’est vers l’ouest !

Selon l’opinion commune, le mémoire de Coriolis de 1835 a attiré l’attention qu’il méritait en 1851 seulement, après l’expérience du pendule de Foucault[10]. Il est probable que ce soit plutôt le débat controversé, engendré par le mémoire de Bertrand de 1848, qui a eu pour effet d’accroître l’attention et l’intérêt portés aux travaux de Coriolis. L’année suivante, lors d’un cours public, Jacques Babinet (1794-1872) expliqua comment la rotation de la Terre affecte les courants marins. Dans le public se trouvait un certain Léon Foucault, journaliste et vulgarisateur de talent, qui non seulement rédigea un compte-rendu de la conférence pour le Journal des débats (30 juin 1849), mais commença également à s’interroger sur la façon dont la rotation de la Terre affecte le mouvement à sa surface…

 (janvier 2019)