De l’influence de l’acide carbonique de l’air sur la température terrestre

  • INFORMATION
  • ACTUALITÉ
  • ANALYSE
  • EN SAVOIR PLUS
  • À TÉLÉCHARGER
De l’influence de l’acide carbonique de l’air sur la température terrestre
Auteur : Svante Arrhenius (1859-1927) - chimiste suédois, prix Nobel de chimie 1903.
Auteur de l'analyse : Sylvain Cros - Docteur de l’École des Mines de Paris - ParisTech
Publication :

“On the influence of Carbonic Acid in the Air upon the Temperature of the Ground”, The London, Edimburgh and Dublin Philosophical Magazine and Journal of Science. Vol. XXXXI, 5th serie, pp. 237-276, April 1896.

Année de publication :

1896

Nombre de Pages :
40
Résumé :

C’est un des textes fondateurs de la climatologie : Arrhenius calcule qu’un doublement de la quantité de CO2 dans l’air peut provoquer un réchauffement planétaire d’environ 5°C. Un résultat étonnamment d’actualité quand les scientifiques du Groupe d’experts intergouvernemental sur l’évolution du climat estiment cette valeur dans une fourchette allant de 2,5 à 4,5 °C (GIEC 2007).

Source de la numérisation :
University of Southern California (USC)
Tags: 
Arrhenius
Cros
atmosphère
climat
dioxyde de carbone
effet de serre
globe terrestre
Langley
Pouillet
réchauffement
spectre
température
Terre
Tyndall
Mise en ligne :
mars 2011
Envoyer la référence de la page

Lauréat du prix Nobel de chimie en 1903, Arrhenius était aussi un passionné de cosmogonie – l’étude des origines de l’univers et de la vie. En souhaitant expliquer les mécanismes des cycles de glaciation, Arrhenius s’appuie sur les propriétés radiatives de l’atmosphère dans l’infrarouge – et notamment sur les travaux de Fourier, Pouillet et Langley – pour démontrer que la composition chimique de l’air est un facteur déterminant des variations de la température terrestre. Il fait partie des nombreux scientifiques de l’époque qui réfutent la théorie de James Croll (1821-1890) attribuant des causes astronomiques aux glaciations, théorie finalement approfondie et admise grâce, notamment, aux travaux de Milutin Milankovitch (1879-1958) dans les années 1920. Arrhenius calcule qu’un doublement de la quantité de CO2 dans l’air peut provoquer un réchauffement planétaire d’environ 5°C. Un résultat étonnamment d’actualité quand les scientifiques du Groupe d’experts intergouvernemental sur l’évolution du climat estiment cette valeur dans une fourchette allant de 2,5 à 4,5 °C (GIEC 2007). Les calculs d’Arrhenius sont aujourd’hui reconnus comme erronés : cependant, malgré le fait que la relative précision de ses résultats soit fortuite, ses travaux sont précurseurs de modèles quantitatifs de l’effet de serre utilisés de nos jours par les climatologues. Ils les utilisent pour quantifier un risque de changements climatiques brusques et irréversibles du à l’émission croissante de CO2. Paradoxalement à nos yeux, Arrhenius écrit dans son ouvrage de vulgarisation paru en 1906, que l’émission de dioxyde de carbone du à l’essor de la révolution industrielle représenterait une solution pour atténuer les conséquences de la prochaine glaciation !

 

Sylvain Cros, ancien élève de l’université Denis Diderot (Paris VII), Docteur de l’École des Mines de Paris, est spécialiste de la modélisation du rayonnement atmosphérique et de l’observation de la Terre depuis l’espace; il a été chercheur à l’institut national de la recherche agronomique (INRA) d’Avignon et à l’École Polytechnique.

 

 

Sylvain Cros

 

 

Awarded the Nobel Prize in Chemistry in 1903, Arrhenius was also fascinated by cosmogony, or the study of the origins of the universe and life. Driven by a desire to explain the mechanisms controlling glacial cycles, he turned to the radiative properties of the atmosphere in the infrared zone – and in particular, the works of Fourier, Pouillet and Langley – to demonstrate that the chemical composition of the air is a crucial factor in determining variations in the earth’s temperature. He was one of a number of scientists at this time who refuted the theory of James Croll (1821–1890), which attributed glaciations to astronomic causes, a theory which would eventually be developed and recognised by the scientific community, notably thanks to the work of Milutin Milankovitch (1879–1958) in the 1920s. Arrhenius calculated that a doubling of the quantity of CO2 in the air could lead to global warming of around 5° C. This result is surprisingly relevant today given that the scientists of the Intergovernmental Panel on Climate Change (IPCC) estimate this value to lie between 2.5 and 4.5° C. Arrhenius’s calculations are now known to be incorrect. Yet while the relative precision of his results was somewhat fortuitous, Arrhenius’s research was a precursor to the quantitative models of the greenhouse effect which are used by climatologists today, particularly when calculating the risk of sudden and irreversible climate change as a result of increasing CO2 emissions. Though it seems paradoxical to us, in a work of popular science published in 1906, Arrhenius writes that the emission of carbon dioxide due to increasing industrialisation would actually prove beneficial in terms of reducing the effects of the next glaciation!

 

 

A graduate of Denis Diderot University (Paris VII), Sylvain Cros completed his PhD at the École des Mines de Paris. He is specialised in modelling atmosopheric radiation and observing the earth from space. He has been a researcher at the French National Institute for Agricultural Research (INRA) in Avignon and at the École Polytechnique.

De l’influence de l’acide carbonique de l’air sur la température terrestre
Sylvain Cros - Docteur de l’École des Mines de Paris - ParisTech
Résumé
Svante Arrhenius émet l’hypothèse que le cycle des glaciations terrestres (depuis les temps géologiques) repose sur les variations naturelles de la quantité de vapeur d’eau et de dioxyde de carbone (CO2) dans l’atmosphère. Il établit une relation quantitative entre la variation de concentration de CO2 et celle de la température moyenne de la surface de la Terre. Il en déduit qu’un doublement de la quantité de CO2 dans l’air peut provoquer un réchauffement planétaire d’environ 5°C. Un résultat étonnant d’actualité quand les scientifiques du Groupe d’experts intergouvernemental sur l’évolution du climat (GIEC) estiment cette valeur dans une fourchette allant de 2,5 à 4,5 °C (1). Les calculs d’Arrhenius sont aujourd’hui reconnus comme erronés : cependant, malgré le fait que la relative précision de ses résultats soit fortuite, les travaux d’Arrhenius sont précurseurs de modèles quantitatifs de l’effet de serre utilisés de nos jours par les climatologues.

 

 

Figure 1: Svante Arrhenius (1857-1929). Image Fondation Nobel.

Figure 1: Svante Arrhenius (1857-1929). Image Fondation Nobel.
Avant Arrhenius
La question de l’origine de la température de la surface terrestre a beaucoup évolué au cours du XIXe siècle. Un consensus s’établit progressivement sur le fait que le Soleil est la seule source de chaleur influençant les basses couches de l’atmosphère et que celle-ci joue rôle significatif dans l’équilibre thermique à l’origine de la température du globe.
En 1824, Joseph Fourier (1768-1830) applique sa théorie de la chaleur pour expliquer les origines de la température du globe terrestre (2). Il suppose qu’elle est la conséquence de la combinaison de trois sources distinctes de chaleur : le rayonnement solaire, la température de l’espace et la chaleur interne de la Terre. Il démontre que cette dernière est négligeable mais pense que l’espace est pourvu d’une température similaire à celles des régions polaires terrestres (en fait elle est beaucoup plus froide). Concernant la chaleur provenant du Soleil, il esquisse une théorie de l’effet de serre en affirmant que l’atmosphère est plus transparente au rayonnement solaire qu’au rayonnement réémis par la Terre (rayonnement infrarouge encore mal connu à l’époque et appelé « chaleur obscure »), maintenant un excès de chaleur près de la surface terrestre.
C'est ainsi que la température est augmentée par l'interposition de l'atmosphère, parce que la chaleur trouve moins d'obstacle pour pénétrer dans l'air, étant à l'état de lumière, qu'elle n'en trouve pour repasser dans l'air lorsqu'elle est convertie en chaleur obscure (3).

Certains aspects manquent, et notamment le fait que ce n'est pas directement l'absorption du rayonnement infrarouge terrestre par l’atmosphère qui réduit les pertes d'énergie vers l'espace, mais plutôt le fait que si l'atmosphère absorbe du rayonnement infrarouge, elle en émet aussi – et c'est cette émission qui apporte un supplément d'énergie à la surface. Il faudra ensuite attendre 1861 pour que John Tyndall (1820-1893) montre que la vapeur d’eau et le gaz carbonique sont responsables de cet effet de serre, en raison des bandes d’absorption qu’ils présentent dans l’infrarouge.

L’effet de serre dans le bilan radiatif de l’atmosphère

 

Tel qu’il est connu de nos jours, l’effet de serre est une des composantes du bilan radiatif de l’atmosphère terrestre, tel que ce bilan apparaît ci-dessous.

Figure 2 : Bilan radiatif de l’atmosphère terrestre (couche grise en haut) [Schéma extrait de A. Moatti, Les Indispensables astronomiques et astrophysiques pour tous, Odile Jacob 2009]. La constante solaire, égale à 1367 W/m², mesure la quantité d’énergie solaire reçue par 1m² de surface perpendiculaire aux rayons, à une distance d’une u.a. (distance Terre-Soleil). Cette chaleur est captée par la Terre suivant le disque qu’elle présente au Soleil (de surface π R²) et est moyennée sur toute sa surface extérieure (soit 4π R²) : le rayonnement solaire incident moyen à la surface terrestre est donc 1367/4 = env. 342 W/m² (valeur qui apparaît en haut à gauche).

Figure 2 : Bilan radiatif de l’atmosphère terrestre (couche grise en haut) [Schéma extrait de A. Moatti, Les Indispensables astronomiques et astrophysiques pour tous, Odile Jacob 2009]. La constante solaire, égale à 1367 W/m², mesure la quantité d’énergie solaire reçue par 1m² de surface perpendiculaire aux rayons, à une distance d’une u.a. (distance Terre-Soleil). Cette chaleur est captée par la Terre suivant le disque qu’elle présente au Soleil (de surface π R²) et est moyennée sur toute sa surface extérieure (soit 4π R²) : le rayonnement solaire incident moyen à la surface terrestre est donc 1367/4 = env. 342 W/m² (valeur qui apparaît en haut à gauche).

Le rayonnement infrarouge terrestre (la chaleur obscure) est figuré en bas à droite, à 390W/m². Il est absorbé par des molécules de l’atmosphère (vapeur d’eau, CO2) à hauteur de 370W/m² (et libéré dans l’espace à hauteur de la différence, soit 20W/m²). Les mêmes molécules émettent un rayonnement dans les mêmes longueurs d’onde, à hauteur de 330W/m² vers la surface terrestre : c’est l’effet de serre.

 

Claude Pouillet (1790-1868), quant à lui, avait publié en 1838 un mémoire sur « les pouvoirs rayonnants et absorbants de l'air atmosphérique, et sur la température de l’espace ». Il marque son temps en commençant à mesurer et à quantifier les échanges radiatifs à travers l'atmosphère. Ceci ouvre la voie au calcul des échanges d'énergie et des températures à la surface de la Terre, qui en découlent. Il détermine notamment la constante solaire (puissance moyenne de rayonnement perçue au sommet de l’atmosphère) à 1228 W/m2, soit à peine 10 % inférieure à l’estimation actuelle qui est de 1367 W/m2. Il estime la température de l’espace en démontrant qu’elle est beaucoup plus faible que ne l’avait supposé Fourier. Il élabore une représentation simplifiée du système Terre-espace-Soleil et une modélisation correspondante adaptée au calcul de la température de surface. Les lois du rayonnement du corps noir étant encore mal établies à son époque, il attribue au Soleil une température de 1734 K. Il faudra attendre 1879 et la loi de rayonnement de Stefan-Boltzmann pour que Joseph Stefan (1837-1893) estime une température très proche des 5800 K actuellement reconnus.

 

A la fin du XIXe siècle, il ne fait plus aucun doute que le rayonnement émis par la Terre et l’atmosphère – que l’on nomme toujours chaleur obscure –, est un rayonnement électromagnétique à longueur d’onde infrarouge. Samuel Pierpont Langley (1834-1906) n’a pas seulement tenté d’être l’un des pionniers de l’aviation : il s’intéresse aussi au rayonnement du Soleil et à son influence sur le climat terrestre. Son apport majeur dans ce domaine est certainement la mise au point du spectrobolomètre (voir encadré), un appareil complexe et imposant permettant d’effectuer des mesures d’intensité de rayonnement pour des longueurs d’ondes séparées.
Avec cet instrument, Langley peut mesurer le spectre d’émission d’un objet à température ambiante ou peu élevée (entre 0°C et 500°C).
Nous associons habituellement la notion de spectre à la lumière, il y a ainsi au premier abord, une certaine étrangeté à la notion de « spectre » formé par un corps froid tel que la glace. Une surface gelée n’est pas seulement capable de rayonner de la chaleur vers un corps encore plus froid, mais d’après nos conceptions actuelles d’énergie de rayonnement, elle est capable de donner un spectre, qu’il soit possible ou non de le déterminer (4).

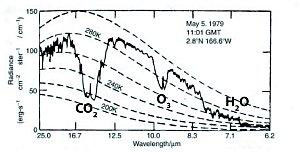
Langley détermine le spectre d’émission d’un objet à 100°C. Il obtient ainsi la première confirmation que, dans les basses couches de l’atmosphère, les spectres du rayonnement solaire et du rayonnement émis par la surface de la Terre (d’une température moyenne de 15°C) couvrent deux domaines spectraux disjoints. Il valide ainsi de manière expérimentale l’hypothèse de Fourier sur l’existence d’un effet de serre atmosphérique :

D’un point de vue d’astronome, parce que nous trouvons que la chaleur rayonnée depuis le sol est d’une nature presque totalement différente de celle reçue par le soleil, le phénomène important par lequel la haute température de surface de la planète est maintenue peut être étudié avec, nous l’espérons, des résultats fructueux en rapport avec les recherches décrites ici (5).

 

Spectres comparés du rayonnement solaire et du rayonnement terrestre

 

Le spectre du rayonnement solaire – au sommet de l’atmosphère – couvre les longueurs d’onde de 0,2 à 3 µm, avec un maximum en autour de 0,5 µm (dans le visible). Près de la surface, ce spectre voit sa partie supérieure à 1 µm significativement réduite, absorbée par les basses couches de l’atmosphère.

 

 

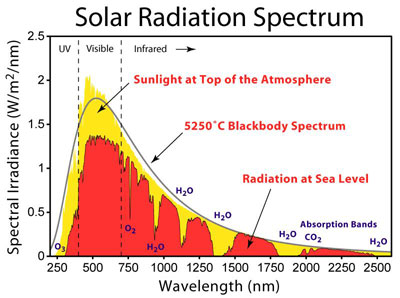
Figure 3 : Spectre du rayonnement solaire (schéma Wikipedia).

Figure 3 : Spectre du rayonnement solaire (schéma Wikipedia). La surface jaune figure le spectre du rayonnement à son arrivée dans l’atmosphère, avec une longueur d’onde entre 200 et 3 000 nm (le maximum étant dans le domaine visible entre 400 et 700 nm). La surface rouge figure le spectre du rayonnement après sa traversée de l’atmosphère (soit au niveau de la mer) : il a perdu une partie significative de son étendue, notamment au-delà de 1000 nm, par absorption du rayonnement par les molécules d’eau atmosphérique. On notera, côté gauche de la figure, l’absorption significative des ultraviolets, notamment les plus énergétiques entre 100 et 300 nm.

Le spectre d’émission de la Terre, quant à lui, couvre le domaine de l’infrarouge entre 1 à 50 µm, avec un maximum autour de 13 µm. Le rayonnement aux longueurs d’onde communes aux deux spectres (entre 1 et 3 µm) est relativement faible dans les basses couches. Les spectres solaire et terrestre peuvent donc être considérés comme disjoints.

 

 

Figure 4 : Spectre du rayonnement terrestre observé par le satellite Nimbus 4 (Source :Richard Tuckett, Climate change : observed impacts on planet Earth, Elsevier 2009).

Figure 4 : Spectre du rayonnement terrestre observé par le satellite Nimbus 4. Les courbes en pointillés correspondent à des rayonnements de corps noirs ayant des températures différentes. (Source :Richard Tuckett, Climate change : observed impacts on planet Earth, Elsevier 2009).

 

 

D’autre part, avec son spectrobolomètre, Langley tente de mesurer la température de la Lune en analysant le rayonnement infrarouge émis par cette dernière. L’absence d’atmosphère de ce satellite rend cette tâche très difficile car la température de la face visible de la Lune varie fortement (entre 100 et 280 K) en fonction de sa phase. Langley ne peut finalement pas exploiter ces données.

 

 

Le bolomètre de Langley, basé sur le prisme de sel gemme

 

Cet instrument, conçu par Langley dans les années 1870, a été perfectionné depuis, mais le principe en est toujours en usage ; il convertit en chaleur le rayonnement électromagnétique incident.

 

 

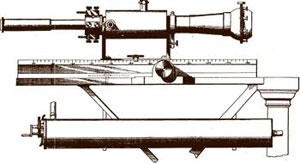
Figure 5 : Bolomètre utilisé par Langley (Annals of the Astrophysical Observatory of the Smithsonian Institution, Volume I, 1900)

Le bolomètre (gr. bolè, radiation) reçoit le rayonnement sur une plaque métallique. La mesure de la résistance électrique de cette plaque permet d’estimer sa température avec une extrême précision (de 10-5 à 10-6 °C), et d’en déduire la puissance du rayonnement incident. L’ajout d’un prisme de sel gemme permet au rayonnement incident de se décomposer en plusieurs directions. Chaque angle de déviation correspond à une longueur d’onde particulière. Par un système rotatif manuel, la plaque réceptrice du bolomètre est orientée selon l’angle associé à la longueur d’onde à mesurer.

 

 

La question d’Arrhenius
Svante Arrhenius commence son texte en posant une question très pertinente sur l’influence de l’absorption atmosphérique. Permet-elle à la température moyenne de la surface du globe d’atténuer les variations journalières et saisonnières comme l’affirme Tyndall ou bien détermine-t-elle cette température moyenne ? Il interroge :
Beaucoup de choses ont été écrites au sujet de l’influence de l’absorption de l’atmosphère sur le climat. Tyndall en particulier a signalé la grande importance de ce phénomène. Selon lui, les variations journalières et annuelles de la température étaient essentiellement atténuées par ce mécanisme. Un autre aspect de la question, qui éveille depuis longtemps l’attention des physiciens, est le suivant : la température moyenne à la surface du globe est-elle d’une quelconque manière affectée par la présence de gaz absorbant la chaleur dans l’atmosphère ?

L’énoncé de cette question permet de fixer le niveau des connaissances admises en 1896, au moment où il écrit. Oui, l’atmosphère peut absorber du rayonnement. Oui, son rôle est significatif dans l’équilibre thermique Terre-Soleil-espace. Mais a-t-elle un de rôle modérateur de variations ? Ou bien un rôle de déterminateur d’une moyenne ? Après avoir cité Tyndall qui défend la première thèse, Arrhenius enchaîne avec les mentions d’une bibliographie remontant jusqu’à Fourier et son principe de l’effet de serre pour appuyer plus sérieusement la deuxième assertion, plus fondamentale en termes de conséquences.

Arrhenius explique clairement que pour répondre à cette question, il faut connaître l’intensité du rayonnement tellurique (émis par la Terre) qui est absorbé par l’atmosphère en quantifiant la capacité d’absorption de cette dernière. Il est connu que l’absorption dépend de la longueur d’onde du rayonnement. Il propose alors de calculer les coefficients d’absorption spectraux de la vapeur d’eau d’une part et du CO2 d’autre part.

 

 

Détermination du spectre d’absorption de l’atmosphère terrestre … à l’aide du rayonnement de la Lune
Arrhenius va donner une seconde vie aux observations spectrobolométriques de Langley. En effet, il pense que la Lune et la Terre ont une température du même ordre de grandeur ; par conséquent, mesurer le rayonnement de la Lune à travers l’atmosphère équivaut à étudier le rayonnement d’un corps à la température de 15°C, tel que la Terre.
Langley avait mesuré le rayonnement émis par la Lune pour vingt et une différentes longueurs d’ondes réparties entre 1 et 9,5 µm. Une correction, tenant compte de la phase et de l’angle d’élévation de la Lune avait été appliquée à chaque mesure afin de les rendre comparables entre elles. En outre, Langley avait relevé l’humidité relative mesurée près du sol pour chacune de ses observations.
Arrhenius va utiliser ces données pour déterminer le spectre d’absorption dans le proche infrarouge séparément pour la vapeur d’eau et le CO2. Il doit donc associer à chacune des observations (puissance de rayonnement pour 21 longueurs d’ondes), la concentration de vapeur d’eau verticalement intégrée sur une colonne atmosphérique (désignée par W dans son texte et ultérieurement dans ce document), ainsi que celle du CO2 (désignée par K). Il va pour cela émettre deux hypothèses.
La première concerne la vapeur d’eau – il suppose que W est proportionnel à la masse d’air (6) et à l’humidité relative mesurée près du sol :
La quantité de vapeur d’eau est en partie proportionnelle à la « masse d’air », et en partie à l’humidité, exprimée en grammes d’eau par mètre cube. J’ai choisi comme unité pour la vapeur d’eau la quantité de vapeur d’eau traversée par un rayon vertical lorsque l’air en contient 10 grammes par mètre cube à la surface de la Terre.

Les mesures avec des ballons sondes (radiosondages) ou des satellites permettent actuellement d’obtenir des valeurs précises de W en tenant compte de la répartition verticale de la concentration en vapeur d’eau. En 1896, estimer W à partir de l’humidité du sol et de la masse d’air est certainement la solution la plus astucieuse. Toutefois, avec cette méthode, une bonne estimation de W nécessite que tous les profils verticaux de la vapeur d’eau soient identiques partout et à tout instant, ce qui est évidemment rarement le cas. Arrhenius mentionne lui-même les limites de cette hypothèse lors de l’interprétation de ces premiers résultats qu’il ne juge pas satisfaisants :

Cet effet est probablement du au fait que la vapeur d’eau dans l’atmosphère, qui est supposée avoir varié de manière proportionnelle avec l’humidité à la surface de la Terre, n’avait pas toujours la répartition idéale et uniforme avec la hauteur qui était présumée.

La deuxième hypothèse concerne l’absorption simultanée par le CO2 et la vapeur d’eau. Il suppose que seuls ces deux gaz peuvent absorber le rayonnement infrarouge. Il suppose également que la transmission de l’atmosphère dans l’infrarouge peut s’exprimer comme le produit de la transmissivité due à la seule présence de CO2 et de celle due à la seule présence de vapeur d’eau, ce qui correspond à l’équation suivante :

Avec T la transmission totale de l’atmosphère, θ l’angle de déviation du prisme du bolomètre (correspondant à une longueur d’onde particulière), Arrhenius nomme x et y les coefficients d’absorption respectivement pour le CO2 et la vapeur d’eau. Cette équation essentielle n’apparaît malheureusement pas dans le texte, elle peut toutefois se déduire par les résultats présentés dans le tableau II (p. 244). La qualification de x et y n’est pas juste dans le sens où ces coefficients correspondent à des coefficients de transmission et non d’absorption. Néanmoins, cette deuxième hypothèse est correcte car les spectres de vapeur d’eau et de CO2 ne sont pas statistiquement corrélés entre eux. Autrement dit, les longueurs d’onde où la vapeur d’eau absorbe le rayonnement ne correspondent quasiment pas à celles où le CO2 est absorbant. Cependant, Arrhenius néglige l’absorption significative due à d’autres gaz à effet de serre comme le méthane ou l’ozone, dont l’effet est inconnu à son époque (7).
Arrhenius s’attend à une fonction décroissante du rayonnement en fonction de la concentration en vapeur d’eau et en CO2 dans l’atmosphère. Supposant alors que les observations doivent aussi être classées par périodes de temps afin d’éviter les variations de ce qu’il nomme la « pureté du ciel », il trie les données en quatre périodes.
Les résultats ne sont pas plus cohérents. Il applique alors un facteur de correction sur chacune des quatre valeurs moyennes de rayonnement afin de contraindre ses résultats vers ses attentes. Arrhenius justifie cette correction en page 241, sans réelles explications :
Je suis arrivé à la conviction qu’aucune erreur systématique n’est introduite dans les calculs ci-dessous par cette façon de procéder.

Il calcule alors ce qu’il appelle les coefficients spectraux d’absorption pour la vapeur d’eau et le CO2 (tableau II, p. 244). Il compare ses résultats à ceux déjà publiés. Il trouve des bandes d’absorption entre 5 et 8 µm, qu’il attribue au CO2, en accord avec les travaux de Friedrich Paschen (1865-1947) mais en désaccord avec ceux d’Anders Jonas Angström (1814-1874). Actuellement, nous savons que la vapeur d’eau a une absorption beaucoup plus forte dans cette région spectrale que le CO2. Ce dernier a une bande centrée à 4,7 µm dont l’intensité ne peut pas justifier l’existence d’un effet de serre. L’ozone et le méthane, également absorbants dans cette région, n’ont par ailleurs pas été pris en compte.

Mais le problème fondamental de cette expérience est surtout l’absence d’observations à 15 µm. En effet, une bande de forte absorption du CO2, inconnue à l’époque, contribue de manière essentielle au rôle de ce gaz dans l’effet de serre (cf. figure 4). L’absorption du CO2 détectée par Arrhenius peut en fait être considérée comme « un artefact de sa méthode (8) ».

 

 

Somme spectrale et angulaire : calcul de l’absorption totale moyenne
À partir de ses coefficients d’absorption spectraux, déterminés par des mesures de rayonnement lunaire, Arrhenius explique sa méthode pour calculer l’absorption totale moyenne du rayonnement solaire par l’atmosphère terrestre.
Il doit d’abord procéder à une intégration spectrale. Après avoir noté que la surface de la Lune pouvait atteindre des températures de 100°C, il ne précise pas comment il adapte son spectre d’absorption pour un corps de 15°C comme la Terre. Néanmoins, il trouve des valeurs d’absorption intégrées tout à fait correctes par rapport aux connaissances actuelles pour W égal à 1 (soit 10 grammes de vapeur d’eau dans un kilogramme, comme Arrhenius le définit) et K égal à 1, soit une concentration en CO2 de 300 ppmv ou 300 millionièmes de volume de CO2 dans un volume d’air (9).
Les coefficients d’absorption ayant été corrigés pour correspondre à un rayonnement traversant l’atmosphère verticalement, une intégration angulaire doit être effectuée afin d’obtenir l’absorption totale de l’atmosphère dans toutes les directions. Il propose une nouvelle méthode appelée « approximation diffuse » (voir encadré ci-dessous). Il s’agit de déterminer un angle pour lequel la transmissivité du rayonnement est très proche de la somme des transmissivités dans toutes les directions. Cet angle est désigné par l’inverse de son cosinus et peut-être assimilé, comme l’indique Arrhenius, à un chemin optique. Cette méthode astucieuse permet de s’affranchir de calculs intégraux longs et fastidieux et est utilisée de nos jours par la plupart des modèles numériques d’optique atmosphérique.

 

L’approximation diffuse – la méthode d’Arrhenius toujours utilisée

 

 

Le rayonnement diffusé dans l’atmosphère peut être considéré comme isotrope ; ses propriétés ne dépendent pas de sa direction. L’intégration spatiale de grandeurs comme la transmissivité τ ne dépend donc que de l’épaisseur D de la couche parcourue par le rayonnement. La transmission totale se calcul par l’intégrale selon l’angle du parcours θ :

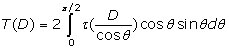
Arrhenius propose de calculer cet intégrale en recherchant la longueur que doit parcourir le rayonnement total pour que sa fraction absorbée soit la même que la somme des fractions absorbées des rayonnements élémentaires de chaque directions. Une approximation de l’intégrale est possible en déterminant un angle particulier dont l’inverse du cosinus vaut α. La transmission totale devient :

α, appelé facteur de diffusion, est déterminé empiriquement par Arrhenius à partir des variations de ses coefficients d’absorption en fonction du chemin optique. Il propose la valeur de 1,61. La plupart des modèles de transfert radiatif utilisent toujours cette approximation avec une valeur de 1,66. Remarquable résultat d’Arrhenius, faisant gagner un temps significatif aux calculs numériques actuels.

 

 

Le modèle de l’effet de serre : équilibre thermique du système Terre-atmosphère-espace
Arrhenius introduit cette partie des travaux en notant que Pouillet a déjà effectué ces calculs mais que ceux-ci doivent être réactualisés. Il fait certainement référence à la loi de rayonnement du corps noir de Stefan-Boltzmann – inexistante du temps de Pouillet – à partir de laquelle Arrhenius fonde son modèle d’équilibre thermique. Les équations présentées dans son texte correspondent aux modèles actuels de l’effet de serre à une couche (les grandeurs physiques sont supposés verticalement constantes à l’intérieur de la couche, y compris K, W et la température). Il pose néanmoins deux hypothèses invalidées par les connaissances actuelles : - l’émissivité et l’absorptivité de la surface terrestre ne varient pas selon la longueur d’onde (hypothèse donnée par l’équation 1, p. 255). Ceci est faux pour les surfaces les plus réfléchissantes comme la neige et les déserts. - l’absorption par l’atmosphère du rayonnement solaire réfléchi par la surface terrestre est négligée (équation 2, p. 256); or celle-ci est très importante particulièrement au-dessus des surfaces très réfléchissantes comme les déserts et les surfaces recouvertes de neiges ou de glaces).

 

Il discute ensuite de la prise en compte de la neige et de la couverture nuageuse, les surfaces les plus réfléchissantes pour le rayonnement solaire, alors que ses deux hypothèses précédentes, erronées, rendent cette considération vaine. Il aborde l’influence des profils verticaux de température pour introduire une notion d’altitude d’émission et de température d’émission. Il place celle du CO2 à 15 km et la vapeur d’eau à 233 m. Si actuellement une réelle différence d’altitude est constatée, ces données paraissent toutefois extrêmes. Il conclue finalement que tous ces phénomènes se compensent et qu’il n’a pas besoin de modifier son équation 3 (p. 256).

 

 

Calcul de la variation de la température de surface en fonction de la concentration en CO2
Arrhenius utilise le modèle à une couche qu’il vient de décrire pour calculer la température de la Terre et sa variation en fonction de K et W. Pour la vapeur d’eau, il compile un grand ensemble de données météorologiques et il en déduit, sans réelle justification, que l’humidité relative à la surface de la Terre est à peu près constante. Ceci lui permet d’écarter la vapeur d’eau afin d’obtenir une relation entre la variation de température et la concentration en CO2.
Arrhenius obtient, sur la base de ses mesures et de ses calculs mais sans donner de formule précise, un résultat important qui est toujours d’actualité :
Donc, si la quantité d’acide carbonique augmente en progression géométrique, l’augmentation de la température se fera selon une progression arithmétique.

Plus particulièrement, un doublement de la concentration du CO2 entraîne une augmentation de la température moyenne de la Terre d’environ 5°C, ce qui est très proche de la fourchette de 2,5 à 4,5°C prévue par le dernier rapport du GIEC. Toutefois, il a été démontré que le modèle à effet de serre à une couche n’est pas pertinent pour le calcul de réchauffement en réponse à augmentation de CO2. Il eût été nécessaire de bien prendre en compte l’épaisseur de l’atmosphère ainsi que la variation verticale des échanges radiatifs dans l’atmosphère, autrement dit le profil vertical de température.

 

 

Les conséquences géologiques
Dans la dernière partie de son texte, Arrhenius s’appuie sur les travaux de Gustaf Högbom (1857-1940) en citant longuement son mémoire (10). Ce dernier analyse les variations passées de la concentration de CO2 dans l’atmosphère et Arrhenius explique qu’elles coïncident avec les fortes variations de la température moyenne de la Terre à l’origine des périodes de glaciations.
S’il écarte les facteurs astronomiques (les variations de la position de la Terre par rapport au Soleil), démontrés ultérieurement par Milutin Milankovitch (1879-1958), Arrhenius entreprend une considération assez visionnaire des effets de rétroaction du système climatique. Sans entrer dans des calculs complexes, il démontre que la température globale de la Terre a un effet conséquent sur l’enneigement, ces phénomènes agissant à leur tour sur cette température globale moyenne :
Les variations géographiques annuelles et journalières de température seraient partiellement atténuées si la quantité d’acide carbonique était augmentée. L’inverse serait le cas (du moins jusqu’à une latitude de 50° par rapport à l’équateur) si l’acide carbonique diminuait en quantité. Cependant, je suis enclin à croire dans ces deux cas que l’action secondaire due au retrait ou à l’avancée de la couverture neigeuse jouerait un rôle plus important.

Les rétroactions, et particulièrement celles liées aux surfaces enneigés et aux nuages sont toujours au cœur des incertitudes sur les prévisions du climat à long terme.

Il conclut en mentionnant le géophysicien Luigi de Marchi (1857-1936) qui énumère les possibles raisons des variations passées de la température globale en ne retenant que la variation de la transparence de l’atmosphère, comme le pense Arrhenius (11). Il est étonnant de nos jours de constater que les raisons des variations du climat énoncées par le géophysicien italien sont aujourd’hui toutes retenues comme des causes pertinentes (facteurs astronomiques, changement du couvert végétal, distribution spatiale des continents et océans, transparence de l’atmosphère).

 

 

Conclusion
Arrhenius est connu pour être le premier scientifique à avoir quantifié la variation de la température de la Terre du à une variation de la concentration de CO2 dans l’atmosphère. Il occupe une place particulière parmi les précurseurs de la climatologie notamment parce que ses travaux correspondent à la principale question traitée par les rapports successifs du GIEC : quelle est la fourchette d’augmentation de la température globale pour une variation de CO2 donnée ? L’exactitude étonnante de ses résultats par rapport aux connaissances actuelles reste néanmoins fortuite. Malgré les imperfections de ses calculs concernant l’absorption atmosphérique et une modélisation trop simple de l’effet de serre, les travaux d’Arrhenius impressionnent toujours les climatologues d’aujourd’hui par la vision globale de la problématique des variations naturelles du climat qu’ils dénotent. Arrhenius souligne l’importance de la prise en compte des rétroactions climatiques et considère le cycle du carbone comme phénomène clé des variations temporelles de la température globale moyenne de la Terre.

 

Mars 2011

 

 

 

Logo BibNum

 

(1) 4ème rapport du GIEC, 2007.

(2) Voir dossier BibNum, analyse par James Lequeux de l’article de Fourier (Mémoire sur la température du globe terrestre et des espaces planétaires, Mémoires de l'Académie royale des sciences de l'Institut de France, vol. 7 1827, p. 569-604)

(3) Joseph Fourier, op. cit.

(4) Langley, S. P., 1886 : “Observations on invisible heat-spectra and the recognition of hitherto unmeasured wave-lengths, made at the allegheny observatory”, American Journal of Science, 31 (181), 1-12.

(5) Langley, op. cit.

(6) La masse d’air est une grandeur physique sans unité qui correspond à l’épaisseur optique de l’atmosphère traversée par un rayonnement d’une longueur donnée. La masse d’air peut s’interpréter comme le « pouvoir absorbant » de l’ensemble des composants de l’atmosphère pour une longueur d’onde particulière.

(7) Le consensus scientifique sur la considération du méthane et de l’ozone comme gaz à effet de serre ne date que du début des années 1990. Avant les années 1970, les techniques de mesures de concentration atmosphérique de ces gaz n’étaient pas considérées comme valides. La contribution de ces deux gaz sur l’effet de serre total– en termes de forçage radiatif - est d’environ 10 %, celles de la vapeur d’eau et du CO2 sont respectivement de 60 et 26 % (National Oceanic and Atmospheric Administration, NOAA).

(8) Cf. J.L. Dufresne, Mémoire d’habilitation à diriger les recherches, L'effet de serre: sa découverte, son analyse par la méthode des puissances nettes échangées et les effets de ses variations récentes et futures sur le climat terrestre, Université Pierre et Marie Curie, janvier 2009.

(9) Arrhenius ne propose pas dans son article de valeur absolue de concentration en CO2, il ne travaille qu’avec des valeurs relatives. Le choix de 300 ppmv est motivé par le fait que cette valeur est celle de la concentration de CO2 estimée pour l’ère préindustrielle. La concentration actuelle de CO2 est estimée à 380 ppmv (GIEC 2007).

(10) G. Högbom, Svensk kemisk Tidskrift, Bd vi, p. 169, 1894.

(11) Luigi de Marchi, Le cause dell’era glaciale, premiato dal R. Istituto Lombardo, Pavia, 1895.

 

ARTICLE BIBNUM

 

 

 

À LIRE (LIVRES)

 

 


Svante Arrhenius, Thomas C. Chamberlin, James Croll, Joseph Fourier, Claude Pouillet, John Tyndall, Sur les origines de l'effet de serre et du changement climatique, Éditions La ville brûle, 2010. [recueil de textes traduits – les quelques citations d’Arrhenius en français dans l’analyse BibNum ont été reprises de cet ouvrage]

 

 


Hervé Le Treut, Nouveau climat sur la Terre, Flammarion, 2009.

 

 


Emmanuel Leroy-Ladurie, Trente-trois questions sur l’histoire du climat, Hachette Pluriel Références, 2010.

 

 


Gérard de Moor, Le transfert radiatif en météorologie dynamique, Collection cours et manuel – Direction de la météorologie, Météo-France, 2007.

 

 


Sylvain Cros, Création d’une climatologie du rayonnement solaire incident en ondes courte à partir d’images satellitales, thèse de doctorat, École Nationale Supérieure des Mines de Paris, 2004, 138 pp.

 

 

À LIRE (ARTICLES)

 

 

Sandrine Bony, Jean-Louis Dufresne, « Processus régissant la sensibilité climatique », La météorologie, No. 56, pp. 29-32, mars 2007.