La théorie de la chaleur de Fourier appliquée à la température de la Terre
- INFORMATION
- ACTUALITÉ
- ANALYSE
- EN SAVOIR PLUS
- À TÉLÉCHARGER
Mémoire sur la température du globe terrestre et des espaces planétaires, Mémoires de l'Académie royale des sciences de l'Institut de France, vol. 7 (1827), p. 569-604 [republication de « Remarques générales sur les températures du globe terrestre et des espaces planétaires », Annales de Chimie et de Physique, vol. 27 (1824), p. 136-167]
1824
Fourier applique sa théorie de la chaleur à la température du globe terrestre, en distinguant trois causes de cette température : 1°/ les rayons du Soleil ; 2°/ la température de l’espace ; 3°/ la chaleur interne datant de la formation de la Terre.
Fourier applique sa théorie de la chaleur à la température du globe terrestre, en distinguant trois causes de cette température : 1°/ les rayons du Soleil ; 2°/ la température de l’espace ; 3°/ la chaleur interne datant de la formation de la Terre. Il démontre que la cause n°3 est négligeable, contrairement à ce qu’on croyait à l’époque. Il fait une erreur sur la cause n°2, surestimant la température de l’espace en l’assimilant à celle des régions polaires (depuis lors la mesure de la température la plus basse pour certaines régions de la Lune a été de −238°C). Enfin, à propos de la cause n°1, la principale, Fourier indique le rôle régulateur des courants marins et des vents sur la température terrestre ; il analyse la « chaleur obscure » du globe terrestre (son rayonnement infrarouge thermique) ; il esquisse l’idée, à la suite de Saussure, de l’effet de serre (l’atmosphère oppose « moins d’obstacles à la chaleur lumineuse affluente qu’à la chaleur obscure, qui retourne dans l’autre sens dans l’espace extérieur ») ; visionnaire, il imagine même « les effets de l’industrie humaine », alors balbutiante, sur la température terrestre. Son mémoire est un texte fondateur de ce qu’on appelle à présent la climatologie.
James Lequeux, ancien élève de l’École normale supérieure, a été astronome à l’Observatoire de Paris et rédacteur en chef de la revue Astronomy and Astrophysics. Membre de l’Union astronomique internationale, il est l’auteur de nombreux articles scientifiques et de livres d’histoire des sciences ou de vulgarisation scientifique (chez EDP Sciences notamment).

Les observations citées sont bonnes et l’existence d’une source interne de chaleur dans la Terre est bien mise en évidence par la marquise ; elle parle ailleurs du volcanisme qui en est une autre preuve. Mais ce qui est incompris par elle et par tout le monde, et le restera jusqu’à Fourier, est que l’absence de variations annuelles de la température au delà d’une certaine profondeur dans la Terre ne signifie nullement que la chaleur provenant du Soleil ne pénètre pas dans le sol : l’effet loin de la surface en est simplement moyenné au cours du temps, comme nous allons le voir avec Fourier.
Buffon pense que la Terre a été formée à très haute température, comme « un petit soleil détaché du grand » et se refroidit continuellement. En tant que maître de forges, il fabrique des boulets de canon en fer et peut étudier leur refroidissement. Puis, ayant constaté que le temps de refroidissement est inversement proportionnel au diamètre du boulet, ce qui est exact pour de petites sphères mais faux pour de grandes (voir l’encadré 2), il extrapole ses mesures à la Terre afin de savoir comment elle s’est refroidie : il trouve qu’il lui a fallu 2 936 ans pour parvenir à un état où elle s’est solidifiée et a cessé d’être incandescente (admirons la précision sur le chiffre !), puis 74 832 ans « environ » (sic !) pour parvenir à l’état présent. Ce résultat ne lui pose pas de problème, car on ignore totalement à l’époque quelles sont les échelles de temps des phénomènes terrestres – on soupçonne cependant qu’elles sont bien plus longues que les quatre millénaires résultant de la généalogie biblique. Buffon prévoit que, le refroidissement continuant, toute vie disparaîtra dans 93 000 ans : la Terre ne sera plus alors qu’un globe gelé inerte.
Joseph Fourier (1768-1830)

Né dans une famille pauvre et orphelin de bonne heure, Joseph Fourier est instruit par les Bénédictins à l’École militaire d’Auxerre. Il est destiné à l’état ecclésiastique, mais ses dons en mathématiques sont tels qu’il est nommé professeur dans cette école à l’âge de 16 ans. Il fait partie en 1794 de la première promotion de l’École normale supérieure. Il est remarqué par Legendre et par Monge, et prend part à l’expédition d’Égypte. Il devient secrétaire de l’Institut d’Égypte et rédige l’introduction de la Description de l’Égypte. Napoléon le nomme en 1802 préfet de l’Isère, poste qu’il occupe à la satisfaction générale jusqu’à la Restauration, qui le destitue et le laisse sans ressources. Cependant, le Préfet de Paris, M. de Chabrol, qui l’estime, lui trouve un emploi au Bureau de la statistique de la capitale. Fourier est élu en 1817 à l’Académie des sciences dont il devient secrétaire perpétuel en 1822, puis à l’Académie française en 1826. C’est à Grenoble, aux rares heures de liberté que lui laisse sa charge préfectorale, qu’il élabore sa Théorie analytique de la chaleur. Les développements mathématiques de Fourier sont peu estimés par Lagrange, par Laplace et par Poisson, car ils ne sont pas toujours rigoureux, mais visent à un résultat utile ; ils sont cependant si novateurs que la consécration finira par venir, très longtemps après sa mort (voir Kahane, Le retour de Fourier, Académie des Sciences, 2005). Les travaux de Fourier sur les séries trigonométriques sont à l’origine de remarquables développements en physique mathématique au 20e siècle, au point que l’on peut le considérer comme le fondateur de cette discipline. (D’après Arago, « Éloge historique de Joseph Fourier », Mémoires de l’Académie royale des sciences, 14, 1833, et Dhombres & Robert, Fourier, créateur de la physique mathématique, Belin 1998)
Le mémoire commence par un exposé général, dont les différents points sont examinés plus en détail à partir de la p. 575. Fourier définit d’abord de façon très claire, p. 569-570, les différentes sources de chaleur de la surface terrestre :
Puis il tente d’évaluer l’importance relative de ces trois sources à l’aide de sa théorie mathématique de la chaleur, à propos de laquelle il indique avec fierté que rien d’équivalent n’existait auparavant. Remarquons en passant que, comme beaucoup de ses contemporains, Fourier pense que la chaleur est un fluide, le fluide calorique, qui imprègne plus ou moins tous les corps et se propage par conduction selon les lois qu’il a établies. D’autres, qui sont une minorité, pensent que la chaleur est un état d’agitation interne plus ou moins grand des corps, ce qui correspond à nos connaissances actuelles. De plus, la chaleur peut être transmise dans l’espace par rayonnement : il s’agit alors de la chaleur rayonnante, dont on n’a pas encore établi à l’époque de Fourier la totale identité avec le rayonnement électromagnétique. Mais peu importe : les résultats obtenus par Fourier ne dépendent nullement de la nature physique de la chaleur.
Fourier n’en donne pas de démonstration dans ce texte, mais on peut la trouver ailleurs, dans son mémoire de 1820 Sur le refroidissement séculaire du globe terrestre (2). Il montre du même coup que la chaleur qui provient de l’intérieur du globe est négligeable vis à vis de celle qui provient du Soleil, qui n’a cependant pas été mesurée à l’époque : elle le sera pour la première fois en 1838 par Claude Pouillet (1790-1868), qui obtient 1230 W/m2 au dessus de l’atmosphère perpendiculairement à la direction du Soleil (la valeur moderne (3) est 1367 W/m2).

La propagation de la chaleur et l’échauffement de la Terre
Rappelons les notions suivantes : - la chaleur spécifique massique c, qui est l’énergie nécessaire pour augmenter d’un degré K l’unité de masse d’un corps. Elle s’exprime en J kg-1 K-1 ; - la conductivité thermique λqui est la densité de flux d’énergie (flux par unité de surface perpendiculaire à la direction de propagation) qui traverse l’unité de longueur du corps soumis à une différence de température unité. Elle s’exprime, comme sa définition l’indique, en W m-1 K-1 ; - la diffusivité thermique D = λ/ρc, ρ étant la masse spécifique du corps (exprimée en kg m-3). Elle s’exprime en m2 s-1. Sous sa forme générale, l’équation de la chaleur s’écrit :
λ∇T + P = ρc∂T/∂t ,
où ∇ est l’opérateur laplacien, ∂2/∂x2 + ∂2/∂y2 + ∂2/∂z2 en coordonnées cartésiennes, et P la puissance produite dans l’unité de volume du milieu au point courant. Fourier aborde deux problèmes. L’un d’eux est celui de la variation de la température en fonction de la profondeur x alors que la surface du sol est portée à une température variable : le problème est à une dimension et P = 0 puisqu’il n’y a pas création de chaleur à l’intérieur du sol. L'équation de la chaleur se réduit alors à sa forme la plus connue :
∂T/∂t = D∂2T/∂x2,
En supposant que la température superficielle varie sinusoïdalement avec une amplitude ΔTO et une période p, la solution de cette équation est :
ΔT(x) = ΔT0 exp(iωt+iax) exp(-ax) , avec ω = 2π/p et a = (π/pD)1/2
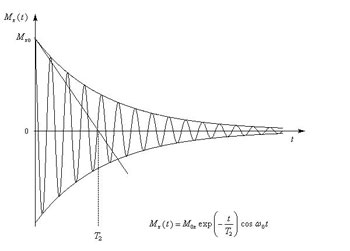
L’amplitude des variations diminue donc exponentiellement avec la profondeur, avec une échelle de hauteur 1/a = (pD/π)1/2 (échelle correspondant à une amplitude divisée par e = 2,72) ; les variations sont déphasées, par rapport aux variations en surface, de 2π par échelle de hauteur. En prenant pour le sol D ≈ 10-6 m2 s-1, on obtient pour les variations diurnes (p = 86 400 s) une échelle de hauteur de 17 cm, et pour les variations annuelles (p = 3,16 107 s) une échelle de hauteur de 3,2 m, en accord avec les observations (Fourier utilise l’équation à l’envers pour déterminer D à partir de la mesure de ces échelles de hauteur). Ces quantités ne sont que des ordres de grandeur, car elles varient évidemment avec la nature du sol.
L’autre problème que se pose Fourier est celui du refroidissement par conduction d’une sphère – la Terre – de température initiale élevée et uniforme. Fourier montre, dans son mémoire de 1820, que, toutes choses égales par ailleurs, le temps de refroidissement est proportionnel au rayon de la sphère si celle-ci est suffisamment petite pour garder une température uniforme, et proportionnel au carré de ce rayon si la sphère est très grande. Il montre également, en réduisant le problème à une dimension (ce qui revient à supposer plane la surface locale de la Terre), que le gradient de température en surface est lié au temps de refroidissement t depuis une température T0 par la relation :
∂T/∂x = T0/(πtD)1/2 .
Cette formule a été retrouvée vers 1860 par Lord Kelvin : bien que déjà résolu par Fourier, le problème est souvent appelé problème de Kelvin. En prenant par exemple T0 = 3 000°C, ∂T/∂x = 0,03°C par mètre et D ≈ 10-6 m2 s-1, valeur obtenue à partir des mesures des variations diurnes ou annuelles de la température du sol en profondeur (voir ci-dessus), on obtient un temps de refroidissement d’environ 108 années. Ce calcul ne tient pas compte du transfert de chaleur par convection dans le manteau, ni de la production d’énergie par la décomposition de l’uranium et d’autres éléments radioactifs, phénomènes inconnus au XIXe siècle : le résultat est donc grossièrement inexact. Fourier estime que le flux de chaleur λ∂T/∂x qui sort de la surface de la Terre ferait fondre 3 m d’épaisseur de glace en 100 ans, ce qui correspond à un flux de 0,3 W m-2 en unités modernes. Les estimations récentes donnent 0,08 W m-2 en moyenne sur l’ensemble de la Terre, dont près de 60% provient de la radioactivité terrestre naturelle. Cette valeur est plus faible que celle de Fourier, car celui-ci n’avait pu estimer qu’une valeur locale, valable seulement pour le continent ouest-européen.
On ne peut être plus clair ; ici on voit le mathématicien qui a remarqué que l’équation de la chaleur est linéaire, et que l’on pouvait donc traiter séparément la moyenne du rayonnement solaire (« l’action perpétuelle des rayons solaires ») et ses variations. Puis Fourier ajoute (p. 572) :
Fourier remarque donc que les courants marins et les vents tendent à uniformiser les températures sur la Terre. Nous verrons plus loin qu’il a malgré tout sous-estimé l’importance de ces effets. Mais voici qui est encore plus intéressant à nos yeux :
Ainsi, les masses océaniques et glaciaires contribuent à élever la température terrestre, puisqu’elles laissent plus facilement entrer la « chaleur lumineuse » que sortir la « chaleur obscure ». Suivant le même principe, Fourier a aussi compris l’existence d’un effet de serre dû à l’atmosphère : le rayonnement thermique de la Terre est partiellement retenu par l’atmosphère. Cet effet avait été suggéré dès 1780 par Horace Bénédict de Saussure (1740-1799), ce que mentionne d’ailleurs Fourier p. 585 ; mais il faudra attendre 1861 pour que John Tyndall (1820-1893) montre que la vapeur d’eau et le gaz carbonique en sont responsables, en raison des bandes d’absorption qu’ils présentent dans l’infrarouge, et 1896 pour que Svante Arrhenius (1859-1927) en fasse les premières estimations quantitatives.

Fourier et Pouillet ont aussi sous-estimé, voire oublié, l’inertie thermique et l’effet de serre qui diminuent le contraste jour-nuit.
Novembre 2010

(1) Sous ce terme, il convient de comprendre que la température sur Terre dépend « de la température commune des espaces planétaires ».
(2) Annales de chimie et de physique, 13 (1820), p. 418-438. Résumé dans Œuvres de Fourier, Gauthier-Villars, Paris, 1888-1890, t. 2, p. 271-288, accessible par Gallica.
(3) cf. Pouillet, Mémoire sur la chaleur solaire, sur les pouvoirs rayonnants et absorbants de l'air atmosphérique et sur la température de l'espace, Bachelier, Paris 1838, et Lequeux, François Arago, un savant généreux, EDP Sciences et Observatoire de Paris, 2008, p. 327.
(4) Dont la cause principale est, rappelons-le, l’inclinaison de 23,5° de l’axe de rotation de la Terre par rapport au plan d’écliptique.
(5) Voir Lequeux, Le Verrier, savant magnifique et détesté, EDP Sciences et Observatoire de Paris, 2009, p. 306-311.
 Dhombres, Jean, & Robert, Jean-Bernard, 1998. Fourier, créateur de la physique mathématique, collection « Un savant, une époque », Belin, Paris : l’ouvrage de référence.
Dhombres, Jean, & Robert, Jean-Bernard, 1998. Fourier, créateur de la physique mathématique, collection « Un savant, une époque », Belin, Paris : l’ouvrage de référence.

Lequeux, James, 2008. François Arago, un savant généreux, EDP Sciences et Observatoire de Paris, Les Ulis et Paris.

Lequeux, James, 2009. Le Verrier, savant magnifique et détesté, EDP Sciences et Observatoire de Paris, Les Ulis et Paris.
fourier-texte.pdf

fourier-analyse.pdf






