Annales de mathématiques pures et appliquées

 

 

Les Annales de mathématiques pures et appliquées sont le premier grand périodique de l’histoire de cette discipline. Publié de 1810 à 1832, ce journal s’imposa dans la communauté mathématique française et européenne comme une référence : il impliqua près de 140 mathématiciens de nombreux pays, du simple professeur de collège au plus illustre académicien ou professeur de l’école Polytechnique. Ils y écrivirent plus de 900 articles ayant trait à toutes les branches des mathématiques de l’époque, mécanique comprise.

Il n’était évidemment pas question de publier sur le site de BibNum l’intégralité de ce document, que nous avons d’ailleurs fait numériser et mettre en ligne sur : http://www.numdam.org (1).

En revanche, le Prospectus, sorte d’éditorial paru en introduction au premier numéro des Annales en juillet 1810, est un excellent document pouvant servir d’entrée dans le journal lui-même : Gergonne (et son très effacé corédacteur durant les deux premières années, Thomas Lavernède, alors professeur de mathématiques comme lui au lycée de Nîmes) y dit ses intentions éditoriales, ses motivations, ce qu’il espère publier et les effets escomptés de cette « périodisation » des publications mathématiques, en opposition à la forme alors dominante de diffusion du savoir : les ouvrages d’invention mathématique (de Lagrange, Carnot, Arbogast, Legendre, Monge, etc.) et les « Elémens*» (2) à caractère davantage didactique (pensons plus particulièrement aux traités de S.F. Lacroix).

1. APERÇU DE LA BIOGRAPHIE ET DE L'ŒUVRE DE GERGONNE

Joseph-Diez Gergonne est né à Nancy le 19 juin 1771, et mourut à Montpellier le 4 avril 1859. Il suivit les cours du collège de Nancy, alors dirigé par des chanoines, et s’intéressa surtout, et de très bonne heure, aux mathématiques et aux sciences physiques.

Après une brève carrière militaire durant laquelle il impressionna, lors de sa prestation au concours d’entrée à l’Ecole d’artillerie de Châlons, le mathématicien Sylvestre-François Lacroix – proche de Monge, de Laplace, et donc des mathématiciens influents de l’Ecole Polytechnique -, il obtint sur concours une chaire de mathématiques à l’Ecole Centrale de Nîmes en mars 1796. On le retrouve en 1804 au lycée où il a été nommé, par décret impérial, professeur de mathématiques transcendantes.

Pendant la première décennie du XIX° siècle, outre son travail d'enseignant, Gergonne occupa diverses fonctions à l'Académie de Nîmes. Mais surtout, grand admirateur des savants éclairés de la Révolution (Monge, Bailly, Laplace...), il tenta de les convaincre de fonder un journal scientifique consacré aux mathématiques. Les seules publications de ce type étaient alors les Mémoires de l'Académie des sciences, qui paraissaient épisodiquement, et le Journal de l'Ecole polytechnique, consacré uniquement aux travaux de celle-ci.

Après avoir tissé un réseau de correspondants et d'abonnés potentiels, Gergonne se « résigna » (le mot est de lui) à publier ce journal qui à ses yeux faisait défaut dans le monde éclairé des « géomètres » de son époque.

Fort de la renommée rapide de ses Annales et de l'estime de tous les mathématiciens européens, il fut nommé en 1816 professeur de mathématiques spéciales au collège royal de Montpellier, puis professeur d’astronomie à la faculté des sciences de la même ville. En 1819, il obtint de celle-ci l’habilitation à ouvrir un cours de philosophie des sciences, fait nouveau dans l'histoire de l'enseignement : le but de ce cours était de combler « une lacune fâcheuse qui existe dans l'ensemble de l'enseignement des facultés de médecine et des sciences » (3). Il enseignera ensuite la physique, sur proposition de l'un de ses anciens élèves, François Guizot (1787-1874), dont on connaît l’important devenir politique.

Nommé recteur de l’académie de Montpellier à la suite des Trois Glorieuses en 1830, il abandonnera la publication des Annales un an plus tard, trop occupé par ses nouvelles fonctions (4).

C'est l’œuvre mathématique de Gergonne qui est restée gravée dans l'histoire de la discipline, ses essais plus philosophiques étant tombés dans l'oubli jusqu'à une période récente. Pourtant, les deux aspects, le mathématique et le philosophique, sont indissociables. Les avancées mathématiques de l'époque provoquaient de tels bouleversements dans les modes de pensée et de raisonnement comme dans la formulation, l'acceptation et la représentation des concepts anciens ou émergents, qu'elles relevaient très souvent des deux champs. Nous en voulons pour preuve le fait que, dans les Annales de Gergonne, ouvrage bien représentatif de son temps, sont souvent classées dans la rubrique "Philosophie mathématique" les avancées essentielles concernant par exemple:

On a essentiellement retenu de Gergonne, outre le rôle de premier plan joué par son journal dans l'histoire des mathématiques, sa polémique avec Poncelet sur le dernier point, et plus particulièrement sur la paternité du principe de dualité (5). Ce débat, déjà prévisible dans un échange de vues sur les intérêts respectifs des géométries analytique et synthétique dès le T. VIII (1817-1818), s'exacerbera à la suite des rapports défavorables que fit Cauchy à l'Académie des Sciences sur les mémoires de Poncelet et à la publication d'un article de Gergonne sur les propriétés de l'étendue au T. XVI (1825-1826).

Mais l'apport mathématique de Gergonne ne se limite pas à cette question, loin s'en faut. Dans les seules Annales, il a laissé pas moins de 272 contributions (articles, lettres) dans tous les domaines des mathématiques, des applications à la physique, de la philosophie mathématique.

2. LES ANNALES ET LEUR IMPACT

Les Annales de Gergonne sont donc un document fondamental de l’histoire des sciences (et pas seulement des mathématiques). A leur suite, la presse périodique mathématique spécialisée allait se développer en France (Journal de mathématiques pures et appliquées de J. Liouville à partir de 1836, Nouvelles annales de mathématiques, journal des candidats aux Ecoles Polytechnique et Normale à partir de 1842) et en Europe (Journal für die reine und angewandte mathematik de Crelle, dit « Journal de Crelle », à partir de 1826 en Allemagne, Correspondance de Quételet au royaume des Pays-Bas puis en Belgique à partir de 1826, etc.) en suivant leur exemple, voire en récupérant les réseaux d’auteurs de Gergonne (dont en particulier celui des anciens élèves de l’Ecole Polytechnique).

Les Annales de Gergonne furent donc le premier grand périodique du 19ème siècle consacré uniquement aux mathématiques, et nul ne doute que son contenu se rapporte essentiellement à ce que nous nommons aujourd'hui ainsi. Cependant, le terme de géomètre est souvent préféré à celui de mathématicien. Certes, nous sommes au début du XIX° siècle, mais l'héritage classique pèse encore, y compris dans les dénominations, et en particulier dans ce cas: l'éternel géomètre" de Platon, le rang de "grand géomètre" attribué à Apollonius, et celui plus modeste de "géomètres" donné aux arpenteurs des rives du Nil, sont les exemples traditionnels que Gergonne reprend lui-même dans un article sur la synonymie mathématique [T. 8, 1817-1818, p. 156] :

Gergonne nous renseigne à la fois sur la persistance de l’emploi du terme de « géomètres », et sur sa propre vision des mathématiques, les seules « sciences exactes » à ses yeux. Finalement, les géomètres s’occupent de bien d’autres choses que de géométrie mais travaillent dans des domaines relevant de l’exactitude des raisonnements et des calculs, au sens de la logique déductive héritée d’Aristote et de Port Royal (et que Gergonne enrichit dans un long article de « dialectique rationnelle » au T.7, 1816-1817, p. 189-228), domaines qui seuls peuvent se retrouver sous l’appellation de « mathématiques » au sens où il l’entend. Le Prospectus permet d’apprécier les démarcations faites par le rédacteur entre « mathématiques pures », « sciences exactes » et applications :

Ces Annales seront principalement consacrées aux Mathématiques pures, et surtout aux recherches qui auront pour objet d'en perfectionner et d'en simplifier l'enseignement. Le titre de l'ouvrage annonce assez d'ailleurs que, si l'on n'y doit rien rencontrer d'absolument étranger au Calcul, à la Géométrie et à la Méchanique* rationnelle, les rédacteurs sont néanmoins dans l'intention de n'en rien exclure de ce qui pourra donner lieu à des applications de ces diverses branches des sciences exactes.

La dernière précaution permettra d’élargir le champ des mathématiques appliquées par exemple à des questions d’arithmétique politique, offrant ainsi une tribune au polémiste Gergonne qui publiera en 1815 et 1820 deux articles sur les méfaits du vote censitaire (6) . Mais, à de rares exceptions près, la seule discipline classée dans ces mathématiques appliquées que nous ne trouverons plus dans les revues ultérieures est celle de « philosophie mathématique » que Gergonne n’annonce d’ailleurs pas dans son Prospectus, si ce n’est peut-être dans l’expression « l’art de conjecturer » :

Ainsi, sous ce rapport, l'Art de conjecturer, l'Economie politique, l'Art militaire, la Physique générale, l'Optique, l'Acoustique, l'Astronomie, la Géographie, la Chronologie, la Chimie, la Minéralogie, la Météorologie, l'Architecture civile, la Fortification, l'Art nautique et les Arts mécaniques, enfin, pourront y trouver accès. On aura soin, au surplus, de consulter, à cet égard, le vœu du plus grand nombre des souscripteurs, et de s'y conformer scrupuleusement.

Un document de référence, publié en 1810, permet de situer les disciplines retenues par Gergonne par rapport à ce que l’on entendait officiellement par « mathématiques » à l’Institut : le Rapport à l’Empereur sur le progrès des sciences, des lettres et des arts depuis 1789, de Jean-Baptiste Delambre, et plus particulièrement de sa section I (mathématiques).

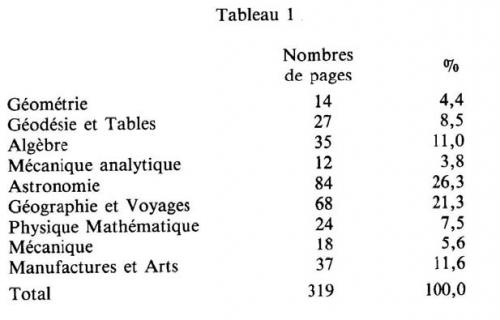
Ce tableau analytique est dû à Jean Dhombres (7) qui par ailleurs le compare aux champs mathématiques dans les mémoires de la première classe de l’Institut avant 1808. Les Annales de Gergonne sont donc bien un journal uniquement consacré aux mathématiques et à leurs applications, si l’on prend ces dernières en un sens assez large partagé à l’époque. Le souci premier des éditeurs (les « recherches qui auront pour objet d'en perfectionner et d'en simplifier l'enseignement ») sera en revanche largement contredit : un nombre important d’articles sont inaccessibles au commun des élèves ou des professeurs de collèges de l’époque, et exposent simplement le fruit de recherches et d’avancées en dehors du contexte scolaire, ou du moins à un niveau (école polytechnique, facultés, académies nationales) où les découvertes ont autant leur importance que la présentation didactique.

Le début du Prospectus nous indique la motivation première :

C'est une singularité assez digne de remarquer que, tandis qu'il existe une multitude de journaux relatifs à la Politique, à la Jurisprudence, à l'Agriculture, au Commerce, aux Science physiques et naturelles, aux Lettres et aux Arts; les Sciences exactes, cultivées aujourd'hui si universellement et avec tant de succès, ne comptent pas encore un seul recueil périodique qui leur soit spécialement consacré, un recueil qui permette aux Géomètres d'établir entre eux un commerce ou, pour mieux dire, une sorte de communauté de vues et d'idées; un recueil qui leur épargne les recherches dans lesquelles ils ne s'engagent que trop souvent en pure perte, faute de savoir que déjà elles ont été entreprises; un recueil qui garantisse à chacun la priorité des résultats nouveaux auxquels il parvient; un recueil enfin qui assure aux travaux de tous une publicité non moins honorable pour eux qu'utile au progrès de la sciences.

Et Gergonne ajoute en note de bas de page :

On ne saurait, en effet, considérer comme tels, le Journal de l'école Polytechnique, non plus que la Correspondance que rédige M. Hachette (8): recueils très précieux sans doute, mais qui, outre qu'ils ne paraissaient qu'à des époques peu rapprochées, sont consacrés presque uniquement aux travaux d'un seul établissement.

L’ambition est clairement affichée : établir une « émulation » (un « commerce d’idées ») au sein d’une « communauté » (celle des « géomètres » partageant justement une « communauté de vues et d’idées ») qui se reconnaîtrait et se ferait reconnaître, et assurer la « publicité » de travaux utiles « au progrès de la science », tout en garantissant à leurs auteurs de pouvoir ainsi s’assurer de la reconnaissance de leur « priorité des résultats nouveaux ». Le succès de l’entreprise, comme l’intérêt que suscitent encore aujourd’hui les Annales, seront révélateurs a posteriori de la pertinence de ces objectifs.

Emulation, publicité, communauté : arrêtons-nous un instant sur ces trois termes.

Gergonne insiste plus loin sur ce point dans le même document :

Chaque numéro des Annales offrira un ou plusieurs Théorèmes à démontrer, un ou plusieurs problèmes à résoudre. Les Rédacteurs, dans le choix de ces théorèmes et problèmes, donneront la préférence aux énoncés qui pourront leur être indiqués par leurs correspondans*; et ils consigneront, dans leur recueil, les démonstrations et solutions qui leur seront parvenues; ils espèrent ainsi provoquer chez les jeunes géomètres une utile et louable émulation. Personne n'ignore d'ailleurs combien ces sortes de défis ont ajouté de perfectionnement à l'analise*, au commencement du dernier siècle ; et il n’est point déraisonnable de penser qu'en les renouvelant, on peut, peut-être, lui préparer encore de nouveaux progrès.

L’émulation et les controverses s’exerceront bien au-delà des simples défis que représentaient les théorèmes non démontrés. Citons-en trois exemples, dont les deux premiers sont restés gravés dans l’histoire des mathématiques.

1. Le premier concerne le conflit en paternité, dont nous avons déjà parlé, entre Gergonne et Poncelet en 1826 sur le principe de dualité dans la géométrie projective. Le débat n’a pas été clos à l’époque, mais a été l’occasion de voir s’affirmer une branche des mathématiques qui montra par la suite son efficience. Les historiens ont depuis fait la part des choses, et rendu à César ce qui appartient à César, en montrant qu’en fin de compte les deux hommes avaient également participé, quoique suivant des approches différentes, à ce progrès des mathématiques en géométrie.

2. Le second a trait là-aussi à une revendication de paternité, mais sur le chapitre de la représentation géométrique des nombres imaginaires en 1814. Il implique tout d’abord Français et Argand, le premier publiant un essai sur cette représentation, le second répondant peu après par une lettre où il accuse Français d’avoir plagié son propre Essai qu’il avait publié en 1806, et en en adressant à Gergonne une version révisée que le rédacteur des Annales s’empresse de publier. Se joindront à cette polémique vite apaisée - Français reconnaissant ses torts, mais expliquant en quoi il était finalement innocent dans cette accusation de plagiat - Gergonne lui-même et l’algébriste Servois dans le cadre d’un débat élargi – philosophique, cette fois- sur la pertinence et la nécessité de cette référence à la géométrie pour légitimer les nombres complexes. L’Essai d’Argand de 1806 est à ce point fondamental dans l’histoire des mathématiques que nous y reviendrons, nous l’espérons, en le publiant sur BibNum avec une note historique et une étude de son contenu et des textes connexes (mathématiques et philosophiques).

3. Le troisième exemple, moins célèbre, est davantage représentatif de ce que Gergonne cherchait à produire au sein de l’ensemble de la communauté enseignant dans les nouvelles institutions issues de la Révolution et de l’Empire (collèges, lycées, Ecole Polytechnique, facultés, etc.). Il met en jeu pas moins de cinq acteurs (dont Gergonne lui-même). Le débat a commencé par une revendication de paternité entre Bret et Bérard sur une démonstration (9). D'autres protagonistes, Rochat et Du Bourguet, apportant leurs contributions a priori indépendantes sur le même sujet, se trouvent impliqués dans la polémique (10). Celle-ci se termine enfin, sur le sujet et entre les protagonistes initiaux, par un règlement de comptes peu courtois. La rixe s'est étendue sur un an et demi! Qu'y ont gagné les mathématiques? Le débat a fait avancer non seulement les considérations analytiques sur les coniques, mais plus généralement sur le théorème fondamental de l'algèbre. Le travail de Gauss est cité, et a donc davantage de chances d'être connu dans la communauté mathématique de l'époque. Des portes sont ouvertes aux autres professeurs et mathématiciens isolés qui n'avaient pas tous les moyens parisiens d'accès à l'information la plus récente. L'anecdote, a priori négligeable, a donc finalement servi l'histoire des mathématiques. Elle montre en outre l’intérêt de la fréquence mensuelle que Gergonne avait voulue pour son journal.

La promotion des travaux des mathématiciens ainsi visés se fera de deux façons différentes :

1. La première, déjà largement pratiquée dans les journaux savants des siècles précédents (le Journal des savans*, The Mathematical Repository, les Philosophical Transactions, etc.) consistera en des comptes-rendus d’ouvrages. Gergonne écrit à ce propos dans son Prospectus :

Enfin, un objet auquel on se propose de donner, dans ces Annales, une attention toute particulière, à raison de l'extrême utilité que le public peut en retirer, c’est l'annonce et l'analise* des ouvrages nouveaux, tant nationaux qu'étrangers, relatifs aux sciences mathématiques et aux autres sciences qui en dépendent.

Il restera fidèle à cette intention jusqu’au dernier numéro. Et la publicité qu’il fera par exemple au Journal de Crelle conduira à de fructueux échanges d’articles entre les deux personnages.

2. La publication des articles s’inscrivant dans la ligne éditoriale, quels qu’en soient les auteurs, et sans censure de classe ou de champ disciplinaire. On trouvera en effet tout au long des 22 années de publication des contributions d’élèves de collèges comme de membres d’académies ou de professeurs de facultés ou de grandes écoles, français ou étrangers, et la diversité des rubriques dont nous reparlerons plus loin vient confirmer l’esprit d’ouverture qui animait le rédacteur.

La « communauté » est donc très large.

Gergonne exprime une frustration liée à son éloignement de la capitale et de ses élites :

Les Rédacteurs des Annales sentent fort bien tout ce que la distance où ils se trouvent du centre des lumières peut ajouter de difficultés à leur entreprise; mais, plus jaloux de leur réputation et de l'estime des savans * que soigneux de leurs intérêts pécuniaires, ils sont résolus de faire tomber sur eux seuls tous les sacrifices auxquels la position peu commode où ils se trouvent doit inévitablement les exposer.

Il avoue son échec à convaincre les mêmes élites à fonder (avec lui) un tel journal :

Ils [les rédacteurs] avaient même fait, auprès de quelques personnes plus à portée et mieux en état qu'eux de l'exécuter, les démarches pressantes pour les solliciter à l'entreprendre; et le non succès de ces démarches a seul pu les enhardir à s'en charger eux-mêmes.

Et il veut intéresser ces élites :

Ils [les rédacteurs] osent croire (…) que les savans* même qui pourraient le mieux se passer des secours qu'un ouvrage de la nature de celui-ci est susceptible d'offrir, ne dédaigneront pas néanmoins d'accorder leur encouragement honorable à une entreprise dont le succès ne peut que contribuer encore à l'avancement de ces mêmes sciences.

Mario Otero et Jean Dhombres y ont vu la volonté d’un homme de donner la parole aux « oubliés », à une « communauté enseignante » isolée dans ses établissements de province (11). L’insistance que Gergonne mettra à obtenir le titre de correspondant de l’académie, ses engagements politiques avant et pendant sa carrière rectorale, ses courriers innombrables aux ministres, nous font plutôt penser à une volonté de se hisser à la hauteur de ces mêmes élites. Mais le résultat n’en est pas moins là. Si nous ne disposons pas de registres des abonnés, la population d’auteurs nous renseigne cependant sur la double réussite de son entreprise : la communauté enseignante dans son ensemble est représentée, et les mathématiciens de renom finiront par adhérer à son journal en y publiant des articles entre 1820 et 1830. En outre, on voit se constituer les différentes hiérarchies dans les instances du savoir en France : le titre d’ « ancien élève de l’Ecole Polytechnique » apparaît rapidement comme une référence, peu de temps finalement après la création de l’école.

Cependant, si l’on considère la première décennie de publication (1810-1820), on constate que le réseau des polytechniciens et des professeurs et élèves à Polytechnique publie essentiellement dans le Journal de cette école, ou dans la Correspondance de Hachette : bien que l’on ne puisse pas considérer ces deux publications comme des périodiques dédiés aux mathématiques (à cause de leurs contenus touchant à toutes les sciences, et de l’irrégularité de leur parution), c’est bien dans leurs pages que s’écrivent alors les avancées théoriques en mathématiques significatives d’une « spécialisation » de celles-ci. Les Annales de Gergonne sont donc finalement au départ une tribune offerte à ceux qui n’ont pas accès à ces deux publications (dont Gergonne lui-même).

Les contenus : une difficile classification

On voit dès le premier numéro la volonté de Gergonne de faire des mathématiques une vraie « spécialité », avec ses « ca­tégories ». Son Prospectus l’affirme, on l’a vu. Et l’organisation même de son journal en rubriques très spécialisées va dans le même sens, donnant l’impression d’une excessive dispersion tant sa volonté de classification, qui était selon lui la première condition toute aristotélicienne à l’organisation de savoirs scientifiques, le pousse à multiplier les rubriques, exercice délicat mais qui offre l’avantage d’un accès facilité aux contenus : les tables de fin de volumes sont en effet claires, détaillées, et permettent en outre de connaître les qualités et origines d’un grand nombre d’auteurs.

Les notes de bas de pages, ou les articles intitulés « notes sur l’article précédent » ajoutés par le rédacteur apportent en outre des informations complémentaires souvent fondamentales.

Enfin, les articles de « mathématiques appliquées » (optique, catoptrique, gnomonique, dynamique, hydrodynamique, météorologie, statique) répondent bien à l’intention première des éditeurs : ne « rien exclure de ce qui pourra donner lieu à des applications de ces diverses branches des sciences exactes ».

On est donc en principe devant ce que l’on peut considérer comme le premier journal consacré aux mathématiques en tant que spécialité scientifique à part entière, et animé et alimenté par un rédacteur et des auteurs qui préfigurent ce que nous nommons aujourd’hui des « spécialistes ». L’exemple du journal de Gergonne inspira, on l’a dit, l’allemand Crelle qui fonda en 1826 son propre mensuel, et les échanges d’articles entre les deux périodiques marquent une globalisation, une internationalisation des connaissances et de leur spécialisation.

Mais Gergonne est un personnage de transition, héritier des mathématiciens-philosophes des siècles précédents, et ses Annales sont ainsi représentatives d’une évolution de la connaissance scientifique de leur temps vers la spécialisation. Gergonne publie son journal dans un contexte de nécessité due à l’émancipation des mathématiques des anciennes disciplines dont elles relevaient (la mécanique et la philosophie - et à l’intérieur de celle-ci, la logique -), et à une difficulté croissante à les appréhender sans entrer dans une approche de spécialiste : la création des grandes écoles depuis 1793 - sous l’impulsion des scientifiques qui accompagnèrent les réformes -puis la création de l’Université par Napoléon, des lycées, des académies, des classes préparatoires, etc. font partie, comme l’édition d’un journal de mathématiques, de cette prise de conscience . Les mathématiques deviennent une matière à part entière, se dégageant peu à peu, sous l’influence d’un positivisme de plus en plus affirmé, des influences de la métaphysique et de la philosophie.

Il y a donc encore une ambivalence qui rattache les Annales de Gergonne aux journaux littéraires et savants du 18ème siècle. Un élément déterminant pour la compréhension de cette ambivalence et de ce polymorphisme du journal est l’étude de sa rubrique de « philosophie mathématique », présente tout au long de la publication.

CONCLUSION

Le Siècle des Lumières, la Révolution et l'Empire ont apporté les bouleversements que l'on sait, au plan des idées comme de la politique et des institutions. Dans le champ scientifique, si des instances existaient déjà avant 1793 (les sociétés savantes, dont l'académie royale, les académies étrangères et de province; des universités peu exigeantes et souvent laxistes, des écoles militaires d'assez bonne tenue), si les échanges et les publications étaient de plus en plus nombreux, il manquait une cohérence à l'ensemble car les frontières entre les diverses sciences étaient encore floues, et la communication par le seul bais des correspondances privées ou des ouvrages ne permettait pas une réactivité suffisante. L'œuvre de Gergonne, comme son Prospectus l’annonce, aura permis de délimiter plus précisément le champ mathématique, de faire un inventaire quasi-exhaustif des connaissances et des avancées de l'époque en la matière, de donner à la création mathématique un caractère démocratique en ne la réservant pas aux seules élites, d'apporter, çà et là, un formalisme nouveau propre à éclairer les sciences empiriques, et de jeter les bases, par des considérations d'ordre épistémologique, didactique ou de logique formelle, comme par de modestes ou de primordiales avancées mathématiques, des progrès à venir: la simple étude des concepts en germe dans les Annales est à ce titre passionnante. En outre, avec elles, une forme moderne de communication et d’échanges dans les mathématiques était née : celle du périodique, plus ouvert, plus réactif, donc plus adapté à la rapide évolution des savoirs au 19ème siècle.*

(1) Grâce aux compétences du programme CNRS « NUDAM » de numérisation des archives de mathématiques, et à l’accord du ministère de la culture via la bibliothèque municipale de Nîmes, détentrice de l’un des rares exemplaires complets du journal.

(2) Nous signalerons par un * les mots écrits dans leur orthographe d’origine : élémens, analise, mechanique, etc.

(3) Registre des délibérations de la faculté des sciences de Montpellier de 1812 à 1846, Archives de l'Université de Montpellier; cité dans : Cécile de Saint-Victor, La fâcheuse lacune: John Stuart Mill à Montpellier, Bulletin Historique de la ville de Montpellier, N°14, 1990, pp. 18-24.

(4) Voir à ce sujet notre chapitre : Joseph-Diez Gergonne (1771-1859). Le zèle d’un fonctionnaire et l’esprit critique d’un libre penseur in : « Le recteur d’académie. Deux cents ans d’histoire », J.-F. Condette et H. Legohérel (Dir.), Cujas, Paris, 2008.

(5) Avant de le définir dans son article du T. XVI (1825-1826), Gergonne avait déjà mis en jeu le principe de dualité, par exemple au T.XV: Recherche des lois générales qui régissent les polyèdres, "Géométrie élémentaire", pp. 157-164.

(6) J.D. Gergonne, Quelques remarques sur les élections, les assemblées délibérantes et le système représentatif, dans : Annales de Mathématiques Pures et appliquées, T. VI, pp. 1-11, juillet 1815 ; Sur les élections et le système représentatif, dans : Annales de Mathématiques Pures et appliquées, T. X (année 1819-1820), pp. 281-288.

(7) Rapports à l’Empereur sur le progrès des sciences, des lettres et des arts. I/ Sciences mathématiques, par Jean Baptiste Delambre. Réédition Belin, Paris, 1889, avec préface de Jean Dhombres.

(8) Gergonne fait référence ici à la Correspondance scientifique de l'Ecole Polytechnique de J.N.P. Hachette, parue de 1804 à 1816.

(9) Au tome II, dans la rubrique Géométrie analytique, Bret, alors professeur de mathématiques transcendantes au lycée de Grenoble, signe un article intitulé Discussion sur des équations du second degré entre deux variables (daté de janvier 1812; pp. 218-224). Il étudie dans un premier temps les coniques à centre, pour terminer sur une construction des la parabole " fondée sur cette propriété de la parabole rapportée soit à son axe soit à ses diamètres, savoir: que la sous-tangente est double de l'abscisse du point de contact". Le 7 juillet 1812, Bérard, principal et professeur de mathématiques au collège de Briançon, signe une lettre au rédacteur des Annales dans le T. III (pp. 97-98) dans laquelle il revendique la paternité de la méthode employée par Bret "qui, à la rédaction près, est exactement celle que l'on trouve à la page 75 de mes Opuscules mathématiques (un volume in 8°; chez Louis, libraire, rue de Savoie, N°6, Paris), publiée en 1810; méthode que je lui avais communiquée dès le mois d'août 1808." Ne mettant pas en cause " l'honnêteté et la délicatesse de M. Bret, la réputation dont il jouit comme géomètre", il suppose poliment "qu'ayant perdu la communication que je lui en avais faite, il n'a publié cette méthode sous son nom que parce qu’il a cru, en effet, ne la devoir qu'à ses propres réflexions."

(10) Toujours dans le tome II, pages 3231-335, Rochat, professeur de navigation à Saint Brieux, donne une autre méthode concernant la "construction des formules qui servent à déterminer la grandeur et la situation des diamètres principaux, dans les courbes du second degré rapportées à deux axes rectangulaires quelconques."; et Du Bourguet, professeur de mathématiques spéciales au lycée impérial, apporte sa "démonstration du principe qui sert de fondement à la théorie des équations" [T. II; pp. 338-340]. Bret, entre-temps devenu professeur à la faculté des sciences de l'académie de Grenoble, répond aux deux précédents, le 7 mai 1812, dans une lettre à Gergonne, en relevant une négligence de Rochat, et en démontrant que le "principe" de Du Bourguet n'est pas correctement établi et que, Gauss ayant démontré que toute équation est décomposable en facteurs réels du second degré, ce principe n'en est qu'une "vulgaire conséquence"[T. III; pp. 31-34]. La polémique se poursuivra tout au long de pas moins de sept autres lettres et articles, et aura couvert les années 1811-1812-1813 (Tomes II, III et IV).

(11) Jean Dhombres et Mario Otero, Les Annales de mathématiques pures et appliquées, le journal d'un homme seul au profit d'une communauté enseignante, in E. Ausejo, M. Hormigón (éd.), Messengers of mathematics, Madrid, 1993, pp. 1-53.