
Cournot : un savant éclectique et précurseur
Antoine Augustin Cournot (1801-1877) fut un scientifique polyvalent. Mathématicien de formation, il s’intéressa assez vite à l’économie. Alors que les économistes qui le précédèrent travaillaient essentiellement de façon qualitative, sans utiliser de raisonnements mathématiques autres que de simples calculs algébriques élémentaires, Cournot fut le premier à faire appel à l’analyse mathématique
(1) pour traiter des problèmes économiques ; à ce titre, de nombreux économistes le considèrent comme le fondateur de l’économie scientifique. Ses travaux sont aujourd’hui considérés comme étant à la base de la théorie moderne des prix ; ils annoncent la création du
marginalisme (2).
Cournot est aussi considéré comme un précurseur de l’économétrie et de la théorie des jeux ; en effet, d’une part, il chercha à construire une loi empirique de la demande à partir d’observations ce qui est précisément un objet essentiel de l’économétrie, et, d’autre part, il construisit un modèle de compétition entre deux firmes et anticipa ainsi la notion d’équilibre développée plus tard par J.F. Nash, lauréat du Prix Nobel d’économie en 1994 ; il fallut attendre plus d’un siècle pour voir se développer ces deux disciplines désormais incontournables en économie.
Toutefois, les mérites des travaux économiques de Cournot ne furent reconnus qu’à titre posthume. Cela peut probablement être expliqué par la période pendant laquelle l’auteur vécut ; elle se situe en effet juste entre deux courants économiques majeurs : d’une part, la période classique des XVIIème et XVIIIème siècles, avec comme représentants célèbres Smith, Ricardo, Malthus ou encore Say, et, d’autre part, la période néo-classique de la fin du 19ème siècle, avec des savants tels que Jevons, Walras, Menger, Marshall ou Hicks.
Cournot fut encore un grand pédagogue, auteur notamment d’un cours d’analyse mathématique
(3) dans lequel il exposa de façon claire et pratique les fondements de l’analyse en insistant sur les motivations et les liens entre les matières présentées ; il y réalisa notamment une remarquable synthèse des résultats connus à l’époque, où il compara les approches de Leibniz et de Newton.
Enfin, Cournot est aussi réputé pour ses travaux de nature philosophique, spécialement pour ses travaux sur le hasard et le calcul des probabilités
(4).
Première apparition de l’analyse mathématique en économie
Le chapitre que nous avons sélectionné est issu d’une des premières œuvres de Cournot, à savoir « Recherches sur les principes mathématiques de la théorie des richesses »
(5) en 1838. Comme le mentionne l’auteur dans sa préface :
Je me propose d’établir dans cet essai que la solution des équations générales, auxquelles donne lieu la théorie des richesses, dépend essentiellement, non pas de l’algèbre élémentaire, mais de cette branche de l’analyse qui a pour objet des fonctions arbitraires, assujetties seulement à satisfaire à certaines conditions
(6).
Cette approche de l’économie était assurément inédite à cette époque ; de fait, l’auteur lui-même écrivait :
C’est là, je le confesse, un plan qui doit m’attirer tout d’abord la réprobation des théoriciens accrédités. Tous se sont élevés comme de concert contre l’emploi des formes mathématiques
(7).
Pour l’anecdote, signalons que, conformément aux attentes de l’auteur, cet ouvrage n’a guère connu de succès à sa publication, au point que le mathématicien se décida, vingt-cinq ans plus tard, à réécrire complètement son livre, à le rebaptiser simplement « Principes de la théorie des richesses » et à n’utiliser cette fois qu’un « langage littéraire ». Notre analyse portera essentiellement sur la première version de l’ouvrage, celle de 1838.
@@@@@@@
De manière plus précise, Cournot s’intéressa essentiellement aux « fondements de la théorie des valeurs échangeables » en basant son raisonnement sur « un seul axiome », à savoir que « chacun cherche à tirer de sa chose ou de son travail la plus grande valeur possible ».
Dans le passage choisi est considérée la « demande », aussi appelée par l’auteur « débit » d’un bien : la demande annuelle D dépend du prix unitaire p et, le plus souvent, de façon inverse : plus le prix augmente, et plus la quantité demandée va, en général
(8), diminuer, mais cette dépendance n’est d’habitude pas de type proportionnel. Bien plus, comme le signale le savant,
puisque tant de causes morales, et qu’on ne peut énumérer ni mesurer, influent sur la loi de demande, il est clair qu’on ne doit pas s’attendre à ce que cette loi puisse être exprimée par une formule algébrique.
C’est pourquoi, Cournot fait appel au concept mathématique de fonction, en supposant que
le débit ou la demande annuelle D est, pour chaque denrée, une fonction particulière F(p) du prix p de cette denrée.
Sans donner à la fonction de demande une forme algébrique explicite, Cournot se contente de lui imposer certaines hypothèses générales et très naturelles : la fonction F est supposée décroissante, continue et même dérivable
(9) en donnant notamment les explications suivantes :
Une denrée est ordinairement d’autant plus demandée qu’elle est moins chère (p.48) (…) les variations de la demande seront sensiblement proportionnelles aux variations du prix, tant que celles-ci seront de petites fractions du prix originaire (p.54) (…) la loi de la demande ou du débit est une fonction continue, c’est-à-dire qui ne passe pas soudainement d’une valeur à une autre, mais qui prend dans l’intervalle toutes les valeurs intermédiaires. Bien sûr, il peut exister des cas de non continuité, mais de même que le frottement use les aspérités et adoucit les contours, ainsi la triture du commerce tend à supprimer ces cas exceptionnels (p.55)
Maximisation du revenu total
Au lieu de s’interroger, comme ses prédécesseurs, sur les origines et la formation de la valeur, Cournot s’est donc demandé dans quelles conditions la valeur est la plus grande possible : cette formalisation nouvelle possède le grand avantage de pouvoir se traduire aisément en langage mathématique. Ainsi, conformément à son « axiome » de base, l’auteur a cherché à rendre maximal le revenu total égal à la valeur totale débitée annuellement. A cet effet, il se proposa de maximiser la fonction R : p → R(p) = pF(p) qui exprime le revenu, à savoir le prix multiplié par la quantité demandée. On peut donner une représentation graphique de cette dernière fonction avec les indications de l’auteur. En effet, dans le plan dont l’axe horizontal se rapporte aux prix p et l’axe vertical aux valeurs de
R(p), la courbe, située dans le premier quadrant, part de l’origine (car
R(0) = 0), croît avant de décroître vers l’axe horizontal (car
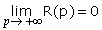
: en effet, au fur et à mesure que le prix augmente, la quantité demandée diminue pour s'annuler "à la limite").
La fonction pF(p) s’évanouit encore quand p devient infini, ou en d’autres termes on peut toujours assigner par la pensée au nombre p une valeur assez grande pour que la denrée cesse d’être demandée et produite à ce prix.
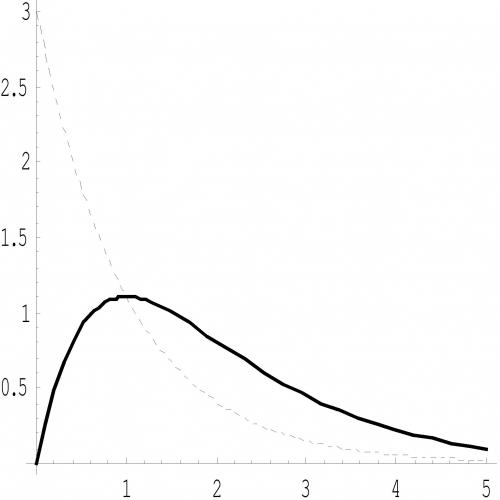
Figure 1 : représentation des courbes de demande F(p) (en pointillés) et de revenu pF(p) (en gras).
Le problème à résoudre consiste à trouver le point où cette courbe atteint son point le plus haut. Analytiquement, la réponse à cette question est fournie par le théorème de Fermat relatif aux maxima (10), c’est-à-dire par l’annulation de la dérivée de la fonction R par rapport à la variable p : elle est donc donnée par l’équation suivante :
F(p) + pF’(p) = 0 (1)
Remarquons que Cournot appelle « notation de Lagrange » la dérivée F’ de la fonction de débit D. La question étudiée est également résolue par l’auteur géométriquement à partir de la représentation graphique de la fonction donnant la quantité demandée F(p) en fonction du prix p.
Cournot affirme (voir figure 2) qu’au maximum, « le triangle ont (…) est isoscèle, de sorte qu’on a oq = qt ». En effet, sachant qu’on a toujours
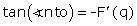 et
et 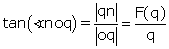 , donc le triangle est bien isocèle.
, donc le triangle est bien isocèle.
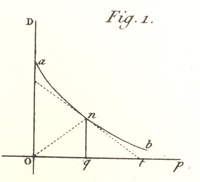
Figure 2: première figure dans la planche du livre de Cournot. Elle représente la fonction F(p) en fonction du prix p.
Mais, l’égalité
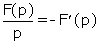
est toute théorique puisque la fonction de demande est inconnue explicitement. C’est pourquoi, Cournot propose de déterminer concrètement le prix assurant le maximum recherché en examinant les variations des grandeurs considérées.
Prémisses du concept économique d’élasticité
Dans le texte original, l’auteur a fait appel aux variations de la demande et du prix en valeurs absolues : lorsque le prix p augmente de Δp, la demande D devient alors égale à D - ΔD, d’où ΔD > 0 puisque la fonction de débit est supposée décroissante.
On peut ensuite penser que Cournot remplace, dans l’égalité (1), F’(p) par 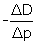 , pareille approximation étant couramment utilisée à son époque (11). Un tel passage du discret, avec les variations ΔD et Δp, au continu, avec la dérivée F’(p), peut être rigoureusement expliqué de nos jours de deux manières : soit classiquement en faisant tendre Δp vers 0, soit dans le cadre de l’analyse non standard (12) en choisissant Δp infiniment petit. Observons au passage que Cournot travaillait déjà dans l’esprit de l’analyse non standard, pourtant créée plus d’un siècle plus tard, ainsi qu’en atteste notamment le phrase suivante : « la fonction p F(p) s’évanouit encore quand p devient infini ». Ainsi donc, l’auteur s’intéresse au signe de l’expression E =
, pareille approximation étant couramment utilisée à son époque (11). Un tel passage du discret, avec les variations ΔD et Δp, au continu, avec la dérivée F’(p), peut être rigoureusement expliqué de nos jours de deux manières : soit classiquement en faisant tendre Δp vers 0, soit dans le cadre de l’analyse non standard (12) en choisissant Δp infiniment petit. Observons au passage que Cournot travaillait déjà dans l’esprit de l’analyse non standard, pourtant créée plus d’un siècle plus tard, ainsi qu’en atteste notamment le phrase suivante : « la fonction p F(p) s’évanouit encore quand p devient infini ». Ainsi donc, l’auteur s’intéresse au signe de l’expression E = 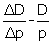 , qui se retrouve aisément dans la condition (1). En effet, pour autant que l’on assimile le rapport
, qui se retrouve aisément dans la condition (1). En effet, pour autant que l’on assimile le rapport 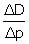 à la valeur de la dérivée la loi de demande, on a :
à la valeur de la dérivée la loi de demande, on a :
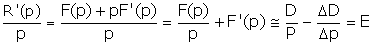
La dérivée R’ est négative ou positive (d’où la fonction R est décroissante ou croissante), selon que E < 0 ou E > 0 respectivement. De façon équivalente, Cournot écrit :
(…) selon que l’on aura
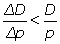
ou
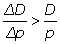
, l’accroissement de prix Δp fera augmenter ou diminuer le produit pF(p) ; et l’on saura conséquemment si les deux valeurs p, p + Δp (…) tombent en deçà ou au-delà de la valeur qui porte au maximum le produit en question.
Or, les inégalités envisagées par Cournot peuvent évidemment s’écrire sous la forme équivalente 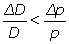 ou encore
ou encore 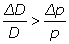 . Cela revient alors à comparer les variations relatives de la demande et du prix, ce qui convient bien aux raisonnements des économistes. Ces deux dernières inégalités mises en avant pour résoudre son problème, soit s’écrivent de façon équivalente
. Cela revient alors à comparer les variations relatives de la demande et du prix, ce qui convient bien aux raisonnements des économistes. Ces deux dernières inégalités mises en avant pour résoudre son problème, soit s’écrivent de façon équivalente 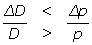 ou encore
ou encore 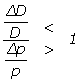 . Ces considérations permettent de penser que Cournot avait déjà perçu tout l’intérêt du concept économique d’élasticité, dont la paternité est pourtant souvent attribuée à l’anglais A. Marshall (1842 – 1924). En effet, dans son célèbre ouvrage Principles of Economics (1890), Marshall recourait au rapport des variations relatives de la demande et du prix et appelait ce rapport « élasticité » (13) de la demande. Depuis lors, les économistes évoquent, selon les situations étudiées, deux types d’élasticité que l’on nomme fréquemment « élasticité-arc » et « élasticité-point » ; il est remarquable de constater que Cournot entrevoyait déjà ces deux possibilités.
. Ces considérations permettent de penser que Cournot avait déjà perçu tout l’intérêt du concept économique d’élasticité, dont la paternité est pourtant souvent attribuée à l’anglais A. Marshall (1842 – 1924). En effet, dans son célèbre ouvrage Principles of Economics (1890), Marshall recourait au rapport des variations relatives de la demande et du prix et appelait ce rapport « élasticité » (13) de la demande. Depuis lors, les économistes évoquent, selon les situations étudiées, deux types d’élasticité que l’on nomme fréquemment « élasticité-arc » et « élasticité-point » ; il est remarquable de constater que Cournot entrevoyait déjà ces deux possibilités.
Deux types d’élasticité
Reprenons les notations de Cournot. Le rapport 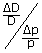 se nomme aujourd’hui « élasticité-arc » (de la demande D lorsque le prix p augmente de Δp). Cette appellation provient du fait que ce rapport dépend de l’arc de la courbe de demande comprise entre les abscisses p et p + Δp. Cette notion s’emploie le plus souvent quand l’on se trouve dans un cas discret où la demande est fournie sous la forme d’un tableau donnant les valeurs de D pour différentes valeurs de p. Lorsque la fonction
se nomme aujourd’hui « élasticité-arc » (de la demande D lorsque le prix p augmente de Δp). Cette appellation provient du fait que ce rapport dépend de l’arc de la courbe de demande comprise entre les abscisses p et p + Δp. Cette notion s’emploie le plus souvent quand l’on se trouve dans un cas discret où la demande est fournie sous la forme d’un tableau donnant les valeurs de D pour différentes valeurs de p. Lorsque la fonction 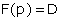 est dérivable, on considère alors l’ « élasticité-point »
est dérivable, on considère alors l’ « élasticité-point » 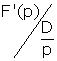 ; en d’autres termes, l’élasticité-point est le rapport entre la valeur, appelée marginale, F’(p) et la valeur moyenne D/p ; ce rapport ne dépend que du point d’abscisse p sur la courbe de demande et non plus de Δp. Ces deux concepts d’élasticité-arc et d’élasticité-point sont proches l’un de l’autre en valeur absolue si l’on remarque, comme l’avait fait Cournot, que F’(p) peut être approché par
; en d’autres termes, l’élasticité-point est le rapport entre la valeur, appelée marginale, F’(p) et la valeur moyenne D/p ; ce rapport ne dépend que du point d’abscisse p sur la courbe de demande et non plus de Δp. Ces deux concepts d’élasticité-arc et d’élasticité-point sont proches l’un de l’autre en valeur absolue si l’on remarque, comme l’avait fait Cournot, que F’(p) peut être approché par 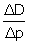 lorsque Δp est petit.
lorsque Δp est petit.
L’élasticité-prix
Pour terminer notre analyse, épinglons ce signe supplémentaire, et à nouveau précurseur, de la perspicacité de Cournot. Dans le dernier paragraphe de l’extrait, les biens sont classés
en deux catégories, selon que leurs prix courants restent inférieurs ou supérieurs à la valeur productrice du maximum de p F(p),
c’est-à-dire selon que l’élasticité est (en valeur absolue) inférieure ou supérieure à l’unité.
C’est ce qu’on appelle à présent des biens inélastiques ou élastiques. Remarquons encore que lorsque la loi de la demande est traduite géométriquement par une droite
(14), le raisonnement géométrique fourni par Cournot s’avère particulièrement efficace : le triangle isocèle construit sur le maximum de Cournot (figure 3) permet de distinguer aisément le caractère élastique ou inélastique des biens, ainsi que le cas d’élasticité unitaire.
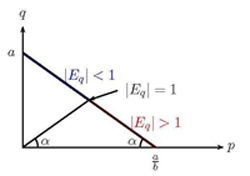
Figure 3 : Les trois types d’élasticité, en fonction du maximum de Cournot. Le point E = 1 est le maximum de la courbe pF(p) tel que donné par Cournot en figure 2 ci-dessus. Pour simplifier, prenons l’exemple D = -10p + 100 ; le maximum de Cournot (qui maximise Dp) est à p = 5 ; l’élasticité est E = pF’(p)/F(p) = -10p/(-10p + 100). À gauche (p < 5), ce sont les biens inélastiques ou faiblement élastiques (|E| < 1) : le prix est inférieur au maximum de Cournot, une augmentation de prix n’entraîne pas une diminution importante de la demande : par exemple, p = 3, une augmentation de prix de 10% entraîne une baisse de 4,3% de la demande (D baisse de 70 à 67). Au maximum de Cournot (p = 5), ce sont les biens d’élasticité unitaire (|E| = 1) : une augmentation de prix de 10% entraîne une baisse de 10% de la demande (D baisse de 50 à 45). À droite (p > 5), ce sont les biens fortement élastiques (|E| > 1) : le prix est supérieur au maximum de Cournot, une augmentation de prix entraîne une diminution plus importante de la demande : par exemple, p = 8, une augmentation de prix de 10% entraîne une baisse de 40% de la demande (D baisse de 20 à 12).
Pour reprendre les notations de la figure ci-dessus, les biens peu élastiques (|E| < 1) peuvent être des biens « nécessaires », dont le prix est inférieur au maximum de Cournot, et dont le besoin subsiste même en cas d’augmentation de prix ; entre dans cette catégorie la nourriture par exemple. Les biens fortement élastiques (|E| > 1) peuvent être
(15) des biens « superflus », dont le prix est supérieur au maximum de Cournot ; entrent dans cette catégorie les produits de luxe par exemple.
Comme l’indique Cournot :
La demande pourrait être en raison inverse du prix ; ordinairement, elle croît ou décroît dans une proportion beaucoup plus rapide : observation qui s’applique surtout au plus grand nombre des produits manufacturés. D’autres fois, au contraire, la variation de la demande est moins rapide ; ce qui paraît (chose singulière) s’appliquer également aux choses les plus nécessaires, et aux choses les plus superflues. Le prix des violons, celui des lunettes astronomiques, baisserait de moitié que probablement la demande ne doublerait pas ; car cette demande est déterminée par le nombre de ceux qui cultivent l’art ou la science auxquels ces instruments se rapportent (…) Le bois de chauffage qui est au contraire une denrée des plus utiles, pourrait doubler de prix, par suite des progrès du défrichement ou de l’accroissement de la population, probablement bien avant que la consommation annuelle de bois eût été réduite de moitié ; un grand nombre de consommateurs étant disposés à retrancher sur les autres dépenses plutôt que de se passer de bois.
C’est la naissance du concept d’élasticité en économie, qui après Cournot sera développé par Léon Walras (1834-1910) et Alfred Marshall (1842-1924).

(1) L’analyse mathématique est née quelques décennies plus tôt, principalement grâce aux travaux d’Isaac Newton et de Gottfried Leibniz.
(2) Théorie économique selon laquelle la valeur économique résulte de l’ « utilité marginale » ; elle fut créée, aux environs de 1870, indépendamment par William Jevons (1835-1882) en Angleterre, Léon Walras (1834-1910) en Suisse et Carl Menger (1840-1921) en Autriche.
(3) Le titre de cet ouvrage, publié en 1841, est le suivant : « Traité élémentaire de la théorie des fonctions et du calcul infinitésimal »
(4) La naissance rigoureuse de la théorie des probabilités remonte à la présentation axiomatique qu’en fit le russe Kolmogorov vers les années 1930.
(5) Nous nous référerons au texte original, de la Librairie de l’Université Royale de France chez L. Hachette, publié aux éditions Bizzarri.
(6) Cournot, 1838, p. IX.
(8) Il existe trois situations classiques pour lesquelles la quantité demandée croît en même temps que le prix : a) Le paradoxe de Giffen qui concerne la consommation de biens de grande nécessité, par exemple le pain ; en effet, une hausse de prix du pain absorbe une part importante du revenu d'un travailleur, de sorte que celui-ci doit parfois renoncer à se procurer d'autres denrées, plus luxueuses mais aussi plus coûteuses, et les remplacer par du pain. b) L'effet Veblen, lorsqu'un bien est convoité pour son prix élevé, principalement en fonction de la signification sociale de son achat. Il en est ainsi pour certains objets de luxe, comme le diamant, qui seraient probablement moins demandés si leur prix était moins élevé. c) La spéculation : lorsqu'une hausse de prix est annoncée et que les consommateurs croient en la poursuite de ce mouvement des prix : ils peuvent alors augmenter leur demande, par exemple pour faire des "provisions".
(9) En réalité, Cournot supposait simplement continue la fonction F, car, à son époque, les concepts de continuité et de dérivabilité étaient souvent confondus.
(11) Cette démarche est encore pratiquée par de nombreux économistes contemporains.
(12) Cette présentation moderne de l’analyse mathématique a été initiée, vers les années 1960, par le mathématicien américain A. Robinson ; celui-ci a étendu le corps classique des nombres réels à celui des nombres dits « hyperréels » au sein duquel se trouvent notamment des nombres infiniment petits (voir l’onglet « Pour en savoir plus »).
(13) Marshall désignait encore l’élasticité par l’appellation responsiveness, car il était probablement conscient de la différence entre le concept économique étudié et la perception courante qu’en donne la physique : effectivement, l’élasticité traduit bien la façon dont une grandeur réagit sous l’influence de la variation d’une autre, mais, en économie, ne se réfère pas à un retour à sa situation initiale.
(14) C’est la cas lorsque la fonction de demande est affine. Cette hypothèse est très souvent supposée en première approche par les économistes qui parlent alors de demande linéaire.
(15) Nous donnons ici une simplification du premier ordre : l’élasticité faible (resp. forte) ne correspond pas en toutes circonstances aux biens nécessaires (resp. superflus). La citation de Cournot qui suit le montre bien (voir aussi note 8 ci-dessus).




![]() et
et 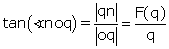 , donc le triangle est bien isocèle.
, donc le triangle est bien isocèle.
![]() , pareille approximation étant couramment utilisée à son époque (11). Un tel passage du discret, avec les variations ΔD et Δp, au continu, avec la dérivée F’(p), peut être rigoureusement expliqué de nos jours de deux manières : soit classiquement en faisant tendre Δp vers 0, soit dans le cadre de l’analyse non standard (12) en choisissant Δp infiniment petit. Observons au passage que Cournot travaillait déjà dans l’esprit de l’analyse non standard, pourtant créée plus d’un siècle plus tard, ainsi qu’en atteste notamment le phrase suivante : « la fonction p F(p) s’évanouit encore quand p devient infini ». Ainsi donc, l’auteur s’intéresse au signe de l’expression E =
, pareille approximation étant couramment utilisée à son époque (11). Un tel passage du discret, avec les variations ΔD et Δp, au continu, avec la dérivée F’(p), peut être rigoureusement expliqué de nos jours de deux manières : soit classiquement en faisant tendre Δp vers 0, soit dans le cadre de l’analyse non standard (12) en choisissant Δp infiniment petit. Observons au passage que Cournot travaillait déjà dans l’esprit de l’analyse non standard, pourtant créée plus d’un siècle plus tard, ainsi qu’en atteste notamment le phrase suivante : « la fonction p F(p) s’évanouit encore quand p devient infini ». Ainsi donc, l’auteur s’intéresse au signe de l’expression E = ![]() , qui se retrouve aisément dans la condition (1). En effet, pour autant que l’on assimile le rapport
, qui se retrouve aisément dans la condition (1). En effet, pour autant que l’on assimile le rapport ![]() à la valeur de la dérivée la loi de demande, on a :
à la valeur de la dérivée la loi de demande, on a :![]()
![]() ou encore
ou encore ![]() . Cela revient alors à comparer les variations relatives de la demande et du prix, ce qui convient bien aux raisonnements des économistes. Ces deux dernières inégalités mises en avant pour résoudre son problème, soit s’écrivent de façon équivalente
. Cela revient alors à comparer les variations relatives de la demande et du prix, ce qui convient bien aux raisonnements des économistes. Ces deux dernières inégalités mises en avant pour résoudre son problème, soit s’écrivent de façon équivalente ![]() ou encore
ou encore 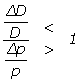 . Ces considérations permettent de penser que Cournot avait déjà perçu tout l’intérêt du concept économique d’élasticité, dont la paternité est pourtant souvent attribuée à l’anglais A. Marshall (1842 – 1924). En effet, dans son célèbre ouvrage Principles of Economics (1890), Marshall recourait au rapport des variations relatives de la demande et du prix et appelait ce rapport « élasticité » (13) de la demande. Depuis lors, les économistes évoquent, selon les situations étudiées, deux types d’élasticité que l’on nomme fréquemment « élasticité-arc » et « élasticité-point » ; il est remarquable de constater que Cournot entrevoyait déjà ces deux possibilités.
. Ces considérations permettent de penser que Cournot avait déjà perçu tout l’intérêt du concept économique d’élasticité, dont la paternité est pourtant souvent attribuée à l’anglais A. Marshall (1842 – 1924). En effet, dans son célèbre ouvrage Principles of Economics (1890), Marshall recourait au rapport des variations relatives de la demande et du prix et appelait ce rapport « élasticité » (13) de la demande. Depuis lors, les économistes évoquent, selon les situations étudiées, deux types d’élasticité que l’on nomme fréquemment « élasticité-arc » et « élasticité-point » ; il est remarquable de constater que Cournot entrevoyait déjà ces deux possibilités.![]() se nomme aujourd’hui « élasticité-arc » (de la demande D lorsque le prix p augmente de Δp). Cette appellation provient du fait que ce rapport dépend de l’arc de la courbe de demande comprise entre les abscisses p et p + Δp. Cette notion s’emploie le plus souvent quand l’on se trouve dans un cas discret où la demande est fournie sous la forme d’un tableau donnant les valeurs de D pour différentes valeurs de p. Lorsque la fonction
se nomme aujourd’hui « élasticité-arc » (de la demande D lorsque le prix p augmente de Δp). Cette appellation provient du fait que ce rapport dépend de l’arc de la courbe de demande comprise entre les abscisses p et p + Δp. Cette notion s’emploie le plus souvent quand l’on se trouve dans un cas discret où la demande est fournie sous la forme d’un tableau donnant les valeurs de D pour différentes valeurs de p. Lorsque la fonction ![]() est dérivable, on considère alors l’ « élasticité-point »
est dérivable, on considère alors l’ « élasticité-point » 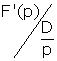 ; en d’autres termes, l’élasticité-point est le rapport entre la valeur, appelée marginale, F’(p) et la valeur moyenne D/p ; ce rapport ne dépend que du point d’abscisse p sur la courbe de demande et non plus de Δp. Ces deux concepts d’élasticité-arc et d’élasticité-point sont proches l’un de l’autre en valeur absolue si l’on remarque, comme l’avait fait Cournot, que F’(p) peut être approché par
; en d’autres termes, l’élasticité-point est le rapport entre la valeur, appelée marginale, F’(p) et la valeur moyenne D/p ; ce rapport ne dépend que du point d’abscisse p sur la courbe de demande et non plus de Δp. Ces deux concepts d’élasticité-arc et d’élasticité-point sont proches l’un de l’autre en valeur absolue si l’on remarque, comme l’avait fait Cournot, que F’(p) peut être approché par ![]() lorsque Δp est petit.
lorsque Δp est petit.

 Les œuvres complètes de Cournot sont rassemblées dans 10 tomes publiés par la Librairie Philosophique J. Vrin. Certaines sont aussi numérisées par BnF-Gallica, la plupart des tomes étant accessibles par internet sur le site LiNuM (faire une recherche Cournot dans le champ).
Les œuvres complètes de Cournot sont rassemblées dans 10 tomes publiés par la Librairie Philosophique J. Vrin. Certaines sont aussi numérisées par BnF-Gallica, la plupart des tomes étant accessibles par internet sur le site LiNuM (faire une recherche Cournot dans le champ).
 • Analyse infinitésimale : le calculus redécouvert, par Bair J. et Henry V , éditions Academia-Bruylant, Louvain-la-Neuve, 2008.
• Analyse infinitésimale : le calculus redécouvert, par Bair J. et Henry V , éditions Academia-Bruylant, Louvain-la-Neuve, 2008.





