L'étude de la chaînette résulte d'un défi lancé par Jacques Bernoulli et relevé avec succès par Leibniz, ainsi que par Jean Bernoulli et Huygens : trouver la courbe décrite par un fil suspendu à ses deux extrémités. Stimulé par le succès de cette première recherche, Jean Bernoulli posa et résolut des problèmes similaires : forme que prend une lame horizontale fixée d'un côté avec un poids suspendu de l'autre, forme prise par un linge rempli de liqueur, courbure d'une voile.
Il était de coutume au 17e siècle de se lancer des défis par revue interposée. Leibniz, par exemple, mit au défi les cartésiens, dans le cadre de la controverse sur les lois du choc, dite « querelle des forces vives », de trouver la courbe le long de laquelle un corps pesant tombe à vitesse verticale constante (courbe isochrone). Proposé dans la Nouvelle République des Lettres de septembre 1687, ce problème reçut la solution de Huygens en octobre de la même année, et celle de Leibniz parut en 1689 dans la revue qu’il avait créée, les Acta Eruditorum. Un autre exemple célèbre est celui de la brachistochrone, « courbe de plus brève descente », qui s’avéra, grâce au nouveau calcul différentiel, être non pas un cercle, comme le croyait Galilée, mais une cycloïde ; le défi avait été lancé par Jean Bernoulli dans les Acta Eruditorum en juin 1696, et relevé par Leibniz en mai 1697.
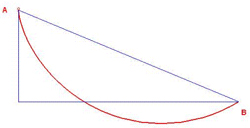
Figure 1 : Courbe brachistochrone. L’arc de cycloïde AB (en rouge) est la courbe suivant laquelle un poids partant de A arrivera le plus vite en B.
C’est également dans cette revue que Jacques Bernoulli proposa à Leibniz, en mai 1690, d’examiner si son nouveau calcul pourrait résoudre le problème de la chaînette ; Leibniz le résolut en effet, sans en publier la solution, pour laisser aux autres mathématiciens le temps de s’y exercer, jusqu’à la fin de l’année 1690. Huygens, Jacques et Jean Bernoulli réussirent dans les délais (1).
Il faut noter que certaines courbes étudiées par Leibniz étaient déjà connues, et que beaucoup de leurs propriétés avaient déjà été établies par des moyens purement géométriques ou par des méthodes pré-différentielles. C’est le cas de la cycloïde, par exemple ; le calcul différentiel pouvait alors s'enorgueillir d'avoir considérablement simplifié des preuves de propriétés déjà établies. La chaînette au contraire est une courbe découverte grâce au nouveau calcul, qui peut donc se vanter de faire réellement progresser l'art d'inventer, auquel Leibniz tenait tant. L'auteur laisse entendre en outre qu'il a remarqué et utilisé le premier le lien entre cette courbe et les logarithmes, lien qui permet de "construire" ceux-ci avec un simple fil suspendu.
Je me suis aperçu en effet que la fécondité de cette courbe n’a d’égale que la facilité de sa réalisation, ce qui la met en tête de toutes les Transcendantes. De fait, nous pouvons l’obtenir et la tracer à peu de frais, par une construction de type physique, en laissant pendre un fil ou mieux une chaînette (de longueur invariable). Et dès que nous disposons, grâce à elle de son tracé, nous pouvons faire apparaître (…) tous les Logarithmes que nous pouvons souhaiter (…)
Nous débrouillerons le texte difficile de Leibniz en donnant d’abord l’équation différentielle de la chaînette, absente du texte bien qu’elle en soit le fondement. Nous en déduirons la construction point par point de la chaînette, et inversement la construction des logarithmes à partir d’un « fil suspendu », puis quelques unes des propriétés de la chaînette énoncées sans démonstration par l’auteur.

Figure 2 : La chaînette est la forme prise par un fil, ou une chaîne, suspendu par ses deux extrémités à hauteur égale.
Equation de la chaînette
On peut la retrouver grâce à un passage de Montucla
(2) : « Nous croyons ne pouvoir nous dispenser de mettre ici les lecteurs géomètres un peu sur la voie de la solution de ce curieux et difficile problème. Nous emprunterons pour cela la subtile analyse qu'en a donnée Jean Bernoulli dans ses
Lectiones calculi integralis. »
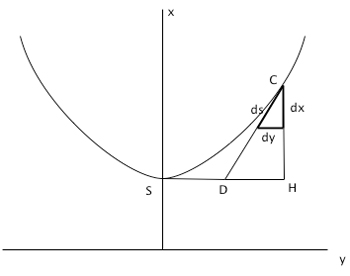
Figure 3 : L'équation de la chaînette, établie par Jean Bernoulli, découle de la similitude du triangle CDH et du triangle caractéristique (dx, dy, ds). On notera l’inversion des axes par rapport aux conventions actuelles. La constante a ci-dessous est l’abscisse du point S (sur l’axe vertical).
Le raisonnement de Jean Bernoulli est fondé sur une propriété de statique, selon laquelle le poids de la section SC du fil (proportionnel à la longueur s de cette section) est à la tension constante (notée a) du fil en S comme CH est à DH, où CD est la tangente au fil en C (fig.2) En reprenant le texte (légèrement modernisé) de Montucla, nous pouvons établir cette propriété comme suit.
L’équilibre d’une portion SC du fil (fig.2) résulte de l’équilibre de trois forces : la tension a du fil en S, la tension T du fil en C, et le poids s (moyennant un certain choix d’unité) de la portion de fil SC. Les tensions sont des « puissances » (des forces) dirigées par les tangentes aux points concernés ; la tension en S est donc dirigée horizontalement, et la tension en C est dirigée suivant CD
(3).
En prenant les composantes des trois forces ramenées au point D, nous avons donc : - horizontalement : a et T× cos CDH, donc a = T× cos CDH - verticalement : le poids s et T× sin CDH, donc s = T× sin CDH
On en déduit 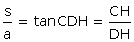
En faisant intervenir le triangle caractéristique en C à la courbe,
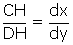
.
L'équation différentielle de la chaînette est donc : 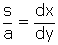 "équation qui, traitée avec adresse", nous dit Montucla, "se réduira à celle-ci :
"équation qui, traitée avec adresse", nous dit Montucla, "se réduira à celle-ci : 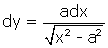 ". Le traitement "adroit", que Montucla laisse aux bons soins du lecteur géomètre, devait ressembler à ceci : comme
". Le traitement "adroit", que Montucla laisse aux bons soins du lecteur géomètre, devait ressembler à ceci : comme 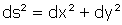 ,
, 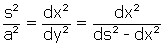 , donc
, donc 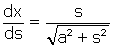 et par conséquent, en intégrant,
et par conséquent, en intégrant, 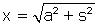 d'où
d'où 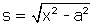 . En reportant cette valeur de s dans l'équation de départ
. En reportant cette valeur de s dans l'équation de départ 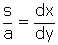 , on obtient l’équation cherchée :
, on obtient l’équation cherchée :
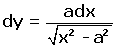 (1).
(1).
On notera que l’on obtient l'équation
(4) d'une partie seulement de la courbe, la partie croissante, parce que les coordonnées sont des couples de nombres
positifs. Les ennuis que peut provoquer une telle restriction, à une époque où les nombres négatifs n'ont pas encore droit de cité, sont éventuellement compensés ici par des considérations de symétrie : on a la même courbe "de l'autre côté".
Construction de la chaînette
Voici une construction géométrique de la courbe, sans l’aide d’aucun fil ni d’aucune chaînette, et sans présupposer aucune quadrature, construction qu’on doit à mon sens juger la plus parfaite qu’on puisse obtenir pour les transcendantes et la plus conforme à l’analyse.
Le texte qui suit ce passage est difficile pour un lecteur contemporain, et ceci d’autant plus que Leibniz, elliptique en diable comme souvent, et qui n’a même pas donné l’équation de la chaînette, ne justifie pas non plus le lien entre celle-ci et une « courbe logarithmique », lien pourtant essentiel dans son texte.
Voici une dérivation possible à cette époque (5). On a 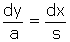 , et nous avons vu que
, et nous avons vu que 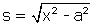 , donc
, donc 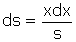 . Par conséquent (6) :
. Par conséquent (6) : 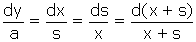 .
.
A une constante additive près, on aura donc
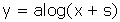
; la constante se détermine en posant la condition y = 0 pour x = a (fig.2), ce qui donne :
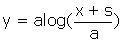
(car pour y = 0, on a s = longueur de l’arc = 0)
et on prendra a = 1 comme le suggère Leibniz, d’où finalement :
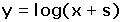 (2)
(2).
Nous avons remarqué plus haut que l’équation
(1) ne concerne qu’une moitié de la courbe. L’autre moitié, symétrique de la première par rapport à l’axe vertical, aura pour équation :
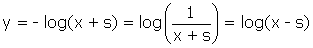 (3)
(3)
puisque 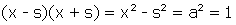 .
.
Le principe de construction de la chaînette d’équation (2) et (3) est donc le suivant : une fois construite une courbe logarithmique, prenons deux points de celle-ci d’abscisses y et – y. Les ordonnées correspondantes nous donnent x+ s et x - s, et l’ordonnée x du point de la chaînette d’abscisse y sera donc la demi-somme des deux ordonnées précédentes.
Pour débrouiller maintenant la construction de la courbe logarithmique telle que l’expose Leibniz, il suffit d’avoir à l’esprit que celle-ci relie des points dont les abscisses y sont en progression arithmétique tandis que les ordonnées correspondantes x sont en progression géométrique. Pour construire un logarithme de base donnée k > 1, donc une courbe de type (x= log
ky, y) il procède en substance comme suit : les premiers points sont (1 ; k), (-1 ; 1/k), (0 ; 1). Pour avoir ensuite l’ordonnée du point d’abscisse ½, on construit la « moyenne proportionnelle
(7) »
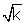
entre 1 et k ; de même, l’abscisse du point d’ordonnée -1/2 est la « moyenne proportionnelle » entre 1 et 1/k, c’est-à-dire
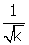
. Nous avons donc construit, en abscisse, une suite arithmétique de raison ½, et en ordonnée, une suite géométrique de raison
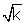
.
On continue en extension, en construisant de proche en proche des points (n;k
n) et (-n;k
-n), puis des points (n+1/2 ; k
n+1/2), où k
n+1/2 est obtenu comme moyenne proportionnelle de k
n et k
n+1. On continue aussi par dichotomie : on placera au point d’abscisse ¼ la moyenne proportionnelle de 1 et de
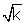
et ainsi de suite pour tous les autres segments, de façon à obtenir en abscisse une suite arithmétique de raison ¼ et en ordonnée une suite géométrique de raison k
1/4. En termes actuels, il s’agit d’une construction point par point de la courbe x=k
y ou y=ln
kx.
Inversement, trouver les logarithmes de nombres à partir de la chaînette (fig. 4)
Inversement, si la Chaînette est construite physiquement, en suspendant un fil ou une chaîne, nous pouvons grâce à elle établir autant de moyennes proportionnelles que nous souhaitons, et trouver les Logarithmes de nombres, ou les nombres de Logarithmes, donnés.
Transcrite en langage actuel, la construction de Leibniz est la suivante. La chaînette d’équation
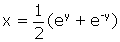
étant tracée “en laissant pendre un fil” (fig.3), elle passera donc par le point de coordonnées (y = lna ; x =
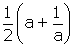
) pour un a > 0 quelconque. Pour construire lna connaissant a, on prendra donc a sur l’axe des x, on construira
(8)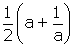
que l’on reportera sur ce même axe, et on prendra l’un des deux antécédents sur l’axe des y : cela donne, il est vrai, deux solutions correspondant à lna et ln(1/a), mais elles sont considérées par Leibniz comme toutes deux positives, et par conséquent égales. Inversement, si l’on veut construire a connaissant lna, on utilisera encore le point de la chaînette d’abscisse lna. En effet son ordonnée est
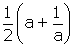
, donc
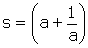
est connu ; pour obtenir a, il ne reste plus qu’à construire deux segments p et q inverses l’un de l’autre et dont la somme s est donnée. Comme le dit Leibniz, c’est un jeu d’enfant : on peut prendre par exemple les abscisses les points d’intersection de la droite x+ y = s et de l’hyperbole xy = 1.
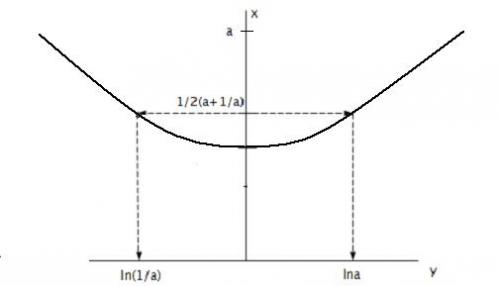
Figure 4 : Construction de lna à partir du tracé de la chaînette (ici on a pris pour exemple a=2)
L’auteur énonce ensuite toute une série de propriétés de la chaînette sans aucune démonstration, sans même avoir donné une équation de la courbe. Nous allons maintenant retrouver ces propriétés, avec les instruments d'époque, à la façon d'un auteur de manuel de la fin du XVIIe siècle.
Tangente en un point de la chaînette (fig. 5)
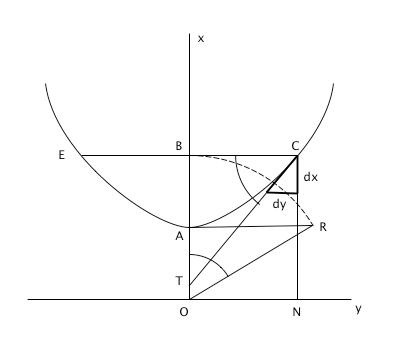
Figure 5 : Propriétés de la chaînette. En plaçant R sur une parallèle à Oy de façon que OR = OB : la tangente CT est telle que l’angle BCT est égal à l’angle AOR, AR est égal à l’arc AC, et l’aire du domaine mixtiligne AONCA est égale à celle du rectangle de côtés OA et AR.
Soit à déterminer la tangente CT en C à la chaînette de sommet A, avec OA = a. Plaçons le point R tel que OR = OB sur une parallèle à Oy passant par A. En tenant compte de l’équation (1) et du fait que le triangle CBT est semblable au triangle caractéristique en C à la courbe, on aura :
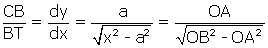
. Mais comme OB = OR,
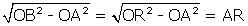
, d'où finalement : CB/BT=OA/AR.
Les triangles BCT et AOR sont donc semblables, donc l'angle
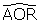
est égal à l'angle
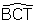
et par suite les angles
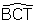
et
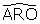
sont complémentaires : Leibniz appelle cela l’“antiparallélisme” des droites CT et OR.
Je nomme ici en abrégé antiparallèles les droites OR et TC faisant avec les parallèles AR et BC des angles ARO et BCT non pas égaux, mais néanmoins complémentaires. Les triangles OAR et BCT sont donc semblables.
D’où la construction de la tangente CT : placer le point R comme indiqué précédemment, puis construire1 la droite antiparallèle à OR passant par C.
Rectification d'un arc de chaînette (fig. 5)
Soit à trouver un segment de droite de même longueur s que l'arc AC.
En établissant l’équation de la courbe, nous avons vu que
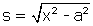
, par conséquent :
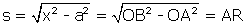
, comme nous l'avons vu plus haut.
Donc l'arc AC a même longueur que le segment AR.
Quadrature (fig. 5)
Soit à carrer le domaine mixtiligne AONCA. Son aire est
(10) :
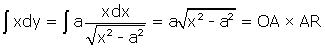
Le domaine a donc une aire égale à celle du rectangle de côtés OA et AR.
Comme le dit Leibniz, « nous voyons également que les arcs sont proportionnels aux aires quadrilignes », puisque l’arc de courbe AC, qui a pour longueur celle du segment AR, est proportionnel à l’aire OA×AR du domaine AONCA.
Centre de gravité d'une portion de courbe (fig. 5)
Soit à trouver le centre de gravité de la portion de courbe CAE, où E est le symétrique de C par rapport à l'axe des abscisses. Par symétrie, le centre de gravité a une ordonnée nulle. L'abscisse du centre de gravité d'un système fini de points d'abscisses xi et de masses mi, de masse totale M, est égale par définition à
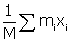
. En passant à une infinité de points d'une courbe d'abscisses x, et en supposant que la masse est proportionnelle à la longueur, la masse totale sera s et la masse de chaque point sera ds : l'abscisse du centre de gravité sera donc
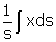
. Comme s =
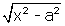
,
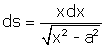
, et par suite :
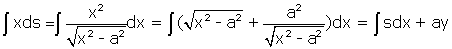 d'après la formule (1).
d'après la formule (1).
Mais 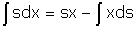 (fig. 5) d'où
(fig. 5) d'où 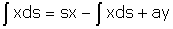 soit
soit 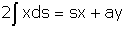 . L'abscisse du centre de gravité est donc :
. L'abscisse du centre de gravité est donc : 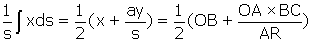 . Cette dernière formule correspond à la construction indiquée par Leibniz, puisque la « quatrième proportionnelle (11) » z de AR, BC et OA est définie par
. Cette dernière formule correspond à la construction indiquée par Leibniz, puisque la « quatrième proportionnelle (11) » z de AR, BC et OA est définie par 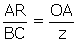 , d’où
, d’où 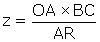 .
.
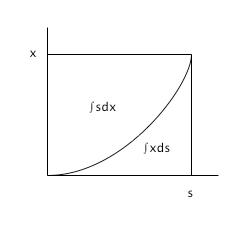
Figure 6 : Ce que l'on appelle aujourd'hui la formule d'intégration par parties ∫xds + ∫sdx = sx se lit directement sur une figure. C'est le fait tout simple que les deux "triangles mixtilignes" sont "complémentaires", selon les propres termes de Leibniz.
En guise de conclusion : postérité mathématique de la chaînette.
Comme le souligne Marc Parmentier, « Notons enfin qu’en exposant méthodiquement les propriétés remarquables de la chaînette, Leibniz ébauche avec une admirable netteté le plan d’étude d’une courbe : établissement des tangentes, rectification d’un arc, calcul d’aire, centre de gravité d’un arc, centre de gravité de l’aire, surface et volume du solide de révolution ».
Découverte comme solution d’un problème de physique, l’équation de la chaînette a connu un important développement purement mathématique sous la forme du cosinus hyperbolique. L’idée, que l’on doit à Vincenzo Ricatti en 1757, et qui fut développée par Jean-Henri Lambert à partir de 1761
(12), est qu’en posant
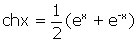
et
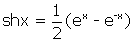
, on a
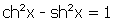
; par conséquent, (x = cht ; y = sht) est une équation paramétrique de l’hyperbole
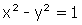
. Le cosinus hyperbolique ch et le sinus hyperbolique sh jouent donc, par rapport à l’hyperbole, un rôle analogue à celui des cosinus et sinus ordinaires par rapport au cercle, puisque (x = cost ; y = sint) est une équation paramétrique du cercle unité
(13)Ainsi la chaînette (d’équation y = ch x), mise en évidence grâce à l’analyse de ses propriétés physiques, sera à l’origine de deux développements mathématiques importants, la trigonométrie hyperbolique et le calcul différentiel.
(ce texte a été repris et adapté par l’auteur à partir du livre IREM qu’il a coordonné Textes fondateurs du calcul infinitésimal, 2006, avec l’aimable autorisation des éditions Ellipses)

(1) Comme l’indique Marc Parmentier dans ses annotations au texte de Leibniz (éditions Vrin) :
Le prestige historique de la question et le concours instauré solennellement par Leibniz avaient mis la chaînette dans tous les esprits et lui ouvrirent pour les années à venir la carrière d’une nouvelle cycloïde. Toutefois, la particularité de la chaînette, ce qui a sans doute contribué à son prestige, est de ne pas être une courbe mécanique au sens de Descartes mais une courbe statique. A ce titre, elle surclasse la cycloïde dans l’échelle des transcendantes dans la mesure où on ne peut pas la construire par une composition de mouvements.
(2) Histoire des mathématiques, Tome II, page 468.
(3) Point important, la tension
a en
S est indépendante du choix du point
C.
(4) Avec les notations actuelles, cette équation s’intègre en :
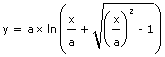
. Le lecteur pourra vérifier que
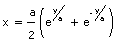
, ce qui est bien l’équation d’une chaînette, avec l’inversion des axes habituelle chez Leibniz.
(5) D’après une idée de Dominique Bénard, de l’Irem du Mans (Institut de recherche sur l’enseignement des mathématiques).
(6) On applique ici une propriété liée aux fractions, si a/b = c/d, alors ce rapport est égal à (a+c)/(b+d).
(7) De nos jours, nous dirions plutôt moyenne géométrique : la moyenne géométrique de
a et de
b est la racine carrée du produit
ab, que l’on peut construire à la règle et au compas à partir de deux segments de longueur a et b. Il en est de même de la construction progressive des puissances entières de
k à partir d’un segment unité et d’un segment de longueur
k.
(8) Un segment de longueur a étant donné, on peut en effet construire géométriquement un segment de longueur 1/
a, puis la demi-somme des précédents.
(9) Ce type de construction était facile : une fois le point R construit, on connaissait l’angle AOR qu’on reportait sur BC en C pour construire l’angle BCT.
(10) Ici comme dans le paragraphe suivant, nous faisons le calcul “à la Leibniz”, sans préciser les bornes. De nos jours, on écrirait plutôt :
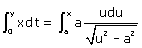
etc.
(11) C'est-à-dire le quatrième terme entrant dans l’égalité de quotients qui suit.
(13) D’autant que, comme Euler l’a établi en 1740, on a
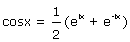
et
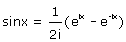




![]()
![]() "équation qui, traitée avec adresse", nous dit Montucla, "se réduira à celle-ci :
"équation qui, traitée avec adresse", nous dit Montucla, "se réduira à celle-ci : ![]() ". Le traitement "adroit", que Montucla laisse aux bons soins du lecteur géomètre, devait ressembler à ceci : comme
". Le traitement "adroit", que Montucla laisse aux bons soins du lecteur géomètre, devait ressembler à ceci : comme ![]() ,
, ![]() , donc
, donc ![]() et par conséquent, en intégrant,
et par conséquent, en intégrant, ![]() d'où
d'où ![]() . En reportant cette valeur de s dans l'équation de départ
. En reportant cette valeur de s dans l'équation de départ ![]() , on obtient l’équation cherchée :
, on obtient l’équation cherchée :![]() (1).
(1).![]() , et nous avons vu que
, et nous avons vu que ![]() , donc
, donc ![]() . Par conséquent (6) :
. Par conséquent (6) : ![]() .
.![]() (3)
(3)![]() .
.

![]()
![]() d'après la formule (1).
d'après la formule (1).![]() (fig. 5) d'où
(fig. 5) d'où ![]() soit
soit ![]() . L'abscisse du centre de gravité est donc :
. L'abscisse du centre de gravité est donc : ![]() . Cette dernière formule correspond à la construction indiquée par Leibniz, puisque la « quatrième proportionnelle (11) » z de AR, BC et OA est définie par
. Cette dernière formule correspond à la construction indiquée par Leibniz, puisque la « quatrième proportionnelle (11) » z de AR, BC et OA est définie par ![]() , d’où
, d’où ![]() .
.

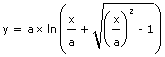 . Le lecteur pourra vérifier que
. Le lecteur pourra vérifier que  Gottfried Wilhelm Leibniz, Naissance du calcul différentiel, Traduction, introduction et commentaire de Michel Parmentier, Vrin, 2000, 504 p. Article original pp. 192-199, reproduit avec l’aimable autorisation des éditions Vrin.
Gottfried Wilhelm Leibniz, Naissance du calcul différentiel, Traduction, introduction et commentaire de Michel Parmentier, Vrin, 2000, 504 p. Article original pp. 192-199, reproduit avec l’aimable autorisation des éditions Vrin. Hémily, groupe d’histoire des sciences de l’IREM de Lyon, Textes fondateurs du calcul infinitésimal, Ellipses et Hémily, 2006 (sous la direction de O. Keller)
Hémily, groupe d’histoire des sciences de l’IREM de Lyon, Textes fondateurs du calcul infinitésimal, Ellipses et Hémily, 2006 (sous la direction de O. Keller)