Théorie analytique de la chaleur
- INFORMATION
- ACTUALITÉ
- ANALYSE
- EN SAVOIR PLUS
- À TÉLÉCHARGER
Théorie analytique de la chaleur, F. Didot père et fils, 1822 ; extrait chap. III, sections I & II, p. 159-177.
1822
Dans ce texte fondateur, Fourier pose, à partir d’une solution particulière de l’équation de la chaleur, les fondements de la « transformée de Fourier » d’une fonction, c’est-à-dire sa représentation par une série de fonctions trigonométriques. Ce concept aura de nombreuses applications en physique mathématique (acoustique, traitement du signal, thermodynamique) et en informatique (traitement d’images, ondelettes).
Dans ce texte fondateur, Fourier pose, à partir d’une solution particulière de l’équation de la chaleur, les fondements de la « transformée de Fourier » d’une fonction, c’est-à-dire sa représentation par une série de fonctions trigonométriques. Ce concept aura de nombreuses applications en physique mathématique (acoustique, traitement du signal, thermodynamique) et en informatique (traitement d’images, ondelettes).
L’intérêt de l’extrait choisi par J.-Ph. Villeneuve, et de l’analyse qu’il développe, est de montrer comment Fourier calcule effectivement les coefficients de la série trigonométrique correspondant à la fonction v(x, y) = e-mx cos my, solution particulière de la chaleur.
Sur l’ouvrage dans sa globalité, laissons parler H. Poincaré (in Théorie analytique de la propagation de la chaleur, 1895, cité par J. Gabay) : « La théorie de la chaleur de Fourier est un des premiers exemples de l'application de l'analyse à la physique ; en partant d'hypothèses simples qui ne sont autre chose que des faits expérimentaux généralisés, Fourier en a déduit une série de conséquences dont l'ensemble constitue une théorie complète et cohérente. Les résultats qu'il a obtenus sont certes intéressants par eux-mêmes, mais ce qui l'est plus encore est la méthode qu'il a employée pour y parvenir et qui servira toujours de modèle à tous ceux qui voudront cultiver une branche quelconque de la physique mathématique. J'ajouterai que le livre de Fourier a une importance capitale dans l'histoire des mathématiques et que l'analyse pure lui doit peut-être plus encore que l'analyse appliquée. »
Après avoir complété une maitrise en mathématiques et un doctorat en philosophie des mathématiques, a commencé, en 2007, à enseigner les mathématiques au Cégep de Rimouski (QC, Canada). Ses recherches portent sur l’histoire des mathématiques (principalement l’analyse au XIXe siècle), le calcul différentiel et intégral, et l’impact de la généralisation sur le développement des connaissances mathématiques. Il a écrit des articles pour le site CultureMath et pour la revue Tangente. Il est chroniqueur pour le Bulletin de l’Association mathématique du Québec.

Joseph Fourier (1768-1830) publia la Théorie analytique de la chaleur en 1822 comme un résumé de ses travaux de 1807 à 1821 sur la propagation de la chaleur dans un solide. Cet ouvrage compte plus de 650 pages et 20 figures. Il est divisé en 433 articles (qui sont en fait des paragraphes) regroupés en neuf chapitres.

Dans les deux premiers chapitres, Fourier présente les définitions des notions physiques utilisées (le thermomètre, p. 19 ; la température, p. 21 ; la quantité de chaleur [1], le 0 degré et le 1 degré [2]), des exemples de propagation de la chaleur dans certains solides (un anneau, une sphère, un cylindre, une barre rectangulaire infinie) et finalement le modèle mathématique de la propagation de la chaleur dans un solide.
L’étude de la propagation de la chaleur dans un solide revient à trouver la température au point (x, y, z) du solide au temps t. Fourier note cette fonction v(x, y, z, t) et affirme qu’elle est la solution de l’équation différentielle suivante [3] :
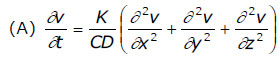
où K est la conductivité du solide, C la chaleur nécessaire pour élever l’unité de poids de la substance d’une température de 0 à 1, et D le poids par unité de volume (densité). Autrement dit, C*D est la capacité calorifique par unité de volume [4].
|
L’équation de la chaleur de Fourier (1822) expliquée par Schrödinger (1946)
Dans son remarquable ouvrage, Qu’est-ce que la vie ? (1946), le physicien Erwin Schrödinger donne un exemple simple permettant d’inférer l’équation de la chaleur[5]. On prend un bac rempli d’eau, on verse du permanganate de potassium (colorant violet) à gauche du bac. Apparaissent des volutes violettes, denses à gauche et beaucoup moins denses à droite :
Après un temps plus ou moins long, la solution va s’harmoniser de manière uniformément violet pâle. Pourtant, chacune des molécules de permanganate se meut indépendamment des autres, avec les mêmes chances d’aller à droite ou à gauche (mouvement de type brownien) : il n’y a pas de raison a priori, au niveau microscopique, que la concentration de la solution s’harmonise. Faisons alors une analyse en découpant la solution en petites tranches de largeur Δx, de concentrations très voisines, diminuant de la gauche vers la droite. Si l’on prend le plan de gauche de la tranche centrale (figurée en gras sur la figure), même s’il y a mouvement brownien – donc aléatoire –, il y aura plus de molécules le traversant de la gauche vers la droite que de molécules le traversant dans l’autre sens, tout simplement parce qu’il y a plus de molécules à gauche du plan qu’à droite. Ceci se produira aussi sur le plan de droite de la tranche centrale, mais quand on fait son bilan global, cette tranche gagne plus sur son plan de gauche qu’elle ne perd sur son plan de droite, et ceci est vrai tant qu’il existe un différentiel de concentration dans la solution. Schrödinger introduit ainsi de manière imagée la fameuse équation de la diffusion. La concentration C de la solution en une tranche Δx varie dans le temps en fonction de la variation des différentiels de concentration entre tranches voisines :
K est un facteur de proportionnalité, l’autre facteur de droite, en dérivée seconde, dérive du raisonnement ci-dessus : à travers le plan de gauche, le transfert se fait en fonction du gradient de concentration ΔC/Δx à l’abscisse x ; à travers le plan de droite le transfert se fait en fonction du gradient de concentration ΔC/Δx à l’abscisse x + Δx ; quand on fait le bilan global de la tranche, comme ci-dessus, à savoir qu’on retranche ce qu’on perd à droite de ce qu’on gagne à gauche, c’est la dérivée seconde d²C/dx² qui apparaît. |
@@@@@@@
Le Chapitre III (§163 et ss) est le chapitre le plus important d’un point de vue mathématique. Fourier y applique le modèle de propagation de la chaleur à un solide particulier, le solide rectangulaire illimité, et développe une technique pour représenter une fonction particulière par une série trigonométrique (une série composée de cosinus et de sinus). Il généralise sa technique pour représenter une fonction « arbitraire » par une série trigonométrique : ce seront les séries de Fourier. Elles constituent l’innovation de Fourier.
Notons aussi que Fourier ajoute le terme ‘arbitraire’ pour s’opposer à la définition d’une fonction proposée en 1748 par Euler. Dans Introduction à l’analyse infinitésimale, Euler avait défini une fonction comme une expression analytique et une fonction était continue si elle n’était composée que d’une seule expression. Fourier écrit :
La fonction fx désigne une fonction entièrement arbitraire, c’est-à-dire une suite de valeurs données, assujetties ou non à une loi commune, et qui répondent à toutes les valeurs de x comprises entre 0 et une grandeur quelconque X. [Fourier, 1822, §418, p. 554-555]
Fourier se retrouve ainsi dans la transition entre la notion de fonction du XVIIIe siècle (la fonction comme une expression analytique) et celle du XIXe siècle (la fonction comme une correspondance biunivoque entre deux ensembles). Or, il n’est pas clair que la fonction sera « entièrement arbitraire », car Fourier utilisera l’hypothèse que la fonction sera représentable en série de Maclaurin.
D’ailleurs, quelques années avant Fourier, Daniel Bernoulli[6] avait présenté un contrexemple à la définition d’Euler[7] en montrant que la série trigonométrique y = a sin px/L + b sin 2px/L + g sin 3px/L + ... était une solution de l’équation différentielle des cordes vibrantes de longueur L. Cette série trigonométrique a un autre intérêt car elle devient une superposition de courbes sinusoïdales dont les fréquences sont des multiples de la fréquence initiale de la corde. Dans le droit fil de cette remarque de Bernoulli, la série de Fourier d’une fonction permettra de réécrire la fonction périodique comme une somme de fonctions dont les fréquences sont des multiples entiers de la fréquence initiale. Avec l’ère numérique, ces séries auront beaucoup d’applications, comme nous le soulignerons en conclusion.
Ce chapitre III se compose de 7 sections, dont les sections II et VI sont importantes d’un point de vue mathématique. Les deux premières sections ont été sélectionnées comme texte BibNum au sein du traité Théorie analytique de la chaleur. Elles seront d’abord analysées, puis les autres sections seront résumées.
Le problème de la propagation de la chaleur dans un solide rectangulaire infini
Dans les sections I et II, Fourier étudie le problème de la propagation de la chaleur, donne une solution particulière, développe une technique pour trouver des coefficients d’une série trigonométrique puis s’intéresse à la convergence de cette série trigonométrique. En fait, la solution particulière au problème de la propagation de la chaleur a la forme d’une équation différentielle, et la technique développée par Fourier mettra de montrer que la solution de l’équation différentielle est une solution au problème. Reprenons en détails ces résultats.
@@@@@@@
Fourier commence avec l’étude de la propagation de la chaleur dans un solide particulier. Il considère (§164) une masse solide homogène compris entre deux plans verticaux B et C qui sont coupés perpendiculairement par un plan A. C’est un prisme à base rectangulaire dont les côtés B et C sont infinis. Il le nomme le solide BAC (fig. 1). Une source de chaleur (de l’eau bouillante) est placée sur le plan A, et de la glace sur les plans B et C. On parlerait aujourd’hui de 100 degrés Celsius et de 0 degré Celsius. Chaque plan conserve une température constante pendant l’observation. La chaleur se propage dans le solide et la température deviendra stationnaire : Fourier parle d’état final comme le seul état qui subsiste de lui-même (p. 160).
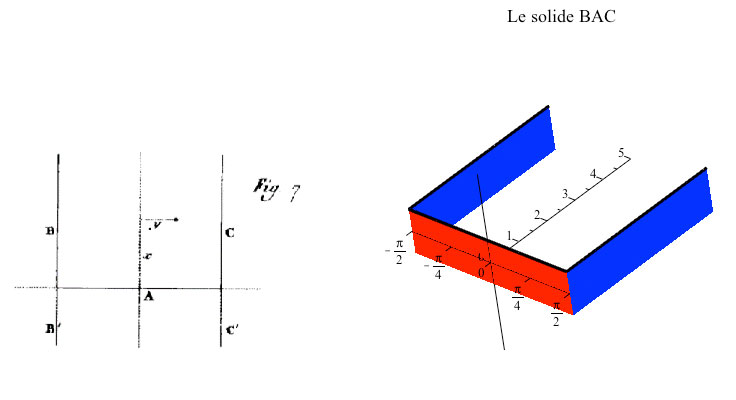
Figure 1 : La figure de gauche est celle donnée par Fourier à la fin du livre ; la figure de droite est une interprétation contemporaine. La température est de 0°C sur les surfaces bleues (surfaces B et C) et de 100°C sur la surface rouge (surface A).
Au §165, Fourier fait une coupe d’épaisseur infinitésimale du solide parallèle au plan XY (celui représenté par les axes gradués à droite). Il obtient une lame rectangulaire infinie dont les côtés B et C (resp. l’extrémité A) demeurent à température initiale de 0 degré (resp. 1 degré). Comme ces lames infinitésimales sont superposées, Fourier affirme qu’il n’y a aucune perte de chaleur sur la surface de chaque lame et que l’objectif est maintenant de déterminer la température stationnaire en tout point d’une lame (figure 2).
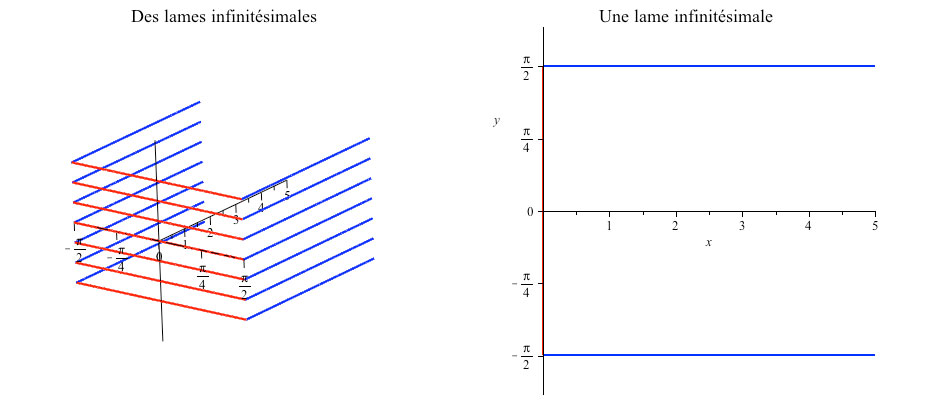
Figure 2 : Le solide est placé dans un système de coordonnées puis divisé en lames d’épaisseur infinitésimale en z. Dans le plan XY, l’axe des x coupe la lame en son milieu et la droite A est prise par convention d’une longueur égale à p sur l’axe des y. Ainsi 0 £ x < ¥, -p/2 £ y £ p/2, -¥ < z < ¥. La température est de 0°C sur les lignes bleues et de 100°C sur les lignes rouges.
Fourier utilise ensuite (§166) l’équation générale de la propagation de la chaleur dans un solide :
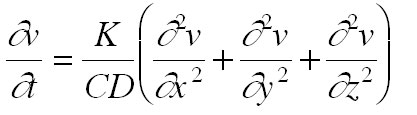
Il pose ![]() , car on cherche une solution en (x, y) dans le plan formé par la lame, et
, car on cherche une solution en (x, y) dans le plan formé par la lame, et 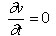 , car la température est stationnaire (on cherche l’état final dans lequel il n’y a plus de variation de chaleur). Ainsi, l’équation devient :
, car la température est stationnaire (on cherche l’état final dans lequel il n’y a plus de variation de chaleur). Ainsi, l’équation devient :
(a) 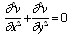
L’objectif est donc de trouver la fonction v(x, y) qui satisfasse les conditions suivantes :
- l’équation (a) ci-dessus ;
- v(x, -p/2) = v(x, p/2) = 0 (bords bleus à température 0) ;
- v(0, y) = 1 (bord rouge à température 1) ;
- Si x est très grand, alors v(x, y) doit être très petit (« puisque toute la chaleur sort du seul foyer A »).
Fourier donne une explication plus complète de la condition (4) plus loin dans le texte :
La chaleur n’étant fournie que par la source constante A, il ne peut en parvenir qu’une portion extrêmement petite dans les points de l’espace, qui sont très éloignés du foyer. Le reste se détourne de plus en plus vers les arrêtes infinies B et C, et se perd dans les masses froides qu’elles terminent.
Une solution particulière
Afin de trouver une fonction qui satisfait les conditions (1) à (4), Fourier s’intéresse au §167 à un type particulier de fonctions : v(x, y)= F(x)f(y).
La condition (1) produit alors l’équation différentielle suivante :
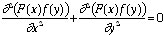
L’objectif est de trouver F(x) et f(y). On écrit :
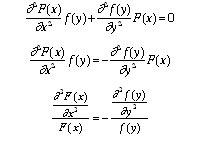
La condition (1) devient alors:
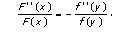
S’agissant de deux fonctions à variables indépendantes, elles ne peuvent être égales entre elles qu’à une constante[8] :
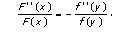
Il obtient donc F(x) = e-mx et f(y) = cos my et la solution à l’équation différentielle devient :
v(x, y) = e-mx cos my
Cette fonction vérifie la condition (1). Restent les autres conditions. Au §168, il traite des conditions (2) et (4). Pour la condition (4), la constante m doit être positive, car l’exponentielle e-mx doit tendre vers 0 lorsque x tend vers l’infini. Quant à la condition (2), v(x, -p/2) = v(x, p/2) = 0, m doit être impair afin que le cosinus s’annule. Ainsi, v(x, y) = e-mx cos my, avec m = 1, 3, 5, 7, …
Remarquant au §169 que chaque valeur m = 1, 3, 5, 7,… produit une solution à l’équation différentielle (a), il pose :
(b) v(x, y) = ae-x cos y + be-3x cos 3y + ce-5x cos 5y + de-7x cos 7y + …
a, b, c, d, … étant des constantes à déterminer. Afin de satisfaire la condition (3), c’est-à-dire v(0, y) = 1, on écrit :
1 = ae-0 cos y + be-3.0 cos 3y + ce-5.0 cos 5y + de-7.0 cos 7y + …
Il s’agit alors de résoudre l’équation :
1 = a cos y + b cos 3y + c cos 5y + d cos 7y + …, avec -p/2 £ y £ p/2,
qui peut être vue comme une façon d’exprimer une fonction (la fonction constante 1) par une série trigonométrique.
Comment trouver les coefficients d’une série trigonométrique ?
L’objectif de la section II (intitulée « Premier exemple de l’usage des séries trigonométriques dans la théorie de la chaleur ») est de développer une technique permettant de trouver les coefficients a, b, c, … de l’équation
1 = a cos y + b cos 3y + c cos 5y + d cos 7y + …
Cette technique est importante, car elle sera généralisée à la section VI pour développer une fonction « arbitraire » en série de cosinus et de sinus. Par contre, cette technique n’est plus utilisée aujourd’hui, car elle ne satisfait plus les critères de rigueur.
Fourier commence (§171) par calculer les dérivées successives de l’équation initiale :
1 = a cos y + b cos 3y + c cos 5y + d cos 7y + …
0 = a sin y + 3b sin 3y + 5c sin 5y + 7d sin 7y + ...
0 = a cos y + 32b cos 3y + 52c cos 5y + 72d cos 7y + ...
0 = a sin y + 33b sin 3y + 53c sin 5y + 73d sin 7y + ...
Et ainsi de suite.
Il pose ensuite y = 0 et obtient un système ayant une infinité d’équations et une infinité d’inconnues :
1 = a + b + c + d + ...
0 = a + 32b + 52c + 72d + ...
0 = a + 34b + 54c + 74d + ...
0 = a + 36b + 56c + 76d + ...
Et ainsi de suite.
Au §172, il tronque ce système pour obtenir m équations à m inconnues. Pour chaque valeur m, on trouvera un système :
|
m = 2 1 = a + b 0 = a + 32b
|
m = 3 1 = a + b + c 0 = a + 32b + 52c 0 = a + 34b + 54c
|
m = 4 1 = a + b + c + d 0 = a + 32b + 52c + 72d 0 = a + 34b + 54c + 74d 0 = a + 36b + 56c + 76d |
Ainsi, chaque inconnue recevra une valeur différente pour chaque système obtenu (pour autant qu’elle y figure). Fourier écrit :
La quantité a, par exemple, recevra une valeur pour le cas de deux inconnues, une autre pour le cas de trois inconnues, ou pour le cas de quatre inconnues, ou successivement pour le plus grand nombre […] La valeur d’une des inconnues, pour le cas où leur nombre est infini, est la limite vers laquelle tendent continuellement les valeurs qu’elle reçoit au moyen des éliminations successives. Il s’agit donc d’examiner si, à mesure que le nombre des inconnues augmente, chacune des valeurs a, b, c, d, … etc. ne converge point vers une limite finie, dont elle approche continuellement.
L’idée est donc, que l’inconnue a se résout en une solution, disons a2, pour le système m = 2, a3 pour le système m = 3, etc. Ainsi 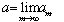 . Pour trouver cette limite, il faut résoudre le système pour un m donné et étudier comment se comporte l’ajout d’inconnues au système[9]. Cette technique n’est plus valide aujourd’hui : en quoi les solutions d’un système m par m convergeraient vers les solutions d’un système infini ?
. Pour trouver cette limite, il faut résoudre le système pour un m donné et étudier comment se comporte l’ajout d’inconnues au système[9]. Cette technique n’est plus valide aujourd’hui : en quoi les solutions d’un système m par m convergeraient vers les solutions d’un système infini ?
Fourier considère alors le système à 7 inconnues.
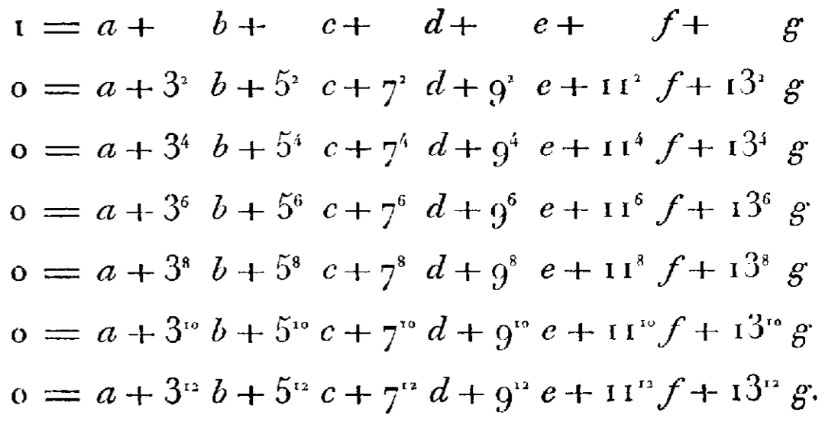
Pour éliminer g, il multiplie la première équation par 132 puis lui soustrait la seconde équation. Il répète le procédé pour les autres équations et obtient le système (c) suivant, à 6 équations et 6 inconnues (g ayant disparu) :
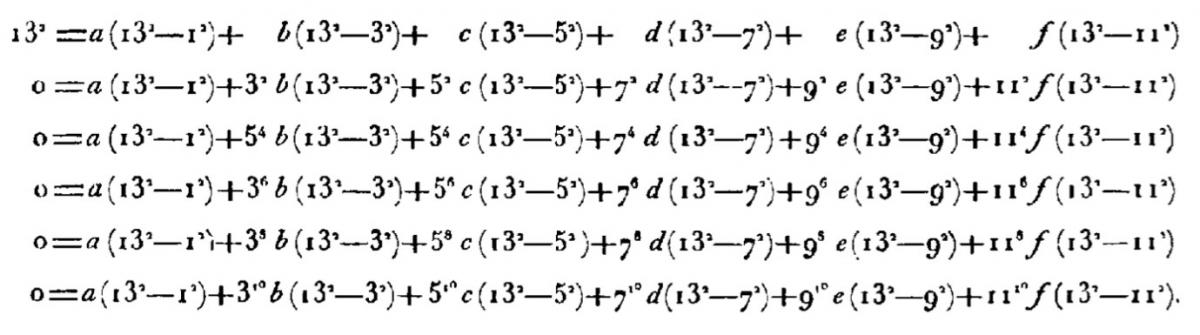
Il réutilise le même procédé pour éliminer les autres inconnues afin d’en conserver seulement qu’une seule (par exemple, pour éliminer f, il faut multiplier la première équation par 112). Il obtient :
a(132 – 12)(112 – 12)(92 – 12)(72 – 12)(52 – 12)(32 – 12) = 1321129272523212
Ainsi ![]()
Fourier explique au §173 les conséquences de l’ajout d’une inconnue dans le système d’équations :
Si l’on avait employé un nombre d’équations plus grand d’une unité [considéré par exemple m = 8 au lieu de m = 7], on aurait trouvé, pour déterminer a, une équation analogue à la précédente, ayant au premier membre un facteur de plus, savoir : 152 – 12, et au second membre 152, pour nouveau facteur. La loi à laquelle ces différentes valeurs de a sont assujetties est évidente, et il s’ensuit que la valeur de a, qui correspond à un nombre infini d’équations, est exprimée ainsi :
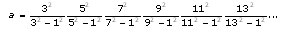
ou[10] 
Or, cette dernière expression est connue et, suivant le théorème de Wallis, on en conclut que a = 4/p.
Rappelons que la formule de Wallis est :
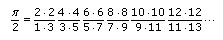
La valeur de l’inconnue a est donc 4/p. La justification de Fourier est la suivante : il trouve une analogie[11] et, comme il obtient un résultat connu (la formule de Wallis), il en conclut que la suite converge. Cette justification, reposant sur une analogie et sur un résultat par ailleurs connu, était acceptée à cette époque mais ne l’est plus aujourd’hui.
@@@@@@@
Fourier explique ensuite comment trouver la valeur des autres inconnues. Il trouve d’abord la formule générale lorsqu’une variable est ajoutée au système (§174). Par exemple, pour l’inconnue f, en posant que F correspond à la valeur de f par résolution du système à 6 inconnues et 6 équations, alors la solution du système augmenté d’une inconnue sera 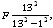 , exactement comme ci-dessus ; pour le système à 8 inconnues et 8 équations, la solution pour f sera
, exactement comme ci-dessus ; pour le système à 8 inconnues et 8 équations, la solution pour f sera 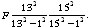 .
.
On voit maintenant la récurrence :  Il reprend l’argument avec b, c, d et a, en faisant la remarque suivante :
Il reprend l’argument avec b, c, d et a, en faisant la remarque suivante :
La question est donc réduite à déterminer la valeur de a dans le cas d’une inconnue, la valeur de b dans le cas de deux inconnues, celle de c dans le cas de trois inconnues, et ainsi de suite pour les autres inconnues.
S’appuyant sur cette remarque, il résout les systèmes de m par m afin de trouver les valeurs de a, b, c, d, etc. (§175). Pour l’inconnue f, il obtient[12], en conformité avec la récurrence ci-dessus :
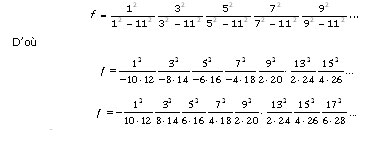
L’objectif est maintenant de faire apparaitre la formule de Wallis. Détaillons le calcul implicitement fait par Fourier. Au numérateur, il manque 11*11. Au dénominateur, il faut former des couples de facteurs pairs identiques (2*2, 4*4, 6*6, etc.). Pour les produits 2*2 jusqu’à 20*20, Fourier regroupe les premiers facteurs jusqu’au dénominateur de 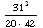 ; pour les autres couples de facteurs identiques, Fourier jumelle le deuxième facteur avec le premier facteur un peu plus loin dans la suite des facteurs – tout en remarquant qu’il manque un 22 au dénominateur. On peut alors appliquer la formule de Wallis :
; pour les autres couples de facteurs identiques, Fourier jumelle le deuxième facteur avec le premier facteur un peu plus loin dans la suite des facteurs – tout en remarquant qu’il manque un 22 au dénominateur. On peut alors appliquer la formule de Wallis :
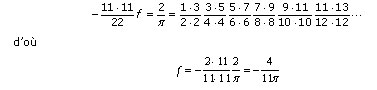
Il applique cette technique aux autres inconnues. Il faut en fait trouver le facteur qui multiplie la valeur de l’inconnue pour obtenir p/2, via la formule de Wallis. Pour b, c’est  , pour c, c’est
, pour c, c’est 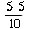 . Ainsi les valeurs des coefficients sont :
. Ainsi les valeurs des coefficients sont :
a = 4/p, b = -4/3p, c = 4/5p, d=-4/7p
Au §177, il conclut en substituant ces valeurs dans l’équation à résoudre:
1 = 4/p cos y – 4/p*1/3 cos 3y + 4/p*1/5 cos5y – 4/p*1/7 cos 7y + …
d’où, en factorisant 4/p :
p/4 = cos y – 1/3 cos 3y + 1/5 cos5y – 1/7 cos 7y + … avec –p/2 < y < p/2
Questions de convergence
Dans les deux derniers articles de la section II, Fourier s’intéresse à la convergence d’une série particulière : la série cos y – 1/3 cos 3y + 1/5 cos5y – 1/7 cos 7y + … qui converge vers p/4 pour –p/2 < y < p/2. Au §177, il donne d’abord une justification analytique. La définition analytique de convergence est :
Il serait aisé de prouver que cette série est toujours convergente, c’est-à-dire, en mettant au lieu de y un nombre quelconque, et en poursuivant le calcul des coefficients, on approche de plus en plus d’une valeur fixe, en sorte que la différence de cette valeur à la somme des termes calculés, devient moindre que toute grandeur assignable.
Cette définition est à rapprocher de celle produite par Cauchy en 1821 dans le Cours d’analyse : une série est convergente si la suite de ses sommes partielles converge[13]. Rappelons qu’à cette époque, la question de la convergence des séries est relativement nouvelle et qu’elle n’était pas définie de façon indépendante des critères de convergence. L’apport de Fourier n’est pas plus décisif, il se contente de renvoyer à une « démonstration que le lecteur peut suppléer ».
@@@@@@@
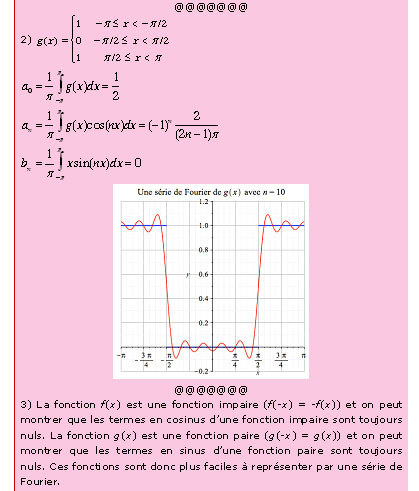
Au §178, Fourier donne une justification géométrique de la convergence de la série. La fonction est y = cos x – 1/3 cos 3x + 1/5 cos 5x – 1/7 cos 7x + … et elle s’approche de la droite y = p/4 ou y = -p/4 lorsque des termes sont ajoutés dans la série (Figure 3). La fonction vers laquelle la série converge est discontinue aux multiples impairs de p/2. Cette fonction permet de nos jours la modélisation de signal.
Figure 3 : Graphique des quatre premiers termes de la série cos x – 1/3 cos 3x + 1/5 cos 5x – 1/7 cos 7x + … Cette série est couramment utilisée de nos jours dans le traitement du signal ; 3bis, en bas : logo de l’Institut Fourier (CNRS à Grenoble (Fourier avait été – aussi – préfet de l’Isère sous Napoléon). On retrouve à gauche les formes sinusoïdes figurant ci-dessus ; on pourra aussi voir une certains similarité avec les crêtes montagneuses autour de cet institut situé dans les Alpes.

Les autres sections du chapitre
Dans la section III (Remarques sur ces séries), Fourier présente une autre technique pour justifier la convergence de la fonction y = cos x – 1/3 cos 3x + 1/5 cos 5x – 1/7 cos 7x + … vers les droites y = p/4 ou y = -p/4 : la série est tronquée, puis dérivée, manipulée (application d’identité trigonométrique), et finalement intégrée. La question de la permutation de l’intégration et la dérivation d’une série n’est pas abordée (Darboux présentera en 1875 des conditions de permutation). Il applique cette technique à d’autres fonctions dont y = sin x – 1/2 sin 2x + 1/3 sin 3x – 1/4 sin 4x + …
Dans la section IV (solution générale), il revient avec la solution générale du problème simplifiée
(b) v = ae-x cos y + be-3x cos 3y + ce-5x cos 5y + de-7x cos 7y + …
devient
p/4*v = e-x cos y – 1/3e-3x cos 3y + 1/5e-5x cos5y – 1/7e-7x cos 7y + …
Il affirme que cette série est « extrêmement » convergente, car chaque terme de la série se superpose pour donner lieu à la variation de chaleur. Il présente ensuite une étude physique de la chaleur et étudie la somme de deux fonctions (aujourd’hui appelée la convolution).
Dans la section V (Expression finie de la solution), il revient à l’équation différentielle  et propose de la résoudre dans le plan complexe. Il remplace dans v les cosinus par leur expression en exponentielle complexe (.
et propose de la résoudre dans le plan complexe. Il remplace dans v les cosinus par leur expression en exponentielle complexe (. .
.
@@@@@@@
La section VI (Développement d’une fonction arbitraire en séries trigonométriques) est très importante d’un point de vue mathématique. Fourier présente une généralisation de la technique de la section 2 et utilise l’hypothèse que la fonction est développable en série de Maclaurin afin de représenter une fonction « arbitraire » en séries, maintenant appelées des séries de Fourier. À la page 240, il introduit la notation 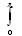 pour désigner l’intégrale de 0 à p et donne une explication du choix de cette notation à la page 252 (Cauchy avait cité Fourier dans son Résumé[14]). Au §235, il résume la section VI comme suit :
pour désigner l’intégrale de 0 à p et donne une explication du choix de cette notation à la page 252 (Cauchy avait cité Fourier dans son Résumé[14]). Au §235, il résume la section VI comme suit :
- La convergence : Fourier affirme que les séries de Fourier convergent vers la fonction pour tout x, ce qui n’est pas tout à fait exact. D’une part, Fourier impose des conditions à la fonction dans sa démonstration, par exemple le fait qu’elle soit infiniment dérivable. D’autre part, en 1829, le mathématicien allemand Peter Gustav Lejeune Dirichlet (1805-1859) s’intéressera à la convergence des séries de Fourier de fonctions[15]. Il en conclura – ce qui sera appelé les conditions de Dirichlet – qu’une fonction périodique est développable en série de Fourier si elle est continue par morceaux, si les limites à gauche et à droite des discontinuités existent, si elle a un nombre fini d’extrémums, enfin si la dérivée est bornée en tout point de continuité.
- La convolution : les séries de Fourier d’une somme de deux fonctions sont données par la convolution des deux fonctions.
- La forme générale : Les séries de Fourier ont la forme suivante :

Enfin, dans la section VII (Application à la question actuelle), Fourier explique la solution de la propagation de la chaleur selon les résultats obtenus.
La postérité du texte
Ce texte de Fourier a amené des résultats mathématiques et scientifiques importants.
En mathématiques, outre la question de la convergence abordée par Dirichlet en 1829, Bernhard Riemann (1826-1866) posa le problème inverse dans son article de 1854. En termes contemporains, les problèmes deviennent :
- Soit f(x) une fonction définie sur [0, 2p] à valeurs réelles. Sous quelles conditions la série de Fourier converge-t-elle vers f(x) :
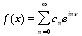 avec
avec 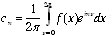 ?
? - Soit une série trigonométrique convergente
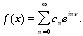 . Sous quelles conditions, les coefficients de la série sont-ils les coefficients de Fourier :
. Sous quelles conditions, les coefficients de la série sont-ils les coefficients de Fourier : 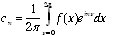 ?
?
Dans ces deux problèmes, l’objectif est de trouver les conditions à imposer à la fonction (continue, continue par morceaux, intégrable au sens de Riemann) et de déterminer le type de convergence (uniforme, ponctuelle, en moyenne). Fourier s’intéressa au problème (1), Riemann au problème (2).
En 1872, Georg Cantor (1845-1918) étudie l’unicité de la convergence des séries de Fourier (si une série trigonométrique S converge ponctuellement vers 0 pour tout x, alors S est la série nulle, c’est-à-dire que an = bn = 0, pour tout n) ; ses recherches le conduisirent à développer la théorie des ensembles. En 1873, Paul du Bois-Reymond (1831-1889) démontre l’existence d’une fonction continue dont la série de Fourier ne converge pas à l’origine. En 1900, Lipót Féjer (1880-1959) démontre que les séries de Fourier convergent en moyenne vers f, lorsque f est continue. En 1905, Henri Lebesgue (1875-1941) s’intéressera aux séries de Fourier de fonctions intégrables au sens de Lebesgue et en 1907, Ersnt Fischer (1875-1959) et Frédéric Riesz (1880-1956) démontreront que les fonctions {1, cos(nx), sin(nx) : n Î R} forment une base orthonormée pour les fonctions dont le carré est intégrable au sens de Lebesgue :

Calculer une série de Fourier d’une fonction L2 revient à exprimer cette fonction dans la base orthonormée.
@@@@@@@
En physique, les séries de Fourier permettent notamment le traitement numérique de sons et d’images. Le son est une variation de la pression d’air perçue par les oreilles : lorsque celle-ci est périodique, on obtient une onde caractérisée par une longueur d’onde et une fréquence. L’oreille humaine peut entendre des sons de 20 Hz à 20 000 Hz. Comme c’est un phénomène périodique, il est modélisable par séries de Fourier.
D’une part, un son peut être généré par une série de Fourier. On se choisit une fréquence initiale perceptible à l’oreille et on calcule les séries de Fourier d’une fonction de signal.
D’autre part, un son peut être modélisé par une série de Fourier. La technique consiste à faire un échantillonnage du son à intervalles de temps régulier et de construire n termes de la série de Fourier à partir de cet échantillon. La modélisation d’un son par une série de Fourier permet d’éliminer le bruit, c’est-à-dire les sons dont les fréquences ne sont pas multiples de la fréquence initiale : les séries de Fourier agissent ainsi comme filtre.
mars 2015
@@@@@@@
Annexe – quelques erreurs dans l’impression du texte de Fourier :
- p. 163 Erreur mathématique (m devient être m2)
- p. 168 Erreur de syntaxe (x = 0 et non y = 0)
- p. 170 Troisième équation, figure un 54 au lieu d’un 34
- p. 174 Erreur dans la formule de Wallis 2*2/1*3 (Fourier l’avait trouvée)
- p. 174 Erreur de syntaxe (a = 2*2/p et non 2*p/2)

[1]. L’unité est la quantité de chaleur nécessaire pour convertir 1 kilogramme de glace d’une température de 0 en de l’eau liquide à une température de 0 (§25).
[2]. Le degré 0 et le degré 1 sont, par convention posée par Fourier, la température de la glace fondante et la température de l’eau bouillante dans un vase donné à une pression donnée (§24, §26).
[3]. Fourier applique ce modèle à différents solides, puis le déduit de principes physiques (p. 134-135).
[4]. Fourier remarque à la page 154 que C est toujours multiplié par D.
[5]. Le texte de cet encadré est issu d’A. Moatti, Récréations mathéphysiques, Le Pommier, 2010. L’image est issue du livre d’E. Schrödinger.
[6]. Fourier en parle à la page 249.
[7]. La définition d’Euler sous-entend une suite finie d’expressions analytique et non une somme infinie.
[8]. Fourier écrit m et non m2, que nous utiliserons ici. En choisissant m2, on obtient la solution de l’équation différentielle v(x, y) = e-mx cos my. Sinon, il aurait fallu introduire cosÖmy, ce qui n’est pas très agréable d’écriture.
[9]. Fourier utilisera à nouveau cette technique dans la section 6 (p. 213).
[10]. Par la différence de carrés A2 – B2 = (A – B)(A + B), on développe le dénominateur.
[11]. L’ajout d’une équation conduit à un résultat analogue et permet de trouver le terme général de la suite des facteurs de la solution am.
[12]. Il y a une légère confusion dans le texte sur l’utilisation du symbole f : il est parfois utilisé par Fourier pour la solution générale du système infini (le coefficient du terme cos 11y de l’équation (b)), et parfois pour la solution du système 6 par 6.
[13]. Voir à ce sujet J.-Ph. Villeneuve, « Cauchy, une nouvelle conception du calcul intégral », BibNum, octobre 2014.
[14]. Voir J.-Ph. Villeneuve, BibNum, op. cit.
[15]. Dirichlet, P. G. Lejeune, 1829, « Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données, » Journal für die reine und angewandte Mathematik, 4, p. 157-169.
HISTOIRE DES SCIENCES
 |
|
 |
|
 |
|
SITE INTERNET
- Une "promenade" illustrée, par un de nos auteurs BibNum, Alain Juhel, dans la théorie analytique de la chaleur de Fourier (ici).
MANUELS UNIVERSITAIRES
 |
|
 |
|
 |
|
L'OUVRAGE DE FOURIER
 |
|
textefourier.pdf

analyse-fourier-vf2.pdf







