Pour ma génération, la littérature française du XVIIe siècle fut un pain quotidien. La Fontaine à l'école. Le trio sacré Corneille, Molière, Racine, de la classe de 4e à la 1ère (une pièce par trimestre). Pascal et Descartes (les philosophes, pas les savants). Sans oublier Boileau, La Bruyère, La Rochefoucauld, voire Bossuet.
J'ai aimé cette littérature mais, venu le temps du choix, je suis allé vers les mathématiques.
Ainsi, j'ai une connaissance de la littérature du XVIIe siècle, et j'ai étudié les mathématiques. Suis-je bien placé pour comprendre à peu de frais ce texte mathématique du XVIIe siècle qu’est le Brouillon Projet d'une atteinte aux événements des rencontres du Cône avec un Plan de Girard Desargues (1591-1661) ? Non. Si je rouvre Corneille ou Racine, ils sont là aussitôt, mais si j’ouvre Desargues, il m’apparaît comme lettre morte, et n'éveille aucune des émotions qui m'ont attiré vers les mathématiques. Que révèle cette incapacité à lire Desargues ?
@@@@@@@
Le texte de Desargues est un classique : il est à l'origine de la géométrie projective (c’est-à-dire l'étude de ce qui, dans les figures, reste inchangé après projection). Cela n'aurait pas suffi à me donner envie de le consulter. Se reporter aux textes anciens n'est pas un geste familier chez les mathématiciens ; en général, ce n'est pas ainsi que le savoir circule entre eux. Mais ce texte-ci a une propriété remarquable : l’effet littéraire réussi par son titre. Brouillon Projet d'une atteinte aux événements des rencontres du Cône avec un Plan – cet imposant festival de mots est autrement plus savoureux que Géométrie, de Descartes, ou Traité sur les Coniques, de Pascal ! Le lecteur commence par ne rien saisir. Puis il surmonte son étourdissement. Ce n'est pas si compliqué. Au XVIIe siècle, « événement » signifie « issue d'une affaire ». L'affaire dont il est question est la « rencontre » d'un cône et d'un plan. Pas de difficulté non plus avec le terme « rencontre » : même s'il a une allure moins savante, il équivaut à notre moderne « intersection ». Quant à « brouillon projet d'une atteinte », mettons cette formule sur le compte de ce qui relèverait aujourd'hui de la fausse modestie, ou de la prudence académique. Bref, ce texte étudie les divers cas de figures qu'on obtient quand un cône coupe un plan. Et la façon alambiquée dont Desargues annonce son intention a de quoi faire sourire.
Géométries projective, descriptive, etc.
Desargues introduit la notion de "point à l’infini" (voir par exemple haut de page 23 : « …les touchantes possibles à la figure à distance finie ou infinie aux points que le bord donne à ces diamétrales conjuguées, où l’on voit que les droites nommées asymptotes, ou qui ne rencontrent le bord de la figure à aucune distance finie, y tiennent lieu tout ensemble et de diamétrales de la figure, et de touchantes à ses bords à distance infinie. ») ; cette notion est à la base de la géométrie projective. Comme indiqué, celle-ci est l'étude de ce qui, dans les figures, reste inchangé après projection, alors que la géométrie euclidienne est l'étude de ce qui reste invariant après déplacement (on peut voir celle-ci comme la science des figures qui se tracent à la règle et au compas). La géométrie projective comporte moins d'axiomes que la géométrie euclidienne et par suite elle est plus générale.
Application de la géométrie projective, et donc descendante des conceptions de Desargues, la géométrie descriptive représente les figures de géométrie dans l’espace par leurs projections sur un plan horizontal et sur un plan vertical. Développée par Monge, elle a été une étape dans la résolution de ce vieux problème qu'est la représentation des objets à trois dimensions. Les deux projections constituent une épure (utilisée notamment en dessin industriel). L’épure ci-dessous montre un cas d’intersection d’un cône avec un plan.
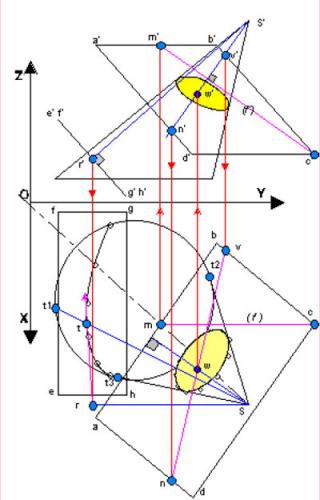
Figure 2 :
Projections descriptives de coupe d’un cône par un plan (dessin © Christian Vaillant, site
http://choumac44.free.fr)
Seulement, le titre est une chose, le texte en est une autre. L’amphigouri qui fait le charme du premier disparaît totalement du second. On n'y trouve plus que de la géométrie et, qui plus est, rédigée de façon sèche. Or je n'ai pas grand goût pour la géométrie (j’étais spécialisé en théorie des nombres). Du coup, essayer de décrypter le texte m'intéresse peu. Somme toute, le titre m'a entraîné sur une fausse piste. Je m'attendais à une langue plaisante parce que fleurie, je tombe sur des coups de trique ! C'est une mésaventure banale, au fond. Il n'est guère de titre qui n'engendre ce genre de malentendus. Sans y songer, le lecteur tient pour allant de soi que le contenu du livre va correspondre à ce qu'il imagine à partir du titre. En fait, il n'y a aucune raison pour que, sollicitée par le titre, son imagination aille dans la direction qu'a prise l'auteur. (Si c’était le cas, l’auteur n’aurait à écrire que le titre, laissant au lecteur le soin d’en déduire tout le corps de l’ouvrage...)
Parcourant néanmoins le Brouillon Projet, je me suis senti comme Fabrice à Waterloo. Si les professeurs, les encyclopédies, les dictionnaires, ne répétaient pas à l'envi qu'il est fondateur, je ne m'en serais jamais rendu compte. C'est que, pour estimer l'apport de Desargues et évaluer son influence, il faut connaître bien l'état de la géométrie avant lui et l'état après lui, puis les comparer. Une telle entreprise exige une érudition qu’on n’atteint guère que si on est historien professionnel des mathématiques.
Mes tentatives de lecture échouent dès le début, car elles butent sur la batterie serrée de définitions qui ouvre le texte. Ordonnance de droites, ordonnance de plans, but d'une ordonnance, tronc, nœud, rameau, branche, borne, arbre, brin de rameau plié à son tronc, rectangles gemeaux entre eux... Certains de ces termes sont encore utilisés en mathématiques (arbre, nœud, par exemple), mais leur sens n'a rien à voir avec celui que leur donne Desargues. L'effort de mémoire demandé au lecteur moderne n'est secouru ni par la familiarité avec la langue littéraire classique – je n'ai pas souvenir qu'elle se préoccupe de « rectangles gemeaux entre eux » ! - ni par les connaissances en mathématiques actuelles, lesquelles prennent les problèmes autrement que Desargues et usent de termes différents. Le vocabulaire du Brouillon Projet a plus vieilli que celui du Cid, pourtant contemporain. Cela ne tient pas seulement au fait qu'on m'a familiarisé en classe avec le Cid. Le vocabulaire du Brouillon Projet a vieilli parce qu'il est précis. Le Cid parle d'honneur et d'amour : le sens de ces termes assez généraux a peu changé depuis Corneille. Desargues, lui, a besoin de donner un sens précis aux termes qu’il introduit, parce qu'il veut cerner l'essentiel de la situation géométrique et éviter les ambiguïtés. Il participe là d'un effort que je crois voué à un inachèvement perpétuel : les hommes n'arrivent jamais à l'essentiel, jamais à la chose même, n’éliminent jamais toute ambiguïté. Ils croient y parvenir mais, de génération en génération, les contextes et les regards changent. Alors, ce qui passe pour essentiel et clair à une époque paraît secondaire ou confus à la suivante, si bien que les termes précis choisis pour cerner l’essentiel perdent de leur pertinence, et leur sens finit dans l'oubli. Dans la mesure où les mathématiques sont plus précises que la littérature, leurs textes sont voués à vieillir plus vite.
@@@@@@@
Un des mots définis par Desargues reste usité : « involution ». C’est d’ailleurs l'importance qu’il a donnée à la notion d'involution qui vaut à Desargues son prestige actuel.
Mais son acception ne nous est pas familière pour autant, les mathématiciens ayant, justement, changé de point de vue. Ils font avec cette notion ce qu'ils font toujours : ils la réélaborent, chaque époque transmet sa réélaboration à la suivante, et la notion évolue au point de devenir méconnaissable. Quant à Desargues, évidemment, il ne pouvait pas deviner que la notion d'involution resterait comme sa contribution majeure. Alors, dans le Brouillon Projet, ce terme est présenté au milieu d’une foule d’autres qui, eux, sont tombés en désuétude. Le passage du temps a fait ainsi naître une hétérogénéité, et le lecteur actuel a l’impression comique que ce pauvre Desargues mélange tout : il place sur un pied d’égalité un terme durable, promis à assurer sa gloire, et des termes éphémères, voués à l’oubli.
Involutions d’hier et d’aujourd’hui
Chez Desargues, des points sur une droite sont en involution quand ils sont dans une certaine position les uns par rapport aux autres – il en donne la définition page 4 du Brouillon Projet :

Une involution, au sens moderne, est une application qui, réalisée deux fois de suite, ramène au point de départ. Le lien entre ces notions réside dans le fait que les points en involution au sens de Desargues peuvent être transformés les uns dans les autres par une involution au sens moderne du terme.
Obstacle supplémentaire à la lecture : le texte que j'ai téléchargé est un fac-similé de l'édition originale (1639). Il faudrait donc le lire dans la présentation de l'époque. En soi, le fait que le titre ne soit pas exactement ce que j'ai dit jusqu'ici, mais BROVILLON PROIECT D'VNE ATTEINTE AVX evenemens des rencontres du Cone avec un Plan ; le fait que Desargues emploie couple au féminin ; que, en général (mais pas toujours), sa typographie confonde presque les s et les f; que sa ponctuation soit parfois aberrante par rapport aux usages actuels ; qu'il parle de poincts et de droictes, et appelle « imposition de nom » ce que nous appelons « définition » – tous ces faits sont des détails, et ne devraient pas gêner la lecture. Certes. La vérité force cependant à admettre qu'ils captent et détournent une partie de l'attention, qu’ils rendent le texte étrange à nos yeux, l’opacifient, donc imposent un effort supplémentaire. Cela montre au passage que ma familiarité avec les écrivains du XVIIe siècle est biaisée ; mon contact avec eux est indirect, puisqu'il se fait via des rééditions conformes à l'orthographe et à la typographie du XXe siècle, fort différentes des leurs.

Figure 3 : L’intersection d’un cône et d’un plan vue sur une image de rêve... Mais le rêve n’est pas la réalité. Cette image n’apporte donc aucun élément sur la vieille question des rapports entre mathématiques et réalité ! (Mont Fuji Yama, photo Joe Jones WikiCommons) (on s’attachera à trouver les deux plans de coupe du cône).
L'intersection d'un plan avec un cône de révolution est une courbe plane, appelée conique. On obtient une conique propre quand le plan n'est pas perpendiculaire à l'axe du cône, et ne passe pas par son sommet. On distingue trois sortes de coniques propres en fonction de l'angle d'inclinaison du plan avec l'axe du cône. Si cet angle est supérieur à l'angle d'ouverture du cône, l'intersection est une ellipse ; si l'angle d'inclinaison est inférieur à l'angle d'ouverture, c'est une hyperbole ; si les deux angles sont égaux, c'est une parabole.
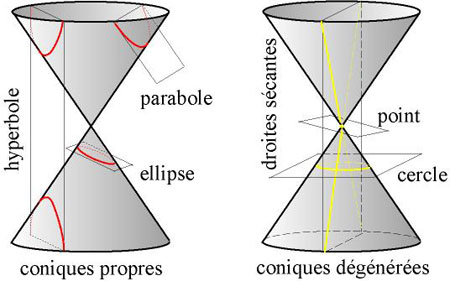
Figure 4 : Coniques propres et dégénérées (WikiCommons, Christophe Dang Ngoc Chan)
Quand le plan est perpendiculaire à l'axe du cône, l'intersection est un cercle. Quand le plan contient le sommet du cône, l'intersection est une conique dégénérée : un couple de droites sécantes, si l'angle d'inclinaison du plan avec l'axe du cône est inférieur à l'angle d'ouverture du cône ; une droite, si ces angles sont égaux ; un point, si l'angle d'inclinaison est supérieur à l'angle d'ouverture.
Surprise : le Brouillon Projet ne contient pas de figures ! J'ai commencé par sourire, en me disant que Desargues avait agi comme Bourbaki, ce célèbre mathématicien collectif du XXe siècle, dont un parti pris ostensible était de ne faire aucune figure dans ses traités de géométrie. Mais je touche là une autre limite de mon entreprise. Télécharger via Internet est une médiation sur laquelle je n'ai aucun contrôle. Or un historien des mathématiques m'a expliqué que l’usage du XVIIe siècle était de rassembler les figures sur des feuilles à part, qui se déplient en accordéon à la fin du volume ; les robots chargés de numériser les œuvres ne les reproduisent pas. De fait, Desargues écrit dès le premier paragraphe :
Il ne fera pas malaifé (...) de choifir entre les figures celle qui à raport au periode qu’on lit, ou de faire ces figures fur le difcours.
Desargues a donc dû publier certaines figures, sans renvoi dans le texte, et en laisser d’autres au soin du lecteur. Pour savoir lesquelles, il faut consulter en bibliothèque un exemplaire sur papier. Les archives sont un passage obligé de l'historien, les téléchargements ne dispensent pas du contact direct avec les originaux. En l'occurrence, l'historien René Taton (1915-2004) a effectué ce travail, mais cela ne permet quand même pas de connaître les figures publiées par Desargues : les planches manquent sur le seul exemplaire connu de l'édition originale
(1).

Figure 5 : On ne connaît pas de portrait de Desargues, sinon celui dû au peintre académique Théobald Chartran (1849-1907) dans son tableau du grand escalier de la Sorbonne "Pascal, en compagnie de Desargues et du père Mersenne, expose à Descartes ses projets d'expérience sur la pesanteur de l'air, place Royale (1643)". Il y a peu de chances que ce portrait soit ressemblant. Mais Pascal, précisément, écrivait : « Lorsqu’on ne sait pas la vérité d’une chose il est bon qu’il y ait une erreur commune qui fixe l’esprit des hommes (...) car la maladie principale de l’homme est la curiosité inquiète des choses qu’il ne peut savoir et il ne lui est pas si mauvais d’être dans l’erreur que dans cette curiosité inutile » (Pensées, Éd. Lafuma, Seuil, 1963, p. 596). Regardons ce portrait comme s’il était fidèle, donc, et tenons-nous en là.
@@@@@@@
Une conception répandue, qui prend tantôt une forme savante, tantôt une forme pédagogique, veut que les mathématiques progressent de façon linéaire ou cumulative. La forme savante de cette conception n'est en général pas explicitée de façon aussi brutale que je vais le faire, mais je la crois néanmoins présente dans beaucoup d'esprits. Elle revient à ceci : « Puisque je viens après Desargues, je bénéficie des connaissances obtenues depuis, donc j'en sais plus que lui. Du coup, même si je suis intrinsèquement moins doué, je suis, grâce au progrès, plus fort que lui ». Une telle lecture de l'histoire des mathématiques donne un agréable sentiment de supériorité, mais elle manque de pertinence – mon échec à lire Desargues en témoigne. Chaque génération, en fait, crée sa propre intelligence des choses. Il n’y a pas une façon fixe de poser les problèmes, suivie d’une progression vers leur solution : la façon même dont on les pose est susceptible de varier. L'image du nain monté sur des épaules de géants est trompeuse. Ce que le nain voit grâce à sa position en hauteur, les géants qui le portent ne le voient pas ; ils ne peuvent donc pas l’aider à le comprendre et à l’interpréter. C’est à lui de le faire.
La pédagogie, maintenant. Lors des débats sur l'enseignement, il se trouve toujours un participant pour proposer l'histoire des mathématiques comme aide à la pédagogie : l’élève comprendrait mieux les notions si l’enseignant expliquait leur histoire. Pareille suggestion sous-entend que les œuvres des anciens sont à lire comme l'ébauche des nôtres – un peu comme un exercice scolaire est censé être l'ébauche du travail plus élaboré que l'élève fera plus tard. En fait, les mathématiques sont une perpétuelle remise en chantier, une exploration de pistes qui se révèlent plus souvent mauvaises que bonnes. Les travaux sont pris dans une histoire qui les mène dans des directions imprévisibles, le « bon » point de vue sur tel ou tel problème change avec le temps, chaque époque retravaille. Se plonger dans l’état d’esprit d’un mathématicien ancien exige donc un long entraînement. Je ne conteste pas l’utilité d’expliquer aux élèves, lors de digressions, que les notions évoluent : cela leur ferait sentir la force du temps, qui métamorphose tout, même les mathématiques. Mais leur demander d’acquérir une connaissance technique de l’histoire des mathématiques, comme on leur demande d’acquérir une connaissance technique des mathématiques, serait une entreprise d’ampleur excessive. L'histoire d'un problème mathématique n'est pas une voie facilitant l'approche de ce problème : elle est un autre problème. (Bien sûr, l’histoire des mathématiques comprend aussi des anecdotes, lesquelles offrent des occasions de respirer au milieu d’un cours difficile.)
@@@@@@@
Le Brouillon Projet a été étudié par nombre d’auteurs, dont il a suscité les commentaires. Voilà qu’il s’est montré capable d’inspirer quelqu’un qui n’en a lu guère plus que le titre. Interprétons cela comme un indice supplémentaire de sa puissance !
Septembre 2011

(1) Comme l’indique René Taton dans son minutieux travail de recherche des manuscrits de Desargues, « Découverte d'un exemplaire original du "Brouillon project" sur les Coniques de Desargues », Revue d'histoire des sciences et de leurs applications, 1951, vol. 4, p.176-181 (en ligne Persée).








 René Taton, L’œuvre mathématique de G. Desargues, par René Taton, PUF (1951)
René Taton, L’œuvre mathématique de G. Desargues, par René Taton, PUF (1951)
 Marcel Chaboud, Girard Desargues : bourgeois de Lyon, mathématicien, architecte, Aléas (1996)
Marcel Chaboud, Girard Desargues : bourgeois de Lyon, mathématicien, architecte, Aléas (1996) Actes du colloque Girard Desargues, Paris-Lyon, organisé en 1991 par le Centre François Viète, Association Girard Desargues
Actes du colloque Girard Desargues, Paris-Lyon, organisé en 1991 par le Centre François Viète, Association Girard Desargues Sur les pas de Girard Desargues, mathématicien et architecte lyonnais, Bibliothèque municipale de Lyon, février 2011
Sur les pas de Girard Desargues, mathématicien et architecte lyonnais, Bibliothèque municipale de Lyon, février 2011