Géométrie des rencontres
- INFORMATION
- ACTUALITÉ
- ANALYSE
- EN SAVOIR PLUS
- À TÉLÉCHARGER
« Questions proposées. Théorèmes appartenant à la géométrie de la règle », Annales de mathématiques pures et appliquées, tome 9 (1818-1819), p. 289-291 ; « Mémoire sur la théorie des moments considérés comme rencontre de lignes droites », Journal de l’École polytechnique, 24e cahier, tome XV (1835) p.133-141 + 1 planche de figures.
1819 | 1835
Démonstration originale d’un résultat géométrique de concourance de droites par l’utilisation des propriétés des résultantes de force en statique.
Le nom de Coriolis est universellement connu ; la carrière et les autres contributions de ce savant sont nettement moins connues (comme la définition physique du mot travail, en 1826). Ici, il use d’une démarche peu habituelle : démontrer un résultat de géométrie (la concourance de droites) en utilisant la statique (forces et moments). C’était là le confluent de ses deux intérêts majeurs : d’une part les mathématiques, qu’il professait à Polytechnique, et d’autre part la statique et la dynamique, à laquelle son nom restera lié (par la force de Coriolis).
Il apporte ici un jalon original sur un sujet connu depuis l’Antiquité (c’est le problème de Ménélaüs d’Alexandrie, au IIe siècle), développé par l’Italien Jean Ceva au XVIIe siècle, et repris par Lazare Carnot trente ans avant Coriolis. Il s’inscrit aussi dans la démonstration de théorèmes duaux, grâce à la géométrie projective notamment – celle-ci avait été imaginée en 1639 par Girard Desargues et développée par le collègue de Coriolis, Jean-Victor Poncelet.
Alexandre Moatti est ancien élève de l’École polytechnique, ingénieur en chef des Mines, docteur en histoire des sciences. Il est directeur de la publication de BibNum, auteur d’ouvrages scientifiques et d’un blog www.maths-et-physique.net

« Sur la théorie des moments considérés comme analyse des rencontres de lignes droites » : tel est le titre de l’article de 1835 de Coriolis. Sommes-nous de nos jours capables de comprendre un tel titre ? – il s’agit en fait d’une démarche peu habituelle : démontrer un résultat de géométrie (la concourance de droites) en utilisant la statique (forces et moments)…
J’avoue pour ma part avoir eu une certaine difficulté, à l’occasion de travaux sur l’œuvre de Coriolis, à bien m’imprégner de ses deux articles sur les moments. Et je ne suis pas certain d’y être totalement arrivé dans le présent article… Il est d’ailleurs rare qu’un enseignant ou un pédagogue avoue tâtonner sur le sujet qu’il traite – pourtant c’est bien le cas ici. Aussi vous proposé-je de transformer ce talon d’Achille (généralement tenu secret, on l’a dit) en un atout dans notre démarche commune, la mienne à l’écriture de cet article, la vôtre à sa lecture.
L’enjeu pour vous et moi sera de comprendre ces deux articles (1819 et 1835), si concis et singuliers de Coriolis, à la lumière des méthodes et des notations modernes – celles-ci sont là pour nous rassurer, pour nous conforter dans l’idée que nous avons bien compris sinon démontré le résultat. Le texte de 1835 ne fait appel qu’à des projections géométriques : il n’utilise pas de coordonnées cartésiennes. Je n’en utiliserai pas non plus… en revanche j’utiliserai l’algèbre vectorielle, bien utile pour la notion de moments – que Coriolis n’utilise pas, cette fois-ci pour cause puisqu’elle n’existait pas de son temps !
|
Le mystère Coriolis
Une célébrité quasi universelle, liée à la force à laquelle il a donné son nom. Un personnage pourtant quasi anonyme, ainsi qu’une œuvre et une carrière scientifiques méconnues. Qui était donc Gaspard-Gustave de Coriolis (1792-1843) ? Il est l’aîné de la branche moins fortunée d’une ancienne famille aristocratique française (parlement de Provence). Après la tourmente révolutionnaire (son père était capitaine aux Gardes du Roi jusqu’en…1792), la famille s’exile à Nancy, et Coriolis intègre l’École polytechnique en 1808, puis le corps des Ponts et Chaussées. Assez peu intéressé par la carrière d’ingénieur des Ponts en province, il devient début 1817 répétiteur d’analyse à l’École polytechnique (cours d’Augustin Cauchy). Il y passera toute sa vie, répétiteur de ce cours jusqu’en 1838, date à laquelle il devient directeur des études dans cette École, poste qu’il conserve jusqu’à sa mort en 1843. Il est aussi professeur à l’École des ponts et chaussées et à l’École centrale (créée en 1829). Mais son sujet d’intérêt principal est la mécanique, et notamment « la théorie des machines », à laquelle il consacre un traité magistral en 1829. Il y formalise la notion de travail, notion toujours en vigueur à l’heure actuelle. En 1831 et 1835, il étudie les équations du mouvement relatif et en tire les notions de force d’entraînement et de force centrifuge composée (plus tard : force de Coriolis) (1). La même année, 1835, il publie une Théorie mathématique des effets du jeu de billard, ouvrage qui reste de référence. Membre de l’Académie des sciences en 1836, il est pris, lorsqu’il devient directeur des études à Polytechnique à partir de 1838, dans des luttes d’influence qui lui pèsent. Il regrette de ne plus pouvoir se consacrer à la science (il avait abandonné, pour des raisons déontologiques étant directeur des études, toutes ses charges de professorat). De santé fragile, miné par ces querelles académiques et politiques, il s’éteint en 1843, à cinquante et un ans, sans doute de la tuberculose qu’il avait contractée jeune.
Figure 1 : Un portrait inhabituel de Coriolis, ca. 1833. Ce portrait est en possession d’un de ses lointains parents, M. Jean de Coriolis, baron de Limaye (Coriolis lui-même n’a pas eu de descendants) (photo A. Moatti) |
« La géométrie de la règle »
Donnons d’abord le sujet brut (tel qu’il apparaît dans l’article de 1819) – on pourrait même dire dans toute sa brutalité.


Il s’agit d’une « question proposée » aux lecteurs, en 1819, dans les Annales de mathématiques pures et appliquées, ou Annales de Gergonne, car elles avaient été créées en 1810 par Jean-Dominique Gergonne (2). Ce n’est pas un article, c’est un exercice, un problème – un peu comme ces devinettes et jeux mathématiques de nos journaux contemporains.
Comme l’indique son titre, il se rapporte « à la géométrie de la règle ». Qu’est cela ? De nos jours, on a du mal à comprendre ces classifications et surtout l’intérêt qu’avaient les mathématiciens jusqu’assez tard au XIXe siècle pour ces constructions à la règle, à la règle et au compas… C’était une autre vision des nombres, d’avant la mise en évidence des nombres transcendants (par Liouville en 1844) (3), d’avant les infinis de Cantor. On construisait les nombres à la règle et au compas, et on obtenait assez (tauto-)logiquement des nombres… constructibles (4), qui d’ailleurs ne constituent qu’une petite partie des nombres algébriques. La « géométrie de la règle », à laquelle se rapporte le sujet proposé de 1819, est plus réductrice encore : elle n’utilise que la règle, pas le compas – elle ne s’autorise pas le recours à la notion de distance (prise entre les pointes du compas et rapportée à un autre endroit), elle ne s’occupe que de directions, de rectilinéarité.
Continuons à observer la forme de ce texte. Il n’est pas signé – ce qui n’est pas anormal s’agissant d’un simple problème en deux pages, et non d’un résultat scientifique avec démonstration à l’appui. Par ailleurs Coriolis n’a alors que vingt-sept ans, il n’a encore jamais rien publié – depuis seulement deux ans répétiteur à Polytechnique (1817), il est inconnu du monde scientifique. Comment sait-on alors que le « problème posé » en 1819 est de lui ? Coriolis nous donne le fil d’Ariane dans l’introduction de son article de 1835, seize ans plus tard :
[…] Dans un mémoire composé en 1811 pour un concours à l’École des Ponts et Chaussées […] Je crois qu’à cette époque on n’avait pas encore considéré les moments comme fournissant une analyse propre à résoudre certaines questions de la géométrie des rencontres (5). Depuis j’ai étendu ces considérations, et j’en ai déduit un assez grand nombre de théorèmes dont plusieurs ont été publiés en 1819 dans les Annales de Mathématiques.
Dans notre investigation sur l’auteur de la « question proposée » de 1819, nous avons trouvé une autre preuve d’attribution à Coriolis. C’est Gergonne lui-même, dans un article (6) ultérieur de 1827, qui indique :
Au commencement de 1819 M. Coriolis me transmet, sans démonstration, un élégant théorème relatif à la géométrie de la règle. Sans même songer à la manière dont il pourrait être démontré, j’écris aussitôt son corrélatif à sa suite, et je les propose tous deux dans mon recueil (tome IX, p. 289).
Les deux « questions proposées » en 1819 sont indistinctes l’une de l’autre dans la forme (l’une est numérotée I, l’autre II) : nous savons donc que la première est de Coriolis et la seconde de Gergonne – c’en est le problème dual.
Coriolis et la « théorie des moments »
Donc : comment Coriolis en vient-il à s’intéresser à cela ? Ce sujet traverse en effet sa vie de mathématicien pendant vingt-cinq ans. En 1811 déjà, alors élève au Corps des ponts à sa sortie de Polytechnique, âgé de 19 ans, il produit sur le sujet un mémoire qui obtiendra un second prix – hélas ce type de mémoire n’était pas conservé par les Ponts et il n’en reste plus trace. En 1835, il indique :
Je le fais moins pour ces théorèmes en eux-mêmes que pour bien montrer l’essence de la théorie des moments.
Coriolis adorait la théorie – et « l’essence d’une théorie » est une expression que l’on trouve plus souvent en philosophie qu’en sciences mathématiques… Comment Coriolis avait-il été mis au contact, dès ses études, avec cette théorie ? Le traité de référence à ce moment est celui de Louis Poinsot (1777-1859, polytechnicien de la première promotion, X1794) : les Éléments de statique (1803), ouvrage constamment réédité pendant soixante-quinze ans. Poinsot fit une carrière très académique qui le tint éloigné de Polytechnique (on peut le rapprocher de Biot, lui aussi polytechnicien de la première promotion, qui eut une carrière fort éloignée de son ancienne école) : mais, de 1809 à 1811, il est brièvement professeur d’analyse et de mécanique à Polytechnique, quand Coriolis y fait ses études. Peut-être est-ce à son contact que Coriolis s’initie à la « théorie des moments » ?
|
Rappels sur la théorie des moments
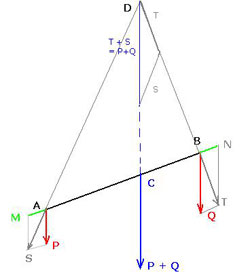
Trouver la résultante de deux forces coplanaires et dont les directions sont sécantes est aisé (règle du parallélogramme). Trouver la résultante de deux forces toujours coplanaires mais de directions parallèles et de même sens est chose moins aisée, et ouvre la voie à la théorie des moments. Soient deux forces parallèles P au point A et Q au point B. Supposant que l'état global n’est pas affecté si l'on ajoute une paire de forces opposées, on applique une paire de forces opposées M en A le long de BA et N en B le long de AB (7) :
La résultante de P et M est S et celle de Q et N est T. Les deux droites supports des forces S et T se rencontrent, elles, en un point D. Appliquées provisoirement en D, leur résultante prend une amplitude S + T, égale à P + Q, et un sens parallèle à celui de P et de Q. Sa droite support est dirigée vers un point C sur AB. C est le point d’application de la résultante P + Q ; la loi des triangles semblables donne par ailleurs BC/DC = N/Q et AC/DC = M/P, et l’on déduit puisque M= N la règle des moments : P x AC = Q x BC. |
Une résolution graphique
Le mémoire de 1835 de Coriolis est nettement moins elliptique que la « question proposée » de 1819. 1835, c’est l’annus mirabilis de Coriolis, l’année de la publication du « second théorème » (force de Coriolis) et de son magistral ouvrage Théorie mathématique des effets du jeu de billard. Dans ce volume XV du Journal de l’École polytechnique, où Coriolis travaille comme répétiteur depuis 1817, quatre articles successifs de Coriolis paraissent, dont le « second théorème » et notre texte sur la théorie des moments.
Mais examinons sans plus tarder les constructions géométriques faites par Coriolis dans cet article, qui nous aideront à comprendre son résultat, notamment son 1er théorème.
Si l’on conçoit dans l’espace (fig. 4) une suite de n points auxquels on donne les numéros de (1) à (n) ; si l’on joint ces points deux à deux dans l’ordre des numéros pour en faire un polygone […] Si sur chaque côté ou sur son prolongement on prend comme on voudra un point, et qu’on le désigne par la réunion des numéros des points par où passe la droite sur laquelle il est pris, c'est-à-dire par (12), (23), (34), etc.
Coriolis choisit donc n points (appelons-les de première génération) sur chacune des droites formant les côtés du polygone. Regardons cela avec l’exemple n=5 dans le plan illustré par Coriolis dans son article de 1835 :
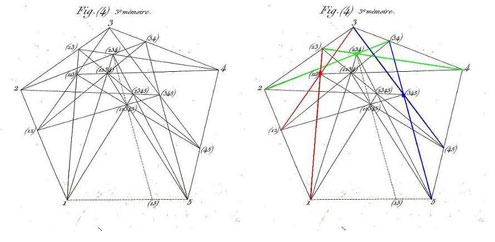
Figures 3 et 3bis : figure (4) de Coriolis, dupliquée par nous, premières étapes. (à g.) On choisit 5 points numérotés de 1 à 5, et sur chacun des côtés, cinq autres points notés (12), sur le côté reliant 1 à 2, (23), etc. ; (à dr.) on relie les points 1 à (23), et (12) à 3 – ces deux droites rouges nous donnent un point rouge noté (123) ; on relie 2 à (34) et (23) à 4 –ces deux droites vertes nous donnent un point vert noté (234) ; on relie 3 à (45) et (34) à 5 – ces deux droites bleues nous donnent un point bleu noté (345).
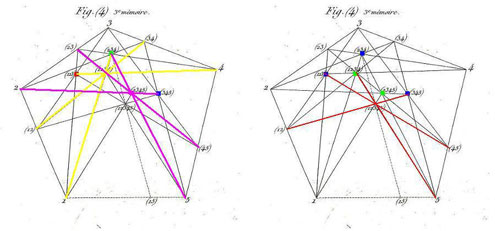
Figures 3ter et 3quater : figure (4) de Coriolis, dupliquée par nous, étapes suivantes. (à g.) On a reporté les points rouge, vert, bleu de la figure précédente. On relie (lignes jaunes) le point rouge (123) à 4, le point 1 au point vert (234), enfin les points (12) et (34) : ces trois droites jaunes sont concourantes en un point jaune noté (1234). On relie (lignes roses) le point vert (234) à 5, le point 2 au point bleu (345), enfin les points (23) et (45) : ces trois droites roses sont concourantes en un point rose noté (2345) ; (à dr.) étape finale pour 5 points, figure de Coriolis – attention on a changé les couleurs des points : les points de troisième génération (123), (234) et (345) figurent en bleu, et les points de quatrième génération (1234) et (2345) figurent en vert. On relie alors le point 1 au point vert (2345), le point (12) au point bleu (345), le point bleu (123) au point (45), le point vert (1234) au point 5 : ces quatre droites rouges sont concourantes en un point rouge noté (12345).
En partant de n points, on arrive à la concourance en un point de (n-1) droites. Voici donc le théorème visualisé à défaut d’être démontré : mais, à mon sens, cette visualisation est une précieuse assistance à la démonstration que nous tâchons d’esquisser ci-après – pour faire cette démonstration (mon rôle) comme pour la comprendre (votre rôle).
Suivons la démonstration de Coriolis
Coriolis semble démontrer son résultat en une phrase, comme si c’était évident :
Si l’on regarde les points de la première série comme des points d’application de forces parallèles dont les rapports de grandeurs soient tels que chaque point de la seconde série soit le point d’application de la résultante des deux forces répondant aux deux numéros successifs de la première série, c'est-à-dire aux extrémités du côté sur lequel se trouve ce point de la seconde série ; il est clair que chacune des deuxième, troisième, quatrième séries de droites contiendra le centre des premières forces appliquées aux points portant les numéros qui sont contenus dans la réunion des indices des deux points par où elles passent : elles devront donc se rencontrer au centre unique de ces forces parallèles.
Dans cette longue phrase, à peine plus explicite que la « question posée » de 1819, où donc interviennent les moments ? Ils interviennent quand Coriolis parle du « rapport de grandeurs » entre forces. Essayons d’expliquer cela :
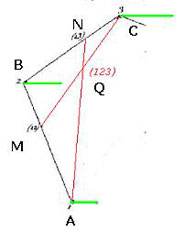
Figure 4
On choisit au point A une force de direction quelconque et d’amplitude FA arbitraire (en vert, figure 4). On applique alors au point B une force parallèle, telle que les moments en M s’équilibrent sur le segment AB : FA x AM = FB x MB (8) donc FB = FA x AM/MB ; idem en N, FB x BN = FC x NC donc FC = BN/NC x FB = BN/NC x AM/MB x FA. Au point M s’applique (cf. relation de Poinsot ci-dessus) la résultante FM = FA + FB ; au point N s’applique la résultante FN = FB + FC.
La résultante entre FA en A et FN en N vaut FA + FN = FA + FB + FC et s’applique au seul point Q du segment [AN] qui annule les moments sur le segment : FA x AQ = FN x QN. Mais ce même point Q a une propriété particulière, il annule aussi les moments sur le segment [MC], ce qu’on démontre dans l’encadré ci-dessous.
|
« Théorème fondamental » du triangle
Avant de nous expliquer sur ce titre pompeux, égrenons nos formules : FA∧ AM + FB∧ BM = 0 (définition de M) (1) FB∧ BN + FC∧ CN = 0 (définition de N) (2) (FA + FB) ∧ MQ + FC∧ CQ = 0 (définition de Q) (3) Calculons alors la somme de moments suivante : FA∧ AQ + (FB + FC) ∧ NQ = FA∧ AM + FA∧ MQ +FB∧ NQ+ FC∧ NC+ FC∧ CQ = FB∧ MB (1) + FA∧ MQ + FB∧ NQ + FB∧ BN (2) + FC∧ CQ = FA∧ MQ + FB∧ (MB + NQ + BN) + FC∧ CQ = (FA + FB) ∧ MQ + FC∧ CQ = 0 (3) En faisant (2) – (3) + (1), on peut obtenir plus rapidement ce même résultat: FA∧ AQ + (FB + FC) ∧ NQ = 0 (4) Donc le point Q annule aussi les moments sur [AN] – démontrons toutefois qu’il est bien sur ce segment. Petite subtilité ici, les forces F sont colinéaires donc proportionnelles à un vecteur de base i sur leur direction, et (4) nous donne alors la relation sans produit vectoriel : FA x AQ + (FB + FC) x NQ = 0 (4bis) Cette relation est entre les vecteurs AQ et NQ, auxquels sont affectés des coefficients barycentriques. Or, qu’est-ce qu’une relation entre deux vecteurs sinon (a minima) une relation de colinéarité ? Les trois points A, N, Q sont donc alignés. Le point Q, défini comme annulant les moments sur [MC], appartient aussi au segment [AN] où il annule aussi les moments. On tirera enfin des trois premières une autre relation (5) : FA∧ AQ + FB∧ BQ + FC∧ CQ = FA∧ (AM + MQ) + FB∧ (BM + MQ) + FC∧ CQ = FA∧ MQ + FB∧ MQ + FC∧ CQ (1) = 0 (3) Cette relation totalement symétrique en A, B et C montre que le point Q est le point d’application de la résultante FA + FB + FC et annule les moments de ces trois forces : FA∧ AQ + FB∧ BQ + FC∧ CQ = 0 (5)
@@@@@@@
Nous ne faisons que retrouver ici un théorème de base de la géométrie du triangle – nous l’appelons fondamental par clin d’œil (théorème fondamental de l’algèbre, de l’arithmétique), mais aussi parce qu’il est fondamental dans notre sujet coriolisien. En transformant les produits vectoriels en relations entre vecteurs, comme ci-dessus (en posant simplement FA = FAi, etc. et en éliminant i), on retrouve la géométrie barycentrique du triangle, avec les coefficients (scalaires cette fois-ci) FA en A, FB en B, FC en C. La relation (5) ci-dessus s’exprime alors : FA x AQ + FB x BQ + FC x CQ = 0 qui est la définition du barycentre, de même que les relations (1) à (4) ci-dessus sont elles aussi l’expression de barycentres. Ce même « théorème fondamental » du triangle s’énonce parfois ainsi : soit Q le barycentre de [(A, FA), (B, FB), (C, FC)] | AQ rencontre BC en N si et seulement si FB x BN + FC x CN = 0. |
Ce qui précède montre comment des calculs de moments – ou les recherches de barycentres, équivalentes (9) – nous amènent à des concourances de droites en ces barycentres. Si l’on reformule la phrase de Coriolis ci-dessus, avec ses notations : au point (1), on fixe une force de direction et d’amplitude arbitraires (cf. figure 4 ci-dessus); au point (2) on applique une force parallèle, d’amplitude donnée par la formule des moments par rapport au point (12); ainsi la résultante, somme des deux forces, a (12) pour point d’application (seul point du segment qui annule les moments) ; et ainsi de suite jusqu’au point (n). La résultante des forces en (1), (2) et (3) aura un et un seul point d’application, annulant les moments en (1), (2) et (3), ainsi qu’en (12) et (3), et en (1) et (23). Le raisonnement se répète dans la série de points successifs : à chaque fois le point d’application de la résultante, envisagé de plusieurs manières différentes, est le point de concours d’un certain nombre de droites. On a ainsi (n – 2) points où se croisent deux droites, (n – 3) points où se croisent trois droites, (n – p) points où se croisent p droites, et finalement 1 point où se croisent (n – 1) droites. La phrase de Coriolis est d’une grande économie de mots, mais même s’il est synthétique on peut suivre son raisonnement.
Le lecteur, pour s’en convaincre (j’aime assez ce genre de phrase, suivie généralement d’un futur), pourra étudier la figure suivante et sa légende.
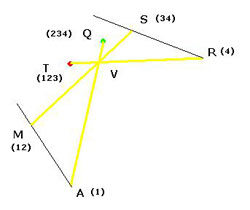
Figure 5 : (issue de figure 3ter ci-dessus) (Les points A, M, Q sont les mêmes que dans la figure 5, et le point S figure comme point (34) dans les figures 3).Traçons le segment MS, et définissons le point V comme celui qui annule les moments sur ce segment. Par des calculs analogues à ceux de l’encadré ci-dessus, s’agissant du même jeu de forces F1, F2, F3, F4, on démontre que V est aussi le point qui annule les moments sur RT, et qu’il est sur ce segment ; que V est aussi le point qui annule les moments sur AQ, et qu’il est sur ce segment. Les trois droites concourent donc en V, qui est appelé (1234) par Coriolis.
Avant Coriolis, Ceva et d’autres
Coriolis résout le sujet de manière originale – il semble que personne ne l’ait fait ainsi avant lui. Cependant, nous l’avons vu, la résolution par les moments diffère peu de la résolution par les barycentres, en affectant un coefficient à chaque sommet d’un polygone. Un certain nombre d’auteurs affectaient (virtuellement, on imagine) une masselotte différente à chaque sommet d’une figure. Coriolis reconnaît une antériorité à cette méthode quand il écrit en note de bas de page :
M. Olivier […] vient de me montrer un traité publié en 1678 par Jean Céva, sous le titre de De rectis lineis invicem secantibus statica constructio. On voit par le titre (10) même que cet ouvrage contient l’idée de ce petit Mémoire.
Il faut dire que l’ouvrage, écrit en latin, n’est pas d’un accès facile et on comprend que Coriolis ait pu ne pas le connaître (et inversement l’on s’étonne qu’Olivier le connût) – en voici un extrait :

Même au temps de Coriolis, 150 ans après la parution de ce traité en latin, il n’est pas sûr que de nombreux mathématiciens aient pu le comprendre ; en tout cas Théodore Olivier (11), répétiteur à Polytechnique, le connaissait – quoique mathématicien mineur, sans doute était-il plus érudit que Coriolis.
|
Théorème de Ceva
Mais si Giovanni Ceva, ou Jean Céva (1647-1734), reste connu, c’est parce qu’il a donné son nom à un théorème extrait de son ouvrage de 1678.
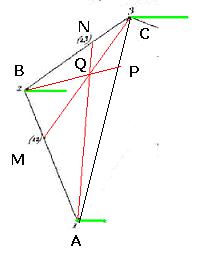
Figure 6 (reprise de figures 4 et 5) Le théorème de Ceva dit que les trois droites sont concourantes si et seulement si :
Démontrons-le dans un sens. On suppose la relation (6) valide. On affecte les poids α en A, β = α x MA/MB en B, γ = α x PA/PC. Comme αMA = βMB, M est le barycentre de A (α) et B (β) On a donc la relation vectorielle suivante : α MA + β MB = 0 En suivant le même raisonnement pour α et γ, on a : α PA + γ PC = 0. On déduit de (6) que βNB = γNC, donc : β NB + γ NC = 0 On définit Q comme le barycentre des trois points : α QA + β QB + γ QC = 0 donc α QM + α MA + β QM +β MB + γ QC = 0 donc (α + β) QM + γ QC = 0 Donc les trois points Q, M, C sont alignés (de même Q, N, A et Q, B, P) : donc les droites sont concourantes.
@@@@@@@
Démontrons-le dans l’autre sens. Soit un point Q dans le triangle. On trace les « céviennes » issues de Q, c'est-à-dire les segments issus de chacun des sommets et passant par Q ; elles sont concourantes. On affecte des coefficients barycentriques α (12) en A, β = α AM/BM en B, et en C γ = β CN/BN. On définit enfin un point Q’ qui annule les moments sur [AN]. On a donc : α MA + β MB = 0 β NB + γ NC = 0 α Q’A + (β + γ) Q’N = 0 On reconnaît les trois relations (1), (2), (3) de l’encadré ci-dessus. Avec le même calcul que ci-dessus (que l’on refait), on obtient : (α + β) Q’M + γ Q’C = α Q’A+ α AM + β Q’B + β BM + γ Q’C = α Q’A + β Q’N + β NB + γ Q’N + γ NC = 0 Le point Q’ est sur le segment [AN] par définition ; il est aussi sur le segment [MC] par la relation de colinéarité ci-dessus. Il est au croisement de ces deux segments et est donc confondu avec Q. On tire aussi : α QA + β QB + γ QC = α QA + β QN + β NB + γ QN + γ NC = 0 Donc Q est bien le barycentre des trois points A (α), B (β), C (γ). Soit maintenant P’ le point barycentre sur [AC] α P’A + γ P’C = 0. Calculons la somme des moments suivante : β QB + (α+ γ) QP’ = β QB + α QA + α AP’ + γ QC + γ CP’ = 0 Donc le point P’ est sur le segment [QB] (colinéarité des vecteurs). Comme il est aussi sur le segment [AC], c’est le point de rencontre de ces deux segments, donc P’= P. On a ici redémontré une variante du « théorème fondamental », à savoir que si Q est le barycentre, la droite BQ coupe AC en un point P tel que α PA + γ PC = 0. On en déduit alors facilement que les coefficients « font la ronde » : NB/NC x PC/PA x MA/MB = γ/β x α/γ x β/α = 1
@@@@@@@
On peut maintenant se demander quelle est l’utilité du théorème de Ceva – d’ailleurs quelle est l’utilité d’un théorème en général ? On peut en dire que le théorème de Ceva permet de transformer un problème de concourance de droites en un problème de calcul de distances. |
Qu’apporte Coriolis par rapport à Ceva ? Comme il le dit lui-même dans sa note de bas de la page de tête de son article – note visant à faire connaître l’originalité de ses travaux :
[…] je n’ai trouvé dans l’auteur italien, parmi les propositions que je donne ici, que la neuvième et la deuxième appliquée au triangle […]
La première proposition (n -1 droites concourantes à partir de n points) est en effet différente du théorème de Ceva. Ceva semble n’avoir travaillé que sur le triangle, c’est pourquoi la deuxième proposition de Coriolis, valable pour tout polygone (pas seulement un triangle), même gauche (non plan), le généralise :
On aura ainsi un polygone fermé et un point sur chaque côté. Les segments formés par ces points sur les côtés pourront se classer en deux séries dont chacune sera composée de ceux qui n’ont pas d’extrémité commune, ou, en d’autres termes, de ceux qui ne sont pas adjacents. Le produit de tous les segments d’une série sera égal au produit des segments de l’autre série.
Nous ne démontrerons pas cette deuxième proposition mais nous y retrouvons les produits des distances du théorème de Ceva pour le triangle :
(notations figure 6)
AM, BN, CP première série de segments non adjacents
MB, NC, PA seconde série de segments non adjacents
AM x BN x CP = MB x NC x PA
@@@@@@@
Il est un autre auteur qui avait travaillé sur ce sujet : il s’agit de Lazare Carnot (1753-1823), le mathématicien et général révolutionnaire, ministre de l’Intérieur des Cent-Jours. Coriolis emprunte aussi à la tradition de Carnot dans ses résultats de mécanique (en théorie des machines, sur la notion de travail par exemple) : bien que ces deux savants se ressemblent fort peu, on ne peut manquer de remarquer le même intérêt qu’ils portent à des sujets fort analogues, en mécanique (théorie des machines) comme en géométrie (rencontre de droites et alignement de points). La notion de « transversale » chez Carnot (13) est duale de la notion de cévienne – elle conduit à des résultats analogues à ceux présentés par Coriolis (qui cite Carnot dans son 3e théorème de l’article de 1835, p. 137). C’est pour nous l’occasion de poursuivre sur cette notion de dualité en géométrie projective, et ce d’autant que chacun des deux articles de 1819 et de 1835 donne un ou plusieurs résultats duaux : en 1819, c’est Gergonne lui-même qui ajoute le résultat dual à celui de Coriolis, et en 1835, c’est Coriolis qui le fait dans son neuvième théorème (généralisant le théorème de Ménélaüs, dual de celui de Ceva).
Un peu de géométrie projective appliquée au triangle
Imaginée, entre autres, par Girard Desargues (1591-1661) (14) et largement développée par Jean-Victor Poncelet (1788-1867), polytechnicien bien connu de Coriolis(15), la géométrie projective (16) associe, à tout point [resp. toute droite] du plan, une droite [resp. un point] d’un autre plan. Les relations entre points et droites sont conservées, de sorte que deux droites du premier plan sont transformées en deux points du deuxième, et que le point d’intersection des deux droites est transformé en la droite passant par les deux points. Ainsi, trois droites concourantes dans l’un deviennent-ils trois points alignés dans l’autre. Un côté d’un triangle, dans le plan de départ, devient un point dans le plan d’arrivée. Un sommet du triangle initial, intersection de deux côtés, devient une droite reliant dans le plan d’arrivée les points qui sont les images des côtés initiaux : l’image d’un triangle est un triangle, les côtés ayant été en quelque sorte intervertis avec les sommets.
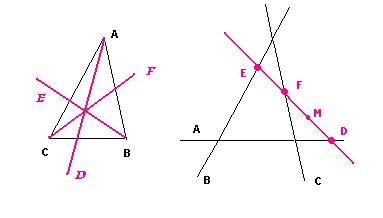
Figure 7 : Triangle de sommets ABC (à g.), et son dual, un triangle de cotés encore notés A, B, C (à dr.). Le sommet A (à g.) devient une droite A (à dr.). Le côté AB (à g.) devient un point à l’intersection des droites A et B (à dr.) (point non marqué dans la figure). La relation (à g.) « la droite cévienne D contient le point A » se transforme (à dr.) en « le point D appartient à la droite A ». Les deux autres céviennes E (resp. F) (à g.) se transforment en deux points E (resp. F) (à dr.) situés sur B (resp. C). La relation (à g.) « les trois droites céviennes E, D, F concourent en un point M » se transforme (à dr.) en « les trois points D, E, F sont alignés sur une droite, la transformée de M ».
Cette dualité projective conduit au théorème de Ménélaüs (17), dual du théorème de Ceva. Soit un triangle (à dr.), coupé par une « transversale » – c'est-à-dire par une droite coupant ses trois côtés en D, E, et F :
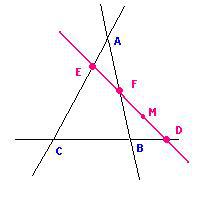
Figure 8 : Figure 7-dr. dans laquelle A, B, C redeviennent les sommets du triangle (marqués en rouge).
On a alors la relation suivante :
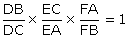
C’est réciproquement une condition nécessaire et suffisante d’alignement : soient trois points D (sur BC), E (sur AC), F (sur AB) – ils sont alignés si et seulement si la condition ci-dessus est vérifiée. Cette condition peut être démontrée par les moments, comme nous l’avons fait pour celle de Ceva.
@@@@@@@
On peut d’ailleurs revenir sur une autre correspondance duale, figurant dans l’article d’origine de Coriolis (1819). Nous avons indiqué ci-dessus que Gergonne, lors de la parution en 1819 ajoute une question de son cru à celle de Coriolis, le problème « corrélatif » :
Soit n droites arbitraires […] se coupant consécutivement. Désignons l’intersection de chaque droite avec celle qui porte le numéro immédiatement supérieur par l’ensemble de leurs indices […] Par ces points d’intersection, soient menées des droites indéfinies […] Considérons les intersections deux à deux, au nombre de n – 2, de celles de ces droites […] En continuant le même procédé, on obtiendra des droites, au nombre de n - 4 […] et enfin, une droite unique, sur laquelle n – 1 points se trouveront situés.
La question posée par Coriolis en 1819 traite de l’obtention d’un point de concours de (n-1) droites – c’est un problème « de type Ceva » (recherche de concourance de droites). Le problème dual que Gergonne ajoute à sa suite consiste en l’obtention d’une droite qui aligne (n – 1) points – c’est un problème de type Menelaüs (recherche d’alignement de points).
Une théorie… aussi très pratique
Finalement, quel est l’apport de Coriolis sur ce sujet connu depuis l’Antiquité (pour le problème de Ménélaüs), développé par Ceva au XVIIe siècle, et repris par Carnot trente ans avant Coriolis ? Ces résultats sont, on l’a vu, très similaires ; mais Coriolis donne des démonstrations concises, fondées sur la théorie des moments, et il généralise les résultats de Ceva sur le triangle (donc plan) à un polygone à n côtés, non nécessairement plan (tout ce qu’il propose s’applique à un polygone gauche). Il ne faut donc pas sous-estimer la vision de ce dernier sur ce sujet qui l’amuse toute sa vie, et son approche m’a pour ma part amusé – j’espère que ce fut votre cas aussi.
À signaler que, de manière tout à fait étonnante, Coriolis ne se contente pas des neufs théorèmes de son article : il donne une application pratique du premier théorème (celui de la concourance des droites), destinée à tester l’aptitude d’un dessinateur à tracer des lignes :
Ce théorème, quand on l’applique à des points sur un plan, donne un moyen commode de vérifier l’exactitude que met un dessinateur au trait à tracer des lignes et à marquer leur rencontre ; si toutefois il ne connaît pas l’énoncé ci-dessus. Pour cela on lui posera les points de la première série, puis on lui prescrira de les joindre […] Alors il se trouvera plusieurs des droites qu’il aura tirées qui devront se rencontrer au même point, s’il les a bien tracées et s’il a marqué avec précision les points de rencontre. C’est donc ce qu’on reconnaîtra d’un coup d’œil.
Cette incise montre la vision fort opérationnelle des questions de géométrie ou de mécanique qu’avait Coriolis. Caractéristique de l’ « ingénieur-savant », sa démarche vers l’amont (appliquer des principes de mécanique à la géométrie) se double d’une inventivité à l’aval : de la géométrie à la « mécanique appliquée », ici le dessin « industriel », auquel se rapporte cette incise.
(mai 2014)
(je remercie Maxime Bourrigan, Damien Gayet, Julien Melleray pour leurs relecture et commentaires de cet article)

1. Sur les articles de 1831 & 1835 sur le mouvement relatif, voir l’analyse d’A. Moatti, BibNum, octobre 2011.
2. Sur le « Prospectus », avant-propos par Gergonne du premier numéro de sa revue (1810), voir l’analyse de Christian Gérini, BibNum, septembre 2008.
3. Sur l’article de 1844 de Liouville, voir l’analyse de Michel Mendès France, BibNum, septembre 2008.
4. Le théorème de Wantzel (1837) démontre qu’un nombre constructible est solution d’un polynôme de degré 2n. On peut le considérer comme un premier jalon de la théorie des nombres.
5. C’est cette jolie expression de Coriolis, « géométrie des rencontres », que nous avons choisie comme titre de notre propre article.
6. En annotation d’un article de Poncelet, « Notes sur divers articles du bulletin des sciences de 1826 et 1827, &c. », Annales de mathématiques pures et appliquées, tome 18 (1827-1828), p. 125-142 [Numdam].
7. Cette explication est issue de Poinsot, via l’article d’Ivor Grattan-Guinness, « La notion de couple en mécanique : réhabiliter Poinsot », BibNum, janvier 2013.
8. Comme les forces sont parallèles, on peut raisonner ici en vectoriel (FA, AM) comme en scalaire (FA, AM).
9. Avec la convention posée par Coriolis de prendre des forces de même direction (peu importe cette direction). En prenant des forces et non des masselottes, Coriolis n’est pas très éloigné de la notion de produit vectoriel.
10. Coriolis ne juge pas bon de le traduire : à l’époque tout le monde comprenait ce titre, qu’on pourrait traduire « À propos d’une construction par la statique de droites mutuellement sécantes ».
11. Théodore Olivier (1793-1853), polytechnicien (X1811), était mathématicien, répétiteur à Polytechnique. Il fut un des fondateurs de l’École centrale en 1829, et par la suite (1839) professeur de géométrie descriptive au Conservatoire national des arts et métiers.
12. Le choix de est arbitraire puisqu’il y a proportionnalité des coefficients barycentriques.
13. Pour une étude de la conceptualisation de la notion de transversale chez Carnot : Karine Chemla, « Lazare Carnot et la généralité en géométrie. Variations sur le théorème dit de Ménélaüs », Revue d’histoire des mathématiques, 4 (1998), p. 163–190.
14. Voir à ce sujet l’analyse par Didier Nordon d’un texte de 1639 de Desargues, BibNum, septembre 2011.
15. Ils avaient une promotion d’écart et leurs parcours et travaux se croiseront entre 1815 et 1830, parfois avec quelques heurts – Poncelet était assez belliqueux sur ses antériorités, Coriolis ne l’était pas.
16. Comme l’écrit Serge Mehl (Chronomath), « la déferlante axiomatique de la période des mathématiques modernes a éliminé des programmes de mathématiques ces éléments fondamentaux de la géométrie projective». Elle était enseignée dans les lycées jusqu’aux années 1970 – Mehl cite une référence de livre scolaire : Géométrie, classe de Terminale C-E, par Marcel Condamine, Coll. P. Vissio, Éd. Delagrave - 1971.
17. Du nom du mathématicien Ménélaüs d’Alexandrie (70-140 ap. J.-C.).
LIVRES
 |
|
 |
|
 |
|
ARTICLES
 |
|
 |
coriolis-texte-retravaille.pdf

coriolis-analyse.pdf



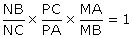 (6)
(6)

