Legendre et la méthode des moindres carrés
- INFORMATION
- ACTUALITÉ
- ANALYSE
- EN SAVOIR PLUS
- À TÉLÉCHARGER
« Appendice sur la méthodes des moindres quarrés », annexe (p.72-80) à l’ouvrage Nouvelles méthodes pour la détermination des orbites des comètes, Firmin-Didot, Paris, 1805.
1805
C’est la première apparition de la « méthode des moindres carrés » pour trouver les valeurs les plus probables dans une série d’observations, qui sera développée par Gauss, et par Laplace. Elle est une des bases de l’analyse statistique.
La méthode du maximum de vraisemblance et celle des moindres carrés sont les outils de la théorie des erreurs ou de l'estimation, utilisés tous les jours dans toutes les sciences d'observation. L’exposé par Legendre en 1805 de la méthode des moindres carrés n'est pas probabiliste mais purement algébrique : il traite le problème algébrique de la détermination des quantités dans un système d'équations surdéterminé. Gauss démontrera en 1809 la loi normale (dite « loi de Gauss », ou « courbe en cloche ») en considérant que si une quantité a été obtenue par plusieurs observations, faites avec le même soin dans des circonstances semblables, la moyenne arithmétique des valeurs observées sera la valeur la plus probable de cette quantité. La synthèse entre l’approche de Legendre en 1805, mais surtout celles de Gauss et Laplace en 1809 et 1810, impose la loi normale comme loi quasi universelle. En effet, même si la distribution individuelle des erreurs ne suit pas une loi normale, celle des moyennes des erreurs suit sous certaines conditions (indépendance, lois identiques), une loi normale. Son usage se révèlera fondamental en analyse statistique.
Jean-Jacques Samueli est docteur d'État ès sciences physiques et auteur scientifique ; il a été notamment chef du service d'instrumentation nucléaire à l'Institut de Physique Nucléaire de Lyon.

Querelle entre Legendre et Gauss sur la paternité de la méthode
Gauss, dans son traité Theoria motus corporum coelestium (4) publié en 1809, indique qu’il utilisait cette technique depuis 1795. Il écrit : Au reste, ce principe, dont nous avons fait usage depuis 1795, a été donné dernièrement par Legendre dans ses Nouvelles méthodes pour la détermination des orbites des comètes, Paris, 1806 ; on trouvera dans cet ouvrage plusieurs conséquences que le désir d'abréger nous a fait omettre.
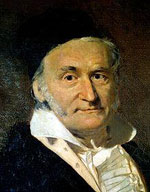
Cette affirmation de Gauss irrita Legendre. Il écrit à Gauss, quelque temps après, en 1809 (Gauss, Werke, Band. 10/1, p. 380) : Je ne vous dissimulerai donc pas, Monsieur, que j’ai éprouvé quelque regret de voir qu’en citant mon mémoire …, vous dites principum nostrum …Il n’est aucune découverte qu’on ne puisse s’attribuer en disant qu’on avait trouvé la même chose quelques années auparavant ; mais si on n’en fournit pas la preuve en citant le lieu où on l’a publiée, cette assertion devient sans objet et n’est plus qu’une chose désobligeante pour le véritable auteur de la découverte. En Mathématiques il arrive très souvent qu’on trouve les mêmes choses qui ont été trouvées par d’autres et qui sont bien connues; c’est ce qui m’est arrivé nombre de fois, mais je n’en ai point fait mention et je n’ai jamais appelé principum nostrum un principe qu’un autre avait publié avant moi. Vous êtes assez riche de [votre] fonds, Monsieur, pour n’avoir rien à envier à personne; et [je suis] bien persuadé au reste que j’ai à me plaindre de l’expression seulement et nullement de l’intention …
Dans une lettre à Laplace datée de 1812 (Werke, Band 10/1 pp. 373-374) Gauss déclare, pour sa part : J’ai fait usage de la méthode des moindres carrés depuis l’an 1795 (…) Cependant mes applications fréquentes de cette méthode ne datent que de l’année 1802, depuis ce temps j’en fait usage pour ainsi dire tous les jours dans mes calculs astronomiques sur les nouvelles planètes. (…). Au reste j’avais déjà communiqué cette même méthode, beaucoup avant la publication de l’ouvrage de M. Legendre, à plusieurs personnes, entre autres à Mr. Olbers en 1803. Ainsi, pouvais-je dans ma théorie parler de la méthode des moindres carrés, dont j’avais fait depuis sept ans mille et mille applications (…). Pouvais-je parler de ce principe, -que j’avais annoncé à plusieurs de mes amis déjà en 1803 comme devant faire partie de l’ouvrage que je préparais,-comme d’une méthode empruntée de Mr. Legendre? Je n’avais pas l’idée, que Mr. Legendre pouvait attacher tant de prix à une idée aussi simple, qu’on doit plutôt s’étonner qu’on ne l’a pas eue depuis 100 ans, pour se fâcher que je raconte, que je m’en suis servi avant lui ? … Mais j’ai cru que tous ceux qui me connaissent le croiraient même sur ma parole, ainsi que je l’aurais cru de tout mon coeur si Mr. Legendre avait avancé, qu’il avait possédé la méthode déjà avant 1795.
![]()
![]()
![]()
(etc.)
Où E, E', E"...sont les erreurs à rendre minimales. Legendre utilise une méthode empirique, simple à mettre en œuvre, qui consiste à rendre minimale la somme des carrés des erreurs et qu'il justifie par la phrase :
![]()
![]()
et nous désirons que cette somme soit minimale par rapport aux inconnues x, y, z,...
![]()
que l'on peut écrire, avec les notations de Legendre :
![]() , avec
, avec ![]()
etc.
![]()
![]()
![]()
...............................................
![]() ,
,
![]()
et donc ![]() , c'est-à-dire la moyenne arithmétique des valeurs mesurées.
, c'est-à-dire la moyenne arithmétique des valeurs mesurées.
![]()
Cette valeur de X rendra maximale la probabilité d'observation des mesures observées x1, ..., xn et donc d’observation des erreurs e1, ...en. Il s'agit de rechercher X, donc f, de sorte que ![]() soit maximum. Le produit
soit maximum. Le produit ![]() est maximum lorsque la somme
est maximum lorsque la somme ![]() est maximale. En dérivant par rapport à X on obtient la condition
est maximale. En dérivant par rapport à X on obtient la condition
![]() (1)
(1)
![]()
Gauss induit que, pour vérifier l’équation (1), on a, pour i allant de 1 à n,
![]()
En prenant k(xi – X), Gauss prend ainsi une fonction linéaire en xi, fonction impaire la plus simple (la fonction f d’erreur étant nécessairement paire – même probabilité d’erreur dans un sens ou dans l’autre –, la dérivée de son logarithme est nécessairement impaire). On a alors, en intégrant,
![]() soit :
soit :
![]()
c'est à dire la densité de la loi de probabilité dite normale.
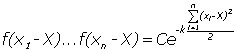 est maximum (ce qui est recherché d'après ce qui précède) lorsque la somme des carrés des écarts des mesures
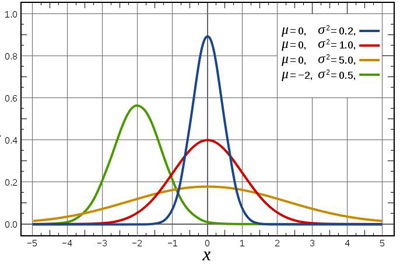
est maximum (ce qui est recherché d'après ce qui précède) lorsque la somme des carrés des écarts des mesures La loi normale la plus générale (dite de Laplace-Gauss) fait intervenir une valeur moyenne μ et un écart type σ.
Une explication du raisonnement de Gauss par Joseph Bertrand

L'histoire de la méthode des moindres carrés est singulière. Legendre, qui, le premier, l'a proposée, en 1805, aux calculateurs, ne la rattachait à aucune idée théorique. Gauss, qui depuis longtemps en faisait usage, a publié, en 1809, une démonstration acceptée sans contestation.
(…)
Si des grandeurs l1, l2,…, ln ont été observées, la probabilité d'une erreur comprise entre z et z + dz, pour l'une d'elles, étant φ(z)dz, la probabilité du concours des erreurs z1, z2,…, zn est proportionnelle à
φ(z1) φ(z2)… φ(zn) (1)
et ce produit doit être rendu maximum. La fonction φ(z) restant inconnue, le problème paraît insoluble. L'hypothèse la plus plausible est, d'après le résultat du calcul, celle qui rend minima la somme
z1² + z2² +….zn² (2)
Si le produit (1) est maximum quand la somme (2) est minima, il doit rester constant en même temps que celle-ci et la fonction φ(z) doit satisfaire à une équation de la forme
φ(z1) φ(z2)… φ(zn) = F(z1² + z2² +….zn²)
On déduit de cette équation bien connue
φ(z) =G e-k²z²
C'est la loi proposée en 1809; elle seule peut justifier la règle qu'on en a déduite.
(…)
Toutes les équations, dans la théorie de Gauss, sont réduites au premier degré (…) on peut, z étant très petit, remplacer φ(z) par son développement
![]()
Les erreurs constantes (8) étant écartées, c'est une des hypothèses de Gauss, on a φ(z) = φ(-z) et, par conséquent, φ’(0) = 0 et φ’’’(0) = 0. On peut, puisqu'on est convenu de négliger z² par rapport à z, négliger z4 par rapport à z2 et réduire φ(z) à la forme
![]()
Mais on a, dans les mêmes conditions,
G e-k²z²= G – Gk²z²
Si donc on pose G = a, k = - b²/a, on aura
φ(z) =G e-k²z²
La fonction φ(z), quelle que soit sa forme véritable, est réductible, dans les conditions où l'on veut résoudre le problème, à celle que Gauss avait proposée d'abord.
(extrait de Joseph Bertrand, Sur la méthode des moindres carrés, C.R.A.S., Paris, Tome CVI, n°16, 1888, pp. 1115-1117).
Le théorème de la limite centrale
Le théorème de la limite centrale établit que la somme d'un grand nombre de réalisations de variables aléatoires indépendantes et ayant la même loi de distribution est approximativement distribuée suivant la loi normale si les variables aléatoires ont une variance finie. Abraham de Moivre avait établi le théorème en 1733 pour une loi binomiale et Laplace approxima en 1811 la loi binomiale par la loi normale. Le théorème de la limite centrale est appelé de nos jours le second théorème fondamental des probabilités, le premier étant la loi des grands nombres de Jacob Bernoulli qui indique que la moyenne des réalisations de variables aléatoires indépendantes ayant la même loi de distribution et une espérance finie converge vers la valeur de cette espérance mathématique.

Le nombre de travaux concernant ces théorèmes étant historiquement très élevé, Lucien Le Cam a commenté avec humour, en 1986, l'histoire du Théorème de la limite centrale [The central limit theorem around 1935. Statistical science, volume 1, 1986, pp.78-96.] (traduction): Au commencement, il y eut De Moivre, Laplace, et de nombreux Bernoullis et ils engendrèrent des théorèmes de la limite, et les hommes avisés dirent que cela était bien et ils donnèrent au théorème le nom de Gauss. Puis vinrent de nouvelles générations qui trouvèrent que le théorème avait une validité expérimentale mais manquait de rigueur. Alors vinrent Chebychev, Liapunov et Markov et ils prouvèrent le théorème et Polya voyant l'usage des moments déclara que le nom Théorème de la limite centrale devait être utilisé. Puis vint Lindeberg et il dit que cela était élémentaire car Taylor avait développé ce qui demandait à être développé, et il le dit deux fois (...)
Dans la théorie des moindres carrés, on cherche à estimer un vecteur ![]() [1 x r], ayant ses r composantes inconnues, à partir de N observations
[1 x r], ayant ses r composantes inconnues, à partir de N observations ![]() reliées linéairement à
reliées linéairement à ![]() , mais comportant des erreurs
, mais comportant des erreurs ![]() . On a
. On a ![]() où
où ![]() est une matrice connue de N x r éléments avec N ≥ r, la colonne de rang r étant pleine.
est une matrice connue de N x r éléments avec N ≥ r, la colonne de rang r étant pleine.
L'estimation de la moyenne du vecteur ![]() noté
noté ![]() , consiste alors à choisir la matrice K selon une approche probabiliste ou une approche algébrique afin d'obtenir l'estimation
, consiste alors à choisir la matrice K selon une approche probabiliste ou une approche algébrique afin d'obtenir l'estimation
![]()
Août 2010

(1) Aujourd'hui, la loi de probabilité continue d'une variable aléatoire X est représentée par une densité de probabilité f, la fonction f étant positive, intégrable, d'intégrale égale à 1, telle que : P(X = x) = f(x) dx est la probabilité que la variable prenne ses valeurs dans un intervalle élémentaire (x, x + dx). La primitive F de la densité de probabilité f est appelée fonction de répartition.
(2) Dans ce cas, on dispose de nombreuses mesures (ou résultats d’observations) des valeurs exactes recherchées, donc de plus d’équations que d’inconnues : c’est en ce sens que le système est surdéterminé.
(3) Le texte est daté du 15 ventôse an 13 (6 mars 1805). Il fut reproduit par Puissant dans son Traité de Géodésie, édité par Courcier toujours en 1805 (pages 137-141) puis republié dans la deuxième édition de l’ouvrage de Legendre en 1806. L’originale des Nouvelles méthodes pour la détermination des orbites des comètes de 1805 a pour éditeur Didot, et l’édition de 1806 a été éditée par Courcier.
(4) Theoria motus corporum coelestium in sectionibus conicis solem ambientium, Auctore Carolo Friderico Gauss, Hamburgi sumptibus Perthes et Besser, 1809, page 210 et seq.
(5) Theoria motus corporum coelestium in sectionibus conicis solem ambientium, Auctore Carolo Friderico Gauss, Hamburgi sumptibus Perthes et Besser, 1809, page 210 et seq.
(6) À ce propos, Gauss écrit : « On a coutume de regarder comme un axiome l'hypothèse que si une quantité a été obtenue par plusieurs observations immédiates, faites avec le même soin dans des circonstance semblables, la moyenne arithmétique des valeurs observées sera la valeur la plus probable de cette quantité, sinon en toute rigueur, du moins avec une grande approximation, de telle sorte que le plus sûr soit toujours de s'y arrêter ».
(7) « Sur les intégrales définies et leur application aux probabilités et spécialement à la recherche du milieu qu'il faut choisir entre les résultats des observations », Mémoires de l'Institut National des sciences et des arts ; sciences mathématiques et physique, 11, 1811, pp. 279-347.
(8) Bertrand fait ici référence aux erreurs systématiques habituellement faites dans les mesures. La méthode des moindres carrés nécessite de les éliminer et de ne tenir compte que des erreurs aléatoires - d'où la symétrie de la courbe d'erreurs par rapport à l'axe des y.
(9) Une variable aléatoire centrée réduite a une espérance mathématique E(X) nulle et un écart type égal a 1. Par rapport à une variable aléatoire quelconque X, la variable centrée réduite est une variable translatée et homothétique ![]() .
.
(10) Roger Mansuy, analyse du manuscrit Sur la résolution numérique des systèmes d'équations linéaires écrit par Cholesky, Bibnum septembre 2008.
Annexe

La densité de la loi normale apparaît page 212 de l'ouvrage de Gauss, Theoria motus corporum, 1809.
 Analyse du manuscrit d’André-Louis Cholesky intitulé « Sur la résolution numérique des systèmes d’équations linéaires », par Roger Mansuy (BibNum octobre 2008)
Analyse du manuscrit d’André-Louis Cholesky intitulé « Sur la résolution numérique des systèmes d’équations linéaires », par Roger Mansuy (BibNum octobre 2008)

E. Barbin et J.P. Lamarche (2004) : Histoires de probabilités et de statistiques, Ellipses.

J.J. Samueli, J.C. Boudenot (2006) : Trente livres de mathématiques qui ont changé le monde, Ellipses.

J.J. Samueli, J.C. Boudenot (2009) : Une histoire des probabilités, Ellipses.

J. Dutka (1990). Robert Adrain and the method of least squares. A.H.E.S. 41, 171-184.

A. Hald (1998) : A history of mathematical statistics from 1750 to 1930, Wiley.

A. Hald (2006) : A History of Parametric Statistical Inference from Bernoulli to Fisher, 1713-1935, Springer.

C.C. Heyde and E. Seneta (1977) : I.J. Bienayme, Statistical Theory Anticipated, Berlin, Springer Verlag.

O.B. Sheynin (1966) : “Origin of the theory of errors”, Nature, vol. 211, pp. 1003 - 1004.

S. Stigler (1986). The History of Statistics: The Measurement of Uncertainty before 1900, Belknap Press of Harvard University Press, Cambridge, MA.
legendre-texte.pdf

legendre-analyse.pdf




