Lambert et l’irrationalité de π (1761)
- INFORMATION
- ACTUALITÉ
- ANALYSE
- EN SAVOIR PLUS
- À TÉLÉCHARGER
Mémoire sur quelques propriétés remarquables des quantités transcendantes et logarithmiques, Histoire de l’Académie royale des sciences et belles-lettres (1761), Berlin, chez Haude et Spener, libraires de l’Académie royale (1763).
1761
Ce texte d’une grande diversité est la preuve de l’irrationalité de π et l’acte de naissance des fonctions hyperboliques (sinus et cosinus hyperboliques).

 Le texte de Lambert (1761) occupe une position charnière dans l'histoire de l'irrationalité et de la transcendance.
Le texte de Lambert (1761) occupe une position charnière dans l'histoire de l'irrationalité et de la transcendance.
- 1 - Dans l'histoire du nombre π, cette première preuve d’irrationalité est évidemment capitale.
- 2 - Il marque le début de la formulation précise de la notion de transcendance, et pose la conjecture correspondante pour les deux nombres remarquables e et π.
- 3 - Il constitue à ce titre un jalon essentiel sur la route de la réponse négative au problème de la quadrature du cercle : c'est le coup d'accélérateur sur un problème qui stagne depuis son exposition au Vème siècle avant J.-C.
- 4 - Enfin, Lambert y définit ce que nous appelons aujourd'hui les fonctions hyperboliques (sinus et cosinus hyperbolique), en justifiant, figure à l'appui, que l'on parle d'une "trigonométrie hyperbolique".

 The text by Lambert we will examine here (1761) occupies a pivotal place in the history of irrationality and transcendence.
The text by Lambert we will examine here (1761) occupies a pivotal place in the history of irrationality and transcendence.
- In the history of number π, this first proof of irrationality is clearly crucial.
- It marks the beginning of a precise formulation of the notion of transcendence, and sets out the corresponding conjecture about the two remarkable numbers e and π.
- It constitutes an essential milestone on the road to negating the problem of squaring the circle, catalysing the resolution of a problem that had stagnated since it was first exposed in the 5th century BCE.
- Lastly, Lambert defines what we now call hyperbolic functions (hyperbolic sine and cosine), by justifying, with a supporting figure, the notion of “hyperbolic trigonometry”.


Born in 1954, Alain Juhel is a graduate of the École normale supérieure (Cachan). He is agrégré in mathematics and is maths teacher in MPSI classe préparatoire at Lycée Faidherbe, Lille (website www.mathouriste.eu)

Le texte de Lambert (1761) que nous étudions ici occupe une position charnière dans l'histoire de l'irrationalité et de la transcendance.
Si un mathématicien ne se méprend pas sur la valeur du texte de Lambert, c'est bien Charles Hermite : après sa victoire sur la transcendance de e, ne dit-il pas, en introduction à une démonstration simplificatrice du résultat de Lambert : « Tout ce que je puis, c'est de refaire ce qu'a déjà fait Lambert, seulement d'une autre manière... »
Lexique
Irrationalité : un nombre est rationnel lorsqu'il est quotient d'entiers, irrationnel sinon.
Transcendance : un nombre est transcendant lorsqu'il n'est racine d'aucune équation à coefficients entiers, de quelque degré que ce soit.
Quadrature du cercle : Construire, à la règle et au compas, un carré d'aire égale à celle d'un cercle de rayon unité ; cela revient à construire ainsi √ π.


Figure 1 : Colonne Lambert à Mulhouse, sa ville natale (à gauche). Elle porte une méridienne en souvenir de ses travaux d'astronomie. Détail, à droite : Médaillon en l’honneur de Lambert figurant sur la colonne.
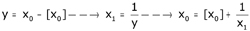
où [x0] désigne, suivant l'usage, la partie entière de x0, alors le nombre initial x0 est irrationnel : la non terminaison en est la preuve ! Euler n'avait donc eu qu'à obtenir – certes, un peu mystérieusement – une jolie fraction continue illimitée, mais aux termes parfaitement réguliers, pour y lire l'irrationalité de e :
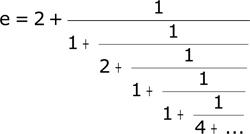
ou, écrit de manière plus compacte, [2,1,2,1,1,4,1,1,6,...1,1,2n,1,1...]
Malheureusement, ∏ se révèle plus coriace. On peut, comme nous l'avons fait avec l'exemple numérique de l'encadré ci-dessous, obtenir, à partir de valeurs décimales de plus en plus précises, autant de termes que l'on voudra ; mais aucune régularité dans ce développement n'est apparue, ni à Euler, ni à aucun autre mathématicien... ∏ apparaît ainsi comme un nombre « plus compliqué » que e : la suite des décimales, soit le développement en série
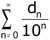
est imprévisible pour e comme pour ∏, mais du moins e retrouvait-il une forme régulière avec un développement d'une autre forme : il n'en va plus de même pour ∏.
Fractions Continues
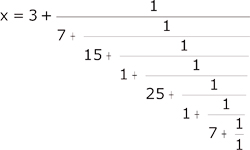
Tout nombre rationnel peut s'écrire en x = a + 1/y, a entier et y>1 ; on peut alors réitérer le procédé, qui revient à la répétition de l'algorithme d'Euclide, correspondant à la division euclidienne. Ainsi, soit à développer x = 314159/100000. On écrira successivement
• 100000 = 7 x 14159 + 887
• 14159 = 15 x 887 + 854
• 887 = 1 x 854 + 33
• 854 = 25 x 33 + 29
• 33 = 1 x 29 + 4
• 29 = 7 x 4 + 1
L'algorithme d’Euclide se termine, et il en est de même pour tout rationnel. Ainsi :
qu'on écrit par commodité :
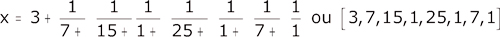
Les fractions "intermédiaires" :
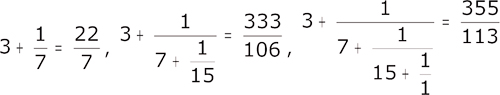
portent le nom suggestif de réduites.
Plus généralement, on peut étudier des fractions à termes quelconques,
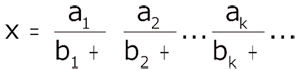
dont les réduites successives (fractions tronquées au rang n) sont calculées par l'algorithme suivant , très intéressant puisqu'il ne comporte aucune division :
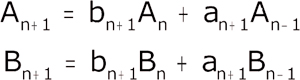
L'attaque exige donc une stratégie plus élaborée; c'est là que réside toute l'originalité du travail de Lambert. En voici les ingrédients essentiels:
Comme dans les autres questions de ce type, ce merveilleux outil sera ultérieurement éliminé sur l'autel des simplifications: la preuve d'Euler est supplantée par celle attribuée à Fourier (1815) (3) ; Liouville efface lui-même, dans son deuxième article sur la construction de Transcendants remarquables (1844), les fractions continues qu'il employait dans un premier temps (4) ; Hermite, enfin, donne, dans une lettre à Borchardt (1873) des preuves de l'irrationalité de ∏ et ∏² où ne figure plus aucune fraction continue, quoiqu'elles portent, dans leur inspiration, la marque indélébile d'approximations rationnelles construites à partir de fraction continues. Cela ne va d'ailleurs pas sans occasionner quelques regrets de la part d’Hermite (5) :


Figure 2 : Histoire de l’Académie royale des sciences et belles-lettres de Berlin (1761), dont est extrait le texte de Lambert. Les comptes-rendus sont à l’époque en français. (exemplaire de la bibliothèque lettres et sciences humaines de l’Université de Lille).
L'article est long, mais, nous prévient Lambert à la fin du §2, c'est d'abord le prix à payer pour que la rigueur du raisonnement soit inattaquable. Et, une fois ce principe accepté, le coût supplémentaire pour quelques résultats remarquables devient trop faible pour qu'on s'en prive ! Ce sont justement ceux-ci qui font de ce texte bien plus qu'une simple preuve d'irrationalité... Dégageons le plan et les paragraphes-clefs auxquels on pourra limiter une première approche du texte, afin de ne pas s'y perdre.
Et de rappeler le paradoxe de ces quadrateurs acharnés (l'Académie des Sciences en viendra, en 1775, à refuser l'examen des solutions proposées dans l'espoir de leur éviter de sombrer dans la folie) :
Ce texte sera, effectivement, d'une rigueur exemplaire et tranchera fortement, en cela, avec ceux qui l'encadrent, qu'il s'agisse d'Euler avant lui, ou de Legendre après lui (1795), qui laissent des zones d'ombre, tant sur leurs inspirations que sur la convergence des fractions qu'ils emploient.
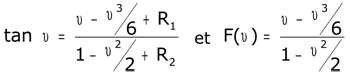
Dans le cas de F (obtenue en ignorant les restes), nous saurions fort bien opérer en vue d'un développement en fraction continue limitée. Il suffirait de remplacer les nombres par des polynômes en ![]() , la division euclidienne des entiers par celle des polynômes, et l'on obtiendra le début de la fraction :
, la division euclidienne des entiers par celle des polynômes, et l'on obtiendra le début de la fraction :
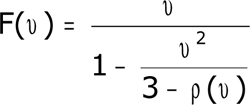
Aller jusqu'aux puissances 5 au numérateur et 4 au dénominateur confirmera les 1 et 3 obtenus, et fera apparaître un nouveau terme, etc. À cette intuition qui le guide, Lambert ajoute un calcul soigné des restes successifs; voilà donc le développement trouvé, mais pas démontré, car, Lambert en est bien conscient –beaucoup plus qu'Euler – dire "et ainsi de suite, indéfiniment" ne suffit pas.
Détail du calcul
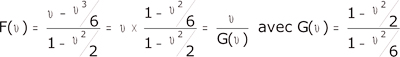
En opérant par division par puissances croissantes :
![]()
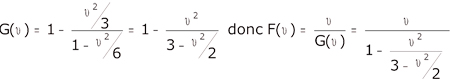
Dans ce cas, sa preuve d'irrationalité est faite: il n'a manipulé que des entiers, l'algorithme ne s'arrête pas, donc le nombre tan u sera une quantité irrationnelle toutes les fois que l'arc u sera une partie aliquote du rayon.
Et Lambert de conclure au début du §16:
Car le raisonnement par l'absurde qu'il envisage supposera ∏/4 rationnel (commensurable au rayon) mais pas forcément à numérateur 1 (partie aliquote)
Lambert nous avait, en fait, prévenu dès le §3:
Il exhibe les premières réduites: c'est un calcul inverse de nos développements simplifiés. Puis il démontre la formule (classique) de calcul séparé des numérateurs et dénominateurs de la réduite An/Bn, que nous écririons en termes modernes
An+1 = (2n+1).w An - An-1
Bn+1 = (2n+1).w Bn - Bn-1
L'algorithme est matérialisé dans un tableau de calcul des premiers numérateurs et dénominateurs partiels.
Il y parvient au §29 pour le dénominateur, au §30 pour le numérateur, par exemple:
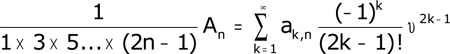
La seule lacune de sa preuve est sans doute à ce point : il fait tendre n vers l'infini, et se prévaut du fait que
![]()
pour conclure ; cependant Lebesgue (6) a montré que la rédaction pouvait être complétée très rigoureusement. D'ailleurs, il souligne pour terminer l'excellente qualité de convergence des approximants ; on peut aujourd'hui – plus aisément qu'à l’époque de Lebesgue – l’apprécier à l'aide d'un tracé réalisé par ordinateur. Il qualifie l'écart entre tan u et la réduite An / Bn en ces termes :
Il ne serait pas tout à fait exact de dire que c'est le premier développement en fraction continue d'une fonction – ce qui est bien plus qu'un nombre ! Euler avait développé exp (x) à partir d'équations différentielles. Mais, si l'on compare ce développement à notre découpage de la preuve de Lambert, des trois étapes, Euler n'avait guère réalisé que la première : on est donc en présence d'un tournant remarquable dans l'approximation des fonctions.
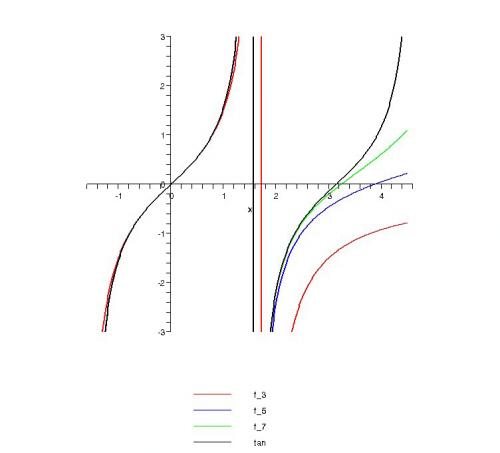
Figure 3 : Approximants de la fonction tangente employés par Lambert. La notation f_n sous les courbes désigne la réduite qui prend en compte les dénominateurs partiels jusqu'à ![]() ²/2n.
²/2n.

dont il trouvera les détails dans le document à télécharger ci-dessous, ou dans le livre de Lebesgue. Observons enfin que, si l'on connaissait bien, depuis Lord Brouncker (1655) un développement de ∏ en fraction continue généralisée
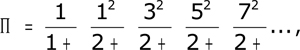
le critère précédent ne s'y appliquait pas : la fraction ne convergeait pas assez rapidement. Le procédé de Lambert était donc parfaitement novateur !
Il pose alors les deux séries, qu'il somme en termes d'exponentielles, par exemple
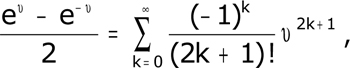
et développe leur quotient en observant que la seule différence est le remplacement de tous les signes – par des +
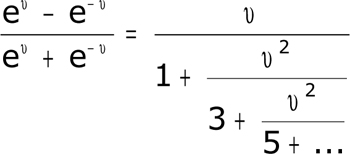
Les notations d'aujourd'hui (cosh, sinh, tanh) ne sont pas encore présentes, mais l'essentiel n'est pas là : non content d'observer que l'on passe des secondes aux premières en changeant u en iu – Euler l'avait fait avant lui ! – il tient à en donner une interprétation géométrique, figure à l'appui, en joignant au cercle x² + y² = 1 l'hyperbole x² - y² = 1, tangente en son sommet A (1,0) au cercle.
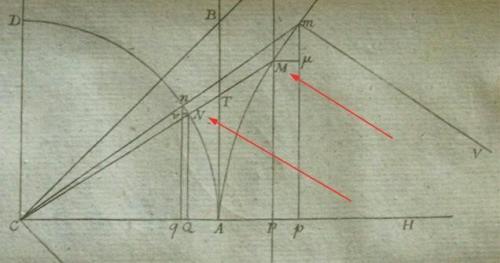
Figure 4 : Planche jointe à la fin de l’article de Lambert (détail). On reconnaît le tracé du quart de cercle AD et de la branche d’hyperbole AM. On a fléché en rouge les points courants M sur l’hyperbole et N sur le cercle (photographie A. Juhel).
Une sécante commune est issue du centre C des deux coniques, coupe le cercle en N(x,y) et l'hyperbole en M(ξ,η) ; introduisant le paramètre u comme double de l’aire du secteur hyperbolique AMCA, Lambert démontre que
![]()
De la même manière que les fonctions cos (![]() ) et sin (
) et sin (![]() ) paramètrent le cercle, les fonctions cosh (u) et sinh (u) paramètrent l’hyperbole : nous venons donc d'assister, aux notations près, à la naissance des fonctions hyperboliques.
) paramètrent le cercle, les fonctions cosh (u) et sinh (u) paramètrent l’hyperbole : nous venons donc d'assister, aux notations près, à la naissance des fonctions hyperboliques.
Et, lorsque u est entier ou inverse d'un entier, il conclut
Le grand mot – transcendance – est lâché, pourtant il n'a ici qu'un sens encore vague : irrationnel au delà de tout ce que l'on pourrait imaginer. Ce sens était déjà présent dans son annonce à la fin du §2 :
Mais les trois derniers paragraphes vont aller bien au delà, et indiquer le chemin, tant à Wantzel pour les questions de constructibilité qu'à Hermite pour la démonstration de la transcendance du nombre e.
Suit la définition moderne d'un nombre algébrique ! Car non seulement Lambert donne une liste d'exemples explicites suggérant un "empilement" arbitraire de radicaux de tous ordres et d'opérations algébriques entre eux
mais surtout il définit comme tels les racines d'équations d'ordre quelconque à coefficients entiers, hors de toute formule explicite :
le &c (etc.) suggérant clairement un degré quelconque, ainsi x5 - 5x + 1, pour laquelle il n'y a pas de formule de résolution connue (théorème d'Abel-Ruffini), et plus généralement xn - 5x + 1, avant de conclure :
En effet, il convient de préciser la nature des coefficients : e est racine de l'équation x – e = 0 … mais les coefficients ne sont pas rationnels (se rapporte à la même unité) et, mettant e pour coefficient, il y entrerait une quantité transcendante. Le théorème dit donc que e ou ∏ – entre autres – ne sont racines d'aucune équation à coefficients rationnels ou, ce qui revient au même après réduction au même dénominateur, entiers.
Résoudre la quadrature du cercle, ce serait construire √∏ à la règle et au compas, et donc ∏, or
Ici, Lambert se montre sans doute lecteur avisé de la Géométrie de Descartes, où l'auteur a montré comment construire sommes, produits et racines carrées. D'un autre côté, il n'ignore pas que l'on bute depuis 2000 ans sur un problème contemporain de la quadrature du cercle, la duplication du cube, ou problème de Délos, qui équivaut à la construction de ![]() , a rationnel donné. Aussi précise-t-il, fort d'un échec pratique valant conjecture d'impossibilité théorique:
, a rationnel donné. Aussi précise-t-il, fort d'un échec pratique valant conjecture d'impossibilité théorique:
Il faudra pourtant encore trois quarts de siècle pour que Wantzel (1837) résolve définitivement la question. Mais l’intuition de la non-constructibilité était en germe dans la conclusion de l’article de Lambert :

Pour plus de détails sur les démonstrations, et pour situer plus précisément cet épisode dans l'histoire de l'irrationalité :
Quelques références sur π, classées en fonction de leur accessibilité: d'une excellente vulgarisation, très complète mais lisible par un "honnête homme" de notre époque jusqu'à un recueil exhaustif des textes qui constituent les jalons de son histoire.

Jean-Paul Delahaye, Le fascinant nombre π, Belin-Pour la Science 1997.

Pierre Eymard, Jean-Pierre Lafon, Autour du nombre Pi, Hermann 1999.

Henri Lebesgue, Leçons sur les Constructions Géométriques, Gauthier-Villars 1949, Jacques Gabay 1987.

Jonathan Borwein, Peter Borwein, Lennart Berggren, Pi : A Source Book, Springer-Verlag 2004.
LAMBERT_PROPRIETES.pdf

lambert-analyse-2015.pdf

24-lambert-analysis.pdf





