La leçon de cosmographie d’Hervé Faye sur les comètes

Nous avons célébré en 2014 le bicentenaire de la naissance d’Hervé Faye (1814-1902) et, à cette occasion, le Bulletin de la Société des amis de la bibliothèque et de l’histoire de l’École polytechnique (SABIX) a consacré le numéro 55 de septembre à cet astronome, célèbre en son temps, qui fut témoin et acteur des grandes mutations de l’astronomie au XIX^e siècle, à l’Observatoire de Paris, à l’Académie des sciences et au Bureau des longitudes. Au nombre de ses premières contributions à la science des astres, on compte la découverte et l’étude de la comète périodique qui porte son nom (1843). Il occupa également des positions importantes dans l’instruction publique puisqu’il fut professeur à Polytechnique, recteur de l’académie de Nancy, inspecteur général et même, de manière très éphémère, ministre. Aussi avons-nous décidé d’étudier ici le chapitre V du livre cinquième qu’il consacre aux comètes dans ses Leçons de cosmographie de 1852.

Figure 1 : Faye, professeur d’astronomie à Polytechnique, croqué par un de ses élèves, le futur général Maurice Pellé (X1882) (©Archives famille Pellé)

Avant d’entrer dans l’analyse du texte, disons quelques mots de la place de la cosmographie dans l’enseignement secondaire (1). Elle est introduite en 1833 dans le cursus de mathématiques de la classe de rhétorique – l’équivalent de notre actuelle classe de Première. Mais les humanités dominent le parcours scolaire, les sciences sont réduites à portion congrue et les professeurs qualifiés font cruellement défaut. Pour ne pas parler des manuels scolaires composés par une nébuleuse d’auteurs divers (militaires désœuvrés, membres de sociétés savantes, ecclésiastiques), peu soucieux des directives officielles. Nombreux sont donc les établissements dans lesquels la cosmographie est peu ou pas enseignée. Arrive alors la réforme de 1852 (2), dite de la bifurcation. Jusque-là, le diplôme de fin d’études était le baccalauréat ès-lettres : les titulaires de ce sésame qui souhaitaient s’engager dans une carrière scientifique pouvaient alors passer un baccalauréat ès-sciences. À partir de 1852, deux filières distinctes, l’une littéraire et l’autre scientifique, sont établies. De nombreux enseignants de valeur rédigent alors des manuels conformes aux programmes officiels. Tel est le cas de l’ouvrage qui nous occupe.

@@@@@@@

Les Leçons de cosmographie d’Hervé Faye sont structurées en cinq « livres » ou parties. Les trois premières sont consacrées à la Terre (ses deux mouvements, sa figure et ses dimensions) ; la quatrième traite de la Lune, la cinquième, sur laquelle nous allons nous arrêter, étudie les planètes et leurs satellites ainsi que les comètes ; la dernière s’intéresse aux étoiles.

Dès le titre du chapitre V du livre cinquième, Faye circonscrit son propos : « Les comètes ; leurs orbites ; leur aspect et leur constitution physique – comètes périodiques. », conformément aux directives émanant du ministère pour la section sciences, mais en des termes légèrement différents – le texte officiel du 30 août 1852 proposant une rubrique « Des comètes. Noyau ; chevelure ; queue. Petitesse de la masse des comètes. Nature de leurs orbites. Comètes périodiques. Comète de Halley. Comète de Biela. Son dédoublement. » Notons en particulier que le programme qui se veut purement descriptif se garde d’examiner la « constitution physique ».

Le paragraphe d’introduction permet à Hervé Faye de distinguer le monde des comètes de celui des planètes. Ce dernier présente deux caractéristiques : il est stable et connu pour l’essentiel. Avec la découverte de Neptune (1846), la plupart des « discordances » entre les « prévisions théoriques » et les « faits » ont disparu. Hervé Faye passe ici sous silence les anomalies du périhélie de Mercure qui vont occuper le découvreur de Neptune Urbain Le Verrier jusqu’à sa mort en 1877. L’idée d’une planète perturbatrice d’Uranus l’ayant conduit au triomphe, Le Verrier tente de reproduire le même schéma avec une planète infra-mercurielle, appelée Vulcain, qu’il cherchera en vain (3). Autant les planètes sont donc connues, selon Faye, autant pour ce qui concerne les comètes, « leur origine et leur nature sont inconnues ». Seule certitude à leur sujet, leur matière « obéit aux lois de la mécanique, comme celle de tous les corps de notre système ».

Les orbites des comètes

La première rubrique du chapitre traite des « orbites des comètes ». Comme les planètes, elles satisfont aux lois de Kepler mais « sous une forme un peu plus générale ». En effet, l’orbite cométaire n’est pas nécessairement une ellipse : « c’est une section conique dont le soleil occupe un foyer ». La présentation des sections coniques nous semble singulière puisque Faye regroupe d’une part ellipse et hyperbole et d’autre part cercle et parabole considérés comme « cas particuliers ». Les explications fournies en note de bas de page ne reposent pas sur la section du cône mais sur la déformation de l’ellipse par suite du déplacement des foyers. Ce regroupement des sections coniques par couple n’est pas pérenne dans l’exposé puisque quelques lignes plus loin, l’auteur lie cercle et ellipse d’une part et parabole et hyperbole d’autre part, en utilisant le critère plus usuel orbite fermée / orbite à branches infinies.

Il explique ensuite qu’en première approximation, la parabole est privilégiée, les éléments de celle-ci pouvant être déterminés à partir de trois observations. S’appuyant sur la fig. 108, il a préalablement expliqué le processus calculatoire. Celui-ci repose sur l’application de la loi des aires – actuellement appelée deuxième loi de Kepler (4) (alors qu’elle fut historiquement la première formulée par l’astronome). Faye détaille ensuite les cinq éléments de l’orbite que l’astronome doit déterminer (inclinaison du plan de l’orbite sur l’écliptique, longitude du nœud ascendant et du périhélie, distance périhélie, époque du passage au périhélie). Faye termine le paragraphe par une remarque importante : les planètes parcourent toutes leur orbite dans le sens direct tandis que la moitié des comètes connues sont de sens rétrograde.

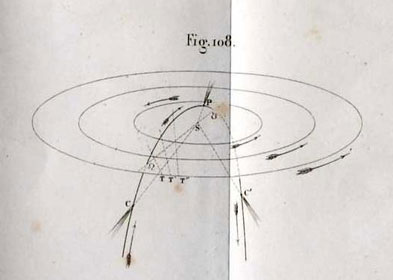
Figure 2 : La figure 108 de Faye, dans la planche de figures à la fin de l’ouvrage

L’aspect des comètes

Une nouvelle différence avec les planètes est mise en avant dans le deuxième paragraphe sur l’  « aspect des comètes ». Celles-ci ne présentent pas « une forme géométrique et invariable », contrairement à celles-là. Selon leur position par rapport au Soleil, la forme originelle – ronde ou ovale, comme sur la fig. 107 – va s’altérer et les comètes vont revêtir des apparences diverses, présentant un noyau, une queue, une chevelure, termes que Faye explique en détail. La matière dont elles sont constituées est d’une extrême ténuité et laisse filtrer la lumière n’engendrant aucune réfraction. D’où l’aveu d’ignorance de Faye sur « l’état physique » des astres cométaires qui ne sont « ni liquides, ni solides, ni même gazeux ». La diaphanéité est rassurante car :

On voit par-là combien peu les effets mécaniques du choc d’une comète contre la Terre sont à redouter ; la moindre toile d’araignée opposerait peut-être plus d’obstacle à une balle de fusil.

Dans cette phrase, Faye fait référence aux frayeurs soulevées par les comètes auxquelles Lalande en 1773 puis Arago en 1832 (comète de Biela) durent faire face.

Faye clôt le paragraphe sur l’influence décisive du Soleil : « on dirait que la chaleur solaire joue un rôle capital dans le phénomène des queues », qui se dirigent toujours « à l’opposite du soleil ». Queues dont l’apparition est le symptôme de la destruction de la « solidarité » des parties de la comète entre elles.

Les comètes périodiques

Le paragraphe suivant permet à Faye de s’attarder sur les comètes périodiques, celles dont l’orbite est elliptique. Paradoxalement, ce sont les éléments paraboliques qui permettent de reconnaître une même comète lors de deux apparitions. D’où l’importance cruciale de la détermination de ceux-ci. Afin d’illustrer la méthode, Faye choisit deux exemples : la comète de Halley et celle de Biela dont il donne les éléments lors de plusieurs apparitions. Il rend hommage à Halley qui calcula les éléments de nombreuses comètes observées lors des siècles antérieurs et qui put ainsi prouver que les apparitions de 1531, 1607 et 1682 correspondaient à une seule et même comète à laquelle on donna son nom. Faye se contente de signaler que le retour de 1758 fut prédit par Halley sans rappeler que le calcul précis par Lalande, Clairaut et Mme Lepaute fut considéré en son temps, en France, comme un triomphe de la théorie de la gravitation newtonienne. La période de la comète de Halley (environ 76 ans) est longue. Tel n’est pas le cas de celle de Biela qui réapparaît tous les 6 ans ¾ et qui, lors de son retour de 1846, se dédoubla sans que les astronomes soient en mesure d’expliquer le phénomène (5). Faye émet, avec beaucoup de circonspection, l’hypothèse que la comète a rencontré une des petites planètes situées entre Mars et Jupiter. La comète de Biela présente un autre intérêt majeur : sa trajectoire « perce le plan de l’écliptique très-près de l’orbite terrestre ». C’est donc elle qui fut responsable de la terreur de 1832 décrite dans l’encadré (6). La crainte fut alimentée par une confusion entre l’orbite de la Terre et la place de la Terre sur son orbite. Lorsque la comète croisa l’orbite terrestre en 1832,

la Terre était bien éloignée du point où la collision aurait pu avoir lieu.

Notons que, conformément au programme officiel, Faye se contente des comètes de Halley et de Biéla et n’évoque pas la comète périodique qui porte son nom.

Importance astronomique des comètes

Dans le paragraphe suivant, « Importance astronomique des comètes », Faye revient sur les différences majeures entre planètes et comètes, ces dernières ne participant « en rien à la merveilleuse stabilité du système solaire ». La diversité y règne tant au niveau de l’inclinaison du plan de l’orbite sur l’écliptique que de l’excentricité de l’ellipse. Leur marche hasardeuse est le siège de « perturbations considérables » nées du passage à proximité d’une planète massive. Ces perturbations sont mises à profit par les astronomes pour déterminer la masse de planètes dépourvues de satellites, comme Mercure (grâce à la comète d’Encke). Hervé Faye dresse un parallèle entre cet apport scientifique des comètes et les désastres qu’elles étaient supposées annoncer autrefois :

Autrefois les comètes passaient, dans l’imagination des peuples, pour les avant-coureurs de quelques grands désastres ; elles annonçaient, croyait-on, la peste, la guerre, la famine ou la mort des rois ; aujourd’hui elles servent à faire connaître la masse de quelques planètes dépourvues de satellites.

@@@@@@@

Faye termine son chapitre par un dernier point fort surprenant, « Absence de milieu résistant dans les espaces célestes », totalement absent du programme officiel. Les comètes qui « traversent l’espace en tous sens » s’y meuvent « comme si l’espace était vide ». L’un des débats majeurs du XIX^e siècle fait ainsi subrepticement son apparition dans un chapitre de manuel scolaire, celui de l’existence d’un éther résistant dont la communauté savante cherche la preuve expérimentale. La note de bas de page rappelle que certains astronomes – parmi lesquels Faye ne se trouvait pas – crurent la trouver dans des anomalies du mouvement de la comète d’Encke. Ce qui peut justifier l’irruption de l’absence du « milieu résistant » dans un chapitre consacré aux comètes.

Figure 4 : Photo contemporaine de la comète périodique 2P/Encke. Elle a été découverte en 1786 –c’est la comète à plus courte période, de 3,3 ans. Même si la comète est ici « d’apparence stellaire » (ayant une forme peu différente des étoiles voisines, car on ne voit pas de queue de comète), elle en est fondamentalement différente : incommensurablement plus proche de la Terre, entourée du fameux halo lumineux, et enfin ne faisant que refléter la lumière solaire (alors qu’une étoile est sa propre source de lumière) (photo Jim Scotti, NASA, janvier 1994).

@@@@@@@

Deux cents ans après la naissance de Faye, la science du XXI^e siècle a réussi le bel exploit d’envoyer le petit robot Philae, porté par la sonde spatiale Rosetta, sur la comète 67P/Churyumov-Gerasimenko. L’engouement du grand public pour ce spectacle a dépassé les espérances du milieu scientifique. Mais les comètes ont toujours suscité la passion – et il nous est apparu intéressant de relire les écrits d’un astronome dont la comète figure dans le catalogue sous la mention 4P/Faye (7). Ces quelques pages rédigées pour un manuel scolaire sont un témoignage de ce que pouvait savoir un homme cultivé du milieu du XIX^e siècle. Six ans après la découverte de Neptune par Urbain Le Verrier (8), « au bout de sa plume » – selon l’expression d’Arago – la France est la nation reine de la mécanique céleste. Aussi ne sommes-nous pas étonnés de voir l’essentiel du propos de Faye consacré aux éléments de l’orbite et à l’exploitation des perturbations. La comparaison établie entre comète et planète repose essentiellement sur des considérations de mouvement. Contrairement à ses homologues allemande ou anglo-saxonne, l’astronomie française, qui demeure entre les mains des polytechniciens et compte peu de physiciens dans ses rangs, s’intéresse peu à la nature des astres (9). De l’observation des interactions entre comète et lumière, Faye se contente de déduire que

leur matière est disséminée à un point dont aucune substance terrestre ne peut nous donner l’idée.

Terminons sur les qualités pédagogiques de Faye qui bâtit en peu de pages un panorama synthétique de la connaissance cométaire, accessible aux élèves de l’enseignement secondaire. Le discours qui comporte quelques images bienvenues, comme celle de la toile d’araignée déjà évoquée, est clair, précis, descriptif, selon les recommandations officielles. La seule liberté que se permette Faye est la mention rapide, en fin de propos, du fameux débat sur l’existence du « milieu résistant » qui aura encore de belles décennies devant lui.

(février 2015)