Textes fondateurs de la science
analysés par les scientifiques d´aujourd´hui
analysés par les scientifiques d´aujourd´hui
Sur les variations séculaires des éléments elliptiques des sept planètes
- INFORMATION
- ACTUALITÉ
- ANALYSE
- EN SAVOIR PLUS
- À TÉLÉCHARGER
Sur les variations séculaires des éléments elliptiques des sept planètes
Auteur : Urbain Le Verrier (1811-1877) - Astronome et mathématicien français
Auteur de l'analyse :
Alain Juhel - Agrégé de mathématiques, professeur en Spéciales MP au lycée Faidherbe de Lille
Publication :
« Sur les variations séculaires des éléments elliptiques des sept planètes principales : Mercure, Vénus, la Terre, Jupiter, Saturne et Uranus », Journal de mathématiques pures et appliquées, 1° série, tome 5 (1840), p. 220-254.
Année de publication :
1840
Nombre de Pages :
35
Résumé :
Le Verrier effectue, en posant les équations différentielles des mouvements des sept planètes (avant sa découverte de Neptune), des travaux mathématiques précurseurs sur ce qui deviendra la théorie des matrices, les valeurs propres, la diagonalisation de matrices [publié dans le cadre des Célébrations nationales 2011 – Le Verrier].
Source de la numérisation :
Numdam (MathDoc)
Mise en ligne :
septembre 2011
Le Verrier effectue, en posant les équations différentielles des mouvements des sept planètes (avant sa découverte de Neptune en 1846), des travaux mathématiques précurseurs sur ce qui deviendra la théorie des matrices, utilisant notamment l’équivalent des valeurs propres ou de la diagonalisation d’une matrice. Il relie aussi cela à l’analyse astronomique du problème, distinguant les "grosses" planètes, plus perturbatrices, Jupiter, Saturne, Uranus et les quatre "petites", Mercure, Vénus, Terre et Mars, ce faisant décomposant son système matriciel 7×7 en deux blocs de 4 et 3.
[publié dans le cadre des Célébrations nationales 2011 – Le Verrier].
Alain Juhel, né en 1954, est ancien élève de l'École normale supérieure de Cachan, agrégé de Mathématiques, professeur en Mathématiques Spéciales MP au lycée Faidherbe de Lille (site personnel http://www.mathouriste.eu/)
Le Verrier et la première détermination des valeurs propres d'une matrice
Alain Juhel - Agrégé de mathématiques, professeur en Spéciales MP au lycée Faidherbe de Lille
Figure 1 : Le Verrier fait partie des 72 savants honorés par Gustave Eiffel sur sa tour (face La Bourdonnais).
Les Hasards d'une Carrière
Urbain Le Verrier (1811-1877) doit sa célébrité mondiale à la découverte de Neptune en 1846 (1). Rien pourtant ne le prédisposait à une carrière d'astronome : entré à l'École polytechnique en 1831, il en sort huitième en 1833 et poursuit sa formation à l'École d'application des Tabacs : aussi, ses deux premiers articles scientifiques ont trait à la chimie du phosphore, essentielle dans la fabrication des allumettes. Mais pour éviter une affectation en province, il démissionne de l'Administration des Tabacs et postule à une place de répétiteur en chimie à l'École polytechnique. Il échoue : elle revient à Regnault, qui s'illustrera dans cette discipline. Mais un deuxième poste est vacant, en astronomie, qu'il obtient, car il est bon mathématicien. Et cela va lui servir immédiatement : son premier article résout, sous couvert d'astronomie, un problème que Laplace lui-même, « le Newton Français », n'avait osé aborder frontalement dans sa Mécanique Céleste.
Cet article se décline en fait en trois variantes : le texte choisi pour notre étude, paru au Journal de Mathématiques Pures & Appliquées (alias Journal de Liouville) en 1839 est, comme le fait observer l'auteur en première page, un extrait détaillé de celui qui paraîtra dans la Connaissance des Temps pour l'An 1843, éditée en 1840 (2). Il a été présenté sous forme de Mémoire à l'Académie des Sciences, et drastiquement réduit à une note de trois pages dans les Comptes Rendus de celle-ci, en date du 16 Septembre 1839. Les Commissaires, Arago – qui encouragea les débuts de Le Verrier, puis le pressa d'abandonner les questions de stabilité des orbites pour se consacrer à la recherche de Neptune –, Savary et Liouville, avaient préconisé sa publication dans le Recueil des Savants Étrangers (3), mais ce sont finalement les deux revues citées qui furent choisies.
Figure 2 : (à g.) Statue de Le Verrier, devant l'Observatoire de Paris (Henri Chapu, 1889); (à dr.) Le recueil Connaissance des Temps où fut publié l'article « jumeau ».
Un Problème d'Astronomie...
Le Verrier commence, dans le §1, par un rappel succinct du problème : le mouvement elliptique képlérien de chaque planète, considérée comme soumise à la seule attraction du Soleil, n'est qu'une première approximation, au demeurant de fort bonne qualité en raison de la prépondérance de la masse solaire sur celle des satellites. C'est aussi le seul cas où l'on sache calculer l'orbite et sa loi horaire de parcours, et l'on ne manque pas de soumettre à cet exercice les étudiants dès leur première année après le Baccalauréat. Mais la lumineuse simplicité de la loi de Newton – tout le monde attire tout le monde !– est, paradoxalement, la source d'une redoutable complexité : dès que le nombre de corps en interaction excède deux, il n'y a plus aucune formule exacte pour exprimer les mouvements, pourtant parfaitement déterminés (4).
La présence de plusieurs planètes autour du Soleil rend la détermination de leurs mouvements beaucoup moins aisée. Elles agissent les unes sur les autres […] et par là elles sont sans cesse entraînées hors de l'ellipse qu'elles décriraient si elles n'étaient soumises qu'à l'action du Soleil.
La providence mathématico-physique qui valide, en première approche, le traitement du système solaire comme n systèmes Soleil-planète indépendants, c'est la décroissance de la force d'attraction en 1/r² : celle qui émane d'un autre corps que le Soleil (dont la forte masse, au numérateur, compense la distance lointaine, au dénominateur) est la plupart du temps négligeable, sauf si cet autre corps est à la fois proche de la planète étudiée (au moins à certaines époques) et massif : ainsi, Jupiter perturbe légèrement le mouvement de Mars. Si la traque de Neptune fut entreprise un peu plus tard, en 1845, c'est bien parce que les prédictions imparfaites du mouvement d'Uranus (découverte en 1781) laissaient supposer l'existence d'une planète troublante – au sens d'une perturbation de la trajectoire.
@@@@@@@
Les astronomes sont aussi gens de pratique: ils doivent construire des éphémérides, quitte à se baser sur une méthode approchée, pourvu que la précision soit satisfaisante pour les calculs envisagés. Lagrange a imaginé, en 1767, l'astuce suivante : considérer que l'ellipse du mouvement képlérien se déforme lentement au cours du temps :
Il est donc permis de considérer chacune des planètes comme se mouvant sur une ellipse de forme et de position variable. D'ailleurs, la petitesse des masses perturbatrices rend les variations séculaires de éléments elliptiques fort lentes et négligeables dans un intervalle de quelques années.
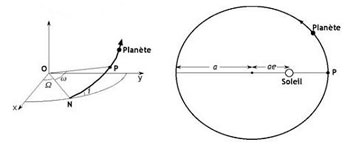
Figure 3 : Paramètres d'une orbite elliptique (figure extraite « La Découverte de Neptune (1846) », James Lequeux, BibNum, op.cit.). Sur un intervalle de temps petit ou « de taille raisonnable », le mouvement réel, complexe et non calculable, ne diffère pas significativement du mouvement sur une ellipse ; on caractérise celle-ci dans l'espace par 6 paramètres, d'une part situant son plan dans l'espace, d'autre part indiquant sa forme dans son plan. Lorsque l'intervalle de temps grandit, cette approximation ne peut rester indéfiniment valable, mais on peut imaginer que l'ellipse a légèrement varié, en considérant désormais que ses quantités caractéristiques ne sont plus fixes, mais fonctions de la variable t (le temps).
Le Verrier s'intéresse à deux de ces paramètres : l'excentricité e et la longitude ϖ du périhélie. Le premier mesure l'écart relatif entre centre et foyer ; le second est un angle permettant de placer dans l'espace le point le plus proche du Soleil, donc de positionner le grand axe. De façon clairement équivalente, il substitue à e et ϖ les paramètres h et l , définis par
h = e cos ϖ , l = e sin ϖ
qui seront assujetties à varier avec le temps ; ce sont elles qui seront désormais étudiées.
...Qui devient un problème d'Analyse...
Quand on applique les lois de la physique à des grandeurs qui varient, on obtient, en général, des équations différentielles. Si, comme c'est le cas ici, plusieurs quantités sont simultanément étudiées, on obtient des équations « mêlées », ce qui est encore bien plus compliqué ! On parle alors d'un système différentiel. Toutefois, en raison même du procédé d'approximation imaginé par Lagrange et employé par Laplace, à qui Le Verrier emprunte sans autre commentaire (5) ses formules, celui-ci est linéaire, seule classe que l'on sache entièrement résoudre, en théorie du moins. Car, en pratique, cette résolution passe... par le travail que Le Verrier sera le premier à faire !
Ce système comporte 14 équations pour 14 fonctions inconnues, deux pour chacune des 7 planètes connues à l’époque (avant la découverte de Neptune). Il est de la forme qui suit, où les dérivées premières des fonctions inconnues sont données, chacune, par une combinaison linéaire de ces mêmes fonctions. Nous avons écrit un système analogue au système (2), §2 de Le Verrier, en regroupant les équations différemment : d'abord toutes celles qui déterminent les dérivées de h1 , … , h7 , puis celles de l1 ,…, l7 (Le Verrier, lui, l'a écrit dans l'ordre des planètes):
La structure étant la même, nous pouvons observer et comprendre le travail de Le Verrier sur le cas plus simple (II). On peut aussi adopter une écriture par blocs, dont la concision est commode
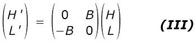
H et L représentent des colonnes de 7 termes, et la matrice B est une matrice 7 x 7. Le système complet admet alors la même écriture que le système (I)... à ceci près que chaque équation y est remplacée par un groupement de 7 équations.
Cette forme très particulière permet de traiter un système de 7 équations seulement, mais du second ordre (c'est à dire, faisant intervenir les dérivées secondes). Par exemple, le système (I) peut s'écrire (en dérivant la première et en y reportant la seconde, que l'on conserve pour déduire l1 de h1, une fois celle-ci calculée) :
{ h1'' (t) + α².h1 (t) = 0 ; α.l1 (t) = h1' (t) (I')
On détermine facilement h1 : on sait qu'elle est de la forme
h1 (t) = U.cos (αt) + V.sin (αt) = N.sin (αt + ζ)
où U, V , N, ζ sont des constantes. Les deux formes sont équivalentes.
@@@@@@@
On peut faire exactement le même travail sur (III), et l'on est ramené à résoudre le système 7x 7, dont la matrice est A = B²
{ H'' (t) + B².H (t) = H'' (t) + A.H (t) = 0 (III')
Par exemple, on vérifie aisément que le système (II) se ramène à
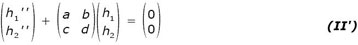
où a,b,c,d se calculent facilement selon les règles classiques d'un produit de matrices (6): a = α² + β γ ; b = α β + β δ.
… Et qui finit en problème d'Algèbre!
Il s'agit désormais de « démêler » ces équations. Ainsi, si nous avions, au lieu de (II'), un système de même forme, mais avec des coefficients nuls aux places de b et c, soit
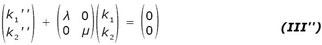
nous aurions deux équations analogues à (I') – sept à partir du système (III'). Leur nombre importe peu, il suffirait de répéter autant que nécessaire la tâche. Ce qui compte pour assurer qu'on aura effectivement des mouvements périodiques, ce sont les signes de λ et μ : ils doivent tous deux être strictement positifs. Faute de quoi, il se produirait une chose encore pire : les solutions ne seraient plus bornées (par exemple de type exponentielles), ce qui signifierait que le système solaire ne serait plus stable ! On comprend mieux pourquoi Le Verrier a emprunté ses formules à Laplace : si le premier est préoccupé de la précision des éphémérides, le second étudiait très précisément la stabilité du système solaire. Il n'y a donc pas un problème théorique d'un côté, un problème pratique d'un autre : tout dépend du passage de la forme (II) à la forme (II'') et de la détermination des nombres λ et μ... ou de sept nombres similaires, lorsqu'on passe du cas d'école au cas réel.
@@@@@@@
Le problème qui se pose ainsi est très exactement celui de la détermination des valeurs propres et de la diagonalisation d'une matrice. Disons sans plus attendre que Le Verrier ne peut le formuler en ces termes, car la théorie des matrices ne verra le jour qu'en 1858 avec le mathématicien britannique Arthur Cayley (1821-1895), et ne diffusera que très lentement dans le monde scientifique, essentiellement à partir des années... 1920-1930 (7)! Ce qui est aujourd'hui banal pour un étudiant de première année était donc loin de l'être pour les pionniers. Une fois de plus, nous allons observer quel merveilleux confort, quelle facilité apportent des notations modernes... et quelle marche délicate a dû être celle des défricheurs.
Pour passer de (III) à (III''), l'idée naturelle est de faire un changement de fonctions inconnues, prenant les anciennes (les hi) comme combinaisons linéaires des nouvelles (les ki)
ou, en forme concise, forme qui a l'avantage d'être valable que le nombre d'inconnues soit 2, 7, ou... n quelconque :
H (t) = QK (t),
forme qui, les coefficients p, q, r, s – plus généralement pi j – étant constants, se dérive en H' (t) = QK' (t). Le système (II’) s'écrit alors
QK'' (t) + AQK (t) = 0 , soit
K'' (t) + Q -1 A Q K (t) = 0 (II'')
Le problème est alors devenu purement algébrique : trouver une matrice Δ diagonale, et une matrice Q (inversible) telle que
Δ = Q -1 A Q (D)
d'où le nom attribué au problème: diagonalisation de la matrice A.
Si nous le supposons un instant résolu, nos équations sont démêlées, chacune est facile à résoudre : on obtient les fonctions sinusoïdales k1 , … , k7 puis, par les combinaisons linéaires indiquées par (CF) les fonctions hi. Le Verrier ne fait rien d’autre : son système (5), au §3, pose pour principe, certes un peu empirique, mais tellement naturel, que les fonctions recherchées auront cette forme. Le mouvement apparaît comme une addition de divers mouvements périodiques, « donc » combinaison linéaire de sinus dont il restera à déterminer, pour chacun, l’amplitude N et la phase ζ .
Mais il faut avant cela rechercher les coefficients diagonaux de D, λ et μ dans le cas n = 2.
Digression : le Calcul qui a fait reculer Laplace.
C'est sur la difficulté de ce travail que s'ouvre le §4:
Les intégrales (5) peuvent donner à la rigueur toutes les circonstances des variations des éléments des orbites. Mais, ainsi que Lagrange l'a remarqué, elles sont d'une discussion très difficile.
Laplace n'a pas été plus chaud pour tenter l'aventure, en dépit des capacités de calculateur dont il fait preuve dans la Mécanique Céleste. Il a donc prouvé, par un argument très courant en Physique – la détermination d'une intégrale première du système –, que les variations sont bornées. Le Verrier rappelle cette argument dans son §4, dont la lecture peut rester accessoire. Pour le système très simple (I), cela consisterait à multiplier sa première équation par h1 (t), la seconde par l1 (t) pour obtenir
h'1'(t).h1(t) + l'1 (t).l1 (t) = 0, qui s'intègre en
h1(t)² + l1 (t)² = k²
ce qui fournit le résultat : ces deux fonctions sont bornées. Le cas de (II) n'est guère plus difficile à traiter.
Valeurs Propres « pour les nuls »!
Si l'on écrit la relation (D) sous la forme équivalente
Q Δ = A Q (D')
Comme Δ est diagonale, la relation se traduit, colonne par colonne, en
A Qj = λj Qj
soit par exemple dans le cas n=2 :
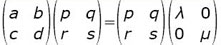en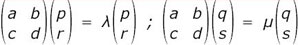 
Ce qui amène à poser les définitions usuelles suivantes :
→ λ est valeur propre de A s'il existe un vecteur (colonne), non nul, x tel que A x = λ x [1]
→ x est dit vecteur propre associé. → On peut écrire encore [1] sous la forme (A – λIn ) x = 0 [2], où In est l’opérateur identité.
→ Un x non nul n'existera que si la matrice (A – λIn ) n'est pas inversible, ce qu'on écrit par la condition portant sur le déterminant
P(λ) = dét (A – λIn ) x = 0 [3]
→ [3] est l'équation caractéristique, et la fonction P du premier membre le polynôme caractéristique; on voit assez facilement, au moins sur les exemples, qu'il est de degré n. Exemple :
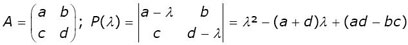
→ Si P(λ) a n racines distinctes, A est diagonalisable, et la matrice Q constituée en accolant n vecteurs propres, chacun relatif à l'une des valeurs propres réalise une telle diagonalisation:
Δ = Q -1 A Q (D)
Ce qui est inhumain au point de dissuader Laplace de l'entreprendre, c'est la perspective du calcul algébrique d'un déterminant d'ordre 7 : c'est enfantin à l'ordre 2 (cf. encadré), faisable à l'ordre 3 si on sait un peu d'algèbre... et généralement très désagréable au-delà. Le Verrier y revient dès l'entrée du §6 :
Le calcul de cette équation, déjà compliqué quand on ne considère pas plus de quatre planètes simultanément, devient impraticable par les moyens ordinaires de l'élimination quand on considère sept planètes.
Le problème n'est donc résolu qu'en théorie :
→ calculer le polynôme caractéristique P(λ); → chercher ses racines.
Notons tout de même la deuxième partie du travail, enfantine elle aussi à l'ordre deux (résoudre une équation du second degré) ne sera pas tout à fait une partie de plaisir à l'ordre 7... mais Le Verrier va réussir, par un ultime argument astronomique, à scinder le calcul en deux: une matrice 3 x 3, une matrice 4 x 4.
Former le Polynôme Caractéristique
Comment Le Verrier va-t-il réussir à poser, puis à effectuer ce calcul sans matrice ni déterminant ? Suivons sa méthode, présentée au §6, avec la matrice A du problème (II') ; elle repose sur la résolution des systèmes. Il écrirait, notant g plutôt que λ son inconnue, (A – gI2) x = 0 [2] en (système (14) dans le texte) :
(a-g) N + bN’ = 0 cN + (d-g)N’ = 0
On calcule N et N' par
[(a – g)(d – g)– bc ]. N = 0 [(a – g)(d – g)– bc ]. N' = 0
équations que Le Verrier écrit de façon résumée
DN = 0 ; DN' = 0
Elles ne fourniront que la solution triviale N = 0 , N' = 0, et partant ne seront d'aucun intérêt... sauf si D = 0. On reconnaît alors en D... le polynôme caractéristique de A ! Le déterminant du système donne en effet la condition à laquelle il a une autre solution que (0,0) : il n'est donc pas surprenant qu'il apparaisse en facteur de chacune des quantités à calculer.
Voilà donc la théorie réglée en pensée : si l'on conduit une résolution du système par éliminations successives des inconnues, on obtiendra le polynôme caractéristique au moment où, ayant éliminé toutes les autres , la dernière inconnue sera exprimée par 0/D, sauf si D = 0 bloque ce calcul (9).
D étant le dénominateur commun à toutes les inconnues. Or on peut considérer ces résultats comme les équations finales provenant de l'élimination de toutes les indéterminées excepté une, et par là on voit que l'équation finale en g dont nous avons besoin, n'est autre que l'équation D = 0.
La Méthode des Traces
Mais en pratique, ce serait inextricable, note Le Verrier dès l'introduction du §6 :
Le calcul de cette équation, déjà compliqué quand on ne considère pas plus de quatre planètes simultanément, devient impraticable par les moyens ordinaires de l'élimination quand on considère sept planètes.
D'où l'introduction d'une nouvelle méthode de calcul, qui repose sur deux objets très simples, mais que l'auteur ne met guère en lumière simultanément :
1. Les fonctions symétriques des racines, vieil ingrédient de l'étude des équations;
2. La trace d'une matrice, que l'on définit comme somme de ses coefficients diagonaux.
Si le premier est explicitement mentionné dès le début du §6, le second apparaît une bonne page plus loin, et le rapprochement ne sera fait, de manière rapide, qu'à la fin.
Fonctions symétriques des racines
Prenons l'exemple d'un polynôme de degré 3 en λ. P(λ) = λ3 + uλ2+ v λ + w = ( λ – α )( λ – β )( λ – γ ) selon qu'on l'écrit en forme développée ou factorisée; cette dernière fait apparaître ses racines α , β, γ.
u = – ( α + β + γ )
v = α β+ β γ + γ α
w = – α βγ
Ce sont les fonctions symétriques élémentaires des racines. D'autres fonctions symétriques en α , β, γ sont dites sommes de Newton :
S1 = α + β + γ
S2 = α2 + β2 + γ2
S3 = α3 + β3 + γ3
Connaissant u, v, w, on calcule aisément S1, S2, S3, et inversement. Il suffit donc, pour connaître un polynôme, de connaître les sommes de Newton de ses racines. De telles relations d'aller et retour existent pour tout degré n. Le calcul est juste un peu plus technique; Newton a donné dans ce but des formules auxquelles son nom est resté attaché.
Le Verrier va alors utiliser le subterfuge suivant : plutôt que calculer les coefficients de P, c'est à dire les fonctions symétriques élémentaires, calculer les sommes de Newton correspondantes, sous la forme de traces de matrices (sans le dire de cette manière, bien sûr). Tout part d'une remarque sur la forme de P, que l'on fait aujourd'hui sous sa forme déterminantale
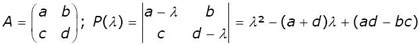
Le produit des termes de la diagonale de ce déterminant est le seul à intervenir dans les termes de plus haut degré n et dans les termes de degré n - 1 ; on le constate facilement sur le cas n = 2.
Cette équation sera du septième degré, car le produit (g-a)(g-b')(g-c'')... donnera le terme g7 qui ne pourra être déduit par aucun autre. Du même produit dépend en outre le coefficient du second terme de l'équation ; car […] on voit qu'il ne peut contenir deux des coefficients compris dans une même colonne verticale, ou dans une même ligne horizontale des équations (14).
Ainsi, dans le cas n = 2, on cueille le terme S1 = ( a + d ) sur la matrice, si l'on est moderne... ou sur le système différentiel, ce qui revient au même, si l'on est adepte de la cuisine traditionnelle !
Il n'y a plus qu'à trouver les autres. On voit aisément, par simple application de la définition, que la matrice A2 a pour valeurs propres les carrés de celles de A, et ainsi de suite à chaque puissance : dans le cas à racines deux à deux distinctes, on le voit grâce aux formules (D) liant A à sa réduite diagonale Δ
Δ = Q -1 A Q , Δ2 = Q -1 A2 Q , Δ3 = Q -1 A3 Q , …
On peut certes objecter qu'on n'est pas sûr d'être dans ce cas... avant d'avoir déterminé les racines, mais l'expérience montrera que c'est bien ce qui se produit (10).
L'algorithme de Le Verrier consiste donc → à calculer les puissances de la matrice A, jusqu'à un ordre égal à sa taille; → puis, calculer les traces, ou somme des coefficients diagonaux, de chacune d'elles.
Comme il ne dispose pas du produit matriciel, le carré est évalué par la dérivation du système différentiel : les dérivées secondes sont exprimées à l'aide des dérivées premières, et l'opération d'élévation au carré se fait implicitement par la réutilisation du système initial pour chasser toute dérivée du membre de droite : c'est ce que nous avons fait, nous aussi, lors de la présentation du problème (passage de (III) à (III')). Le Verrier résume ainsi son algorithme
Il n'est pas besoin de plus longues explications pour apercevoir qu'on obtiendra la somme des cubes, des quatrièmes puissances... des racines, au moyen des dérivées troisième, quatrième … de h, h' … Et d'ailleurs, quand on aura les sommes des puissances semblables des racines jusqu'à la septième, il sera facile de calculer les coefficients de l'équation par les fonctions symétriques. Cette marche est assez simple [...]
Lorsque n = 2, on obtient
et enfin, si l’on se rapporte aux coefficients λ et μ du système (III’) page 6 :
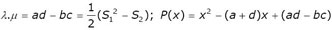
Travaux pratiques !
Exemple 1 : un cas d'école :
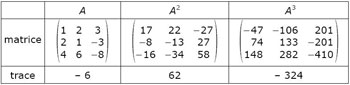
On calcule les coefficients u, v, w de P(λ) = – λ3 + uλ2+ v λ + w en fonction de S1, S2, S3, ce que l'on fait à partir des relations (11) :
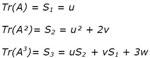
Le calcul est sans difficulté, et, comme la matrice provient... d'un livre de mathématiques, on factorise le polynôme caractéristique dès qu'on a vu la racine – 2 :
P(λ) = – λ3 – 6 λ2+13 λ + 42 = – ( λ + 7 )( λ + 2 )( λ – 3 )
Exemple 2 : le vrai calcul de Le Verrier :
Le Créateur du Monde, lui, est un peu plus farceur : il n'a pas prévu que les calculs s'arrangent aussi miraculeusement ! Mais heureusement, avec un ordinateur, voire une simple calculette programmable, les calculs s'effectuent très rapidement.
Comment Le Verrier procédait-il à son époque ? Ce serait une boutade à peine exagérée que de le considérer comme un des pionniers du tableur et... du calcul parallèle, pointe de la modernité de nos ordinateurs. À un détail près : les circuits de processeurs arithmétiques d'alors étaient des êtres humains ! L'observatoire employait une armée de calculateurs, gens ayant une bonne habileté arithmétique, mais sans connaissances scientifiques particulières, qui exécutaient sans comprendre une suite d'opérations dont l'astronome avait préparé la marche sur des feuilles de calculs. On pourrait aussi bien, dans une école primaire aujourd'hui (12), partager les 16 opérations que réclament le produit de deux matrices 4 x 4 en 32 élèves, chacun faisant le calcul d'un terme (4 multiplications et 3 additions), un terme étant confié à deux personnes dont le résultat n'est validé que s'il est identique pour les deux, et repris sinon ! (Contrôle et minimisation des erreurs n'étaient alors pas une mince affaire). Chaque participant effectue un calcul dont le sens lui échappe, et dont seul le coordinateur connaît la signification...
Le problème porte sur une matrice 7 x 7 qui – curieusement ? – ne figure pas dans l'article du Journal de Liouville. Mais on la trouve dans la Connaissance des Temps, dont beaucoup d'items sont les mêmes, mot pour mot, ou très proches : cet homme qui maîtrisait le tableur maniait aussi le « copier-coller » avec aisance. Le Verrier allège alors la tâche avec une considération simplificatrice : si une matrice a cette forme
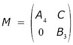
où les lettres majuscules symbolisent des blocs (A4 est un carré 4 x 4, B3 un carré 3 x 3, C a donc 4 lignes et 3 colonnes), le polynôme caractéristique de M est le produit de ceux de A et B. La situation n'est pas tout à fait celle-ci, mais elle en est toute proche : tous les coefficients du bloc 3 x 4, en bas à gauche, sont inférieurs à 0.001. On peut donc faire comme s'ils étaient nuls sans, probablement, altérer beaucoup les valeurs propres. Et voilà la détermination d'un polynôme de degré 7 remplacée par celle de deux facteurs de degré 4 et 3, et, surtout, les calculs de puissance matricielle limités efficacement en taille et en nombre de produits.
Figure 4 : Le système 7x7, brut, dans la Connaissance des Temps pour l'An 1843. Remarquer la petitesse des quatre premiers coefficients dans les trois dernières lignes.
Cet état de fait n'a rien d'un miracle : il y a une bonne raison astronomique à cela. Les planètes peuvent être divisées en deux groupes, les trois "grosses" : Jupiter, Saturne, Uranus et les quatre "petites": Mercure, Vénus, Terre et Mars. Or, si les grosses font ressentir leur attraction aux petites, ces dernières, certes, agissent sur les grosses... mais si peu ! C'est exactement ce que traduit le système : en première approximation, on peut donc considérer comme autonome le système des trois grosses planètes, ce qui correspond à B3 et chercher ses valeurs propres, puis traiter le système des quatre petites planètes. Le Verrier donne seulement, dans son article, le polynôme et les racines pour les deux blocs ; voici l'essentiel du calcul pour celui de taille 4.
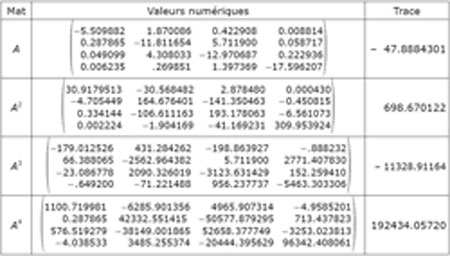
Grâce aux relations sur les fonctions symétriques, Le Verrier obtient alors :
P(λ) = λ4 – 47.88843 λ3 + 797.2789.λ2 – 5349.457 λ + 12296.555
et les racines (13)
λ1 = 5.29870, λ2 = 7.57404, λ3 = 17.15266, λ4 = 17.86303
La méthode a été améliorée, du point de vue algorithmique, par le Français Jean-Marie Souriau (1948) et le Russe Dimitri Faddeev (1949), tout en restant basée sur le principe du calcul du polynôme caractéristique.
La Question de la Précision
Elle se pose dans toute détermination numérique ; dans ce qui précède, deux circonstances invitent à s'interroger : 1. Si l'on avait estimé A à quatre (respectivement à trois, deux) décimales, la valeur des racines en aurait-elle été notoirement affectée, ou aurait on obtenu des précisions « cohérentes » ? Par exemple, en arrondissant les coefficients à 2 décimales, obtiendrait on des valeurs propres arrondies à 2 décimales des résultats précédents ? 2. En découplant le système des grosses planètes de celui des petites, on a commis une erreur de méthode. Quelles sont ses répercussions ?
Qualitativement, la question peut se reformuler ainsi : les valeurs propres varient-elles continûment avec la matrice ? (ou les racines avec les coefficients d'un polynôme?). Quantitativement, peut-on garantir des bornes effectives sur la variation du résultat à partir de celle des données ? Heureux les étudiants d'aujourd'hui : rien n'est plus facile que de se faire une idée expérimentale à l'aide d'un logiciel retournant les valeurs propres, il n'en manque pas ; on ne peut que les encourager à étudier ainsi les deux questions posées. Une étude théorique sérieuse n'a pas été entreprise avant le XXe siècle. On n'en appréciera que davantage le travail esquissé par Le Verrier dans son §9, à partir de la différenciation des formules exprimant les fonctions symétriques des racines : il est clair que l'importance du problème ne lui avait pas échappé et là encore, il se révèle un pionnier lucide.
La suite du calcul des valeurs propres
Le deuxième mathématicien, dans l'ordre historique, à se lancer à l'assaut des valeurs propres va opérer une rupture de méthode radicale. Karl Gustav Jacobi (1804-1851) met au point en 1844 une méthode itérative de résolution des systèmes, correspondant à la construction d'une suite de matrices. A priori, ce n'est pas le même problème ! Mais voilà qu'à la fin de son article, Jacobi remarque :
La méthode décrite ici est encore plus intéressante quand les équations ont la forme suivante.
en l'occurrence, le système (14) du §6 de Le Verrier ! (ci-dessous)
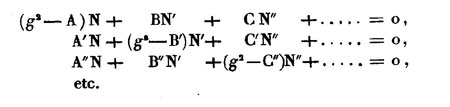
C'est ainsi que Jacobi obtient une méthode itérative de calcul des valeurs propres comme sous-produit d'une méthode itérative de résolution des systèmes, dont il ne donne qu'une idée assez vague, précisant (14) :
Je me contente ici de ces indications car j'ai l'intention d'exposer, dans un travail ultérieur, l'application de cette méthode aux perturbations séculaires des sept planètes principales. On verra par là, grâce aux calculs effectués avec le plus grand soin par mon savant ami, M. le Docteur Seidel, de Munich, que ma méthode présente des avantages notables sur celle de M. Le Verrier, pour la rapidité et la sûreté avec lesquelles on parvient à déterminer le résultat final.
La nouveauté, c'est que l'on court-circuite ainsi le polynôme caractéristique : on vise directement la diagonalisation en construisant des matrices qui s'approchent de plus en plus d'une matrice diagonale. Or, à partir de 1950, les calculs des ingénieurs, parallèlement à l'essor des ordinateurs, concernent des matrices de taille de plus en plus grande. Les méthodes itératives s'adaptent parfaitement à l'évolution conjointe de la taille des problèmes, de celle des mémoires et de la vitesse de calcul. Le procédé de Le Verrier devient impraticable dès qu'on est amené à rechercher les racines d'un polynôme de degré supérieur à quelques dizaines... C'est pourquoi le développement des méthodes de calcul numérique des valeurs propres a suivi la voie proposée par Jacobi et non celle de Le Verrier ; l'une des plus utilisées aujourd'hui est la méthode "QR" de John Francis (1961). Le lecteur désireux d'en savoir plus sur cette évolution au XXe siècle trouvera un bon point de départ dans l'article, ci-dessous référencé (15).
La suite de l'étude du système solaire
Revenons brièvement à la question d'astronomie qui a motivé ces découvertes mathématiques : la variation des éléments elliptiques des orbites, parmi lesquelles figure en bonne place celle du périhélie. En 1841, Le Verrier s'intéresse particulièrement à celui de Mercure.
Figure 5 : Relevé manuscrit, par Le Verrier, d’éléments de Mercure (Document Observatoire de Paris).
La méthode des perturbations explique l'avance du périhélie de toutes les planètes... sauf celui de Mercure. Il aura beau reprendre la question en 1849, espérant renouveler le coup d'éclat de la découverte de Neptune (1846) en émettant l'hypothèse d'une nouvelle planète troublante – déjà baptisée Vulcain ! – ses tentatives seront vaines, et pour cause : l'explication viendra de la Relativité générale d'Einstein (1915), dont ce sera la première confirmation !
Figure 6 : Brouillon et première parution de l'article d'Albert Einstein sur la Relativité Générale.
Figure 7 : L'explication de l'avance du périhélie de Mercure clôt l'article ! On remarque cité le nom de « Leverrier ».
Quant à la stabilité du système solaire, elle sera malmenée – pour le très long terme, évidemment – par Poincaré et ses prémisses de la théorie du chaos en 1889….
C'est donc dans un contexte historique très riche que s'inscrit cet article de Le Verrier : les mathématiques pures (le polynôme caractéristique), appliquées (la méthode des traces) y ont été mises au service d'une astronomie classique alors à son sommet, avant qu'elle ne doive tenir compte de deux théories essentielles au XXe siècle : celle de la Relativité et celle du Chaos déterministe.
Septembre 2011
(1) Voir l'article de James Lequeux : La Découverte de Neptune (1846), sur BibNum (juin 2010).
(2) L'écart des dates n'est pas une anomalie: pour être utilisables, les éphémérides du mouvement des planètes doivent être publiés avec une certaine avance...
(3) C’est-à-dire « étrangers à l'Académie » (qui n'en sont pas membres).
(4) Il n'y aura pas d'avancée théorique avant les célèbres travaux d'Henri Poincaré sur le Problème des Trois Corps en 1889. Et, plus d'un siècle plus tard, le domaine reste un sujet de recherche pointu et ardu.
(5) Un simple renvoi au tome 2 de la Mécanique Céleste, §55.
(6) Un simple renvoi au tome 2 de la Mécanique Céleste, §55.
(7) Voir par exemple, sur BibNum, l'analyse par Roger Mansuy de l'article de Cholesky « Sur la résolution numérique des systèmes d’équations linéaires ». Daté de 1910, le texte de Cholesky ne contient pas encore une seule matrice
! (8) CF = changement de fonctions.
(9) Pour le dire autrement, ce D serait le dénominateur des célèbres formules de Cramer: quelle que soit la taille du système, toutes les inconnues sont calculées avec le même dénominateur, ou la nullité de celui-ci empêche l'expression d'une solution unique.
(10) Le résultat est tout à fait général, c'est l'illustration que nous limitons à ce cas par souci de simplicité.
(11) La troisième s'obtient à partir de l'équation : on l'écrit pour chacune des trois racines, et on somme. C'est un cas particulier des formules de Newton !
(12) On fait ici l'hypothèse – hasardeuse ou téméraire – que les élèves y savent additionner et multiplier... ou disposent d'une calculette 4 opérations.
(13) Il ne dit rien de la méthode employée à cet effet.
(14) Traduction de Colette Bloch pour le livre J-L Chabert & al. Histoires d'Algorithmes (Belin, 2010).
(15) Gene H. Golub, Henk.A. van der Vorst, “Numerical Progress in Eigenvalue Computation in the 20th Century” (en ligne). D'un niveau toutefois nettement plus élevé que celui de cet article.
À LIRE (ARTICLES ET SITES)
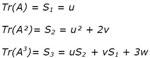
James Lequeux : La Découverte de Neptune (1846), analyse d’un texte de Le Verrier – juin 2010.
Site Web Alain Juhel, page consacrée à Le Verrier.
À LIRE (LIVRES)
James Lequeux : Le Verrier, savant magnifique et détesté (EDP Sciences, 2009).
Jean-Luc Chabert, Évelyne Barbin, Michel Guillemot, Anne Michel-Pajus, Histoire d'Algorithmes (Belin, 1994).
EXPOSITION TEMPORAIRE
Bicentenaire d’Urbain Le Verrier à l’Observatoire de Paris : exposition jusqu’au 30 octobre 2011 (lien).
POUR ALLER PLUS LOIN (MATHÉMATIQUES)
Émile Durand, Solutions Numériques des Équations Algébriques, vol 2 (Masson, 1961).
Gene H. Golub, Henk.A. van der Vorst , Numerical Progress in Eigenvalue Computation in the 20th Century (lien).
Moïse Sibony, Jean-Claude Mardon, Analyse numérique T1 : Systèmes Linéaires et non Linéaires (Hermann, 1984).
Jean-Marie Souriau, Une Méthode pour la Décomposition Spectrale et l'Inversion des Matrices (CRAS 227, 1948) (lien).
Wikipedia (Allemand), mise en œuvre de l'algorithme à la manière de Souriau et Faddeev (lien).texte-le-verrier.pdf
>> Téléchargez le texte d'Urbain Le Verrier
Sur les variations séculaires des éléments elliptiques des sept planètes - Version PDF (1.72 Mo)
Analyse-Le-Verrier.pdf
>> Téléchargez l'analyse d'Alain Juhel
Le Verrier et la première détermination des valeurs propres d'une matrice - Version PDF (811.37 Ko)
société des amis de la bibliothèque de l'X