Dans un de ses "best-sellers", Portrait du Gulf Stream (Seuil 2005), le romancier Erik Orsenna consacre un chapitre à Gaspard-Gustave de Coriolis (1792-1843) et le conclut ainsi : « Et rien n’indique que notre Gaspard Gustave ait jamais mis le pied sur un bateau ni qu’il se soit jamais intéressé à la mer. Le fait est là : pour les siècles des siècles, Coriolis est celui qui a expliqué l’influence de la rotation de la Terre sur le parcours des vents et des courants ».

Figure 1 : (à gauche) Cyclone dans l’hémisphère nord (sens inverse des aiguilles d’une montre) : ouragan Olga le 28 novembre 2001 dans l’Atlantique ; (à droite) Cyclone dans l’hémisphère sud (sens des aiguilles d’une montre) : Australie le 20 février 2002 – on reconnaît la côte sud de l’Australie (images NASA)
C’est ainsi que le nom de Coriolis est universellement connu ; néanmoins la carrière et les autres contributions de ce savant sont nettement moins connues, de même que la façon dont il arrive aux « forces centrifuges composées », auxquelles son nom sera donné. C’est ce que nous essaierons de décrire dans le présent article, sans omettre de rappeler les autres contributions de Coriolis : c’est lui qui le premier donne la définition physique du mot travail en mécanique dans un mémoire présenté en 1826 à l’Académie (alors qu’il n’en est pas encore membre). Il est aussi l’auteur d’une véritable « théorie du travail » dans son ouvrage majeur et austère, le
Calcul de l’effet des machines (1829). Il écrit par ailleurs une
Théorie mathématique des effets du jeu de billard (1835), rare exemple dans l’historiographie des sciences où un sujet est complètement traité
(1), sans guère d’apport ultérieur possible.
@@@@@@@
La naissance de la « force de Coriolis » se fait à travers deux textes complémentaires : - Le « Mémoire sur le principe des forces vives dans les mouvements relatifs des machines », lu le 6 juin 1831 à l’Académie des sciences, publié dans le Journal de l’École polytechnique en septembre 1832 (21e cahier, tome XIII), publié aussi des les Mémoires des savants étrangers. - Le « Mémoire sur les équations du mouvement relatif des systèmes de corps », publié dans le Journal de l’École polytechnique en 1835 (24e cahier, tome XV).
Le second mémoire évoque les « forces centrifuges composées », qui prendront par la suite le nom de « force de Coriolis ». Le premier mémoire jette les bases de calcul pour le second résultat, mais il comprend aussi la notion nouvelle à cette époque des « forces d’entraînement ». Ce vocable est resté, bien que Coriolis n’en soit pas crédité.
Une autre différence importante entre les deux mémoires montre l’évolution du travail de Coriolis : le premier, on le verra, révèle une égalité scalaire – elle porte sur les forces vives dans le mouvement relatif (la force vive est ½mv²). Le deuxième révèle une égalité vectorielle, plus puissante, portant sur le principe de la dynamique dans le mouvement relatif. A posteriori, le résultat du premier mémoire devient un simple cas particulier de celui du second mémoire : par projection de l’identité vectorielle sur la courbe du mouvement, on obtient l’identité scalaire du premier mémoire – puisque la force centrifuge composée « ne travaille pas », sa projection est nulle dans la direction du mouvement.
Poisson présente à l’Académie le premier mémoire
Un document d’approche intéressant de ce « Mémoire sur le principe des forces vives dans les mouvements relatifs des machines » est le rapport qu’en fait Poisson en séance du 31 octobre 1831 de l’Académie des sciences. Comme souvent, le texte du rapporteur permet de mieux comprendre le texte, puisqu’il tire ce qui lui en semble essentiel, et qu’il remet le texte en perspective.

Figure 2 : Siméon-Denis Poisson (1781-1840). Polytechnicien, auteur de nombreuses contributions en mathématiques, en mécanique rationnelle et en physique mathématique.
Poisson commence par rappeler le « principe des forces vives » tel que posé par d’Alembert :
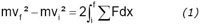
L’accroissement des « forces vives », entre deux positions successives du système, est égal au double de l’intégrale, prise entre ces limites, de la somme des forces qui ont agi sur tous ces corps multipliés chacun par l’élément de sa direction ; intégrale que l’on appelle à l’époque la quantité d’action due à ces forces.
Poisson poursuit en indiquant que Coriolis établit le principe des forces vives, non dans le cas de mouvements absolus, mais dans le cas de mouvements relatifs, par exemple à l’intérieur d’une machine : dans le membre de gauche (les forces vives mv²), ce sont les vitesses relatives qui interviennent dans ce cadre ; dans le membre de droite (la quantité d’action), il faudra retrancher les forces d’entraînement.
Ceci conduit, dans le texte de Coriolis, après quatre pages de calculs précis, au principe suivant qu’il écrit avant de l’énoncer :
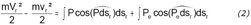
Cette équation renferme ce théorème, que le principe des forces vives a encore lieu dans le mouvement relatif aux axes mobiles, pourvu qu’aux quantités d’action
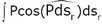
, calculées avec les forces données P et les arcs dsr décrits dans ce mouvement relatif, on ajoute d’autres quantités d’action qui résultent des forces Pe, qui sont égales et opposées à celles qu’il faudrait appliquer à chaque point mobile pour lui faire prendre le mouvement qu’il aurait s’il était invariablement lié aux axes mobiles.
Comparons les deux équations (1) et (2) : - Coriolis, comme à son habitude, renvoie le facteur 2 en dénominateur du membre de gauche de l’équation (alors qu’il est chez Poisson, en (1), en multiplicateur du côté gauche). Poisson, en géomètre adepte de la « mécanique rationnelle », ne considérait que les « forces vives » définies par mv². Coriolis, pédagogue, proposait d’appeler forces vives la quantité ½mv² : c’est cette acception qui sera le fondement de la notion ultérieure d’énergie cinétique. - Dans l’équation (2), le premier terme du membre de droite correspond au membre de droite de l’équation (1). Mais apparaît dans l’équation (2) un autre terme, celui des forces d’entraînement. Compte tenu de la similitude de forme de ces deux équations, on peut considérer que l’équation (2) de Coriolis est une généralisation (dans le cadre d’un mouvement relatif) du principe des forces vives de Lagrange.
Analyse du mémoire de 1831
Ce mémoire, relativement complexe, comprend 20 pages et 6 pages d’annexe : bien qu’a posteriori il n’apparaît que comme un cas particulier du résultat du second mémoire, il est plus volumineux et plus calculatoire que ce dernier, qui fait 13 pages – en fait, les résultats du second mémoire étaient en germe dans le premier : Coriolis pour définir la « force centrifuge composée » n’aura qu’à reprendre à mi-chemin les calculs de son premier mémoire.
Dès l’introduction (partie A), Coriolis commence par poser les bases de son résultat :
…on peut appliquer l’équation des forces vives en y faisant entrer les vitesses relatives, et les quantités d’action ou de travail qui se rapportent aussi aux mouvements relatifs. Mais dans ces quantités d’action, en outre des forces qui sont immédiatement données et qui concourent au moment absolu, il faut en considérer d’autres dont il est facile d’indiquer la nature : elles sont opposées aux forces qu’il faudrait appliquer aux points matériels du système s’ils étaient libres, pour les obliger à conserver par rapport aux plans mobiles les positions relatives qu’ils ont à un moment donné (…)
Mais, dès le départ aussi, Coriolis met en garde contre la fausse évidence de l’énoncé :
(…) on se méprendrait si l’on regardait la proposition comme évidente, même dans cet exemple assez simple. Il est si peu évident qu’on doit introduire ces forces, que l’on arriverait à des résultats faux si l’on procédait ainsi pour toute autre équation que celle des forces vives.
Coriolis résume ainsi la portée du mémoire, tout en anticipant, de manière encore non consciente, les résultats du second mémoire. L’introduction des « forces d’entraînement » – et de celles-ci uniquement – n’est valable que pour le principe des forces vives, et aboutit au principe des forces vives dans le mouvement relatif, énoncé en
(2) ci-dessus (ce que René Dugas
(2) appellera « premier théorème de Coriolis »).
Coriolis résume ainsi la portée du mémoire, tout en anticipant, de manière encore non consciente, les résultats du second mémoire. L’introduction des « forces d’entraînement » – et de celles-ci uniquement – n’est valable que pour le principe des forces vives, et aboutit au principe des forces vives dans le mouvement relatif, énoncé en (2) ci-dessus (ce que René Dugas1 appellera « premier théorème de Coriolis »).
@@@@@@@
La partie (B) du mémoire (p.272-277), après l’introduction, est la plus théorique et de portée la plus générale. Coriolis se place dans le cas de deux repères normés mais non orthogonaux, l’un pour les axes fixes, l’autre pour les axes mobiles, et donne les relations existant entre les coordonnées cartésiennes d’un même point dans les deux repères de la manière la plus générale. De la même manière, il exprime dans leur plus grande généralité les liaisons qui existent au cours du mouvement L = 0, M = 0, etc., et utilise les multiplicateurs de Lagrange pour projeter l’expression de ces liaisons sur les axes mobiles. Cette généralité est importante pour Coriolis, qui insiste (p.279) : « sans rien particulariser sur ces mouvements ».
Cette partie aboutit au résultat principal du texte, le « premier théorème de Coriolis », rappelé en (2) ci-dessus.
D’importantes coquilles dans le Journal de l’École Polytechnique
La lecture des mémoires de Coriolis est assez difficile du point de vue mathématique, mais de plus certaines coquilles à des endroits cruciaux obligent le lecteur (que ce soit le lecteur actuel ou celui de l’époque) à des rectifications s’il veut suivre le raisonnement :
- p. 273, en bas, dernier système d’équations : remplacer x’, y’, z’ par x1, y1, z1. - p. 274, en bas, avant-dernier système d’équations : remplacer dans le membre de gauche dx par dx1 ; ôter les coefficients m dans les trois équations ; dans la deuxième équation, membre de droite, remplacer le second dy par dη.
- p. 274, en bas, dernier système d’équations : remplacer dans le membre de gauche de2x par de2x1 (idem pour y, z).
- p. 279, équation (C) : remplacer v par vr.
- p. 279, dernière équation, enlever le premier terme m.
- p. 280, équation (D), manque cos après le produit vrve.
- p. 281, équation concluant la partie, facteur 2 en trop.
- p. 283, dernière équation, d²a au lieu de da.
- p. 284, dernier système d’équations, de nombreuses incohérences : remplacer les parenthèses (xdy – zdz) par (xdy – ydx), (ydz – xdy) par (ydz – zdy) ; seule la deuxième parenthèse (zdx – xdz) est correcte.
- p. 291, première équation, les indices e (pour entraînement) s’appliquent aux vitesses et non aux masses ; manque m dans le dernier terme.
- p. 291, deuxième équation, erreur de signe dans le dernier terme.
@@@@@@@
La partie (E) est la plus longue et la plus difficilement accessible du mémoire, car elle ne semble donner aucun résultat particulier par rapport à
(2). Coriolis détaille le dernier terme de la formule
(2), nouveau dans l’équation des forces vives, terme qui est à la base du premier théorème de Coriolis :
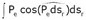
. Il avait dès l’énoncé de son théorème le souci de l’expliciter :
Nous indiquerons plus loin le moyen de représenter ces forces et de simplifier les calculs des quantités d’action qui leur sont dues [p. 277, juste après le premier théorème qui introduit les forces d’entraînement Pe] Revenons au calcul de
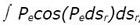
, en ne nous occupant plus des forces dues au mouvement de l’origine des axes mobiles [p. 282]
Coriolis n’évoquera que huit pages plus loin (p.290) le mouvement possible de l’origine, pour aussitôt annuler son effet dans la pratique (en considérant un mouvement rectiligne uniforme de l’origine des plans mobiles). Cette partie (E) aboutit à la formule la plus générale de l’expression du nouveau terme de l’équation des forces vives, en détaillant ce terme qui résulte des « forces d’entraînement »:
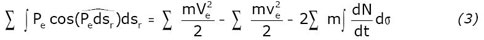
Le terme
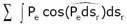
faisant son apparition dans l’équation des forces vives du mouvement relatif en
(2) est lié à deux facteurs, qu’on voit en
(3) :
- Le dernier terme à droite représente la variation de la vitesse de rotation des axes mobiles : quand celle-ci est uniforme, ce terme est nul. Mais Coriolis tient à donner le résultat dans sa plus grande généralité, ce que le titre de sa partie (E) indique (« Expression générale de la quantité d’action qu’il faut introduire dans l’équation des forces vives, en raison du mouvement des axes mobiles »). - Le premier terme (toujours à droite de l’équation) est la différence des forces vives due à la différence des vitesses d’entraînement dans le temps. Cette partie de l’équation est en effet à rapprocher du principe traditionnel des forces vives (1) : la variation d’une quantité d’action correspond à la variation des forces vives liées aux vitesses, en utilisant cette fois-ci les vitesses d’entraînement. Mais on ne saurait se contenter de cette analogie avec le principe traditionnel des forces vives, et il faut ajouter un second facteur, qui est la variation de la vitesse des axes mobiles dans le temps, représentée par le deuxième terme.
Ainsi, cette partie (E) complète bien le premier théorème : Coriolis vise à ramener à une expression connue (la première partie de (3)), et à voir quelle est la différence induite par son théorème, ce qui l’amène au dernier membre à droite de l’équation (3). On constate le souci de Coriolis de se rapprocher le plus possible du principe des forces vives traditionnel, et ainsi de s’inscrire, sur le fond comme sur la forme, dans la tradition lagrangienne de la mécanique rationnelle.
Coriolis et la roue à aubes courbes de Poncelet
Jean-Victor Poncelet (1788-1867), autre polytechnicien ingénieur-savant, avait obtenu en 1825 le prix de mécanique de l’Académie des sciences pour l’invention de sa roue à aubes courbes (en remplacement de la roue à ailettes plates). L’avantage majeur de cette invention, immédiatement adoptée par les fabricants de roues à moulins, était que l’eau de la rivière ou du bief entrait tangentiellement à l’aube (grâce à sa forme courbe) : ainsi toute l’énergie de l’eau était utile dans l’aube, alors que dans la roue à ailettes plates (à droite ci-dessous), l’eau arrivait avec un angle d’attaque, il y avait choc contre l’aube et déperdition d’énergie – le rendement n’était pas optimal.
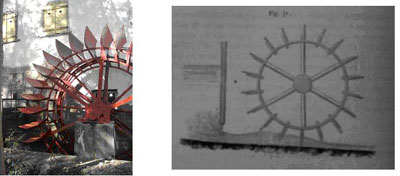
Figure 3 : La roue à aubes courbes ("à la Poncelet") du moulin de Lütterbach (Alsace), à gauche ; une roue à aubes planes, extrait de l’Introduction à la mécanique industrielle de Poncelet, à droite.
Coriolis ne conteste bien évidemment pas l’utilité de l’aube courbe par rapport à l’aube plate. Mais, dans son Calcul de l’effet des machines (1829), il avait déjà relevé une première erreur dans la théorie qu’avait faite Poncelet de sa roue (3). Dans son article de 1831 ici analysé, Coriolis fait (p. 294) une seconde objection importante et montre que le rendement même théorique ne peut être égal à 1, contrairement à ce que prétendait Poncelet : On peut appliquer les formules générales des articles précédents à la question du mouvement de l’eau dans les aubes courbes des roues de M. Poncelet. Si l’on considère l’aube comme un canal où l’eau se meut pendant qu’il est entraîné d’un mouvement de rotation uniforme, la valeur de Vr sera donnée dans ce cas par (…)
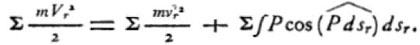
(…) Suivant la forme ordinaire des aubes courbes, la gravité se rapprochera davantage de la direction de dsr, c'est-à-dire de la tangente au canal que forme l’aube, pendant la descente de l’eau que pendant son ascension ; il s’ensuit que ΣmVr²/2 est plus grand que Σmvr²/2, et qu’ainsi l’eau sort de la roue avec une force vive relative plus grande que celle qu’elle y avait en entrant. Dit plus simplement, l’eau rencontre une pente de l’aube plus faible quand elle monte que quand elle descend, car entre temps la roue a tourné : lors du mouvement de descente, l’inclinaison de l’aube est déjà plus proche de la verticale puisqu’elle va bientôt relâcher l’eau (pour une particule d’eau donnée, l’inclinaison de l’aube à « l’amenée d’eau » n’est pas la même qu’au « dégagé d’eau »). Dans le calcul théorique de Poncelet, l’eau entre avec toute sa vitesse sur l’aube (grâce à la courbure) et sort avec une vitesse absolue nulle. Coriolis corrige ce dernier point en indiquant que compte tenu du travail de la gravité (la roue ayant tourné), la vitesse absolue en sortie d’aube est non nulle – ce qui était fatal au rendement de 1 : si l’eau garde une vitesse absolue au dégagé, ceci signifie que cette vitesse (cette "force vive") n’a pas été utilisée dans la roue. Le principe de Carnot nous dit « qu’il n’y a pas de repas gratuit » – pas de création de force vive : si l’eau a une vitesse absolue non nulle en sortie d’aube, elle emporte une partie des forces vives de l’ensemble du cycle…
Analyse du mémoire de 1835
Paradoxalement, l’article de 1835 « Mémoire sur les équations du mouvement relatif des systèmes de corps », qui contient le résultat de la « force de Coriolis » (« second théorème de Coriolis » pour reprendre l’expression de R. Dugas), est moins complexe et moins long que l’article de 1831. Les résultats du second article sont largement en germe dans le premier article
(4).
Comparaison avec le premier mémoire
Dès l’introduction de son second mémoire, Coriolis rappelle les limites de son article de 1831, à savoir qu’il ne s’appliquait qu’au principe des forces vives – c’est à dire à l’identité scalaire qui représente le bilan énergétique du mouvement – et non à d’autres équations du mouvement relatif, comme le principe fondamental de la dynamique f = mγ, égalité vectorielle. Coriolis va généraliser la démarche dans son second mémoire, en se posant les questions suivantes : peut-on utiliser les termes de correction liés aux vitesses d’entraînement dans d’autres équations du mouvement que le principe des forces vives ? si ce n’est pas le cas, peut-on « donner une expression simple des nouveaux termes de correction » ? Coriolis y répond dès son introduction :
Pour établir une équation quelconque de mouvement relatif d’un système de corps ou d’une machine quelconque, il suffit d’ajouter aux forces existantes deux espèces de forces supplémentaires ; les premières sont toujours celles auxquelles il faut avoir égard pour l’équation des forces vives, c’est à dire que ce sont des forces opposées à celles qui (…) ; les secondes sont dirigées perpendiculairement aux vitesses relatives et à l’axe de rotation des plans mobiles ; elles sont égales au double du produit de la vitesse angulaire des plans mobiles multipliée par la quantité de mouvement relatif projetée sur un plan perpendiculaire à cet axe.
Le mémoire de 1831 donnait une égalité scalaire, celle des forces vives. Le mémoire de 1835 donne une égalité vectorielle, beaucoup plus puissante, s’appliquant aux lois vectorielles du mouvement lui-même – comme le principe de la dynamique de Newton. Coriolis montre immédiatement, dans son introduction, que le résultat de 1831 est un cas particulier de son second résultat, autrement dit vérifie le résultat de 1835 dans le cas particulier du principe des forces vives : en effet, les seconds termes de correction (la « force de Coriolis Fc ») étant perpendiculaires aux vitesses relatives, le cosinus Fc dsr est nul ; seuls subsistent, dans le membre de droite du principe des forces vives, les premiers termes de correction, ceux du premier mémoire.
C’est dans cette disparition de ces forces centrifuges composées que consiste le théorème que j’ai présenté à l’Académie des Sciences, en 1831. Il devient maintenant un cas particulier de l’énoncé plus général sur l’introduction des ces forces centrifuges composées.
Analyse du résultat et comparaison avec les notations modernes
La démonstration de Coriolis est largement engagée dans le mémoire de 1831. Il se sert d’un résultat intermédiaire du premier mémoire (p. 275) pour aboutir très vite au résultat de son second mémoire (p.146), en donnant l’équation du mouvement comme suit :
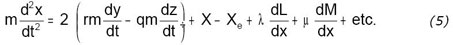
Analysons les différents termes de cette équation du mouvement, qui est une équation vectorielle en x, y, z (nous n’avons écrit que l’équation en x) : - Le terme de gauche de l’égalité représente mγ, γ étant l’accélération dans le repère mobile. - Le deuxième terme de droite (X) représente les forces appliquées, mesurées dans le repère mobile. - Le troisième terme de droite (Xe) représente le terme correctif du premier mémoire, tel que défini par Coriolis (en fait l’opposé des « forces d’entraînement »). - Enfin, le premier terme de droite représente l’opposé de la « force centrifuge composée », dont Coriolis donne les trois composantes sur les axes mobiles :
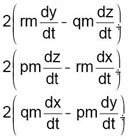
On reconnaît là l’expression précise des coordonnées de la force de Coriolis, force qu’on écrit en notations modernes :
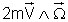
(produit vectoriel), le vecteur
V étant le vecteur vitesse dans le repère mobile, de coordonnées (dx/dt, dy/dt, dz/dt), le vecteur Ω étant la vitesse angulaire de rotation des « plans mobiles », de coordonnées (p, q, r).
Notons aussi que l’équation du mouvement [
(5) ci-dessus pour la coordonnée
x, et les deux autres équations non représentées pour les coordonnées
y et
z] constitue une équation vectorielle analogue à la l’équation newtonienne de la dynamique
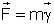
. Coriolis réécrit donc ainsi une équation vectorielle du mouvement relatif, qui n’est plus
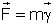
, mais à laquelle on a ajouté deux termes correctifs,
Fe la force d’entraînement, et
Fc la force de Coriolis :
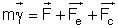
La désignation de « forces centrifuges composées »
Coriolis utilise l’appellation « forces centrifuges composées » (au pluriel) pour désigner le terme correctif Fc. Il est intéressant de voir comment et pourquoi Coriolis introduit ce terme, ce d’autant que la notion de force centrifuge n’est pas utilisée dans le premier mémoire. Coriolis fait l’analogie dès le début du second mémoire.
Ces dernières ont la plus grande analogie avec les forces centrifuges ordinaires. Pour mettre en évidence cette analogie, il suffit de remarquer que la force centrifuge est égale à la quantité de mouvement multipliée par la vitesse angulaire de la tangente à la courbe décrite, et qu’elle est dirigée perpendiculairement à la vitesse et dans le plan osculateur, c’est à dire perpendiculairement aussi à l’axe de rotation de la tangente. Ainsi, pour passer de ces forces centrifuges ordinaires aux secondes forces dont les doubles entrent dans l’énoncé précédent, on n’a qu’à remplacer la vitesse angulaire de la tangente par celle des plans mobiles, et substituer à la direction de l’axe de rotation de cette tangente, la direction de l’axe de rotation de ces mêmes plans mobiles.
Si l’on essaie de traduire cette analogie en termes modernes (et bien que maintenant cette analogie entre force centrifuge et force centrifuge composée ait été complètement abandonnée dans la présentation et l’enseignement de la force de Coriolis), on peut poser la comparaison suivante : -
Force centrifuge simple : elle a une valeur scalaire
mVω (quantité de mouvement
mV multipliée par vitesse angulaire de la tangente ω) ; elle a une direction perpendiculaire à la vitesse et « à l’axe de rotation de la tangente
(5) ». -
Force centrifuge composée (
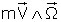
) : elle a une valeur scalaire mVΩ (quantité de mouvement
mV multipliée par vitesse angulaire des plans mobiles Ω
(6)) ; elle a une direction perpendiculaire à la vitesse et « à l’axe de rotation des plans mobiles ».
C’est ce qui permet à Coriolis d’écrire, à propos des « forces centrifuges composées » :
Ces dernières forces ont la plus grande analogie avec les forces centrifuges ordinaires.
Si l’on peut expliquer ainsi l’analogie avec la force centrifuge, à aucun moment Coriolis n’explique l’utilisation du terme « composées »: on peut penser que la vitesse de rotation Ω est composée – par l’intermédiaire du produit vectoriel – avec la vitesse du mobile V.
On notera au passage que Coriolis définit une notion de force centrifuge composée dont le double intervient dans son résultat, ce qui l’oblige à parler à chaque fois du « double des forces centrifuges composées ». On ne peut manquer de remarquer qu’il s’était élevé auparavant contre l’emploi du terme « forces vives » pour mv², obligeant toujours à parler de la seule quantité physique intéressante, ½mv², comme « la moitié des forces vives ».
On voit donc que, pour passer des forces centrifuges ordinaires aux secondes forces dont les doubles entrent dans les équations du mouvement relatif, il suffit de substituer en même temps, à l’axe de rotation de la tangente, à la vitesse angulaire, et à la quantité de mouvement du point mobile ; l’axe de rotation des plans mobiles, la vitesse angulaire de ces plans, et la quantité de mouvement projeté sur un plan perpendiculaire à cet axe. Ces secondes forces centrifuges (…), on peut les nommer forces centrifuges composées.
L’acception moderne de la force de Coriolis est bien 2mV∧Ω, avec le coefficient 2 ; Coriolis n’a quant à lui pas franchi le pas d’inclure le coefficient 2 dans ce qu’il désigne sous le nom de « forces centrifuges composées ».
@@@@@@@
On notera par ailleurs la différence entre les titres des deux mémoires : le premier ne porte que sur « le principe des forces vives dans les mouvements relatifs des machines » ; le second sur « les équations du mouvement relatif des systèmes de corps ». Le terme « équations du mouvement » prime sur le terme « principe des forces vives », et le généralise ; le terme « mouvement relatif de systèmes de corps » prime sur le terme « mouvements relatifs des machines », et le généralise. La portée du second mémoire est beaucoup plus générale ; comme le pluriel a disparu au profit du singulier, le terme « machines » a disparu ; et, de fait, les applications du second mémoire dépasseront largement le cadre de l’étude des machines : le pendule de Foucault, la météorologie, le géomagnétisme terrestre font intervenir les équations vectorielles du mouvement contenues dans le second mémoire – ce alors que ces applications ne font intervenir ni le principe des forces vives ni une quelconque conservation de l’énergie.
Ampère (1830), force d’entraînement et force de Coriolis
Dans un article (7) précédant ceux de Coriolis, et que celui-ci cite, Ampère met en évidence ces deux forces, mais dans un cas particulier (figure ci-dessous) et sans donner d’interprétation à ces forces.
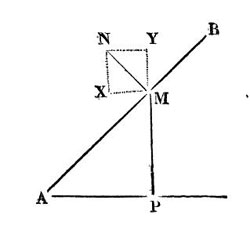
Figure 4 : Un tube AB tourne dans un plan vertical autour d’un point A. Une sphère M est mobile dans le tube (dessin de l’article d’Ampère 1830)
On a 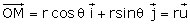 ,
, 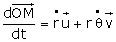 (v étant le vecteur normal - sinθ i + cosθ j), en dérivant à nouveau (sachant que du/dt = θ’v, et dv/dt = - θ’u) :
(v étant le vecteur normal - sinθ i + cosθ j), en dérivant à nouveau (sachant que du/dt = θ’v, et dv/dt = - θ’u) :
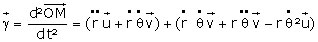
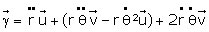 (1)
(1)
Le premier terme en r’’u est l’accélération du mobile dans le repère propre au tube. Le second terme se rapporte au « premier théorème de Coriolis » (1831) –c’est l’accélération d’entraînement. On prend un point N situé en M mais indissolublement lié au tube (r’=0). On a
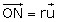 , puis
, puis 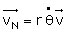 , et
, et 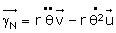
Le troisième terme en (1) correspond à l’accélération de Coriolis (8) appliquée au mobile M dans son repère propre :
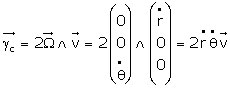
La formule (1) nous amène ainsi au principe des forces vives eu égard au mouvement relatif (identique à Coriolis 1835) :
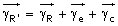
Les accélérations correspondant respectivement à : celle dans le repère lié aux axes fixes (R’) ; celle dans le repère lié aux axes mobiles (R), l’accélération d’entraînement ; enfin l’accélération de Coriolis. L’article d’Ampère contient donc, par anticipation – mais dans un cas très particulier et sans rapport avec la généralité du système telle qu’étudiée par Coriolis – les résultats de ce dernier : ceux sur la force d’entraînement (1831) et ceux sur les forces centrifuges composées (1835).
Le pendule de Foucault (1851) – une application ?
De son vivant, Coriolis a la satisfaction de voir la force centrifuge composée entrer dans les manuels de mécanique rationnelle. Mais il était sans doute loin d’imaginer ce qui allait se passer à peine huit ans après sa mort – une vérification expérimentale étonnante de la force centrifuge composée dans un domaine fondamental sans rapport avec la théorie des machines !
C’est presque un cas d’école en histoire des sciences, où deux résultats liés sont mis en évidence
indépendamment à si peu de temps d’intervalle (une quinzaine d’années). D’autant plus que tout sépare Foucault de Coriolis : Foucault est physicien (
cf. ses expériences sur la vitesse de la lumière
(9)), intéressé par l’astronomie, plutôt expérimental,
self-made man (son premier diplôme est sa thèse de physique en 1853, à trente quatre ans), par ailleurs journaliste scientifique (au
Journal des Débats) et vulgarisateur ; Coriolis est d’une autre génération (vingt-sept ans les séparent), de formation mathématique, plutôt théoricien, brillant polytechnicien ingénieur des Ponts, fort peu porté sur la communication ou la vulgarisation scientifiques
(10).

Figure 5 : L'expérience du pendule de Léon Foucault au Panthéon de Paris, en 1851. Ce pendule est réinstallé au Panthéon en 1995 (© Illustration Conservatoire national des arts et métiers).
D’ailleurs, leurs chemins ne se sont pas croisés – leurs résultats arrivent tout à fait indépendamment. Dugas (op. cit.) enfonce le clou comme suit en concluant son chapitre IV consacré au mouvement relatif :
Force centrifuge composée au sens de Coriolis et pendule de Foucault sont deux conquêtes essentielles de la mécanique, l’une d’origine surtout mathématique, l’autre fruit d’une géniale intuition de physicien, que les traités aujourd’hui classiques réunissent dans une même explication rationnelle, mais qui sont nés séparément : ce n’est pas la lecture de Coriolis qui a inspiré l’expérience de Foucault.
Costabel
(11) s’est aussi penché sur ce sujet. En ce qui concerne l’aspect théorique, il pense que les promoteurs de la mécanique au XVIIIe siècle et au début du XIXe étaient « plus préoccupés de développer toutes les conséquences mathématiques des principes posés pour l’analyse dynamique du mouvement que d’instituer une réflexion sur l’incidence que pouvait avoir dans cette analyse l’attention portée au repère du mouvement » – il souligne dans ce contexte le caractère remarquable de la démarche de Coriolis. En ce qui concerne l’aspect pratique, il indique avec raison que le pendule de Foucault doit plus « au sens aiguisé de l’expérimentation de son auteur plutôt qu’à une claire vision théorique du problème ». Et, paraphrasant Dugas dans un style moins concis mais plus académique, il conclut, à propos de ces deux résultats :
Nées séparément, les traités classiques les réunissent depuis le début du XXe siècle dans une même explication rationnelle, mais si celle-ci a mis longtemps à s’élaborer, c’est précisément à cause de la difficulté à faire ressortir de ces deux conquêtes leur leçon commune et essentielle.
![Figure 6 : Explication graphique du pendule de Foucault par l’effet Coriolis. À gauche, le pendule lancé de midi vers 6h est dévié vers sa droite par la force de Coriolis, il arrive à environ 7h (point rouge) ; disque suivant, on a remplacé le point rouge à 7h par un point noir : lancé de ce point vers 1h, le pendule est dévié vers sa droite par la force de Coriolis et arrive à 2h (point rouge), et ainsi de suite. Sur ces quatre schémas, en eux allers-retours du pendule, le plan d’oscillation de celui-ci a déjà tourné d’un quart de tour (NB : la représentation est ici schématique, la rotation du plan du pendule se fait en fait bien plus lentement, mais suivant ce même schéma). Comme écrit Foucault [1851], « il m’a semblé que la masse du pendule peut être assimilée à un projectile qui dévie vers la droite quand il s’éloigne de l’observateur » (dessins A. Moatti)](/files/u1/Figure-5_22.jpg)
Figure 6 : Explication graphique du pendule de Foucault par l’effet Coriolis. À gauche, le pendule lancé de midi vers 6h est dévié vers sa droite par la force de Coriolis, il arrive à environ 7h (point rouge) ; disque suivant, on a remplacé le point rouge à 7h par un point noir : lancé de ce point vers 1h, le pendule est dévié vers sa droite par la force de Coriolis et arrive à 2h (point rouge), et ainsi de suite. Sur ces quatre schémas, en eux allers-retours du pendule, le plan d’oscillation de celui-ci a déjà tourné d’un quart de tour (NB : la représentation est ici schématique, la rotation du plan du pendule se fait en fait bien plus lentement, mais suivant ce même schéma). Comme écrit Foucault [1851], « il m’a semblé que la masse du pendule peut être assimilée à un projectile qui dévie vers la droite quand il s’éloigne de l’observateur » (dessins A. Moatti)
Reich et la déviation des corps vers l’Est
Mais un autre résultat expérimental, moins connu de nos jours et moins étudié que le pendule de Foucault, avait été découvert auparavant, dans un tout autre contexte. Ferdinand Reich, chimiste et physicien allemand (1799-1882) avait mis en évidence en 1833 la déviation des corps pesants vers l’Est : dans un puits de mine de Freiberg (Saxe), d’une profondeur de 158 m, il avait mesuré en moyenne, après 106 essais, une déviation de 28,3 mm. Cette déviation vers l’est se calcule conformément à la formule vectorielle de Coriolis 2
v∧Ω : elle vaut 2/3ωT
0hcosα, où
ω est la vitesse de rotation de la Terre,
h la hauteur de chute, T
0 le temps de chute (T
0 = √(2h/g)) et
α la latitude du lieu. Poisson lui-même, dans une communication de 1837 à l’Académie des sciences
(12), avait étudié cette déviation des graves, reprenant les expériences de Reich – mais sans faire de lien avec les travaux de Coriolis, datant de deux ans auparavant.
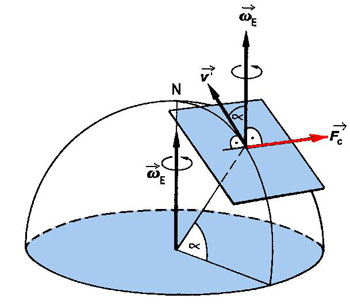
Figure 7 : Représentation de la force de Coriolis, dirigée vers l’Est pour un mobile situé se rapprochant de l’axe de rotation de la Terre (Fc = 2mvwωsinα). Pour être le plus concis possible pour décrire l’effet Coriolis (dans le cas simplifié d’un mobile à la surface terrestre, on a le choix entre deux assertions équivalentes : 1°/ tout mobile se rapprochant de l’axe de rotation terrestre subit une déviation vers l’est, tout mobile s’en éloignant subit une déviation vers l’ouest ; 2°/ tout mobile dans l’hémisphère Nord subit une déviation vers sa droite ; tout mobile dans l’hémisphère Sud subit une déviation vers sa gauche.
Foucault connaissait ce résultat à travers l’article de Poisson qui le mentionne. Or, comme il le note à propos de cet effet de déviation, « le pendule présente l’avantage d’accumuler les effets et de les faire passer du domaine de la théorie dans celui de l’observation
(13) ». Ce sont bien les remarquables conditions d’expérimentation « qui minimisent l’amortissement des lentes oscillations [du pendule] et permettent de prolonger assez longtemps l’observation pour profiter de "l’accumulation des effets" » (Costabel,
op. cit.).
Il est à noter que Foucault cite Poisson, mais pas Coriolis dont il ne connaissait pas les travaux, comme on l’a dit : sa référence théorique est celle de l’effet de déviation de Poisson. Notons aussi que la vision de Foucault se développe dans des domaines sans rapport avec ceux de Coriolis – l’astronomie fondamentale et la mécanique céleste : il veut démontrer le mouvement diurne de la Terre, comme l’indique le titre de son article de 1851 aux Comptes-rendus.
Le débat Bertrand-Babinet-Delaunay sur l’érosion des cours d’eau (1859)
Ce n’est que progressivement que le corps scientifique en arrive à accepter le concept de Coriolis dans toute sa généralité, en le sortant de son champ d’application initial et en faisant abstraction de l’approche démonstrative de Coriolis. Après avoir été redémontré de manière cinématique et extrait de la théorie des machines, le théorème de Coriolis permettra d’expliquer un certain nombre de phénomènes, comme le pendule de Foucault ou l’érosion des cours d’eau.
C’est Charles-Eugène Delaunay (1816-1872) qui, en France, contribuera le plus à faire comprendre la généralité d’application des résultats de Coriolis. En 1856, dans son Traité de mécanique rationnelle, il n’utilise qu’une forme passive sans citer Coriolis :
La seconde force apparente a reçu le nom de force centrifuge composée.
Mais le mouvement est lancé : c’est en utilisant cette force que Delaunay donne une base théorique à l’expérience de Foucault : quatre ans après celle-ci, ceci constitue une de ses premières explications dans un manuel.

Figure 8 : Charles-Eugène Delaunay (1816-1872). Polytechnicien, il est astronome et mathématicien.
@@@@@@@
Quelque temps après, en 1859, un débat assez virulent a lieu entre Joseph Bertrand, Babinet et Delaunay, où ce dernier va évoquer de manière déterminante Coriolis, contre Bertrand
(14).
Jacques Babinet (1794-1872), en ce qui le concerne, parle d’un théorème de Foucault qui « rectifie et complète plusieurs théories admises et professées par des savants du premier ordre » selon lequel un point libre marchant vers l’ouest avec une vitesse acquiert « vers le nord, c'est-à-dire vers la droite », une vitesse relative égale à ωasinλ. Mais c’est surtout Delaunay qui ouvre, en défense de Babinet, une joute avec Bertrand sur l’usure des cours d’eau – qui est une application de la force de Coriolis : Bertrand pensait que seuls les cours d’eau dirigés suivant les méridiens érodaient leur rive droite (et non les cours d’eau dirigés d’est en ouest) ; Delaunay lui montre le contraire.
Pour ce faire, Delaunay fait explicitement référence à Coriolis, tout en mettant l’accent sur la simplification faite de sa démarche :
L’étude de ces mouvements relatifs, la recherche des particularités qu’ils présentent et qui peuvent les faire distinguer des mouvements absolus, est extrêmement délicate. La marche qui me semble la plus convenable pour y arriver, consiste à s’appuyer sur une théorie fort ingénieuse que nous devons à Coriolis, et qui a été tellement simplifiée dans ces dernières années, qu’elle a pu être introduite dans l’enseignement ordinaire de la mécanique rationnelle : je veux parler de la théorie des forces apparentes dans les mouvements relatifs.
Delaunay donne acte à Coriolis du fait qu’il a nommé la force centrifuge composée, qu’il en a « complètement déterminé la valeur, la direction et le sens », et qu’elle
(…) donne lieu à la rotation du plan d’oscillation du pendule, dans l’expérience de M. Foucault ; c’est elle qui produit les mouvements qu’on observe dans le gyroscope du même physicien ; c’est elle enfin qui intervient dans le mouvement des cours d’eau, et qui tend à porter les eaux vers la rive droite de leur lit.
Il donne l’expression simplifiée de la force centrifuge composée 2mωasinα. Le débat se poursuit ensuite entre Delaunay et Bertrand. Ce dernier confirme sa répugnance à utiliser « les forces centrifuges composées de Coriolis » ; c’est précisément parce qu’elles sont « fictives » qu’elles « ne paraissent pas de nature à faire bien comprendre le mécanisme du phénomène ». Mécanisme du phénomène [sic] que Bertrand ne semble pas bien comprendre lui-même, puisqu’il arrive à un résultat erroné sur les cours d’eaux est-ouest : peut-être est-ce, aussi, pour Bertrand, une manière de rejeter sa propre faute sur Coriolis ? Laissons là aussi le mot conclusif, particulièrement pertinent, à Delaunay :
M. Bertrand (…) semble répugner à se servir des forces fictives de Coriolis pour arriver à l’explication des phénomènes réels qui nous manifestent l’existence de la rotation de la terre. Je n’ai pas la prétention de dire que la théorie de Coriolis peut seule en rendre compte. Mais je viens de faire voir que cette théorie conduit très facilement à une idée nette et précise de la manière dont les choses doivent se passer. J’ajoute que de quelque manière qu’on raisonne, en suivant une autre marche, on doit arriver identiquement aux mêmes résultats (…)
Finalement, il semble que ce débat de 1859 à l’Académie des sciences, avec cette prise de position de Delaunay, acte le fait qu’il convient d’attribuer à Coriolis l’idée et la théorisation des forces centrifuges composées
(15). Les arguments effectifs apportant un bémol à la théorie de Coriolis (approche par la dynamique trop compliquée, possibilité de faire les calculs dans un repère inertiel sans forces « fictives ») ont certes été reconnus, mais le corps savant lui attribue l’idée originelle et le cite. À partir de cette date, l’ensemble des applications afférant à la théorie de Coriolis (pendule de Foucault, érosion des cours d’eau) lui est clairement rattaché, même si l’on parle non de
force de Coriolis mais de
forces centrifuges composées. Par exemple, en 1863, dans un mémoire assez scolaire à l’Académie
(16), Finck explique un passage de l’
Astronomie d’Arago sur la déviation des corps graves en s’aidant de « la théorie des mouvements relatifs de Coriolis », et en utilisant ses équations : le pli est pris d’utiliser les résultats de Coriolis dans des domaines qui n’étaient pas les siens.
Cette force entre progressivement, aussi, dans les traités les plus académiques de mécanique rationnelle. À titre d’exemple, quelques décennies plus tard, Paul Appell, dans son Traité de mécanique rationnelle de 1896, mentionne la « force centrifuge composée ». En 1930, le cours de Paul Painlevé à l’École polytechnique mentionne à dix reprises la « force centrifuge composée », en indiquant lors d’une des occurrences « force centrifuge composée ou force de Coriolis ».
La force de Coriolis en météorologie
Anders Persson s’est spécialisé dans l’histoire de la force de Coriolis dans ce domaine, sur ses acceptions et sur la façon de la présenter. Il la relie de manière intéressante à la force centrifuge simple, et par ailleurs est assez radical sur la façon de l’expliquer :
À l’inverse de l’inertie "normale", qui résiste aux changements du mouvement d’un corps, la force inertielle de Coriolis résiste à ces déplacements en essayant, par un mouvement circulaire, de ramener le corps à sa position d’origine. Toute explication mathématique ou intuitive de la force de Coriolis qui entrerait en conflit avec la notion de mouvement inertiel circulaire serait donc incomplète ou fausse.
Figure 9 : formation (dans le sens inverse des aiguilles d’une montre dans l’hémisphère Nord) d’un cyclone autour d’une dépression. Les flèches bleues indiquent la force d’attraction des vents, toujours vers le centre de la dépression (de la haute vers la basse pression) ; les flèches rouges indiquent la déviation de Coriolis, toujours orientées vers la droite de la trajectoire. Lorsque la masse d’air s’approche (un des quatre côtés ici), elle est déviée vers sa droite ; elle est amenée à tourner, subissant encore la force de Coriolis (cette fois-ci centrifuge par rapport au centre de la dépression) opposée à la force bleue, centripète. Les masses d’air tourbillonnent ainsi au lieu d’aller en ligne directe vers le centre de la dépression (schéma WikiCommons, Roland Geider).
L’application de la force de Coriolis au domaine météorologique ne viendra pas de France : nous avons vu que nos physiciens français, de Foucault à Delaunay, ont déjà largement étendu le domaine originel d’application de la force centrifuge composée, et lui ont donné une légitimité en relation avec Coriolis.
Persson date de 1858 (à peu près à la même époque que les débats français entre Bertrand et Delaunay) l’introduction d’une force centrifuge rotatoire en météorologie, sous l’impulsion de William Ferrel (1817-1891) :
If a body is moving in any direction, there is a force arising from the earth’s rotation, which always deflects it to the right in the northern hemisphere, and to the left on the southern.
L’approche de Persson est intéressante. À rebours de la majorité des scientifiques, il pense que l’approche de Coriolis par la dynamique est, en tout cas pour la météorologie, beaucoup plus féconde qu’une approche par la cinématique – il regrette que les travaux de Coriolis n’aient pu être véritablement connus qu’avec la réédition Jacques Gabay de 1990 (!). Selon lui, si les découvertes majeures en ce domaine ont été faites « sans connaissance particulière » des travaux de Coriolis, leur diffusion eût évité à son avis de nombreuses interprétations erronées en météorologie – il rend d’ailleurs en conclusion un bel hommage à Coriolis :
C’est pourquoi il est tout à fait qualifié de prêter ainsi son nom à la force éponyme. Eût-il été avec nous aujourd’hui, sans doute eût-ce été un des rares qui l’eût comprise et enseignée correctement !
Nous n’entrerons pas ici plus avant dans l’histoire de la force de Coriolis en météorologie – d’autant que c’est là un domaine qui était sans doute encore plus étranger aux préoccupations de Coriolis que ne l’était la mécanique céleste de Foucault. De la même manière que nous avons pu situer et dater en France l’attribution aux travaux de Coriolis des effets de la « force centrifuge composée » (l’utilisation de cette désignation étant une claire référence aux travaux de 1835 de Coriolis), il serait intéressant de situer à quelle date ce même concept de force centrifuge composée, ou de force de Coriolis, commence à se répandre hors de France, dans le domaine météorologique notamment. Mais ceci dépasse largement le cadre du présent article.
Octobre 2011

(1) Cet ouvrage faisait suite à l’invention dans les années 1820 par le joueur Mingaud, ancien officier de l’armée napoléonienne, de la « queue à procédé », munie d’une rondelle hémisphérique à son extrémité permettant des effets de type « rétro ». Cette invention, à l’origine du jeu moderne du billard, avait profondément renouvelé le jeu – auparavant la queue de billard était à extrémité carrée, ce qui ne permettait aucun effet.
(2) Histoire de la mécanique, Dunod, 1950 (réédition Jacques Gabay 1996) [voir chap. IV, Mouvement relatif, p. 354-367]
(3) Cette objection était fondée sur le fait que le modèle ne saurait être celui d’une particule unique d’eau montant et descendant sur l’aube, mais d’un filet continu : ainsi « les particules déjà élevées, dont la vitesse est moindre, gênent le mouvement de celles qui sont en dessous et qui ont plus de vitesse » (Coriolis, Calcul de l’effet des machines, 1829, § 105 ; pour discussion de ce point, cf. thèse A.Moatti, 2011, ibid., p.120)
(4) On peut émettre l’hypothèse que le second article, publié en 1835 (soit quatre ans après le premier qui contenait en germe les résultats ultérieurs), était en fait écrit avant 1835 : le JEP mettait en effet un certain temps à publier les articles qu’il recevait. (5) Prenons un point matériel en rotation circulaire uniforme autour d’un axe perpendiculaire au plan : la force centrifuge est orthogonale à la vitesse et à l’axe de rotation.
(6) On suppose ici V et Ω orthogonaux, ce qui ne fait pas intervenir le cosinus de leur angle.
(7) « Dynamique. Solution d’un problème de dynamique, suivie de considérations générales sur le problème des forces centrales », Annales de mathématiques pures et appliquées, 20 (1829-1830), p. 37-58.
(8) Dans les formules de type f = mγ, l’effet Coriolis peut apparaître soit à droite, en tant qu’accélération de Coriolis 2Ω^v, soit être basculé à gauche avec le signe opposé et apparaître comme force de Coriolis 2mv^Ω. Il en est de même de l’accélération d’entraînement : par exemple, un des deux termes de (1), - rθ’²u, peut être basculé de l’autre côté et apparaître en mrθ’²u, désignée comme force d’inertie centrifuge.
(9) Voir Jean-Jacques Samueli, « L’expérience du miroir tournant de Foucault » (1853), BibNum, septembre 2009.
(10) Voir néanmoins Alexandre Moatti « Sur le bruit du tonnerre », analyse BibNum d’un texte de vulgarisation de Coriolis, mai 2009.
(11) Pierre Costabel, Article sur la mécanique in Histoire générale des sciences. La science contemporaine 1. Le XIXe siècle, Dir. René Taton, Quadrige, P.U.F.
(12) « Extrait de la première partie d’un Mémoire sur le mouvement des projectiles dans l’air, en ayant égard à leur rotation et à l’influence du mouvement diurne de la Terre », Comptes-rendus de l’Académie des sciences, 1837, t.5, p.660-668 (séance du 13 novembre 1837).
(13) Léon Foucault, « Démonstration physique du mouvement de la Terre au moyen du pendule », Comptes-rendus de l’Académie des sciences, 1851, p.135-139.
(14) Comptes-Rendus de l’Académie des sciences, séance du 14 novembre 1859, p. 685-693 « Seconde note sur l’influence du mouvement de la Terre », par M. Bertrand ; « Sur le déplacement vers le nord ou vers le sud d’un mobile qui se meut librement dans une direction perpendiculaire au méridien », par M. Babinet ; Observations de M. Delaunay sur la même question ; Réponse de M. Bertrand à M. Delaunay ; puis M. Piobert.
(15) C’est, par exemple, l’avis d’Anders Persson, “How do we understand the Coriolis force?”, Bulletin of the American Meteorological Society, 79, n°7; juillet 1998 (PDF Université de Princeton)
(16) Finck, « Chutes des corps qui tombent d’une grande hauteur », CRAS, 1863 (T.56), p. 957 et ss.





![]()
![]()
![]()

![]()
![]()
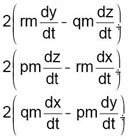
![]()

![]() ,
, ![]() (v étant le vecteur normal - sinθ i + cosθ j), en dérivant à nouveau (sachant que du/dt = θ’v, et dv/dt = - θ’u) :
(v étant le vecteur normal - sinθ i + cosθ j), en dérivant à nouveau (sachant que du/dt = θ’v, et dv/dt = - θ’u) :![]()
![]() (1)
(1)![]() , puis
, puis ![]() , et
, et ![]()
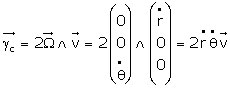
![]()

![Figure 6 : Explication graphique du pendule de Foucault par l’effet Coriolis. À gauche, le pendule lancé de midi vers 6h est dévié vers sa droite par la force de Coriolis, il arrive à environ 7h (point rouge) ; disque suivant, on a remplacé le point rouge à 7h par un point noir : lancé de ce point vers 1h, le pendule est dévié vers sa droite par la force de Coriolis et arrive à 2h (point rouge), et ainsi de suite. Sur ces quatre schémas, en eux allers-retours du pendule, le plan d’oscillation de celui-ci a déjà tourné d’un quart de tour (NB : la représentation est ici schématique, la rotation du plan du pendule se fait en fait bien plus lentement, mais suivant ce même schéma). Comme écrit Foucault [1851], « il m’a semblé que la masse du pendule peut être assimilée à un projectile qui dévie vers la droite quand il s’éloigne de l’observateur » (dessins A. Moatti)](/files/u1/Figure-5_22.jpg)





 Alexandre Moatti, thèse de doctorat d’histoire Paris-I Sorbonne (octobre 2011) : « Gaspard-Gustave de Coriolis (1792-1843) : Un mathématicien, théoricien de la mécanique appliquée » (lien sur blog A. Moatti)
Alexandre Moatti, thèse de doctorat d’histoire Paris-I Sorbonne (octobre 2011) : « Gaspard-Gustave de Coriolis (1792-1843) : Un mathématicien, théoricien de la mécanique appliquée » (lien sur blog A. Moatti)
 TPE sur la force de Coriolis, « l’idée reçue » du sens d’écoulement dans les lavabos (lien)
TPE sur la force de Coriolis, « l’idée reçue » du sens d’écoulement dans les lavabos (lien)








