Thomas Young est considéré comme un génie polymathe, aussi doué pour les langues que pour les sciences. Fondateur de l’optique physiologique et père de la théorie ondulatoire de la lumière, il est également le premier à déchiffrer certains hiéroglyphes égyptiens.

Figure 1 : Thomas Young, 1773-1829 (d’après un portrait peint par Sir Thomas Lawrence, 1769-1830)
Il naît le 13 Juin 1773, à Milverton, dans le Somerset, de l’union de Sarah Davis et de Thomas Young, un marchand d‘habits et un banquier prospère. Peu après sa naissance, il est confié à son grand-père maternel Robert Davis, qui l’élèvera à Minehead, un petit village situé à quelques kilomètres de la maison familiale.
Le jeune Thomas est un élève extraordinairement doué. Il apprend seul dans les livres, épuisant chaque ouvrage en moitié moins de temps que ses précepteurs. En 1782 il intègre une école, à Crompton, qui semble adaptée à sa précocité d’esprit : les élèves y jouissent d’une liberté qui leur permet d’aller à leur propre pas. Pourtant même là, Thomas reste un phénomène. Il en sort en 1786, avec des bases solides en physique newtonienne et en optique. Il parle plus de douze langues, européennes ou orientales, mortes ou vivantes.
Études de médecine
En 1792, il déménage à Londres, et entame des études de médecine à la Hunterian School. Il est accepté en internat au Saint Barthelemy Hospital. Là, en disséquant un œil de bœuf, il découvre le mécanisme de l’accommodation, qu’il explique par une modification de la courbure du cristallin. Il formalise sa théorie dans Observations sur la Vision, qu’il soumet à la Royal Society de Londres le 30 mai 1793. Il n’a pas encore 20 ans.
Young passe l’année 1794 à l’université d’Edinburgh (Écosse), puis se rend en Allemagne. Il obtient un doctorat de sciences physiques à la Georg-August-Universität Göttingen le 30 Avril 1796. Il visite ensuite l’Allemagne, passe par Jena et Berlin, avant de rentrer en Angleterre en février 1797. Cette même année, il hérite de son grand-oncle, le médecin Richard Brocklesby, une maison de Londres, et une rente suffisamment confortable pour lui assurer une indépendance financière.
Thomas s’inscrit à l’Emmanuel College à Cambridge. Il lui faut en effet un diplôme britannique pour intégrer l’Ordre de Médecins et pouvoir exercer. Mais il pense en savoir désormais assez sur le sujet et ne suit pas les cours du cursus. Au contraire, hanté par ses lectures de jeunesse et surtout par des discussions qu’il a eues sur le continent, il se plonge dans l’étude de la physique et des mathématiques. Il acquiert très vite la réputation d’un esprit brillant mais peu sociable, plus intéressé par un calcul difficile ou un instrument ingénieux que par la vie du College.
En 1799, fraîchement diplômé, il s’installe à Londres. Cependant le médecin Young, malgré son talent et son dévouement, a peu de succès. Il lui manque la rondeur des manières, le tact et l’attention au malade que les patients recherchent… Mais c’est en exerçant son art et en s’interrogeant sur le fonctionnement de l’œil et de l’oreille qu’il ouvre ses réflexions à des considérations plus générales et fait le lien entre son et lumière.
Premiers travaux scientifiques
Young publie très vite ses premiers travaux, mais anonymement pour protéger sa crédibilité de médecin, peu compatible avec la réputation sulfureuse qu’ont encore les scientifiques. Il soumet ainsi une série de communications à la Royal Society de Londres :
Son et lumière en janvier 1800, puis Le mécanisme de l’œil en novembre, et
Sur la théorie de la lumière et des couleurs en 1801. Les avancées sont gigantesques : Thomas Young analyse l’astigmatisme pour la première fois, et pose les bases de la vision tricolore – une étude qui sera reprise et complétée par la suite par Hermann von Helmholtz (1821-1894), et vérifiée expérimentalement en 1956 par Gunnar Svaetichin
(1).
Mais ceci n’est que le premier niveau de lecture. Le vent de la révolution que souffle Young mène ailleurs, vers des notions plus souterraines, et plus fondamentales.
@@@@@@@
Plaçons d’abord le décor. Depuis l’Antiquité, la lumière et la vision sont restées pour l’essentiel un mystère. La question de la formation des images sur l’œil a tourmenté des esprits aussi prodigieux que Pythagore, Euclide, Épicure, Aristote… Deux écoles se sont opposées pendant des siècles, jusqu’au Kitab fi’l Manazir du savant persan Ibn al-Haytham qui établit en 1020 que la vision est due à des rayons de lumière émis par les objets vers l’œil.
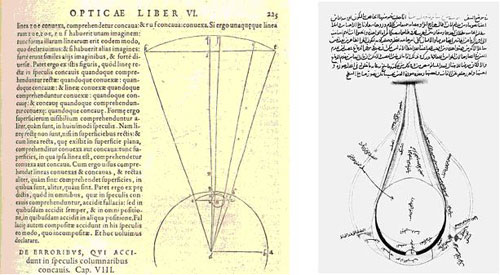
Figure 2 : (à g.) Une figure de l’ouvrage d’Ibn al-Haytham, latinisé en Alhazen (Bassorah v. 965 – Le Caire 1039). Il écrivit son Traité d’Optique de 1015 à 1021.Une traduction latine nous en est parvenue (Opticae thesaurus), traduite par F. Risner en 1572 (disponible en ligne sur la bibliothèque numérique de l’université de Strasbourg –SICD) ; (à dr.) Une figure extraite de l’ouvrage d’Al-Farisi (1267-1320), qui décrit l’anatomie de l’œil d’après les recherches d’Ibn Al-Haytham.
En 1604, dans son Astronomia pars Optica, Johannes Kepler décrit de façon méthodique la formation des images sur la rétine à l’aide de ces rayons, qu’il assume extérieurs et indépendants de l’œil. A la fin du XVIIE siècle, il reste toujours à élucider la nature de ces rayons de lumière (corpuscules ou ondes ?) – et à percer par la même occasion certains phénomènes optiques encore inexpliqués : la réflexion, la réfraction, la dispersion des couleurs par un prisme, et la diffraction.
Christiaan Huygens (1629–1695) propose une approche ondulatoire en 1678, qui s’avère particulièrement commode pour retrouver les lois de Descartes-Snell (réflexion et réfraction). Elle porte aussi en germe une explication du phénomène de diffraction. Mais son formalisme est trop peu développé pour convaincre, et Huygens est incapable d’établir des résultats formels.
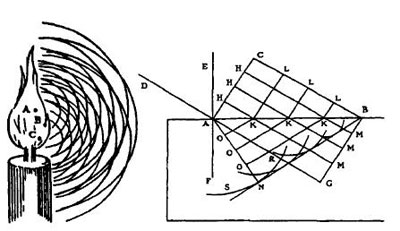
Figure 3 : Décomposition en ondelettes par Ch. Huygens, in Traité de la Lumière paru en 1690.
Puis vient Isaac Newton (1643-1727), avec toute la puissance conceptuelle et la pertinence expérimentale qui imposeront ses théories physiques en Angleterre et partout en Europe. Comme Huygens, il est d’abord tenté par la théorie ondulatoire, mais lui non plus n’arrive pas à un formalisme satisfaisant. Surtout il se heurte au manque d’un outil mathématique adapté. En 1704, après plusieurs années d’un travail minutieux, il tranche la question dans son imposant Opticks. A quelques détails près, la démonstration est magistrale : la théorie corpusculaire explique pratiquement tous les phénomènes optiques en souffrance. Certes le mécanisme des « accès
(2) » qu’il introduit pour modéliser le phénomène d’interférences, est un peu trop complexe. D’ailleurs il peine à traiter la diffraction… Mais cela doit suffire : la lumière est désormais pour tous, presque tous, faite de corpuscules.
Chapitre pratiquement clos, donc.
Au moins pendant le siècle à venir, le temps que l’influence de Newton faiblisse, au moins un peu, et qu’un ingénu, mais pas trop, s’enhardisse à mettre sa théorie en question.
Théorie ondulatoire de la lumière
Dans la communication Son et Lumière qu’il présente à la Royal Society le 16 Janvier 1800, Thomas Young pointe les insuffisances du système newtonien, dont certaines ont déjà été relevées par d’autres, sur le continent, comme Leonhard Euler (1707-1783). Ces « détails » font plus que semer le doute ; pour Young, ils mettent en cause la pertinence de la théorie corpusculaire. Il aboutit ainsi à la nécessité d’une théorie ondulatoire de la lumière, qui se propage par des vibrations de l’éther, et il associe les couleurs aux fréquences de ces vibrations. Près de deux ans plus tard, il récidive et insiste : son mémoire Sur la théorie de la lumière et des couleurs du 12 Novembre 1801 est présenté comme une confrontation, point à point, de ses vues et de celles de Newton sur un certain nombre de concepts. Il réaffirme avec force sa conviction qu’une théorie ondulatoire est juste et suffisante.
Le point d’orgue de la démonstration est incontestablement formulé dans la Proposition VIII, par le principe d’interférence (p. 34 du texte BibNum) :

ce que l’on peut traduire par : « lorsque deux ondulations issues de sources différentes coïncident en direction parfaitement ou de manière très rapprochée, leur effet commun est une combinaison des mouvements de chacune ».
C’est un principe qu’il a déjà appliqué aux harmoniques sonores lors de sa communication Son et Lumière, et qu’il explicite ainsi : si deux ondulations de même fréquence coïncident exactement, le mouvement résultant est le plus intense ; si elles présentent un écart d’une demi-ondulation, le mouvement résultant est le plus faible, voire nul.
La formulation de Young est complexe (il la simplifiera plus tard), mais c’est la première fois dans l’histoire qu’un modèle lève ainsi le voile sur les mécanismes de diffraction et d’interférences.
Il utilise immédiatement cette Proposition VIII pour expliciter un certain nombre de phénomènes, tel que les anneaux colorés de Newton (l’irisation des lames minces sur les niveaux d’égale épaisseur).

Figure 4 :
Irisation de la lumière par une lame mince (expérience de Newton). Newton a laissé son nom à ce phénomène découvert par R. Hooke : en plaquant une lentille convexe L sur une lame plane P, on crée des zones d’air de différentes épaisseurs. S’il est éclairé en lumière blanche, ce système génère des anneaux colorés (observables en A), que Newton explique péniblement à l’aide du mécanisme des « accès » (cf. note 2 ci-dessus). (image S. Bourdreux,
site “La Physique au temps de Sigaud de Lafond”) ;
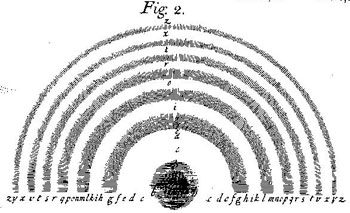
Figure 4bis, ci-dessous :
schéma des « anneaux irisés », extrait de Opticks, d’Isaac Newton (Book II, Part I, Plate I, Edition 1704)
L’argumentaire est étonnamment convaincant. Il l’affine encore lors d’une communication le 1er Juillet 1802, Rapport sur certains cas de production de couleurs, et déduit une Loi Générale qui dit en substance :
La lumière émise par une source qui atteint l’œil par deux chemins différents, présente un maximum d’intensité si les longueurs des chemins sont séparées d’une distance égale à un multiple quelconque d’une certaine longueur ; et un minimum s’il s’agit d’un multiple impair de la moitié de cette longueur ; enfin, cette longueur dépend de la couleur de la lumière.
C’est simple, clairement articulé, complet. Et cela introduit, par la même occasion, la notion de longueur d’onde.
Pourtant Young ne suscite qu’un intérêt modéré. Outre qu’il se dresse comme le monument Newton, la raison en est probablement que sa démarche et ses conclusions restent qualitatives : Young ne les appuie sur aucun développement mathématique, aucun formalisme concret.
La définition d’une théorie physique par Young
En premier paragraphe du texte BibNum, apparaît sous la plume de Young ce qui peut être considéré comme la magistrale définition d’une théorie physique :

Ce que l’on pourrait traduire ainsi : Certes la proposition d’hypothèses, plausibles mais indépendantes de toute observation expérimentale, ne saurait être que de peu d’utilité dans la progression de la connaissance de la nature. Cependant, la découverte de principes uniformes et simples, grâce auxquels un grand nombre de phénomènes en apparence hétérogènes sont ramenés à des lois universelles et cohérentes, doit toujours être regardée comme étant d’une importance considérable pour l’amélioration du raisonnement humain.
Malgré cette position de principe introductive, Young est conscient de la faiblesse de sa démarche, qu’il décide d’étayer par des démonstrations expérimentales. C’est l’objet du fameux mémoire Expériences et calculs relatifs à l’optique physique qu’il présente à la Royal Society le 24 Novembre 1803 et dans lequel il propose le terme d’interférences pour traiter l’interaction des ondulations lumineuses – un terme qui sera repris plus tard par Arago en France pour les travaux de Fresnel.
C’est également dans ce mémoire que Young décrit l’expérience des fentes qui porte aujourd’hui son nom : il montre qu’il est nécessaire de faire intervenir deux ondes issues d’une même source pour observer des franges d’interférences ; en en masquant l’une quelconque des deux, on fait disparaître les franges.

Figure 5 : Expérience des « fentes de Young ». L’onde provenant d’une source en haut, coupée sur la figure (image Wikipedia, Tatoute), arrive au niveau des deux fentes, et se forme une figure d’interférences, où l’intensité lumineuse reçue est représentée en bas (image Wikipedia, Jordgette).

@@@@@@@
Cette notion étant posée, Young en déduit un mécanisme de diffraction par un bord d’écran. Le point mérite que l’on s’y attarde, puisqu’il symbolise un passage de relais virtuel de Young à Fresnel.
La démarche de Young : du principe d’interférence au mécanisme de diffraction
Même si Young est d’abord connu pour son expérience d’interférences lumineuses à deux fentes (dites « fentes de Young »), on lui doit surtout d’avoir initié un modèle performant du mécanisme de diffraction basé sur les interférences. Voici en substance sa démarche : 1- Il se place dans l’hypothèse ondulatoire, qu’il justifie et valide sur des cas simples. Ainsi, dans sa Proposition III (et figure 1 du texte BibNum), il décrit un schéma de transmission à travers une fente qu’il veut compatible avec la théorie ondulatoire. Pour Young, la lumière que l’on observe dans la zone d’ombre est générée, en « ondulations divergentes de faible intensité », par les bords de la fente.
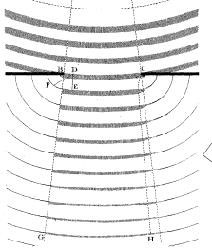
Figure 6 : En haut, extrait de la figure 1 de la planche de figures de Young. Une partie de la lumière transmise, partant d’une source ponctuelle A (non représentée dans l’extrait), se propage en vision directe dans le triangle ABC à travers la fente. L’autre partie, visible dans la zone d’ombre (c'est-à-dire en-dehors du triangle ABC), est générée par les bords d’écran. En bas, figure de diffraction par une fente (image Wikipedia, Jordgette)

2- il développe ensuite le principe d’interférences (Proposition VIII du document BibNum, cf. ci-dessus). 3- il propose un mécanisme de la diffraction basé sur les interférences. Fresnel élargira la portée de ce mécanisme en y intégrant la décomposition en ondelettes de Huygens.
De Young à Fresnel, une nécessaire amélioration
Considérons donc la diffraction par un bord d’écran. Selon Young, elle est le résultat de l’interférence de deux ondes : l’une en vision directe et existant dans la zone éclairée, l’autre diffractée et générée par les discontinuités géométriques du bord d’écran (in
Conférences sur la philosophie naturelle et les arts mécaniques paru en 1807). Lorsque Augustin Fresnel (1788-1827), en 1815, de l’autre côté de la Manche, se penche à son tour, quoiqu’indépendamment, sur les mêmes questions, sa première approche est très similaire à celle de Young. Mais il se rend très vite compte des limites du modèle qui, notamment, prévoit une différence selon que le bord est arrondi ou franc. Or ses expériences sont formelles : ce ne sont pas les effets de bord qui gouvernent la diffraction. Serait-ce plutôt l’ouverture entière ?... Adaptant le concept d’ondelettes introduit par Huygens un siècle plus tôt, Fresnel considère l’ouverture de l’écran comme constituée d’un grand nombre de sources élémentaires, à chacune desquelles il attribue une phase. Au contraire de ses prédécesseurs, il adosse son intuition à un puissant formalisme mathématique. C’est un travail d’orfèvre, qui lui prend quatre années. Au final, expériences et calculs correspondent admirablement, confirmant la justesse du mécanisme qui s’érige très vite en Principe de Huygens-Fresnel
(3).
Le 16 Octobre 1819, dans une lettre qu’il adresse au jeune Français, Thomas Young s’incline et reconnaît la supériorité conceptuelle du modèle de Fresnel. Pour autant, sa propre contribution reste indéniablement pertinente et on lui doit d’avoir jeté les bases d’une théorie qui a révolutionné la conception de la lumière.
Un esprit universel
Mais revenons au parcours de Young, dont il convient de compléter le portrait.
En 1801, la jeune Royal Institution of Great Britain lui propose d’enseigner la philosophie naturelle. Il accepte et crée une cinquantaine de cours qu’il donne à partir de janvier 1802. Le programme est varié (mécanique, hydrodynamique, physique générale, mathématiques), très ambitieux et reflète son éclectisme scientifique. Young choisit une logique de conférences : il s’adresse volontairement à un public averti plutôt qu’à une assemblée d’étudiants. Du coup, son cours peine à convaincre. Il l’abandonne en 1803, mais publie en 1807 un volumineux Conférences sur la philosophie naturelle et les arts mécaniques, où il regroupe ses notes de cours. Signe de sa formidable créativité, Young y introduit le module qui porte son nom et qui caractérise la déformation élastique d'un matériau sous la contrainte qui lui est appliquée.
Son goût et le talent qu’il a développé très jeune pour les langues poussent Young vers l’étude des textes égyptiens anciens. L’aventure commence en juin 1814, quand un ami lui apporte un papyrus écrit en démotique. Très vite Young se prend au jeu et s’attaque à la Pierre de Rosette – dont le texte est répété en grec, démotique et hiéroglyphes –, et qui est exposée au British Museum depuis 1802. Guidé par son intuition et sa méthode mathématiques, il propose une traduction conjecturale astucieuse, qui le mène à la transcription de quelque 220 cartouches – dont une partie sera confirmée par le déchiffrement complet de Champollion (1790-1832) en 1822.
En 1827, Thomas Young est élu Associé étranger de l'Académie des sciences de l'Institut de France. Honneur rare, et l’un des seuls qu’il reçoit de son vivant.
Sa santé se détériore brutalement en 1828, lors d’un voyage à Genève. Il est atteint de difficultés respiratoires en février 1829, et s’éteint le 10 mai de la même année à Londres.
Janvier 2011
L’auteur tient à remercier Alexandre Moatti pour sa relecture attentive et son travail d’iconographie sur le manuscrit.

(1) G.Svaetichin, « Spectral response curves from single cones », Actaphysiol. Scand. 39, Suppl. 134, 17-46.
(2) Pour Newton, un corpuscule de lumière possède périodiquement, le long de sa trajectoire, des « accès » de transmission aisée et des « accès » de réflexion aisée. Il explique ainsi les franges d’interférence, successivement sombres et claires.
(3) Voir texte BibNum d’analyse (auteur J.L. Basdevant) du Premier mémoire sur la diffraction de la lumière de Fresnel (1815).

















 Jean-Louis Basdevant, Le Mémoire de Fresnel sur la diffraction de la lumière (1815), texte BibNum mai 2009.
Jean-Louis Basdevant, Le Mémoire de Fresnel sur la diffraction de la lumière (1815), texte BibNum mai 2009.








