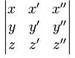Étienne Bézout (1730-1783), qui fut membre de l’Académie royale des Sciences et de l’Académie de Marine, Examinateur des Gardes du Pavillon et de la Marine et des élèves et aspirants au corps royal d’Artillerie ainsi que Censeur royal, est essentiellement connu pour son cours de mathématiques et trois résultats algébriques qui portent son nom. Son cours, best-seller jusqu’à la fin du XIXe siècle et couramment appelé « le Bézout » dans les écrits de Napoléon, Stendhal ou Chateaubriand, fut totalement novateur et s’imposa aussi bien dans les écoles de la Marine et de l’Artillerie, dont Bézout était responsable, que, après la Révolution, dans les Écoles centrales et à l’examen d’entrée de l’École Polytechnique. Ses résultats mathématiques essentiels – le Bézoutien, l’« identité de Bézout » et le « théorème de Bézout » – furent longtemps méconnus ou attribués à d’autres, avant que leur intérêt ne soit démontré et sa paternité reconnue.

Figure 1 : Étienne Bézout (1730-1783). (image université St-Andrews)
Le texte que nous avons choisi de commenter
(1) est l’un de ses deux écrits les plus importants, l’autre étant le traité
Théorie générale des équations algébriques, publié en 1779. C’est aussi le premier de ses travaux de recherche contenant des approches vraiment originales et des résultats fondamentaux.
Dans quel contexte s’inscrit-il ? Bézout, ayant quitté sa ville natale de Nemours vers l’âge de vingt ans pour s’installer à Paris et connaître l’émulation du milieu de la recherche mathématique française, a rapidement fait partie de l’entourage de d’Alembert, dont il devient un disciple. Il collabore à la deuxième édition du Traité de dynamique de ce dernier et, jusqu’en 1760, il travaille sur des sujets de prédilection de l’encyclopédiste, la mécanique et le calcul intégral. Á partir de 1760, sa vie privée (il se marie et devient père en 1761) et professionnelle (il accompagne les académiciens Camus et Nollet dans les écoles du Génie et de l’Artillerie pour faire passer les examens et donner des cours de physique expérimentale) l’éloignent de d’Alembert. Cet éloignement, sans doute en partie voulu aussi, lui permet, en mathématiques, de suivre son penchant pour l’algèbre, déjà fortement sensible dans son approche du calcul intégral. Il va d’abord s’intéresser à la résolution algébrique des équations de degré quelconque et publier un mémoire sur ce sujet en 1762. Les méthodes utilisées en ce domaine sont basées sur l’élimination des inconnues et elles amènent Bézout à s’intéresser plus spécialement à cette partie de l’algèbre, comme il l’écrit dans l’introduction du texte que nous allons étudier :
Les recherches [sur l'élimination] dont je vais exposer les résultats dans ce mémoire, doivent naissance à celles dont je continue de m'occuper sur la résolution algébrique des équations
(2). Quelque route qu'on prenne pour résoudre ce dernier problème, on aura toujours à éliminer plusieurs inconnues [...] c'est donc préparer les voies que de travailler à perfectionner les méthodes d'élimination ; & pour y parvenir, le problème qu'on doit se proposer est, ce me semble, de déterminer à quel degré doit monter l'équation résultante de l'élimination [p. 288]
Mais Bézout a compris l’intérêt du sujet et entrevoit d’ailleurs l’insolubilité des équations de degré supérieur ou égal à 5 par des méthodes algébriques :
Si les méthodes d'élimination n'avoient d'autre utilité que leur application à la résolution algébrique des équations, je me serais contenté de ce qui peut avoir rapport à ce dernier objet […] mais ces méthodes ont une application beaucoup plus étendue […] En effet, si on a des méthodes pour résoudre, par approximation […] lorsqu'on n'a qu'une seule équation, on n'en a pas de même […] lorsque les relations des inconnues restent dispersées dans plusieurs équations ; ainsi
quand même on serait condamné pour toujours à résoudre par approximation (3), les méthodes d'élimination n'en seraient pas moins indispensables [p. 288].
Donc, dans le mémoire « Recherches sur le degré des équations résultantes de l'évanouissement des inconnues et sur les moyens qu'il convient d'employer pour trouver ces équations », qu’il présente à l’Académie des sciences en 1764
(4) et que nous allons étudier, Bézout fait le point de ses travaux et de ses résultats sur le sujet de l’élimination, comme un récapitulatif avant de se consacrer à sa nouvelle charge d’Examinateur des écoles de la Marine. Cette charge, il en entrevoit la lourdeur puisqu’elle va l’obliger à de nombreux mois de déplacements dans les ports et à l’écriture d’un cours complet de mathématiques. Son amertume d’être détourné de ses recherches apparaît dans le texte à propos de certains résultats qu’il sait pouvoir être améliorés :
Au reste, je crois ces méthodes encore très susceptibles de perfection [...] c'est un travail auquel j'invite ceux qui seront assez heureux pour avoir plus de temps à dépenser que moi [p. 329]

Figure 2 :
Le socle de la statue de Bézout à Nemours. On lit « Théorie générale des équations algébriques ». (photo Alain Juhel, site
Mathouriste)
Le contexte mathématique
Le problème général de l’élimination peut s’énoncer ainsi : Un certain nombre d'inconnues et de relations polynomiales entre ces inconnues étant donné, y a-t-il des valeurs de ces inconnues qui vérifient toutes ces relations ? Et dans le cas d’une réponse positive, quelles sont-elles ? Pour résoudre ce problème, on cherche à déduire des relations polynomiales données, une équation dans laquelle ne subsiste plus, au maximum, qu'une seule inconnue. On dit alors que l'on a « éliminé » les autres. Cette équation donnera une condition d'existence, d'où l'on pourra tirer éventuellement les valeurs de l'inconnue restante qui, une fois calculées, permettront de trouver celles des autres.
Il s’agit de trouver la « condition d’existence » permettant d’éliminer x dans le système suivant :
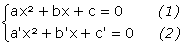
Notations préliminaires On introduit la notion moderne de déterminants sur la matrice
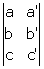
Le premier déterminant est 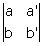 , appelons-le ΔC = ab’ – ba’, et par permutation les deux autres déterminants ΔA = bc’ – cb’ et ΔB = ca’ – ac’.
, appelons-le ΔC = ab’ – ba’, et par permutation les deux autres déterminants ΔA = bc’ – cb’ et ΔB = ca’ – ac’.
Méthode d’élimination 1 On élimine les termes en x² en multipliant (1) par a’ et (2) par a. On obtient : xΔC = ΔB. On reporte cette « valeur » de x dans le système :
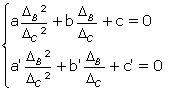
De nouveau, multipliant la première par b’ et la deuxième par b et en retranchant, on obtient : ΔB²= ΔA ΔC, ce qui est la condition d’existence cherchée.
Méthode d’élimination 2 Même première étape. On obtient : xΔC = ΔB. En anticipant sur la méthode de Bezout ci-après, on trouve une autre façon de symétriser le système afin d’éliminer le second degré : on multiplie (1) par a’x + b’ et (2) par ax + b. Le système devient :
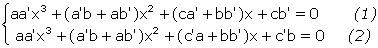
ce qui donne par soustraction xΔB = ΔA, et amène par élimination de x à la même condition ΔB²= ΔA ΔC.
Nota La condition d'existence ΔB²= ΔA ΔC , ou (ab'-ba')(c'b-b'c)=(a'c-ac')², est une relation entre coefficients réels, si x est la seule inconnue. Mais a, b, c, a', b', c', peuvent aussi être des polynômes réels en y, et la relation devient alors une équation en y – ce qu’on appelle la résultante du système –, dont la résolution permet d'avoir les x correspondants.
Dans son mémoire, Bézout commence par faire l'historique en citant trois noms : Newton, Euler et Cramer. Il veut, comme il le dit lui-même,
ne point envelopper dans [son] travail ce qui peut appartenir à d'autres . [p. 289]
Faisons donc le point sur le problème de l'élimination au moment où il écrit son texte, d’une part pour éclairer ses propos et d’autre part pour mieux comprendre l’apport et l’originalité de son travail.
Ce problème s'était essentiellement porté jusque-là sur le cas de deux équations à deux inconnues, correspondant à la recherche des points d’intersection de deux courbes planes. On le résolvait surtout par substitution, ce qui entraînait des facteurs superflus dans l'équation finale.
Newton, avait, dans son Arithmetica universalis en 1707, donné sans explications les formules de la résultante, sans facteurs superflus, pour deux équations de degré n chacune, avec n = 1, 2, 3 ou 4. Par ailleurs, le nombre de points d'intersection de deux courbes planes était pour lui, de toute évidence et sans démonstration, le produit des degrés des deux courbes. Et, de fait, jusque vers le milieu du XVIIIe siècle, il était admis et non démontré, qu'une courbe de degré m et une courbe de degré n, se coupaient en (ou en au plus) m.n points.
Euler est le premier qui ait exprimé le besoin d’une démonstration et qui en ait donné une, même si celle-ci n’est pas exacte. Il la présente en 1748 à l'Académie des Sciences de Berlin, dans un écrit intitulé « Démonstration sur le nombre de points où deux lignes des ordres quelconques peuvent se couper », qui sera publié en 1750. Euler, comme d’Alembert, avait donné en 1746 une démonstration, lacunaire mais sérieuse, du théorème fondamental de l'algèbre, pour un polynôme à une variable à coefficients réels. Énoncé sous une forme actuelle, il dit que, tout polynôme à une variable, de degré n et à coefficients réels, a n racines réelles ou imaginaires. Euler l’étend donc, par analogie, à un polynôme dont les coefficients sont eux-mêmes polynomiaux, mais aucun résultat, à son époque, ne le lui permettait. Sa démonstration qui actuellement pourrait se reprendre en changeant bien des points et en se plaçant dans la clôture algébrique de ℝ (X) – c'est à dire la clôture du corps des fractions rationnelles sur ℝ - est donc inexacte et le trouble lui-même à certains moments. Par ailleurs, s’il « démontre » – avec toutes les restrictions précédentes – que le degré de la résultante est le produit des degrés des deux équations, il ne peut arriver à écrire la résultante elle-même puisqu’il ne peut écrire les racines qu’il suppose exister. Sa méthode n’est donc pas constructive.
Dans les travaux d'Euler sur l'élimination, il faut citer aussi le chapitre XIX du tome 2 de l'ouvrage Introductio in analysin infinitorum (1748) dont Bézout a pu s’inspirer mais en améliorant la méthode et en en changeant les buts, nous y reviendrons, et un deuxième mémoire « Nouvelle méthode d'éliminer les quantités inconnues des équations » qu'il présente la même année que Bézout, en 1764, à l'Académie des sciences de Berlin et qui sera publié en 1766. Euler, dans ce mémoire, ne s’intéresse qu’à deux équations. Après avoir démontré les formules d'élimination que Newton donne sans explications dans son Arithmetica Universalis, il obtient la résultante en écrivant que les deux équations ont une racine commune, ce qui le ramène à une méthode proche de celle de son mémoire de 1748, avec les mêmes défauts.

Figure 3 : Gabriel Cramer (1704-1742), mathématicien suisse (image université St-Andrews).
Cramer, cité lui aussi par Bézout, publie à Genève en 1750 l'Introduction à l'analyse des lignes courbes algébriques, dans lequel, bien qu'il ne semble pas avoir eu connaissance du mémoire d'Euler de 1748 – publié lui aussi en 1750 –, il emploie la même idée (présentée sous une forme différente), pour arriver au même résultat sur les intersections de courbes planes, et il pense être le premier à l'avoir démontré. Sa démonstration comporte donc les mêmes erreurs que celle d’Euler et les mêmes imprécisions ; elle ne conduit pas à l’écriture de la résultante. Un autre point est présent dans l’ouvrage de Cramer, l'élimination dans les systèmes linéaires qui l’amène à ses célèbres formules pour les solutions de ces systèmes. Nous verrons que Bézout, rendant hommage à Cramer, reprendra, à sa façon, la formation du déterminant en lui donnant une très grande importance dans son œuvre.
@@@@@@@
Étienne Bézout résume lui-même son travail dans l'introduction du mémoire :
Je réduis, dans ce mémoire, tout le travail de l'élimination, à quelques degrés que montent les équations, je le réduis, dis-je, à éliminer des inconnues au premier degré [p. 291]
Nous allons expliciter cette idée originale de Bézout et la façon dont il l'emploie. En ramenant la résolution d'un système quelconque à celle d'un système linéaire homogène, il écrit l'équation résultante comme condition d'existence de solutions non nulles à ce système linéaire, c’est-à-dire en annulant le déterminant
(5). On peut dès lors comprendre le cheminement de son ouvrage qui se déroule en plusieurs étapes : - améliorer, selon lui, la formation du déterminant d'un système linéaire, à l’aide d’une nouvelle méthode ; - ramener le calcul de la résultante à celui du déterminant d'un système linéaire homogène ; - appliquer cette idée, d’abord, à la recherche du degré de la résultante de 2 équations à 2 inconnues, puis de n équations à n inconnues, avec
n > 2 ; - puis l’appliquer pour mettre au point une méthode performante de calcul de la résultante, dans le cas de deux équations à deux inconnues (méthode qui a apporté le Bézoutien).
La grande originalité du travail de Bézout sur l'élimination est là : pour lui, la résultante est toujours donnée par le déterminant d'un système linéaire. Cette idée est tout à fait nouvelle et sera son fil conducteur.
Les systèmes linéaires
L'ouvrage de Cramer, Introduction à l'analyse des lignes courbes, est bien sûr connu de Bézout quand il écrit son mémoire de 1764. Voici l’hommage qu’il rend au savant genevois, même si lui-même pense avoir apporté quelques améliorations à l'application de ses formules :
Il n'y a encore que fort peu de temps qu'on a une méthode pour trouver la valeur des inconnues dans les équations du 1er degré d'une manière simple & sans que cette valeur soit compliquée de quelque facteur inutile ; [...] M. Cramer a donné une règle générale pour les exprimer toutes débarrassées de ce facteur : j'aurais pu m'en tenir à cette règle ; mais l'usage m'a fait connaître que quoiqu'elle soit assez simple, quant aux lettres, elle ne l'est pas de même à l'égard des signes lorsqu'on a au-delà d'un certain nombre d'inconnues à calculer ; j'ai donc cru devoir revenir sur cet objet. (p.291)
Bézout explique alors ce qu'il propose, c'est-à-dire ce que nous appellerions une règle de construction du déterminant, qu'il énonce sans la démontrer : au lieu de compter pour chaque terme les « dérangements » et en déduire son signe, comme le proposait Cramer, il indique qu’il « réduit le travail à n'exiger d'autre attention que celle qu'il faut pour écrire des lettres ».
Ce n'est pas la résolution d’un système quelconque qui intéresse Bézout ; mais, un système homogène étant donné, il se propose de trouver la condition pour qu'il ait des solutions non toutes nulles. Il énonce sa règle dans le lemme 1 :
Soient a, b, c, d, &c., les coefficients de ces inconnues dans la première équation. a', b', c', d', &c., les coefficients de ces inconnues dans la seconde équation a'', b'', c'', d'', &c., ceux de la troisième & ainsi de suite. […] Formez les deux permutations ab & ba & écrivez ab – ba ; avec ces deux permutations & la lettre c formez toutes les permutations possibles en observant de changer de signe toutes les fois que c changera de place dans ab & la même chose à l'égard de ba ; vous aurez
abc – acb + cab – bac + bca – cba (6).
Avec ces six permutations et la lettre d, formez toutes les permutations possibles, en observant de changer de signe à chaque fois que d changera de place dans un même terme ; [...] et ainsi de suite jusqu'à ce que vous ayez épuisé tous les coefficients de la première équation. Alors conservez les lettres qui occupent la première place ; donnez à celles qui occupent la seconde, la même marque qu'elles ont dans la seconde équation ; à celles qui occupent la troisième, la même marque qu'elles ont dans la troisième équation, & ainsi de suite ; égalez enfin le tout à zéro et vous aurez l'équation de condition cherchée [p. 292]
Traduit en termes actuels, cet énoncé affirme qu'un système homogène a des solutions non nulles si et seulement si son déterminant est égal à zéro. Bézout met ensuite ces conditions sous la forme :
ab' – a'b = 0,
(ab' – a'b)c'' + (a"b – ab")c' + (a'b" – a"b')c = 0 &c…
Cette nouvelle forme a deux avantages Le premier, de rendre les substitutions à venir, plus commodes ; le deuxième c'est d'offrir une règle encore plus simple pour la formation de ces formules. En effet, il est facile de remarquer 1° que le premier terme de l'une quelconque de ces équations, est formé du premier membre de l'équation précédente, multiplié par la première des lettres qu'elle ne renferme point, cette lettre étant affectée de la marque qui suit immédiatement la plus haute de celles qui entrent dans ce même membre ; 2° Le deuxième terme se forme du premier, en changeant dans celui-ci la plus haute marque en celle qui est immédiatement au–dessous & réciproquement, & de plus en changeant les signes ; 3° Le troisième, se forme du premier, en changeant dans celui-ci la plus haute marque en celle de deux numéros au–dessous & réciproquement, & de plus en changeant les signes ; 4° Le quatrième, se forme du premier, en changeant dans celui-ci la plus haute marque en celle de trois numéros au-dessous & réciproquement, & changeant les signes, & toujours de même pour les suivans. (p. 294). Il ajoute en corollaire : Chacun des termes de l'équation de condition a donc essentiellement le même nombre de facteurs, & ces facteurs sont tellement combinés que jamais, dans un même terme, il ne s'y en rencontre deux qui appartiennent à une même inconnue.
Il faut remarquer que la recherche de Cramer sur les systèmes linéaires, l'amène à calculer ce que Gauss appellera en 1801 « le déterminant », en tant que dénominateur commun des solutions. Celle de Bézout, nous l'avons vu, l'amène au déterminant comme objet dont l’annulation exprime la condition pour qu'un système linéaire homogène ait d'autres solutions que la solution nulle. Il cherche les conditions d'existence de telles solutions pour un système, ce que représente la résultante dans le cas général.
Sa règle d'écriture a deux caractéristiques, elle donne en même temps les termes et leurs signes et elle procède par récurrence sur le nombre d'inconnues et donc de coefficients d'une équation. Il est remarquable que sa règle non démontrée – sans doute obtenue par induction à partir des cas n = 2,3, 4 –, en plus de sa simplicité, donne les mises en forme suivantes que Bézout présente très clairement :
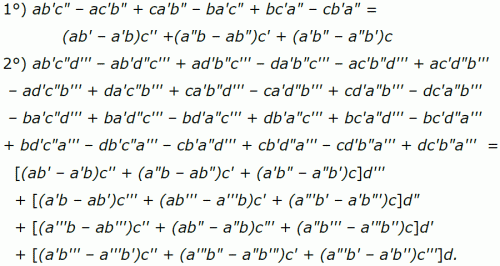
On reconnaît ce que l’on appelle actuellement le développement d'un déterminant suivant les éléments d'une ligne ou d'une colonne, faisant apparaître les déterminants mineurs correspondants.
Calcul d’un déterminant avec ses déterminants mineurs
Le déterminant d’ordre 3 (appellation et notations modernes) se calcule ainsi :
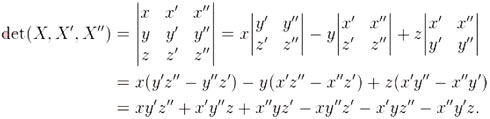
On retrouve la formule de Bézout ci-dessus pour un système de trois équations à trois inconnues. Le calcul d’un déterminant d’ordre 4 se fait par induction de la même manière, faisant intervenir des déterminants d’ordre 3, et aboutissant à la formule de Bézout d’ordre 4. On appelle déterminants mineurs les déterminants intermédiaires intervenant dans le calcul (déterminants d’ordre 2 pour le calcul de celui d’ordre 3, déterminants d’ordre 2 et 3 pour le calcul de celui d’ordre 4).
Application à la recherche du degré de la résultante
Bézout rend hommage, nous l'avons vu, à ses prédécesseurs dans le domaine de l'élimination : Newton, Euler et Cramer. Mais il constate que les résultats de Newton,
lorsqu'on les applique à des degrés un peu élevés conduisent à des équations qui, à la vérité, renferment les racines utiles au problème, mais qui en admettent en même temps d'inutiles, & cela en nombre d'autant plus grand, que le nombre des équations & le degré de chacune deviennent plus élevés [p. 289]
Celles d’Euler et Cramer, performantes pour deux équations, ne le sont plus dès qu'on dépasse ce nombre car
telle est la nature de ces méthodes, qu'elle exige que pour éliminer on compare les équations deux à deux : or [...] ce procédé conduit à des équations beaucoup plus élevées qu'il ne faut |p. 289]
Car ceci est un autre point qui distingue Bézout de ses prédécesseurs. Ils ne se sont intéressés qu’au cas de 2 équations à 2 inconnues, persuadés que le cas de
n équations à
n inconnues se ramenait facilement à celui-là par itération. Bézout, lui, a compris l’inadéquation de ce procédé qui apporte des facteurs superflus – et donc de fausses racines – et complique encore plus les calculs
(7).
Pour remédier à ces défauts, il entreprend, pour éliminer une inconnue, de : - traiter toutes les équations en même temps ; - ramener l'élimination à la résolution d'un système linéaire ; - trouver le degré de la résultante, c'est-à-dire, du polynôme en la ou les inconnue(s) restante(s).
Sa démarche consiste, n équations à n inconnues de degrés quelconques étant données, - à les multiplier chacune par un polynôme à coefficients indéterminés ; - à égaler la somme de tous ces produits à zéro, obtenant ainsi ce qu'il appelle « l'équation-somme » ; - à annuler dans cette équation tous les coefficients de l'inconnue qu'il a choisi d'éliminer, grâce aux indéterminées des différents polynômes multiplicateurs.
Il s'attaque ainsi en même temps à deux problèmes : déterminer les degrés des polynômes multiplicateurs et celui de la résultante – partant du principe qu'il n'y a, les inconnues restantes étant choisies, qu'une résultante à un coefficient multiplicateur près.
Le cas de deux équations à deux inconnues
Bézout commence par calculer le degré de la résultante pour deux équations à deux inconnues et il s'explique :
Non que je prétende décider ma méthode préférable à celle que Mrs. Euler & Cramer ont donnée pour ce cas seulement, mais parce que cette méthode étant uniforme, j'ai cru me rendre plus clair en fortifiant l'analogie par la réunion de ce cas avec les autres, & en même temps parce que dans un travail aussi long que l'est souvent celui de l'élimination, il n'est pas inutile de multiplier les méthodes sur lesquelles les Calculateurs peuvent porter leur choix [p. 291]
À ce stade, une clarification s'impose. La méthode qu'il va utiliser est celle des coefficients indéterminés exposée par Euler en 1748 dans son
Introductio in analysin infinitorum, chapitre XIX, pour trouver la résultante de deux équations à deux inconnues. Mais Euler ne l'a pas utilisée
pour calculer le degré de la résultante, alors que c'est ce que va faire Bézout. Celui-ci a donc raison de dire qu'il n'utilise pas la même méthode qu'Euler et Cramer, pour calculer le degré de la résultante, et non la résultante elle-même. Comme nous allons le voir, cette méthode n'a en effet rien de commun avec les méthodes d'Euler du mémoire « Démonstration sur le nombre des points où deux lignes des ordres quelconques peuvent se couper », et celle de Cramer, fondées toutes les deux sur l’idée qu’une équation à une variable de degré
n a
n racines, quels que soient les coefficients, et sans pouvoir préciser ce que peuvent être ces racines – en langage actuel : sans préciser dans quel corps cela peut être vrai
(8).
Bézout, qui est sans doute conscient – comme eux-mêmes semblent l’avoir été – des lacunes de leurs démonstrations, ne l’exprime pas et ne présente modestement sa méthode que comme une autre façon de calculer le degré de la résultante. Pourtant il va donner ainsi la première démonstration correcte du fait qu'une courbe de degré m et une courbe de degré m’, sans composante commune, se coupent au plus en m.m’ points.
Soient les deux équations :
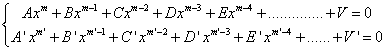
dans lesquelles
A, B, C, D, E, etc.,
A', B', C', D', E', etc., sont des polynômes en la deuxième inconnue
y, de degrés respectifs :
p,
p + 1,
p + 2,
p + 3, etc.
(9), et
p',
p' + 1,
p' + 2,
p' + 3, etc., il multiplie les deux équations respectivement, par les polynômes (
L) et (
L') suivants :
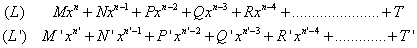
et obtient donc, pour que chaque puissance de x disparaisse dans l'équation-somme, le système ci-dessous (à m + n + 1 équations) :
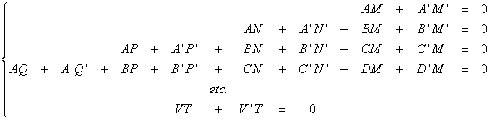
avec les conditions m + n = m' + n', et m + n + 1 = n + 1 + n' +1 (i.e. autant d'équations que d'inconnues). Les valeurs de n et n' sont alors fixées, n=m' – 1 et n'=m – 1, et le déterminant du système doit être nul pour que les inconnues puissent être différentes de 0. Les coefficients d'une même inconnue sont des polynômes dont les degrés sont en progression arithmétique de raison 1.
Il se sert alors du lemme II qu'il a démontré au début de son mémoire :
Soient n suites arithmétiques de raison k et de premiers termes a, b, c, etc. a b c d e etc. a+k b+k c+k d+k e+k etc. a+2k b+2k c+2k d+2k e+2k etc. a+3k b+3k c+3k d+3k e+3k etc. etc. etc. etc. etc. etc. etc. dans quelque ordre qu’on ajoute n termes de cette progression, tels que deux d’entre eux ne soient jamais ni dans la même ligne, ni dans la même colonne, la somme sera toujours
(a+b+c+d+e+….) +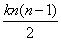 [p. 296].
[p. 296].
Il en est de même s’il y a des lacunes dans le tableau, en sommant comme premiers termes, ceux qui sont ou devraient être en première ligne.
Par application immédiate aux suites arithmétiques des degrés en y des coefficients A, A', B, B', C, C', etc., qui se retrouvent dans le système linéaire en M, M', N, N', P, P', etc.,
p p'
p+1 p'+1 p p'
p+2 p'+2 p+1 p'+1 p p'
p+3 p'+3 p+2 p'+2 p+1 p'+1
etc. etc. etc. etc. etc. etc.
on trouve que le degré de chaque terme du déterminant du système sera au plus égal à
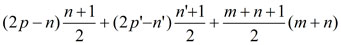
Or, l’annulation de ce déterminant donne l'équation résultante du système de départ, donc soit G le maximum possible du degré de cette résultante :
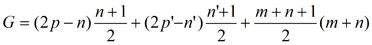
ou encore comme n = m’ – 1 et n’ = m – 1,
G = mm' + mp' + m'p
@@@@@@@
Il faut faire ici quelques remarques importantes.
Deux polynômes Q(x,y) et Q’(x,y) étant donnés d’ordre respectivement m et m’ en x, Bézout a montré que :
- il existe un polynôme non nul L(x,y) d'ordre au plus m' – 1 en x, et un polynôme non nul L'(x,y) d'ordre au plus m – 1 en x, tels que L.P + L'.Q = 0 soit une équation en une seule inconnue y, si et seulement si, le déterminant du système obtenu en égalant à zéro tous les coefficients des différentes puissances de x, dans L.P + L'.Q, est nul ; - la résultante qu'il obtient étant le déterminant d'un système dont les coefficients sont des polynômes en y, Bézout est sûr que c'est, elle-même, un polynôme en y, puisqu'il ne fait que des multiplications et des sommes de polynômes. Euler et Cramer manipulant des fractions et des racines de polynômes, n’ont pas montré ce point de façon convaincante. - si les deux équations de départ sont de degrés respectifs m et m', alors p = p' = 0 (10), et on retrouve, dans la formule donnant G, pour maximum du degré de la résultante le produit des degrés des équations, m.m'.
Donc, Bézout a démontré, sans aucun point obscur ou discutable, que deux courbes planes de degrés respectifs m et m', se coupent au plus en m.m' points. Avant même la généralisation qu'il fera en 1779, pour un nombre quelconque d'équations et d'inconnues, cela justifie déjà que le théorème correspondant porte son nom.
En revanche, Euler a montré que sa résultante – celle du mémoire de 1748 – ne contient aucun facteur superflu et donc ne peut donner aucune racine étrangère au problème, alors que Bézout donne une condition nécessaire pour que le système ait des racines, mais ne démontre pas qu'elle est aussi suffisante, ce qui est pourtant le cas
(11). Peut-être, connaissant déjà le résultat d'Euler et de Cramer, et étant arrivé au même degré, Bézout estimait-il qu'il ne pouvait y avoir de facteur superflu dans sa résultante, d'après le résultat même de ses prédécesseurs.
Ce qui différencie la méthode de Bézout de 1764 de celle d'Euler dans l’Introductio in analysin infinitorum de 1748.
Nous avons dit au paragraphe précédent que la méthode donnée par Bézout pour la résultante est celle d’Euler dans son Introductio in analysin infinitorum. Nous avons vu aussi que, même s'il ne l'explicite pas puisque ce n'est pas son but, Bézout obtient l'équation résultante.
Qu’est-ce donc qui différencie leurs deux méthodes d'obtention de cette équation ?
Elles suivent la même idée de départ : multiplier chacune des équations par un polynôme à coefficients indéterminés, chacun de ces deux polynômes ayant pour degré, par rapport à l’inconnue qui apparaît dans l'écriture, celui de cette inconnue dans l'équation qu'il ne multiplie pas, moins un. À partir de là, Euler identifie les coefficients des deux polynômes produits, ce qui lui permet d'obtenir, m étant le degré en y de la première équation et n celui de la seconde, un système d'équations linéaires de m + n – 1 équations à m + n – 2 inconnues. Mais chez lui, à cause de certains coefficients choisis, le système n'est pas homogène. Il calcule les coefficients indéterminés avec les m + n – 2 premières équations, et, en plaçant ces valeurs dans la dernière équation, il obtient la résultante.
Quels sont les défauts de ce procédé ?
Le système n'étant pas homogène, il n'est pas sûr qu'il y ait des solutions mais Euler ne s'en préoccupe pas. Les solutions sont généralement des fractions rationnelles – c’est d'ailleurs le cas des exemples qu'il donne – et demandent donc dans la mise au même dénominateur pour revenir à des polynômes, des calculs longs et susceptibles d’éliminer des racines à cause des ensembles de définition des fractions, ce dont Euler ne tient pas compte.
Pour sa part, Bézout, après avoir multiplié lui aussi chaque équation (d'ordres respectifs m et m' en x) par un polynôme à coefficients indéterminés (d'ordres respectifs m’ – 1 et m – 1 en x), fait la somme des deux produits et égale à zéro les coefficients de tous les termes. Mais chez lui le système obtenu de m + m' équations à m + m' inconnues, est homogène. Il trouve donc l'équation résultante, comme condition d'existence pour des solutions non toutes nulles qu’il n'a pas besoin de calculer, et ne travaille ainsi que sur des polynômes. On le voit, la même idée de départ est utilisée de façon plus élégante, plus rapide et surtout plus sûre chez Bézout.
En revanche, si l'on examine ces deux procédés d'un point de vue actuel, on constate qu'ils nous conduisent à la même matrice carrée que nous noterons Mr (matrice résultante), et qui, avec les notations de Bézout, est d'ordre m + m' et est égale à :
Mr = 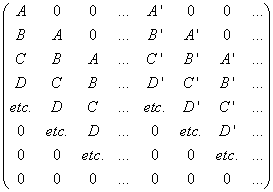
C'est le déterminant de Mr qui est appelé aujourd'hui le résultant du système
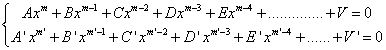
Donc, si on peut attribuer à Euler la première idée qui a conduit finalement à cette matrice résultante, c'est Bézout qui a pensé à utiliser l’annulation de son déterminant comme condition nécessaire à la résolution du système des deux équations. Cette condition est la résultante cherchée.
D'autre part, Euler utilise la méthode des coefficients indéterminés de façon classique, c'est-à-dire en identifiant des termes et en calculant les coefficients pour les remplacer dans une des équations obtenues. Il suppose implicitement que ces coefficients existent, et il cherche leurs valeurs, valeurs dont il a besoin.
Bézout, lui, se sert seulement des coefficients indéterminés comme outils pour construire sa résultante. Il n’a pas besoin de connaître leurs valeurs et d’ailleurs il ne les cherche pas. Il veut uniquement connaître leur condition d'existence, qui est l’équation cherchée. L'utilisation que fait Bézout des coefficients indéterminés n'est donc pas l'utilisation classique, et par la suite, dans son ouvrage de 1779, il continuera à les employer d'une façon très originale et surtout constructive.
Le cas de trois équations à trois inconnues
Si, pour deux équations à deux inconnues, la détermination du degré est donc pleinement réussie – car les conditions permettent de déterminer sans ambiguïté n, n' et G –, il n'en est pas de même quand on augmente les nombres d'équations et d'inconnues.
Voulant éviter de traiter les équations deux par deux, Bézout va, là aussi, essayer de se ramener à un système linéaire, et d’appliquer les principes exposés au début de l’étude du mémoire.
Quand il les applique aux cas de trois équations à trois inconnues, x, y, z, il est obligé, puisqu'il n'envisage que l'élimination d'une inconnue dans son calcul, d'appliquer sa méthode deux fois, c'est à dire qu'il devra obtenir trois polynômes pour éliminer x et obtenir un premier polynôme en y, z ; puis trois autres pour un second polynôme en y, z ; enfin, il devra éliminer y ou z dans les deux équations trouvées.
Bézout commence donc par éliminer x. Les notations sont analogues aux précédentes.
Soit trois équations de degrés respectifs en x, m, m’, m", dans lesquelles les coefficients A, B, C, etc., A', B', C', etc., A", B", etc., sont des polynômes à deux inconnues y et z, telles que les degrés de A, B, C, etc., A', B', C', etc., A", B", C", etc., soient respectivement p, p + 1, p + 2, etc., p', p' + 1, p' + 2, etc., p", p"+1, p"+2, etc. Les polynômes multiplicateurs de chaque équation ont pour degrés respectifs en x, n, n', n".
Bézout suppose, pour que les termes de plus haut degré de l'équation somme puissent s'annuler, que : m + n = m' + n' et m + n ≥ m" + n".
On doit avoir m + n + 1 = n + 1 + n' + 1 + n" + 1, c'est à dire autant d'équations que d'inconnues, donc n' = m – n" – 2 et n = m' – n" – 2.
Par un raisonnement analogue à celui du paragraphe (c) précédent, sur le degré du déterminant du système obtenu en annulant les coefficients de x dans l'équation-somme, il obtient, G étant le degré de ce premier polynôme en y, z :
G=mm' + pm’ + p'm – m – m' + m" – p – p' + p" + 1 – (p + p' – p" + m + m' – m" – n" – 2)n", où n" est indéterminé.
Pour avoir G minimum, il annule la dérivée de G par rapport à n", ce qui donne :
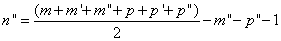
Cette valeur de n" ne pourra pas toujours être prise car on doit avoir : 1) n" entier positif ; 2) le terme entre parenthèses pair ; 3) m + n ≥ m" + n" ; 4) m' – 2 ≥ n", puisqu'on suppose m' ≤ m.
Donc il prend n" =
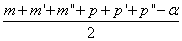
–
m" –
p" – 1, où α est « la plus petite valeur possible ».
Dans ce cas, Bézout ne peut pas trouver de formule qui lui donne de façon certaine le meilleur résultat pour G, puisque le choix de n" reste aléatoire. Il reconnaît le caractère insatisfaisant de son résultat puisqu'il écrit :
Si l'on ne peut parvenir à donner à n, n', n", des valeurs positives, qu'en rendant G plus grand qu'il ne serait par la combinaison des équations deux à deux, on aura recours à ce dernier moyen. (p. 305)
ce qui le ramène à la méthode de ses prédécesseurs.
Bézout traite alors quelques exemples pour montrer les avantages de sa méthode.
Soit p = p' = p" = 0 & m = m' = m", par élimination en prenant les équations deux à deux, l’équation finale a pour degré m4, alors que par sa méthode, il arrive à [(3m² + 1)/4]² si m est impair et [3m²(3m²/4 + 1)]/4 si m est pair. Il donne le tableau suivant, où la première méthode est l’usuelle avant lui (traiter les équations deux par deux), et la deuxième méthode la sienne :
si m = 2 3 4 5 6 7
1re méthode G=16 81 256 625 1296 2401
2e méthode G=12 49 156 361 756 1369
Bézout examine ensuite les cas où le nombre d’équations et d’inconnues est n supérieur ou égal à 4. Il trouve alors, outre la longueur des calculs exigés puisqu'il n'élimine les inconnues que les unes après les autres, que ces calculs ne lui permettent pas d’aboutir à des résultats satisfaisants.
Nouvelle méthode pour trouver la résultante
Il revient ensuite sur le cas de deux équations, mais pour calculer la résultante d'une autre façon, puisqu’il connaît, dorénavant, son degré.
Il envisage d'abord le cas de deux équations à deux inconnues de même degré m en x :
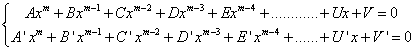
Il multiplie : - la première équation par A' et la deuxième par A, la différence est de degré m – 1 ; - la première équation par A'x + B' et la deuxième par Ax + B, la différence est de degré m – 1 ; - la première équation par A'x² + B'x + C' et la deuxième par Ax² + Bx + C, la différence est de degré m – 1 ; etc.
jusqu’à avoir m équations, chacune de degré m – 1.
Il considère chaque puissance de x comme inconnue et obtient donc un système de m équations à m ‑ 1 inconnues.
Grâce au résultat sur les équations linéaires donné au début, il peut dire que le déterminant du système de m équations à m inconnues, obtenu à partir de celui qu'il a construit, en multipliant la colonne des constantes par une même lettre, doit être égal à zéro pour qu'il y ait des solutions.
Contrairement à la précédente, cette méthode d'obtention de la résultante est entièrement une création de Bézout. On remarque qu'elle n'utilise pas de coefficients indéterminés, mais seulement les coefficients des équations de départ. De plus, le calcul est plus facile que celui du résultant puisque l'ordre du déterminant obtenu est seulement m au lieu de m + m' = 2m.
Si l’on note les deux équations de départ f(x) = 0 et g(x) = 0, et les polynômes multiplicateurs
fm = A, fm-1 = Ax + B, fm-2 = Ax² + Bx + C, etc., fm-i = Axi + Bxi-1 + etc.,
f1 = Axm-1 + Bxm-2 + Cxm-3 + …+ U,
gm = A', gm-1 = A'x + B', gm-2 = A'x² + B'x + C', etc., gm-i = A'xi + B'xi-1 + etc.,
g1 = A'xm-1 + B'xm-2 + C'xm-3 + … + U',
on peut écrire, avec nos notations actuelles, le système sous la forme :
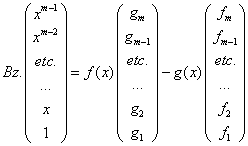
où la matrice Bz est égale à
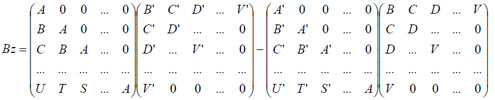
Cette matrice
Bz a été appelée par Sylvester en 1853, le « Bézoutien »
(12) en hommage à son inventeur.
Mutatis mutandis, on peut remarquer qu’elle a une forme analogue à celle d’un déterminant primaire, c'est-à-dire de type
xy’ – x’y.

Figure 4 : Le mathématicien anglais James Joseph Sylvester (1814-1897) (WikiCommons)
L'équation obtenue en écrivant l’annulation du déterminant du Bézoutien, est, d'après ce qui précède, la résultante du système :
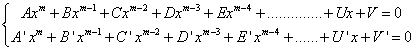
Cette annulation est la condition nécessaire et suffisante pour que ce système ait des solutions.
Bézout, dans son mémoire, ne se demande pas si la condition est suffisante, mais comme le degré du Bézoutien est m² + mp + mp', il ne doit pas considérer comme indispensable de le montrer, sans doute pour les mêmes raisons que pour le résultant.
En fait le système a une solution si et seulement si Dét Bz = 0 ou si et seulement si Dét Mr = 0.
Il envisage maintenant le cas où les deux équations à 2 inconnues sont de degrés différents en x, m et m’, avec m’ < m :
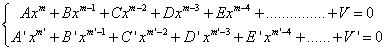
Il essaie le même genre de procédé, mais cela s'avère moins simple.
Bézout multiplie :
- la première par A' et la deuxième par A et fait la différence qui est de degré m – 1 en x ;
- la première par A'x + B' et la deuxième par, la différence est de degré m – 1 en x ;
- la première par
A'x² + B'x + C' et la deuxième par
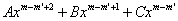
, la différence est de degré
m – 1 en
x ; etc.
jusqu’à avoir m’ équations, chacune de degré m – 1.
Puis il multiplie chacune de ces équations par un coefficient indéterminé, et la deuxième équation de départ par :
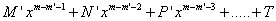
Une fois tous ces produits obtenus, il les ajoute et égale à 0 la somme des coefficients de chaque puissance de x. Par les formules du lemme II précédent, il obtient l’équation de condition.
En fait, dans ce cas, il retombe sur la première méthode puisque ce n'est plus un système d'équations où les inconnues sont des puissances de x qu'il obtient, mais un système où les inconnues sont les coefficients indéterminés introduits
(13). Bézout poursuit en cherchant à simplifier les calculs, mais ne trouve plus un niveau de généralité et de simplicité intéressant.
Il le trouve encore moins lorsqu'il veut passer à des équations à un plus grand nombre d’inconnues. Il est, là encore, comme dans sa première méthode, confronté aux mêmes difficultés de détermination des exposants et à des calculs longs et aléatoires. Bézout en est d'ailleurs très conscient :
Au reste, je crois ces méthodes encore très susceptibles de perfection, & il y a un grand nombre de cas où en suivant les principes sur lesquels elles sont fondées, on parvient à trouver des routes plus faciles. [...] c'est un travail auquel j'invite ceux qui seront assez heureux pour avoir plus de temps à dépenser que moi. [p. 328-329]
Cette dernière remarque, figurant dans la dernière partie du mémoire lu le 29 février 1764, fait allusion à la perspective de nouvelles charges – nous l’avons vu – liées à l’enseignement des Gardes du Pavillon et de la Marine et le conduisant à se rendre à Brest dès mars 1764.
Le théorème de Bézout pour les polynômes à une variable
Le tout dernier paragraphe du mémoire d'Étienne Bézout est le suivant :
On peut encore appliquer à beaucoup d'autres usages cette manière de combiner les équations, particulièrement à la recherche du commun diviseur de plusieurs quantités complexes. En effet, si deux, trois ou un plus grand nombre de quantités complexes ont un diviseur commun composé, par exemple, de x, & de telles autres quantités qu'on voudra, on peut supposer que chacune de ces quantités est zéro, parce qu'elle le deviendrait en effet, si on mettait pour x sa valeur qu'on aurait en égalant ce diviseur à zéro : alors ou le diviseur est d'une, ou de deux ou d'un plus grand nombre de dimensions ; il n'y a donc qu'à chercher quels sont les polynômes indéterminés par lesquels il faudrait multiplier chaque équation pour qu'en égalant à zéro la somme des produits, il n'y restât que les deux derniers termes, si le commun diviseur doit être d'une dimension, ou les trois derniers, s'il doit être de deux dimensions, & ainsi de suite. Je me contente d'indiquer cet usage. [p. 337-338]
Bien que la phrase ne soit pas très claire sur le nombre de variables considérées, car il ne parle que de
x mais ajoute des « quantités complexes
(14) » et « telles autres quantités qu'on voudra », on comprend ce qui suit : - Bézout considère la première méthode qu'il a exposée, celle de la multiplication par des polynômes indéterminés ; - il se place dans le cas où le résultant est égal à zéro, nécessaire pour que les polynômes aient des solutions communes ; - dans ce cas, il essaye d'annuler seulement les coefficients des termes en
x pour des exposants de
x supérieurs à 1, ou 2, etc., ce qui va lui donner
m + n – 2, ou
m + n – 3, etc.. équations à
m + n inconnues, qu'il pourra toujours résoudre en fonction de deux, ou trois, etc., inconnues choisies ; - grâce à cela, il aura avec les deux (ou trois, etc.) derniers coefficients, deux (ou trois, etc.) équations à deux (ou trois, etc.) inconnues ; - suivant la compatibilité de ce dernier système, il pourra conclure s'il a ou non atteint le degré du PGCD.
Bézout énonce donc que le PGCD de plusieurs polynômes est la somme du produit de ces polynômes par des polynômes à coefficients indéterminés. La détermination de ces coefficients donne le PGCD et indique son degré, donc le nombre de racines communes aux polynômes de départ. Mais il se contente « d'indiquer cet usage », sans expliciter davantage.
Quelle est la voie indiquée par Bézout ? Tout d'abord il ne précise pas le nombre d'inconnues qu'il considère, mais il semble se placer dans le cas le plus général de n équations à n inconnues. Or, la méthode des polynômes indéterminés n'a été, on l'a vu, couronnée de succès que pour deux équations à deux inconnues. Il ne peut donc l'appliquer que dans ce cas. Restreignons-nous donc au cas de deux inconnues.
Bézout semble penser que cette méthode va toujours permettre d'éliminer les termes qu'il faudra pour arriver au PGCD. Or, il est bien clair que, deux polynômes P(x, y) et Q(x, y) étant donnés, s'il existe deux polynômes L(x, y) et L'(x, y), tels que L.P + L'.Q = 1, alors P et Q n'ont pas de racine commune et pas de diviseur commun. Mais la réciproque n'est pas vraie. Il suffit de considérer les deux polynômes x et y dans K[x,y] qui n'ont aucun diviseur commun autre que 1 – bien qu'ils aient une racine commune (0,0) –, mais pour lesquels on ne peut trouver aucun L et aucun L' tels que L.x + L'.y = 1.
Le seul cas qui reste à considérer est donc celui d'une seule inconnue, c'est-à-dire celui du système :
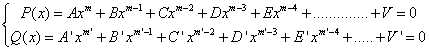
où A, A', B, B', C, C', etc., sont des nombres et non des polynômes.
On sait que dans K[X], avoir une racine commune et avoir un diviseur commun sont deux propriétés équivalentes, contrairement au cas de plusieurs variables. Il est, là aussi, bien clair que, deux polynômes P(x) et Q(x) étant donnés, s'il existe deux polynômes L(x) et L'(x), tels que L.P + L'.Q = 1, alors P et Q n'ont pas de racine commune et pas de diviseur commun. Examinons la réciproque. Bézout a montré qu'il existe un polynôme non nul L(x) de degré au plus m' – 1 et un polynôme non nul L'(x) de degré au plus m – 1, tels que L.P + L'.Q = 0, si et seulement si le Résultant du système est nul. Donc si le résultant de P et Q n'est pas nul, c'est à dire si P et Q n'ont pas de racine commune, cela signifie que le système
Mrx 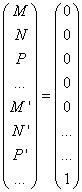 où M, N, &c.., M', N', &c. sont des nombres, a une solution.
où M, N, &c.., M', N', &c. sont des nombres, a une solution.
On obtient donc « l’identité de Bézout
(15) »: Les polynômes
P(x) et
Q(x) sont premiers entre eux, si et seulement si, il existe un couple unique de polynômes
L(x) et
L'(x) tels que
L.P + L'.Q = 1 , avec le degré de (
L) strictement inférieur au degré de
Q, et le degré de
L' strictement inférieur au degré de
P.
Plus généralement, dans K[X], l'affirmation qui termine le mémoire de Bézout est vraie, le PGCD de deux ou plusieurs polynômes peut être trouvé comme somme du produit de ces polynômes par d'autres polynômes, puisque K[X] est un anneau principal. On peut donc énoncer une nouvelle forme, telle qu’elle est aujourd’hui bien connue, de son théorème :
Pour que (Pi)i=1, 2, &c.., n soit une famille d'éléments de K[X] premiers entre eux dans leur ensemble, il faut et il suffit qu'il existe une famille (Ai)i=1, 2, &c., n de polynômes de K[X] telle que 1=Σi=1, 2, &c.., nAi.Pi.
Conclusion sur ce mémoire de 1764
Ce mémoire, présenté à l'Académie royale des sciences le 1er février 1764, est la première œuvre marquante de Bézout, non seulement par ses résultats mais aussi par ses démarches innovantes sur plusieurs points.
Bézout est le premier à concevoir et à énoncer l'idée que la recherche de la résultante d'un système de n équations à n inconnues, peut toujours se ramener à l'étude de systèmes linéaires homogènes.
Il est aussi le premier, grâce à cette optique, à concevoir la résultante comme la condition d'existence de solutions non nulles de ces systèmes, et ramène donc son calcul à celui d'un déterminant.
Cela lui permet d'être le premier à donner explicitement une démonstration satisfaisante du théorème sur le degré de la résultante de deux équations à deux inconnues et donc sur le nombre maximum de points d'intersection de deux courbes planes.
Relié à cette démonstration, Bézout est le premier à envisager le PGCD de deux polynômes comme la somme du produit de ces polynômes par d’autres polynômes
(16). De façon implicite, on l'a vu, cela entraîne l'un des deux théorèmes qui porte son nom, celui sur la condition nécessaire et suffisante pour que des polynômes à une variable soient premiers entre eux.
Enfin ce mémoire contient une façon tout à fait nouvelle de calculer la résultante, la méthode du « Bézoutien ». Il connaît toujours actuellement des développements notoires. L'intérêt de cette matrice – son ordre (qui est la moitié de celui du Résultant), sa symétrie – a réapparu depuis les années 1970, grâce, entre autres, au développement des possibilités de calculs dû à l'informatique. En effet, des articles récents qui paraissent aujourd'hui dans des revues aussi bien d'algèbre linéaire et d'analyse que de physique ou d'informatique, montrent que les propriétés du Bézoutien semblent bien en faire un outil de plus en plus utilisé.
L'importance de ce mémoire ne fut reconnue qu'au XIXe siècle, bien après sa parution, comme toute l’œuvre de Bézout d’ailleurs. Comme l'écrivit H.S. White, président de l’American Mathematical Society, en 1909 :
Yet what a commentary on the futility of the best efforts is found in the fact that both Jacobi and Minding, only 60 years later, published investigations as new whose methods and results were in effect identical with Bézout's ! At least this showed not that his work was unnecessary, but only that he was in advance of his time
(17).
Annexe – Point de vue actuel, à partir de quelques exemples
Pour illustrer le fait que « deux courbes de degré m et n se coupent en mn points » – Bézout dit « en au plus mn points » –, sauf si elles ont une composante commune, voici quelques exemples. Ils montrent le rapport entre la résultante que l’on trouve après élimination d’une inconnue, la figure et le nombre de points d’intersection tels qu’on les considère aujourd’hui.
1/ Cas où tous les points d'intersection sont réels et distincts
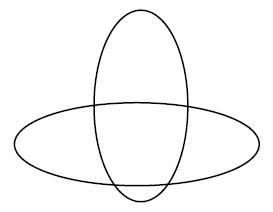
Ces deux ellipses, x² + (y – 0,5)²/4 = 1 (verticale) et x²/4 + y² = 1 (horizontale), ont quatre points d'intersection à coordonnées réelles que l’on « voit ».
Exemple de calcul de résultante
Il s’agit ici d’un « calcul à la main », loin des méthodes générales et puissantes de Bézout, mais qui permettent d’illustrer ses résultats. En multipliant la 2nde équation par 4 et en la retranchant de la première, on obtient :
y= 15y² - 12,25
En élevant cette identité au carré, puis en remplaçant y² par 1 – x²/4, on obtient après quelques calculs la résultante en x :
225 x4 – 326 x2 + 105 = 0
La résultante en x est de degré 4 : 225x4 – 326x2 – 465 = 0 avec 4 racines réelles distinctes, correspondant à des y réels.
2/ Cas d'intersection à l'infini uniquement

Prenons un cas simple de deux droites strictement parallèles y = x et y = x+1. La résultante en x est : 1 = 0, elle n’a donc pas de solution, ni réelle ni imaginaire. Les deux droites étant de degré 1, elles se rencontrent en un point, le point à l'infini. Il est à noter que les deux directions opposées comptent pour un seul point.
3/ Cas ayant à la fois des intersections réelles et d’autres à l’infini :
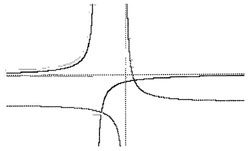
C'est le cas de deux hyperboles xy + x - 1 = 0 et xy + y + 3= 0. La résultante en x est seulement du 2e degré : x² - 3x – 1 = 0. Elle a deux solutions réelles qui correspondent à deux y réels, d'où les deux points d'intersection que l'on « voit ». Les deux équations étant de degré 2, il y a 2x2 = 4 points d’intersection, donc deux points d'intersection à l'infini, celui des asymptotes y = - 1 et y = 0 (à droite comme à gauche), et celui des deux autres x = - 1 et x = 0 (en haut comme en bas). Comme dans le cas 2), les deux directions opposées comptent pour un seul point.
4/ Cas d'une composante commune :
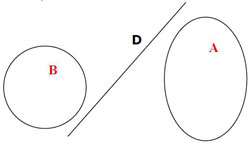
Soient les courbes d'équation :
x3 – y3 + xy2 – yx2 – 5x2 – 5y2 – x + y + 5 = 0
x3/4 – y3 + xy2 – yx2/4 – 5x2/4 – 5y2 – 7x + 7y + 35 = 0
La première est représentée par l'union de la droite D et du cercle B (c’est en effet le produit de x2 + y2 – 1 = 0 par x – y – 5 = 0). La deuxième par l'union de la droite D et de l'ellipse A. La résultante en x est 0 = 0, équation toujours vérifiée : il y a une infinité de points d'intersection réels, ceux de la droite D.
5/ Cas de points multiples :
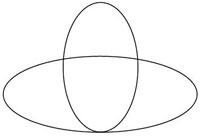
Voici les deux ellipses x2/4 + y2 = 1 (horizontale) et x2 + (y – 1)2/4 = 1 (verticale). leur résultante en x est : 225 x4 – 224 x2 = 0. Elle a quatre solutions dont une racine double (x = 0), qui correspondent à quatre points d'intersection à coordonnées réelles, le point le plus bas de la figure étant un point double (le point 0,-1 ; les deux autres points d’intersection sont x = &plumn;4/15√14, y = 13/15). Cas encore plus parlant, y = 0 et y = xn, ont un seul point d'intersection, l'origine, qui est donc un point multiple d'ordre n.
6/ Cas de solutions dans le plan complexe :
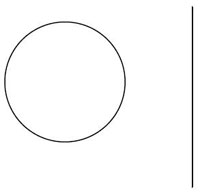
Ici le cercle a pour équation x2 + y2 = 16 et la droite x = 5. La résultante en y est : y2 = –9. Il n’y a donc pas de solutions réelles mais deux solutions complexes qui donnent deux points d'intersection dans le plan complexe, (5, 3i) et (5, –3i).
@@@@@@@
Ces six exemples, très simples, illustrent la différence d'approche du problème entre Bézout et les mathématiciens d'aujourd'hui, et donc une partie du travail qu'accompliront ses successeurs.
Novembre 2013

(1) Texte BibNum (voir référence en note 4 ci-après).
(2) Bézout présentera en 1765, soit un an après le texte qui nous occupe, un mémoire à l’Académie des sciences sur la résolution des équations, problème qu’il n’avait pas abandonné.
(3) Souligné par nous.
(4) Il le lit au cours des séances des 1er, 15, 24 et 29 février 1764 et ce mémoire sera publié dans les Mémoires de l’Académie Royale des Sciences (MARS) de cette année-là.
(5) Bézout n’emploie pas le mot déterminant, ni la notation actuelle.
(6) On accole c à ab en 3e position, puis on le fait remonter en 2e (avec le signe –), puis en 1e (avec le signe +).
(7) La méthode de Newton et d’Euler pour plus de deux équations – Cramer n’aborde pas ce point – est celle que donne d'Alembert en 1756 dans l’article « Évanouir » de l’Encyclopédie : « Quand il y a plus de deux inconnues, par exemple, x, y, z, &c. on réduit d'abord les inconnues à une de moins ; on fait évanouir x ou y, &c. en traitant z & les autres comme une constante ; ensuite on réduit les inconnues restantes à une de moins, & ainsi du reste. Cela n'a aucune difficulté ». Quand on sait que d’Alembert écrivait la même chose en 1781, après avoir pourtant été en 1779 un des deux rapporteurs du traité Théorie générale des équations algébriques de Bézout, on mesure l’incompréhension du travail de ce dernier par son ex-mentor et à quel point leurs rapports s’étaient distendus.
(8) Euler est conscient que « les expressions des racines A, B, C, D, etc., a, b, c, d, etc., sont pour la plupart fort irrationnelles et souvent telles, qu'on ne les peut pas assigner », et qu'il faut montrer que sa résultante est bien un polynôme en x, ce qu’il n’arrive pas à faire contrairement à ce qu’il affirme. Il passe outre en écrivant : « S'il y a dans cette démonstration encore quelque obscurité, cela vient de sa grande généralité ». Cramer, lui, ne fait pas de remarque sur la nature des racines a, b, c, d, etc., mais déplore simplement que ces racines soient inconnues « lorsque l'équation A est d'un degré trop élevé pour que l'Algèbre en puisse donner la solution ».
(9) Pour assurer la généralité de cette construction, Bézout prend bien soin d’expliquer (bas de page 300) qu’ « il faut partir du terme où la somme des exposants de x et y est la plus forte, et retrancher de cette somme l’exposant de x dans le premier terme ». Prenant l’exemple de l’équation a3 x5 y – 2 a4 y2x3 + y8 x – a9 = 0, il remarque que la somme la plus forte est sur le terme , soit 9 ; il retranche de 9 l’exposant de x dans le premier terme, soit 5, ce qui donne p = 9 – 5 = 4. Ainsi, p, p+1, etc. sont-ils des degrés maximaux à chaque fois, le maximum étant atteint au moins une fois : dans cet exemple : pour x5, p = 4 ; pour x2 (terme non présent dans cet exemple) p + 3 = 7 ; pour x, p + 4 =8 (dans ce cas valeur maximale en y effectivement atteinte, par construction).
(10) Si le degré total (degré en x + degré en y) est m, qui est le plus haut degré en x, ceci signifie, de par la construction de Bézout rappelée en note 9, que p = 0 : le terme de plus haut degré en x se confond avec le terme de plus haut degré total.
(11) La démonstration est aujourd’hui aisée, grâce au Résultant (voir page suivante). En effet, soit y0 une racine de la résultante, en prenant pour A, B, etc., A’, B’, etc., leurs valeurs en y0, le système de départ 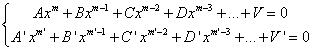 , devient un système à une seule inconnue x. Or le résultant de ce système est nul, d’après le choix de y0, donc il existe un x solution du système, et donc (x, y0), est solution du système de départ.
, devient un système à une seule inconnue x. Or le résultant de ce système est nul, d’après le choix de y0, donc il existe un x solution du système, et donc (x, y0), est solution du système de départ.
(12) Sylvester a appelé Bézoutien la forme quadratique définie par la matrice Bz. Cependant ce nom représente, suivant les auteurs, soit la matrice, soit le déterminant de cette matrice. Il est aussi souvent employé indifféremment dans les deux sens, quand il n'y a pas d'ambiguïté.
(13) C'est en rédigeant, en 1766, la partie « algèbre » de son cours pour la Marine que Bézout trouvera le calcul du Bézoutien dans le cas où m et m' sont différents. Cela nuira longtemps à sa postérité car Jacobi le redécouvrant dans un cours (celui de Bézout), prit ce calcul pour une méthode anonyme et se l’appropria en 1736. Sylvester rétablit Bézout dans ses droits en 1753.
(14) « Une quantité complexe en algèbre, est une quantité comme a + b – c, composée de plusieurs parties a, b, c, jointes ensemble par les signes + et –. » [Encyclopédie, art. « complexe » 1753].
(15) Le théorème analogue dans Z (a et b éléments de Z, sont premiers entre eux si et seulement si, il existe un couple (u, v) dans Z2 tels que au + bv = 1), est souvent appelé de façon impropre, théorème de Bézout, alors qu'il doit être attribué à Bachet de Méziriac (1581-1638), en 1621.
(16) Préfigurant la théorie des idéaux de Dedekind.
(17) White, H. S. « Bezout’s theory of resultants and its influence on geometry », Bulletin of the American Mathematical Society, 15, 1909, p. 332. Bézout a souffert de l’oubli mais aussi du fait qu’ayant publié ses résultats dans son cours, ils ont longtemps été considérés comme des résultats anonymes.



![]()
![]()
![]() , appelons-le ΔC = ab’ – ba’, et par permutation les deux autres déterminants ΔA = bc’ – cb’ et ΔB = ca’ – ac’.
, appelons-le ΔC = ab’ – ba’, et par permutation les deux autres déterminants ΔA = bc’ – cb’ et ΔB = ca’ – ac’.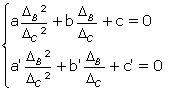
![]()

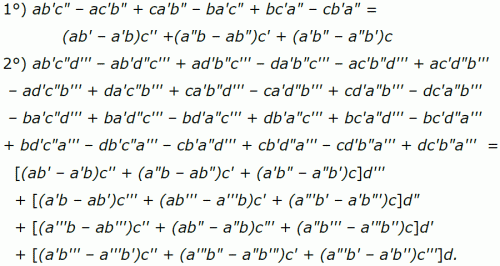
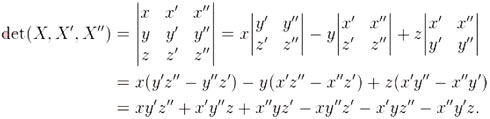
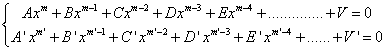
![]()
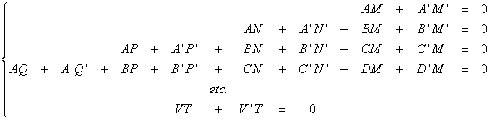
![]() [p. 296].
[p. 296].![]()
![]()
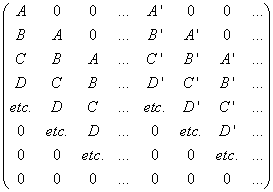
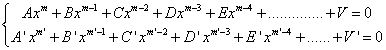
![]()
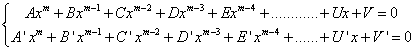
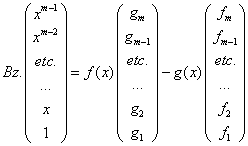
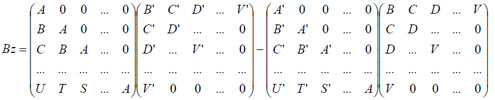

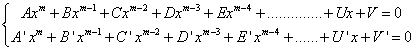
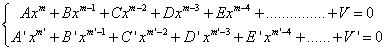
![]()
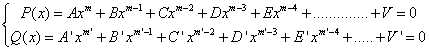
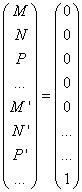 où M, N, &c.., M', N', &c. sont des nombres, a une solution.
où M, N, &c.., M', N', &c. sont des nombres, a une solution.






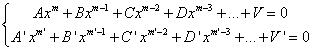 , devient un système à une seule inconnue x. Or le résultant de ce système est nul, d’après le choix de y0, donc il existe un x solution du système, et donc (x, y0), est solution du système de départ.
, devient un système à une seule inconnue x. Or le résultant de ce système est nul, d’après le choix de y0, donc il existe un x solution du système, et donc (x, y0), est solution du système de départ.




 « Bézout futé », blog chou romanesco, novembre 2013 (lien). Des graphiques intéressants d’intersection de courbes algébriques, en prolongement de l’annexe de l’article BibNum.
« Bézout futé », blog chou romanesco, novembre 2013 (lien). Des graphiques intéressants d’intersection de courbes algébriques, en prolongement de l’annexe de l’article BibNum. Newton, I., Arithmetica universalis, Londres, 1707.
Newton, I., Arithmetica universalis, Londres, 1707. Newton, I., The mathematical papers of sir Isaac Newton, éd. par D.T.Whiteside, Cambridge Univ. Press, 7 vol., 1967-1981.
Newton, I., The mathematical papers of sir Isaac Newton, éd. par D.T.Whiteside, Cambridge Univ. Press, 7 vol., 1967-1981. Euler, L., Introductio in analysin infinitorum, Lausanne, 1748, Trad.française par J. B. Labey, 2 vol., Paris, 1796-1797.
Euler, L., Introductio in analysin infinitorum, Lausanne, 1748, Trad.française par J. B. Labey, 2 vol., Paris, 1796-1797. Euler, L., « Démonstration sur le nombre des points où deux lignes des ordres quelconques peuvent se couper », Mémoires de l'Académie des sciences et belles-lettres de Berlin, 4, (1748), Berlin, 1750, p. 234-248 (lien)
Euler, L., « Démonstration sur le nombre des points où deux lignes des ordres quelconques peuvent se couper », Mémoires de l'Académie des sciences et belles-lettres de Berlin, 4, (1748), Berlin, 1750, p. 234-248 (lien) Cramer, G., Introduction à l'analyse des lignes courbes algébriques, Genève, 1750.
Cramer, G., Introduction à l'analyse des lignes courbes algébriques, Genève, 1750. Euler, L., « Nouvelle méthode d'éliminer les quantités inconnues des équations », Mémoires de l'Académie des sciences et belles-lettres, 20, (1764), Berlin,1766, p. 91-104.
Euler, L., « Nouvelle méthode d'éliminer les quantités inconnues des équations », Mémoires de l'Académie des sciences et belles-lettres, 20, (1764), Berlin,1766, p. 91-104. Bézout, E., Cours de mathématiques à l’usage des gardes du Pavillon et de la Marine, t. III, Paris, 1766.
Bézout, E., Cours de mathématiques à l’usage des gardes du Pavillon et de la Marine, t. III, Paris, 1766. Bézout, E., 1779 : Théorie générale des équations algébriques, Paris, 1779.
Bézout, E., 1779 : Théorie générale des équations algébriques, Paris, 1779. Jacobi, C. G. J., « De eliminatione variabilis e duabus aequationibus algebraicis », J. reine angew. Math., 15 ,1836, p. 101-124.
Jacobi, C. G. J., « De eliminatione variabilis e duabus aequationibus algebraicis », J. reine angew. Math., 15 ,1836, p. 101-124. Sylvester, J. J., « On a theory of syzygetic relations of two rational integral functions, comprising an application to the theory of Sturm's functions, and that of the greatest algebraic common measure », Philosophical Transactions, vol. 143, 1853, p. 407-548.
Sylvester, J. J., « On a theory of syzygetic relations of two rational integral functions, comprising an application to the theory of Sturm's functions, and that of the greatest algebraic common measure », Philosophical Transactions, vol. 143, 1853, p. 407-548.