À propos de l'existence des nombres transcendants

  • INFORMATION
  • ACTUALITÉ
  • ANALYSE
  • EN SAVOIR PLUS
  • À TÉLÉCHARGER
Joseph Liouville
À propos de l'existence des nombres transcendants
Auteur : Joseph Liouville (1809-1882)
Auteur de l'analyse : Michel Mendes France - Mathématicien, professeur émérite à l’Université de Bordeaux
Publication :

Comptes-rendus de l'Académie des sciences, séance du lundi 13 mai 1844

Année de publication :

1844

Nombre de Pages :
3
Résumé :

Dans ce texte, Liouville est le premier à mettre en évidence un nombre transcendant (c’est à dire non algébrique) ; il résume cela comme « des classes très étendues de quantités dont la valeur n’est ni rationnelle ni même réductible à des irrationnelles algébriques », c’est à dire « une grande quantité de nombres qui ne sont pas algébriques ».

Source de la numérisation :
n.c.
Tags: 
1844
Académie des Sciences
algèbre
Liouville
Mendes France
nombres transcendants
Mise en ligne :
septembre 2008
Envoyer la référence de la page
La première phrase du mémoire de Liouville du 13 mai 1844 est en elle-même tout un programme : « Des classes très étendues de quantités dont la valeur n’est ni rationnelle ni même réductible à des irrationnelles algébriques ». Autrement dit l’existence en grande quantité de nombres qui ne sont ni irrationnels ni algébriques (solutions d’une équation algébrique) : Liouville est le premier à avoir cette idée ; il explique même comment construire un nombre non algébrique. C’est la découverte des nombres non algébriques, qui seront désignés comme nombres de Liouville avant d’être appelés nombres transcendants. Liouville examine la décomposition en fraction continue d’un nombre x solution d’une équation algébrique. Il démontre simplement que le dénominateur du « quotient incomplet » (développement en fraction continue arrêté à un stade donné) du nombre algébrique x est borné par une formule donnée. Il construit ensuite des nombres dont le développement en fraction continue ne respecte pas cette formule : ils sont donc non algébriques. Par la suite, le mathématicien français Hermite démontra le caractère transcendant de e (1873), et le mathématicien allemand Lindemann celle de π (1882).

 

 

 

(Michel Mendes France, ancien élève de l’École polytechnique, est mathématicien, professeur émérite à l’Université de Bordeaux).

 

 

 

Liouville, le découvreur des nombres transcendants
Michel Mendes France - Mathématicien, professeur émérite à l’Université de Bordeaux
 
 
 
En deux notes de 1844 aux comptes rendus de l’Académie des Sciences, Joseph Liouville établit l’existence des nombres transcendants. Qu’est-ce qu’un nombre transcendant ? Un nombre x est dit algébrique s’il est solution d’une équation polynomiale de type :

Formule 1

où a, b,…., g, h sont des entiers donnés non tous nuls. Ainsi, par exemple, les nombres suivants sont algébriques :

formule 2

Si le polynôme ne peut se factoriser en deux polynômes, n s’appelle le degré du nombre algébrique. Les nombres de degré algébrique 1 correspondent exactement aux nombres rationnels. Les autres nombres algébriques sont dits irrationnels : dans la liste ci-dessus, les degrés respectifs sont 1, 1, 2, 6, 2.

Avant Liouville, on pouvait croire que tous les nombres étaient algébriques. Après lui, on savait qu’il en existait d’autres : un nombre non algébrique est dit transcendant.
@@@@@@@
Liouville donne deux preuves de l’existence de tels nombres ; toutes deux s’appuient sur la théorie des fractions continues pour établir le résultat fondamental suivant :

Si x est un nombre algébrique réel de degré n supérieur ou égal à 2 (donc irrationnel), alors il existe une constante positive non nulle C telle que, pour tout nombre rationnel

p/q, on a :formule 3

Autrement dit, même si l’ensemble des rationnels est dense, un nombre algébrique irrationnel se laisse mal approcher par les rationnels.

L’inégalité de Liouville peut s’établir de façon élémentaire sans faire appel aux fractions continues, que Liouville utilise : c’est pourquoi nous nous écarterons de cette partie de son texte, néanmoins pour aboutir au même résultat. Voici une preuve de cette inégalité. Le théorème des accroissements finis – bien connu de tout étudiant en première année de mathématiques à l’université – affirme que pour toute fonction réelle continue et dérivable f, il existe un nombre t compris entre x et p/q tel que :

formule 4

Si donc x est réel algébrique, il existe un polynôme à coefficients entiers non tous nuls tel que f(x) = 0, et l'égalité précédente implique :

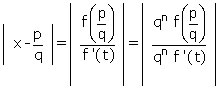
formule 5

Nous allons chercher à minorer cette quantité par une quantité de type A/qn (inégalité de Liouville).

 

 

Démonstration de l’inégalité de Liouville

 

Cherchons d’abord à minorer le numérateur qn f(p/q). Comme le fait remarquer Liouville, cette quantité, qu’il appelle f(p,q), est égale à apn + bpn-1 +…. + hqn : c’est un nombre entier. Liouville avait pris la précaution d'indiquer que le polynôme f avait été « débarrassé de tout facteur commensurable », c’est-à-dire réduit à la forme où il n’admet que des solutions irrationnelles. Cette précaution prise, le numérateur ne peut jamais être nul ; s’agissant d’un nombre entier (positif ou négatif), sa valeur absolue est toujours minorée par 1. Cherchons à présent à majorer la quantité |f’(t)| figurant au dénominateur, en rappelant que t est compris entre p/q et x. On choisit p/q tel que – 1 < x – p/q < 1. Alors, f’ étant une fonction polynomiale bornée sur l’intervalle [x – 1, x + 1], elle prend sur ce segment des valeurs finies, qu’on peut majorer, pour reprendre la notation de Liouville, par une quantité A constante : |f’(t)| < A. En reportant ci-dessus, après avoir minoré le numérateur et majoré le dénominateur (avec C = 1/A), on obtient l’inégalité de Liouville :

 

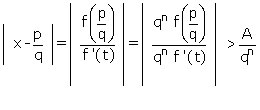
formule 6

@@@@@@@
Une fois établie cette inégalité, Liouville mentionne rapidement en une phrase la façon dont il construit un nombre non algébrique (« Nous citerons en particulier la série… »). Détaillons la deuxième partie de sa « découverte ». Il observe que le nombre

formule 7 (on prend a = 10 dans l’exemple qu’il donne en fin d'article)

est « trop bien approché » par les sommes partielles formule 8, d'où il conclura que y est transcendant.

Détaillons ce calcul.

 

 

La série de Liouville est un nombre transcendant

 

Examinons la quantité formule 9= 0,0000…….01…….. : le premier 1 apparaît à la position (N+1)! après la virgule, et d’autres 1 apparaissent, de plus en plus espacés. On peut donc majorer cette quantité par exemple par le nombre où 2 apparaît à la position (N+1)! après la virgule, suivi de 0 :

formule 10

Pour toute quantité positive non nulle C, cette dernière quantité est majorée par formule 11dès lors que N est assez grand pour que formule 12(rappel : qN = 10N!). Donc, pour tout n donné, pour toute quantité positive non nulle C, on a pu trouver une infinité de p/q (à savoir les pN/qN pour N assez grand) tels que formule13 Ceci contredit l’inégalité de Liouville et permet de conclure que y est transcendant. On notera au passage qu’un nombre algébrique irrationnel ne peut être « approché de trop prés » par des nombres rationnels (inégalité de Liouville), en revanche certains nombres transcendants peuvent être ainsi « approchés ».

@@@@@@@
Bien des années plus tard, Georg Cantor montre que « presque tous » les nombres sont transcendants, ce qui est évidemment assez surprenant puisqu’on est bien plus familiarisé avec les racines d’équation polynomiales ! En 1873, Charles Hermite établit la transcendance de e , puis suivant des idées assez proches, Ferdinand Lindemann montre en 1882 que π est transcendant. Ce dernier résultat règle une fois pour toutes le vieux problème de la quadrature du cercle ! On se convaincra en effet qu’à partir de la longueur unité, toute construction avec la règle et le compas ne peut donner que des nombres algébriques (d’ailleurs de degré 1,2,4,8,16, etc. – théorème de Wantzel). Si la quadrature du cercle était possible, π serait algébrique, ce qui est absurde.
Depuis, bien des familles de nombres transcendants ont été mises à jour. Si a ≠ 0 ou 1, et si b est irrationnel, tous deux algébriques, alors ab est transcendant (A.O. Gelfond et Th. Schneider, 1934). En particulier, puisque eπ = (-1)(-i), on voit que eπ est transcendant. En 1955, K.F.Roth améliore l’inégalité de Liouville et montre que pour tout x algébrique irrationnel, pour tout ε positif, il existe une infinité de p/q irréductibles tels que |x- p/q| > 1/q2+ε. Ceci lui vaudra la très convoitée médaille Fields en 1958.
La théorie des nombres transcendants est aujourd’hui florissante, sans doute grâce aux beaux travaux du mathématicien Alan Baker dans les années 1960-70, pour lesquelles il recevra lui aussi la médaille Fields (1970).
La morale de cette histoire est, me semble t-il, que les deux notes de Liouville, quoique parfaitement élémentaires, sont d’une grande profondeur. Seul un grand mathématicien peut découvrir des idées simples et néanmoins très riches.

 

 

 

 

 

À LIRE

 

 


Article de Michel Mendes France, professeur à l’Université de Bordeaux I : Nombres transcendants et la diagonale de Cantor, Revue « Images des mathématiques 2006 ». http://www.math.cnrs.fr/imagesdesmaths/pdf2006/Mendes.pdf

 

 


Article Wikipedia sur les nombres de Liouville, premiers nombres transcendants à être mis en évidence. http://fr.wikipedia.org/wiki/Nombre_de_Liouville