Sur le mouvement d’un corps qui tombe d’une grande hauteur

 

Nous vous proposons ici et pour la première fois la version originale de l'analyse en anglais.

La version française est à la suite.

 

 

 

From Aristotle to Galileo

From the 17^th century well into the 19^th century the deflection of falling objects was a hotly debated subject, first as a way to prove or disprove the Copernican theory, later about the details of the deflection. This paper from 1803 “Mémoire sur le mouvement d’un corps qui tombe d’une grande hauteur” by Laplace is a scientific milestone in this debate:

• It was written to predict the likely deflection of objects dropped in a mine shaft for a campaign to prove the rotation of the Earth;
• It was made in an unofficial competition with the renowned German mathematician Friedrich Gauß who had got the same assignment ;
• Both arrived at the correct result and were thereby the first scientists to derive and physically interpret what was later to become known as the “Coriolis Effect”.

The experiments of deflection of falling bodies was an answer to a problem already posed by Aristotle and repeated by anti-Copernicans: if the Earth was spinning around its axis an object dropped from a tower would be “left behind”, i.e. deflected to the west (1). In Galileo’s (alleged) experiment at the tower of Pisa the objects landed at the base with no obvious deflection. But this was, according to Galileo and other supporters of the Copernican model, not an indication that the Earth did not move since the objects took part in the Earth’s rotation. As everybody could see: an object dropped from a mast on a sailing ship in full motion would also land at the foot of the mast.

 

 

The naïve model

The debate could have ended here if the anti-Copernicans had based all their opposition on a possible westerly deflection. What the scientists among them actually claimed was that objects would move differently depending on if the Earth was moving or not. And here they could score several points. Galileo had himself admitted in his famous Dialogo sopra i due sistemi del mondo in 1632 that since the top of the tower was further away from the Earth’s centre, the rotational velocity at the top would be slightly larger than at the surface. An object falling from the top would therefore overtake the tower and land slightly ahead, to the east of it.

If we put this reasoning into mathematics, we will find that an object dropped in northern Italy (at 43° N) from a tower of 100 m height will take 4.515 seconds to reach the ground. Since the rotational velocity at the top is 5.3 mm/sec faster than at the surface, the object will, when it reaches the surface, have “moved ahead” by 24 mm. (fig.1).

 

 

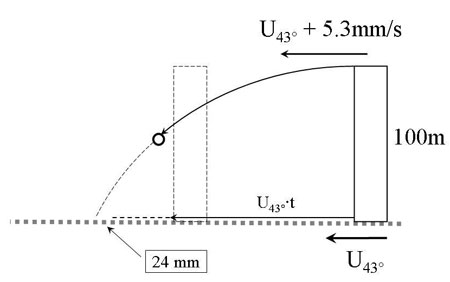
Figure 1: A simplistic model of the deflection of vertically falling objects. Because the top of a tall building due to the earth’s rotation moves faster than the bottom of the building, an object dropped from the top will, with its slightly higher horizontal velocity, reach the surface ahead of an object moving with the surface velocity.

 

Such small deviations were at Galileo’s time difficult to confirm by measurements. Even worse, the deflection according to this simplistic model is not quite correct and yields results which are 50% too large. This is because we have ignored the curvature of the earth. During the 4.5 seconds the object falls, the tower and its environment move 1½ kilometre to the east. Not a long distance, but the curvature of the Earth’s surface, although very small, cannot be neglected. It is to their scientific credit that both the Copernicans and the anti-Copernicans realised this and the debate concentrated on the kind of trajectory the falling object would follow.

 

 

The Italian debate

To simplify the investigation they chose to focus on objects dropped from a tower at the equator. To allow the dropped objects to be free to continue their fall also after they had reached a distance to the earth centre equal to its radius (=surface) they designed a quite ingenious mental picture of the Earth at the equator halved in two hemispheres.

 

 

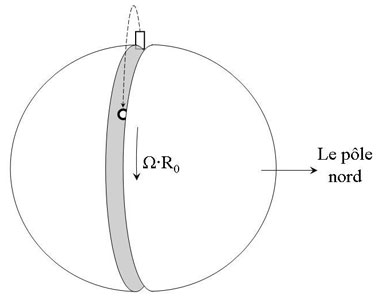
Figure 2: In order to allow the falling bodies to continue their journey the Italian scientists imagined the Earth as two separate hemispheres.

 

 

With the underlying ground no longer flat but spherically curved the trajectory could no longer be a parabola (or part of a parabola). So what was it? In his Dialogue 1632 Galileo suggested a semicircle with a diameter equal to the radius of the Earth. This was a pure speculation on his side, had no basis in his mechanical theories and was also against the generally accepted view that the object would follow a spiral trajectory, most likely an Archimedean spiral trajectory towards the Earth’s centre. But five years later he changed his mind and agreed in Dialogue 1638 with the prevailing view. Both sides were in full agreement that the object would come to rest at the centre of the Earth.

 

 

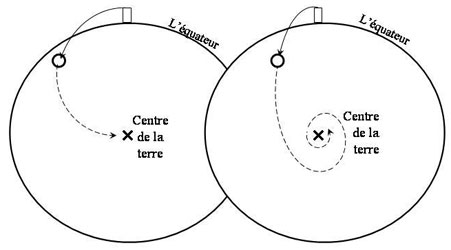
Figure 3: It was taken as an axiom by all scientists in the early 17^th century that an object, able to penetrate the earth without any loss of speed, would end up at the centre of the Earth. The only disagreement was the type of trajectory that would carry it to the centre. Galileo initially suggested a semi-circle (left) against the prevailing opinion which favoured a spiral, most likely an Archimedean spiral (right).

 

 

The debate that followed has been taken by modern historians of science as a textbook example of how the tremendous power of “mental or intellectual inertia” and of the very slow and gradual way in which even “superior minds” succeed in liberating themselves from the traditional and habitual, what the English 17^th century philosopher Francis Bacon called “idola tribus”. Because what everybody agreed on, that the falling body would end up in the centre of the earth, was fundamentally wrong! It was fundamentally wrong because it effectively prevented the scientists to even reach approximate or qualitatively correct solutions!

The debate therefore became very confused. So for example in 1667 Giovanni Alfonso Borelli (1608-1679) put forward a hypothesis that curved motion was composed of one rectilinear tangential motion and one accelerated towards the centre. We now know this is perfectly true, but his idea was rejected, also by himself and his followers, when it was found that the falling object would then not reach the centre of the Earth!

 

 

Newton’s “fancy”

The Italian debate quickly “spilled over” to England. David Gregory (1659-1708), one of the members of the Royal Society, reported this Italian debate in 1668. It fuelled the interest in the problem also in England, and in 1674 Robert Hooke published a book with the title “An Attempt to Prove the Motion of the Earth”. One of the methods he suggested was to observe the deflection of objects dropped from high buildings. He had also qualitatively foreseen Newton’s laws in Principia:

• All celestial bodies have an attraction or gravitational power towards their own centres;
• A body put in motion in a straight line will continue to move until it by some power is deflected into a curved motion;
• The nearer the object the stronger this attractive power.

 

Hooke had thereby conceived gravity as an attractive force drawing a body downward, rather than being an Aristotelian “tendency to fall” within the body itself. Hooke’s profound physical intuition was acquired through numerous experiments, perhaps several hundreds. His remarkable physical intuition and understanding was based on mechanical analogues rather than mathematical reasoning and would have a crucial importance to the development of Newton’s thinking.

 

@@@@@@@

 

In November 1679 Robert Hooke, in his capacity as newly elected Secretary of the Royal Society, wrote a letter to Isaac Newton. His intention was to draw Newton into a discussion on planetary motion, in particular the reason for the elliptical orbits of the planets. But Newton had something else on his mind, what he called “a fancy of my own”: the deflection of objects dropped from a high altitude as proof of the Earth’s rotation.

Much later in his life Isaac Newton would tell his friends that it was in 1666, while watching apples fall from the tree in his family garden, that made him speculate about earthly bodies and the moon being attracted by the same gravitational forces. What has made scholars skeptical is that it was in 1726, sixty years after the alleged event, and at a time when Newton was engaged in priority argument with other scientists. In 1666 he was developing ideas in mathematics and optics, and there is no documentary evidence about deeper thoughts on the nature of gravitation. We also know from the history of science that such profound theoretical concepts rarely appear “out of the blue”.

However, if we place the “falling apple event” thirteen years later, in 1679, it gains much more credibility. Newton had spent most of that summer and autumn at his family home in Lincolnshire. His mother had just died and he had to attend to family matters. There had been a lot of opportunities to see apples fall in the family garden.

 

 

The elliptic path

The exchange of letters that followed with Hooke during the winter 1679-80 shows that Newton had not yet achieved a deeper understanding of celestial mechanics. His first idea was to suggest, like the general scientific opinion of the time, that a falling object would, in principle, approach the centre of the earth in a spiral. Thanks to Hooke he came to realize, that it instead would rather follow an elliptic path (figure 4).

 

 

Figure 4: Hooke’s and Newton’s agreed opinion about the elliptical trajectory of a falling body within the earth’s gravitational attraction.

 

 

From this insight, that a falling object follows the same type of orbit as any of the planets around the Sun, it is not far-fetched to infer that the motions of these different bodies might be controlled by the same mechanism – universal gravitation. Still, even for a genius like Newton, it took a few more years to lead into conclusions in “Principia”.

 

 

Gauß and Laplace

More than a century later there was a renewed interest in the problem of the deflection of falling objects. The explanation of the flattening of the poles proved that the earth rotated and settled the dispute among scientists. But it was in some way an indirect proof.

In 1803 an experiment, dropping iron pebbles in a 90 metre deep mineshaft, was conducted in Germany. The event attracted the interest of the scientific community and the 24-year German mathematician Carl Friedrich Gauß and the 53-year French mathematician Pierre Simon de Laplace volunteered to calculate the theoretically expected deflection.

 

 

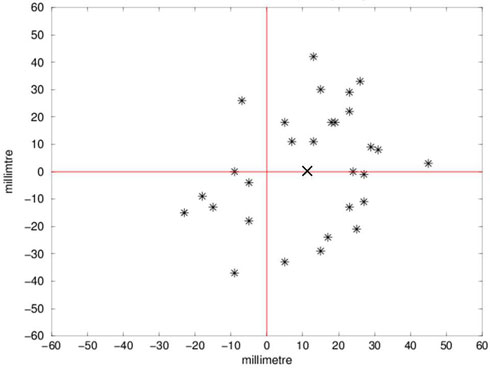
Figure 5: The hit-picture from the Schlebusch experiment 1803. A cross marks the theoretically derived deflection.

 

 

There was an element of competition since Gauß had the year before managed to calculate the orbit of the newly discovered asteroid Ceres, something Laplace had deemed impossible. Both came up with the right answer by deriving the full three-dimensional equation for motions on a rotating earth.

They specifically pointed out that the Coriolis-terms (as we call them) (2) were responsible for the deflection. Gauß and Laplace were thereby the first scientists to contribute to the proof of the rotation of the earth some 50 years before Foucault’s famous pendulum experiment and to analyse correctly the relative motion in connection with rotation, 30 years before Coriolis’ mathematical paper (1835).

 

 

Laplace’s derivation – and the modern one

What makes Laplace’s derivation difficult to follow for modern readers are

• Lack of graphical illustrations. In figure 6, I have made an attempt to show visually what Laplace might have had in mind.
• The mathematical notations of the time. Laplace for example defines the latitude as the angle from the earth’s rotational axis (co-latitude) instead as from the equatorial plane as we now do.
• The use of Cartesian component forms. During the 19^th century British, German and American physicists (not mathematicians) developed for practical reasons, to facilitate intuitive interpretations, the modern vectorial system.
• In order to acquire as exact an estimation as possible, Laplace also wanted to take the possible effect of the air resistance into account.
• Laplace wanted also, with as detailed calculations as possible, try to find if there was a possible minor southerly deflection.

 

 

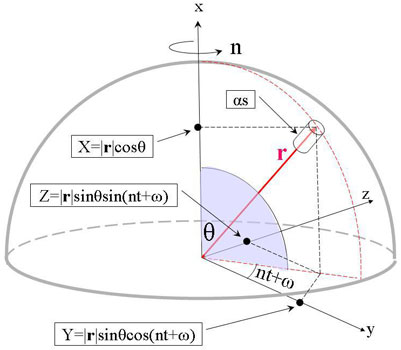
Figure 6: Laplace’s computational model of the Earth with a tower at co-latitude θ (corresponding to latitude 90-θ).

 

 

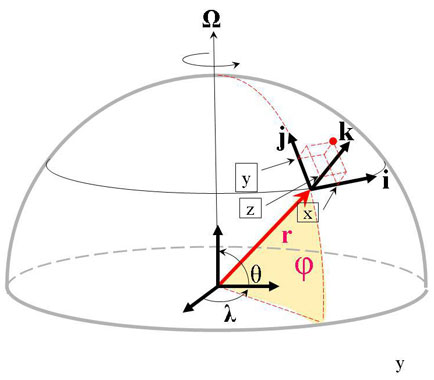
Figure 7: The modern spherical coordinate system with θ, λ and r as axes. Locally a Cartesian x, y and z coordinate system can be defined.

 

 

Laplace derivation does essentially the same as today’s derivations, a coordinate transformation from an absolute frame of reference to a relative, rotating one. The rate of change of vector A as observed in the absolute frame of reference (what Laplace marked x, y and z) and in the relative frame of reference (by Laplace noted as reference frame X,Y and Z) rotating with an angular velocity Ω is described by the very powerful relation :

 

 

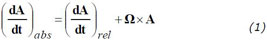
A can be any vector and we choose it to be the position vector r

 

 

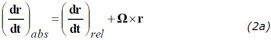
or with v denoting the velocity

 

 

We then apply (1) on the absolute velocity which yields

 

 

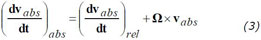
Substituting (2b) into the right hand side of (3) gives

 

 

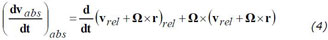
which yields

 

 

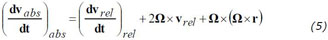
As seen in an absolute frame of reference:

 

 

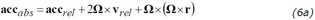
We are, however, interested in the accelerations seen from the relative frame of reference:

 

 

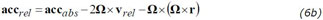
where -2 Ω × v_rel is the Coriolis force (per unit mass) pointing to the right of the motion and - Ω × Ω × r the centrifugal acceleration pointing outward, from the axis of rotation.

 

@@@@@@@

 

Algebraically the three-dimensional components can be found by applying standard mathematics for cross products vectors

 

 

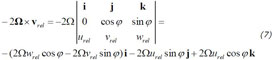
which yields the deflection of east-west or latitudinal motion (u_rel) in the north-south or meridional direction (j) as -2Ωu_relsinφ and in the vertical direction (k) as 2Ωu_relcosφ. The former is the well-known Coriolis effect for horizontal motion, the latter the so called “Eötvös effect” which explains why horizontal motions in the west or east directions make an object lighter or heavier. Meridional motion (v_rel) will only be deflected in the east-west direction (i) with 2Ωv_relsinφ and so will also vertical motion (w_rel) with 2Ωw_relcosφ.

 

Figure 8: Laplace’s derivation of the deflection in component form (p. 112) The entities s, u and v correspond to distances, their first and second derivative to velocities and accelerations. The rotational velocity, corresponding to Ω in modern notation is here represented by n. Laplace has also considered the possible influence due to friction which is seen in the K-terms. In the end the air friction has very little impact on the deflection.

 

 

The interpretation of this -2 Ω × v_rel term

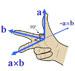
The Coriolis Effect was discovered in the 19^th century mathematicians and physicists have since then struggled to find a good intuitive explanation: why a “ 2”, and why a vectorial cross-product? So far nobody has really succeeded; so we must for the time being accept the term it at face value. On the other hand it is quite easy to understand what the -2 Ω × V_rel term means in physical terms. Thanks to the vector notation that was developed just for the purpose of facilitating physical, intuitive understanding this can be stated as:

 

All relative motions V_rel, or components of relative motions, perpendicular to the rotational axis Ω will be deflected perpendicular both to the motion V_rel and the axis Ω to the right (for a counter clockwise rotation) (3). And all motions, or components of motions, parallel to the rotational axis, will not be affected. (expl. in fig.9).

 

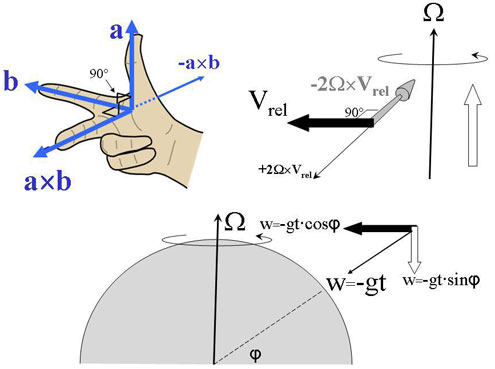
Figure 9: The relation between vectors a, b and their cross products a×b is facilitated through the “règle de la main droite” (left). From this it is easy to see (right) how the relative motion V_rel , a vector perpendicular to the rotational axis Ω is deflected to -2Ω×V_rel . Motions or components of motions, parallel to the rotational axis will not be affected, as indicated by the white vector to the far left.

 

@@@@@@@

 

More specifically, for vertical motion w, where w > 0 for upward motion (the time derivative of the distance to the Earth’s centre) the velocity for free fall (w<0) can be written w= - g.t This can be split up into one component w·sinφ·g·t parallel to the Earth’s axis, and another component, w·cosφ·g·t, perpendicular to it. Only the second component will be deflected to the right by the Coriolis effect.

 

 

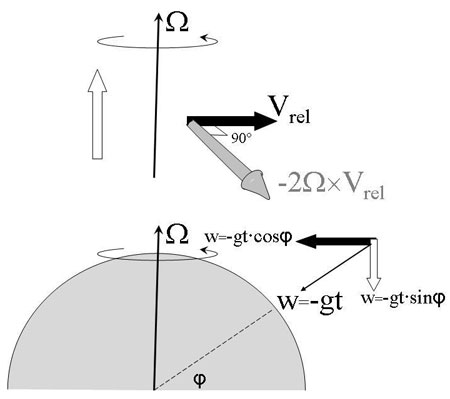
Figure 10: The velocity of a falling body –wg can be split up into one component perpendicular to the Earth’s axis, another parallel to it. The first will be fully deflected, the second not.

 

 

Deflection according to the Coriolis Effect

We can now, like Laplace (and Gauß) in 1803, calculate the deflection of the falling object. We first note that the time (t) it takes for an object to fall from an elevation (h) is

 

 

and it will then increase and when hitting the ground have a velocity

 

 

which can also be expressed as

 

 

or

 

 

To gain clarity the derivations will be conducted for falls at the equator φ=0, where sinφ=0 and cosφ=1. For any calculation away from the equator, Ω can easily be replaced by Ωcosφ

 

 

 

For this vertically moving object we have, according to the cross product display in section 8 a deflection -2Ω×w, with w = -g·t; this can also be written as a second derivative of the position S

 

 

Integrating (9a) over the time of the fall from a height h, with the initial horizontal velocity V₀, yields to

 

 

Since the initial velocity V₀ = 0, further integration yields

 

 

Since our reference point is the base of the tower S₀ = 0 and (8a) yields

 

 

This corresponds exactly to Laplace’s result p.115 (given that we took sinθ =1):

 

 

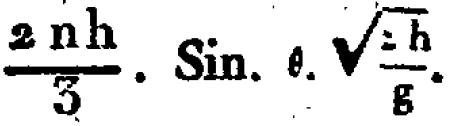
This is again a rather mathematical explanation of the deflection with not much physical “feel”. But, as often is the case in physics, there is more than one mathematical derivation for the same process or mechanism. We will make derivations which Isaac Newton and Johannes Kepler would have been able to do if they had come to think of it!

While the derivation of the deflection using the Coriolis effect was conducted in a relative frame of reference where we were positioned on the Earth and followed its rotation, we will now move into an absolute frame of reference, outside the Earth and look at the motion of the falling objects while they are transported around by the earth rotation.

 

 

Deflection according to Newton’s laws

For our first “Newtonian” derivation we make use of the insight, acquired already by the generation before Newton, that due to the curvature of the Earth the object will be affected by a component of gravity g directed “backward”, which will delay the object’s motion compared to the simplistic model in figure 1.

 

 

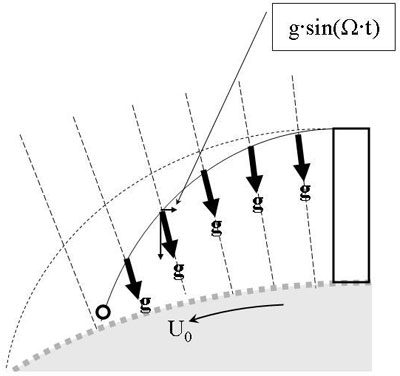
Figure 11: In contrast to figure 1 where the gravitational force lines were parallel and the trajectory a parable, for radially converging force lines the trajectory becomes in principle an ellipse.

 

This backward horizontal acceleration can be simplified because of the smallness of the angle Ω·t

 

 

which integrated yields

 

 

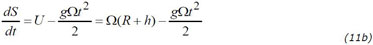
where U = Ω (R+h) is the Earth rotation at the elevation h. Finally we have

 

 

But a point at the ground, towards which the body is falling, is moving with a speed U₀ = Ω·R < U. This velocity difference yields U - U₀ = Ωh and when the body strikes the ground it undershoots by ΔS:

 

 

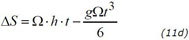
Inserting (8a) into (11d) yields

 

 

where the first term is the distance covered by the tower and the second term the slight deflection back from the tower.

If only Newton had more stubbornly considered the problem of the deflection of his famous falling apples, he would have been able to derive equation (12) already in the late 17^th century and maybe also discovered the Coriolis effect. But he might not have been the first. Indeed it could have been done already some fifty years before by Johannes Kepler.

 

 

Deflection according to Kepler’s 2nd (area) law

Kepler’s 2^nd Law, that radius vector in equal times covers equal areas, was for long thought only to apply to celestial bodies, such as planets or comets. For most of the 1600s this law was not widely understood or accepted, not even by Isaac Newton. It was only during his work on “Principia” in the mid-1680s that he came to realise its validity, but also its shortcomings. It was, for example, only when he questioned one of the fundamental parts of Kepler’s theory (that the trajectory of an orbiting planet has its focus, not in the centre of the sun as stated by Kepler, but in the common centre of mass of the sun and the orbiting planet), that he was able to formulate his third law.

Kepler had never extended his planetary laws to the neighbourhood of the Earth. It was not until the late 18^th century that it was realised that his Second Law, the “Law of areas" could also be applied to also earthly objects and as such it became known as “Conservation of Angular Momentum”.

 

 

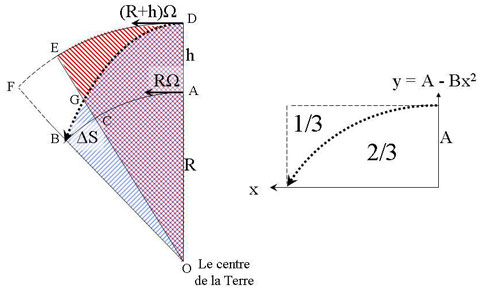
Figure 12a: Seen from outside the falling object follows the trajectory DGB while the top of the tower follows DE, and the base AC. 12b: Any parable inscribed in a rectangle will cover 2/3 of its area.

 

Our dropped object follows an absolute trajectory DGB while the base of the tower follows the trajectory AC (fig. 12a). According to Kepler’s 2^nd law the two areas ODBO (hatched blue and violet) and ODEO (hatched red and violet) are equal, and it is easily seen that the falling object moves ahead of the tower by the distance CB=ΔS.

Since the two motions share the area ODGO (hatched violet), the two not-shared, “leftover” areas DEGD (hatched only red) and area OGBO (hatched only blue) are equal in size. We then add to them the (white) area GEFB making area DFBD = area OEFO.

Considering h << R and the small angles involved (much smaller than in the figure) we approximate BG ≈ BC ≈ FE ≈ ΔS, essentially disregarding the area GBC ≈ 0 and treating GEFB as a rectangle with area ≈ h·ΔS and area OEFO ≈ ΔS (h+R)/2.

From our previous discussion (fig. 4), we know that the trajectory is an ellipse, but for the very short duration we are dealing with now, just a handful of seconds, we can treat the trajectory as a parable.

For the same reason we can treat DFBA as an rectangle with an area =(R+h)Ω·t. From the general rule that for a parable inscribed in a rectangle 2/3 of the rectangle’s area is inside the parable, 1/3 outside (fig. 12b), we can approximately calculate the area DFBD = h·(R+h)·Ω·t/3, and we have

 

 

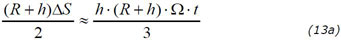
which yields again with (8)

 

 

 

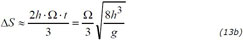
Laplace extension for deflection of vertically projected objects

When Laplace edited his Collected Works in 1805, he slightly modified his 1803 article, also including an analysis of the deflection of an object (like a cannonball) thrown vertically straight upward. This version can be found under the reference P.S.Laplace, De la chute des corps qui tombent d’une grande hauteur, Traité de Mécanique Céleste, T IV, Seconde Partie, Livre X, p. 294-305. (4)

 

 

 

 

Such experiments were indeed conducted in the early 1600’s. In 1627 a German mathematician Joseph Furtenbach from Ulm fired cannonballs vertically and, being sure that they would not come straight down, immediately after the shots climbed up and sat on the cannon’s muzzle. The same experiment was carried out 1634 also by Mersenne, at the request of Descartes. Galileo’s students in Florence conducted in the 1650’s an experiment where the cannon was mounted on a wagon drawn by six horses in a rapid speed to see if the motion of the wagon would make the balls drop differently compared to when the wagon was at rest.

The results were generally inconclusive. Cannonballs were not uncommonly lost, and this gave rise to the belief that they broke away from the earth’s gravity and travelled into space never to return. It is more likely that they were carried away by the strong winds often found high up in the atmosphere.

 

@@@@@@@

 

We now repeat this derivation in the “Coriolian” way Laplace did in 1803 and then how it could have been done in a “Newtonian” and “Keplerian” fashion. First the “Coriolian” with an initial upward velocity V₀ and where the Coriolis deflection at time t is:

 

 

when integrated becomes

 

 

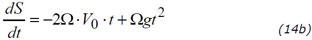
and finally

 

 

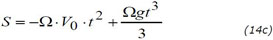
The expression of time as a function of V₀ as presented in (8b) must be doubled since the time it takes for the projectile to reach height h and then descend back to earth is double compared to a fall from height h. This makes

 

 

and we get a deflection

 

 

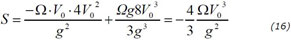
Since S < 0, the deflection is to the west. This result needs a further explanation. For a projectile fired upward in the air and then falling back, one would expect that the deflection during the falling back part of the motion should cancel the deflection during the upward part.

 

 

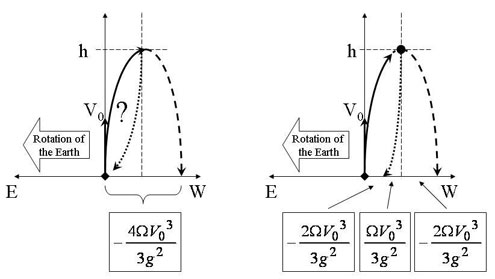
Figure 13: The relative trajectory, relative to the cannon and the ground, of a vertically projected object with initial velocity V₀. Left: Why is the object not deflected back when it falls back to the Earth, as would an object released from rest at the same height? Right: An object released from the same height would fall eastward, but the eastward deflection is not large enough to compensate for the initial westerly deflection. Further, since the projected body is moving westward at its highest point and the released body is at rest, this further adds to their separation.

 

Let us imagine that our upward projected object, when reaching its highest point, by some coincidence, should be close to another projectile, released from rest into a free fall. Since both are on their way down, we might expect them to be close and follow each other. But the projected object is at this highest point, due to the Coriolis effect, not at rest but in horizontal motion to the west. Further, the eastward deflection of the objects starting from rest will anyhow only be half of the westward deflection it is supposed to compensate for (fig. 13).

 

 

The deflection of vertically projected objects according to Newton’s laws

And now, in an absolute frame of reference, according to Newton’s laws, the backward deflection due to the curvature of the earth’s surface as previously discussed:

 

 

 

 

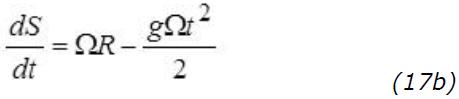
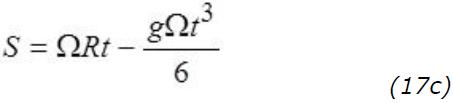
With the expression for the time (15) as above

 

 

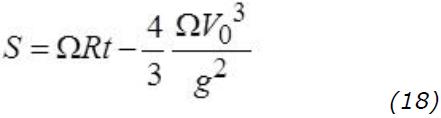
So while the cannon travels a distance ΩRt carried by the Earth rotation, the ball falls slightly behind (S < ΩRt).

 

 

The deflection of vertically projected objects according to Kepler’s 2^nd law

Using Kepler’s 2^nd Law of equal areas we can immediately see that the position where the object is projected vertically upward will overtake the object itself since the area OADBO = area OACO. Both have the area OABO (violet) in common so we can concentrate on (red) area OBCD=R·ΔS/2 and (blue) area ADBA=2Ω·R·t·h/3 which, although an ellipse, can be approximated as a parable inscribed in a rectangle with base=2Ω·R·t and height=h.

 

 

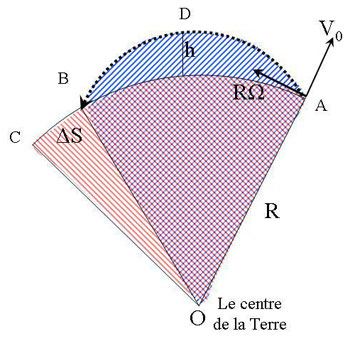
Figure 14: The trajectory of the vertically projected body ADB seen from an absolute frame of reference. During the same time the position of the launch (the “cannon”) has travelled the longer distance ABC. In both cases the “radius vector” covers equal areas OADB=OABC. The trajectory ADB is in reality an ellipse but can here be approximated by a parable.

 

Using (8a) and (15) we integrate over two time periods we find once again the same formula:

 

 

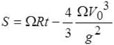
In those days a cannon had a typical exit velocity (V₀) of 400 m/s. With an angle of 45° this would mean both a horizontal velocity and a vertical initial velocity V_0H = V_0V = 283 m/s. It will take the grenade 29 seconds to reach its highest point just above 4 km and almost 58 seconds to reach its target (assuming no air friction) which will be little more than 16 km away. The grenade will undershoot the target by 45 m. So far in the equator region, where 2Ωsinφ is null, and we therefore do not have any horizontal, sideway, deflection.

If we now move to a north Italian latitude of 43° where Ωcosφ = 0.53·10^-4 /sec the projectile will undershoot the target by 17 m. But with a value for 2Ωsinφ = 1.00·10^-4 /sec there will be a sideways deflection of 47 m.

 

 

Other aspects of Laplace’s derivations

As mentioned in the introduction, Laplace made his derivation very consciously in order to also establish the effects of friction and any possible southerly deflection. We will not go into these details, only mention that friction according to Laplace (and subsequent derivations) does not seem to have any significant impact on the deflection.

Concerning a possible southerly, or rather equatorward deflection, was, as we can read in Laplace’s article, a matter of controversy already 200 years ago, Laplace’s calculations showed no such deflection but Gauß’ calculations did; this contributed to keep the issue controversial into our times. Part of the problem is to define “southerly”; is it in relation to the geographical latitude or the geocentric? Laplace and Gauss were not aware of later geodetic work that defined the shape of the earth more exactly than was the case in their times. Today’s agreed wisdom is that the deflection does not exist or is so small that it is over-shadowed by necessary mathematical approximations. Finally, experiments in modern times have so far not found any detectable southerly deflection.

 

 

Why did it take almost 200 years?

We have thus shown that correct expressions for the deflection of a falling object could have been derived already 100 years earlier by Newton or almost 200 years earlier by Kepler. So why didn’t they do it?

In Newton’s case it was because he was never asked. Deflection of falling bodies had been, as we have seen, high on the scientific agenda in the 17^th century, but simplistic calculations (fig. 1) had yielded very small values. Hooke’s experiment had shown a very great spread of measurements and the matter had been regarded as impossible to pursue scientifically.

But also Benzenberg’s measurements (fig. 5) showed large spread and so did Ferdinand Reich’s measurements in a later experiment 1834. By that time the understanding of error statistics had developed, and it was seen a natural thing to compute averages of measurements. Well into the late 18^th century scientists, in particular astronomers, had the habit of trying to find out which of several observations or measurements they had done, was “the best” one. Combining observations would, so it was thought, add the errors.

Thanks to Laplace, Gauß, Legendre (5) and others, it become established that due to the random nature of errors, combining observation would to a large degree cancel out the errors yielding averages that would be more accurate than any randomly chosen observation.

The reason why Kepler would not have been able to apply his 2^nd law on the problem was because it was considered to apply only to celestial motions, not terrestrial. That became clear only after the publication of Newton’s “Principia”. Before that there were even doubts if the law was correct, since it had been derived from observations from only one planet, Mars, with an unusually eccentric orbit.

Finally, Laplace and Gauß managed to calculate the deflection after having derived what we now regard as the “Coriolis Effect”, some 30 years before Coriolis. Why did they, or one of them, not get the credit of later generations? One reason might be that Coriolis’s work dealt with the dynamics of machines and appeared as less far-fetched than Laplace’s and Gauß’s. But more likely, the interest in the behaviour of relative motion in rotating system had its “breakthrough” after Foucault’s famous experiment in 1851. In the ensuing discussions Coriolis’s 1835 paper happened to be more in the scientists mind because the attention it had contracted a few years earlier. French mathematician Joseph Bertrand had 1847-48 claimed that Coriolis had plagiarized results already derived by Alexis Clairault some 100 years earlier. There might be reasons to come back to this story in a later contribution.

 

(August 2014)

 

 

 

 

 

 

---

 

1. D'Aristote à Galilée

Depuis le XVII^e siècle jusqu'assez tard au XIX^e siècle, la déviation des corps tombant fut un sujet ardemment débattu, d'abord pour confirmer ou infirmer la théorie copernicienne – ensuite à propos des caractéristiques de cette déviation.

L'article de 1803 de Laplace, « Mémoire sur le mouvement d’un corps qui tombe d’une grande hauteur », est une étape fondamentale de ce débat :

• Il visait à prédire la valeur de la déviation d'objets lâchés dans un puits de mine, dans le contexte d'une recherche de preuves de la rotation de la Terre ;
• Son auteur était en compétition – non officielle – avec le célèbre mathématicien allemand Friedrich Gauß qui s'était fixé le même objectif ;
• Tous deux arrivèrent au résultat correct et furent ainsi les premiers savants à découvrir et à interpréter correctement ce qui sera plus tard connu sous le nom d' « effet Coriolis ».

Les expériences de déviation des corps constituaient une réponse à un problème déjà soulevé par Aristote, puis par des opposants à la théorie de Copernic : si la Terre tournait autour de son axe, un objet lâché depuis une tour serait « laissé en arrière », c'est-à-dire dévié vers l'ouest. Dans l'expérience  (supposée) de Galilée à la tour de Pise, les objets arrivaient au sol sans déviation  mesurable : mais, selon Galilée et les héliocentristes, ce n'était pas une preuve d'une fixité de la Terre, puisque ces objets étaient entraînés par la rotation terrestre. Comme chacun pouvait le constater, un objet lâché du mât d'un bateau  en mouvement tombait lui aussi au pied du mât.

 

2. Le modèle naïf

Le débat aurait pu s'arrêter là si les opposants à Copernic n'avaient fondé toute leur argumentation sur une éventuelle déviation vers l'ouest. Ces savants imaginaient que les objets tomberaient de manière différente, selon que la Terre tournait sur elle-même ou non. Et là, ils pouvaient marquer quelques points. Galilée avait lui-même admis dans son Dialogo sopra i due sistemi del mondo en 1632 que, comme le sommet d'une tour est plus éloigné du centre de la Terre que ne l'est sa base, la vitesse de rotation au sommet est légèrement plus grande qu'à la base, à la surface de la Terre. Un objet lâché d'en haut dépasserait alors le pied de la tour et en viendrait à tomber légèrement devant, donc à l'est de la tour.

Si nous mathématisons ce raisonnement, nous trouvons qu'un objet lâché d'un promontoire de 100 m de haut en Italie du Nord (à 43°N de latitude) mettra 4,515 secondes à atteindre le sol. Comme la vitesse de rotation sommitale est de 5,3 mm/s supérieure à celle de la surface, l'objet aura « avancé » de 24 mm lorsqu'il atteint le sol (figure 1).

 

 

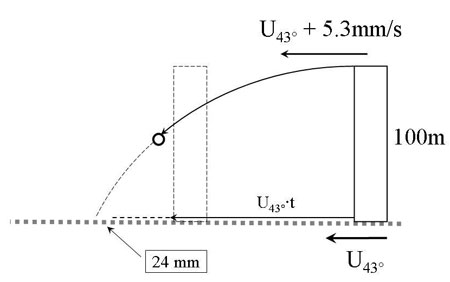
Figure 1: Un modèle simpliste de déviation des corps en chute verticale. Comme le sommet d'un bâtiment élevé se déplace, avec la rotation terrestre, à une vitesse plus grande que le bas de l'immeuble, un objet lâché du sommet arrivera, de par sa vitesse horizontale légèrement supérieure, à l'avant d'un objet se déplaçant à la vitesse de la surface terrestre. 

 

 

De telles petites déviations étaient difficilement mesurables du temps de Galilée. Pire, la déviation calculée selon ce modèle simpliste est erronée et conduit à des résultats de 50% trop importants – car nous avons négligé ici la courbure terrestre... Pendant les 4,5 s. de chute de l'objet, la tour et ce qui l'entoure se déplacent d'1,5 km vers l'est. C'est une courte distance – mais la courbure terrestre, quoique faible, ne peut plus être négligée. Mettons au crédit des coperniciens comme de leurs opposants le fait qu'ils prirent conscience de ce point, ce qui déplaça leur controverse sur le type de trajectoire suivie par l'objet.

 

 

3. Le débat italien

Pour simplifier le propos, tous choisirent de se concentrer sur des objets lâchés d'une tour située sur l’Équateur. Et afin de permettre aux objets de poursuivre fictivement leur trajectoire après leur arrivée au sol, ils imaginèrent une représentation mentale ingénieuse de la Terre, tranchée à l’Équateur en deux hémisphères.

 

 

Figure 2: Pour permettre aux corps chutant de poursuivre leur trajectoire, les Italiens imaginèrent la Terre comme séparée en ses deux hémisphères.

 

 

Avec une surface qui n'était plus plate mais courbée (et donc une attraction vers le centre terrestre qui variait en direction), la trajectoire ne pouvait plus être  parabolique. Alors quelle était-elle ? Dans son Dialogue de 1632, Galilée suggéra un demi-cercle dont le diamètre serait égal au rayon terrestre. C'était pure spéculation de sa part, sans aucun fondement dans ses conceptions de la mécanique, et contraire à la vision largement acceptée d'une trajectoire spirale – vraisemblablement une spirale d'Archimède dirigée vers le centre de la Terre. Six ans plus tard, Galilée changea d'avis et se rangea à l'avis général dans son Dialogue de 1638. Les deux parties, les coperniciens et leurs opposants, étaient en tout cas d'accord sur le fait que l'objet arrivait (fictivement) au centre de la Terre avec une vitesse nulle.

 

 

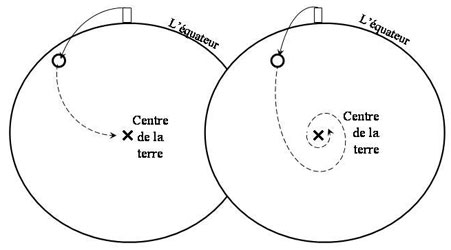
Figure 3: Il était pris comme postulat par les savants du premier XVII^e siècle qu'un objet capable de pénétrer la surface terrestre sans perte de vitesse arriverait au centre de la Terre. Le seul désaccord portait sur le type de trajectoire qui porterait l'objet vers le centre de la Terre. Galilée suggéra initialement un demi-cercle (à gauche), contre l'hypothèse dominante de la spirale, vraisemblablement archimédienne (à droite).

 

 

La discussion qui s'ensuivit a été donnée par les historiens contemporains des sciences comme un cas d'école du pouvoir énorme de « l'inertie intellectuelle et mentale » et de la manière, lente et progressive, suivant laquelle même des « esprits supérieurs » réussissaient à se libérer de leur traditionnelle « idola tribus » – pour reprendre l'expression donnée au XVII^e siècle par Francis Bacon. Car de fait, ce qui recueillait l’accord de tous (l'arrivée du mobile au centre de la Terre) était totalement erroné ! Et erroné aussi parce que cela empêchait tout savant de calculer des solutions même approximativement correctes...

Le débat devint alors confus. Ainsi par exemple en 1667 Giovanni Alfonso Borelli (1608-1679) proposa-t-il une hypothèse suivant laquelle la trajectoire courbe avait une composante rectiligne uniforme, tangentielle à la Terre, et une composante accélérée vers son centre. Nous savons maintenant que c'est parfaitement correct, mais l'idée fut rejetée, aussi bien par lui que par ses successeurs, parce que dans cette hypothèse l'objet n'atteignait pas le centre de la Terre !

 

 

4.Une fantaisie newtonienne

Le débat italien contamina assez vite l'Angleterre. David Gregory (1659-1708), membre de la Royal Society, en fit part à cette assemblée en 1668. Le problème suscita un vif intérêt, et en 1674 Robert Hooke publia un livre intitulé An Attempt to Prove the Motion of the Earth. Une des méthodes suggérées était l'observation de la déviation d'objets lâchés depuis des tours. Il avait aussi prévu de manière qualitative les lois de Newton qui apparaîtront dans les Principia:

• Tous les corps célestes ont une gravitation dirigée vers leur propre centre ;
• Un corps en mouvement rectiligne uniforme continue dans ce mouvement, sauf à être dévié en une trajectoire courbe par une force quelconque ;
• le plus proche est l'objet, la plus forte est l'attraction.

Hooke avait ainsi conçu la gravité comme une force attractive entraînant les objets vers le bas, plutôt qu'une « tendance à tomber » intrinsèque aux corps, comme le voulait Aristote. Hooke avait eu ces profondes intuitions grâce à de nombreuses expériences, peut-être plusieurs centaines. Son sens physique remarquable était fondé sur des analogies mécaniques plus que sur des calculs : il a eu une grande influence sur le développement de la pensée de Newton.

En novembre 1679 Hooke, fraîchement élu secrétaire de la Royal Society, écrit à Newton, en souhaitant ouvrir une discussion sur le mouvement des planètes, et notamment la cause de leur orbite elliptique. Mais Newton avait autre chose en tête, ce qu'il appelait « une fantaisie de mon cru » : la déviation d'objets lâchés d'une grande hauteur, comme preuve de la rotation terrestre.

Beaucoup plus tard, Isaac Newton dira à ses amis que c'était en 1666, alors qu'il regardait des pommes tomber de l'arbre dans le jardin familial, qu'il eut l'idée que les corps terrestres et la Lune obéissent aux mêmes forces gravitationnelles. Ce qui rendit de tous temps les historiens sceptiques est que Newton tint ses propos en 1726, soixante ans après l'événement relaté, et ce alors qu'il était engagé dans une querelle de priorité avec d'autres savants. En 1666, il développait des idées en optique et en mathématiques, et il n'y aucune preuve documentaire d'une idée sur la nature de la gravitation à ce moment-là. Nous savons aussi par l'histoire des sciences que des concepts théoriques si profonds naissent rarement du néant.

Cependant, si nous situons « l'événement de la chute de la pomme » 13 ans plus tard, en 1679, il gagne beaucoup en crédibilité. Newton avait passé la plus grande partie de l'été dans sa maison familiale du Lincolnshire. Sa mère venait de mourir, et il devait s'occuper d'affaires familiales : il y aurait alors eu beaucoup d'occasions de voir des pommes tomber dans ce jardin-là.

 

 

5. La trajectoire elliptique

La correspondance qui s'en suivit avec Hooke pendant l'hiver 1679-1680 montre que Newton n'avait pas encore une compréhension très profonde de la mécanique céleste. Sa première idée avait été – conformément à l'opinion scientifique de son temps – qu'un corps chutant aurait une trajectoire spirale vers le centre de la Terre. Grâce à Hooke il en vient à comprendre que le corps suivrait plutôt une trajectoire elliptique (figure 4).

 

 

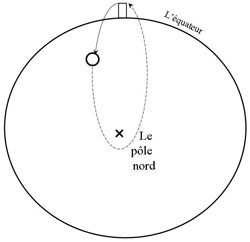
Figure 4: Hooke et Newton étaient d'accords au sujet de la trajectoire elliptique d'un corps tombant, soumis à l’attraction de gravitation terrestre.

 

 

À partir de ces prémisses – une corps en chute suit le même type d'orbite que celle des planètes autour du Soleil, il n'était pas aberrant d'inférer que les mouvements de ces différents corps sont régis par la même loi – la gravitation universelle. Néanmoins, même un génie comme Newton mit quelques années de plus à aboutir à cette conclusion dans les Principia.

 

 

6 Gauß et Laplace

Plus d'un siècle après, on assiste à un regain d'intérêt pour la déviation des corps tombant. L'aplatissement des pôles s'était trouvé être une preuve de la rotation terrestre, ce qui avait tranché le conflit sur le sujet. Mais c'était en quelque sorte une preuve indirecte...

En 1803, a lieu en Allemagne une expérience de lâché de scories de fer dans un puits de mines de 90 m de profondeur. L'expérience suscite l'intérêt de la communauté scientifique ; le mathématicien allemand  Carl Friedrich Gauß, âgé de 24 ans, et le mathématicien français  Pierre-Simon de Laplace, âgé de 53 ans, relevèrent le défi du calcul de la déviation attendue.

 

 

Figure 5: Le schéma des chutes dans l’expérience de 1803 de Schlebusch. La croix indique la déviation théorique.

 

 

La compétition était déjà engagée sur un autre sujet, puisque l'année précédente,  Gauß avait réussi à calculer l'orbite de l'astéroïde Cérès, nouvellement découvert – ce que Laplace avait estimé impossible. Sur la chute des corps, les deux savants donnèrent la réponse correcte, en dérivant l'équation tridimensionnelle complète d'un mouvement sur la Terre en rotation.

Ils notèrent spécifiquement que les termes de Coriolis (comme nous les appelons maintenant )[1] étaient à l'origine de la déviation.  Gauß et Laplace furent donc les premiers savants à donner cette preuve de la rotation terrestre quelques 50 ans avant l'expérience du pendule de Foucault, et à analyser correctement le mouvement relatif aux repères en rotation, 30 ans avant l'article mathématique de Coriolis.

 

 

7. La dérivation par Laplace, comparée à celle d'aujourd'hui

Ce qui rend la dérivation de Laplace difficile à suivre pour le lecteur moderne est:

• Le manque d'illustrations. Dans la figure 6, nous avons tenté de montrer visuellement ce que Laplace avait en tête.
• Les notations mathématiques d'époque. Laplace définit par exemple la latitude comme l'angle depuis l'axe de rotation de la Terre (en fait, pour nous, la colatitude), alors que nous le mesurons depuis l’Équateur.
• L'utilisation de formes cartésiennes de coordonnées. Ce n'est qu'au cours du XIX^e siècle que des physiciens (et non des mathématiciens) britanniques, allemands et américains développèrent, pour des raisons pratiques et afin de faciliter les interprétations, le système de notation vectorielle moderne.
• Pour obtenir l'estimation la plus exacte possible, Laplace avait voulu aussi prendre en considération la résistance de l'air.
• Il voulait enfin, au moyen de calculs les plus détaillés possible, vérifier s'il y avait une possible déviation, mineure, vers le sud.

 

 

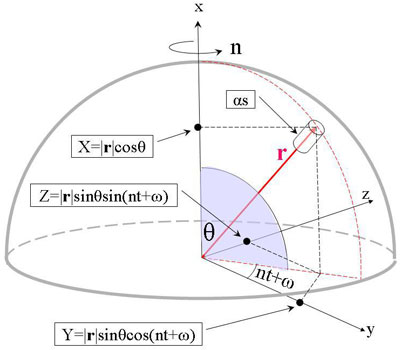
Figure 6: Le modèle de calcul de Laplace pour la Terre, avec une tour à la colatitude θ (correspondant à la latitude 90-θ).

 

 

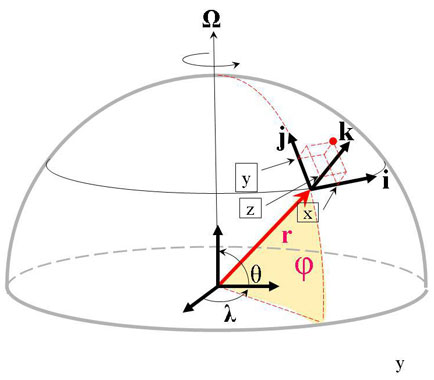
Figure 7 : Le système moderne de coordonnées sphériques θ, λ et r. Localement, un système de coordonnées cartésiennes en x, y et z peut aussi être défini.

 

 

La dérivation de Laplace s'opère de manière analogue aux dérivations modernes : une transformation des coordonnées d'un repère absolu vers un repère relatif en rotation. La transformation du vecteur A telle qu'observée dans le repère absolu (il affecte au vecteur les coordonnées x, y et z) et dans le repère relatif (il affecte les coordonnées X,Y et Z), tournant à vitesse angulaire Ω  est décrite par la très puissante relation suivante:

 

                   

A représente n'importe quel vecteur, choisissons le vecteur position r :

 

 

ou, en notant v la vitesse

 

On applique ensuite (1) à la vitesse absolue, d'où:

 

            

 

En replaçant (2b) du côté droit de (3), on obtient:

 

 

d'où

 

Ainsi donc dans un repère absolu:

 

 

Cependant, nous sommes intéressés par les accélérations dans le repère relatif:

 

 

où -2 Ω × v_rel représente la force de Coriolis  (par unité de masse) déviant le mouvement vers sa droite et - Ω × Ω × r l’accélération centrifuge, dirigée vers l'extérieur, éloignant le mobile de l'axe de rotation terrestre.

 

 

@@@@@@@

 

 

On peut trouver algébriquement les composantes de cette accélération en développant le produit vectoriel :

 

 

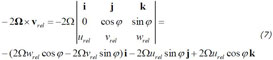
Ce qui conduit à une déflexion du mouvement est-ouest (ou mouvement latitudinal u_rel) dans deux directions – celles où le terme u_rel apparaît : en direction N-S, ou direction méridionale (j), avec une valeur -2Ωu_relsinφ ; et dans la direction verticale (k) avec une valeur de 2Ωu_relcosφ. La première déflexion, bien connue, est l'effet Coriolis, la seconde est « l'effet Eötvös » qui explique pourquoi les mouvements horizontaux vers l'est ou l'ouest rendent un objet plus léger ou plus lourd. Le mouvement méridional (v_rel) ne sera quant à lui défléchi que dans la direction est-ouest (i), avec une valeur de 2Ωv_relsinφ ; il en est de même du mouvement vertical (w_rel), avec une déflexion d'une valeur de Ωw_relcosφ.

 

 

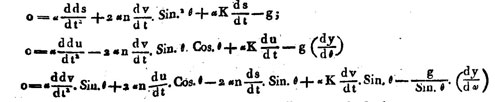
Figure 8: Décomposition par Laplace de la déviation totale en chacun de ses composants (p.112). Les notations s, u et v sont des distances. La vitesse de rotation, Ω en notation moderne, est ici notée n. Laplace a aussi tenu compte du frottement de l'air, donné par les termes en K : en fait, cette composante a très peu d'effet sur la déviation.

 

 

8. L'interprétation du terme -2 Ω × v_rel

L'effet Coriolis a été découvert au XIX^e siècle – depuis lors mathématiciens et physiciens se sont battus pour trouver une explication intuitive qui soit satisfaisante : pourquoi un «- 2 », et pourquoi un produit vectoriel ? À ce stade personne n'y est réellement parvenu ; donc acceptons ce terme tel qu'il apparaît... D'un autre côté, il est assez facile de comprendre ce que signifie en termes physiques la valeur -2 Ω × V_rel. Grâce à la notation vectorielle qui fut justement développée pour faciliter l'interprétation physique, on peut écrire :

 

Tous les mouvements relatifs V_rel (ou les composantes de ces mouvements) perpendiculaires à l'axe de rotation Ω seront déviés, perpendiculairement à la fois au mouvement (V_rel) et à l'axe Ω, vers la droite (pour une rotation antihoraire)[2]. Tandis qu'un mouvement (ou composante de mouvement) parallèle à l'axe de rotation ne sera pas dévié (figure 9).                                         

 

 

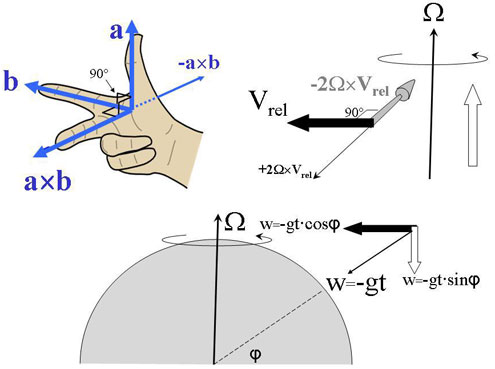
Figure 9: La correspondance entre les vecteurs a, b et leur produit vectoriel a×b est donnée par la règle de la main droite (à g.). De là, il est facile de voir (à dr.) comment le mouvement relatif V_rel , vecteur perpendiculaire à l'axe de rotation Ω, est dévié d'une valeur de -2Ω×V_rel .  Les mouvements parallèles à l'axe ne seront pas déviés, comme l'indique la flèche blanche à l'extrême droite.

 

 

Plus spécifiquement : pour un mouvement vertical w, avec la convention w>0 pour un mouvement ascendant, on peut écrire la vitesse en chute libre (w<0) par la formule w= - g.t. Elle peut être séparée en une composante  w·sinφ·g·t parallèle à l'axe terrestre et une autre composante w·cosφ·g·t perpendiculaire. Seule cette deuxième composante sera déviée (vers sa droite) par l'effet Coriolis.

 

 

Figure 10 : La vitesse d'un corps en chute libre –gt peut être décomposée n un terme perpendiculaire à l'axe terrestre et un terme parallèle. Seul le premier subira une déviation.

 

 

9. La déviation selon l'effet Coriolis

Nous pouvons à présent, comme Laplace (ainsi que Gauß) en 1803, calculer la déviation d'un objet tombant. Notons d'abord que le temps t pris par un objet pour tomber d'une hauteur h est :

 

 

sa vitesse va croître selon la formule :

 

et quand il touche le sol, il aura une vitesse de :

 

 

ou

 

 

Pour la clarté d'exposition, les dérivation seront menées pour une chute à l’Équateur (φ=0, sinφ=0, cosφ=1). Pour un calcul à une autre latitude, on peut remplacer Ω par Ωcosφ.

Pour cet objet en chute verticale, la déviation est (section 8) de  -2Ω×w, avec w = -g·t ; ce qui peut aussi être écrit comme une dérivée seconde de la position S :

 

 

En intégrant (9a) en fonction du temps, pour une chute depuis une hauteur h, avec une vitesse horizontale initiale de V₀, conduit à

 

 

Or en fait la vitesse initiale V₀ = 0, d'où par intégration :

 

 

En prenant comme point de départ des distances le pied de la tour, alors S₀ = 0, et (8a) donne :

 

 

Ce qui correspond exactement au résultat de Laplace p.115 (sachant que nous avons pris sinq =1):

 

 

C'est à nouveau une explication plutôt mathématique de la déviation, avec peu de « sens » physique. Mais, comme souvent en physique, il y a plus d'une dérivation mathématique possible pour le même processus. Faisons les dérivations à la Newton et à la Kepler – comme ceux-ci les auraient faites s'ils y avaient pensé !

Alors que la dérivation que nous venons de faire en utilisant l'effet Coriolis était conduite dans un repère relatif – celui de la Terre sur laquelle nous nous placions, en suivant sa rotation –, nous allons maintenant nous situer dans un repère absolu, en dehors de la Terre, en regardant la chute d'objets et la façon dont ils sont emmenés par la rotation terrestre.

 

 

10. La déviation selon les lois de Newton

Pour notre première dérivation newtonienne, nous utiliserons l'idée (émise avant Newton) selon laquelle la courbure terrestre affecte le corps en chute par un composant gravitationnel dirigé « vers l'arrière », qui en fait le retarde, en comparaison du modèle simpliste présenté en figure 1.

 

 

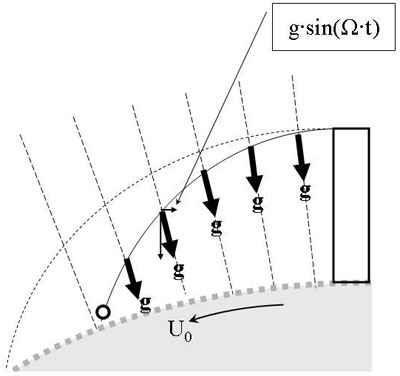
Fig. 11: À la différence de la figure 1, où les lignes de champs gravitationnel étaient parallèles et la trajectoire une parabole, dans ce cas de lignes de champ radiales, la trajectoire est en principe une ellipse.

 

Le calcul de cette accélération arrière peut être simplifié grâce à la petitesse de l'angle Ω·t :

 

 

ce qui par intégration conduit à :

 

 

où U = Ω (R+h) est la valeur de la rotation terrestre à la hauteur h. Finalement l'on obtient :

 

 

         Mais le point de la surface terrestre vers lequel se dirige le mobile est lui-même en mouvement à une vitesse U₀ = Ω·R < U. Cette différence de vitesse U - U₀ = Ωh amène le mobile en-deçà du pied de la tour, à une distance de :

 

 

En insérant (8a), on retrouve :

 

 

Si seulement Newton avait examiné de manière plus tenace le problème de la déviation de ses fameuses pommes détachées de leur arbre, il aurait été capable de dériver la formule (12) déjà au XVII^e siècle, et peut-être aussi de découvrir l'effet Coriolis. Mais il n'aurait pas été forcément le seul : Kepler aurait pu lui aussi le faire 50 ans auparavant.

 

 

11. La déviation selon la 2^nde loi de Kepler (loi des Aires)

Cette 2^nde loi de Kepler, suivant laquelle le rayon-vecteur décrit des aires égales en des temps égaux, n'était pendant longtemps supposée s'appliquer qu'aux corps célestes : planètes, comètes. Au cours du XVII^e siècle, cette loi n'était pas unanimement comprise ni acceptée, même par Newton. Ce ne fut qu'à partir de son travail sur les “Principia” au milieu des années 1680 qu'il comprit la validité de cette loi, mais aussi ses considérants. Ce ne fut, par exemple, que lorsqu'il remit en cause un concept important de la théorie de Kepler (celui selon lequel la trajectoire d'une planète en orbite a son foyer non au centre du Soleil comme imaginé par Kepler, mais au centre de gravité commun de la planète et du Soleil) qu'il fut capable de formuler sa propre loi.

Kepler n'avait jamais imaginé étendre la validité de sa théorie au voisinage terrestre. Ce n'est qu'au cours du XVIII^e siècle qu'il a été réalisé que sa seconde loi, dite « loi des Aires », pouvait aussi être appliquée aux objets terrestres, sous forme d'une loi de conservation du moment angulaire.

 

 

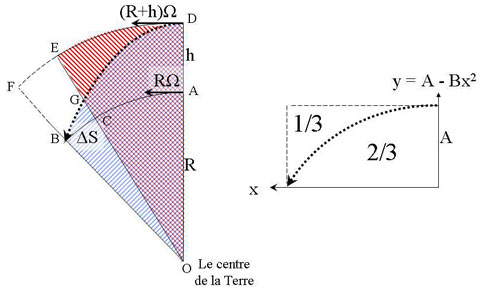
Figure 12a: Le corps tombant suit la trajectoire DGB, alors que le sommet de la tour suit la trajectoire DE, et la base la trajectoire AC.  12b: Toute parabole inscrite dans un rectangle occupe les 2/3 de l'aire de celui-ci.

 

Notre objet tombant suit une trajectoire absolue DGB, alors que le pied de la tour suit AC (figure 12a). Suivant la seconde loi de Kepler, les deux surfaces ODBO (hachurée en bleu et violet) et ODEO (en rouge et violet) sont égales ; et par ailleurs l'objet tombant au point B dépasse donc la tour d'une distance  CB=ΔS.

De cette égalité d'aires on déduit que les deux aires ODGO (hachurée en violet) et DEGD (en rouge) sont égales. On leur ajoute ensuite à chacune l'aire (blanche) GEFB, ce qui donne aire DFBD = aire OEFO.

Considérant h << R, et la petitesse des angles en cause (bien plus petits que sur la figure !), nous prenons l'approximation BG ≈ BC ≈ FE ≈ ΔS, principalement en négligeant l'aire GBC ≈ 0 en en traitant GEFB comme un  rectangle d'aire ≈ h·ΔS, avec l'aire OEFO ≈ ΔS (h+R)/2.

De notre discussion précédente (fig. 4), nous savons que la trajectoire est une ellipse, mais pour les très courtes durées sur lesquelles nous raisonnons là – à peine quelques secondes –, nous pouvons considérer la trajectoire comme parabolique. Pour la même raison, nous pouvons considérer DFBA comme un rectangle d'aire =(R+h)Ω·t. De la règle géométrique d'une parabole inscrite dans un rectangle (fig. 12b), nous pouvons calculer de manière approximative l'aire DFBD = h·(R+h)·Ω·t/3, et nous avons :

 

 

ce qui conduit de nouveau, en insérant (8), à :

 

 

 

 

12. Un complément donné par Laplace pour les objets projetés verticalement.

Quand Laplace publia ses Œuvres en 1805, il modifia légèrement son article de 1803, en incluant l'analyse de la déviation d'un objet lancé verticalement vers le haut (tel un boulet de canon par exemple). Cette nouvelle version peut être trouvée sous la référence « De la chute des corps qui tombent d’une grande hauteur », Traité de Mécanique Céleste, TIV, Seconde Partie, Livre X, p. 294-305 [3].

 

 

 

 

De telles expériences étaient en fait conduites depuis le début du  XVII^e siècle. En 1627, un mathématicien allemand d'Ulm, Joseph Furtenbach, tira des boulets de canon vers le haut et, certain qu'ils ne retomberaient pas droit, grimpait juste après le tir pour s'installer sur la bouche du canon. La même expérience fut menée en 1634 par Mersenne, à la demande de Descartes. Les étudiants de Galilée à Florence menèrent aussi dans les années 1650 une expérience où le canon était monté sur une voiture tirée par six chevaux rapides, afin de voir si cette vitesse conduisait à un résultat différent d'un tir au repos.

 Les résultats étaient en général non conclusifs. Il arrivait que les boulets de canon fussent perdus, et ceci accréditait la fallacieuse croyance suivant laquelle ils échappaient à la gravitation terrestre et partaient dans le cosmos pour ne plus revenir. Il est plus vraisemblable qu'ils étaient emmenés assez loin par les forts vents qu'ils rencontraient dans l'atmosphère.

 

 

@@@@@@@

 

 

Reprenons à présent la dérivation à la Coriolis faite par Laplace en 1803, et voyons comment elle aurait pu être faite dans un mode newtonien ou képlerien. L'accélération de Coriolis avec vitesse initiale V₀ s'écrit :

 

 

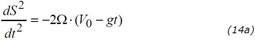
d'où, en intégrant

 

 

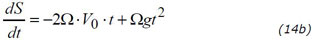
et enfin

 

 

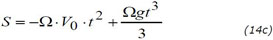
La valeur du temps telle que présentée en (8b) doit être multipliée par deux, puisque le temps mis par le projectile pour atteindre la hauteur h puis redescendre est le double du temps de chute d'une hauteur h. Ce qui donne :

 

 

et donc, en reportant dans (14c), une déviation de :

 

 

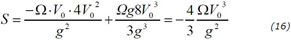
Puisque S < 0, la déviation se fait cette fois-ci vers l'ouest. Ce résultat mérite d'être expliqué plus avant. Pour un projectile tiré dans l'air et retombant ensuite, on pourrait s'attendre à ce que la déviation durant la chute compense la déviation durant l'ascension.

 

 

Figure 13:  La trajectoire relative, à la fois au canon et au sol, d'un objet projeté verticalement avec une vitesse initiale V₀. À g. : Pourquoi ne serait-il pas dévié dans l'autre sens, en retombant sur le sol ?  À dr. : Un  objet lâché de la même hauteur retomberait à l'est, mais cette déviation vers l'est n'est pas assez importante pour compenser la première déviation vers l'ouest. De plus, comme le corps projeté se meut vers l'ouest quand il atteint son apogée, alors que le corps simplement relâché est au départ au repos, la situation n'est pas la même.

 

 

Imaginons que notre projectile envoyé vers le haut s'approche par hasard à son apogée d'un autre corps, relâché de la même hauteur en chute libre. Comme tous deux sont en phase descendante, on attendrait que leurs trajectoires soient très voisines. Mais le projectile parti du sol a, arrivé à son apogée, une vitesse horizontale vers l'ouest, causée par l'effet Coriolis. La déviation vers l'est de l'objet simplement lâché d'en haut ne sera en tout état de cause que de la moitié de  la déviation vers l'ouest qu'elle serait supposée compenser (figure 13).

 

 

13. La déviation d'objets projetés verticalement, selon les lois de Newton

À présent, dans un repère absolu, selon les lois de Newton, la déviation arrière due à la courbure terrestre, vaut, comme précédemment évoqué : 

 

 

 

 

 

 

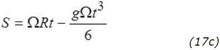
en reprenant pour le temps l'expression (15) ci-dessus

 

 

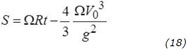
Ainsi, alors que le canon tourne à une vitesse de ΩRt avec la Terre en rotation, le boulet tiré verticalement retombe légèrement derrière le canon  (S < ΩRt).

 

 

14. La déviation d'objets projetés verticalement, selon la 2^nde loi de Kepler

En utilisant cette loi de Kepler des aires égales, nous pouvons immédiatement voir que le canon va dépasser le projectile tiré verticalement, puisque l'aire OADBO = area OACO. Les deux ont en commun l'aire OABO (violette) ; donc nous nous  concentrons sur l'aire (rouge) OBCD=R·ΔS/2 et l'aire (bleue) ADBA=2Ω·R·t·h/3 suivant la formule de la parabole (ici approximant l'ellipse) inscrite dans un rectangle.

 

 

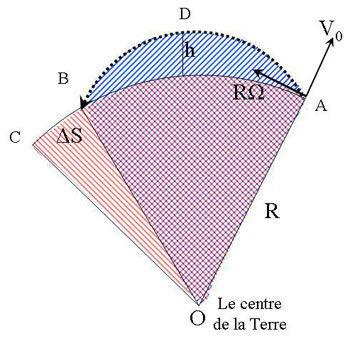
Figure 14: La trajectoire du corps projeté, ADB, vue dans un repère absolu. Pendant la même durée, la position de la base de lancement (le canon) a avancé sur une distance plus longue, ABC. Dans les deux cas, le rayon-vecteur couvre la même aire : OADB=OABC. La trajectoire ADB est en réalité une ellipse mais peut ici être assimilée à une parabole.

 

Avec (8a) et (15) on intègre suivant les deux périodes de temps pour aboutir à nouveau à la même formule :

 

 

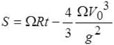
À cette époque, un canon avait une vitesse de sortie (V₀) d'environ 400 m/s. Un angle de lancer de 45° signifie une vitesse horizontale et une vitesse verticale égales à V_0H = V_0V = 283 m/s. L'obus – ou grenade – mettra 29 secondes pour atteindre son apogée à 4 km de hauteur, et 58 secondes à atteindre sa cible  (en négligeant le frottement de l'air), qui sera située à un peu plus de 16 km. L'obus arrivera en fait en-deçà de sa cible d'une distance de 45 m – ceci dans une région équatoriale, avec  2Ωsinφ = 0, et donc sans déflexion horizontale.

Si nous montons à présent à une latitude italienne de 43°, avec Ωcosφ = 0.53·10^-4 /sec, le projectile arrivera en-deçà de sa cible d'une distance de 17 m.  Mais, comme 2Ωsinφ = 1.00·10^-4 /sec, il subira aussi une déflexion de 47 m sur le côté.

 

 

15. Autres aspects de la dérivation de Laplace

Comme indiqué en introduction, Laplace fit ses dérivations de manière consciencieuse, essayant de prévoir les effets du frottement, ainsi que toute déviation vers le sud. Nous n'entrerons pas dans ces détails, mais mentionnerons simplement que le frottement, selon Laplace, n'a pas de conséquence significative sur la déviation.

Concernant une déviation possible vers le sud, ou plutôt dirigée vers l’Équateur – un sujet de controverse il y a 200 ans déjà –, les calculs de Laplace ne montrent pas d'effet, mais ceux de  Gauß oui ; ceci continue à être un sujet controversé de nos jours. Une part du problème est de définir ce que signifie « vers le sud » : est-ce en relation avec la latitude ou avec la forme effective de la Terre ?

Laplace et Gauß ignoraient bien sûr les travaux ultérieurs de géodésie, qui définirent plus précisément la forme de la Terre. De nos jours, la sagesse la plus communément acceptée est que cette déviation-là n'existe pas, ou est d'ordre équivalent à celui des approximations mathématiques indispensables... De fait, des expériences contemporaines n'ont pas permis de mettre en évidence une quelconque déviation vers le sud.

 

 

16. Pourquoi cela prit-il presque 200 ans ?

Nous avons donc montré que les expressions correctes pour la déviation d'un objet tombant auraient pu être déduites 100 ans auparavant par Newton, si ce n'est 200 ans auparavant par Kepler. Alors pourquoi ne le firent-ils pas ?

Dans le cas de Newton, ce fut parce que personne ne le lui demanda. La déviation des corps tombant avait été, comme nous l'avons vu, une priorité de la communauté scientifique au XVII^e siècle, mais des calculs simplistes (figure 1) avaient conduit à des valeurs très faibles. Les expériences de Hooke avaient montré une grande dispersion, et le sujet avait alors été considéré comme impossible à traiter scientifiquement.

Mais les expériences de Benzenberg (figure 5) elles aussi montraient une grande dispersion, comme celles de Reich dans une expérience ultérieur de 1834. À cette époque cependant, la compréhension des erreurs statistiques avait progressé scientifiquement : il devenait plus naturel de calculer une moyenne de mesures.

En effet, jusque tard dans le XVIII^e siècle, les savants, notamment les astronomes, avaient pris l'habitude d'essayer de trouver, parmi leurs nombreuses mesures ou observations, lesquelles étaient « les meilleures ». Combiner des observations ajouterait à l'erreur, croyait-on. Grâce à Laplace, à Gauß, à Legendre [4] et à d'autres, on comprit le caractère aléatoire des erreurs, et que la combinaison d'observations neutraliserait dans une certaine mesure les marges d'erreur, amenant à des moyennes finalement plus précises que n'importe quelle mesure choisie au hasard.

Quant à Kepler, la raison pour laquelle Kepler il n'aurait pas été capable d'appliquer sa deuxième loi est, on l'a vu, sa focalisation sur les corps célestes – il pensait que ses travaux ne s'appliquaient pas aux corps terrestres. Leur validité universelle n'apparut qu'après la publication des Principia de Newton. Avant cela, des doutes étaient même émis sur leur validité tout court, sous prétexte que ces lois avaient été inférées par l'observation d'une planète unique, Mars, à l'excentricité trop marquée.

Finalement, Laplace et Gauß ont réussi à déduire ce que nous appelons à présent « effet Coriolis » quelques 30 années avant Coriolis. Pourquoi n'ont-ils pas été crédités de cela, au moins pour l'un des deux ? Une raison pourrait être que l’œuvre de Coriolis traitait du mouvement des machines, et pouvait apparaître moins spécifique que ces calculs de Laplace ou de Gauß. Mais plus vraisemblablement, l'intérêt pour le mouvement relatif dans des repères en rotation ne se manifesta vraiment – et comment ! – qu'après l'expérience du pendule de Foucault, en 1851. Dans les discussions qui suivirent immédiatement, l'article de 1835 de Coriolis se trouvait être bien présent à l'esprit des savants, car il avait été écrit quelques années auparavant. Le mathématicien français Joseph Bertrand allégua alors que Coriolis avait plagié Alexis Clairault, qui aurait obtenu les mêmes résultats 100 ans avant lui. Il y a matière à revenir sur ce point précis dans une contribution ultérieure...

 

(août 2014)

 

(traduit en français par Alexandre Moatti, publié en mars 2015)