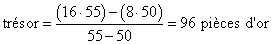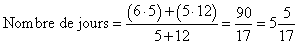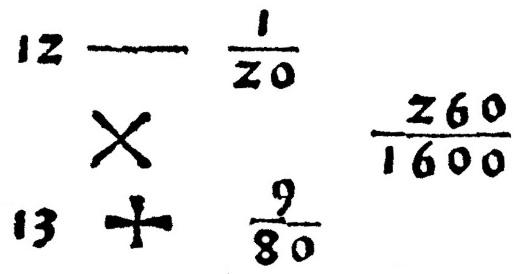Schreyber alias Grammateus : De la « fausse position » aux timides débuts de l’algèbre
- INFORMATION
- ACTUALITÉ
- ANALYSE
- EN SAVOIR PLUS
- À TÉLÉCHARGER
Ayn new kunstlich Buech welches gar gewiss vnd behend lernet nach der gemainen regel Detre welschen practic regeln falsi und etlichen regeln Cosse… (« Un nouveau livre conforme aux arts, qui enseigne avec certitude et prestement la règle de trois commune, la pratique italienne, la règle de la fausse position et l’algèbre… »), Johann Stüchs, Nuremberg, 1518-1521.
terminé en 1518, imprimé vraisemblablement en 1521.
La méthode de la fausse position, aujourd’hui oubliée, était manipulée pour résoudre de nombreux problèmes, comme dans ce texte, où apparaissent aussi les premiers signes algébriques + et –, utilisés de manière opératoire.

Sur le long chemin qui a conduit l’algèbre à sa pleine efficacité, un livre publié à Nuremberg en 1521 mérite d’être tiré de l’oubli. Outre le fait qu’il propose la première utilisation des symboles + et – dans un contexte algébrique, il permet de comprendre pourquoi le procédé de la fausse position est resté longtemps un grand rival de l’algèbre. Les quelques extraits donnés de ce texte illustrent ces deux réalités, présentes dans les premiers ouvrages imprimés d’arithmétique : d’une part la montée en puissance des symboles + et –, et d’autre part la lente progression de l’algèbre en Occident, où elle avait de la peine à concurrencer le procédé de la fausse position. Procédé qui, encore aujourd’hui, peut permettre de résoudre certains problèmes plus facilement qu’en posant des équations algébriques.
L’auteur est Heinrich Schreyber, qui se désignait sous le nom d’Henricus Grammateus (Henri le scribe). Né à Erfurt au plus tard en 1496, il a étudié à Cracovie et surtout à Vienne, où il a rédigé en 1518 ce livre de 124 folios, qui est son ouvrage principal. Fuyant la peste, il a quitté Vienne en 1521 pour Nuremberg, où il a fait imprimer son livre ainsi qu’un version réduite de 40 folios, puis pour Erfurt, avant de rentrer à Vienne où il est mort en 1525, à environ trente ans. Christoff Rudolff, l’auteur du premier ouvrage allemand consacré entièrement à l’algèbre, en 1526, y écrit que c’est par Schreyber qu’il a entendu parler de cette matière pour la première fois, et qu’il « lui en est reconnaissant » (sag im darumb danck).

On the long road that led to algebra becoming the highly effective instrument it is today, a book published in Nuremberg in 1521 deserves to be rescued from oblivion. Besides the fact that it is the first publication to use the + and – symbols in an algebraic context, it also shows why the false position method long remained a worthy rival to algebra. The excerpts from this text illustrate the two realities evident in the first printed arithmetic publications: on one hand, the rise of the + and – symbols, on the other, the slow advent of algebra in the West, where it initially struggled to compete with the false position method. Even today, it is easier to solve certain problems with false position than it is with algebraic equations.
The author is Heinrich Schreyber, who styled himself Henricus Grammateus (Henry the Scribe). Born in Erfurt in 1496 at the latest, he studied in Krakow but mainly in Vienna, where in 1518 he wrote this book, which runs to 124 folios in length. It is his most important work. Fleeing the plague, he left Vienna for Nuremberg in 1521. It was there that he had his book published, as well as an abridged version running to 40 folios. He then left for Erfurt before returning to Vienna, where he died in 1525 at the age of about 30. Christoff Rudolff, author of the first work in German specifically focused on algebra (published in 1526), wrote in this book that it was through Schreiber that he had first heard about this subject, and that he was grateful to him (sag im darumb danck).

Jérôme Gavin est mathématicien. Il enseigne les mathématiques au Collège Voltaire à Genève, en classes terminales notamment. Il a écrit jusqu’ici deux ouvrages en histoire du calcul, avec Alain Schärlig.
Alain Schärlig est mathématicien, et docteur en économie politique. Il est professeur honoraire à la Faculté des Hautes études commerciales de l’Université de Lausanne. Il a écrit à ce jour huit livres en histoire du calcul, dont les deux derniers avec Jérôme Gavin.
Ces ouvrages ont été publiés aux Presses polytechniques et universitaires romandes, la maison d’édition de l’École polytechnique fédérale de Lausanne (EPFL).

Jérôme Gavin is a mathematician. He teaches mathematics at Collège Voltaire in Geneva, where he mainly teaches final-year students. He has co-written two books about the history of calculation with Alain Schärlig.
Alain Schärlig is a mathematician and holds a PhD in political economy. He is honorary professor at the Faculty of Business (HEC), University of Lausanne. He has written eight books about the history of calculation, of which the two most recent were co-written with Jérôme Gavin.
These books are published by the Presses polytechniques et universitaires romandes, the publishing house of the École polytechnique fédérale de Lausanne (EPFL).

Les informations circulent de nos jours à la vitesse de la lumière, et les progrès dans tous les domaines se développent très rapidement. Cela nous fait oublier qu’autrefois tout était infiniment plus lent, autant dans la transmission des connaissances que dans le développement de celles-ci.
Certains considèrent par exemple que l’algèbre « était connue depuis l’an 825 », parce que le plus ancien traité qui en parle, écrit en arabe à Bagdad par Al-Khwarizmi, date de cette époque. Mais ils ne se demandent pas à quelle époque elle est arrivée dans nos contrées (c’est la question de la transmission), ni sous quelle forme elle était connue au Moyen Âge (c’est la question du développement).
C’est pourquoi nous pensons intéressant de montrer d’une part comment l’algèbre était présentée en 1521 en Allemagne, par l’un des premiers auteurs à en parler ; et de faire voir d’autre part qu’elle n’était pas encore considérée comme l’arme absolue, concurrencée qu’elle était par une bien plus ancienne technique, la fausse position.
La Regula Falsi, après l’arithmétique, avant la musique et la comptabilité
La page intermédiaire (ci-dessous) annonce la partie consacrée à la fausse position et à l’algèbre. Cette partie compte 78 pages ; elle est précédée de 95 pages d’arithmétique classique, avec une forte part réservée à la règle de trois ; et suivie de 78 pages traitant de musique, de comptabilité et d’étalonnage des fûts. Loin d’être seulement anecdotique ou esthétique, cette page est d’un grand intérêt pour qui s’intéresse à l’histoire des mathématiques.

On remarque d’abord que la taille des caractères avantage nettement la fausse position, appelée ici Regula Falsi (« règle du faux » en latin), par rapport à l’algèbre, dite Coss en Allemagne à l’époque (par altération de Cosa, « la chose », qui désignait l’inconnue en italien). Cela montre que l’algèbre n’était pas encore, en 1521, la référence en matière de résolution de problèmes. Cette position minoritaire vis-à-vis de la fausse position tenait au fait qu’elle n’était pas encore pleinement efficace, comme on le verra par la suite.
On note aussi sur cette page un paradoxe : dans un livre entièrement consacré au nouveau calcul écrit, rendu possible par les chiffres présentés dans ses premières pages – des chiffres que l’auteur ne présente ni comme indiens ni comme arabes –, la gravure montre uniquement des personnages qui calculent… au moyen de jetons, et sur des abaques ! Et elle apparaît trois fois dans le livre ! C’est le signe qu’en Allemagne, en 1521, le nouveau calcul était encore très minoritaire.
La fausse position
Cette méthode calculatoire, aujourd’hui bien oubliée, était fort connue à l’époque – le lecteur contemporain en trouvera un bref résumé dans l’encadré ci-dessous (1).
|
La fausse position simple
Le procédé de la fausse position, déjà connu des anciens Égyptiens, s’applique aux problèmes linéaires. On pose pour l’inconnue une valeur facile à manier, tout en sachant qu’elle est fausse. On fait la preuve, et on ne trouve évidemment – en général – pas le résultat voulu. On effectue alors une règle de trois entre la valeur fausse, le résultat faux, et ce qu’on devait trouver. Et il en sort la solution juste.
@@@@@@@
Exemple. Un homme a trouvé un trésor, il en a dilapidé la moitié, il a reconstitué un quart, puis dilapidé un huitième ; il lui est resté 50 pièces d’or ; quel était ce trésor ? On pose 8, parce qu’on voit que ce sera pratique. Diminué de moitié, le trésor est réduit à 4. Puis augmenté d’un quart, il se monte à 6. Enfin diminué d’un huitième, il ne vaut plus que 5. Par rapport à 50 qu’il fallait trouver, 5 est le dixième. Donc 8, c’était dix fois trop peu. La solution est 80. On peut noter au passage que les fameux problèmes de robinets, ou de baignoires qui se vident – le mauvais souvenir de nombreux anciens élèves –, se résolvent beaucoup plus facilement par la fausse position que par l’algèbre. Ce n’est pas étonnant : ils ont été créés il y a très longtemps comme illustration de la fausse position, et embarqués par la suite dans le corpus des leçons d’algèbre où ils sont beaucoup moins à leur place. En voici un exemple (Byzance, xive siècle). Un récipient est pourvu de 5 tuyaux ; le premier le remplit en 2 heures, le deuxième en 3 heures, et le troisième en 4 heures ; mais dans le même temps l’un le vide en 6 heures, l’autre en 4 heures. Quand tous sont ouverts en même temps, en combien d’heures remplissent-ils le récipient ? On pose 12 heures. Le nombre de fois que le récipient se remplit est 6 + 4 + 3 – 2 – 3 = 8. S’il se remplit 8 fois en 12 heures, il se remplira 1 fois en 1 ½ heure. La solution est donc une heure et demie. Ce serait bien plus compliqué par l’algèbre ! Autre fausse position possible : on pose 1h. Le récipient s’est rempli de 1/2 + 1/3 + 1/4 (les tuyaux d’amenée) et s’est vidé de 1/6 + 1/4 (les tuyaux de vidange). Il s’est donc rempli aux 2/3 : il sera complètement rempli en 3/2*1h, donc en 1 ½ heure. |
Il existe aussi une autre méthode de regula falsi, c’est celle de la fausse position double. C’est celle que l’auteur utilise ici, même s’il ne le dit pas. Sa description textuelle du procédé étant un peu ardue pour nous – mais on peut tout de même relever qu’elle est très pédagogique –, rappelons brièvement ce procédé dans notre langage moderne. On choisit successivement deux valeurs – les fausses positions, ici x1 et x2 – ; on calcule le résultat qu’elles donneraient, et on note les écarts de ces deux résultats – ici e1 et e2 – vis-à-vis de celui qu’on devrait trouver ; on additionne ou soustrait les produits croisés, selon que les écarts sont de même signe ou non ; on calcule la somme ou la différence des écarts, à nouveau selon que ceux-ci sont de même signe ou non ; et la division par cette valeur donne le résultat juste. En notation algébrique – mais on voit que celle-ci n’est pas très adaptée à la description d’un tel procédé ! – on applique la formule que voici :
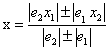 (1)
(1)
Ce qui frappe au premier coup d’œil dans le texte, c’est la grandeur disproportionnée des signes + et –. Ils apparaissent de surcroît là pour la première fois, après une centaine de pages d’arithmétique dont ils sont totalement absents.
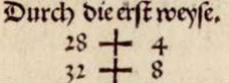
Figure 1 : Grandeur importante du signe +, qui par ailleurs n’a pas une fonction d’opérateur.
Quand on déchiffre le texte, on constate qu’ils ne sont utilisés que comme indicateurs, comme une sorte de sténographie, pour dire qu’il y a excès ou manque ; et donc sans signification opératoire.
Après son explication, Schreyber passe à un exemple… qu’il ne développe pas ! Cela témoigne de la notoriété de la fausse position chez ses contemporains : il ne s’attarde pas sur ce que tout le monde connaît. Mais cinq siècles plus tard, il nous revient d’expliquer ce qu’il passe sous silence !
Il propose de chercher un nombre qui, lorsqu’on multiplie son quart par 8 et que l’on prend la moitié du tout, donne 24. Pour nous qui sommes formés par l’algèbre, la réponse est évidente, c’est 24 :
(x : 4 × 8) : 2 = 24
Et nous voyons aussi que le problème tourne en rond : quelle que soit la valeur choisie comme fausse position, on retombera sur la même valeur comme résultat. Mais ce n’était pas le cas pour les lecteurs du xvie siècle. Auxquels l’auteur propose d’abord d’essayer avec 28.
On suppose donc que le nombre cherché est 28. On prend son quart, 7, que l’on multiplie par huit, 56, que l’on divise par deux, 28. Le résultat étant 28, il y a 4 d’excès par rapport à 24 qu’il faudrait trouver, ce qu’il résume sèchement par « 28 + 4 », pour dire en toutes lettres « si l’on part de vingt-huit, il y a excès, de quatre ». Le second essai est fait avec 32, ce qui donne 32 comme nous pouvons nous y attendre, et un excès de 8 comme le lecteur était censé le découvrir. D’où le résumé « 32 + 8 », pour « si l’on part de trente-deux, il y a excès, de huit ».
Comme il y a deux fois excès, on doit procéder dans la formule (1) à des soustractions : au numérateur (28 × 8) moins (32 × 4), et au dénominateur 8 moins 4 ; soit 96 / 4, et 24 en résultat.
|
La fausse position double
Dans la version double, un peu plus complexe, on pose successivement deux fausses positions, et on calcule l’écart entre chaque résultat faux et ce qu’on devrait trouver. Puis, soit on applique un raisonnement de proportionnalité sur ces écarts, soit on applique une formule (dont on peut montrer qu’elle est équivalente (2)), comme le fait ici Schreyber. Et cela fournit la solution juste. Le choix de la version dépend du problème comme on va le voir, mais on montre que la fausse position double est applicable dans tous les cas ; ce qui fait que certains auteurs anciens ne parlent que d’elle, comme ici Schreyber. Exprimée par Léonard de Pise (dit aussi Fibonacci) en 1202, la formule a la forme suivante (il appelle erreur ce que nous appelons écart) : « La première erreur est multipliée par la seconde position ; et la seconde erreur par la première position. Et si les erreurs sont toutes deux de diminution, ou toutes deux d’augmentation (3), la plus petite somme desdites multiplications est soustraite de la plus grande ; et le reste est divisé par la différence des erreurs ; et ainsi la solution des questions est trouvée : et si une erreur est de diminution, et l’autre d’augmentation, alors les deux multiplications s’additionnent, et la somme est divisée par la somme des erreurs (4). »
Figure 2 : Statue (1863) de Leonardo da Pisa, ou Fibonacci, au Camposanto de Pise (Italie) (photo WikiCommons Hans-Peter Postel, cc-by 2.5)
Exemple (le même que dans l’autre encadré, mais avec une légère modification… qui rend obligatoire de passer à la fausse position double, parce que les anciens – qui ne connaissaient pas l’algèbre – ne voyaient pas qu’il suffisait de transférer la constante 5 de l’autre côté du signe =). Un homme a trouvé un trésor, il en a dilapidé la moitié, il en a reconstitué un quart, puis dilapidé un huitième et enfin récupéré 5 pièces d’or ; il lui est resté 65 pièces d’or ; quel était ce trésor ? Essayons avec la fausse position simple. D’abord avec une fausse position de 8 : 8 – 4 + 2 – 1 + 5 = 10. Puis avec une fausse position de 16 : 16 – 8 + 4 – 2 + 5 = 15. On voit que si l’on double la fausse position, le résultat ne double pas ! Le problème n’est donc plus linéaire. Il faut donc appliquer la fausse position double, et passer par la formule : Première fausse position : 8. Le résultat est 10, il manque 55. Deuxième fausse position : 16. Le résultat est 15, il manque 50.
@@@@@@@
Autre exemple (Chine, IIe siècle avant notre ère). Supposons que l’on ait un muret de 90 cm de hauteur, depuis le sommet duquel pousse un melon, lequel croît d’une longueur de 7 cm par jour, et depuis la base duquel pousse une calebasse, laquelle croît d’une longueur de 10 cm par jour. On demande au bout de combien de jours ils vont se rencontrer. Première fausse position : 5 jours. Le melon a poussé vers le bas de 35 cm, et la calebasse vers le haut de 50 cm. Total 85 cm, il y a 5 cm de déficit. Deuxième fausse position : 6 jours. Le melon a poussé vers le bas de 42 cm, et la calebasse vers le haut de 60 cm. Total 102 cm, il y a 12 cm d’excès. En appliquant la formule telle qu’elle est donnée par Léonard en texte, mais dans notre notation, on calcule le nombre de jours :
On voit au passage que l’expression de la formule sous forme d’un texte (comme le fait Léonard) est plus conviviale que sous forme d’une traduction dans notre notation, comme à la formule (1) ci-dessus. |
Son exemple ayant conduit à deux excès, et donc à des soustractions dans l’application de la formule, Schreyber reprend le même problème avec d’autres fausses positions, pour arriver à un excès et un manque, et illustrer ainsi le cas où l’on procède à des additions. C’est ce qu’il appelle une seconde manière. Il choisit 21 puis 28, ce qui donne un manque de 3 puis un excès de 4, comme l’a corrigé un lecteur de l’exemplaire ayant servi à la numérisation… alors que l’auteur se trompe, et trouve 12 de manque puis 8 d’excès, ce qu’il résume par « 21 – 12 » et « 28 + 8 ». Et c’est bien lui qui se trompe, car deux coquilles de suite, de la part du typographe, de surcroît proportionnelles, sont très peu probables.
Le numérateur de la formule est alors (28 × 3) plus (21 × 4), et le dénominateur 3 plus 4 ; ce qui donne 168 / 7, et à nouveau 24 de résultat.
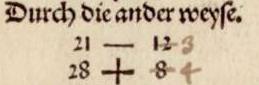
Figure 3 : Avec 28, on est en excès de 4 (après rectification), comme en figure 1 ; avec 21 on est en défaut de 3.
|
Reconstitution du calcul de « fausse position double »
Pour ceux qui tiennent à « démontrer » en termes modernes la formule (1), prenons le problème Kx + b = c, avec les deux fausses positions A1 et A2 : KA1 + b = c + δ1 KA2 + b = c + δ2 On multiplie la première égalité par δ2 et la deuxième par δ1 : KA1δ2 = (c – b)δ2 + δ1δ2 KA2δ1 = (c – b)δ1 + δ1δ2 On soustrait la deuxième égalité à la première : K(A1δ2- A2δ1)= (c – b) (δ2- δ1)
Donc la solution de Kx + b = c est bien donnée par
Figure 4 : Algorismus ratisbonensis de Widmann (ca 1450), folio 137r. Sur un problème qu’il se pose, la position 12 donne un défaut de 1/20 ; la position 13 un excès de 9/80. La différence des deux écarts est 260/1600, et la croix rappelle qu’il faudra faire le « produit en croix » au dénominateur.
Le lecteur pourra s’amuser à résoudre par la fausse position le problème dit de Diophante, où l’on demande combien de temps a vécu la personne suivante : Son enfance occupa un sixième de sa vie ; le douzième fut consacré à l’adolescence ; après un septième de sa vie il se maria ; cinq ans plus tard il eut un fils, qui mourut après avoir atteint la moitié de l’âge de son père ; lequel mourut huit ans après ce décès (5). En prenant par exemple les deux fausses positions A = 72 puis B = 120, on trouve (6) : 72 → 744/7 donc δA = 24/7 120 → 1122/7 donc δB = – 75/7 x = (72*75/7 + 120*24/7 )/(75/7 + 24/7)= 864 / (102/7) = 84 |
Parenthèse : le signe + et le signe –
Comme on l’a dit, Schreyber n’utilise pas les signes + et – en arithmétique ; il ne s’en sert que comme marqueurs en fausse position ; et, comme on va le voir, ce n’est qu’en algèbre qu’il leur donne un rôle opératoire.
Rappelons brièvement la situation de ces deux symboles avant Schreyber, en commençant par les manuscrits. Le symbole + apparaît dans l’Algorismus Ratisbonensis, écrit vers 1450. Le + et le – figurent dans le Codex Dresden C 80 écrit en 1481, mais sous la forme de corrections, que certains attribuent à Johannes Widmann (ca 1460-1498). Le Codex Lips. 1470 enfin, conservé à Leipzig et reflétant un cours donné par Widmann en 1486, contient les deux symboles dans le texte. En un mot : c’est dans ces trois manuscrits, considérés globalement, que les deux symboles apparaissent pour la première fois ; et Widmann y a joué un rôle.
Si l’on passe alors des manuscrits aux livres, c’est l’ouvrage de Widmann qu’il faut considérer en premier. Il a été publié à Leipzig en 1489, sous le titre Behende und hübsche Rechenung auff allen kauffmanschaft (« calcul preste et joli pour tout le monde du commerce »). Le début est consacré très normalement à l’arithmétique, mais il faut attendre le 88e folio pour rencontrer un signe – et un signe +, tous deux opératoires ; et il n’y en aura qu’une douzaine d’autres par la suite. Widmann a donc été le premier à utiliser ces symboles dans un livre, avec cette signification.
Et ce n’est pas son seul coup fumant. Aux folios 201 et 202, il parle de la fausse position. Et dans les schémas qu’il propose pour résumer la situation d’un problème, il utilise à nouveau le + et le –, mais cette fois pour indiquer un excès ou un manque, et donc comme marqueurs.
Schreyber suit donc ici l’invention de Widmann, dont la notation permet d’automatiser la pratique de la fausse position double. Sa révolution à lui, ce sera d’utiliser les mêmes symboles dans un cadre algébrique.

Figure 5 : Ouvrage de Widmann ; à g. page de garde de l’édition originale, Leipzig 1489 (pour mémoire, les premiers ouvrages imprimés par Gutenberg datent de 1452 à 1455); à dr. page de garde, illustrée, de l’édition d’Augsburg 1526 (images MDZ, Bayerische StaatsBibliothek, lien).
L’addition en algèbre
Cet extrait révèle lui aussi l’apparition d’une nouveauté : l’algèbre, telle qu’elle est présentée aux Allemands en 1521. C’est un très joli petit cours de calcul littéral, avec des notations d’une lourdeur difficile à supporter pour nous, mais qui comporte surtout une révolution : les signes + et – opératoires, en première mondiale, très clairement qualifiés d’entrée de jeu comme und (« et ») pour l’un, et comme mynnder (« moins ») pour l’autre. L’usage de ces signes est un grand pas vers l’efficacité de l’algèbre. Avec toutefois cette ironie du sort que celle-ci va lentement tuer la fausse position, qui est pourtant à l’origine de l’usage systématique de ces deux signes.
Réglons d’abord la question de la lourdeur des notations. Elle permet de mesurer la lenteur de l’évolution qui a conduit l’algèbre à son statut d’instrument imparable : à l’époque, elle était loin de constituer le moyen idéal pour résoudre un problème !
Schreyber désigne une constante en lui collant la lettre N et un double-point, comme « 6N: » où nous écririons simplement « 6 ». Il désigne d’autre part une variable du premier degré, qui serait pour nous tout simplement « x », en la notant pri avec aussi un double-point, pour prima, ce qui donne par exemple « 9 pri: » où nous noterions « 9x ». Plus loin – dans d’autres passages – il désignera une variable du deuxième degré par se (pour secunda), une du troisième degré par ter (pour tertia), et ainsi de suite.
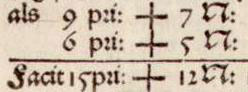
Figure 6 : La première des deux additions.
@@@@@@@
La leçon commence par l’addition de deux binômes comportant un signe +, en colonne à gauche, en parallèle avec celle de deux autres binômes pourvus du signe –, en colonne à droite. Écrites à notre manière, ces deux additions seraient notées comme ceci :
(9x + 7) + (6x + 5) = 15x +12
(6x – 4) + (8x – 10) = 14x – 14
L’auteur passe ensuite à l’addition de deux autres binômes, qui comportent un signe + et un signe –, et dont l’une amène à trouver une constante positive et l’autre une constante négative :
(6x + 6) + (12x – 4) = 18x + 2
(4x + 2) + (6x – 6) = 10x – 4
Il termine enfin par l’addition de deux nouveaux binômes, comportant également des signes contraires, mais où le signe – figure dans le premier et le signe + dans le second :
(6x – 4) + (6x + 2) = 12x – 2
(6x – 2) + (6x + 4) = 12x + 2
Schreyber traite ainsi chaque cas possible par un exemple, plutôt que de donner une règle générale ; et il réserve celle-ci à la fin du passage. Il témoigne ainsi d’une grande capacité pédagogique.
Autre parenthèse : de quand date l’algèbre ?
C’est l’occasion de traiter au passage une question qui n’est pas sans intérêt pour l’histoire des mathématiques : celle de savoir de quand date l’algèbre, dans nos régions et sous sa forme efficace. Lorsque nous situons cette maturité entre la fin du 16e et le début du 17e siècle – par exemple dans une conférence, en relation avec la disparition progressive de la fausse position – une objection jaillit immanquablement de l’assemblée : « mais non, Messieurs, l’algèbre est connue depuis l’ouvrage d’Al-Khwarizmi, qui date de 825 ! »
C’est oublier que le texte de ce grand homme était rédigé en arabe, et qu’il n’a été « publié » qu’autour de 825 qu’à Bagdad, à une époque – le 9e siècle – où régnait dans nos contrées ce que certains ne veulent pas appeler le sombre Moyen Age… mais qui n’était en tout cas pas lumineux pour ce qui touche aux mathématiques.
La première apparition documentée de l’algèbre en Europe – en l’occurrence en Italie – se trouve dans le Liber abaci (« livre du calcul ») de Léonard de Pise, daté de 1202. Elle se situe donc au 13e siècle. En Allemagne, Schreyber a présenté l’algèbre en 1521 comme on vient de le voir, suivi de Rudolff en 1525, puis de Stiefel, qui a mis de l’ordre dans l’ouvrage du précédent en 1591. On est déjà au 16e siècle. Et il en va de même en France, où l’on s’approche de la fin du siècle avec Scheybel en 1550 et Viète en 1591.
Mais il faut encore voir sous quelle forme se sont faites ces apparitions. Avec les « pri: » et les « se: » de Schreyber, et les développements textuels d’autres auteurs – où les lignes successives de nos développements sont remplacées par autant de phrases – on ne peut pas dire que l’algèbre était pleinement efficace. Et c’est bien entre la fin du 16e et le début du 17e siècle, avec l’entrée en force des « x » et des constantes nues, et avec en plus le signe d’égalité inventé par le Gallois Recorde, que l’algèbre a enfin été dans nos contrées l’instrument pleinement efficace que nous connaissons.
La multiplication en algèbre
Cet autre extrait fait pendant au précédent : il montre comment Schreyber amorce sa présentation de la multiplication en algèbre. Et ici aussi, il passe en revue toutes les possibilités : il effectue les produits de deux binômes comportant un signe +, puis de deux autres comportant un signe –, et enfin de deux autres pourvus de signes contraires. Et à chaque fois, il annonce la règle qui s’applique aux signes. Transcrites dans notre notation, ses trois multiplications s’écriraient :
(6x + 6)(5x + 8) = 30x2 + 30x + 48x + 48 = 30x2 + 78x + 48
(6x – 8)(5x – 6) = 30x2 – 40x – 36x + 48 = 30x2 – 76x + 48
(6x + 8)(5x – 7) = 30x2 + 40x – 42x – 56 = 30x2 – 2x – 56
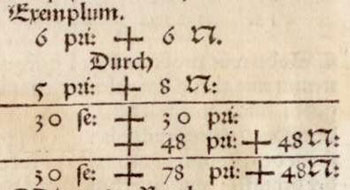
Figure 7 : La première des trois multiplications.
Il conclut son passage par une « règle des signes »… un peu plus verbeuse que celle enseignée dans nos écoles :
Quand les signes sont inverses l’un de l’autre soustrais toujours le plus petit du plus gros, et à ce qui reste mets le signe du plus grand nombre.
Un exemple, par la fausse position et par l’algèbre
Ce premier exemple – l’auteur en donne plusieurs autres – illustre les deux manières, à son époque concurrentes et à égalité, de résoudre un problème : la fausse position d’une part, et « les premières règles de l’algèbre » de l’autre. Et une fois de plus, c’est la fausse position qui est appelée la première.
En choisissant successivement deux fausses positions de 300 et de 240, Schreyber arrive à deux excès, respectivement de 77 et de 57. Et il résume la situation en utilisant deux signes + comme marqueurs :
300 + 77
240 + 57
Contrairement à ce qui serait pour nous évident, il ne s’agit donc pas là de deux additions élémentaires, mais du résumé sténographique d’une étape dans la résolution du problème. L’auteur expédie la suite rapidement : il donne directement le numérateur et le diviseur de la formule, et le résultat. Il considère donc comme évident le développement qui serait pour nous
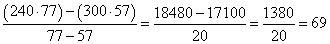
et il ne prend pas la peine d’expliquer pourquoi il faut inverser l’ordre des deux produits du numérateur, et vertu de la règle « tu soustrais le plus petit du plus grand ».
Quant à la résolution par l’algèbre, elle nous donne une bonne image de ce qu’était cette méthode en 1521 : des phrases en continu, qui ne sont pas très opérationnelles ! On peut les comparer à ce qu’écrirait de nos jours un élève débutant, qui noterait scrupuleusement toutes les étapes :
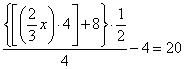
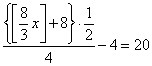
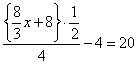
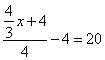
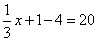
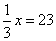
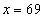
On voit là l’illustration de ce que nous disions ci-dessus : en 1521, il restait encore à l’algèbre quelques progrès à réaliser pour qu’on puisse la considérer comme un instrument efficace !
Rien ne remplace un voyage sur place !
Cet article aura révélé au lecteur francophone un texte injustement méconnu. Il est l’illustration d’une règle importante que nous faisons nôtre : en histoire des mathématiques, rien ne vaut un transport sur place, dans le temps et dans l’espace. C'est-à-dire la remontée à la source, qui offre en prime la saveur très particulière des anciennes notations, et dans le cas particulier celle du vieil allemand.
Mais un autre enseignement découle surtout de ce qui précède : on y comprend pourquoi l’algèbre s’est imposée lentement dans nos contrées. Ce n’est pas seulement parce qu’elle était lourde à employer en l’état ; mais c’était aussi et surtout parce qu’elle subissait la concurrence de la fausse position, bien plus élégante pour les problèmes linéaires.
(Novembre 2014)

1. Ainsi que dans Gavin & Schärlig, Longtemps avant l'algèbre : La Fausse Position, ou comment on a posé le faux pour connaître le vrai..., Presses Polytechniques et Universitaires Romandes, Lausanne, 2012, 222 p.
2. Voir Gavin & Schärlig, Longtemps avant l’algèbre, la fausse position, pp. 22-23.
3. Autrement dit : s’il y a les deux fois manque ou déficit, ou les deux fois excès.
4. Léonard de Pise (Leonardo Pisano), Liber abaci, Pise, 1202, folio 141r du manuscrit, et page 319 de la transcription de Baldassare Boncompagni : Scritti di Leonardo Pisano, volume I, Il Liber Abbaci di Leonardo Pisano pubblicato secondo la lezione del codice Magliabechiano C. I, 2616, Badia Fiorentina, N° 73, Rome, 1857, 459 p.
5. Problème mentionné par Gavin & Schärlig, op. cit., p. 7. Le lecteur se convaincra facilement que c’est un problème de type Kx + b = c.
6. Les fractions ci-dessous ne sont pas des exposants, mais une commodité d’écriture pour indiquer, par exemple, 74 + 4/7 (qu’il ne servait à rien de développer en expression décimale).
À LIRE (LIVRES)
 |
|
 |
|
À LIRE (ARTICLES)
 |
|
 |
|
 |
|
 |
|
LIVRES (TRÈS) ANCIENS
 |
|
 |
|
analyse-schreyber-1520.pdf

144-analysis-schreiberv2.pdf