
Figure 1 : Henri Bouasse (1866-1955), à gauche, et Pierre Duhem (1861-1916), à droite (tous deux en toge de professeur d’université)
Henri Bouasse est né à Paris en novembre 1866, il entre à l’École normale supérieure en 1885, où il fait la connaissance de Pierre Duhem, de cinq ans son aîné ; lequel commence alors sa quatrième année. Les deux hommes s’y lient d’amitié, et resteront amis. Ils feront tous deux la plus grande partie de leur carrière universitaire loin de Paris, Duhem à Bordeaux, Bouasse à Toulouse ; il arrivera à Bouasse de prendre à pied ou en vélo le chemin de Cabrespine, là où Duhem a sa résidence de vacances, dans l’Aude. Il est vrai que la route est belle le long du canal du Midi et dans la Montagne Noire. Leurs divergences d’opinions politique et religieuse ne comptent guère, Duhem est antidreyfusard et fervent catholique, Bouasse est dreyfusard et libre penseur ; mais tous deux portent le même jugement sur l’enseignement en France, ils développent un même intérêt à l’histoire des sciences physiques et font le même examen logique de la théorie physique.
Lorsque Duhem publie l’analyse de Mécanique rationnelle et expérimentale de son ami Bouasse, son propre ouvrage, La théorie physique, son objet et sa structure est déjà paru, en 1906 ; Bouasse, lui aussi, a déjà publié différents articles sur la méthode en physique.

Figure 2 : Page de garde de l’ouvrage de Bouasse (numérisation University of Michigan)
De la mécanique
D’entrée, Duhem contextualise la publication de Mécanique rationnelle et expérimentale afin d’en mieux dégager l’intérêt et l’originalité. Il commence par des considérations générales sur les mathématiques et la physique et sur la place qui est accordée à la mécanique dans l’enseignement en France : celle-ci est séparée en deux disciplines qui, poursuivant des buts différents, semblent inconciliables, à savoir la mécanique rationnelle (qui est pour les mathématiciens une branche de leur discipline) et la mécanique expérimentale (une des branches de la physique expérimentale pour les physiciens). Ceux-ci s’efforcent de ne pas aller plus loin que l’expérience.
Partant d’une réflexion de Bouasse : « Les Mathématiques sont non pas une science comme les autres, mais l’ensemble des formes abstraites de raisonnement nécessitées par les autres. » Duhem y ajoute qu’une forme de raisonnement ne devient un raisonnement que si on lui fournit une matière :
l’ensemble des procédés de déduction que les Mathématiques traduisent en un langage précis ne nous fait, par lui-même, rien connaître ; il n’accroît nos connaissances que si l’on applique ces procédés de déduction à des principes venus d’ailleurs, à des propositions reconnues vraies par l’expérience ; ces propositions issues de l’expérience, d’autre part, demeureraient stériles si la déduction ne les obligeait à produire toutes les vérités dont elles sont grosses ; et la déduction n’atteint sa parfaite rigueur et sa pleine puissance que là où elle peut revêtir la forme mathématique.
Il s’ensuit qu’il n’y a pas de science réelle qui ne résulte de la compénétration des données de l’expérience et de la forme imposée par les mathématiques. Historiquement, cette compénétration s’est établie par la mécanique, et les physiciens, de Descartes à Laplace, ont tenté de réduire la physique à la mécanique, pensant que tous les changements dans le monde pouvaient se réduire à des changements de lieu :
Les plus grands génies ont consacré toutes les puissances de leur raison à tenter cette réduction de la Physique entière à la Mécanique ; leurs efforts avaient semblé, tout d’abord, couronnés par le succès ; mais, bientôt, les essais les mieux conduits d’explication mécanique ont vu se dresser devant eux des objections qu’ils étaient impuissants à renverser (…)
Duhem juge alors que cette grandiose vision, qu’on nomme alors l’atomisme, n’était qu’un beau rêve :
L’affirmation que tout, dans le monde des corps, se peut réduire à la figure et au mouvement est purement gratuite (…)
À côté de la mécanique, science du mouvement local, il est possible de concevoir
une Physique proprement dite, science plus complexe que la Mécanique, où l’on traite non seulement du mouvement local, mais encore d’autres transformations qui ne se réduisent pas au changement de lieu.
Cette physique, qui est la théorie mathématique des modifications de toute espèce dont les corps sont susceptibles, c’est l’
énergétique, elle est adoptée par des physiciens qui, comme Duhem, rejettent l’atomisme et par ceux qui, comme Bouasse, sont suffisamment sceptiques pour adopter l’une ou l’autre selon les phénomènes étudiés, pourvu qu’on ne les mêle pas
(1).
Après avoir distingué le mouvement local des autres changements physiques ou chimiques, Duhem constate qu’il n’existe
dans le monde des corps, aucun phénomène où le mouvement local se trouve dissocié des autres transformations, des variations de la température, des changements d’état physique ou chimique, des modifications électriques ou magnétiques.
Il constate aussi que « jamais, peut-on dire, nous n’observons quelqu’une de ces transformations qu’un certain mouvement local ne l’accompagne. » Duhem montre ensuite que lorsqu’on étudie certains phénomènes, il se peut que seul le mouvement local nous intéresse, et que les autres changements n’ont qu’une influence négligeable, le problème à résoudre est un problème de mécanique pure ; si pour un autre phénomène seul le changement d’une autre grandeur physique nous intéresse parce que le seul qui ne soit pas négligeable, le problème à résoudre est un problème de physique pure
(2). Duhem insiste :
Ces problèmes artificiellement simplifiés, problèmes de mécanique pure ou problème de physique pure, ont donc pour nous, dans un grand nombre de cas, un intérêt immédiat ; non pas qu’en les résolvant nous répondions à toutes les questions qui se posent à propos du problème réel, toujours infiniment complexe, mais parce qu’en les résolvant nous répondons à celles de ces questions qui nous paraissent les plus importantes.
Tel est le compte rendu du travail d’abstraction que doit faire le physicien lorsqu’il aborde un phénomène physique ; ce travail est au cœur des ouvrages de physique de Bouasse, des ouvrages qui couvrent les enseignements de la classe de seconde à la licence, des ouvrages parus avant 1910.
@@@@@@@
La mécanique, telle que la décrit Duhem, est aussi une source d’analogies où tous les physiciens puisent pour concevoir et développer différentes branches de la physique, telle l’acoustique pour l’optique…
La mécanique, source d’analogie : l’acoustique pour l’optique
« Il est clair qu’on ne peut comprendre ce que sont la propagation d’un mouvement vibratoire et une onde stationnaire, en optique et en électricité, que si on le comprend en acoustique. Nul ne disconviendra qu’il est plus facile de se représenter un phénomène quand il est matériel que quand il ne l’est pas, quand il existe réellement que quand c’est une manière de parler. Nous hésiterions à rappeler des choses aussi banales, si l’on ne constatait trop généralement un mépris et une ignorance invraisemblables des phénomènes les plus simples d’acoustique, joints à la prétention de disserter sur les ondes électriques. S’imaginerait-on que l’acoustique perd de son intérêt parce qu’elle confine à la musique ? craindrait-on, en s’appesantissant trop sur l’étude des sons, de faire apparaître qu’on ne sait pas distinguer une octave d’une quinte ? » (extrait de H. Bouasse et L. Brizard, Avant-propos du cours de Physique des classes de mathématiques A et B, programme de 1902, Paris, Delagrave, 1903 ; p. vii)
Il s’ensuit que la mécanique sert de deux manières :
Elle sert d’une manière directe au physicien et à l’ingénieur en donnant réponse à des questions où le mouvement local joue un rôle à ce point prépondérant que les autres transformations y peuvent être négligées. Elle est utile d’une manière indirecte au physicien parce qu’elle lui fournit l’ensemble des types idéaux qui lui serviront, par voie d’analogie, de généralisation, de combinaison, à imaginer ses propres théories.
Le but de la mécanique ayant été ainsi défini, les règles qui doivent diriger son enseignement s’en déduisent, le cours de mécanique doit viser à la résolution de deux sortes de problèmes : l’analyse des mouvements locaux, qui jouent un grand rôle dans les machines industrielles ou les appareils de physique, l’étude des modèles qu’imitent les théories de la physique. Les premiers ont une place prépondérante dans la formation des ingénieurs, les seconds dans celle des physiciens. Ce but peut être respecté si la physique prend place dans les sciences mathématiques ou si, ces dernières étant limitées au domaine des nombres et des figures, la mécanique et l’astronomie prennent place, avec la physique, dans les sciences de la nature.
L’état des lieux
En France, depuis quelques quatre-vingts ans, les règlements qui régissent la licence ès sciences ont établi une ligne de démarcation entre la mécanique et la physique, mettant la mécanique et l’astronomie au nombre des sciences mathématiques et rejetant la physique au voisinage de la chimie
(3).
Les règlements (…) qui sont encore en vigueur pour l’agrégation et le doctorat ont établi une ligne de démarcation entre les Sciences mathématiques et les Sciences physiques. […] Pour mieux marquer que l’expérience n’avait pris, à l’érection de ce monument [NB : la mécanique rattachée aux sciences mathématiques], qu’une part infirme, que la raison raisonnante pouvait se vanter de l’avoir presque en entier construit de ses propres forces, on a donné à ce bel édifice mathématique le nom de Mécanique rationnelle.
Ainsi naquirent en France deux monstres complémentaires : une mécanique rationnelle abîmée dans la contemplation d’êtres mathématiques et dégagée de toute référence à l’expérience, et une mécanique physique et expérimentale tournée vers une physique purement expérimentale soigneusement séparée de toute physique mathématique. Citant Bouasse, Duhem écrit :
Le mathématicien de métier ne s’occupe guère de l’application, et les cas particuliers lui répugnent. Malgré ses efforts, un problème de Mécanique devient vite entre ses mains un sujet de spéculations mathématiques. J’admire que les candidats à l’Agrégation de Mathématiques résolvent les merveilleux rébus offerts à leur sagacité. Généralement un gyroscope se promène sur un hyperboloïde, qui glisse sur un tore, lequel est astreint à rouler et à pirouetter sur un hélicoïde ; … l’énoncé remplit une page de papier ministre. Ces jeunes gens résolvent le problème en 7 heures, comme qui plaisante. Je n’ignore cependant pas qu’en les plaçant devant une machine d’Atwood
(4), on les embarrasserait fort.
Dans cet état des lieux, Duhem ne manque pas d’esquisser une comparaison avec ce qui se passe outre-Rhin, où la division des sciences se fait selon ses vœux :
(…) parmi ces sciences expérimentales, on eût trouvé l’Astronomie et la Mécanique en même temps que la Physique. C’est cette division qui est, je crois, adoptée par les Universités allemandes (…)
Enfin Bouasse vint
Duhem salue dans l’ouvrage de Bouasse, une entreprise qui réunit ce qui n’aurait jamais dû être séparé, la mécanique rationnelle et la mécanique expérimentale. La mécanique de Bouasse est, selon Duhem, rationnelle, car elle pose comme hypothèses un petit nombre de prémisses non démontrées et (…) elle en tire, par voie de déduction mathématique, toutes les conclusions qu’elle énoncera par la suite
(5).
Elle est aussi expérimentale car :
elle n’attribue à ses hypothèses premières aucune évidence immédiate, aucune certitude affirmée par une science antérieure, certitude que le raisonnement déductif transporterait graduellement jusqu’aux ultimes corollaires ; [… et] elle regarde ces corollaires comme n’étant, par eux-mêmes et a priori, ni vrais ni faux ; si elle les tient seulement pour des propositions destinées à fournir une représentation abstraite, simplifiée, approchée des lois expérimentales du mouvement ; si donc elle déclare un ensemble de telles conséquences bon ou mauvais selon qu’il figure bien ou mal, avec une approximation suffisante ou avec d’intolérables inexactitudes, l’ensemble des vérités d’observation dont il doit être l’image.
Le mathématicien qui prétend exposer une mécanique purement rationnelle et Bouasse peuvent faire ensemble un bout de chemin : ils peuvent, à l’aide de calculs identiques, tirer des principes de la mécanique la solution d’un même problème. Mais ils auront des attitudes différentes devant la formule finale. Le mathématicien, qui pense que ses premiers principes ont la certitude d’axiomes, estime que la proposition obtenue est vraie pourvu que son raisonnement soit d’une impeccable rigueur. Le physicien, tel Bouasse, soumet cette proposition au contrôle de l’expérience et la déclare non pas vraie mais utile lorsqu’elle a subit l’épreuve avec succès. Alors que le mathématicien a l’illusion que sa tâche est achevée, Bouasse dresse et règle appareils et instruments. Il consacre ainsi de nombreux articles touchant les précautions qu’exige le maniement de ces instruments, tout ceci donne au livre de Bouasse l’aspect d’un traité de physique et permet à son auteur de déclarer, comme l’affirme Duhem, « qu’il a exposé un cours de Mécanique à la fois rationnelle et expérimentale. »

Figure 3 : Henri Bouasse à l’entrée de son laboratoire.
Plaidoyer pour une révolution de l’enseignement de la mécanique rationnelle
Selon Duhem, les ingénieurs trouveront profit à lire le cours de Bouasse, car celui-ci, ayant horreur des problèmes factices, applique autant que possible les théorèmes de la mécanique à des mécanismes et des machines qui se rencontrent dans les laboratoires et dans l’industrie. Ces machines ayant le plus souvent des mouvements d’une extrême complexité, l’ingénieur qui veut apprécier rapidement les défauts d’une machine pour les corriger doit éviter d’analyser dans ses moindres détails la marche de sa machine, ce qu’il ne peut faire qu’à partir de calculs très laborieux et très longs. Il doit, au contraire, acquérir l’intuition qui lui permet de simplifier à un haut degré les questions posées, négliger une foule d’éléments de ces questions et s’attacher à quelques-uns d’entre eux afin d’atteindre une solution, approchée mais satisfaisante, du problème posé.
Pour être utile au futur ingénieur, il convient, en premier lieu, d’appliquer les théorèmes de la Mécanique à des exemples tirés des mécanismes et des machines qui se rencontrent dans la pratique industrielle ; de fuir ces problèmes artificiellement composés dans le seul but de conduire à telle ou telle équation différentielle d’espèce connue, ces problèmes dont abusent nos leçons et nos examens. […] L’ingénieur aura donc véritablement acquis la forme intellectuelle qui lui convient lorsqu’il usera, pour résoudre les problèmes de Mécanique, très peu de l’esprit géométrique qui déduit et conclut, et beaucoup de l’esprit de finesse qui voit et devine
(6).
Techniciens et physiciens
« […] les cerveaux primaires et les ingénieurs de vingt-septième ordre exceptés, les techniciens admettent qu’un bon technicien est d’abord un honnête théoricien ; j’entends par là non pas un mathématicien en rupture d’intégrale fuchsienne ou abélienne (genre École polytechnique), mais un monsieur qui n’ignore pas la Physique Générale. Un cours de machines ne doit pas être un catalogue […]. Laissons aux uns et aux autres la joie d’être des catalogues vivants, le plaisir d’énumérer les « états » successifs de l’allumage « Proutt », de disserter sur les mérites relatifs du carburateur « Antoine » et de l’hydro-carburateur « Anatole ». On fait ce qu’on peut ! Nous pouvons d’avantage. Quand on s’étonne que nous, physiciens, n’ayons pas de formules pour toutes les circonstances, on se méprend sur le rôle de la Physique. Tandis que pour un but immédiat et strictement pécuniaire, la Technique étudie (tant bien que mal) le phénomène brut, tel qu’il se présente dans la pratique, avec son inextricable complexité, le nombre mal défini de ses variables, la Physique ne retient que les phénomènes schématisés, en quelque sorte stylisés. Cette limitation lui permet des résultats nets et indiscutables : d’où l’établissement de théories reliant les phénomènes. La Physique est autre chose qu’un gagne-sou : c’est une discipline intellectuelle. […] Mais que l’ingénieur ne nous croie pas inutiles. Qu’il prenne conscience du peu de science que renferment ses gros volumes et de la supériorité qu’a le savant (lui-même s’il le désire […]) qui réduit à quelques principes la masse des applications. Il sera d’autant plus fort qu’il aura vérifié les points d’appui de ses connaissances et délimité les fondations de son édifice. » (extrait de H. Bouasse, Cours de thermodynamique, 2e édition, 2e partie, Paris, Delagrave, 1919 ; Introduction, p. vi, vii)
Duhem fait confiance au cours de Bouasse pour habituer le futur ingénieur à « distinguer rapidement l’indispensable justesse de la précision futile, et cela afin de voir simple, partant de voir d’ensemble l’appareil qu’il manie
(7) ». Il indique :
La sûreté avec laquelle M. Bouasse sait simplifier chacun des problèmes pratiques qu’il traite jusqu’au degré voulu, et jusqu’à ce degré-là seulement, est peut-être la qualité la plus rare dont il fasse preuve dans son ouvrage.
Il juge que l’ouvrage est propre à former des physiciens expérimentateurs comme il l’est à former des ingénieurs :
les qualités d’esprit qu’il faut posséder pour manier habilement tel instrument de physique ne diffèrent guère de celles qu’on met en jeu lorsqu’on emploie telle machine.
Duhem remarque d’ailleurs que les instruments de physique et les machines proprement industrielles se rencontrent bien souvent à la fois dans les laboratoires et dans les usines. Il ajoute que « la mécanique n’a pas seulement pour le physicien une utilité directe ; elle a encore une utilité indirecte, et qui n’est pas moindre ; elle lui enseigne l’art de construire des théories physiques. »
Duhem termine son commentaire en imaginant ce que pourrait devenir l’enseignement de la mécanique rationnelle s’il se conformait au modèle complet du cours à faire et des manipulations à installer que Bouasse a donné.
Bouasse : le treuil et son principe de fonctionnement
Dans son Cours de physique, il trace un schéma de treuil :
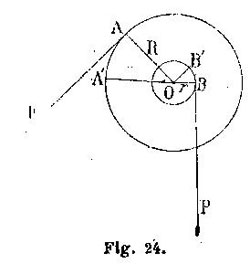
La « grande roue » (rayon R) permet de soulever une charge P autour de la « petite roue » (rayon r), en appliquant une force F (à gauche) inférieure à P. D’après le théorème des moments : F = P x r/R. Voici, extrait du même cours, le dessin d’un treuil de puits (c’est la grande roue à gauche qu’on manœuvre pour faire monter l’eau) :
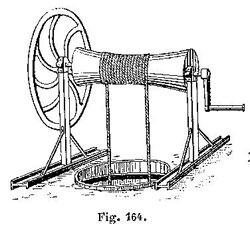
Bouasse insiste sur le fait que le travail total reste le même : (…) ce qu’on gagne en force on le perd en déplacement ; autrement dit, pour déplacer la résistance d’une quantité déterminée, il faut effectuer avec le treuil un travail égal à celui qui serait nécessaire pour arriver au même résultat directement. En effet, on tire avec une force F inférieure à P, mais en tournant la grande roue sur une circonférence plus grande qu’on ne le ferait avec la petite roue, la rotation étant « démultipliée » sur une longueur R/r inversement proportionnelle au rapport F/P (le travail reste constant). De même, avec un palan, on tire avec une force inférieure au poids, mais sur une longueur de corde supérieure. Bouasse donne d’autres exemples de machines utilisant le principe du treuil, comme le « treuil des carriers » : (…) la roue R porte sur son pourtour des tiges normales à son plan et également espacées : l’ouvrier grimpe le long de cette sorte d’échelle et agit par son propre poids.
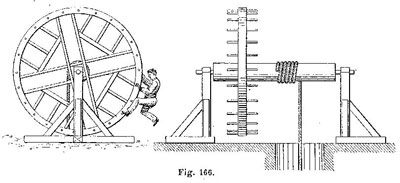
« Treuil de carrier vu de face et de champ » (légende de l’ouvrage)
§ Treuil, in Bouasse et Brizard, Cours de physique, classe de seconde, Paris, Delagrave, 1903 ; p. 33, 34 ; les figures 164, et 166 figurent sur une planche en fin d’ouvrage.
Conclusion
Cette réforme que Duhem appelle de tous ses vœux se fera-t-elle ? Il en doute, d’après lui : « le mal qu’il s’agit de guérir est difficilement guérissable ». Et il a raison d’en douter ! Les mathématiciens continueront encore longtemps à enseigner la même mécanique rationnelle.
Bouasse eut plus de succès auprès des physiciens, ainsi Bruhat publia-t-il un « Cours de physique générale à l’usage de l’enseignement supérieur scientifique et technique ». Comme Bouasse, Bruhat, même s’il ne fait qu’une place modeste à la mécanique
(8), utilise des relations mathématiques qui ne sont pas que la simple transcription mathématique des données d’une expérience, comme elles peuvent l’être dans d’autres cours de physique expérimentale, mais qui sont insérées dans une chaîne de déduction partant de principes clairement posés.
Août 2010

(1) C’est en 1909 qu’Ostwald renonce à ses attaques contre l’atomisme : il considère que les travaux de J. J. Thomson sur l’ionisation des gaz et de Jean Perrin sur le mouvement brownien apportent la preuve expérimentale de la structure atomique de la matière.
(2) Duhem donne à ce propos, en bas de page 148, un exemple méritant d’être relevé : « En bien des cas, cependant, les changements que, d’un instant à l’autre, la température éprouve en chaque masse élémentaire présenteront pour nous un grand intérêt, tandis que nous nous soucierons fort peu des petits déplacements de cette masse. Au morceau de cuivre contractible et dilatable sur lequel portera l’observation, nous pourrons alors substituer par la pensée un solide rigoureusement indéformable et immobile ; à l’imitation de Fourier, nous construirons une théorie de la conductibilité de la chaleur qui sera pure de tout lien avec la Mécanique ».
(3) De fait, ces règlements divers et variés qui se sont succédés pendant plus de quatre-vingt ans ne font que suivre une tradition bien établie : celle-ci apparaît clairement dans les Rapports à l’Empereur sur les progrès des sciences depuis 1789, publiés en 1808, que la physique est divisée entre une physique expérimentale liée à la chimie et une physique mathématique intégrée dans les sciences mathématiques.
(4) Sur Bouasse et la machine d’Atwood, on peut consulter R. Locqueneux, « Bouasse et l’esprit taupin », BibNum janvier 2010, et notamment la figure 3 (lien).
(5) La conformité des points de vue de Duhem et de Bouasse peut être appréciée en se référant à un article publié un an plus tôt par ce dernier sur la méthode en physique : « La physique cherche dans son domaine à reconstruire le monde, à le déduire par voie purement syllogistique d’un principe général une fois admis. » (Bouasse, « Physique générale, De la méthode dans les sciences, préface de P. Félix Thomas, Paris, Félix Alcan, 1909, p. 121-150 ; p. 124).
(6) Duhem usera souvent du distinguo pascalien entre esprit de finesse et esprit de géométrie. Sur son utilisation par Duhem dans son ouvrage La Science allemande (Hermann, 1915), contre cette dernière assimilée à « l’esprit de géométrie », voir Alexandre Moatti, Einstein, un siècle contre lui (Odile Jacob, 2007).
(7) Dans un article paru en 1909 (« Physique générale, De la méthode dans les sciences », op. cit., p. 153-154), Bouasse montre le passage de certaines branches de la physique générale à des branches de la physique appliquée, par la substitution d’une formule empirique d’allure plus simple à une formule théorique compliquée : « Par exemple la théorie de l’élasticité étant difficile, la théorie de la résistance des matériaux la supplée dans la pratique. Elle contient une théorie approchée de la torsion, une théorie approchée de la flexion, …, toutes théories indépendantes ou à peu près, tandis que la théorie de l’élasticité s’applique à tous ces phénomènes, les coordonne avec une précision malheureusement balancée par une complication de formules effarante. Bien entendu la complication des résultats ne peut en aucune manière être opposée à une théorie dont les postulats sont simples et quasiment nécessaires. Mais la rigueur dans le calcul de la résistance des matériaux est un luxe si parfaitement inutile, qu’il vaut mieux des théories partielles plus simples, même un peu fautives, qu’une théorie plus satisfaisante mais délicate à manier ».
(8) Les cours d’électricité, de thermodynamique et d’optique de Bruhat, publiés respectivement en 1924, 1926 et 1930 étaient les cours qu’il avait enseignés à la population mâle de la Sorbonne et de la rue d’Ulm ; les cours de mécanique qu’il publie en 1934, sont ceux qu’il avait enseignés aux sévriennes.



















