L’os d’Ishango

On conviendra qu’un objet aussi prometteur, source de tant d’enthousiasme, mérite une place dans un site consacré à l’histoire des sciences. Voyons donc de quoi il s’agit, et examinons sous les angles technique, historique et méthodologique les interprétations mathématiques (4) qui fondent sa célébrité.

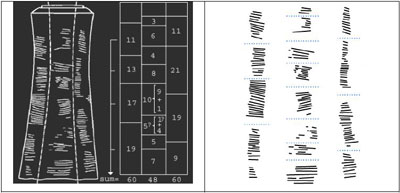
Prenons la colonne du milieu : d’après l’auteur, 3 serait doublé en 6, 4 en 8 et 5 en 10. Mais le 5 et le 10 sont douteux : l’un des paquets de 5 est sérieusement illisible, et le 10 pourrait être en réalité 9. De plus, on ne comprend pas pourquoi, en cas de duplication de 5, 3 et 4, le groupe de cinq encoches serait figuré deux fois, contrairement au groupe de trois et de quatre qui ne le sont qu’une seule fois. Et quel est le rôle de ce 7, qui n’est ni duplication ni doublé ? A moins qu’il ne faille lire au bas de la colonne du milieu non pas 10, 5, 5 et 7, mais 10, 4, 5 et 7, auquel cas nous aurions le double de 7 avec 10+4 et le double de 5 avec 10.

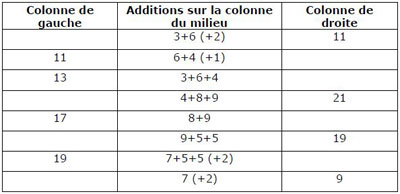
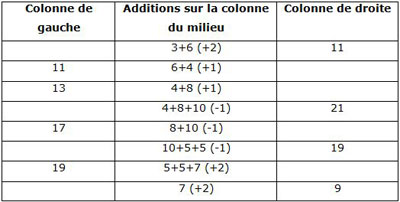
La justification ne change pas. Pour le calcul de la première ligne, par exemple :

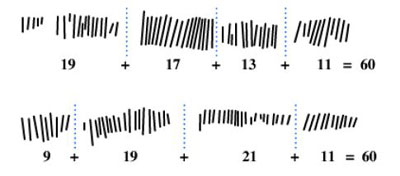
Où voit-on les bases 3 et 4 ? Dans la colonne du milieu, selon les auteurs, puisque nous avons, de haut en bas : - 3 puis 6, donc 3 puis 3x2 - 4 puis 8, donc 4 puis 4x2 - 9 ou 10, donc 4x2+1 ou 4x2+2 deux fois 5 « pour montrer deux manières d’obtenir le nombre composé 5 en ajoutant 1 ou 2 aux bases 3 et 4 (10) - 7 « montre comment obtenir le nombre composé 7 en additionnant les bases 3 et 4 (11) »

Où voit-on la base 12 ? D’une part, comme nous l’avons dit, dans les totaux de chaque colonne qui sont des multiples de 12. Et d’autre part, affirment les auteurs, par le fait que dans la colonne du milieu : - 6 intervient dans deux des additions supposées (deux premières lignes du tableau ci-dessus) : 2x6 = 12 - 4 intervient dans trois des additions supposées : 3x4 = 12 - 8 intervient dans trois des additions supposées : 3x8 = 24 = 2x12

n.c.

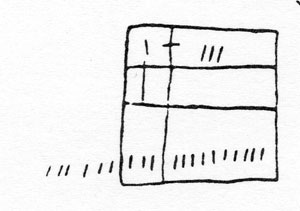
Et voici la réalité. Il s’agit d’un aide-mémoire à usage du porteur d’un message destiné à un certain groupe. Le message est le suivant :

Et l’aide mémoire fonctionne ainsi :

Il y aurait beaucoup d’autres exemples. Ces deux là sont suffisamment cruels pour les auteurs de fables mathématiques, il n’est pas besoin d’en rajouter.

• - que parmi toutes les marques possibles (points, encoches, parties du corps etc.) certaines soient choisies comme « collections-types » (30) spécialement chargées d’exprimer des pluralités. - que pour comparer deux ensembles d’objets, on ne le fasse plus directement, par correspondance élément par élément entre ces deux ensembles, mais que l’on opère par l’intermédiaire de la collection-type. - que la collection-type soit organisée en une suite ordonnée de degrés de quantité, par exemple : I, II, III, etc. s’il s’agit d’entailles index, annulaire, majeur, etc. s’il s’agit de parties du corps, de telle sorte qu’avec « III » ou « majeur », par exemple, on comprenne à la fois l’aspect cardinal (trois) et ordinal (troisième).

Août 2010

(1) Outil fabriqué en masse au Paléolithique inférieur par l’homo erectus et l’homo ergaster, à partir de -1,5 millions d’années.

(2) « Ishango, 22000 et 50 ans plus tard : le berceau des mathématiques ? »

(3) Els Cornelissen, Ivan Jadin et Patrick Semal. “Ishango, a history of discoveries in the Democratic Republic of Congo (DRC) and in Belgium”, dans : Dirk Huylebrouck (éd.), Ishango, 22000 and 50 years later : the cradle of mathematics ? 28/02-02/03 2007, pp.23-39. Brussel, Koninklijke Vlaamse Academie Van Belgie Voor Wetenschappen En Kunsten.

(4) Nous laisserons de côté l’interprétation en termes de calendrier lunaire défendue par Alexander Marshack, aujourd’hui généralement abandonnée.

(5) Cité par Alexander Marshack dans Les racines de la civilisation, Plon, 1972, p.23.

(6) Vladimir Plester and Dirk Huylebrouck : ‘The Ishango Artefact : the Missing Base12 Link’. Forma, 14, 1999, pp.339-346.

(7) Vladimir Plester and Dirk Huylebrouck : ‘An Interpretation of the Ishango Rods’, dans les Actes du Congrès déjà cités, pp. 139-170.

(8) Idem.

(9) Idem. À noter que la numérotation babylonienne est sexagésimale (base 60), en utilisant un symbole (le clou) en base 10 et un autre (le chevron) en base 6. Voir l’analyse par B. Rittaud de ce document sur BibNum.

(10) Idem.

(11) Idem.

(12) Idem.

(13) Idem.

(14) Jean-Pierre Adam s’est amusé avec les diverses dimensions d’une guérite de marchande de billets de loterie, avenue de Wagram à Paris ; il lui a fait avouer entre autres la distance Terre-Soleil, le nombre pi, le cycle de Meton. Jean-Pierre Adam : Le passé recomposé. Chroniques d'archéologie fantasque. Editions du Seuil, 1988.

(15) Pour une critique détaillée, on pourra consulter : Olivier Keller, Aux origines de la géométrie, le Paléolithique et le monde des chasseurs-cueilleurs, Vuibert, 2004, pp16-18.

(16) B.L. Van der Waerden : Geometry and Algebra in Ancient Civilizations. Springer, 1983.

(17) Frolov, B.A. ‘Comment on Alexander Marshack's paper’. Current Anthropology (1979) 20 (3):605-607. Du même auteur : ‘Aspects mathématiques dans l’art préhistorique’, communication au Symposium international d’art préhistorique, Valcamonica, 1968. Et ‘Les bases cognitives de l’art préhistorique’, communication au Symposium de Valcamonica, 1979.

(18) Un grand nombre de baguettes sont reproduites dans : Marthe Chollot-Varagnac, Les origines du graphisme symbolique. Essai d’analyse des écritures primitives en préhistoire. Fondation Singer-Polignac, 1980.

(19) The World’s Earliest Portait-30.000 Years Old’. 2 oct. 1937.

(20) Pour les amateurs : le même article présente une belle aiguille d’os, avec trois colonnes bien distinctes d’encoches bien régulières, tout ce qu’il faut pour fabriquer un instrument arithmétique.

(21) Bogoshi, Naidoo et Webb : ‘The Oldest Mathematical Artefact’. The Mathematical Gazette, vol 71, n°458, déc.1987.

(22) Claudia Zaslavsky : L'Afrique compte ! Nombres, formes et démarches dans la culture africaine. Editions du Choix, 1995. L’original anglais est de 1973.

(23) Germaine Dieterlen : Essai sur la religion bambara. Bruxelles, Editions de l’Université de Bruxelles, 1988, pp 154-155. Réédition de l’ouvrage paru aux Presses Universitaires de France en 1951.

(24) Quatre est féminin parce que les femmes ont quatre lèvres.

(25) La figure n’en comporte que 19.

(26) Dieterlen, ouvrage cité.

(27) Alfred William Howitt : The native tribes of South East Australia. Londres, Macmillan, 1904. Chapitre XI.

(28) Idem, p.695.

(29) Idem.

(30) J’emprunte cette expression au mathématicien français Henri Lebesgue (1875-1941)

(31) Francesco d’Errico : ‘A New Model and its Implications for the Origin of Writing : The La Marche Antler revisited’. Cambridge Archeological Journal, vol 5 (2), 1995, pp 163-206.

(32) Cela fait partie des recherches actuelles de l’auteur, pour une Préhistoire de l’arithmétique à paraître dans quelques mois.

Réponse à l’article « Les fables d’Ishango, ou l’irrésistible tentation

de la mathématique-fiction »

par Vladimir Pletser

Département Sciences, Directorat Vols spatiaux habités et Opérations, Centre de Recherches et de Technologies spatiales, Agence spatiale européenne, Noordwijk, Pays-Bas

et Dirk Huylebrouck

Faculté d’architecture, Université de Louvain, KUL Bruxelles-Gand, Belgique

Nos hypothèses

Depuis la fin des années 1990, les auteurs ont présenté et expliqué les hypothèses suivantes concernant le bâton d’Ishango, découvert par l’archéologue Jean de Heinzelin à la fin des années 1950 :

1. Le bâton d’Ishango, daté de 22 000 ans, peut être considéré comme le plus ancien outil mathématique de l’humanité car l’arrangement des encoches sur trois colonnes suggère une intention arithmétique.
2. De plus, il apparaît que plusieurs bases sont utilisées dans cette arithmétique élémentaire : la base 10 et la base 12 avec ses sous-multiples 3, 4 et 6. L’arrangement géométrique des encoches dans les différents groupements sur les trois colonnes permet de faire d’autres opérations arithmétiques élémentaires.

Ces hypothèses ont été présentées dans plusieurs publications [1-18] et dans des congrès internationaux sur les mathématiques et l’ethno-mathématique.

Les auteurs ont exploré en détail les relations arithmétiques entre les nombres d’encoches. On sait par exemple que les sommes des nombres dans les colonnes de gauche à droite sont 60, 48 et 60, que les nombres de la colonne de gauche peuvent être vus comme des nombres premiers, que des duplications sont vues dans la colonne du milieu, et que les nombres de la colonne de droite peuvent être interprétés comme 10 et 20 plus ou moins 1.

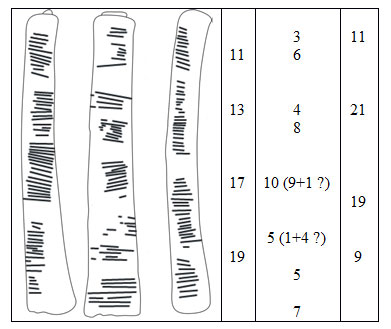
 Figure 1 : Schéma du premier bâton d’Ishango (basé sur un dessin Wikimedia Commons) et les nombres d’encoches correspondant des trois colonnes.

Nos conclusions

Les auteurs ont proposé diverses hypothèses, et rejeté d’autres (comme celle des nombres premiers), arrivant à une conclusion peu spectaculaire : il s’agit probablement d’un outil qui dénombre des événements ou des choses, notés par quelqu’un qui mélangeait les bases 10 et 12.

Toutefois, les auteurs n’ont pas voulu entrer dans les discussions quant à l’utilisation de ce bâton : est-ce un jeu arithmétique, comme le pensait l’archéologue Jean de Heinzelin, son découvreur ; ou un calendrier, suivant l’archéologue Marshack ; ou un outil de comptage tout simplement ; ou autre chose encore ? Les auteurs ont laissé cette discussion aux ethnologues et anthropologues.

Suite à une analyse BibNum

Olivier Keller, dans une analyse BibNum [19], a critiqué le travail des auteurs concernant ce bâton. Il leur a fallu quelque temps avant qu’ils décident de répondre à ces critiques. En effet, les travaux de ce critique n’ont jamais été publiés dans des journaux internationaux, ni dans des revues à évaluation par des pairs. De plus, ce critique n’a jamais participé à aucun congrès scientifique international, où il aurait pu défendre son point de vue, ce qui fait partie de la démarche scientifique. Sans vouloir polémiquer, les auteurs veulent présenter les quelques arguments suivants pour réfuter une à une ces critiques.

Nos réponses

1. L'os, l'outil et son âge

[…] le premier des deux os d’Ishango, est parvenu à la célébrité en se faisant passer pour un texte scientifique marquant […]

Étrange formulation : un os se faisant passer pour un texte scientifique… « carpe je te baptise lapin »

Un fragment de quartz encastré à l’une des extrémités montre qu’il s’agit d’un manche d’outil  […]

Cette hypothèse est soutenue par les archéologues de renom ayant étudié le bâton : Jean de Heinzelin (B), Alison Brooks (USA), John Yellen (USA), Els Cornelissen (B), et est également mentionnée sur le site de l’Institut des Sciences Naturelles de Bruxelles où l’objet est conservé.

 […] on le date ordinairement de 20 000 ans avant nos jours.

La datation admise est de 22 000 ans. Cette datation est obtenue par la méthode du carbone 14, et confirmée par plusieurs autres méthodes archéologiques, comme expliqué par Alison Brooks. La civilisation d’Ishango pourrait même être âgée de 90 000 ans, suivant les travaux de J. Yellen [20].

2. La suspicion sur les encoches

plusieurs [encoches] sont effacées ou à peine visibles, ce qui rend déjà suspecte a priori toute interprétation fondée sur leur dénombrement.

Il conviendrait de ne pas se fonder sur l’observation de photographies ou de reproductions, mais de consulter l’ouvrage original de J. de Heinzelin [21, pp 64-70] décrivant les circonstances de sa découverte, à moins bien sûr qu’il ne faille aussi soupçonner l’illustre archéologue de malhonnêteté intellectuelle. De plus, le technicien et collaborateur de Heinzelin, Marcel Spinglaer, fut un spécialiste reconnu qui ne peut certainement pas être soupçonné.

Prenons la colonne du milieu : d’après l’auteur, 3 serait doublé en 6, 4 en 8 et 5 en 10. Mais le 5 et le 10 sont douteux : l’un des paquets de 5 est sérieusement illisible, et le 10 pourrait être en réalité 9. De plus, on ne comprend pas pourquoi, en cas de duplication de 5, 3 et 4, le groupe de cinq encoches serait figuré deux fois, contrairement au groupe de trois et de quatre qui ne le sont qu’une seule fois.

Où est le problème ? Ne pourrait-on y voir tout simplement deux opérations de duplication (3 => 6 et 4 => 8) et une opération d’addition (10 = 5+5) ?

Et quel est le rôle de ce 7, qui n’est ni duplication ni doublé ? À moins qu’il ne faille lire au bas de la colonne du milieu non pas 10, 5, 5 et 7, mais 10, 4, 5 et 7, auquel cas nous aurions le double de 7 avec 10+4 et le double de 5 avec 10.

Est-ce que l’auteur de ses lignes ne se livre pas lui-même au jeu de supposition qu’il décrie si fort par ailleurs ? Néanmoins, l’interprétation proposée est intéressante et nous en laissons la paternité et la responsabilité à son auteur.

Il est donc clair qu’à partir du moment où l’on a décidé que les paquets d’encoches sont des nombres […]

Il est exact que l’hypothèse de départ de toute interprétation mathématique de ce bâton d’Ishango est l’association à un groupe d’encoches du nombre d’encoches dans ce groupe. Ce critique soutient lui-même cette hypothèse dans ses publications [22, p. 569] et [23] : « Derrière l'énumération à l'aide d'encoches se cache le nombre : l'histoire de l'arithmétique commence. On l'écrira un jour, grâce au grand nombre de monographies consacrées à la numération chez les primitifs, et on mettra en valeur les deux découvertes capitales que nous devons à nos ancêtres illettrés : le nombre et les systèmes de nombres, c'est-à-dire le nombre et le calcul. »

 […] il est assez facile, moyennant quelques petits arrangements, de « faire parler » notre os, et même, en creusant un tout petit peu comme ci-dessus, de lui faire dire des choses contradictoires.

Bien sûr, et la théorie de Ramsey [24] en dit même plus sur toute série finie de nombres, mais restons-en aux « petits arrangements ». On pourrait y voir des nombres premiers (comme suggéré initialement par Heinzelin), ou des triplets de Pythagore, etc. Cependant, si l’on prend la peine de considérer tous les groupements à la fois et de regarder non par le petit bout de la lorgnette mais de considérer l’ensemble, on ne peut qu’être amené à considérer une hypothèse arithmétique. J. de Heinzelin fut très prudent à ce sujet [21, pp 67-70] : « … De l’avis des mathématiciens que j’ai consultés, aucun moyen logique ne peut prouver que ces chiffres sont dus ou non au genre de "hasard" qui intervient par exemple dans un compte de chasses ou de recettes. Cependant chacun oserait dire, je pense, dans l’explication de ce tableau de chiffres, que le sentiment des choses humaines fait pencher pour l’hypothèse arithmétique. S’il y a arithmétique, les calculs se fondent assurément sur les bases 2 et 10 ; l’usage primitif de celles-ci n’est pas fait pour étonner, car elles sont les plus naturelles à l’homme.»

Parmi les (neuf) scientifiques de renom de l’époque que de Heinzelin avait consultés figurent L. Hogben, l’auteur du livre Mathematics for the Million [25], et des spécialistes de l’Université Libre de Bruxelles et d’autres universités.

L’interprétation des nombres 11, 13, 17 et 19 d’encoches figurant sur la colonne de gauche du bâton comme un signe d’une connaissance des nombres premiers a été rejetée par les auteurs dans plusieurs publications. Cependant, la disposition des nombres 11, 13, 17 et 19 appelait une autre explication, par exemple en les considérant respectivement comme 12 ± 1 et 18 ± 1. On obtient alors des indications pointant vers la base 12 (et/ou ses sous-multiples 3, 4 et 6). De plus, les sommes des trois colonnes sont des multiples de 12. Les bases 10 et 20 sont physiologiquement évidentes, mais la base 12 l’est tout aussi bien. On compte avec le pouce d’une main les phalanges des quatre autres doigts, comme il est encore pratiqué de nos jours par certaines populations, et le nombre des douzaines sur l’autre main, donnant un total de 60. Cette interprétation suggère pourquoi 12 et 60 vont souvent de pair, même de nos jours, comme pour la subdivision du temps.

3. Une règle à calcul ?

Ils vont même plus loin que leur prédécesseur en affirmant que les nombres des trois colonnes sont liés de telle sorte que leur ensemble forme une règle à calcul.

Il n’a jamais été affirmé que l’os d’Ishango fût une règle à calcul. Les auteurs décrivent dans leurs publications l’arrangement et les particularités géométriques des encoches dans les différents groupements et émettent l’hypothèse que ce bâton aurait pu servir de support à une méthode de comptage, similaire à une règle à calcul, sans pour autant prétendre qu’il s’agissait d’un tel instrument. Par exemple [7, pp 342] : « […] the proposed hypothesis of considering the bone as an ancient ‘slide rule’ to display simple addition arithmetic fits well with the various notch geometrical patterns. It shows a systematic occurrence of the derived base 12 and the central role that this base played in the proto-mathematics of the ancient Ishango people. »

4. Des additions inventées ?

Il n’y a que quatre additions exactes ; mais comme les auteurs veulent que notre os soit une table d’additions, il leur faut en fabriquer d’autres de force. Par exemple, nous disent-ils, le 3 et le 6 du milieu sont presque en face du 11 de droite ; c’est donc que 3 et 6 ont été additionnés et le résultat mis à droite. Il est vrai qu’il manque 2 (entre parenthèses dans le tableau ci-dessus) : c’est donc que le 2 a été omis pour une raison inconnue ! C’est par le même procédé que Pletser et Huylebrouck inventent trois autres additions, notées sur la deuxième et les deux dernières lignes du tableau ci-dessus avec les nombres manquants entre parenthèses.

En supposant même qu’il s’agisse d’additions, quel profit tirer d’une table aussi brouillonne, où il faut prendre les nombres tantôt par deux, tantôt par trois, et où les résultats sont tantôt à droite et tantôt à gauche ?

[et plus loin] Au congrès de 2007, les auteurs fournissent un schéma supplémentaire en supposant que le cinquième nombre de la colonne du milieu est 10. Cette fois-ci, toutes les opérations sont fausses.

Les auteurs ont essayé d’envisager toutes les possibilités de combinaisons d’opérations d’arithmétique élémentaire entre les nombres d’encoches de la colonne du milieu et ceux des deux autres colonnes, tout en respectant l’arrangement et les formes des encoches [15]. Certaines tentatives donnaient un résultat, d’autres pas. Deux de ces tentatives ont été présentées dans ces tableaux, sans aucune intention malveillante.

Et quel serait l’intérêt de telles additions, dans la mesure où la fusion de trois paquets de 3, 6 et 4 encoches, par exemple, en un seul paquet de 13 n’apporterait rien de plus qu’une lecture plus difficile de ce nombre ?

Si ce n’est qu’elle apporte une illustration visuelle de la somme des trois paquets de 3, 6 et 4 encoches de la colonne du milieu comme un nouveau paquet de 13 encoches dans la colonne de gauche.

5. L'intention des hommes préhistoriques et inconnues 

Il est bien connu qu’avec les premières véritables notations numériques, une telle « addition » n’aurait eu aucun sens, puisque le nombre 13, pour reprendre le cas qui nous occupe, n’aurait jamais été écrit avec 13 encoches régulièrement espacées, mais uniquement sous la forme de paquets distincts, pour en faciliter la lecture ; en Égypte antique par exemple, le hiéroglyphe de 9 n’était pas 9 barres alignées à égale distance les unes des autres, mais 4 barres placées au-dessous de 5 autres, ou plus souvent trois paquets de 3 barres les uns en dessous des autres.

Est-ce une critique ou un argument ? Les auteurs ne comprennent plus ce critique, car d’une part, il décrie leurs interprétations similaires, et d’autre part, voici qu’il propose lui-même l’idée audacieuse du passage d’une représentation d’un paquet de 13 encoches à une représentation plus abstraite d’un nombre, 13. Et là, n’était certainement pas l’intention des hommes préhistoriques d’Ishango qui n’avaient sans doute pas encore découvert la notion des nombres et de leur représentation. Ce passage à l’abstraction et à la représentation des nombres est bien postérieur à la civilisation préhistorique d’Ishango.

De plus, ce critique signale dans sa note 9 de bas de page 9 de [19], la numérotation babylonienne utilisant un symbole (le clou) en base 10 et un autre (le chevron) en base 6. Le nombre 9 s’écrit ainsi avec neuf clous, comme le signale B. Rittaud [26, p.2], cité par ce critique. Alors, deux poids, deux mesures ?

L’affaire ne marche pas, donc il y a des intentions inconnues ! À cela s’ajoutent des spéculations peu convaincantes sur des comparaisons des longueurs ou des inclinaisons des encoches, qui de toute manière ne parviennent pas à justifier les ajouts nécessaires de 2, 1 ou -1 pour donner un semblant de cohérence à l’ensemble.

Concernant les « intentions inconnues » de la première phrase, les auteurs signalent qu’il arrive à ce critique de confesser lui-même son ignorance, par exemple [27, p. 73] : « Pour des raisons que l’auteur ignore, les symboles primitifs sont essentiellement des symboles géométriques.» De plus, ces « spéculations peu convaincantes » font allusion à l’étude de la forme et de la taille des encoches des différentes colonnes qui sont détaillées dans [15].

6. Le choix des nombres sur l'os

S’agissant du cinquième nombre de la colonne du milieu, on peut se demander pourquoi les auteurs ont choisi de prendre 10, avec lequel toutes les additions sont fausses, plutôt que 9, avec lequel quatre sont exactes. La raison est qu’avec 10, le total des nombres de la colonne du milieu est 48, qui est un multiple de 12, comme le total de 60 des colonnes de droite et de gauche. »

Effectivement.

Pour rendre compte du choix des nombres présents sur l’os, Pletser et Huylebrouck avancent en effet l’idée que : « Les nombres 3 et 4 pourraient avoir constitué la base du système arithmétique en usage dans l’ancienne population d’Ishango pour opérer sur les petits nombres, et la base dérivée 12 pour les grands nombres. » Où voit-on les bases 3 et 4 ? Dans la colonne du milieu, selon les auteurs, puisque nous avons, de haut en bas :

- 3 puis 6, donc 3 puis 3 × 2

- 4 puis 8, donc 4 puis 4 × 2

- 9 ou 10, donc 4 ×2+1 ou 4 ×2+2

- deux fois 5 « pour montrer deux manières d’obtenir le nombre composé 5 en ajoutant 1 ou 2 aux bases 3 et 4 »

- 7 « montre comment obtenir le nombre composé 7 en additionnant les bases 3 et 4 »

Effectivement.

7. La combinaison de plusieurs bases

Mais si 5 est écrit deux fois parce qu’il y a deux bases, pourquoi les autres nombres 6, 8, 9 ou 10 et 7 ne figurent-ils qu’une seule fois ? Si l’objectif, d’autre part, avait été de mettre une base en relief, celle-ci apparaîtrait nettement ; on devrait voir clairement deux ensembles de 3 au sein du paquet de 6, deux ensembles de 4 au sein du paquet de 8 et ainsi de suite. Or il n’est rien de tel, il n’y a aucun groupement visible régulier faisant penser à une base.

Il n’a été dit nulle part que le sculpteur d’encoches avait « l’objectif de mettre une base en relief » sur cet os. Les auteurs ne comprennent pas d’où ce critique sort cette remarque.

Les auteurs ont avancé que ce bâton est probablement le témoignage d’un peuple qui comptait en mélangeant les bases 10 et 12 (ou 6). Un Européen écrirait peut-être |||||  |||||  |||| pour compter 14 jours, un homme d’Ishango ||||||   |||||||   ||. La combinaison de plusieurs bases est chose courante et n’est pas étonnante. Par exemple, en français, 77 et 93 réfèrent bien à un passé à bases 10 et 20. Si dans 22 000 ans on retrouve un texte français avec les expressions ‘soixante-dix-sept’ et ‘quatre-vingt-treize’, l’archéologue du futur pourrait en conclure avec raison que la langue française mélangeait les bases 10 et 20. De plus, il y aurait peu de chances que ce texte soit une dissertation savante sur l’arithmétique expliquant l’utilisation de ces différentes bases.

Ensuite, la duplication n’est pas nécessairement une opération d’ajout à l’original d’une copie de l’original, ni une simple multiplication par 2. Il peut s’agir d’une reconstruction d’un nouveau groupe ayant un nombre d’encoches double de celui du groupe initial mais arrangé différemment [15]. Le fait d’exiger de « voir clairement deux ensembles de 3 au sein du paquet de 6, deux ensembles de 4 au sein du paquet de 8 et ainsi de suite » est ce qui pourrait être appelé ‘regarder par le petit bout de la lorgnette’ et fait preuve d’un égocentrisme mathématico-culturel moderne trop simpliste.

Où voit-on la base 12 ? D’une part, comme nous l’avons dit, dans les totaux de chaque colonne qui sont des multiples de 12. Et d’autre part, affirment les auteurs, par le fait que dans la colonne du milieu :

- 6 intervient dans deux des additions supposées (deux premières lignes du tableau ci-dessus) : 2 ×6 = 12

- 4 intervient dans trois des additions supposées : 3 ×4 = 12

- 8 intervient dans trois des additions supposées : 3 ×8 = 24 = 2 ×12 »

Effectivement, mais, comme dit plus haut, la base 12 apparaît également dans la colonne de gauche avec les nombres 11, 13, 17, 19, qui après l’abandon de l’hypothèse des nombres premiers, sont vus comme 12 ± 1 et 18 ± 1.

Nous avons donc la situation suivante : 6 n’est gravé qu’une fois, sous forme d’un groupe de six encoches de la colonne du milieu ; mais comme on a supposé qu’il intervient dans deux additions, et bien que celles-ci soient fausses à cause d’une intention inconnue, cela donne 12 ! De même pour 4 et 8 qui interviendraient trois fois chacun, donnant respectivement 12 et 2 ×12. Est-il possible d’être convaincu par de tels tours de passe-passe dignes de la plus plate littérature numérologique ?

Remettons les choses à leur place. Les bases 3 et 4 sont déduites des opérations élémentaires dans la colonne du milieu et la base 12 est déduite des nombres 12 ± 1 et 18 ± 1 de la colonne de gauche. Les auteurs constatent simplement que les sommes des nombres de la colonne du milieu sont égales à 12 ou à des multiples ou sous-multiples de 12. Ce fait n’est nulle part utilisé comme argument pour renforcer la véracité de l’hypothèse de la base 12 et de ses sous-multiples.

8. Le deuxième os

Jean de Heinzelin a trouvé en 1959, toujours à Ishango, un deuxième os marqué d’encoches, et a proposé en 1998 une interprétation, qui, d’après Pletser et Huylebrouck, confirme ce qui précède. Il ne sera pas utile d’ennuyer beaucoup plus longtemps le lecteur avec cela.

Les auteurs doutent que ce critique ait vu le second bâton, car rien n’avait  été publié à ce sujet avant 2007, à l’occasion d’un congrès dont la communauté scientifique avait été informée par voie d’annonce. Ce critique n'a pas assisté à ce congrès.

Les auteurs pensent que ce point au contraire est du plus grand intérêt. Sur son lit de mort, Jean de Heinzelin avait changé d’avis au sujet de l’interprétation des encoches du premier bâton, y voyant effectivement un outil arithmétique élémentaire utilisant plusieurs bases simples. Cette conclusion n’avait pas été publiée suivant ses dernières volontés et ne pourrait être publiée que quelque temps après sa mort. La surprise des auteurs fut grande de voir leur hypothèse confirmée a posteriori par  Heinzelin, en même temps que l’annonce de l’existence du second os.

Il sera suffisamment édifié en jetant simplement un coup d’œil sur la figure 6 et en lisant ce qui suit : « De Heinzelin ajoutait que le petit tiret sur la colonne E était à la dixième place, et se demandait si cela annonçait "un passage de la base 10 à la base 12" […] Puisque la colonne C a un total de 20 encoches, et la colonne E 18, les bases 6 et 10-20 semblent se faire jour. De plus, il y a deux concordances spatiales entre les rangées : E10 = F1 = G10 et E12 = F2 = G12. » Cet os, selon des hypothèses de De Heinzelin reprises par Pletser et Huylebrouck, pourrait être le témoignage d’un changement de base, avoir eu une fonction didactique, ou même avoir servi dans l’échange entre groupes ethniques, l’un pratiquant la base 10, l’autre une autre base comme 12, 16 ou d’autres encore.

L’archéologue J. de Heinzelin fut une sommité mondiale de l’archéologie. Ses arguments étaient toujours fondés et avaient du poids.

9. Le petit bout de la lorgnette

Rappelons encore une fois que l’on ne peut sérieusement soutenir la présence de bases que si l’on est en face de regroupements clairs et systématiques ; il ne suffit pas que 18 = 3 × 6 pour démontrer pas la présence d’une base 6 !

Et rappelons également que cette manière de voir les choses est contraire à l’esprit scientifique qui présuppose une ouverture d’esprit et l’examen de toutes les hypothèses possibles et plausibles. Ne chercher que « des regroupements clairs et systématiques » est tellement réducteur et fait preuve d’une étroitesse de vue (le petit bout de la lorgnette…) passant toute observation au moule de notre vision moderne et actuelle des choses sans s’interroger sur la manière dont un homme préhistorique aurait pu voir les choses de son point de vue.

Effectivement, 18 = 3 x 6 n’est pas suffisant pour en déduire l’existence d’une base 6 s’il n’y a qu’une seule indication de ce type. Par contre, si plusieurs indications sont présentes comme montré par Heinzelin et d’autres scientifiques pour le premier bâton d’Ishango avec plusieurs exemples d’opérations élémentaires de duplication et d’addition faisant intervenir les nombres 3, 4 et 12, à côté du nombre 10, tout scientifique ayant été formé à la méthode scientifique, c’est-à-dire à l’observation et à la déduction, est en droit de se poser la question s’il n’existe pas effectivement plus qu’un simple hasard et si des corrélations entre les différentes bases ne devraient pas être considérées.

10.  Le comparatisme ethnographique

Les quelques exemples ethnographiques donnés par les auteurs dans les Actes du Congrès de 2007 ne peuvent pas davantage nous convaincre. Car si, chez tel peuple du Congo, on dit l’équivalent de ‘douze-un’ pour notre treize, on peut bien parler de base 12, mais cela signifie justement que la seule façon de dire 13 est de prononcer 12, puis 1 ; l’équivalent graphique serait de graver un paquet de 12, puis une autre encoche bien séparée. Il en est de même avec les nombres simplement figurés avec les doigts. Les Shambaa de Tanzanie montrent 6 en étendant trois doigts de chaque main, et disent l’équivalent de ‘trois-trois’ pour six. Même accord entre le geste et le mot pour 8 qui se dit ‘quatre-quatre’ et se montre avec quatre doigts de chaque main. Il y a désaccord pour 7, qui se dit ‘dix moins trois’ et se montre par 4 doigts de la main droite et 3 de la main gauche ; mais le geste de 7, comme celui de 8 et de 6, sépare nettement les bases 3 et 4, si bases il y a. Or de telles séparations claires systématiques en sous-ensembles de 3, 4 ou 12 encoches n’existent sur aucun des os d’Ishango. Les exemples ethnographiques ne font donc qu’enfoncer un peu plus les théories de Pletser et Huylebrouck.

Il est surprenant de lire le début de cet extrait sous la plume de quelqu’un qui se dit le chantre du comparatisme ethnographique, en s’extasiant même [22, pp. 563-564] : « Le comparatisme ethnographique, qui reconnait cette analogie, ouvre une voie de recherche à peine explorée pour les mathématiques de la préhistoire, mais riche de promesses puisqu'il permet, dans une certaine mesure, de faire parler les trouvailles archéologiques. Et il impose aussi aux hypothèses et théories fondées uniquement sur les documents préhistoriques d'être vérifiées par les documents ethnographiques et inversement. »

Les auteurs ne voient pas comment ni pourquoi « les exemples ethnographiques ne font donc qu’enfoncer un peu plus les théories » des auteurs. Rien ne permet d’affirmer cela comme le fait ce critique. Au contraire même, si celui-ci s’était donné la peine de lire avec attention les différents arguments circonstanciels ethnographiques donnés dans [15].

11.  L'illusion mathématicienne

C’est ce à quoi nous venons d’assister avec les spéculations de Heinzelin, Pletser et Huylebrouck, lesquels ne sont d’ailleurs que les derniers en date d’une longue lignée de victimes de l’illusion mathématicienne ; illusion d’autant plus tentante et fréquente qu’il s’agit de préhistoire.

Une tentative de mots blessants qui n’appelle pas de commentaire.

12. Une question de femmes battues ?

Néanmoins, que les prétendues lectures soient simples ou sophistiquées, toutes reposent sur un même fondement arbitraire, qui  consiste  à  croire  que  des  encoches  ont nécessairement un caractère numérique. Claudia Zaslavsky raconte que certaines femmes africaines font de temps en temps une encoche dans le manche de leur cuillère en bois. Marquent-elles des jours ? Jouent-elles avec des nombres ? Nullement : elles font une marque chaque fois qu'elles reçoivent un coup de leur mari ; et dès que le manche de la cuillère est rempli, elles demandent le divorce.

Les auteurs ont cité Zaslavsky dans leur référence 23, p. 166 de [15]. Plus même, ils ont cité des rapports semblables écrits par des missionnaires et administrateurs du Congo belge qui décrivaient comment et pourquoi de tels bâtons à encoches étaient utilisés.

De plus, il est exact que cette hypothèse ne peut pas non plus être entièrement rejetée. Mais pourquoi alors une femme préhistorique d’Ishango aurait fait des marques aussi sophistiquées avec des groupements qui présentent une telle régularité d’ensemble ? Et surtout pourquoi faire des marques sur trois colonnes ? On peut imaginer qu’elle aurait pu déjà demander le divorce après avoir rempli la colonne du milieu avec 48 encoches, ou à la rigueur celle de gauche ou celle de droite, avec 60 encoches chaque fois !

Bien que ne pouvant pas être formellement rejetée, il est évident que cette hypothèse serait la moins plausible de toutes pour le premier bâton d’Ishango.

Une encoche peut donc n’être qu’une marque, ce qui ne paraît pas grand-chose si l’on est obnubilé par l’arithmétique ; il y a pourtant là la plus importante invention que nous devons à nos ancêtres du Paléolithique supérieur, celle du signe.

Effectivement.

Et à s’égarer dans des spéculations numériques hasardeuses, on gaspille du temps, de l’argent et du papier alors qu’il y a tant à découvrir dans les signes préhistoriques, y compris en ce qui concerne la gestation intellectuelle du concept de nombre, en les confrontant avec la documentation ethnographique.

Si ce critique avait suivi cette recommandation à la lettre, son œuvre scientifique, se limitant à quelques publications au niveau national et répétant les mêmes critiques que celles discutées ici, aurait disparu entièrement.

Les deux contre-exemples ethnographiques donnés par ce critique [19, pp.14-17] sont excellents mais ne sont pas des contre-exemples, bien au contraire. Les auteurs ont repris des exemples semblables dans certaines de leurs publications. Ces histoires montrent surtout un point important : la connaissance a priori de la raison d’être de ces supports marqués ou signés. Autrement dit, une autre source d’information (un écrit, une tradition orale, une information supplémentaire, quel que soit le support) permet le déchiffrement aisé de ces objets.

Les os d’Ishango ont été retrouvés avec d’autres outils et des pointes de harpon [21]. Aucun de ces autres artefacts n’indique un quelconque lien avec les encoches sur les os. Le critique le dit d’ailleurs lui-même [22, p. 567] en parlant de l’os d’Ishango :

De la même façon, aucun document ethnographique ne permet d'étayer la thèse mentionnée plus haut […] d'un chasseur-cueilleur fabriquant une table de nombres premiers, une table de doubles,…

Alors que faire ? Ignorer ces artefacts et les laisser dormir dans un tiroir ou au contraire les étudier et essayer de les déchiffrer ?

Rappelons que l’étude du premier os a été réalisée sans même savoir qu’un second os avait été découvert au même endroit et que la description de ce second os n’a été publiée que plusieurs années après la mort de son découvreur. Or les conclusions auxquelles sont arrivées les auteurs sur le premier os ont été corroborées par après par les conclusions de Jean de Heinzelin sur son lit de mort avant la publication des résultats des auteurs et sans que ceux-ci n’en aient connaissance.

13.  Quelle calculette ?

S’il est désolant que des fictions du style « calculette d’Ishango » circulent et soient souvent prises pour argent comptant, ce n’est pas seulement en raison de leur faiblesse interne et de leur invraisemblance, mais c’est aussi qu’il y aurait mieux à faire avec toute cette documentation venue de l’archéologie et de l’ethnographie.

Les auteurs n’ont jamais employé l’expression « calculette d’Ishango » dans leurs publications et communications. Ils laissent à ce critique la paternité de cette expression.

Conclusions

1. Une conclusion correcte

L’étude du premier os est bien arrivée à une conclusion correcte, bien que peu spectaculaire. Elle a été réalisée sans savoir qu’un second os avait été découvert au même endroit et avant la publication de sa description plusieurs années après la mort de son découvreur. Or les conclusions auxquelles sont arrivées les auteurs sur le premier os ont été corroborées par après par les conclusions de Jean de Heinzelin sur son lit de mort avant la publication des résultats des auteurs et sans que ceux-ci n’en aient connaissance.

2. Un défaut épistémologique

Une meilleure recherche bibliographique aurait permis à ce critique de se faire une opinion sur l’ensemble des éléments, mais on peut douter que ce critique ait une maîtrise suffisante de la langue anglaise, car il tire des éléments hors de leur contexte et utilise des sources de seconde main au lieu de consulter les documents originaux. Enfin, il est vrai que ce n’est pas la première fois que ce critique a des problèmes à lire des publications scientifiques et à se documenter proprement (Voir par exemple [28]).

3. Non-respect de droits d'auteurs

Les auteurs signalent également l’utilisation par ce critique d’images sans respect du droit d’auteur ; ses illustrations sont reprises d’autres articles sans aucune demande d’autorisation, ou du site du Musée des Sciences Naturelles de Bruxelles, sans respect des lois en vigueur.

4. Un vocabulaire douteux, peu académique

Finalement, les auteurs ne résistent pas au plaisir de relever dans ce petit pamphlet les adjectifs et expressions suivantes qui éclairent sur le style de ce critique : « ridicule» ([19], p. 5), « en fabriquer d’autres de force» (p. 7), « aussi brouillonne» (p. 7), « L’affaire ne marche pas» (p. 8), « des spéculations peu convaincantes» (p. 8), « un semblant de cohérence» (p. 8), «de tels tours de passe-passe dignes de la plus plate littérature numérologique» (p. 10), « le même "tour"» (p. 10), « il faut fabriquer des 12» (p. 10), « des bricolages aussi confus» (p. 10), « Il ne sera pas utile d’ennuyer beaucoup plus longtemps le lecteur avec cela. Il sera suffisamment édifié » (p. 10), « On invente ensuite quelque contexte concret et on imagine une histoire pour ne fabriquer en fin de compte qu’une fiction mathématique » (p. 12), « les spéculations » (p. 12), « les derniers en date d’une longue lignée de victimes de l’illusion mathématicienne» (p. 12), « Les sirènes de l’illusion mathématicienne» (p. 12), « le mathématicien naïf» (pp. 12-13), « Quatre est féminin parce que les femmes ont quatre lèvres. » (p. 15), « suffisamment cruels pour les auteurs de fables mathématiques» (p. 17).

Quant aux termes « faiblesse interne et […] invraisemblance » (p. 17), ils seraient mieux accolés à ce petit pamphlet critique.

Les auteurs déplorent ce langage mais ils ne veulent pas entrer dans une vaine polémique pour les raisons expliquées dans l’introduction.

Cependant, ils sont ouverts aux débats d’idées et ils seraient heureux de participer à un échange de points de vue lors d’une conférence.

(juin 2016)

Références mentionnées dans l’article

•  [1] D. Huylebrouck, ‘Puzzles, patterns, drums: the dawn of mathematics in Rwanda and Burundi’, Humanistic Mathematics Network, Journal no 14, November 1996.

• [2] D. Huylebrouck, ‘The Bone that began the Space Odyssey’, The Mathematical Intelligencer, Vol. 18, no 4, p. 56, Autumn 1996.

• [3] D. Huylebrouck, ‘Histoires célestes du Rwanda’, Ciel et Terre, Bulletin de la Soc. Royale Belge d’Astronomie, Météorologie et Physique du Globe, Vol. 113 (2), 83-89, 1997.

• [4] D. Huylebrouck, ‘Counting on hands in Africa and the origin of the duodecimal system’, Wiskunde en Onderwijs (Mathématiques et Education), no 89, 1997.

• [5] V. Pletser, D. Huylebrouck, ‘The Ishango Artefact: the Missing Base 12 Link.’ Proc. Katachi Univ. Symmetry Congress (KUS2), T. Ogawa, S. Mitamura, D. Nagy & R. Takaki (ed.), Paper C11, Tsukuba Univ., Japan, 18 Nov. 1999.

• [6] V. Pletser, D. Huylebrouck, ‘Research and promotion about the first mathematical artefact: the Ishango bone’, Proc. PACOM 2000 Meeting Ethnomathematics and History of Mathematics in Africa, Cape Town, South Africa, 1999.

• [7] V. Pletser, D. Huylebrouck, ‘The Ishango Artefact : the Missing Base 12 Link’, Forma, 14-4, 339-346, 1999.

• [8] D. Huylebrouck, ‘Afrika + Wiskunde’ (in Dutch), VUBPress of the Free University of Brussels, 2005; traduit en français ‘Afrique + Mathématiques’ VUBPress of the Free University of Brussels, 2008.

• [9] D. Huylebrouck, ‘De parabolische vlucht van het Ishangoartefact, de oudste wiskundige vondst’ (Le vol parabolique de l’artefact d’Ishango, la plus ancienne découverte mathématique), Wiskunde en Onderwijs (Mathématiques et Education), n° 101, 2000.

• [10] D. Huylebrouck, F. Dumortier, ‘A Stamp for World Mathematical Year’, European Mathematical Society Newsletter, p. 27, November 2000.

• [11] D. Huylebrouck, ‘Middle column of marks found on the oldest object with logical carvings, the 22000-year-old Ishango bone from the Congo’, sequence A100000, On-Line Encyclopaedia of Integer Sequences, http://oeis.org/, November 2004

• [12] D. Huylebrouck, ‘L'Afrique, berceau des mathématiques‘, Pour la Science, Dossier 47, avril-juin 2005 (6 pages). L’article fut traduit en portugais (au Brésil) et en allemand.

• [13] D. Huylebrouck, ‘Mathematics in (central) Africa before colonisation’, Anthropologica et Praehistorica, Bulletin of the Royal Belgian Association for Anthropology and Prehistory, 135 – 162, Vol. 117, 2006.

• [14] D. Huylebrouck, ‘Report: The ISShango project’, Journal for Mathematics and the Arts, Taylor and Francis, September 2008.

• [15] V. Pletser, D. Huylebrouck, ‘An interpretation of the Ishango rods’, Proc. Conf. ‘Ishango, 22000 and 50 years later: the cradle of Mathematics?’, D. Huylebrouck ed., Royal Flemish Academy of Belgium, KVAB, 139-170, 2008.

• [16] D. Huylebrouck, ‘Foreword to the book Lusona: find the omitted drawings’ by Paulus Gerdes (Mozambique), Lulu Editions, July 2009.

• [17] D. Huylebrouck, R. Matteus Berr, ‘Vermessung’, in ‘Kunstlerhaus catalogue EVO EVO! 200 Jahre Charles Darwin’, I. and P. Braunsteiner eds, Künstlerhaus ISBN 978-3-900926-84-7 Verlag Lehner Wien, 2009.

• [18] D. Huylebrouck, ‘België + wiskunde’ (Belgique + Mathématique), Academia Press Gent, Belgique, 2013.

• [19] O. Keller, « Les fables d’Ishango, ou l’irrésistible tentation de de la mathématique-fiction », Bibnum, août 2010.

• [20] J. Yellen, ‘Ishango and its importance for later African prehistory’ (Ishango et son importance pour la préhistoire africaine), Proc. Conf. ‘Ishango, 22000 and 50 years later: the cradle of Mathematics?’, D. Huylebrouck ed., Royal Flemish Academy of Belgium, KVAB, 63-81, 2008.

• [21] J. de Heinzelin de Braucourt, ‘Exploration du Parc National Albert’, Fascicule 2, Les Fouilles d’Ishango, Instituts des Parc Nationaux du Congo Belge, Bruxelles, 1957.

• [22] O. Keller, « Questions Ethnographiques et Mathématiques de la Préhistoire », Revue de synthèse : 4e S. n° 4, oct.-dec. 1998, p. 545-573.

• [23] O. Keller, « Préhistoire de l'arithmétique, La découverte du nombre et du calcul», in ‘Si le nombre m'était conté’, I.R.E.M. - Histoire des mathématiques, Paris, Ellipse, 2000.

• [24] F.P. Ramsey, ‘On a Problem of Formal Logic’, Proceedings London Mathematical Society, s2-30 (1): 1930, 264–286. doi10.1112/plms/s2-30.1.264

• [25] L. Hogben, « Mathematics for the Million», London, Allen & Unwin, 1936. ISBN-13: 978-0393310719

• [26] B. Rittaud, « À un mathématicien inconnu ! », Bibnum, novembre 2008.

• [27] O. Keller, « Préhistoire de la Géométrie: Premiers éléments d’enquête, premières conclusions », Science et Techniques en Perspective, Vol. 33, Université de Nantes, 1995.

• [28] J. Høyrup, ‘Book review of ‘Préhistoire de la Géométrie: Premiers éléments d’enquête, premières conclusions’ , Isis 87,1 996, 713-714.

@@@@@@@

Note annexe de la rédaction de BibNum

Note de BibNum à/s de Conclusions 3, p. 14 : Les illustrations figurant dans l’article BibNum [19] d’O. Keller sont extraites de publications scientifiques – on peut considérer qu’elles sont libres d’usage pour illustrer un autre article scientifique se rapportant au même sujet (en en précisant l’origine, bien sûr).